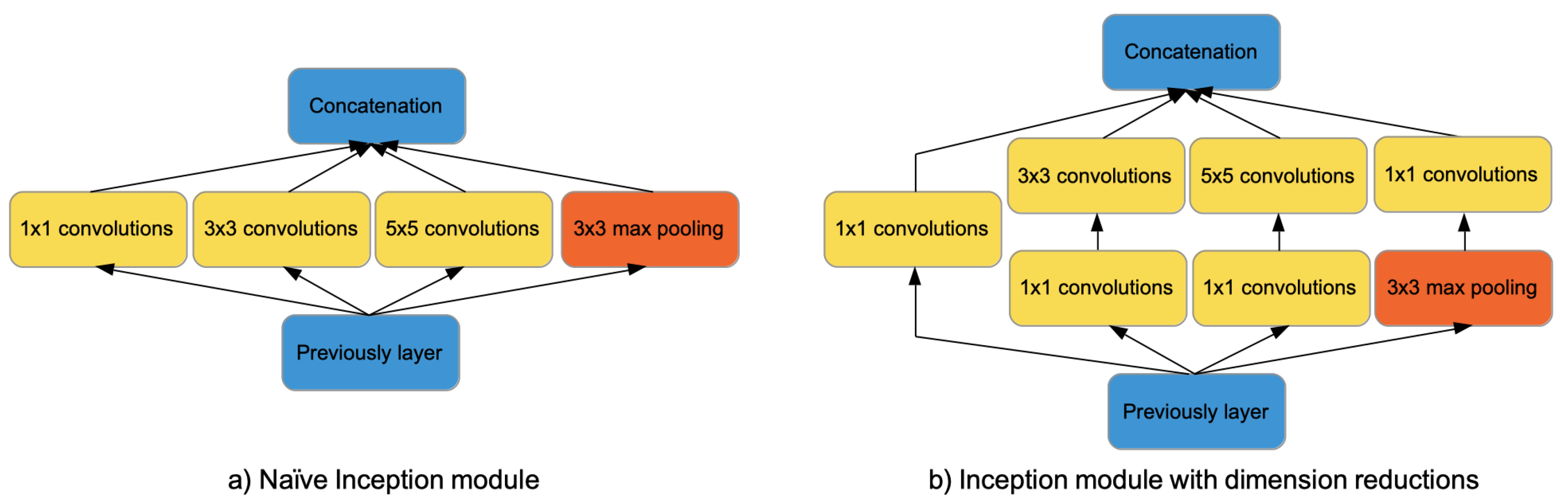
Figure 1.
Inception-V1 modules. On the left side, the naïve Inception module consisting of a pooling layer and convolution filters of size 1 × 1, 3 × 3, 5 × 5. On the right side, the Inception module with dimension reductions obtained adding convolutions of size 1 × 1.
Figure 1.
Inception-V1 modules. On the left side, the naïve Inception module consisting of a pooling layer and convolution filters of size 1 × 1, 3 × 3, 5 × 5. On the right side, the Inception module with dimension reductions obtained adding convolutions of size 1 × 1.
Figure 2.
Inception-V2 module is obtained factorizing filters kernel size 5 × 5 to two 3 × 3 and then factorizing convolutions to a stack of and convolutions.
Figure 2.
Inception-V2 module is obtained factorizing filters kernel size 5 × 5 to two 3 × 3 and then factorizing convolutions to a stack of and convolutions.
Figure 3.
The figure shows with an example how both hard and soft voting work. The ensemble consists of three base models able to predict two possible classes, which are labeled with 0 and 1. Hard voting (left side) predicts the class that obtained the most votes by base models. In the example, the voting policy outputs the class labeled 1, which is predicted by two out of three models. Soft voting (right side) averages the class pseudo-probabilities of the base models (represented in red in the figure) so that the class with the highest average probability is selected.
Figure 3.
The figure shows with an example how both hard and soft voting work. The ensemble consists of three base models able to predict two possible classes, which are labeled with 0 and 1. Hard voting (left side) predicts the class that obtained the most votes by base models. In the example, the voting policy outputs the class labeled 1, which is predicted by two out of three models. Soft voting (right side) averages the class pseudo-probabilities of the base models (represented in red in the figure) so that the class with the highest average probability is selected.
Figure 4.
The main steps of the proposed approach. Basically, it consists of steps aimed at pre-processing the dataset, splitting it to perform a 5-fold cross-validation, buiding and assessing the individual models, and compositing them using a voting ensemble strategy.
Figure 4.
The main steps of the proposed approach. Basically, it consists of steps aimed at pre-processing the dataset, splitting it to perform a 5-fold cross-validation, buiding and assessing the individual models, and compositing them using a voting ensemble strategy.
Figure 5.
The figure shows the slices of a chest scan. It can be observed that the information content of the scan tends to reduce moving toward its ends.
Figure 5.
The figure shows the slices of a chest scan. It can be observed that the information content of the scan tends to reduce moving toward its ends.
Figure 6.
The left side shows an original chest CT slice of size 512 × 512. The right side shows the same chest CT slice after the pre-processing. The slice has been cropped in the center and then scaled to 256 × 256 pixels.
Figure 6.
The left side shows an original chest CT slice of size 512 × 512. The right side shows the same chest CT slice after the pre-processing. The slice has been cropped in the center and then scaled to 256 × 256 pixels.
Figure 7.
A representation of the classification process for the build models. The model obtains in input a CT scan and produces a distribution probability on the possible classification labels.
Figure 7.
A representation of the classification process for the build models. The model obtains in input a CT scan and produces a distribution probability on the possible classification labels.
Figure 8.
Ensemble classifier model. The figure shows an ensemble consisting of 4 individual models. Each model provides a distribution probability on three classes (i.e., Normal, NCP, CP). The output of the individual models is fed to a decision fusion layer that applies a voting strategy. The outcome is obtained averaging the predictions of all models.
Figure 8.
Ensemble classifier model. The figure shows an ensemble consisting of 4 individual models. Each model provides a distribution probability on three classes (i.e., Normal, NCP, CP). The output of the individual models is fed to a decision fusion layer that applies a voting strategy. The outcome is obtained averaging the predictions of all models.
Figure 9.
Individual models—The normalized confusion matrices obtained by the models built using the Inception-V1 and Inception-V3 architectures for a CT scan depth of 25 and 35 slices.
Figure 9.
Individual models—The normalized confusion matrices obtained by the models built using the Inception-V1 and Inception-V3 architectures for a CT scan depth of 25 and 35 slices.
Figure 10.
Individual models—Class-Wise ROC curves for the Inception-V1 and Inception-V3 architectures obtained for a CT scan depth of 25 and 35 slices.
Figure 10.
Individual models—Class-Wise ROC curves for the Inception-V1 and Inception-V3 architectures obtained for a CT scan depth of 25 and 35 slices.
Figure 11.
Inception-V1 individual models—The normalized matrices for the individual models built varying the dropout rate p using a CT scan depth of 25 and 35 slices.
Figure 11.
Inception-V1 individual models—The normalized matrices for the individual models built varying the dropout rate p using a CT scan depth of 25 and 35 slices.
Figure 12.
Inception-V3 individual models—The normalized matrices for the individual models built varying the dropout rate p using a CT scan depth of 25 and 35 slices.
Figure 12.
Inception-V3 individual models—The normalized matrices for the individual models built varying the dropout rate p using a CT scan depth of 25 and 35 slices.
Figure 13.
Soft-voting ensemble models—Normalized confusion matrices obtained for the ensemble models built using the Inception-V1 and Inception-V3 architectures for CT scans with 25 and 35 slices.
Figure 13.
Soft-voting ensemble models—Normalized confusion matrices obtained for the ensemble models built using the Inception-V1 and Inception-V3 architectures for CT scans with 25 and 35 slices.
Figure 14.
ROC curves for ensemble models built using the soft-voting algorithm.
Figure 14.
ROC curves for ensemble models built using the soft-voting algorithm.
Table 1.
CC-CCII dataset. This table reports the number of chest CT scans and slices for patients without lung lesions (i.e., Normal), with common pneumonia (i.e., CP) and with novel coronavirus pneumonia (i.e., NCP). The last row reports the overall size of the dataset.
Table 1.
CC-CCII dataset. This table reports the number of chest CT scans and slices for patients without lung lesions (i.e., Normal), with common pneumonia (i.e., CP) and with novel coronavirus pneumonia (i.e., NCP). The last row reports the overall size of the dataset.
| Class | # CT Scans | # Slices |
|---|
| Normal | 1078 | 95,756 |
| CP | 1545 | 156,523 |
| NCP | 1544 | 156,071 |
| Total | 4167 | 408,350 |
Table 2.
CLEAN-CC-CCII dataset. This table reports the number of chest CT scans and slices for the CLEAN-CC-CCII dataset. The last row reports the overall size of the dataset.
Table 2.
CLEAN-CC-CCII dataset. This table reports the number of chest CT scans and slices for the CLEAN-CC-CCII dataset. The last row reports the overall size of the dataset.
| Class | # CT Scans | # Slices |
|---|
| Normal | 966 | 73,635 |
| CP | 1523 | 135,038 |
| NCP | 1534 | 131,517 |
| Total | 4023 | 340,190 |
Table 3.
The number of chest CT scans used for the training set, validation set and test set for patients without lung lesions (i.e., Normal), with common pneumonia (i.e., CP) and with novel coronavirus pneumonia (i.e., NCP). The last row reports the overall size of the dataset.
Table 3.
The number of chest CT scans used for the training set, validation set and test set for patients without lung lesions (i.e., Normal), with common pneumonia (i.e., CP) and with novel coronavirus pneumonia (i.e., NCP). The last row reports the overall size of the dataset.
| Class | Total | Train | Val. | Test |
|---|
| Normal | 966 | 696 | 77 | 193 |
| CP | 1523 | 1093 | 122 | 308 |
| NCP | 1534 | 1107 | 123 | 304 |
| Total | 4023 | 2896 | 322 | 805 |
Table 4.
Performance measure for multiclass classification.
Table 4.
Performance measure for multiclass classification.
| Measure | Definition | |
|---|
| Precision | | per-class k-th precision |
| Sensitivity | | per-class k-th sensitivity |
| Specificity | | per-class k-th sensitivity |
| Balanced accuracy | | per-class k-th bal. accuracy |
| AUC | | per-class k-th AUC |
| F1-score | | PREC and REC macro-averaged |
Table 5.
Individual models—Overall performance for three-way classification models in terms of accuracy, F1-score, AUC, and MCC for both Inception-V1 and Inception-V3 for varying CT scan depths of 25 and 35 slices.
Table 5.
Individual models—Overall performance for three-way classification models in terms of accuracy, F1-score, AUC, and MCC for both Inception-V1 and Inception-V3 for varying CT scan depths of 25 and 35 slices.
| Model | Depth | ACC | F1 | AUC | MCC |
|---|
| Inception-V1 | 25 | 95.48% | 95.52% | 0.9915 | 0.9149 |
| 35 | 95.67% | 95.70% | 0.9886 | 0.9397 |
| Inception-V3 | 25 | 93.29% | 93.28% | 0.9847 | 0.8743 |
| 35 | 93.89% | 93.99% | 0.9864 | 0.9012 |
Table 6.
Individual models—Class-Wise performances for Inception-V1 and Inception-V3 using 25 and 35 slices in terms of accuracy, precision, sensitivity, specificity, F1-score, Area Under the ROC Curve, and Matthews Correlation Coefficient.
Table 6.
Individual models—Class-Wise performances for Inception-V1 and Inception-V3 using 25 and 35 slices in terms of accuracy, precision, sensitivity, specificity, F1-score, Area Under the ROC Curve, and Matthews Correlation Coefficient.
| Model | Depth | Label | ACC | PREC | SENS | SPEC | F1 | AUC | MCC |
|---|
| Inception-V1 | 25 | Normal | 95.88% | 94.17% | 93.58% | 98.17% | 93.87% | 0.9893 | 0.9068 |
| NCP | 97.21% | 96.76% | 96.38% | 98.04% | 96.57% | 0.9919 | 0.9055 |
| CP | 96.92% | 95.74% | 96.49% | 97.34% | 96.11% | 0.9933 | 0.9157 |
| 35 | Normal | 96.27% | 94.69% | 94.20% | 98.33% | 94.45% | 0.9879 | 0.9276 |
| NCP | 97.15% | 96.88% | 96.18% | 98.12% | 96.53% | 0.9881 | 0.9603 |
| CP | 96.94% | 95.62% | 96.62% | 97.26% | 96.12% | 0.9899 | 0.9289 |
| Inception-V3 | 25 | Normal | 94.18% | 90.47% | 91.41% | 96.96% | 90.94% | 0.9855 | 0.8527 |
| NCP | 95.94% | 97.26% | 93.48% | 98.40% | 95.33% | 0.9852 | 0.8980 |
| CP | 94.96% | 92.06% | 94.99% | 94.93% | 93.50% | 0.9835 | 0.8694 |
| 35 | Normal | 94.44% | 92.26% | 91.30% | 97.58% | 91.78% | 0.9851 | 0.8618 |
| NCP | 96.50% | 97.62% | 94.40% | 98.60% | 95.98% | 0.9893 | 0.9366 |
| CP | 95.53% | 92.37% | 95.97% | 95.09% | 94.13% | 0.9849 | 0.8960 |
Table 7.
Soft-voting ensemble models—Overall performance for three-way classification models in terms of balanced accuracy, macro F1, macro AUC, and multiclass Matthews Correlation Coefficient (MCC) for both Inception-V1 and Inception-V3 for a depth size of 25 and 35 slices.
Table 7.
Soft-voting ensemble models—Overall performance for three-way classification models in terms of balanced accuracy, macro F1, macro AUC, and multiclass Matthews Correlation Coefficient (MCC) for both Inception-V1 and Inception-V3 for a depth size of 25 and 35 slices.
| Model | Depth | ACC | F1 | AUC | MCC |
|---|
| Inception-V1 | 25 | 96.92% | 96.98% | 0.9915 | 0.9563 |
| 35 | 97.06% | 97.03% | 0.9968 | 0.9567 |
| Inception-V3 | 25 | 95.00% | 95.00% | 0.9947 | 0.9268 |
| 35 | 95.42% | 95.46% | 0.9938 | 0.9328 |
Table 8.
Soft-voting ensemble models—Class-wise performances for Inception-V1 and Inception-V3 using 25 and 35 slices in terms of balanced accuracy, precision, sensitivity, specificity, F1-score, Area Under the ROC Curve, and Matthews Correlation Coefficient.
Table 8.
Soft-voting ensemble models—Class-wise performances for Inception-V1 and Inception-V3 using 25 and 35 slices in terms of balanced accuracy, precision, sensitivity, specificity, F1-score, Area Under the ROC Curve, and Matthews Correlation Coefficient.
| Model | Depth | Label | ACC | P |
SEN
| SPE | F1 | AUC | MCC |
|---|
| Inception-V1 | 25 | Normal | 97.08% | 96.24% | 95.34% | 98.82% | 95.79% | 0.9893 | 0.9447 |
| NCP | 98.19% | 98.79% | 97.10% | 99.28% | 97.94% | 0.9919 | 0.9672 |
| CP | 97.93% | 96.12% | 98.31% | 97.55% | 97.20% | 0.9933 | 0.9546 |
| 35 | Normal | 97.47% | 95.78% | 96.27% | 98.66% | 96.02% | 0.9970 | 0.9476 |
| NCP | 98.21% | 98.73% | 97.17% | 99.24% | 97.94% | 0.9972 | 0.9672 |
| CP | 97.78% | 96.53% | 97.72% | 97.83% | 97.12% | 0.9961 | 0.9533 |
| Inception-V3 | 25 | Normal | 95.68% | 93.00% | 93.58% | 97.78% | 93.29% | 0.9942 | 0.9116 |
| NCP | 96.85% | 98.23% | 94.73% | 98.96% | 96.45% | 0.9956 | 0.9439 |
| CP | 96.35% | 93.76% | 96.68% | 96.02% | 95.20% | 0.9942 | 0.9218 |
| 35 | Normal | 96.07% | 94.09% | 94.00% | 98.14% | 94.04% | 0.9921 | 0.9216 |
| NCP | 97.08% | 98.37% | 95.13% | 99.04% | 96.72% | 0.9961 | 0.9482 |
| CP | 96.66% | 94.02% | 97.14% | 96.18% | 95.55% | 0.9931 | 0.9276 |
Table 9.
Performance comparison. This table compares the best performance achieved with the proposed approach and those implemented by Zhang et al. [
14] and He et al. [
26] for NCP versus the rest. The table reports the performance in terms of accuracy, precision, sensitivity, specificity, F1-score and Area Under the ROC Curve.
Table 9.
Performance comparison. This table compares the best performance achieved with the proposed approach and those implemented by Zhang et al. [
14] and He et al. [
26] for NCP versus the rest. The table reports the performance in terms of accuracy, precision, sensitivity, specificity, F1-score and Area Under the ROC Curve.
| Method | ACC | P | SEN | SPE | F1 | AUC |
|---|
| proposed | 98.21% | 98.73% | 97.17% | 99.24% | 97.94% | 0.9972 |
| Zhang et al. [14] | 92.49% | 92.20% | 94.93% | 91.13% | 93.55% | 0.9797 |
| He et al. [26] | 88.63% | 90.28% | 86.09% | 94.35% | 88.14% | 0.9400 |