High-Temperature Thermodynamics Modeling of Graphite
Abstract
:1. Introduction
2. Computational Approaches
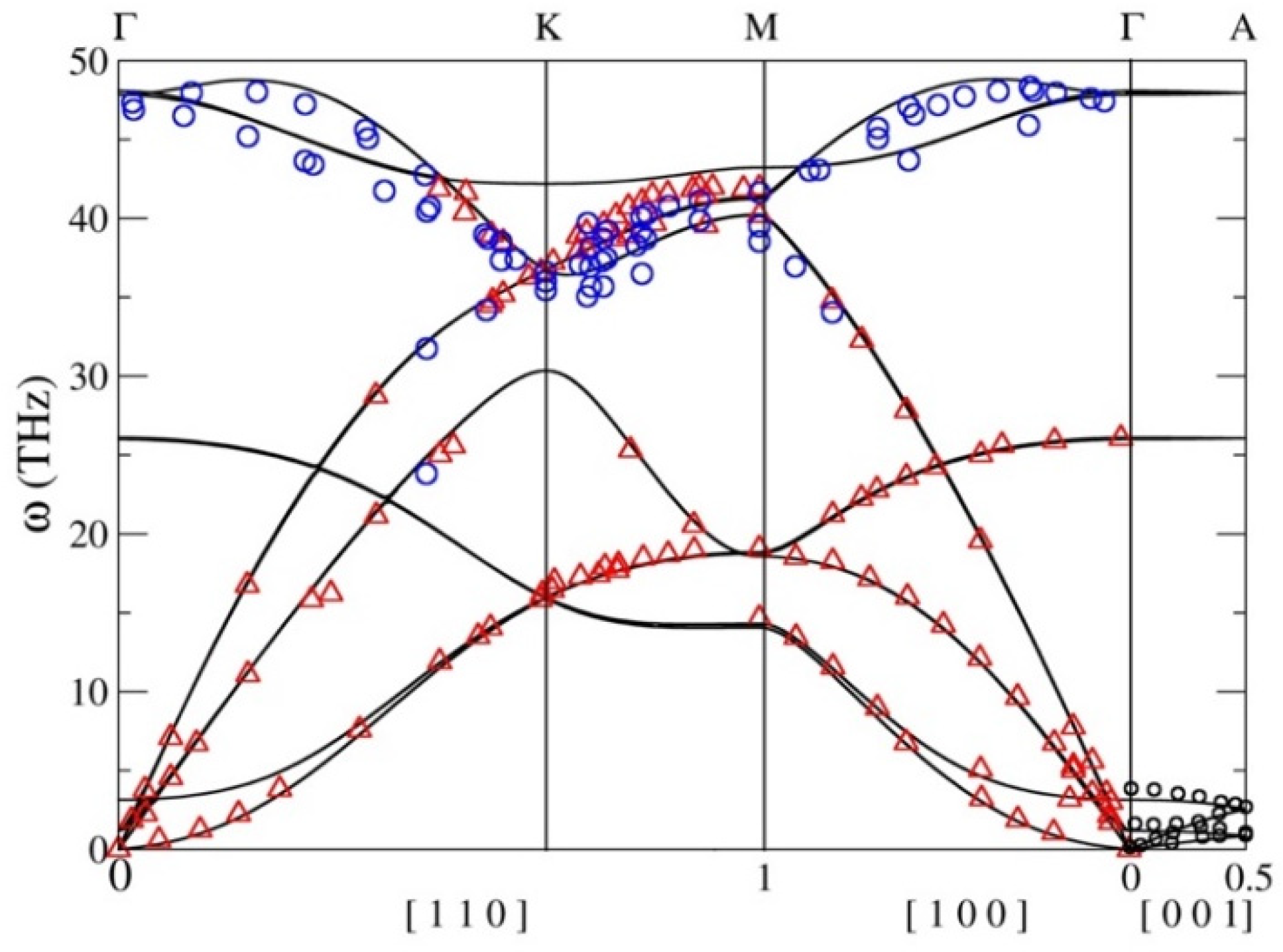
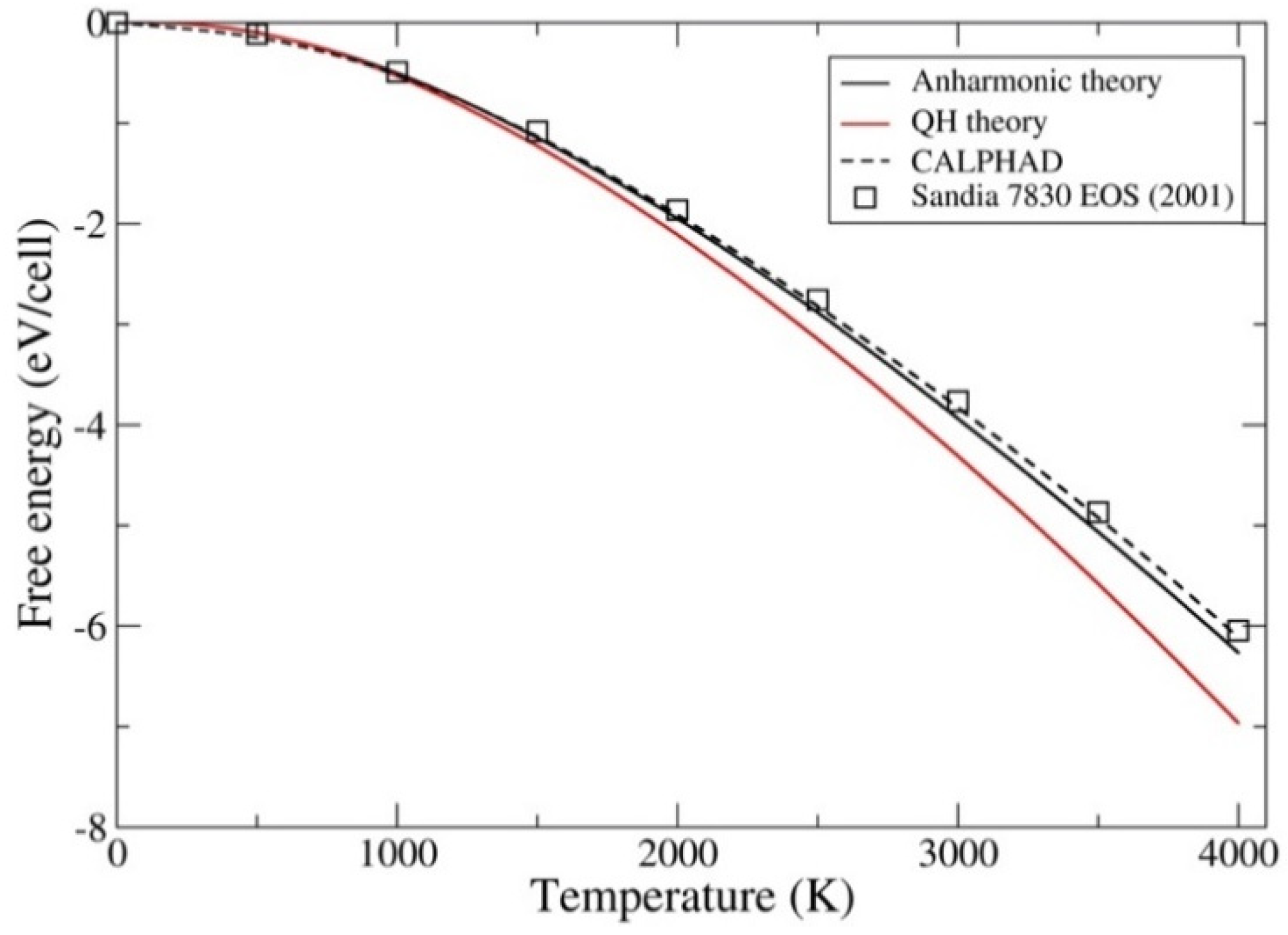
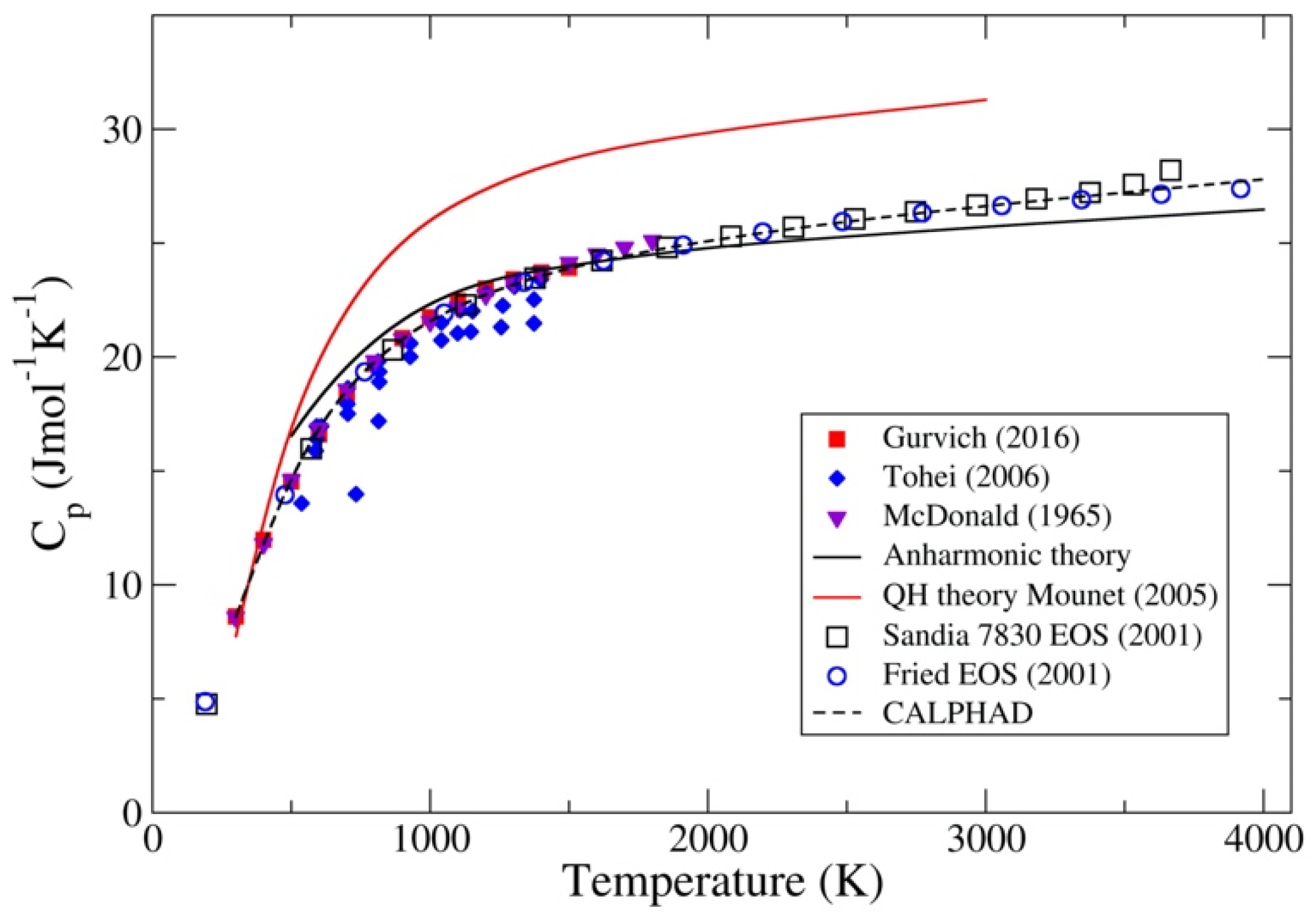
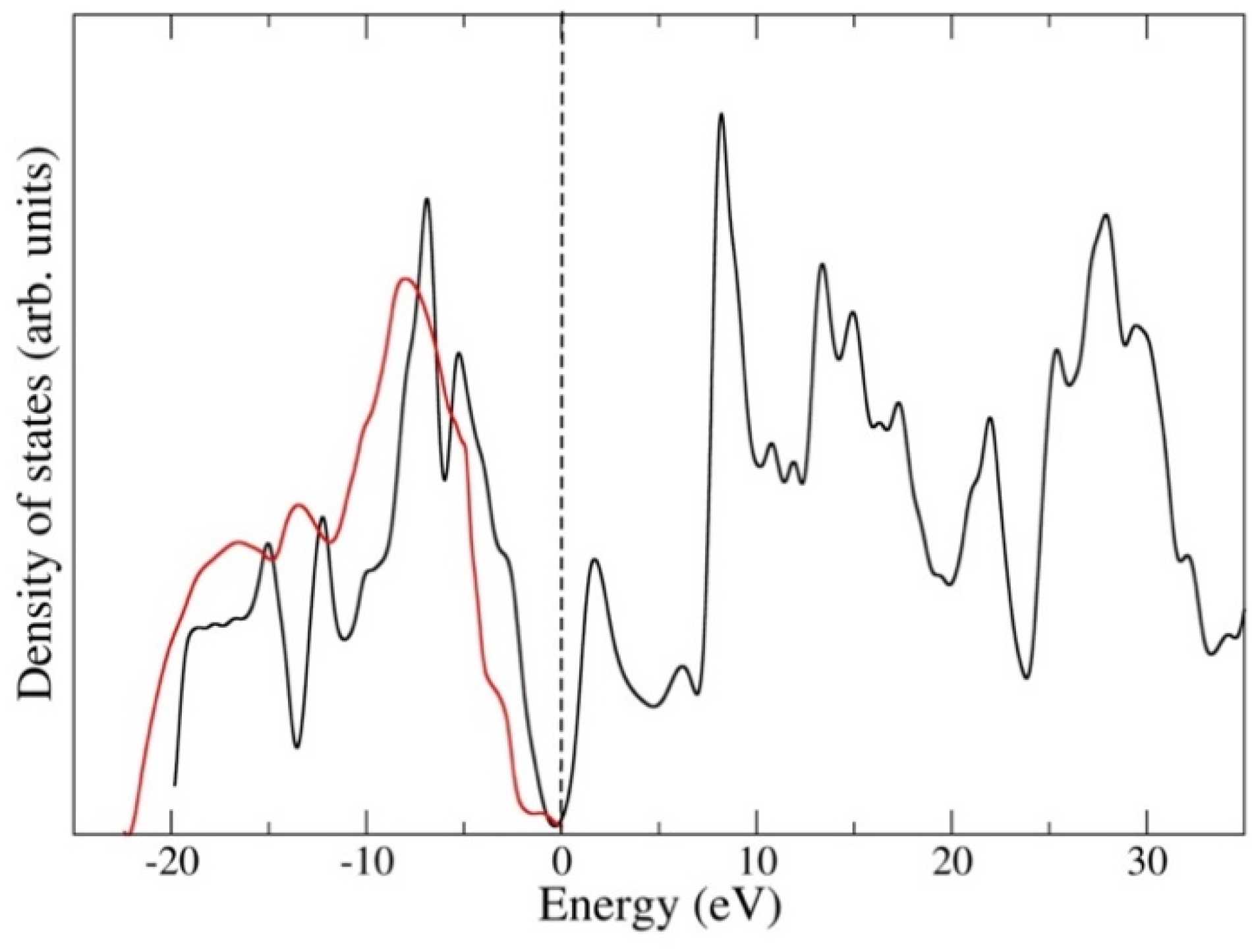
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, R.J.; Bangsaruntip, S.; Drouvalakis, K.A.; Kam, N.W.S.; Shim, M.; Li, Y.; Kim, W.; Utz, P.J.; Dai, H. Noncovalent functionalization of carbon nanotubes for highly specific electronic biosensors. Proc. Natl. Acad. Sci. USA 2003, 100, 4984–4989. [Google Scholar] [CrossRef] [Green Version]
- Limin, J.; Xu, D.; Li, M.; Guo, J.; Fu, H. Casting defects of Ti-6Al-4V alloy in vertical centrifugal casting processes with graphite molds. Met. Mater. Int. 2012, 18, 55–61. [Google Scholar]
- Zhou, X.-W.; Tang, Y.-P.; Lu, Z.-M.; Zhang, J.; Liu, B. Nuclear graphite for high-temperature gas-cooled reactors. New Carbon Mater. 2017, 32, 193–204. [Google Scholar] [CrossRef]
- Gustafson, P. An evaluation of the thermodynamical properties and the P, T phase diagram of carbon. Carbon 1986, 24, 169–176. [Google Scholar] [CrossRef]
- Charlier, J.-C.; Gonze, X.; Michenaud, J.-P. Graphite interplanar bonding: Electronic delocalization and van der Waals interactions. Europhys. Lett. 1994, 28, 403–408. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J.; Hafner, J. Ab initio force constant approach to phonon dispersion relations of diamond and graphite. Europhys. Lett. 1995, 32, 729–734. [Google Scholar] [CrossRef]
- Mounet, N.; Marzari, N. First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives. Phys. Rev. B 2005, 71, 205214. [Google Scholar] [CrossRef] [Green Version]
- Tohei, T.; Kuwabara, A.; Oba, F.; Tanaka, I. Debye temperature and stiffness of carbon and boron nitride polymorphs from first principles calculations. Phys. Rev. B 2006, 73, 064304. [Google Scholar] [CrossRef] [Green Version]
- Bonini, N.; Lazzeri, M.; Marzari, N.; Mauri, F. Phonon anharmonicities in graphite and graphene. Phys. Rev. Lett. 2007, 99, 176802. [Google Scholar] [CrossRef] [Green Version]
- Pisana, S.; Lazzeri, M.; Casiraghi, C.; Novoselov, K.S.; Geim, A.K.; Ferrari, A.C.; Mauri, M. Breakdown of the adiabatic Born-Oppenheimer approximation in graphene. Nat. Mater. 2007, 6, 198–201. [Google Scholar] [CrossRef] [Green Version]
- Lazzeri, M.; Attaccalite, C.; Wirtz, L.; Mauri, F. Impact of the electron-electron correlation on phonon dispersion: Failure of LDA and GGA functionals in graphene and graphite. Phys. Rev. B 2008, 78, 081406(R). [Google Scholar] [CrossRef] [Green Version]
- Avramov, P.V.; Sakai, S.; Entani, S.; Matsumoto, Y.; Naramoto, H. Ab initio LC-DFT study of graphene, multilayer graphene and graphite. Chem. Phys. Lett. 2011, 508, 86–89. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. Entropy driven stabilization of energetically unstable crystal structures explained from first principles theory. Phys. Rev. Lett. 2008, 100, 095901. [Google Scholar] [CrossRef]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. The self-consistent ab initio lattice dynamical method. Comput. Mater. Sci. 2009, 44, 888–894. [Google Scholar] [CrossRef]
- Söderlind, P.; Moore, E.E.; Wu, C.J. Thermodynamics modeling for actinide monocarbides and mononitrides from first principles. Appl. Sci. 2022, 12, 728. [Google Scholar] [CrossRef]
- Souvatzis, P.; Arapan, S.; Eriksson, O.; Katsnelson, M.I. Temperature-driven a-to-b phase transformation in Ti, Zr, and Hf from first-principles theory combined with lattice dynamics. Europhys. Lett. 2011, 96, 66006. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Wills, J.M.; Eriksson, O.; Andersson, P.; Delin, A.; Grechnyev, O.; Alouani, M. Full-Potential Electronic Structure Method; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Maultzsch, J.; Reich, S.; Thomsen, C.; Requardt, H.; Ordejón, P. Phonon dispersion in graphite. Phys. Rev. Lett. 2004, 92, 075501. [Google Scholar] [CrossRef] [PubMed]
- Wirtz, L.; Rubio, A. The phonon dispersion of graphite revisited. Solid State Commun. 2004, 131, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Alfè, D. PHON: A program to calculate phonons using the small displacement method. Comput. Phys. Commun. 2009, 180, 2622–2633. [Google Scholar] [CrossRef]
- Mohr, M.; Maultzsch, J.; Dobardžic, E.; Reich, S.; Milosevic, I.; Damnjanovic, M.; Bosak, A.; Krisch, M.; Thomsen, C. Phonon dispersion of graphite by inelastic X-ray scattering. Phys. Rev. B 2007, 76, 035439. [Google Scholar] [CrossRef] [Green Version]
- Nicklow, R.; Wakabayashi, N.; Smith, H.G. Lattice dynamics of pyrolytic graphite. Phys. Rev. B 1972, 5, 4951–4962. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A. CALPHAD Calculation of Phase Diagrams: A Comprehensive Guide; Pergamon Materials Series; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lukas, H.; Fries, S.; Sundman, B. Computational Thermodynamics: The CALPHAD Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Perron, A.; Turchi, P.E.A.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F.; Kurata, M. Thermodynamic re-assessment of the Pu-U system and its application to the ternary Pu-U-Ga system. J. Nucl. Mater. 2014, 454, 81–95. [Google Scholar] [CrossRef] [Green Version]
- Perron, A.; Turchi, P.E.A.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F. The Pu-U-Am system: An ab initio informed CALPHAD thermodynamic study. J. Nucl. Mater. 2015, 458, 425–441. [Google Scholar] [CrossRef] [Green Version]
- Dinsdale, A. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Kerley, G.I.; Chhabildas, L. Multicomponent-Multiphase Equation of State for Carbon; Sandia Report Sand2001-2619; US Department of Energy (US): Washington, DC, USA, 2001.
- Otero-de-la Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Abbasi-Pérez, D. Gibbs2: A new version of the quasi-harmonic model code. II Models for solid thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Equation of state and thermodynamics of solids using empirical corrections in the quasi-harmonic approximation. Phys. Rev. B 2011, 84, 184103. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Treatment of first-principles data for predictive quasiharmonic thermodynamics of solids: The case of MgO. Phys. Rev. B 2011, 84, 024109. [Google Scholar] [CrossRef]
- Gurvich, L.V.; Iorish, V.S.; Yungman, V.S.; Dorofeeva, O.V. Thermodynamic properties as a function of temperature. In CRC Handbook of Chemistry and Physics Online; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- McDonald, R.A. Heat content and heat capacity of an extruded graphite from 341 to 1723 K. J. Chem. Eng. Data 1965, 10, 243. [Google Scholar] [CrossRef]
- Fried, L.E.; Howard, W.M. Explicit Gibbs free energy equation of state applied to the carbon phase diagram. Phys. Rev. B 2001, 61, 8734–8743. [Google Scholar] [CrossRef]
- Bianconi, A.; Hagström, S.B.M.; Bachrach, R.Z. Photoemission studies of graphite high-energy conduction-band and valence band states using soft-x-ray synchrotron radiation excitation. Phys. Rev. B 1977, 12, 5543–5548. [Google Scholar] [CrossRef]
- Charlier, J.-C.; Gonze, X.; Michenaud, J.-P. First-principles study of electronic properties of graphite. Phys. Rev. B 1991, 43, 4579–4589. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Söderlind, P.; Landa, A.; Hood, R.Q.; Moore, E.E.; Perron, A.; McKeown, J.T. High-Temperature Thermodynamics Modeling of Graphite. Appl. Sci. 2022, 12, 7556. https://doi.org/10.3390/app12157556
Söderlind P, Landa A, Hood RQ, Moore EE, Perron A, McKeown JT. High-Temperature Thermodynamics Modeling of Graphite. Applied Sciences. 2022; 12(15):7556. https://doi.org/10.3390/app12157556
Chicago/Turabian StyleSöderlind, Per, Alexander Landa, Randolph Q. Hood, Emily E. Moore, Aurélien Perron, and Joseph T. McKeown. 2022. "High-Temperature Thermodynamics Modeling of Graphite" Applied Sciences 12, no. 15: 7556. https://doi.org/10.3390/app12157556
APA StyleSöderlind, P., Landa, A., Hood, R. Q., Moore, E. E., Perron, A., & McKeown, J. T. (2022). High-Temperature Thermodynamics Modeling of Graphite. Applied Sciences, 12(15), 7556. https://doi.org/10.3390/app12157556







