Influence of Coupling Effects between Gravel Soil Porosity and Cement Grout Weight on Diffusion Laws and Morphologies of Penetration Grouting

Abstract

The practice and theory of grouting engineering show that both injected medium porosity and grouting fluid weight play an important influence on the diffusion law and morphology of penetration grouting. However, the effects have not been well studied in the context of existing penetration grouting mechanisms. In this paper, the actual diffusion law and morphology of cement grout into the gravel soil are studied on the basis of indoor experiments, mathematical statistics, and theoretical analyses. Then, the three-dimensional space diffusion trajectory equation was quantitatively characterized. The influence of the coupling effect between gravel soil porosity and cement grout weight on diffusion morphologies of penetration grouting was discussed by the definition of the morphological deviation rate. Results show that actual penetration diffusion dimensions of cement grout into the gravel soil differ from that of theoretical values calculated by the penetration grouting mechanism, and its spatial diffusion morphology is approximated as ellipsoid. The coupling effect between gravel soil porosity and cement grout weight have a relatively significant effect on the diffusion morphologies of penetration grouting except for gravel soil with porosity <0.5 infiltrated by Newton-type and <0.4 by power-law-type cement grout, respectively. This influence is particularly significant when Bingham-type cement grout was penetrated into gravel soil with a porosity of >0.5. The research results can provide theoretical support and technical references for the practical grouting engineering of gravel soil.

1. Introduction

Years of engineering practice have shown that grouting technology is a favorable and effective technology to tackle different geotechnical problems. Penetration grouting is one of the earliest geotechnical construction techniques used in the field of grouting. As early as 1802, Charles Berlghy, a French engineer, applied it to repair the Dieppe scour gate project [1,2]. Because it has less influence on the disturbance of the injected medium or material during the grouting process, permeation grouting is now widely used in architecture, highways, railways, subways, mines, tunnels, hydropower, military, and other engineering fields, and has achieved good engineering results [1,2,3].

Currently, many studies have been carried out to find the penetration grouting diffusion laws of grouting fluids in the injected medium. As early as 1938, Maag studied the penetration diffusion law of Newtonian fluid in isotropic homogeneous medium [2]; Zou analyzed the columnar penetration grouting diffusion radius expression for Newtonian fluid [4]; Uddin, Yang, and Li et al. studied the penetration diffusion mechanism of Newton, Bingham, and power-law fluids in sandy stratum [5,6,7,8]; Ye et al. discussed the penetration diffusion mechanism and model based on Newtonian fluid, Bingham fluid, and power-law fluid for shield tunnel grouting [9,10,11]; Dayakar and Yang analyzed the penetration diffusion law of Bingham fluid in gravel soil layers [12,13]; Draganovic and Fang et al. studied the penetration grouting diffusion law considering the percolation effect [14,15,16]; Tiruoatl, Bolisetti, and Sui et al. explored the penetration grouting mechanism of chemical grout in porous media [17,18,19]; Zhou et al. analyzed the penetration diffusion model considering the tortuosity effect [20]; Zhang et al. explored the penetration grouting diffusion law of quick-setting cement in porous media [21]; Yang et al. explored the penetration diffusion laws and mechanisms for Newtonian fluid, Bingham fluid and power-law fluid in the injected media, which were verified by the grouting experiments [22,23,24,25,26,27].

Grouting engineering practice and theoretical studies have shown that both the porosity of the injected medium and the self-weight of the injected fluid have a significant influence on the diffusion law and morphology of penetration grouting [1,2,3,22,23]. However, the current penetration diffusion model has not yet considered the role of the porosity of the injected medium and the cement grout weight on the diffusion law and morphology. The coupling effect of the two on the penetration grouting is still in the exploration stage. On the one hand, cement is the most widely used grouting fluid in the practice of grouting engineering. Based on the rheological properties of fluid, cement grout can be classified as a Newtonian fluid, Bingham fluid, and power-law fluid [1,2]: the cement grout is Newtonian fluid when the water–cement ratio (W/C) is greater than 1.25; that within the range of 0.75–1.25 is Bingham fluid; that within the range of 0.5–0.75 is power-law fluid [28]. Different types of cement grout have different densities, so the gravitational effect of cement grout on the diffusion law and morphology of the penetration grouting is different. For example, the density of power-law cement grout exceeds 1.60 g/cm³ [1,2]. On the other hand, gravel soil is widely developed and distributed in China, which is highly susceptible to induce the formation of natural disasters under the action of earthquakes, heavy rainfall, and human activities, resulting in extremely painful lessons [22,23]. Therefore, the methods of indoor experiments, mathematical statistics, and theoretical analyses adopted by Li were used in this paper to study the influence of the coupling effect of gravel soil porosity and cement grout weight on the diffusion law and morphology of the penetration grouting, which can provide theoretical support and technical reference for practical grouting engineering [24,25,26,29].

2. Experimental Studies

2.1. Experiment Device and Experiment Scheme

The grouting experimental device consists of three parts: a test chamber, pressure supply device, and cement container. [22,23]. The test chamber is composed of steel brackets and Plexiglas plates with an external dimension of 600 mm × 600 mm × 600 mm, which is used to place the gravel soil layer simulation equipment. The cement container mainly consists of a closed steel cylinder, a circular iron frame, and an electronic scale, of which the closed steel cylinder, with a bottom diameter of 15 cm and a height of 40 cm, is designed to bear a pressure of 2.5 MPa, which can fully meet the test requirements. In the experiments, three different grains of 5–10 mm, 3–5 mm, and 1–3 mm were used to simulate gravel soil layers with different properties. The grouting material used was ordinary silicate cement of grade #32.5 produced by Kunming Cement Factory, which is widely used as grouting material in current projects. The experiment was designed by the orthogonal design test method. Three factors were selected: grouting pressure, porosity of gravel soil layer, and water–cement ratio of grouting cement, and three level values were selected for each factor. A total of nine groups of experiments were completed and the specific scheme can be referred to the author’s previous research results by Yang [22,23].

2.2. Penetration Diffusion Laws of Cement Grout in Gravel Soil

The penetration grouting experiments were carried out according to the designed experiment scheme, shown in Figure 1. The penetration diffusion progress of the cement grout in the gravel soil can be divided into three stages.

(1)

Beginning stage: Most of the cement grout diffused rapidly in the gravel soil from the grouting hole along the downward (especially vertical downward (gravity)) direction. A certain amount of cement grout diffused horizontally and laterally around the grouting hole, and only a very small amount of cement diffused to its upper area. In this stage, the cement grout diffusing along the downward direction was much larger than the cement diffusing around the grouting hole horizontally and laterally, both in terms of diffusion speed and diffusion volume.

(2)

Intermediate stage: both the diffusion speed and diffusion volume of cement grout in gravel soil along the downward direction gradually decreased; while the amount of cement grout diffusing horizontally and horizontally around the grouting hole slowly increased, and a certain amount of cement diffused into the gravel soil at the upper part of the grouting hole.

(3)

End stage: Only a very small amount of cement grout penetrated and diffused into the gravel soil at the lower part of the grouting hole. The speed and volume diffusing in the horizontal and lateral part around the grouting hole gradually decreased, while most of the cement penetrated and diffused in the upward direction at this stage.

The diffusion flow pattern and diffusion morphology of cement grout in gravel soil are shown in Figure 2, respectively.

2.3. Spatial Diffusion Morphology

The spatial diffusion morphology of penetration grouting of cement grout in gravel soil was approximated as ellipsoidal morphology with inconsistent diffusion dimensions in three dimensions (Figure 3).

2.4. Experiment Results

The results of three-dimensional spatial diffusion dimensions of cement grout in gravel soil are shown in

Table 1. Three-dimensional spatial diffusion dimensions of cement grout into the gravel soil.

Influencing Factors		Three-Dimensional Spatial Diffusion Dimensions of Cement in Gravelly Soil
Cement Water–Cement Ratio	Porosity of Gravelly Soil /%	Diffusion Dimension in y-axis Direction/cm	Diffusion Dimension in x-axis Direction/cm	Diffusion Dimension in z-axis Direction /cm
1.0	50.74	12.2	9.2	9.8
0.75	45.05	6.8	5.9	6.6
1.25	39.93	12.0	11.5	11.8
0.75	50.74	8.4	7.8	7.6
1.25	45.05	12.5	12.0	12.3
1.0	39.93	11.1	10.6	10.3
1.25	50.74	13.8	12.7	11.8
1.0	45.05	12.1	11.8	11.2
0.75	39.93	6.8	6.5	6.6

.

Table 1 shows that the penetration diffusion dimension of cement grout in gravel soil in the direction of the y axis (vertical) is larger than that in the direction of the x and y axis (horizontal), and the difference between the latter two is not significant.

3. Effect of Coupling Effect of Porosity and Cement Grout Weight on the Diffusion Morphology of Penetration Grouting in Gravel Soil

3.1. Comparison between Experimental Values and Theoretical Values of Penetration Diffusion

According to the penetration grouting diffusion mechanism [1,2,6,7], the penetration grouting diffusion in gravel soil studied in this paper is theoretically spherical diffusion, and the three-dimensional spatial morphology should be a standard sphere, while the three-dimensional diffusion morphology in the experiments is approximately an ellipsoid. The differences between these two are analyzed in this section.

In order to analyze more precisely the difference between the experimental values of penetration diffusion of cement grout in gravel soil and the theoretical values obtained by the penetration grouting mechanism, the equal volume method is used to transform the approximate ellipsoidal three-dimensional morphology into the theoretical equivalent penetration diffusion sphere, i.e.,

$$R=\sqrt[3]{abc}$$

(1)

where R is the radius of the equivalent penetration diffusion sphere of cement grout in gravel soil, cm; a, b, and c are the diffusion dimensions of the x-axis, y-axis, and z-axis of the approximate ellipsoid, cm, respectively.

The theoretical values of the penetration diffusion radius obtained from the penetration grouting diffusion mechanism [1,2,6,7], the equivalent penetration diffusion sphere radius calculated from the experimental measurements, and the difference between the two are shown in

Table 2. Theoretical values of the penetration diffusion radius, the equivalent penetration diffusion sphere radius, and the difference.

Theoretical Values of Penetration Diffusion Radius Obtained from the Penetration Grouting Diffusion Mechanism/cm	Equivalent Penetration Diffusion Sphere Radius Calculated from Experimental Measurements/cm	Difference between the Two Values/%
6.9	10.4	33.65
8.5	6.4	24.71
37.9	11.7	32.48
18.0	7.9	56.11
13.7	12.3	10.22
3.6	10.7	66.36
27.2	12.7	53.31
7.0	11.7	40.17
7.7	6.6	14.29

.

It can be seen in Table 2 that the differences between the theoretical values of the penetration diffusion radius obtained based on the penetration grout diffusion mechanism and the equivalent penetration diffusion sphere radius values calculated from experimental measurements are more than 10%, and even about 70% of the differences are more than 40%. This shows that there is a very large difference between the actual penetration diffusion dimensions of the cement in the gravel soil and the theoretical diffusion values.

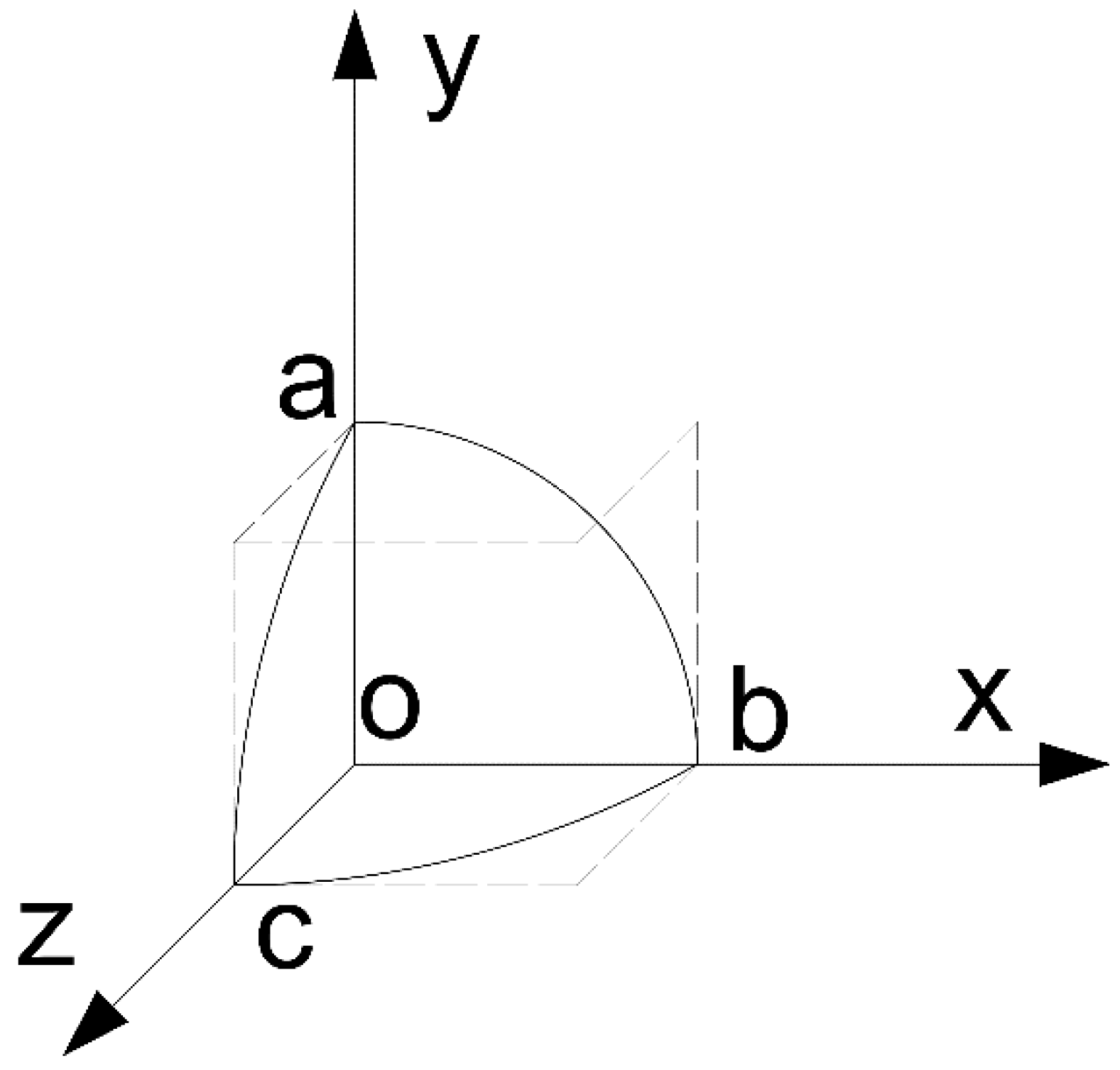
3.2. Three-Dimensional Spatial Diffusion Morphology Model

The above analysis shows that the diffusion of cement grout in gravel soil is approximately ellipsoidal, and the diffusion dimensions in three-dimensional space are not consistent. The diffusion dimensions in the vertical direction differ greatly from those in the horizontal transverse direction.

Therefore, in order to theoretically reveal the three-dimensional spatial diffusion morphology of cement grout in gravel soil and provide some theoretical support for practical engineering, based on the experimental results, the mathematical ellipsoidal geometric trajectory is used this paper to reveal the three-dimensional spatial diffusion morphology of cement grout in gravel soil by penetration grouting, which can be seen in Figure 4.

Where a, b, and c, are respectively the half-line of x-axis, y-axis, and z-axis, of the approximated ellipsoidal morphology by the penetration diffusion of cement grout in the gravel soil. The O point at the center of its geometric trajectory is the location of the grouting hole.

Combining the rectangular equation of the ellipsoid with the experimental results in Table 1, the following equation can be used to describe the three-dimensional spatial diffusion morphology of cement grout by penetration grouting in gravel soil,

$$\frac{x^2}{{(m_1{R}_T)}^2}+\frac{y^2}{{(m_2{R}_T)}^2}+\frac{z^2}{{(m_3{R}_T)}^2}=1$$

(2)

where m₁ is the adjustment coefficient of half-line of x-axis, varying from 0.70 to 1.70, generally taken as 1.20; m₂ is the adjustment coefficient of half-line of y-axis, varying from 0.80 to 1.80, generally taken as 1.30; m₃ is the adjustment coefficient of half-line of z-axis, varying from 0.70 to 1.70, generally taken as 1.20; R_T is the theoretical value of the penetration diffusion radius calculated by the penetration grouting diffusion mechanism.

Equation (2) is the three-dimensional spatial diffusion trajectory equation of cement grout in gravel soil by penetration grouting, which can be used as the calculation model of three-dimensional spatial diffusion dimension parameters. Therefore, this model can be used to predict the three-dimensional spatial diffusion dimension of cement grout in gravel soil by penetration grouting.

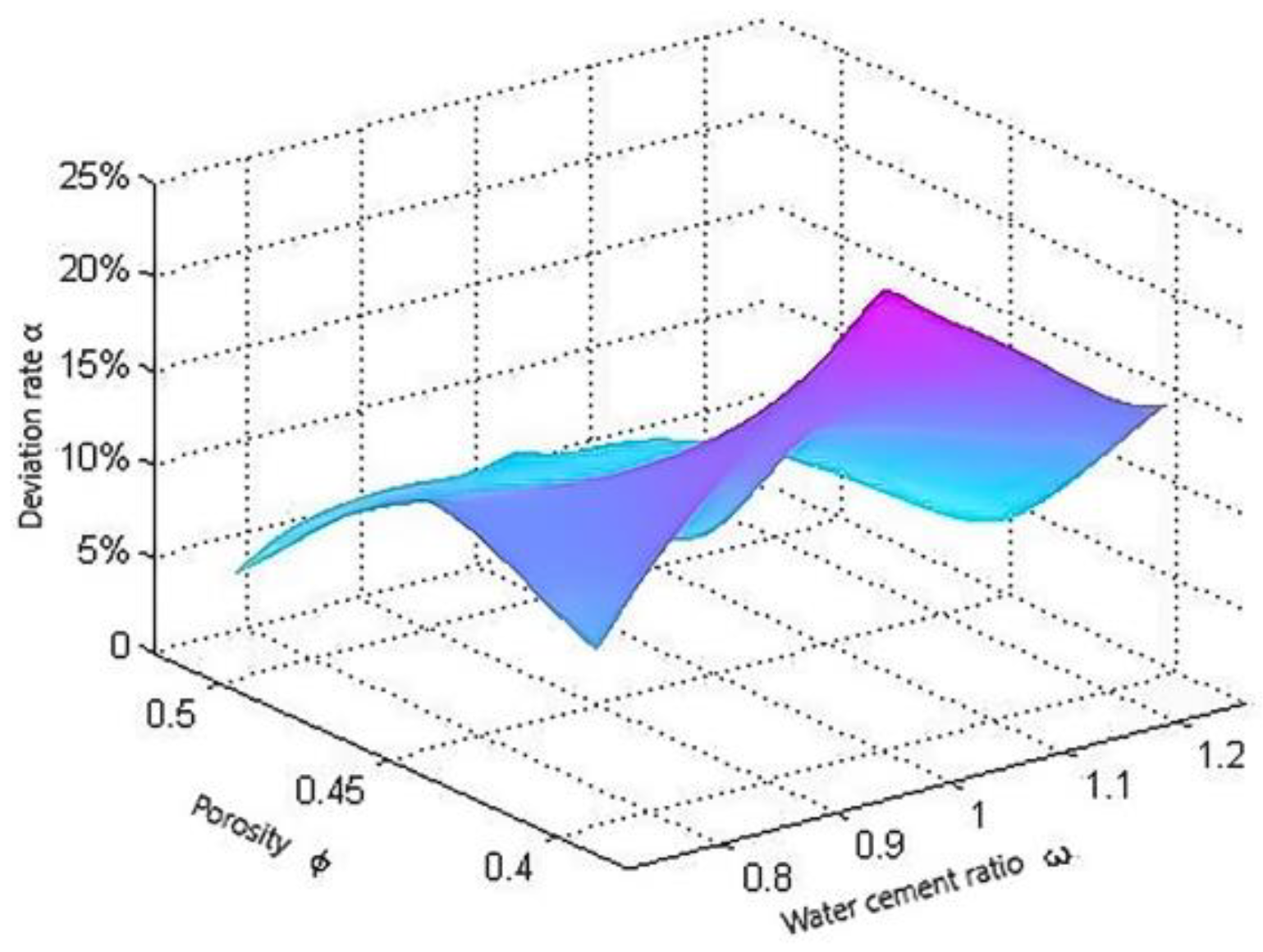
3.3. Effect of Coupling Effect of Porosity and Cement Grout Weight on the Diffusion Morphology of Penetration Grouting in Gravel Soil

As mentioned in the former research of the author [22], the most significant factor affecting the size of cement grout in gravel soil by penetration diffusion is the water–cement ratio. The second factor is gravel soil’s porosity, while grouting pressure’s effect on it is small. The grouting pressure provides the same force from the grouting hole to the cement grout in the surrounding gravel soil by penetration diffusion [1,2]. Therefore, the coupling effect of porosity and self-weight of cement grout has a very important effect on the diffusion morphology of gravel soil infiltration grouting. The effect of grouting pressure on it is relatively small, so the effect of grouting pressure on the diffusion morphology of gravel soil infiltration grouting is not considered in this paper.

Referring to the elliptical flatness theory, this study defines the deviation rate of the three-dimensional spatial diffusion morphology of cement grout in gravel soil to quantify = the effect of the coupling effect of porosity and cement grout weight on the diffusion morphology of infiltration grouting in gravel soil:

$$\alpha =\frac{a-\min (b,c)}{a}$$

(3)

where min (b, c) is the smaller of the x semi-axis and y semi-axis lengths of the ellipsoidal form of cement grout diffusion in gravel soil, and the other meanings are the same as above.

From the experimental results and theoretical analysis, it is known that the deviation rate α can be taken in the range of 0 ≤ α < 1:

1.

When α = 0, the diffusion of cement grout in gravel soil is spherical, and the three-dimensional spatial morphology is a standard sphere.

This indicates that porosity and cement grout weight coupling effect have no influence on the diffusion morphology of penetration grouting in gravel soil, which is the assumption of cement penetration grouting diffusion theory in gravel soil and does not exist in actual grouting penetration diffusion.

2.

When 0 ≤ α < 1, the coupling effect of porosity and cement grout weight has an effect on the diffusion morphology of penetration grouting in gravel soil, and the penetration grouting in gravel soil is ellipsoidal diffusion, and the three-dimensional spatial morphology is approximately ellipsoidal, which is consistent with the actual penetration grouting diffusion; the larger indicates that the effect of coupling effect of porosity and cement grout weight on the diffusion morphology of penetration grouting in gravel soil is also greater.

Based on Equation (3), the deviation rate of the approximated ellipsoidal morphology of porosity and cement grout weight coupling effect on the penetration grouting diffusion of gravel soil can be calculated and shown in

Table 3. Morphological deviation rate of the approximate ellipsoid of the coupling effect between gravel soil porosity and cement grout weight on cement grouts into the gravel soil by penetration grouting.

Water–Cement Ratio ω	Gravelly Soil Porosity ϕ /%	Length of Semi-Axis (Vertical Direction) a/cm	The Smaller of the x and z (Horizontal and Lateral) Semi-Axis Lengths min (b,c)/cm	Approximate Ellipsoidal Morphology Deviation Rate of Infiltration Grout Diffusion α/%
1	0.5074	12.2	9.2	24.59%
0.75	0.4505	6.8	5.9	13.24%
1.25	0.3993	12	11.5	4.17%
0.75	0.5074	8.4	7.6	9.52%
1.25	0.4505	12.5	12	4.00%
1	0.3993	11.1	10.3	7.21%
1.25	0.5074	13.8	11.8	14.49%
1	0.4505	12.1	11.2	7.44%
0.75	0.3993	6.8	6.5	4.62%

and Figure 5.

From the practical investigation, it is known that most of the gravelly soil layers have porosity distribution in the range of 0.35–0.55, and according to the three-dimensional spatial diffusion morphology of cement in gravelly soil, the porosity of gravelly soil can be divided into ϕ ≤ 0.4, 0.4 < ϕ < 0.5 and ϕ ≥ 0.5, and the deviation rate α of diffusion morphology of approximate ellipsoid can also be divided into α ≤ 5% (indicating insignificant effect), 5% < α ≤ 15% (indicating significant effect), 15% < α ≤ 25% (indicating significant effect) and α ≥ 25% (indicating more significant effect) to analyze the effect of the coupling effect of porosity and cement grout weight on the diffusion morphology of gravel soil infiltration grouting.

The effect of porosity and cement grout weight coupling effect on the three-dimensional spatial diffusion laws of gravel soil infiltration grouting is shown in

Table 4. Influence laws of penetration grouting diffusion morphologies of coupling effect between gravel soil porosity and cement grout weight on cement grouts into the gravel soil.

Effect of Cement Grout Weight (Water–Cement Ratio ω)
		Power-Law Type Cement (ω ≤ 0.75)	Bingham Type Cement (0.75 < ω < 1.25)	Newton Type Cement (ω ≥ 1.25)
Gravelly soil porosity ϕ influence effect	ϕ ≤ 0.4	Insignificant (α < 5%)	More significant (5% < α < 15%)	Insignificant (α < 5%)
	0.4 < ϕ < 0.5	More significant (5% < α < 15%)		Insignificant (α < 5%)
	ϕ ≥ 0.5	More significant (5% < α < 15%)	Significant (15% < α < 25%)	More significant (5% < α < 15%)

.

Analysis of Table 4 shows that.

• The coupling effect of cement grout weight and porosity of Bingham-type cement has a more significant effect on the three-dimensional spatial diffusion morphology formed by infiltration in gravelly soil, especially in gravelly soil with porosity over 0.5.
• When the power-law cement is infiltrated into the gravel soil with porosity over 0.4, the coupling effect of its self-weight and porosity has a significant effect on its three-dimensional spatial diffusion morphology; while when the power-law cement is infiltrated into the gravel soil with porosity less than 0.4, the effect is not significant.
• Newtonian cement infiltration into gravelly soil with porosity less than 0.5, the coupling effect of cement grout weight and porosity, effect on its three-dimensional spatial diffusion morphology is not significant; only in the gravel soil with porosity over 0.5, the effect shows a more significant feature.

4. Theoretical Analysis

This section carries out a theoretical analysis of the law of influence of the coupling effect of porosity and cement grout weight on the three-dimensional spatial diffusion morphology of gravelly soil infiltration grouting.

• When the gravel soil porosity ϕ is greater than 0.5, its internal pore size is large, and the majority of pore sizes are larger than the maximum particle size of cement (about 60–100 μm), and the gravitational effect of power law, Bingham and Newton type cement promotes its penetration diffusion in the pore space of gravel soil along the downward (especially vertical (y-axis) downward) direction, inhibiting the horizontal. This results in a difference of almost 10% between the diffusion size of the cement in the gravity (y-axis) direction and the diffusion size in the horizontal lateral (x-axis and z-axis) direction, especially for the Bingham-type cement in the gravelly soil, where the difference is nearly 25%.
• When the gravel soil porosity is in the range of 0.4 < ϕ < 0.5, the internal pore size is large and most of the pore sizes exceed the maximum particle size of the cement (about 60–100 μm), the gravitational effect of the power-law and Bingham-type cement has a better promotion effect on its penetration diffusion in the gravel soil pore space along the downward (especially vertical (y-axis) downward) direction, and it has a more severe inhibition effect on its penetration diffusion in the horizontal In contrast, Newtonian cement is relatively less dense, and its own gravitational effect on the diffusion in the gravel soil along the gravity (vertical downward, y-axis) direction is more than 5% different from that in the horizontal lateral (x-axis and z-axis) direction, while the Newtonian cement is relatively less dense, and its own gravitational effect on the diffusion in the gravel soil along the gravity (vertical downward, y-axis) direction is more than 5% different from that in the horizontal lateral (x-axis and z-axis) direction. The difference between the diffusion size of Newtonian cement in the gravity (y-axis) and horizontal (x-axis and z-axis) directions is within 5%, because of its gravitational effect on the diffusion in the gravity (vertical downward, y-axis) direction and the inhibition of the diffusion in the horizontal lateral (x-axis and z-axis) direction are both greatly weakened.
• When the gravelly soil has a porosity ϕ ≤ 0.4, the internal pore size is small and a part of it does not exceed the maximum particle size of the cement (about 60–100 μm).

  (a)

  When the cement is a power-law fluid, it has a strong gravitational effect due to its higher density, which promotes its penetration and diffusion in the gravel soil along the downward (especially vertical (y-axis) downward) direction and inhibits its penetration and diffusion in the horizontal lateral (x-axis and z-axis) direction in the beginning stage; as the grouting time goes on, the liquid is thicker and thicker due to the smaller water–cement ratio of this type of cement. At the same time, the pore size is smaller, causing most of the pores along the downward direction to be blocked by the cement, inhibiting its diffusion in the gravity (vertical downward, y-axis) direction and promoting its diffusion in the horizontal lateral (x-axis and z-axis) direction, thus resulting in a difference of less than 5% in the diffusion size in both directions.

  (b)

  When the cement is a Newtonian fluid, its gravitational effect is weak and the pore size between the gravelly soil is small, which has a less significant effect on its permeability diffusion along the downward (especially vertical (y-axis) downward) and horizontal transverse (x-axis and z-axis) directions of the gravelly soil, and therefore, the difference in diffusion size caused in these two directions is also less than 5%.

  (c)

  When the cement is Bingham fluid, its gravitational effect is between the gravitational effect of power-law and Newtonian cement, although the pore size inside the gravel soil is small and part of the pores along the downward direction are blocked by the cement, but in the process of penetration diffusion, in general, the gravitational effect of Bingham cement to promote its diffusion along the downward (especially vertical (y-axis) downward) is stronger than that due to part of the pores. The cement blockage and the small size of the pore space inhibit the diffusion; therefore, it results in a better diffusion of Bingham cement along the gravity (vertical downward, y-axis) direction than in the horizontal lateral (x-axis and z-axis) direction, with a large difference (more than 5%) in the diffusion size between the two.

5. Conclusions

• The diffusion pattern of penetration grouting in gravel soil: in the beginning stage, most of the cement slurry penetrates and diffuses rapidly in the gravel soil from the grouting hole along the downward (especially vertical downward due to gravity) direction; in the middle stage, the cement mainly penetrates and diffuses horizontally and laterally around the grouting hole; in the end stage, most of the cement penetrates and diffuses along the upward direction.
• The actual permeate diffusion size of cement in gravel soil is different from the theoretical diffusion value, and it shows a three-dimensional spatial diffusion morphology of nearly ellipsoid; its trajectory equation is quantitatively characterized, which can be used as a computational model for three-dimensional spatial diffusion size parameters, and thus can be used to predict the three-dimensional spatial diffusion size of cement permeate grouting in gravel soil in order to provide guidance for engineering practice.
• The deviation rate of three-dimensional spatial diffusion pattern of cement penetration grouting in gravel soil is defined, and the effect law of coupling effect between gravel soil porosity and cement grout weight on morphologies of penetration grouting is discussed. That is, for Bingham type cement slurry, when the porosity exceeds 0.5, the coupling effect has a significant effect on the three-dimensional spatial diffusion pattern of gravel soil penetration grouting; for power-law type cement slurry, when the porosity exceeds 0.4, the coupling effect has a significant effect, while less than 0.4 is showing insignificant characteristics; for Newton type cement slurry, the coupling effect has a comparable significant effect.

The research results of this paper can provide not only theoretical support for the actual penetration grouting engineering practice of gravelly soil layer, but also provide technical reference for the prevention and mitigation of geological disasters such as landslides that occur in gravelly soil.