Modal Analysis of a Steel Truss Girder Cable-Stayed Bridge with Single Tower and Single Cable Plane

Abstract

The dynamic characteristics of bridge structures are important in wind stability analysis, seismic design, fatigue assessment, health inspection, and maintenance of bridge structures; however, the mechanical and dynamic properties of different bridge types are different. A long-span cable-stayed bridge has the advantages of large flexibility, long natural vibration period, low natural frequency, dense spectrum, and denser modal than those of general structures. In this paper, the dynamic characteristics of a cable-stayed bridge with single pylon and single cable plane in the maximum cantilever stage and the complete bridge are analyzed. The single-tower cable-stayed bridge has some unique characteristics, such as lower cost, and a more beautiful appearance, but its torsional rigidity is lower, which increases the risk of wind damage and earthquake damage. Therefore, a finite element analysis of this bridge in the maximum cantilever state is carried out, and the influences of the main components’ rigidity, the inclination angles of the stayed cables, the supporting conditions, and the locations of the auxiliary piers are analyzed for the sustainability of this type of cable-stayed bridge. The analysis results show that a cable-stayed bridge with single pylon and single cable plane has more flexibility, and that the lateral rigidity and torsional rigidity are smaller. Structure rigidity, dip angles of the stayed cables, and positions of the auxiliary piers all have significant influences on the dynamic characteristics of cable-stayed bridges.

1. Introduction

The natural frequencies, damping, and free vibration features of principal modes of bridge structures are the basis for analyzing the dynamic characteristics of cable-stayed bridges. The dynamic characteristics of bridge structures depend heavily on the stiffness, supporting conditions, and composition system of the structures. Studies on the dynamic characteristics of bridge structures are important for wind stability analysis, seismic design, health inspection, and maintenance of bridge structures [1,2]. At the same time, it is also an important basis to judge whether a bridge structure is intact or not.

With the development of modern bridge technology, bridge development tendencies have become more and more beautiful, complex, and bigger. A single cable-plane cable-stayed bridge is popular because of its advantages, such as beautiful aesthetics, good perspective, navigation, and flood discharge performance. However, a single cable plane structure does not provide enough resistance to torsion capability, which reduces the torsional rigidity of the structure and wind resisting stability. Its dynamic characteristics need to be studied carefully.

If the tower style of a bridge is a single tower, it can reduce costs and increase the sense of beauty. At the same time, it can increase structural flexibility, the risk of wind resistance, and anti-seismic performance. For a single-tower cable-stayed bridge, the auxiliary piers in the side span are helpful to improve the overall rigidity of the structure. For a long-span steel truss girder cable-stayed bridge, the side girder of the steel truss is the largest component which bears the axial force and bending moment, and the force always is the most unfavorable [3,4]. The tension diagonal and crossbeam are the main force members of a steel truss beam. The web members play a stabilizing role. For a cable-stayed bridge with a single central cable plane, the maximum cantilever state is the most unfavorable construction stage and is critical to the closure control. Therefore, the dynamic characteristics of a steel truss girder cable-stayed bridge with single tower and single cable plane should be analyzed.

Through finite element modeling, the dynamic characteristics of bridges can be optimized by modifying different bridge parameters [5,6,7,8,9]. For example, the stiffness [10,11] of each member of a bridge, the constraint conditions [12] of different members and pylons, the influence of concentrated force [13], and the position of auxiliary piers [14] will have a certain impact on the dynamic characteristics of the bridge.

At present, in-depth studies on the dynamic characteristics of bridges have been conducted; however, most studies have been aimed at mainstream bridge types. A cable-stayed bridge with single tower and single cable plane is a unique type of bridge, and there is still a lack of relevant studies. Therefore, the main focus of this study is to investigate the effect of changes in component stiffness, cable inclination angle, and auxiliary piers position on the dynamic characteristics of a single tower and single cable plane cable-stayed bridge and how to optimize them.

Zhou et al. [15] systematically studied the dynamic characteristics of a self-anchored suspension bridge, which is a concrete bridge with a wide deck, and its transverse vibration is worth studying. Ventura C. E. et al. [16] conducted an in-depth study on the dynamic characteristics of the Colquitz river bridge, and the main research direction was to evaluate the seismic resistance of the bridge structure. Roy, S. S. and Dash, S. R. [17] focused on the dynamic characteristics of continuous beam bridges. Although multi-span continuous beam technology is very mature, there are few long-span multi-span continuous beams, which have generally been replaced by cable-stayed bridges or suspension bridges, and still have research value. Xie, X. et al. [18] conducted in-depth research on carbon fiber cables and found that carbon fiber had better mechanical properties than traditional cables and could be widely used in long-span cable-stayed bridges. Casalegno, C. and Russo, S. [19] analyzed the dynamic characteristics of bridges using new materials. They comprehensively compared the main bridge types at this stage including cable-stayed bridges, suspension bridges, continuous rigid frame bridges, etc. [20,21,22,23,24,25,26,27,28,29,30], analyzed the advantages of new bridges, and provided a reference for the construction of similar bridges in the future. The cable-stayed bridge with single tower and single cable plane is a new type of bridge, and its dynamic characteristics have increased research value. However, there are few studies on the influence of girder stiffness, cable inclination, and auxiliary pier location on the dynamic characteristics of a single tower and single cable plane cable-stayed bridge.

In this paper, the finite element analysis software, ANSYS, is used to establish a three-dimensional finite element model of a cable-stayed bridge with single tower and single cable plane, and its natural vibration characteristic is studied. The influence of the maximum cantilever state on the dynamic characteristics of the bridge is analyzed according to changes in parameters of the cable-stayed bridge, such as stiffness of the main components, the inclination angles of the stayed cables, the supporting condition, and the position of the auxiliary piers. Finally, we propose the general rules of the natural vibration characteristic of a steel truss girder cable-stayed bridge with single tower and single cable plane at maximum cantilever state under the influence of parameters.

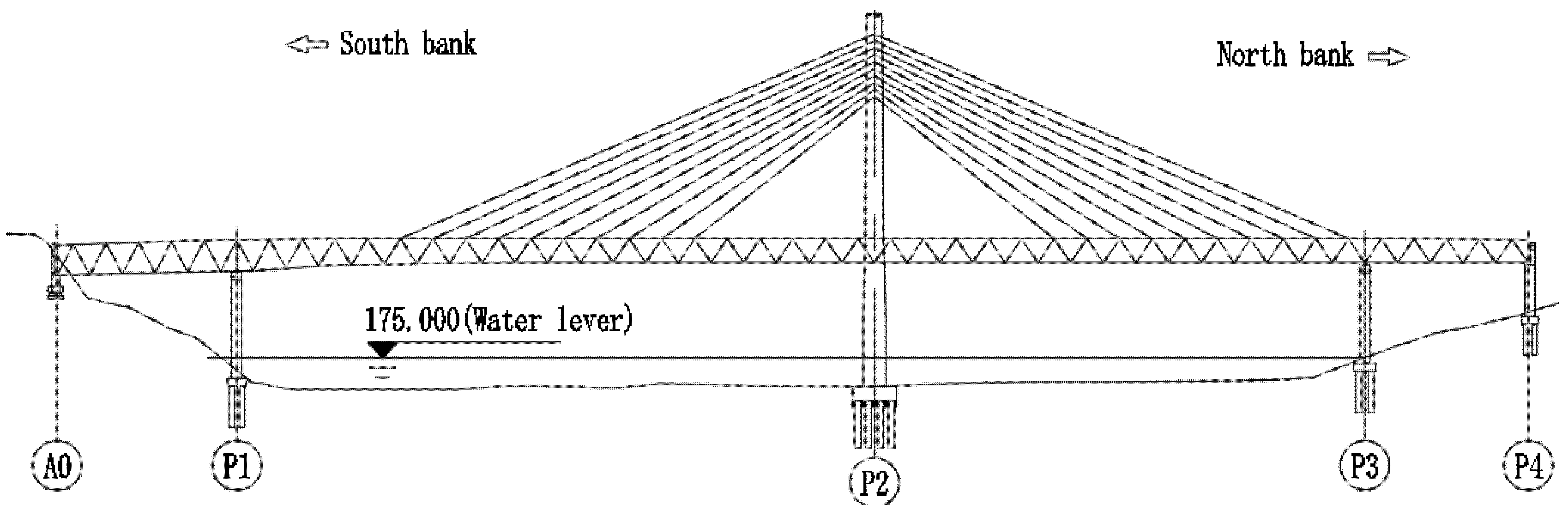
2. Bridge Description

The bridge studied in this paper is a steel truss girder cable-stayed bridge with single tower and single cable plane, whose span arrangement is 88 m + 312 m (main span) + 240 m + 80 m. Because the upper and lower decks are not parallel, the height of the trusses are not constant. The main girder adopts the triangular truss structure, the main girder of the whole bridge has 45 sections, and the length of each section is 16 m. The upper deck of the bridge adopts the orthotropic steel deck. The transverse beams are installed along the longitudinal direction of the bridge. The main truss member and the middle longitudinal beam are all bolted using M30 high strength bolts. The appearance type of bridge tower is Tissot type, the tower height is 172.61 m, and it is constructed of C50 concrete. The in situ bridge is shown in Figure 1. The key sectional diagrams of main girder are shown in Figure 2. The overall drawing is shown in Figure 3.

3. Finite Element Simulation

The finite element model is established in accordance with the actual condition of the bridge structure, which is the basis for analyzing the dynamic characteristics in the maximum cantilever state of this bridge. When establishing the finite element model, the elements are selected according to the following principles: (1) the selected element types must be able to mostly simulate the force characteristics of the structure; (2) it must be able to ensure the calculation results are accurate; (3) the finite element model should be simple and efficient. The calculation effort should be as simple as possible, and analysis of the results should be more convenient.

Based on the finite element analysis software, ANSYS, a three-dimensional finite element model of the actual bridge is established, in which the BEAM4 element is used to simulate the bridge tower, the temporary piers, and the steel truss girder. The BEAM188 element is used to simulate the steel truss girder. Stayed cables are simulated by the spatial bar element, link10, and the elastic modulus of stayed cable is modified using the Ernst formula to satisfy the nonlinear feature of cables. The bridge deck is simulated by the SHELL63 element. The average densities of the cables, steel truss girder, and concrete pylon are calculated by the actual amount of steel and concrete used, and the quality of the bridge deck and other structural members are taken into consideration. The fixed hinge support is installed at the P2 pier, and the longitudinal movable hinge supports are arranged at other piers. The model is established in the order of main tower, main beam, cable, and auxiliary piers. In the construction stage, due to the cantilever assembly method, only the deadweight and temporary construction load are considered. After the whole bridge is built, giving the link10 attribute to the cable, the cable force amplitude modulation is carried out through deadweight. P2 piers are all fixed, and the remaining piers and abutments release UX. After the model is established, the model analysis is carried out. The material parameters used in the finite element model are listed in

Table 1. Material parameters.

Component Names	Poisson Ratio	Elastic Modulus (GPa)	Mass Density (kg/m3)	Linear Expansion Coefficient (10−5 °C)
Pylon (C50 concrete)	0.2	34.5	2.549	1.0
Stayed cables	0.3	195	8.005	1.2
Q370 Steel	0.3	206	7.85	1.2
Rigid arms	0.3	206,000	0.00	1.2
Construction brackets	0.3	206	7.85	1.2
Supports	0.3	100,000	0.00	1.2
Longitudinal connection of beams	0.3	54	7.85	1.2

, the ansys bridge model is shown in Figure 4, and the cable details are shown in Figure 5.

4. Dynamic Characteristic Analysis of the Special Cable-Stayed Bridge

The frequency spectrum of the stayed cables are intense, and the dynamic loads can stimulate more vibration modes in a wide frequency range. Therefore, the dynamic characteristics of long-span cable-stayed bridges are usually adopted using more than 10 vibration modes. In the calculation process of dynamic characteristics, the undamped free vibration equation is adopted and the initial stress effect of the deadweight is taken into consideration; the deadweight stress in the vertical direction of any point in the bridge structure is equal to the mass of the structure per unit area above this point, that is, the deadweight is converted into equivalent load. The subspace iteration method is used to extract the natural vibration frequencies and vibration modes [31,32,33,34]. The first ten natural vibration frequencies and vibration mode characteristics of the bridge at the maximum cantilever state and completion stage are shown in

Table 2. The first ten frequencies and vibration modescharacteristics at the maximum cantilever state and completion stages.

Orders	Natural Vibration Frequencies (Hz)		Cycle (s)	Vibration Modes
1	Cantilever stage	0.174	5.760	The 1st order lateral runout
	Completion stage	20.255	0.049	The 1st order torsion of longitudinal beam
2	Cantilever stage	0.316	3.164	The 1st order vertical runout
	Completion stage	22.777	0.044	The 1st order transverse bending
3	Cantilever stage	0.598	1.672	The 1st order Lateral torsion
	Completion stage	25.600	0.039	The 1st order vertical bending
4	Cantilever stage	0.611	1.638	The 1st order vertical bending
	Completion stage	30.269	0.033	The 2nd order vertical bending
5	Cantilever stage	0.723	1.383	The 2nd order reverse bending
	Completion stage	32.326	0.031	The 2nd torsion of longitudinal beam
6	Cantilever stage	0.856	1.168	The torsion of the girder
	Completion stage	33.933	0.029	bending-torsional coupling
7	Cantilever stage	1.013	0.987	The 1st order vertical bending
	Completion stage	45.683	0.022	Symmetrical vertical bending
8	Cantilever stage	1.021	0.979	Lateral bending torsion coupling
	Completion stage	47.841	0.021	Lateral swing of bridge tower
9	Cantilever stage	1.210	0.826	Auxiliary pier swing
	Completion stage	51.992	0.019	Vertical bending
10	Cantilever stage	1.255	0.797	Auxiliary pier reverse bending
	Completion stage	52.083	0.0192	Bending torsion coupling

, some vibration modes are shown in Figure 6.

It can be seen from Table 2 that the vibration modes of the cable-stayed bridge with single cable plane steel truss girder have the following basic characteristics in the maximum cantilever state and the completion stage.

(1)

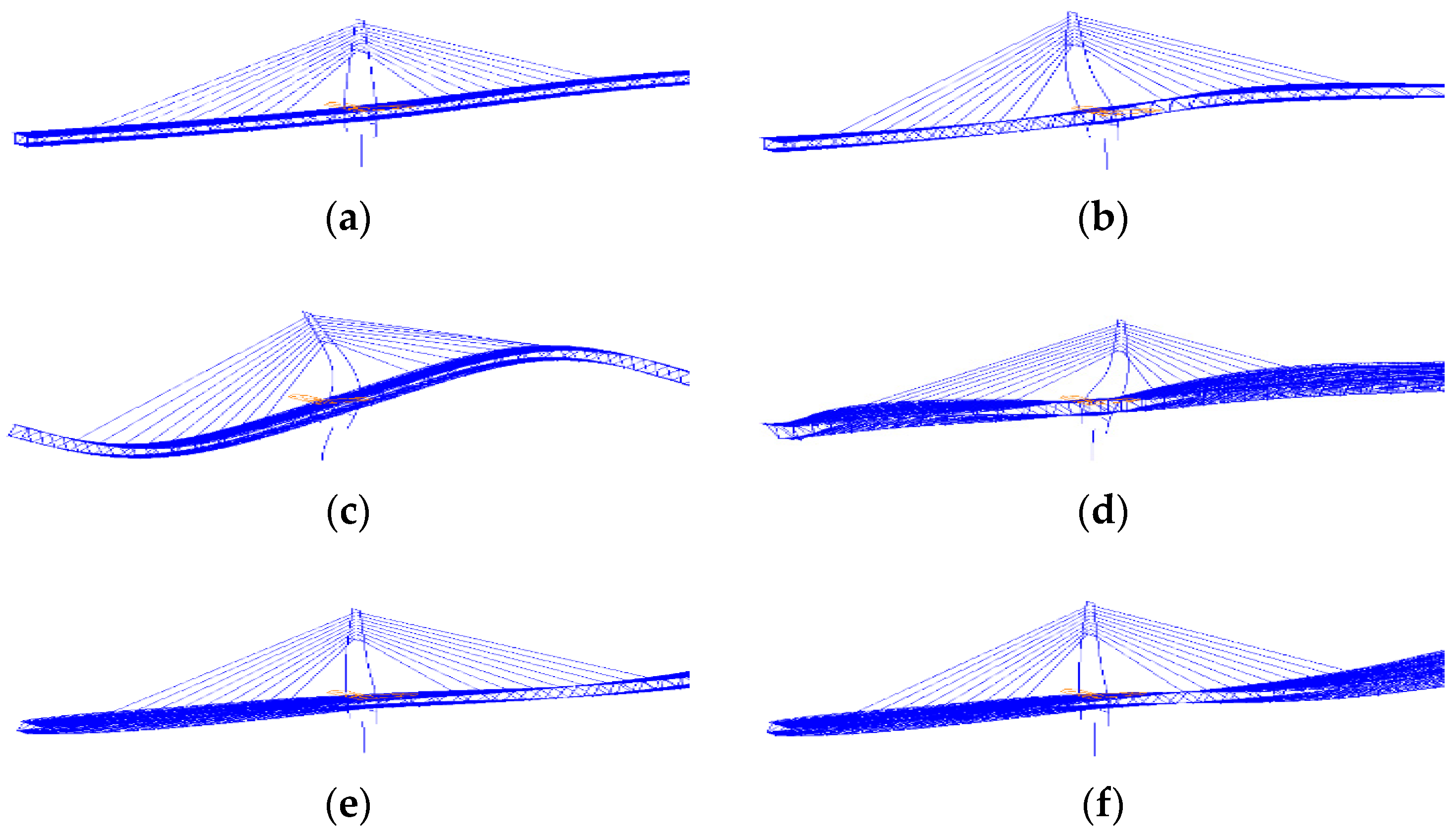
The vibration modes mainly include six kinds of vibration modes, namely lateral vibration, vertical vibration, torsional vibration, vertical bending vibration, lateral bending vibration, and coupled vibration. Among them, the torsion of the main girder appeared in the third order and sixth order. The reason for the torsion of the main beam is that the single cable plane does not provide enough ability to resist torsion, and therefore the torsional rigidity and the torsional frequencies are decreased. Therefore, special attention should be paid to the anti-wind capacity of bridge structures when they are being constructed. Because bridge members have different stiffnesses, the first eight orders are all the vibration modes of the main girder, and the latter two modes are the vibration modes of the auxiliary piers.

(2)

A long-span cable-stayed bridge is very flexible, and therefore, its natural vibration periods are usually longer.Besides, the natural vibration frequency of the bridge is large because the second phase deadload of this bridge is large. The first vibration mode is lateral vibration of the main girder, which is the basic vibration mode of the bridge. Lateral vibration can indicate that the transverse stiffness of the main girder in cantilever stage is less than the longitudinal stiffness. The frequency is greater than 1 Hz when the whole bridge is in the seventh order, which shows that the overall stiffness of the structure is smaller.

(3)

It can be seen from Table 2 that the modes of vibration at the cantilever stage are intense. In the narrow frequency range from 0.174 Hz to 1.254 Hz, 10 vibration modes are distributed, therefore, it is suggested that more vibration modes should be adopted when the dynamic characteristics of this type of cable-stayed bridges are analyzed.

(4)

Compared with the maximum cantilever state, the vibration modes of the completed bridge mainly include lateral bending, vertical bending, and torsion coupling. The steel truss girder cable-stayed bridge with single cable plane in the semi-floating system has relatively large rigidity and a short natural vibration period of 0.049 s. The first-order vibration mode is the longitudinal torsion of the left side beam of the upper deck system, which is the basic vibration mode of the completed bridge. It shows that the rigidity of the left side longitudinal beam is low and it conforms to the maximum force of the side longitudinal beam. The lateral bending vibration mode of the main girder appears earlier than the vertical bending vibration modes, which is consistent with small width span ratio. The bridge adopts the form of a single cable plane cable-stayed bridge, which has the characteristics of poor torsional resistance and low torsional rigidity, therefore, it conforms to the torsional vibration mode of structure in the 5th, 6th, and 10th order modes. The main beam is a steel truss with large structural size; the tower is a concrete tower with relatively small size. Therefore, the stiffness of the main girder of the cable-stayed bridge is smaller than those of the pylon.

5. Influence Analysis of the Main Structural Parameters on Dynamic Characteristics

In view of the steel truss cable-stayed bridge with single tower and single cable plane at the maximum cantilever state, the changes of structural stiffness, inclination angles of the stayed cables, and auxiliary pier position are used to discuss the influence on the natural frequencies or typical mode frequencies.

Scaling represents the ratio of the current stiffness to the original stiffness, it directly reflects the change of frequency, which is an important indicator for subsequent analysis of parameter sensitivity. The scaling equation is as follows:

$$\mathrm{scaling}=\frac{\mathrm{current} \mathrm{stiffness}}{\mathrm{original} \mathrm{stiffness}}$$

The rate of frequency change refers to the change value of the current frequency as compared with the original frequency. It is an important index for analyzing the dynamic characteristics of bridges when parameters change. The equation of rate of frequency change is as follows:

$$\mathrm{rate} \mathrm{of} \mathrm{frequency} \mathrm{change}=\frac{\mathrm{original} \mathrm{frequency}}{\mathrm{current} \mathrm{frequency}}-1$$

5.1. Structural Stiffness

On the basis of the original structure, the stiffness values of the main girder, bridge tower, cable, and other components are changed, and the stiffness value scaling changes from 0.8 to 1.6. The vibration frequencies of typical vibration modes at different working conditions are compared with those of the original model.

The results are shown in Figure 7.

According to Figure 3, the following conclusions can be obtained.

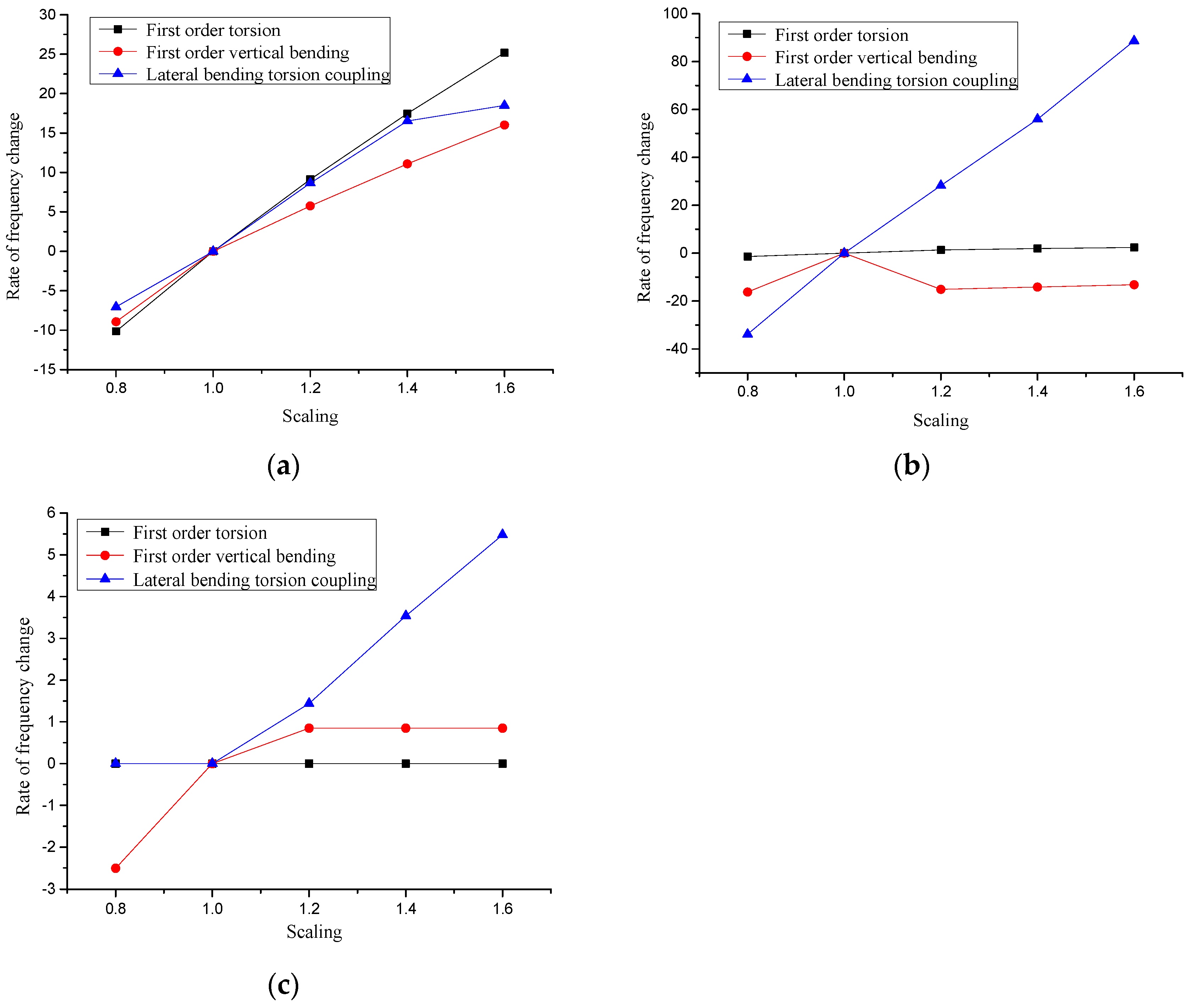
(1)

The stiffness variations of bridge tower and stayed cables have little influence on the frequency changes of the first-order torsion.

(2)

The changes in the stiffness of the bridge tower make the frequency change rate of the first-order vertical bending negative. When the scaling ratio is 1.2 times, the frequency change rate reaches the minimum, approximately −17%. Therefore, the overall stiffness of the bridge can be increased by adding auxiliary piers or auxiliary cables during the construction stage.

(3)

Changes in the stiffness of the main girder can induce, accordingly, the frequency change rate of the first-order torsion, the coupling of the first vertical bending and the lateral bending torsion can change basically linearly, and gradually increase.

(4)

The frequency change rates of the lateral bending torsion coupling are approximately linear, but the frequency variation rate of the pylon stiffness is the maximum. When the scaling ratio is 1.6, the frequency change rate is close to 90%.

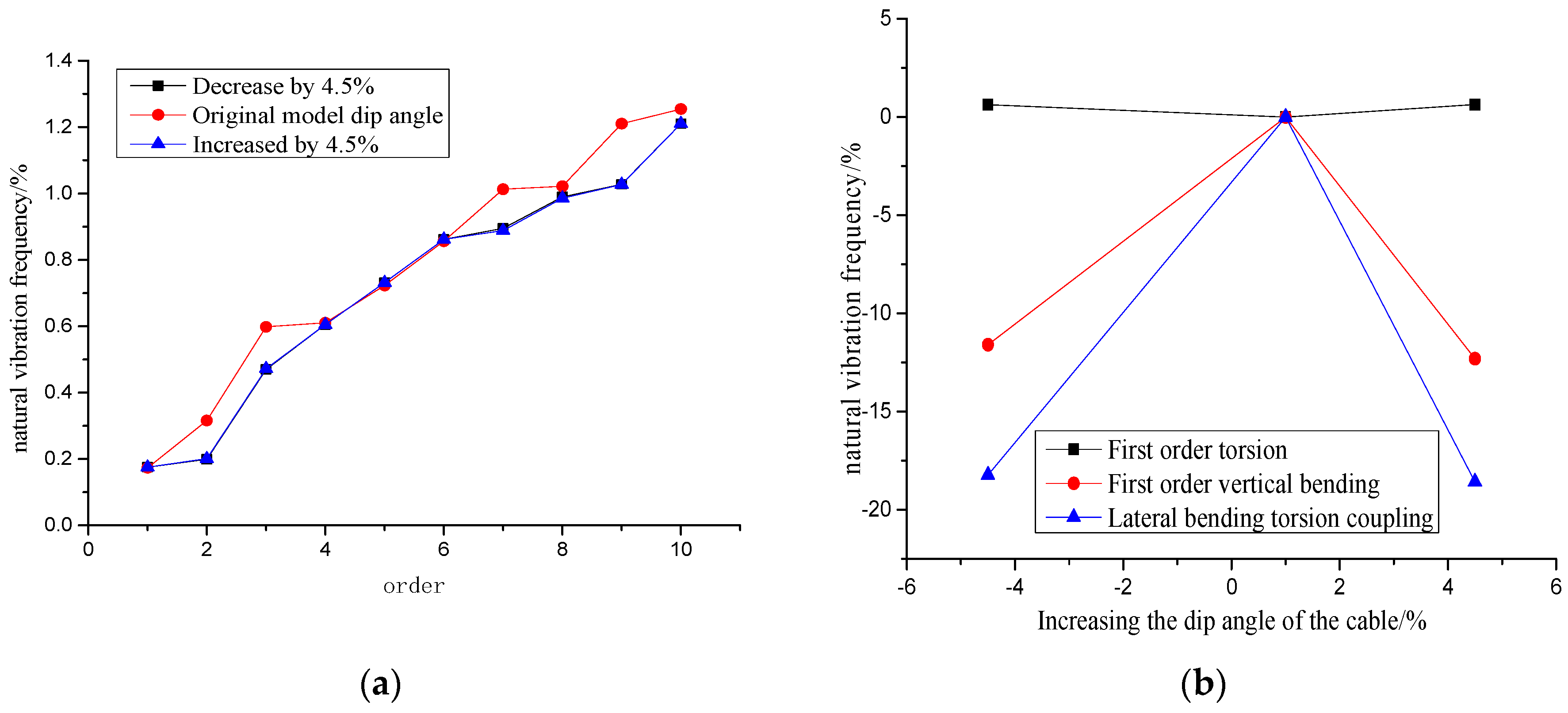
5.2. Inclination Angle Changes of Stayed Cables

The unique shape of this type of cable-stayed bridge in this paper has a wide field of vision, but also makes the mechanical properties of the cable-stayed bridge complicated and unique. Because the torsional stiffness decreases, the difficulty of construction increases accordingly. The effect of inclination angle changes on cables at the maximum cantilever state is not ignored. Therefore, it is necessary to analyze its effects on the dynamic characteristics of cable-stayed bridges.

The influence of inclination angles of the stayed cables is analyzed in three cases. Namely, compared with the original mode, the average inclination angle of cables changes from an increase of 4.5% to a decrease of 4.5%. The analysis results based on the original mode are shown in Figure 8.

Illustrate: 1th Order Means 1th Vibration Mode

It can be seen from Figure 8 that an increase or decrease in the inclination angle can change the first-order torsional stiffness of the structure, but the change is small. However, first-order vertical bending and lateral bending torsional vibration frequency decrease obviously, and the lateral bending torsional vibration mode has the greatest influence. The anchorage accuracy of stayed cables should be strictly controlled during the construction process, the independent inspection system should be established, the cables must be reliably fixed, and auxiliary facilities need to be checked carefully. In a modal analysis, different modes have different participation masses, participation coefficients, and direction factors in the X, Y, and Z directions. For example, in the participation coefficient, the first mode tran-x is −0.04 and tran-y is 18.03, while the second mode tran-x is 45.07 and tran-y is 0.03, which leads to different change rates of different modes under the same parameter, and the curve is not smooth enough, but the curve change trend is the same. Obviously, the change rate of the original cable angle from the first mode to the second mode is greater, which indicates that the dynamic characteristics of the original cable angle are more sensitive than those of the angle increased by 4.5% in the first and second modes.

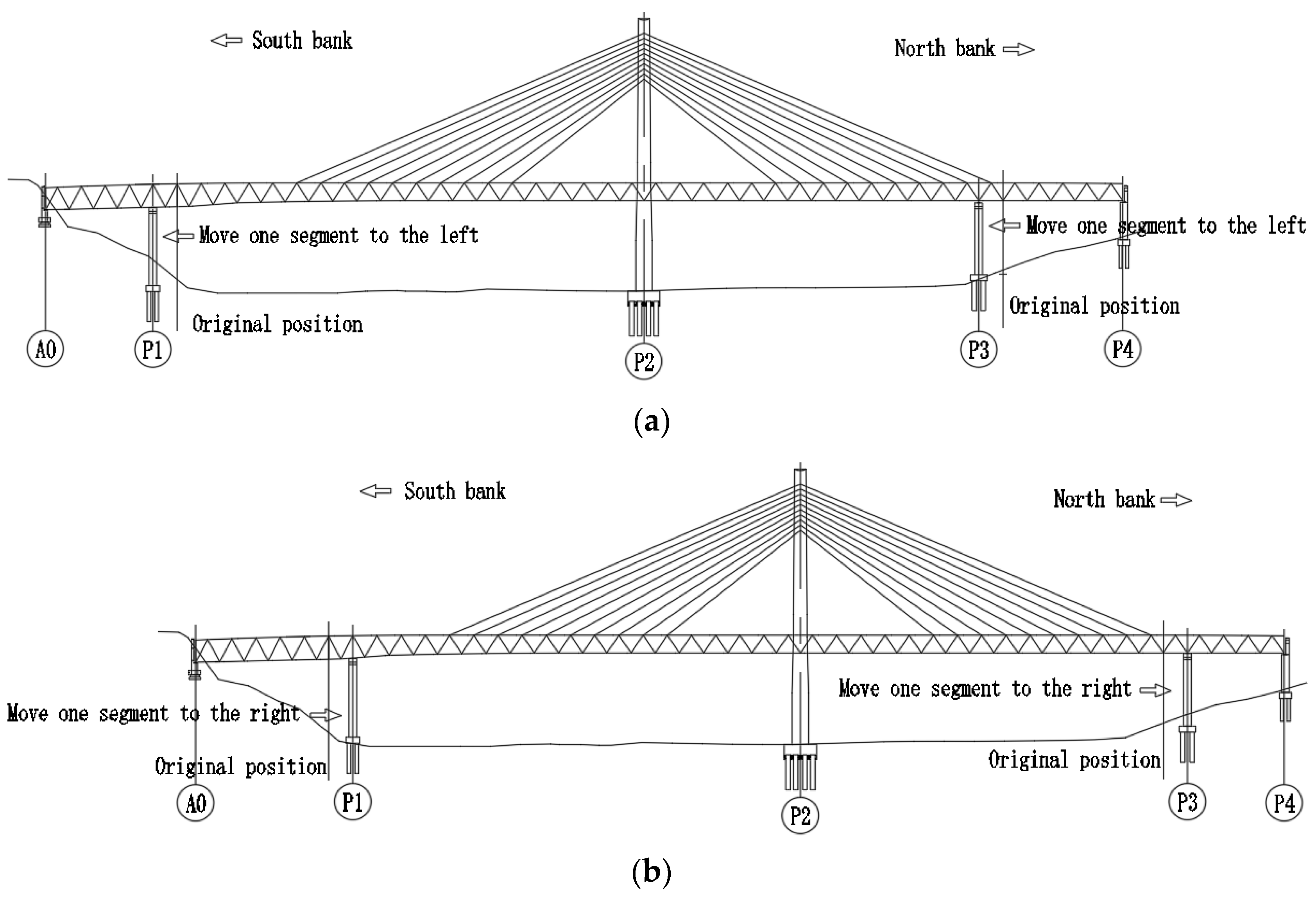
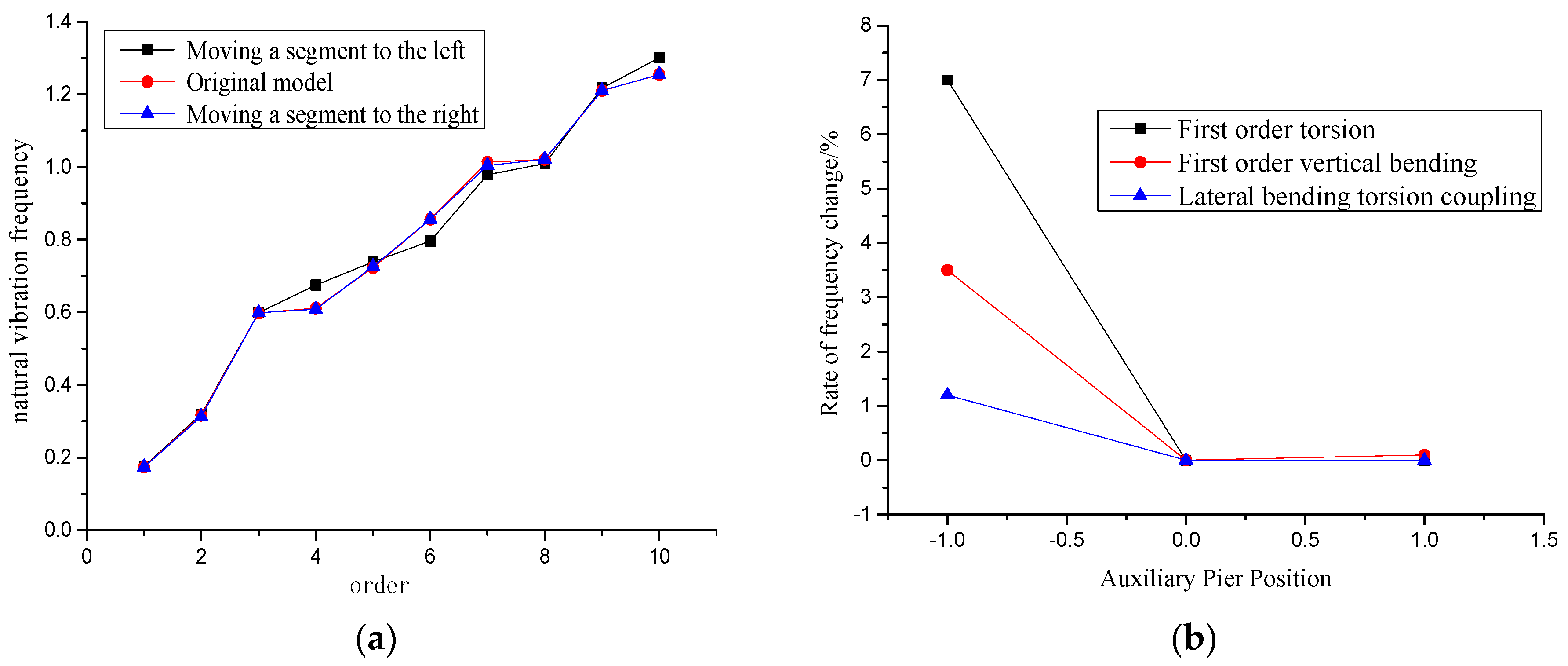
5.3. Position Change of Auxiliary Piers

The addition of auxiliary piers to the side span of a long-span cable-stayed bridge can eliminate the unfavourably dual cantilever state at the early stage of construction, but the setting of auxiliary piers may reduce the seismic performance of the structure. Different positions of auxiliary piers may cause different overall stiffnesses of a structure, and the ratio of the first-order torsion frequency and first-order vertical bending frequency of the structure will change, which change the possibility of flutter failure of a bridge. It is necessary to analyze the influence of the maximum cantilever state auxiliary piers’ position on the dynamic characteristics of the structure. The movement of auxiliary piers are shown in Figure 9, influences of auxiliary piers on the key natural frequencies are shown in Figure 10.

According to Figure 9 and Figure 10, the auxiliary pier’s position has little influence for the first ten orders of frequencies. The influence of the natural frequency is relatively large when the auxiliary pier moves to the left, which has the greatest influence on the first-order vertical bending, reaching 1.2%. The position adjustment of the auxiliary piers to the left has significant influence for the three main vibration modes of the cable-stayed bridge, but the position adjustment of the auxiliary piers to the right has little influence. If both sides of the main tower of the bridge are asymmetric, the longitudinal deviation of the auxiliary piers can emerge easily in the construction process.

6. Conclusions

(1)

Increasing the stiffness of the main girder is helpful to raise the torsional stiffness of the bridge and to enhance the wind resistance stability of the bridge. Increased rigidity of cables, pylons, and girders is helpful to improve the lateral flexural stiffness of structures, but the vertical bending stiffness of structures decreases accordingly with increases in bridge stiffness. However, when the stiffness of the pylon and main beam is 0.8 times that of the original structure, the vibration mode of the structure changes significantly. Slightly reducing the stiffness of the tower and main beam may have a significant impact on the wind resistance and seismic stability design of the bridge.

(2)

An adjustment in the inclination of stayed cables significantly reduces the vertical stiffness and lateral stiffness, and has little influence on the torsional vibration modes. Therefore, the inclination of stayed cables should be treated with great caution.

(3)

As the auxiliary piers moves one segment to the left, the natural frequency increases significantly, Moving one segment to the right, the increase in natural frequency is small. The reason is that when moving to the left of the auxiliary pier, P3 auxiliary pier is already under the stayed cables, reducing the tension of the cable, while the P1 pier is far away from the cable, increasing the tension of the cables. Therefore, the force on the bridge tower is unbalanced, resulting in an increase in the natural frequency of the bridge tower and the main beam, which affects the wind resistance stability of the bridge. Therefore, the location and quantity of auxiliary piers need to be carefully considered according to the actual situation.