Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation
Abstract
:1. Introduction
2. Problem Formulation
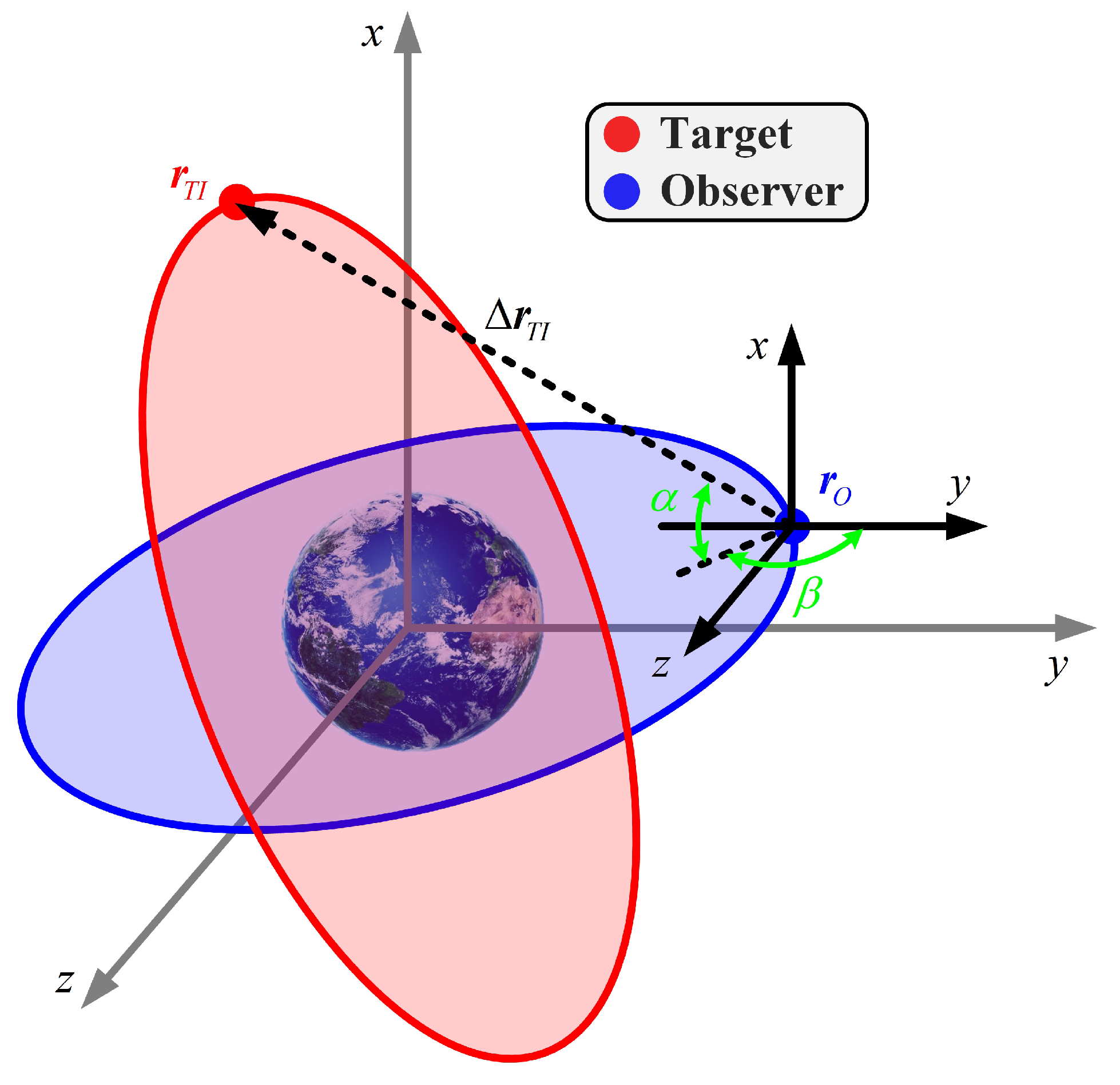
2.1. State Model
2.2. Measurement Model
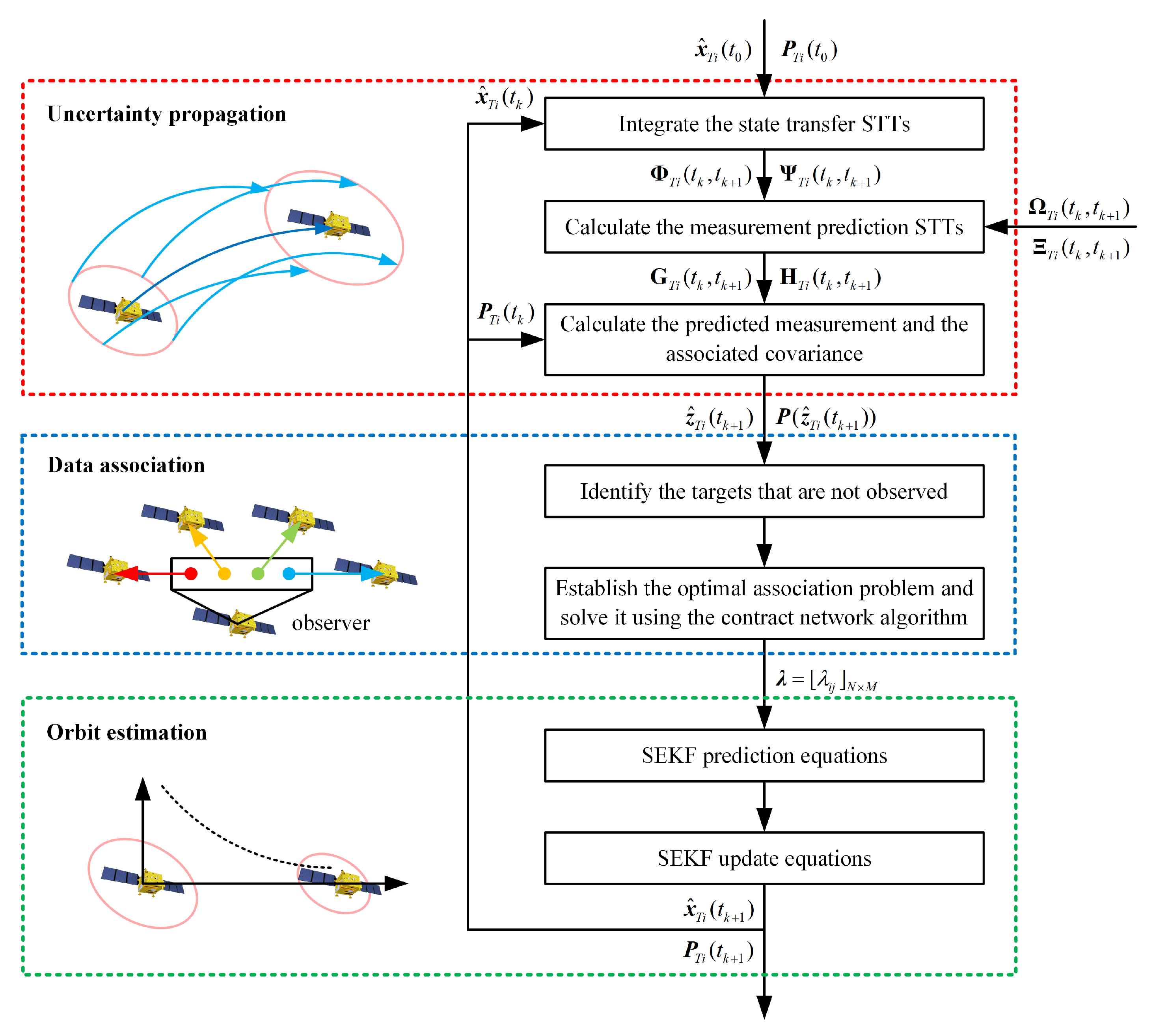
3. Methodology of the Multi-Spacecraft Tracking
3.1. Uncertainty Propagation
3.2. Data Association
3.3. Orbit Estimation
3.4. Overall Procedure
4. Numerical Simulation
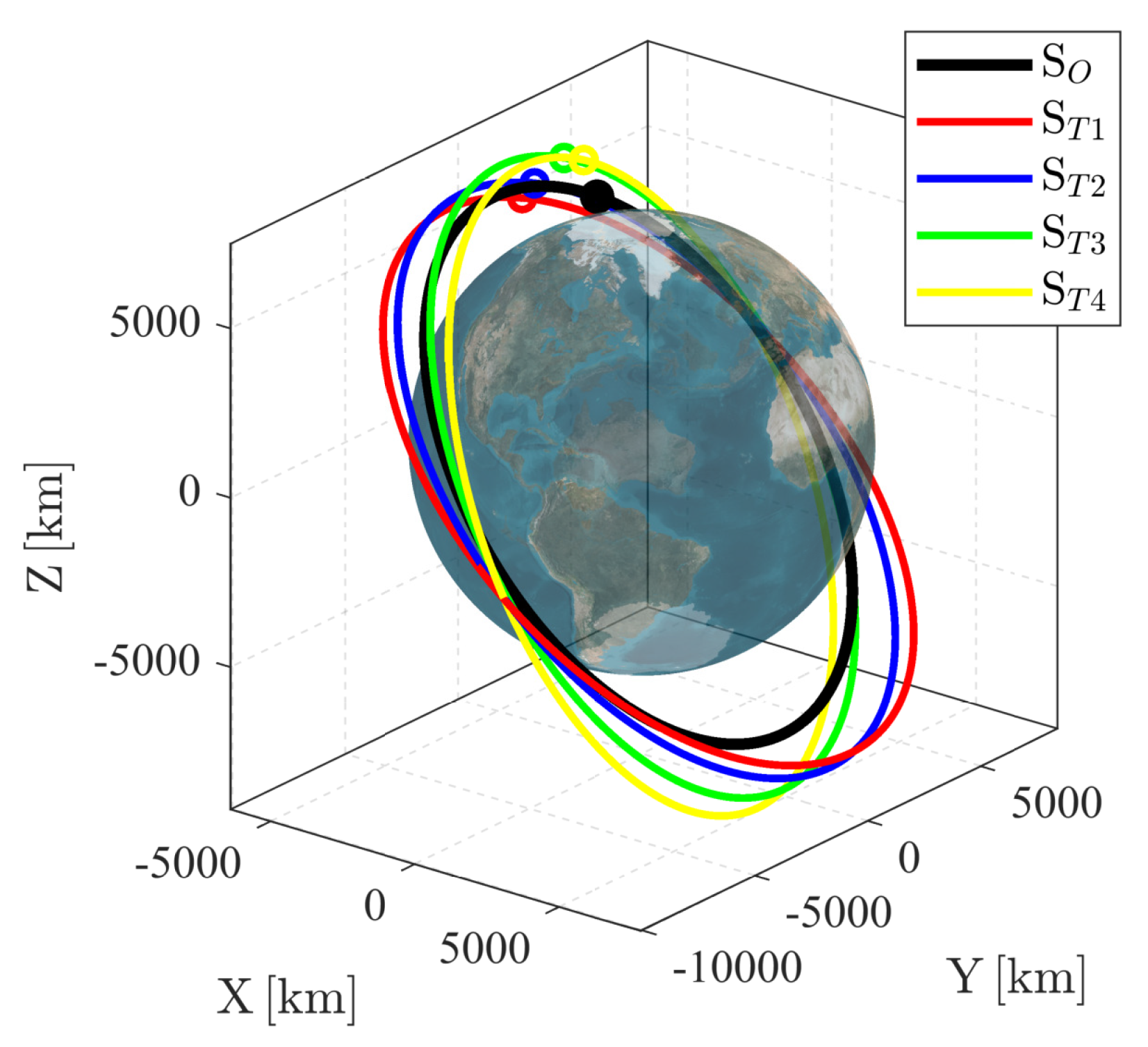
4.1. Scenario Design
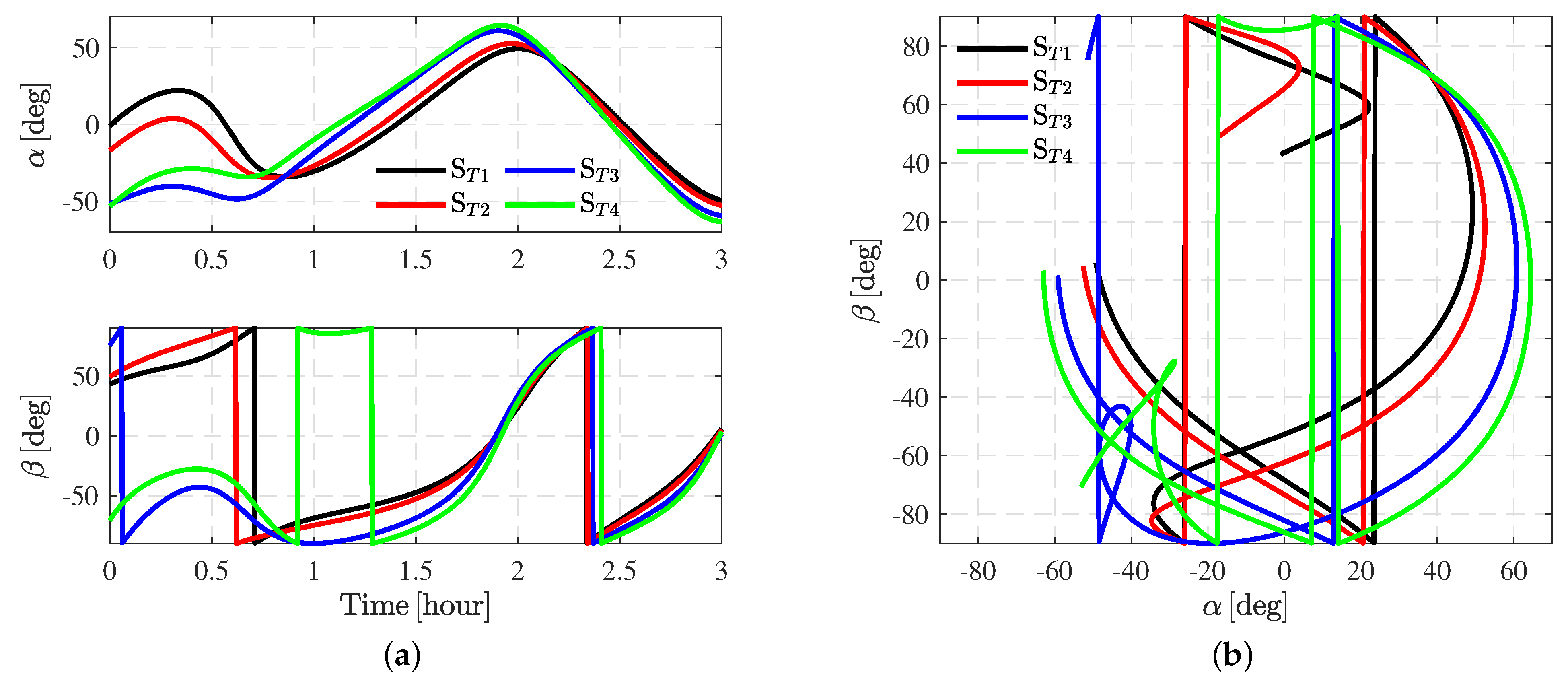
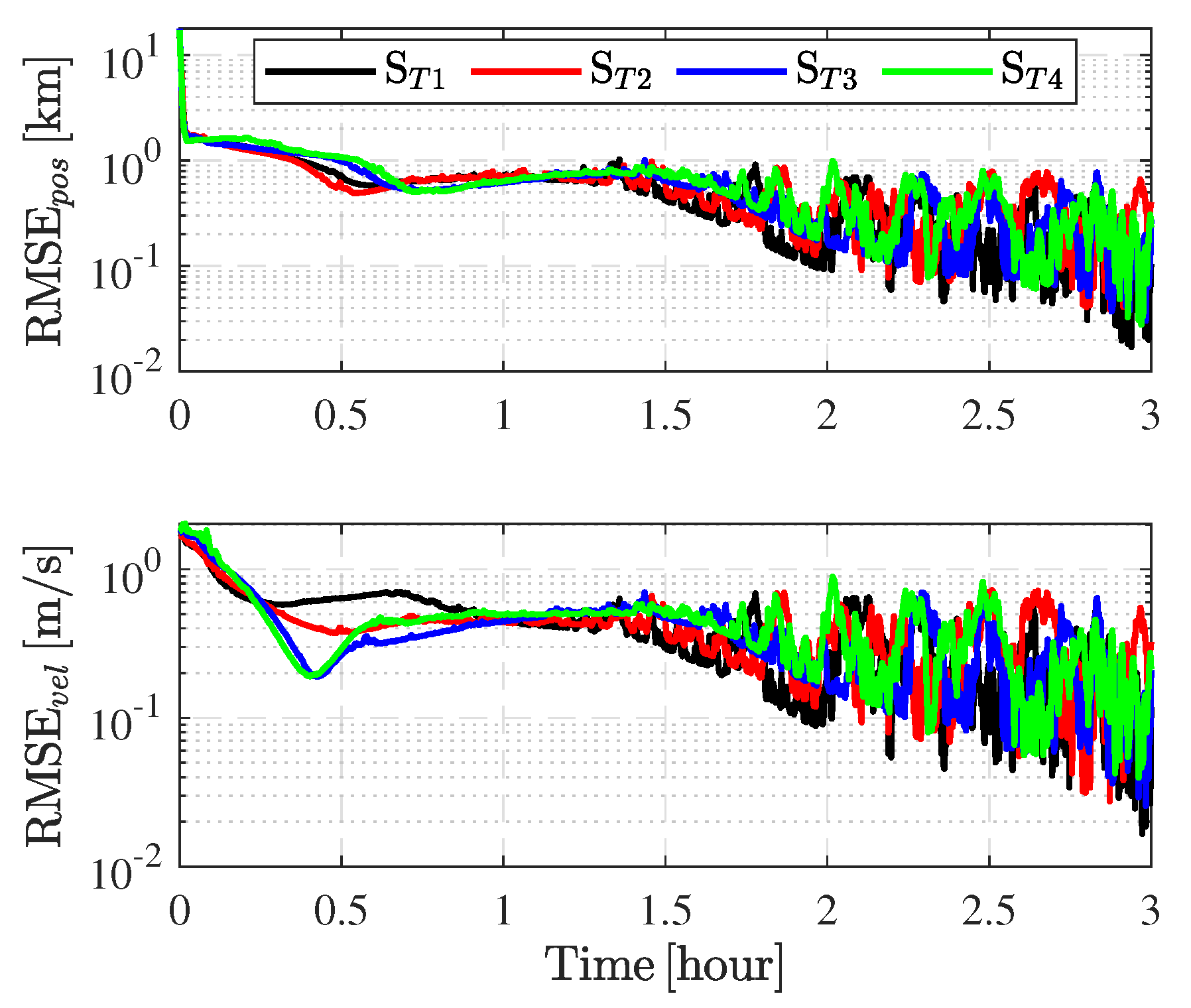
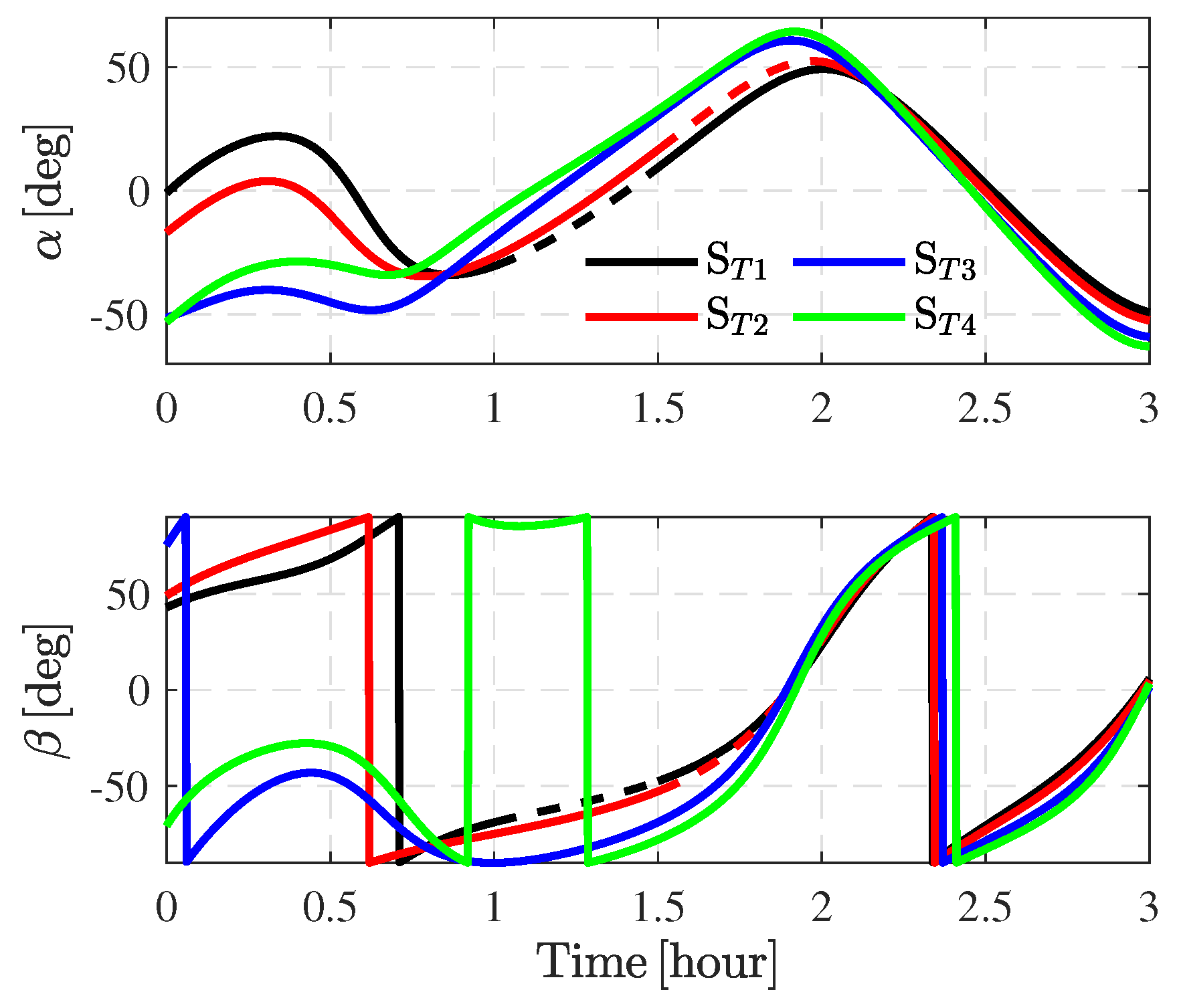
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, S.; Lee, J.; Hwang, I. Maneuvering spacecraft tracking via state-dependent adaptive estimation. J. Guid. Control Dyn. 2016, 39, 2034–2043. [Google Scholar] [CrossRef]
- Ko, H.C.; Scheeres, D.J. Tracking maneuvering satellite using thrust-fourier-coefficient event representation. J. Guid. Control Dyn. 2016, 39, 216–221. [Google Scholar] [CrossRef]
- Serra, R.; Yanez, C.; Frueh, C. Tracklet-to-orbit association for maneuvering space objects using optimal control theory. Acta Astronaut. 2021, 181, 271–281. [Google Scholar] [CrossRef]
- Luo, Y.; Qin, T.; Zhou, X. Observability Analysis and Improvement Approach for Cooperative Optical Orbit Determination. Aerospace 2022, 9, 166. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, X.; Zhao, Z.; Qin, T. Asteroid Approaching Orbit Optimization Considering Optical Navigation Observability. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Zhou, X.; Qin, T.; Meng, L. Maneuvering Spacecraft Orbit Determination Using Polynomial Representation. Aerospace 2022, 9, 257. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, W.; Qiao, D.; Li, X. Effect of orbital shadow at an Earth-Moon Lagrange point on relay communication mission. Sci. China Inf. Sci. 2017, 60, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Tang, Y.; Zhang, L.; Qiao, D. Design of communication relay mission for supporting lunar-farside soft landing. Sci. China Inf. Sci. 2018, 61, 040305. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Barucci, M.A. Analysis of equilibria in the doubly synchronous binary asteroid systems concerned with non-spherical shape. Astrodynamics 2018, 2, 133–146. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Li, P. Frozen orbit design and maintenance with an application to small body exploration. Aerosp. Sci. Technol. 2019, 92, 170–180. [Google Scholar] [CrossRef]
- Colagrossi, A.; Lavagna, M. Fault Tolerant Attitude and Orbit Determination System for Small Satellite Platforms. Aerospace 2022, 9, 46. [Google Scholar] [CrossRef]
- Li, L.-Q.; Xie, W.-X. Intuitionistic fuzzy joint probabilistic data association filter and its application to multitarget tracking. Signal Process. 2014, 96, 433–444. [Google Scholar] [CrossRef]
- Wen, H.; Fan, H.; Xie, W.; Pei, J. Hybrid Structure-Adaptive RBF-ELM Network Classifier. IEEE Access 2017, 5, 16539–16554. [Google Scholar] [CrossRef]
- Oussalah, M.; De Schutter, J. Hybrid fuzzy probabilistic data association filter and joint probabilistic data association filter. Inf. Sci. 2002, 142, 195–226. [Google Scholar] [CrossRef]
- Aziz, A.M. A new nearest-neighbor association approach based on fuzzy clustering. Aerosp. Sci. Technol. 2013, 26, 87–97. [Google Scholar] [CrossRef]
- Sutharsan, S.; Kirubarajan, T.; Lang, T.; Mcdonald, M. An Optimization-Based Parallel Particle Filter for Multitarget Tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1601–1618. [Google Scholar] [CrossRef] [Green Version]
- Habtemariam, B.; Tharmarasa, R.; Thayaparan, T.; Mallick, M.; Kirubarajan, T. A Multiple-Detection Joint Probabilistic Data Association Filter. IEEE J. Sel. Top. Signal Process. 2013, 7, 461–471. [Google Scholar] [CrossRef]
- Sathyan, T.; Chin, T.J.; Arulampalam, S.; Suter, D. A Multiple Hypothesis Tracker for Multitarget Tracking With Multiple Simultaneous Measurements. IEEE J. Sel. Top. Signal Process. 2013, 7, 448–460. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M. Sonar tracking of multiple targets using joint probabilistic data association. IEEE J. Ocean. Eng. 1983, 8, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Svensson, L.; Svensson, D.; Guerriero, M.; Willett, P. Set JPDA Filter for Multitarget Tracking. IEEE Trans. Signal Process. 2011, 59, 4677–4691. [Google Scholar] [CrossRef] [Green Version]
- Rong Li, X.; Bar-Shalom, Y. Tracking in clutter with nearest neighbor filters: Analysis and performance. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 995–1010. [Google Scholar] [CrossRef]
- Chen, X.; Tharmarasa, R.; Pelletier, M.; Kirubarajan, T. Integrated Bayesian Clutter Estimation with JIPDA/MHT Trackers. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 395–414. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Chen, H. Interplanetary transfer optimization using cost function with variable coefficients. Astrodynamics 2019, 3, 173–188. [Google Scholar] [CrossRef]
- Li, X.; Qiao, D.; Jia, F. Investigation of Stable Regions of Spacecraft Motion in Binary Asteroid Systems by Terminal Condition Maps. J. Astronaut. Sci. 2021, 68, 891–915. [Google Scholar] [CrossRef]
- Cui, P.Y.; Qiao, D.; Cui, H.T.; Luan, E.J. Target selection and transfer trajectories design for exploring asteroid mission. Sci. China Technol. Sci. 2010, 53, 1150–1158. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Qiao, D.; Mao, Q.; Jiang, J. Transfer to near-Earth asteroids from a lunar orbit via Earth flyby and direct escaping trajectories. Acta Astronaut. 2017, 133, 177–184. [Google Scholar] [CrossRef]
- Wang, Y.; Qiao, D.; Cui, P. Design of optimal impulse transfers from the Sun-Earth libration point to asteroid. Adv. Space Res. 2015, 56, 176–186. [Google Scholar] [CrossRef]
- Jia, F.; Li, X.; Huo, Z.; Qiao, D. Mission Design of an Aperture-Synthetic Interferometer System for Space-Based Exoplanet Exploration. Space Sci. Technol. 2022, 2022, 9835234. [Google Scholar] [CrossRef]
- Terejanu, G.; Singla, P.; Singh, T.; Scott, P.D. Adaptive Gaussian Sum Filter for Nonlinear Bayesian Estimation. IEEE Trans. Autom. Control 2011, 56, 2151–2156. [Google Scholar] [CrossRef]
- Gelb, A.; Warren, R.S. Direct statistical analysis of nonlinear systems: CADET. AIAA J. 1973, 11, 689–694. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, Z.; Liu, L. Unscented Kalman filter for spacecraft pose estimation using twistors. J. Guid. Control Dyn. 2016, 39, 1844–1856. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M. Active Sampling Based Polynomial-Chaos–Kriging Model for Orbital Uncertainty Propagation. J. Guid. Control Dyn. 2021, 44, 905–922. [Google Scholar] [CrossRef]
- Park, R.S.; Scheeres, D.J. Nonlinear semi-analytic methods for trajectory estimation. J. Guid. Control Dyn. 2007, 30, 1668–1676. [Google Scholar] [CrossRef] [Green Version]
- Roa, J.; Park, R.S. Reduced nonlinear model for orbit uncertainty propagation and estimation. J. Guid. Control Dyn. 2021, 44, 1578–1592. [Google Scholar] [CrossRef]
- Boone, S.; McMahon, J. Orbital guidance using higher-order state transition tensors. J. Guid. Control Dyn. 2021, 44, 493–504. [Google Scholar] [CrossRef]
- Fritsch, G.S.; Demars, K.J. Nonlinear gaussian mixture filtering with intrinsic fault resistance. J. Guid. Control Dyn. 2021, 44, 2172–2185. [Google Scholar] [CrossRef]
- Yang, Z.; Luo, Y.Z.; Lappas, V.; Tsourdos, A. Nonlinear analytical uncertainty propagation for relative motion near J2-perturbed elliptic orbits. J. Guid. Control Dyn. 2018, 41, 888–903. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Luo, Y.Z.; Zhang, J. Nonlinear semi-analytical uncertainty propagation of trajectory under impulsive maneuvers. Astrodynamics 2019, 3, 61–77. [Google Scholar] [CrossRef]
- Zhou, X.; Cheng, Y.; Qiao, D.; Huo, Z. An adaptive surrogate model-based fast planning for swarm safe migration along halo orbit. Acta Astronaut. 2022, 194, 309–322. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Wang, N.; Hoque, M.; Wang, L.; Li, R.; Zhang, Y.; Yuan, H. Real-Time Precise Orbit Determination for LEO between Kinematic and Reduced-Dynamic with Ambiguity Resolution. Aerospace 2022, 9, 25. [Google Scholar] [CrossRef]
- De Weck, O.L.; Scialom, U.; Siddiqi, A. Optimal reconfiguration of satellite constellations with the auction algorithm. Acta Astronaut. 2008, 62, 112–130. [Google Scholar] [CrossRef]
- Zhen, Z.; Wen, L.; Wang, B.; Hu, Z.; Zhang, D. Improved contract network protocol algorithm based cooperative target allocation of heterogeneous UAV swarm. Aerosp. Sci. Technol. 2021, 119, 107054. [Google Scholar] [CrossRef]
- Qin, T.; Qiao, D.; Macdonald, M. Relative orbit determination using only intersatellite range measurements. J. Guid. Control Dyn. 2019, 42, 703–710. [Google Scholar] [CrossRef]
- Qin, T.; Qiao, D.; Macdonald, M. Relative orbit determination for unconnected spacecraft within a constellation. J. Guid. Control Dyn. 2021, 44, 614–621. [Google Scholar] [CrossRef]
- Qin, T.; Macdonald, M.; Qiao, D. Fully Decentralized Cooperative Navigation for Spacecraft Constellations. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2383–2394. [Google Scholar] [CrossRef]


| a/km | e | i/ | / | / | n/ | ||
|---|---|---|---|---|---|---|---|
| Observer | S | 8362 | 0.1007 | 53.60 | 100.60 | 33.00 | 21.51 |
| Target | S | 9381 | 0.1498 | 43.60 | 103.1 | 42.00 | 22.02 |
| S | 9406 | 0.1398 | 48.60 | 103.6 | 42.00 | 22.02 | |
| S | 9456 | 0.1198 | 58.60 | 104.6 | 42.00 | 22.02 | |
| S | 9481 | 0.1098 | 63.60 | 105.1 | 42.00 | 22.02 |
| [−0.5569, 43.1841] | [−16.6373, 49.4247] | [−51.2908, 76.0587] | [−52.8157, −70.0077] | ||
|---|---|---|---|---|---|
| [−0.8393, 43.1550] | 0.6922 | ||||
| [−17.0700, 49.4502] | 0.4117 | ||||
| [−51.7809, 76.4379] | 0.1785 | ||||
| [−53.1513, −69.3724] | 0.1933 |
| [42.3691, 61.2692] | [42.2580, 63.1710] | [41.5619, 66.5737] | [44.3305, 64.0263] | ||
|---|---|---|---|---|---|
| [42.3522, 61.2866] | 0.8767 | 0.1544 | 0.0032 | ||
| [42.2656, 63.1609] | 0.1499 | 0.8682 | 0.0022 | 0.0721 | |
| [41.5623, 66.5585] | 0.0023 | 0.8544 | 0.0008 | ||
| [44.3387, 64.0293] | 0.0029 | 0.0709 | 0.0008 | 0.8576 |
| S | S | S | S | |
|---|---|---|---|---|
| Position/km | 0.6181 | 0.6108 | 0.7004 | 0.7072 |
| Velocity/(m/s) | 0.4487 | 0.4197 | 0.4594 | 0.4514 |
| S | S | |
|---|---|---|
| Position/km | 0.6147 | 0.6169 |
| Velocity/(m/s) | 0.4309 | 0.4078 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, S.; Qin, T. Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation. Appl. Sci. 2022, 12, 7660. https://doi.org/10.3390/app12157660
Zhou X, Wang S, Qin T. Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation. Applied Sciences. 2022; 12(15):7660. https://doi.org/10.3390/app12157660
Chicago/Turabian StyleZhou, Xingyu, Shuo Wang, and Tong Qin. 2022. "Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation" Applied Sciences 12, no. 15: 7660. https://doi.org/10.3390/app12157660
APA StyleZhou, X., Wang, S., & Qin, T. (2022). Multi-Spacecraft Tracking and Data Association Based on Uncertainty Propagation. Applied Sciences, 12(15), 7660. https://doi.org/10.3390/app12157660






