On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations
Abstract
:1. Introduction
2. Seismological Data and Earthquake Sequence Analysis
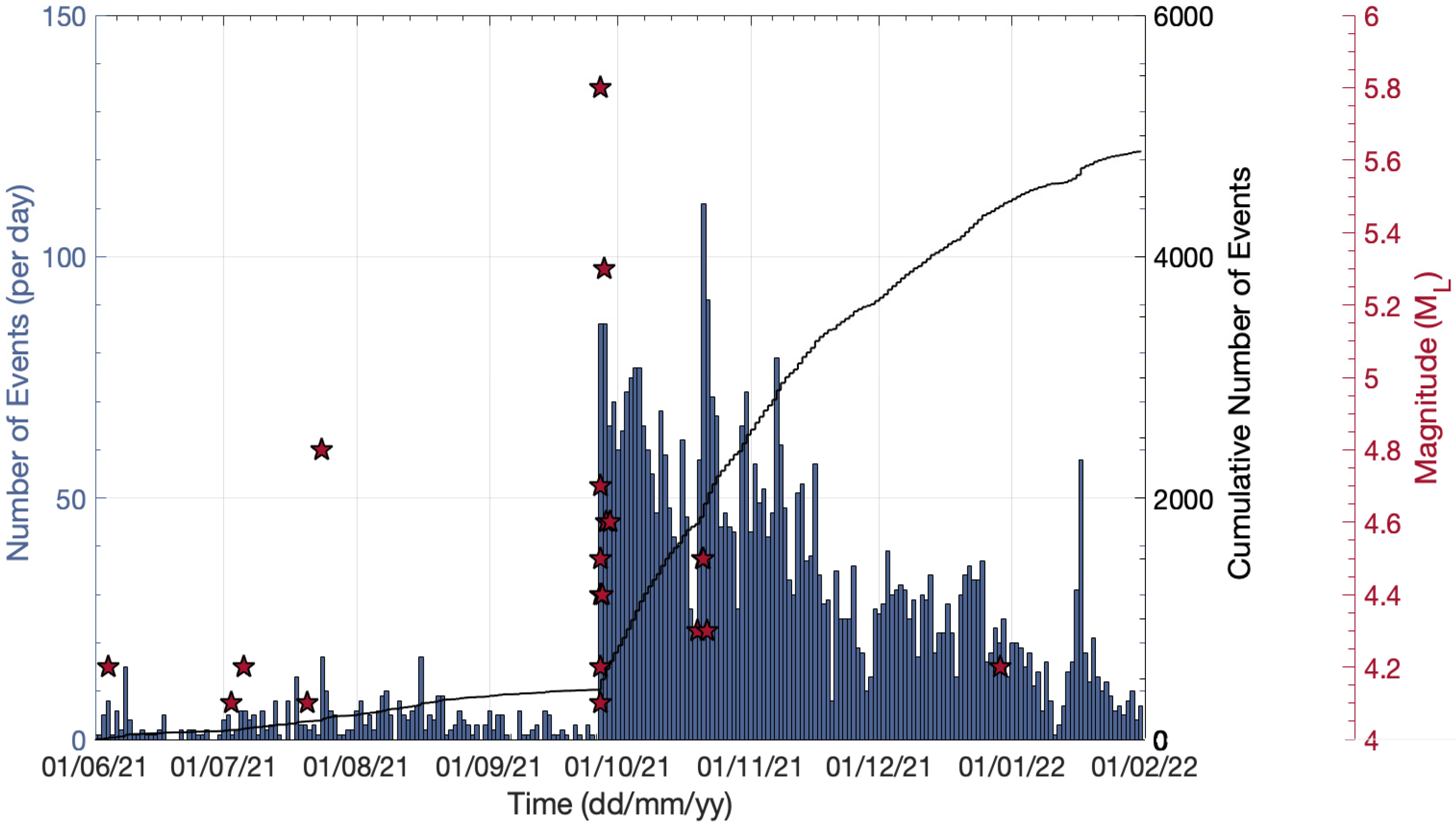
2.1. Data Analysis
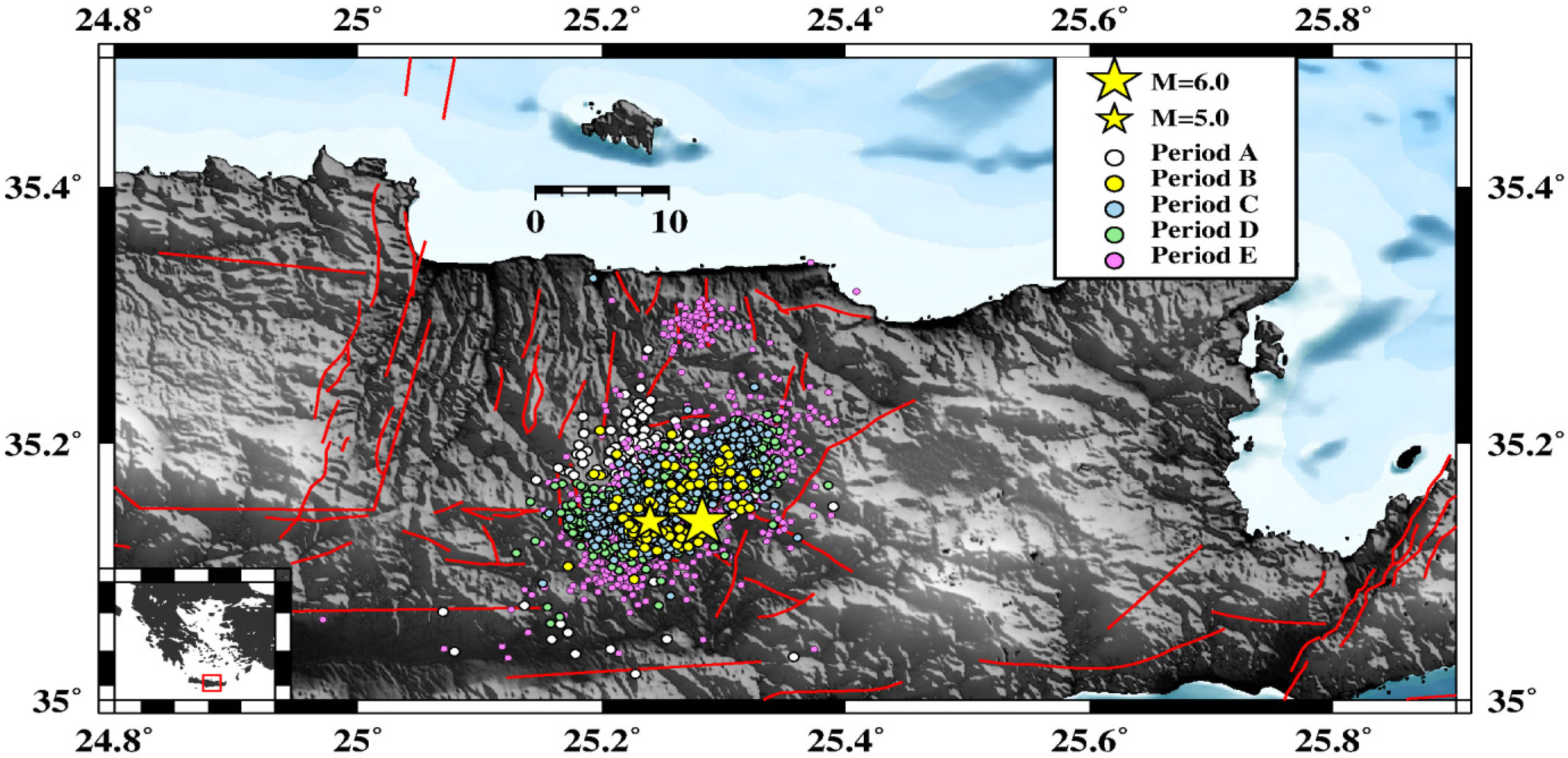
- 13 January–27 September 2021 (period A), consisting of 620 events;
- 27 September–28 September 2021 (period B), the first day of the aftershock sequence and just a few hours before the greatest aftershock (M5.3), composed of 90 events;
- 28 September–12 October 2021 (period C), just after the occurrence of the M = 5.3 aftershock at 04:48 UTC, consisting of 803 events;
- 12 October–31 October 2021 (period D), where the M = 4.0 event took place after a significant decay in the aftershocks number in Arkalochori;
- 1 November–31 January 2022 (period E), which comprises small to moderate magnitude events in a deeper part of the crust (H > 20 km) located near Herakleion.
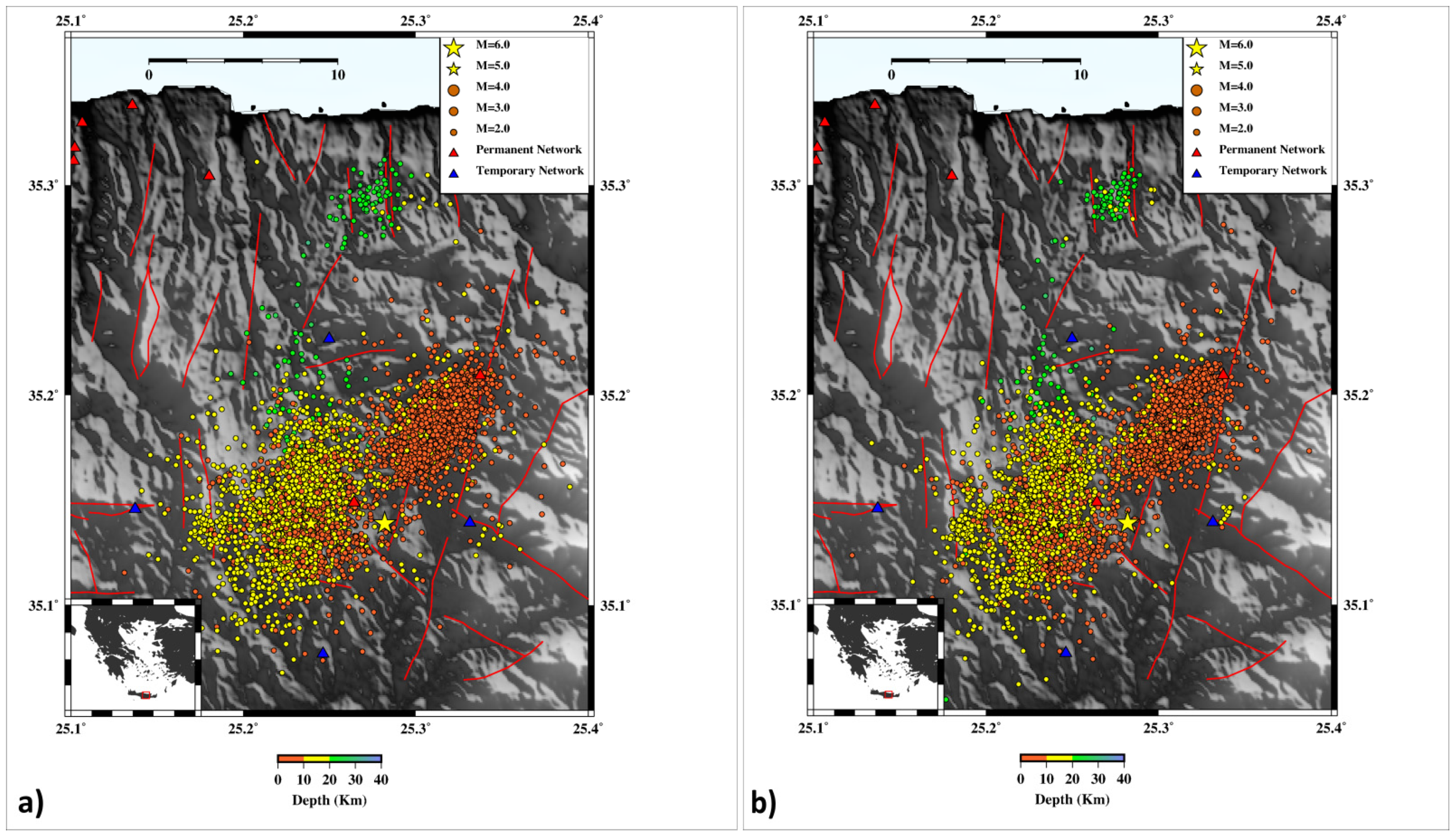
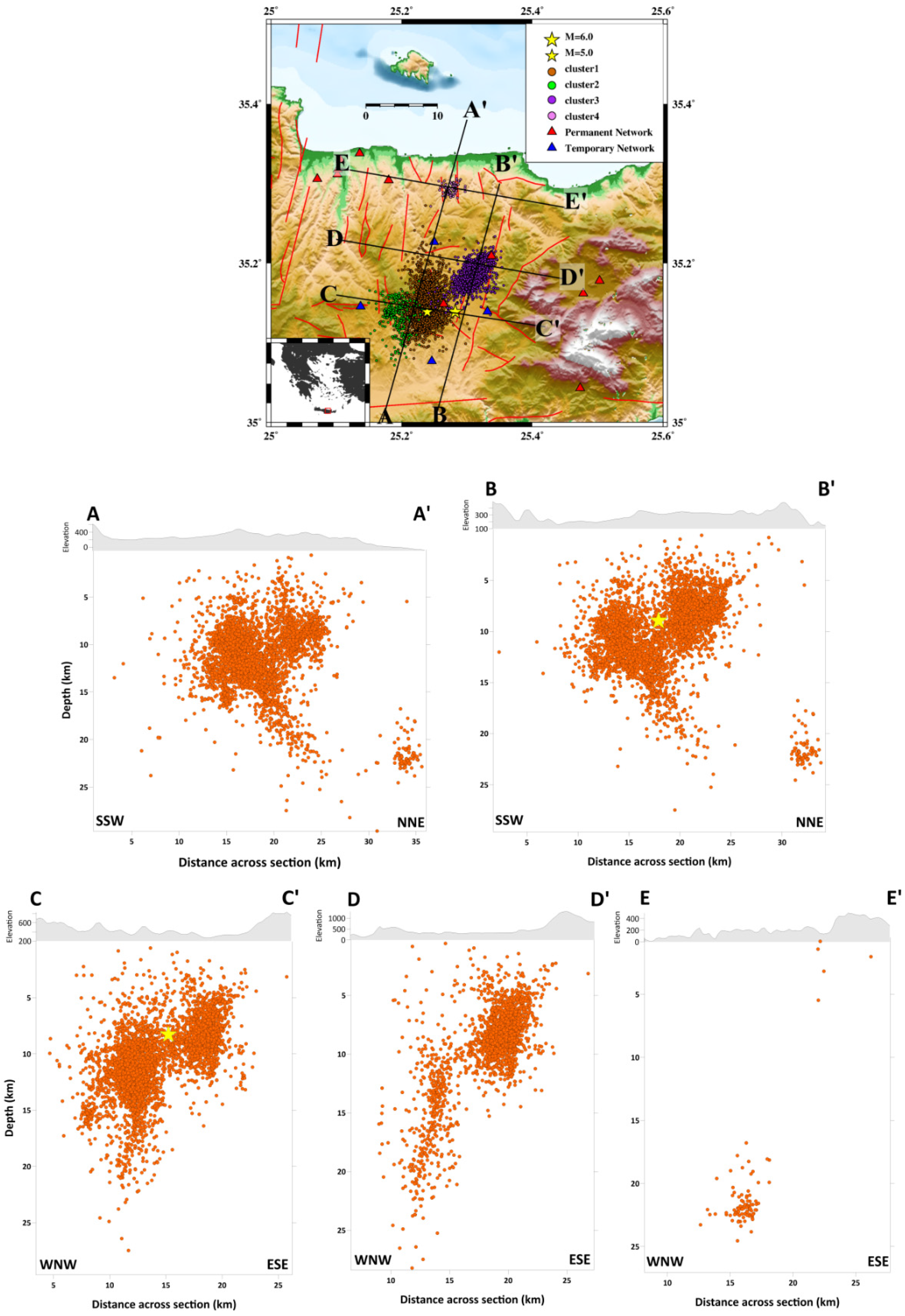
2.2. Hypocentral Relocation of the Earthquake Sequence
3. Travel Time Tomography
4. Co-Seismic Ground Deformation
4.1. Interferometric Data and Results
4.2. GNSS Data and Results
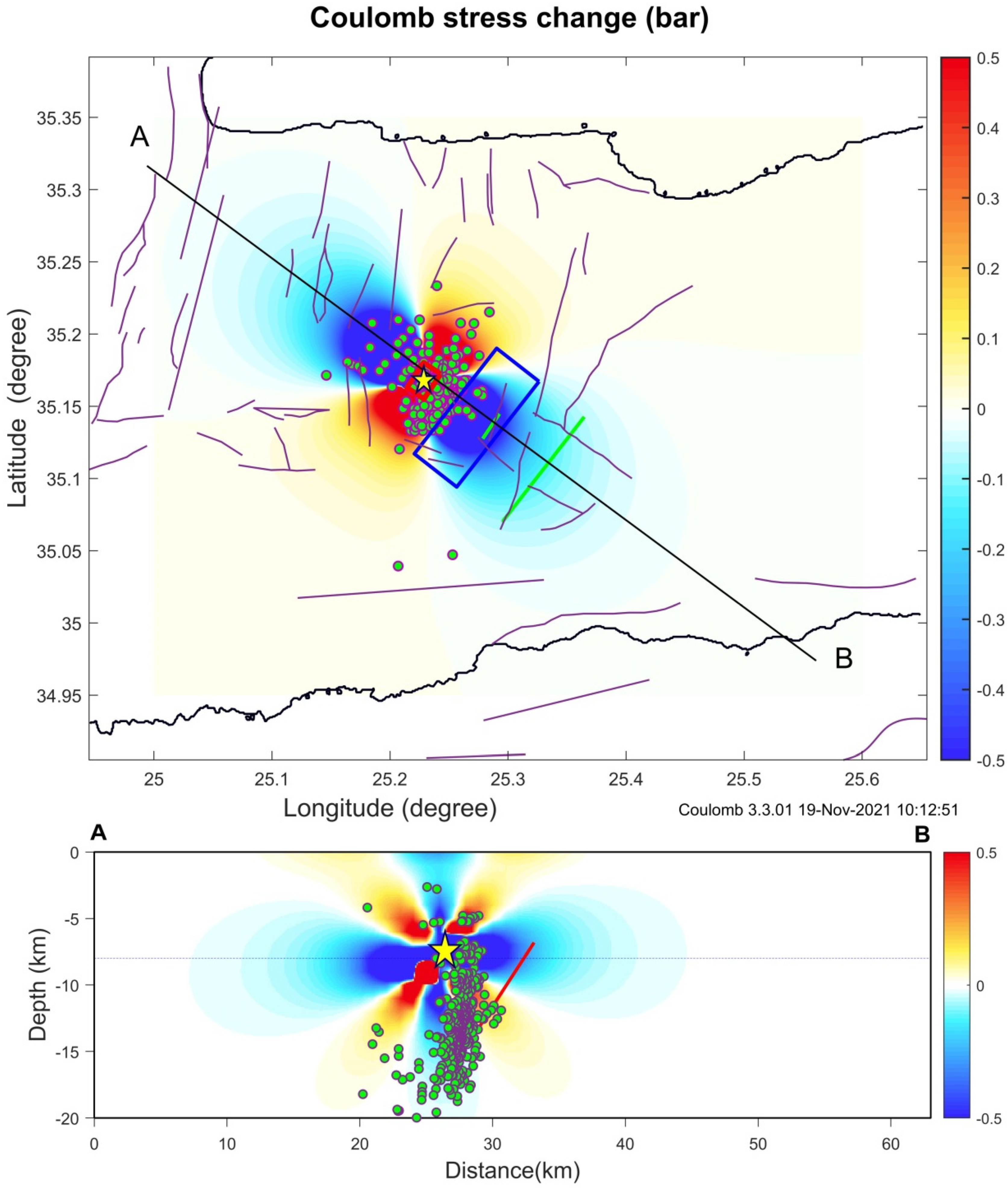
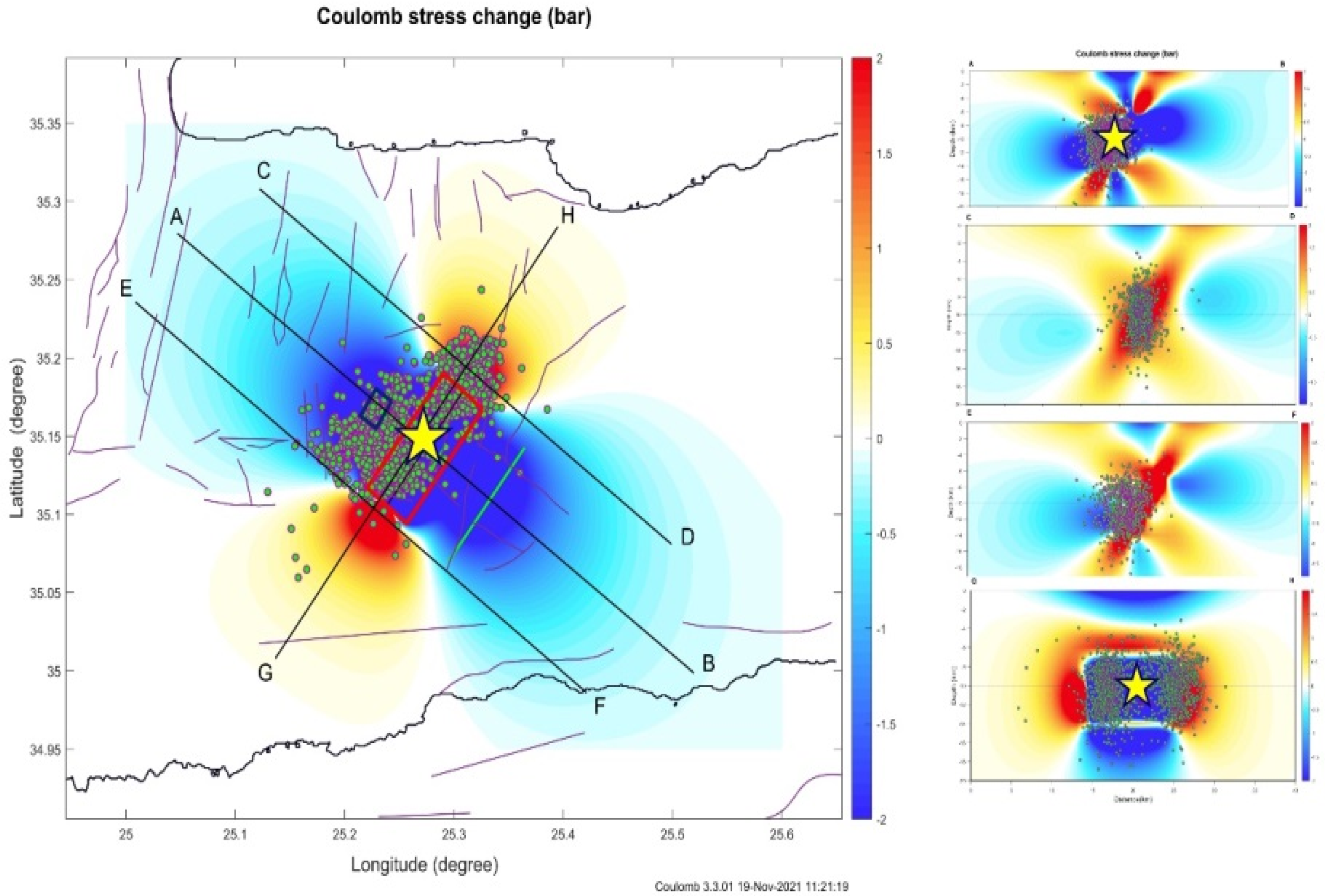
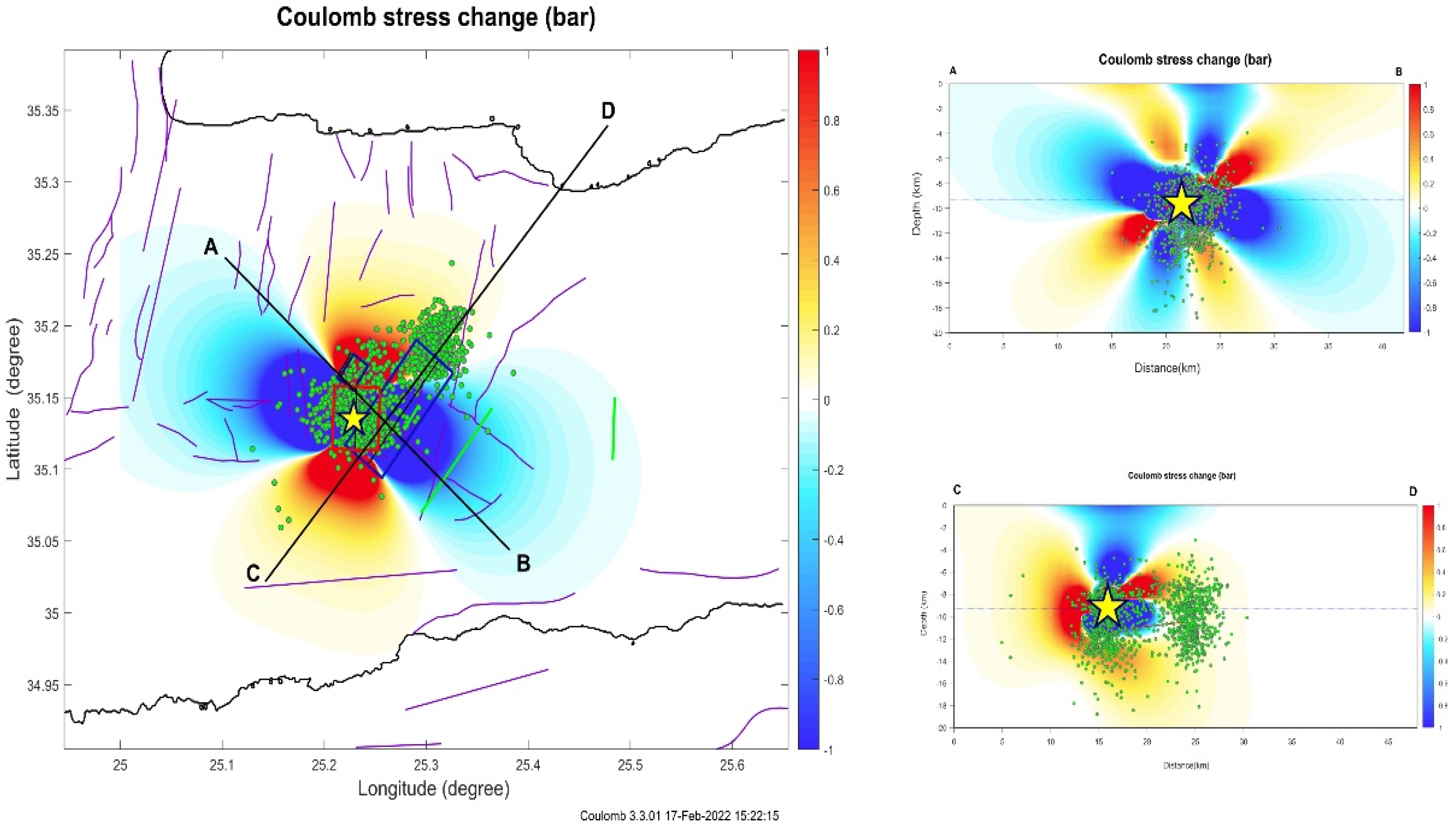
5. Spatial Footprint of Coulomb Stress Changes
6. Frequency-Magnitude Scaling Properties of the Foreshock and Aftershock Sequences in Terms of Non-Extensive Statistical Physics
7. Temporal Properties of the Aftershock Sequence
7.1. Aftershock Production Rate and Modelling
7.2. The Interevent Times Distributions for the Foreshock and Aftershock Sequences
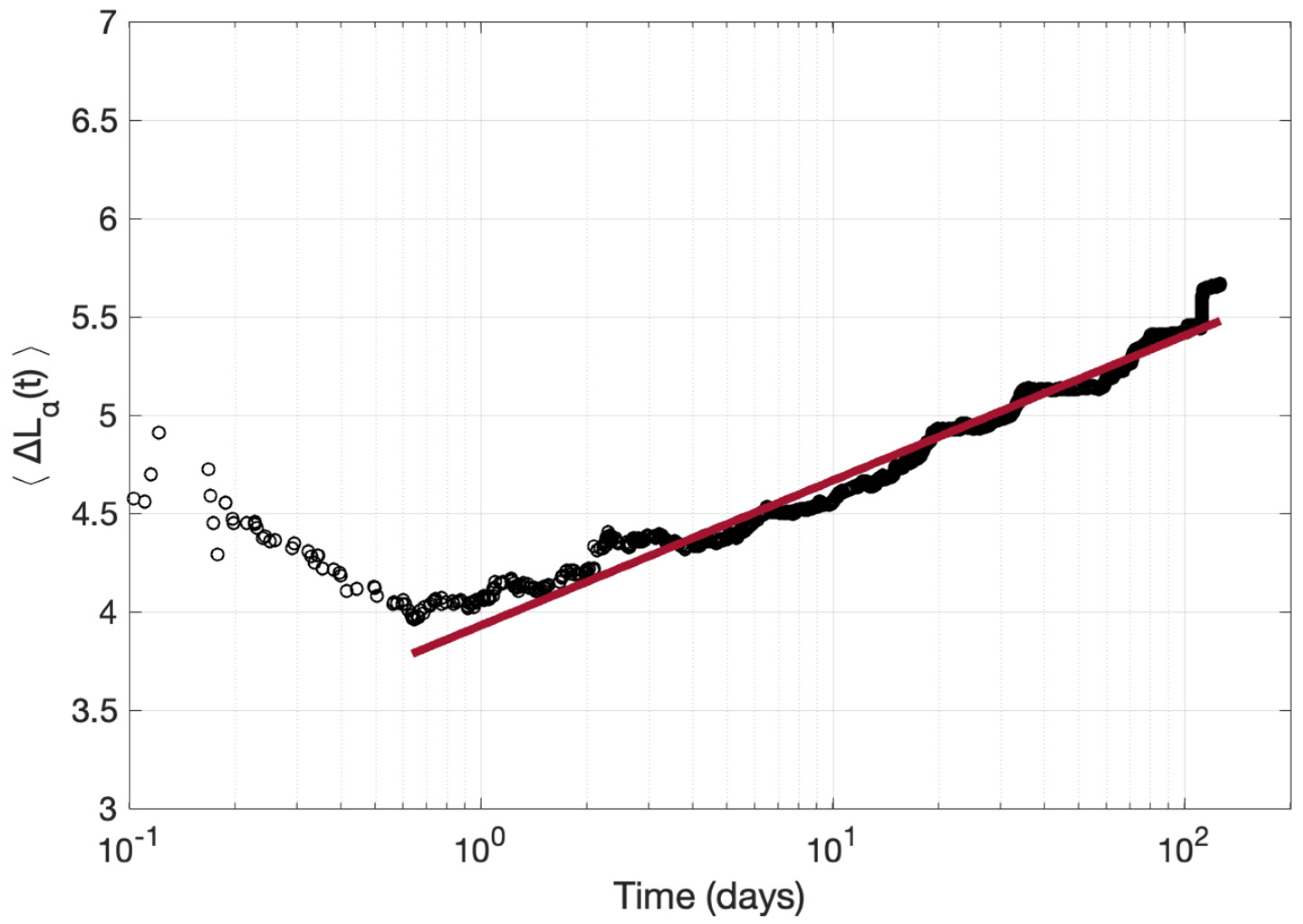
7.3. Scaling of the Aftershocks Focal Zone with Time
8. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delibasis, N.; Drakopoulos, J.K.; Fytrolakis, N.; Katsikatsos, G.; Makropoulos, K.C.; Zamani, A. Seismotectonic Investigation of the area of Crete Island. Proc. Intern. Symp. Hellenic Arc. Trench. 1981, 1, 121–138. [Google Scholar]
- Drakopoulos, J.; Delibasis, N. The focal mechanism of earthquakes in the major area of Greece for the period 1947–1981. Seismol. Lab. Univ. Athens Publ. 1982, 2, 1–72. [Google Scholar]
- Ganas, A.; Parsons, T. Three-dimensional model of Hellenic Arc deformation and origin of the Cretan uplift. J. Geophys. Res. 2009, 114, B06404. [Google Scholar] [CrossRef] [Green Version]
- Kiratzi, A.; Benetatos, C.; Vallianatos, F. Seismic Deformation Derived from Moment Tensor Summation: Application Along the Hellenic Trench (Book Chapter). In Moment Tensor Solutions; D’Amico, S., Ed.; Springer Natural Hazards; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Karakostas, V.; Mesimeri, M.; Vallianatos, F. The Mw 6.7 12 October 2013 western Hellenic Arc main shock and its aftershock sequence: Implications for the slab properties. Int. J. Earth Sci. 2016, 105, 2149–2160. [Google Scholar] [CrossRef]
- Ten Veen, J.H.; Meijer, P.T. Late Miocene to recent tectonic evolution of Crete (Greece): Geological observations and model analysis. Tectonophysics 1998, 298, 191–208. [Google Scholar] [CrossRef]
- Papanikolaou, D.; Vassilakis, E. Thrust faults and extensional detachment faults in Cretan tectono-stratigraphy: Implications for Middle Miocene extension. Tectonophysics 2010, 488, 233–247. [Google Scholar] [CrossRef]
- Fassoulas, C. The tectonic development of a Neogene basin at the leading edge of the active European margin: The Heraklion basin, Crete, Greece. J. Geodyn. 2001, 31, 49–70. [Google Scholar] [CrossRef]
- Caputo, R.; Catalano, S.; Monaco, C.; Romagnoli, R.; Tortorici, G.; Tortorici, L. Active faulting on the island of Crete (Greece). Geophys. J. Int. 2010, 183, 111–126. [Google Scholar] [CrossRef]
- Caputo, R.; Catalano, S.; Monaco, C.; Romagnoli, G. Middle-late quaternary geodynamics of Crete, southern Aegean, and seismotectonic implications. Bull. Geol. Soc. Greece 2010, 43, 400–408. [Google Scholar] [CrossRef] [Green Version]
- Ganas, A.; Kourkouli, P.; Briole, P.; Moshou, A.; Elias, P.; Parcharidis, I. Coseismic Displacements from Moderate-Size Earthquakes Mapped by Sentinel-1 Differential Interferometry: The Case of February 2017 Gulpinar Earthquake Sequence (Biga Peninsula, Turkey). Remote Sens. 2018, 10, 1089. [Google Scholar] [CrossRef] [Green Version]
- Mason, J.; Reicherter, K. The palaeoseismological study of capable faults on Crete. In Minoan Earthquakes-Breaking the Myth through Interdisciplinarity, 1st ed.; Jusseret, S., Sintubin, M., Eds.; Leuven University Press: Leuven, Belgium, 2017; pp. 191–216. [Google Scholar]
- Vassilakis, E. Study of the Tectonic Structure of the Messara Basin, Central Crete, With the AID of Remote Sensing Techniques and G.I.S. Ph.D. Thesis, National and Kapodistrian University of Athens, Athens, Greece, 2006; p. 564. [Google Scholar]
- Ganas, A.; Elias, P.; Kapetanidis, V.; Valkaniotis, S.; Briole, P.; Kassaras, I.; Argyrakis, P.; Barberopoulou, A.; Moshou, A. The 20 July 2017 M6.6 Kos Earthquake: Seismic and Geodetic Evidence for an Active North-Dipping Normal Fault at the Western End of the Gulf of Gökova (SE Aegean Sea). Pure Appl. Geophys. 2019, 176, 4177–4211. [Google Scholar] [CrossRef]
- Zygouri, V.; Koukouvelas, I.; Ganas, A. Palaeoseismological analysis of the East Giouchtas fault, Heraklion basin, Crete (preliminary results). Bull. Geol. Soc. Greece 2016, 50, 563–571. [Google Scholar] [CrossRef] [Green Version]
- Stucchi, M.; Rovida, A.; Gomez Capera, A.A.; Alexandre, P.; Camelbeeck, T.; Demircioglu, M.B.; Gasperini, P.; Kouskouna, V.; Musson, R.M.W.; Radulian, M.; et al. The SHARE European Earthquake Catalogue (SHEEC) 1000–1899. J. Seismol. 2013, 17, 523–544. [Google Scholar] [CrossRef] [Green Version]
- Papazachos, B.C.; Papazachou, C.B. The Earthquakes of Greece; Ziti: Thessaloniki, Greece, 2003; p. 304. [Google Scholar]
- Guidoboni, E.; Comastri, A. Catalogue of Earthquakes and Tsunamis in the Mediterranean Area from the 11th to the 15th Century; INGV-SGA: Rome, Italy, 2005; p. 1037. [Google Scholar]
- Vallianatos, F.; Michas, G.; Hloupis, G.; Chatzopoulos, G. The Evolution of Preseismic Patterns Related to the Central Crete (Mw6.0) Strong Earthquake on 27 September 2021 Revealed by Multiresolution Wavelets and Natural Time Analysis. Geosciences 2022, 12, 33. [Google Scholar] [CrossRef]
- ITSAK. Arkalochori Earthquakes, Μ 6.0 on 27/09/2021 & Μ 5.3 on 28/09/2021: Preliminary Report—Recordings of the ITSAK Accelerometric Network and Damage on the Natural and Built Environment; ITSAK Research Unit: Thessaloniki, Greece, 2021; p. 44. [Google Scholar]
- Triantafyllou, I.; Karavias, A.; Koukouvelas, I.; Papadopoulos, G.A.; Parcharidis, I. The Crete Isl. (Greece) Mw6.0 Earthquake of 27 September 2021: Expecting the Unexpected. GeoHazards 2022, 3, 106–124. [Google Scholar] [CrossRef]
- Vassilakis, E.; Kaviris, G.; Kapetanidis, V.; Papageorgiou, E.; Foumelis, M.; Konsolaki, A.; Petrakis, S.; Evangelidis, C.P.; Alexopoulos, J.; Karastathis, V.; et al. The 27 September 2021 Earthquake in Central Crete (Greece)—Detailed Analysis of the Earthquake Sequence and Indications for Contemporary Arc-Parallel Extension to the Hellenic Arc. Appl. Sci. 2022, 12, 2815. [Google Scholar] [CrossRef]
- Ganas, A.; Hamiel, Y.; Serpetsidaki, A.; Briole, P.; Valkaniotis, S.; Fassoulas, C.; Piatibratova, O.; Kranis, H.; Tsironi, V.; Karamitros, I.; et al. The Arkalochori Mw = 5.9 Earthquake of 27 September 2021 Inside the Heraklion Basin: A Shallow, Blind Rupture Event Highlighting the Orthogonal Extension of Central Crete. Geosciences 2022, 12, 220. [Google Scholar] [CrossRef]
- Hellenic Mediterranean University Research Center (former Technological Educational Institute of Crete). Seismological Network of Crete; 10.7914/SN/HC; International Federation of Digital Seismograph Networks: Crete, Greece, 2006. [Google Scholar]
- Behr, Y.; Clinton, J.F.; Cauzzi, C.; Hauksson, E.; Jónsdóttir, K.; Marius, C.G.; Pinar, A.; Salichon, J.; Sokos, E. The Virtual Seismologist in SeisComP3: A New Implementation Strategy for Earthquake Early Warning Algorithms. Seism. Res. Let. 2016, 87, 363–373. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.H.K.; Lahr, J.C. HYP071 (Revised): A Computer Program for Determining Hypocenter, Magnitude, and First Motion Pattern of Local Earthquakes; U.S. Geological Survey Open File Report 75-311; U.S. Geological Survey: Reston, VA, USA, 1975. [Google Scholar]
- Karakonstantis, A. 3-D Simulation of Crust and Upper Mantle Structure in the Broader Hellenic Area through Seismic Tomography. Ph.D. Thesis, Department of Geophysics-Geothermics, Faculty of Geology, University of Athens, Athens, Greece, 2017. (In Greek). [Google Scholar]
- Delibasis, N.D.; Ziazia, M.; Voulgaris, N.; Papadopoulos, T.; Stavrakakis, G.N.; Papanastassiou, D.; Drakatos, G. Microseismic activity and seismotectonics of Heraklion Area (central Crete Island, Greece). Tectonophysics 1999, 308, 237–248. [Google Scholar] [CrossRef] [Green Version]
- Becker, D.; Meier, T.; Bohnhoff, M.; Harjes, H.P. Seismicity at the convergent plate boundary offshore Crete, Greece, observed by an amphibian network. J. Seismol. 2010, 14, 369–392. [Google Scholar] [CrossRef] [Green Version]
- Klein, F.W. User’s Guide to HYPOINVERSE-2000, a Fortran Program to Solve for Earthquake Locations and Magnitudes, 2002-171; United States Department of the Interior Geological Survey: Menlo Park, CA, USA, 2002; p. 123. [Google Scholar]
- Ganas, A.; Oikonomou, I.A.; Tsimi, C. NOAfaults: A digital database for active faults in Greece. Bull. Geol. Soc. Greece 2017, 47, 518–530. [Google Scholar] [CrossRef] [Green Version]
- Waldhauser, F. hypoDD-A Program to Compute Double-Difference Hypocenter Locations, Open-File Report, 01-113; U.S. Geological Survey: Menlo Park, CA, USA, 2001. [Google Scholar]
- Koulakov, I. LOTOS code for local earthquake tomographic inversion: Benchmarks for testing tomographic algorithms. Bull. Seismol. Soc. Am. 2009, 99, 194–214. [Google Scholar] [CrossRef]
- Jaxybulatov, K.; Koulakov, I.; Ibs-von Seht, M.; Klinge, K.; Reichert, C.; Dahren, B.; Troll, V.R. Evidence for high fluid/melt content beneath Krakatau volcano (Indonesia) from local earthquake tomography. J. Volcanol. Geotherm. Res. 2011, 206, 96–105. [Google Scholar] [CrossRef]
- Toomey, D.R.; Foulger, G.R. Tomographic inversion of local earthquake data from the Hengill–Grensdalur central volcano complex, Iceland. J. Geophys. Res. 1989, 94, 17497–17510. [Google Scholar] [CrossRef]
- Ganas, A.; Fassoulas, C.; Moschou, A.; Bozionelos, G.; Papathanassiou, G.; Tsimi, C.; Valkaniotis, S. Geological and seismological evidence for NW-SE crustal extension at the southern margin of Heraklion Basin, Crete. Bull. Geol. Soc. Greece 2017, 51, 52–75. [Google Scholar] [CrossRef] [Green Version]
- Kassaras, I.; Kapetanidis, V.; Ganas, A.; Tzanis, A.; Kosma, C.; Karakonstantis, A.; Valkaniotis, S.; Chailas, S.; Kouskouna, V.; Papadimitriou, P. The New Seismotectonic Atlas of Greece (v1.0) and Its Implementation. Geosciences 2020, 10, 447. [Google Scholar] [CrossRef]
- Curlander, J.; McDonough, R. Synthetic Aperture Radar: Systems and Signal Processing; John Wiley & Sons.: Hoboken, NJ, USA, 1991; ISBN 978-0-471-85770-9. [Google Scholar]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Massonnet, D.; Rabaute, T. Radar interferometry: Limits and potential. IEEE Geosci. Remote Sens. 1993, 8, 455–464. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar Interferometry. Inverse Probl. 1998, 14, 1–54. [Google Scholar] [CrossRef]
- Elliott, J.; Walters, R.; Wright, T. The role of space-based observation in understanding and responding to active tectonics and earthquakes. Nat. Commun. 2016, 7, 13844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markogiannaki, O.; Karavias, A.; Bafi, D.; Angelou, D.; Parcharidis, I. A geospatial intelligence application to support post-disaster inspections based on local exposure information and on co-seismic DInSAR results: The case of the Durres (Albania) earthquake on November 26, 2019. Nat. Hazards 2020, 103, 3085–3100. [Google Scholar] [CrossRef]
- Sakkas, V. Ground Deformation Modelling of the 2020 Mw6.9 Samos Earthquake (Greece) Based on InSAR and GNSS Data. Remote Sens. 2021, 13, 1665. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038, Erratum in Remote Sens. 2021, 13, 1665. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Briole, P.; Ganas, A.; Elias, P.; Dimitrov, D. The GPS velocity field of the Aegean. New observations, contribution of the earthquakes, crustal blocks model. Geophys. J. Int. 2021, 226, 468–492. [Google Scholar] [CrossRef]
- King, G.C.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Alkan, H.; Büyüksaraç, A.; Bektaş, Ö.; Isik, E. Coulomb stress change before and after 24.01.2020 Sivrice (Elazığ) Earthquake (Mw = 6.8) on the East Anatolian Fault Zone. Arab. J. Geosci. 2021, 14, 2648. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-rich deformation and stress-change software for earthquake, tectonic, and volcano research and teaching—User guide. US Geol. Surv. Open-File Rep. 2011, 1060, 63. [Google Scholar]
- Scholz, C. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Cocco, M.; Rice, J.R. Pore pressure and poroelasticity effects in Coulomb stress analysis of earthquake interactions. J. Geophys. Res. Solid Earth 2002, 107, ESE-2. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Harris, R.A.; Simpson, R.W. Suppression of large earthquakes by stress shadows: A comparison of Coulomb and rate-and-state failure. J. Geophys. Res. Solid Earth 1998, 103, 24439–24451. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Gutenberg, B.; Richter, C. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Teleseismic b values; or, much ado about 1.0. J. Geophys. Res. 1993, 98, 631–644. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Mogi, K. Some discussion on aftershocks, foreshocks and earthquake swarms–the fracture of a semi-infinite body caused by an inner stress origand its relation to the earthquake phenomena (3rd paper). Bull. Earthq. Res. Inst. Univ. Tokyo 1963, 41, 615–658. [Google Scholar]
- Suyehiro, S.; Sekiya, H. Foreshocks and earthquake prediction. Tectonophysics 1972, 14, 219–225. [Google Scholar] [CrossRef]
- Papazachos, B.C. Foreshocks and earthquake prediction. Tectonophysics 1975, 28, 213–226. [Google Scholar] [CrossRef]
- Jones, L.M.; Molnar, P. Some characteristics of foreshocks and their possible relationship to earthquake prediction and premonitory slip on faults. J. Geophys. Res. 1979, 84, 3596–3608. [Google Scholar] [CrossRef]
- Main, I.; Meredith, P.G.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Internat. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Chan, C.-H.; Wu, Y.-M.; Tseng, T.-L.; Lin, T.-L.; Chen, C.-C. Spatial and temporal evolution of b-values before large earthquakes in Taiwan. Tectonophysics 2012, 532–535, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Kato, A.; Obara, K.; Igarashi, T.; Tsuruoka, H.; Nakagawa, S.; Hirata, N. Propagation of slow slip leading up to the 2011 Mw 9.0 Tohoku-Oki earthquake. Science 2012, 335, 705–708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nanjo, K.Z.; Hirata, N.; Obara, K.; Kasahara, K. Decade-scale decrease b value prior to the M9-class 2011 Tohoku and 2004 Sumatra quakes. Geophys. Res. Lett. 2012, 39, 1–4. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Minadakis, G. Foreshock Patterns Preceding Great Earthquakes in the Subduction Zone of Chile. Pure Appl. Geophys. 2016, 173, 3247–3271. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Minadakis, G.; Orfanogiannaki, K. Short-Term Foreshocks and Earthquake Prediction. In AGU Geophysical Monograph Series Book, 1st ed.; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2018; pp. 127–147. [Google Scholar]
- Wiemer, S.; Wyss, M. Minimum magnitude of complete reporting in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Sotolongo-Costa, O.; Posadas, A. Fragment-asperity interaction model for earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin, Germany, 2009. [Google Scholar]
- Silva, R.; França, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Telesca, L. Tsallis-Based Nonextensive Analysis of the Southern California Seismicity. Entropy 2011, 13, 1267–1280. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A 2016, 472, 2196. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Michas, G.; Hloupis, G. Seismicity Patterns Prior to the Thessaly (Mw6. 3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis. Geosciences 2021, 11, 379. [Google Scholar] [CrossRef]
- Vallianatos, F. A non extensive statistical physics approach to the polarity reversals of the geomagnetic field. Phys. A Stat. Mech. Appl. 2011, 390, 1773–1778. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Phys. A Stat. Mech. Appl. 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Vallianatos, F.; Telesca, L. Statistical mechanics in earth physics and natural hazards. Acta Geophys. 2012, 60, 499–501. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Tzanis, A. Evidence of non-extensivity in the seismicity observed during the 2011–2012 unrest at the Santorini volcanic complex, Greece. Nat. Hazards Earth Syst. Sci. 2013, 13, 177–185. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran-Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Evidence of Nonextensive Statistical Physics behavior of the Hellenic Subduction Zone seismicity. Tectonophysics 2013, 608, 1037–1048. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Michas, G. The earthquake intervent time distribution along the Hellenic subduction Zone. Bull. Geol. Soc. Greece 2013, XLVII, 1194–1200. [Google Scholar] [CrossRef]
- Vallianatos, F.; Karakostas, V.; Papadimitriou, E. A Non-Extensive Statistical Physics View in the Spatiotemporal Properties of the 2003 (Mw6.2) Lefkada, Ionian Island Greece, Aftershock Sequence. Pure Appl. Geophys. 2014, 171, 1343–1534. [Google Scholar] [CrossRef]
- Chochlaki, K.; Vallianatos, F.; Michas, G. Global regionalized seismicity in view of Non-Extensive Statistical Physics. Phys. A Stat. Mech. Appl. 2018, 493, 276–285. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non Extensive statistical Seismology: An overview. In Complexity of Seismic Time Series; Measurement and Application; Chelidze, T., Telesca, L., Elsevier, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Omori, F. On after-shocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1894, 7, 111–200. [Google Scholar]
- Utsu, T. A statistical study on the occurrence of aftershocks. Geo-Phys. 1961, 30, 521–605. [Google Scholar]
- Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Ogata, Y. Estimation of the parameters in the modified Omori formula for aftershock frequencies by the maximum likelihood procedure. J. Phys. Earth 1983, 31, 115–124. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Scaling properties, multifractality and range of correlations in earthquake timeseries: Are earthquakes random? In Statistical Methods and Modeling of Seismogenesis; Limnios, N., Papadimitriou, E., Tsaklidis, G., Eds.; ISTE John Wiley: London, UK, 2021. [Google Scholar]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A Stat. Mech. Appl. 2005, 350, 588–596. [Google Scholar] [CrossRef] [Green Version]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and long-range correlations in the earthquake activity at the West Corinth rift (Greece). Nonlinear Processes Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Michas, G.; Benson, P.; Sammonds, P. Natural time analysis of critical phenomena: The case of acoustic emis-sions in triaxially deformed Etna basalt. Phys. A Stat. Mech. Appl. 2013, 392, 5172–5178. [Google Scholar] [CrossRef]
- Chochlaki, K.; Michas, G.; Vallianatos, F. Complexity of the Yellowstone Park Volcanic Field Seismicity in Terms of Tsallis Entropy. Entropy 2018, 20, 721. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Sammonds, P. A non-extensive statistical physics view to the spatiotemporal properties of the June 1995, Aigion earthquake (M6.2) aftershock sequence (West Corinth rift, Greece). Acta Geophys. 2012, 60, 758–768. [Google Scholar] [CrossRef]
- Vallianatos, F.; Pavlou, K. Scaling properties of the Mw7.0 Samos (Greece), 2020 aftershock sequence. Acta Geophys. 2021, 69, 1–18. [Google Scholar] [CrossRef]
- Michas, G.; Pavlou, K.; Avgerinou, S.E.; Anyfadi, E.A.; Vallianatos, F. Aftershock patterns of the 2021 Mw 6.3 Northern Thessaly (Greece) earthquake. J. Seismol. 2022, 26, 1–25. [Google Scholar] [CrossRef]
- Peng, Z.; Zhao, P. Migration of early aftershocks following the 2004 Parkfield earthquake. Nat. Geosci. 2009, 2, 877–881. [Google Scholar] [CrossRef]
- Obana, K.; Kodaira, S.; Nakamura, Y.; Sato, T.; Fujie, G.; Takahashi, T.; Yamamoto, Y. Aftershocks of the December 7, 2012 intraplate doublet neat the Japan Trench axis. Earth Planets Space 2014, 66, 24. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.C.; Lin, C.H.; Peng, Z. Spatial-temporal evolution of early aftershocks following the 2010 ML6.4 Jiashian earthquake in southern Taiwan. Geophys. J. Int. 2014, 199, 1772–1783. [Google Scholar] [CrossRef]
- Frank, W.B.; Poli, P.; Perfettini, H. Mapping the rheology of the Central Chile subduction zone with aftershocks. Geophys. Res. Lett. 2017, 44, 5374–5382. [Google Scholar] [CrossRef]
- Perfettini, H.; Frank, W.B.; Marsan, D.; Bouchon, M. A model of aftershock migration driven by afterslip. Geophys. Res. Lett. 2018, 45, 2283–2293. [Google Scholar] [CrossRef]
- Ariyoshi, K.; Matsuzawa, T.; Hasegawa, A. The key frictional parameters controlling spatial variations in the speed of postseismic-slip propagation on a subduction plate boundary. Earth Planet Sci. Lett. 2007, 256, 136–146. [Google Scholar] [CrossRef]
- Kato, A.; Iidaka, T.; Kurashimo, E.; Nakagawa, S.; Hirata, N.; Iwasaki, T. Delineation of probable asperities on the Atotsugawa fault, central Japan, using a dense temporary seismic network. Geophys. Res. Lett. 2007, 34, L09318. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. 2004, 109, B02304. [Google Scholar] [CrossRef]
- Dieterich, J.H. A constitutive law for earthquake production and its application to earthquake clustering. J. Geophys. Res. 1994, 99, 2601–2618. [Google Scholar] [CrossRef]
- Margaris, B.N.; Hatzidimitriou, P.M. Source spectral scaling and stress release estimates using strong-motion records in Greece. Bull. Seismol. Soc. Am. 2002, 92, 1040–1059. [Google Scholar] [CrossRef]
- Allmann, B.P.; Shearer, P.M. Global variations of stress drop for moderate to large earthquakes. J. Geophys. Res. 2009, 114, B01310. [Google Scholar] [CrossRef] [Green Version]
- Papadimitriou, P.; Voulgaris, N.; Kassaras, I.; Kaviris, G.; Delibasis, N.; Makropoulos, K. The Mw = 6.0, 7 September 1999 Athens Earthquake. Nat. Hazards 2002, 27, 15–33. [Google Scholar] [CrossRef]
- Kapetanidis, V.; Karakonstantis, A.; Papadimitriou, P.; Pavlou, K.; Spingos, I.; Kaviris, G.; Voulgaris, N. The 19 July 2019 earthquake in Athens, Greece: A delayed major aftershock of the 1999 Mw = 6.0 event, or the activation of a different structure? J. Geodyn. 2020, 139, 101766. [Google Scholar] [CrossRef]
- Triantafyllou, I.; Papadopoulos, G.A.; Lekkas, E. Impact on built and natural environment of the strong earthquakes of April 23, 1933, and July 20, 2017, in the southeast Aegean Sea, eastern Mediterranean. Nat. Hazards 2020, 100, 671–695. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Kapetanidis, V.; Karakonstantis, A.; Spingos, I.; Kassaras, I.; Sakkas, V.; Kouskouna, V.; Karatzetzou, A.; Pavlou, K.; Kaviris, G.; et al. First Results on the Mw=6.9 Samos Earthquake of 30 October 2020. Bull. Geol. Soc. Greece 2020, 56, 251–279. [Google Scholar] [CrossRef]
- Karakostas, V.; Tan, O.; Kostoglou, A.; Papadimitriou, E.; Bonatis, P. Seismotectonic implications of the 2020 Samos, Greece, Mw 7.0 mainshock based on high-resolution aftershock relocation and source slip model. Acta Geophys. 2021, 69, 979–996. [Google Scholar] [CrossRef]


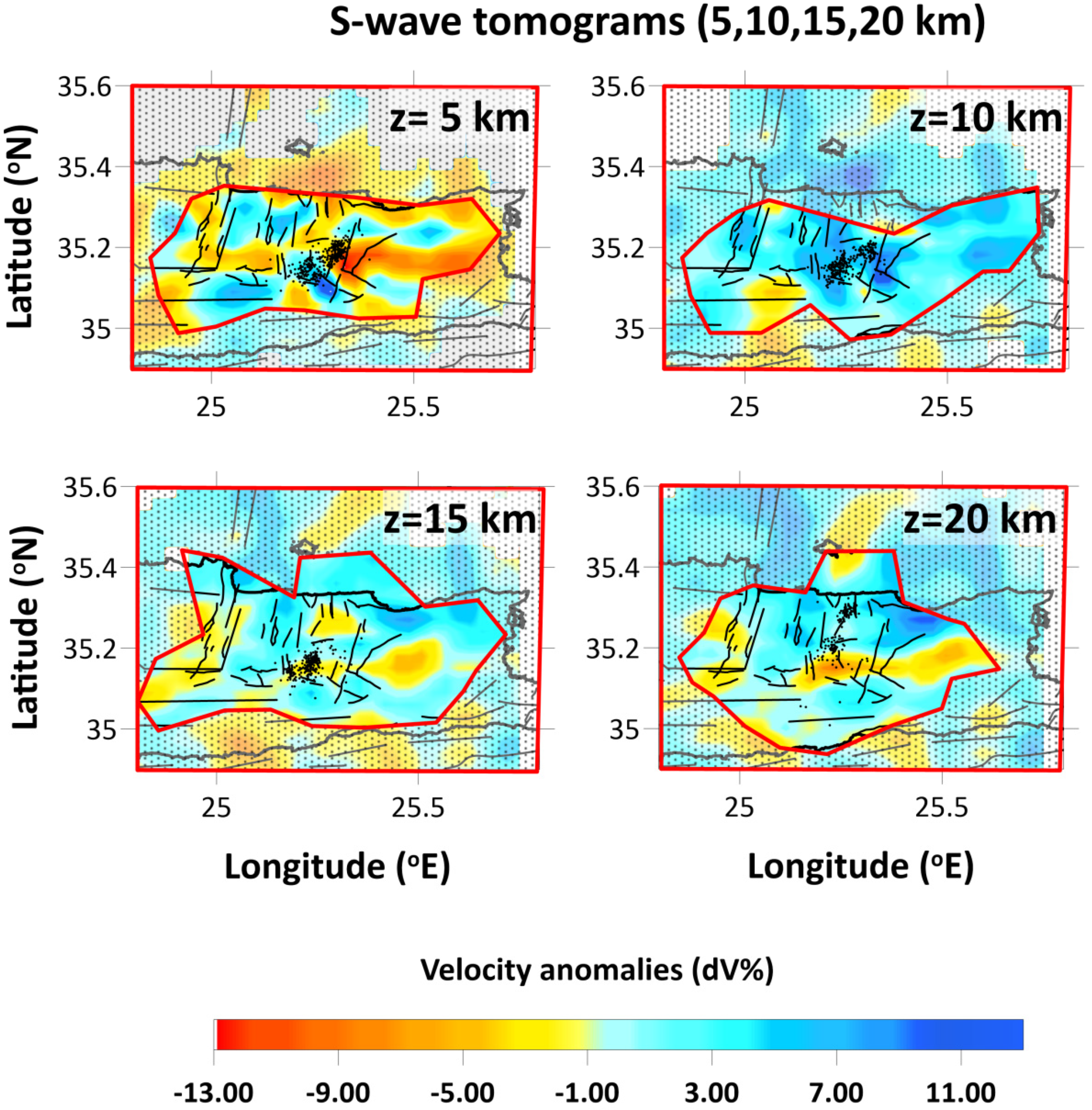
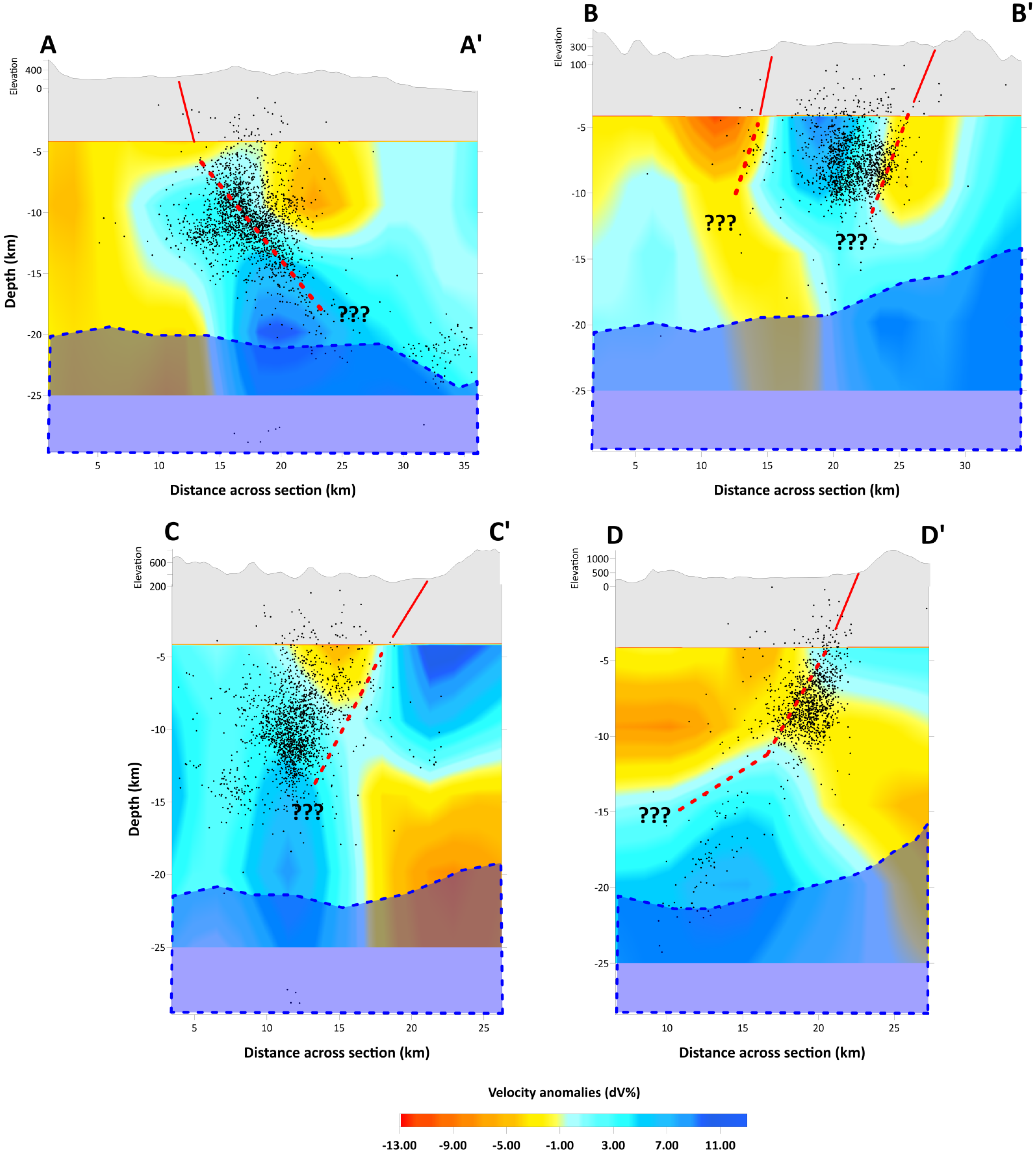
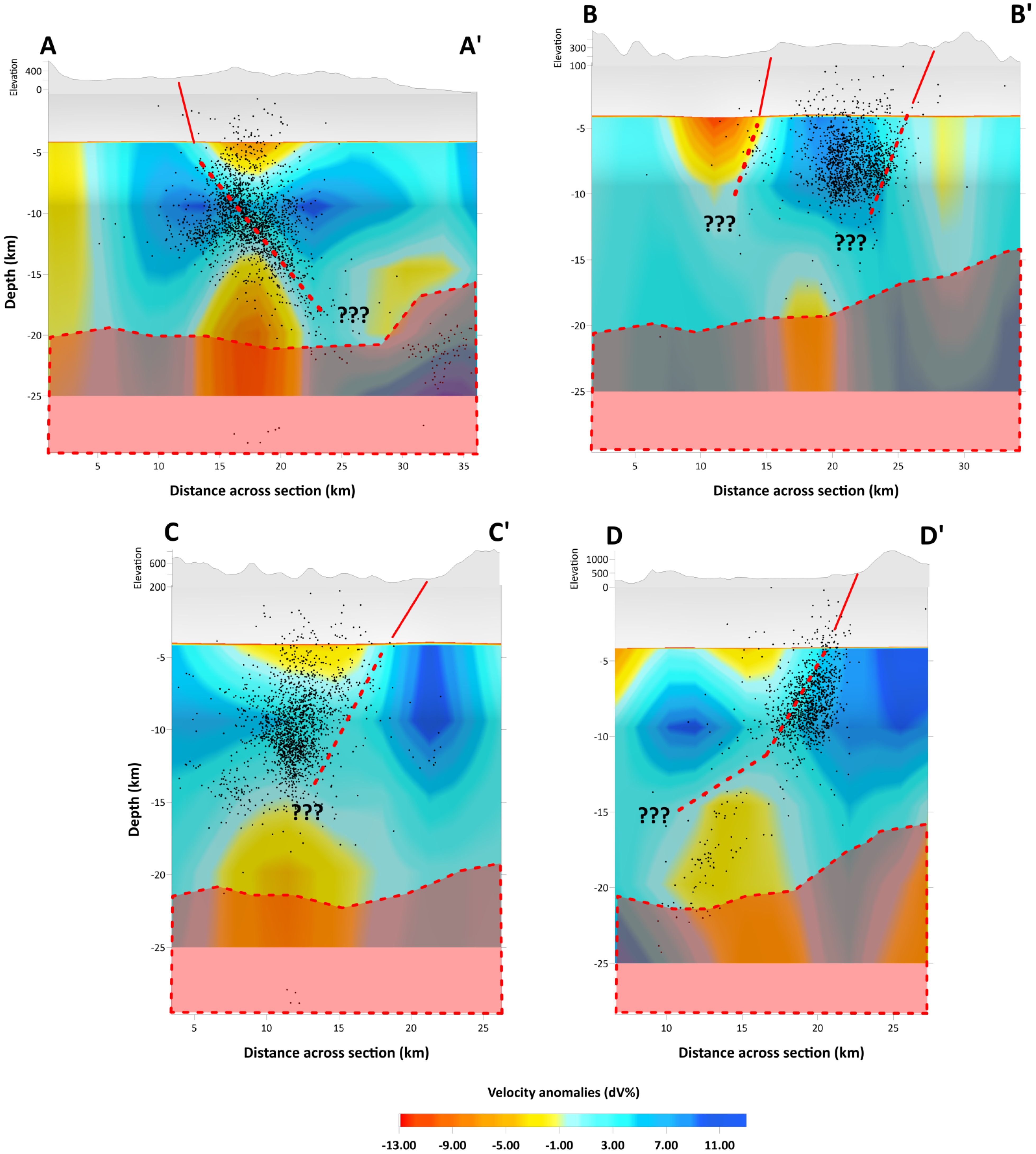
| Model | Model 1 | Model 2 |
|---|---|---|
| Mean RMS (s) | 0.26 | 0.26 |
| Mean ERH (km) | 1.30 | 1.31 |
| Mean ERZ (km) | 4.41 | 4.52 |
| Mean Depth (km) | 9.43 | 13.94 |
| Iteration | P-Residual (s) | P-residual Reduction (%) | S-Residual (s) | S-Residual Reduction (%) |
|---|---|---|---|---|
| 1 | 0.269 | 0.00 | 0.437 | 0.00 |
| 2 | 0.211 | 21.50 | 0.248 | 43.14 |
| 3 | 0.194 | 27.63 | 0.222 | 49.12 |
| 4 | 0.188 | 30.08 | 0.218 | 50.10 |
| 5 | 0.186 | 30.85 | 0.211 | 51.69 |
| Ascending Image Pair | ||||||
|---|---|---|---|---|---|---|
| Satellite | Ref./Repeat | Acquisition | Track | Orbit | Bperp (m) | Btemp (days) |
| S1B | Reference | 23 September 2021 | 102 | 28,828 | −111.36 | 6 |
| S1A | Repeat | 29 September 2021 | 102 | 39,899 | ||
| Descending Image Pair | ||||||
| Satellite | Ref./Repeat | Acquisition | Track | Orbit | Bperp (m) | Btemp (Days) |
| S1A | Reference | 25 September 2021 | 36 | 39,833 | −28.08 | 6 |
| S1B | Repeat | 1 October 2021 | 36 | 28,937 | ||
| Site | Latitude (°) | Longitude (°) | DEast (cm) | DNorth (cm) | DUp (cm) |
|---|---|---|---|---|---|
| ARKL | 35.1339 | 25.2689 | 4.51 ± 0.11 | 7.85 ± 0.14 | −15.45 ± 0.60 |
| HERA | 35.4241 | 25.1415 | −0.54 ± 0.09 | 0.62 ± 0.19 | 0.57 ± 0.39 |
| Date | Hour | Minute | Lat. | Long. | Depth (km) | Mw | Strike | Dip | Rake | Agency | Length | Width | Mo (Nm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 24 July 2021 | 2 | 7 | 35.1676 | 25.2286 | 8 | 4.9 | 214 | 52 | −95 | NOA | 2.3 | 2.56 | 9.116 × 1015 |
| 27 September 2021 | 6 | 17 | 35.1421 | 25.2734 | 10 | 6.0 | 218 | 57 | −85 | GFZ | 7.61 | 10.3 | 1.1 × 1018 |
| 28 September 2021 | 4 | 48 | 35.1356 | 25.2312 | 9 | 5.3 | 182 | 22 | −95 | UOA | 4.41 | 4.88 | 1.30 × 1017 |
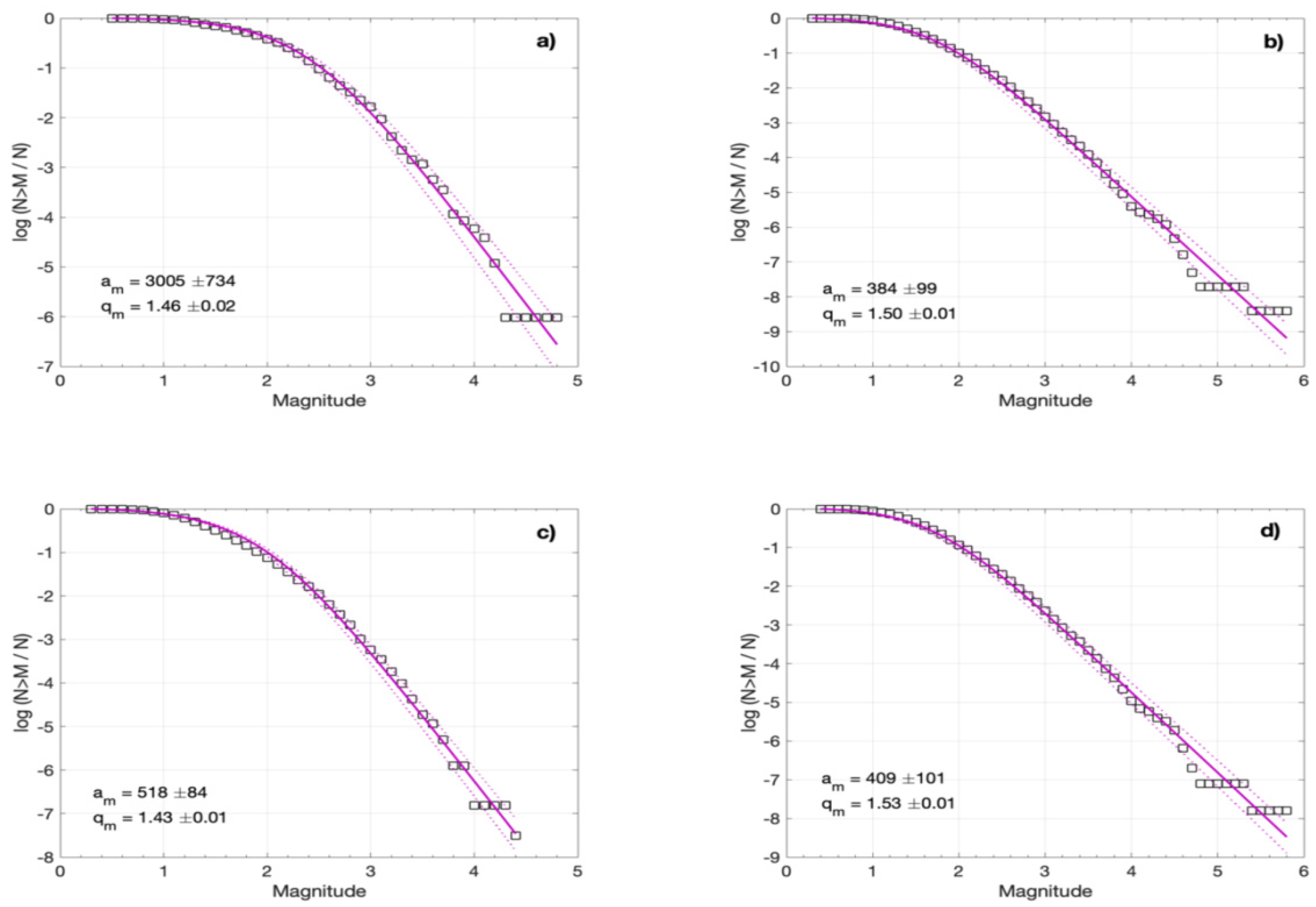
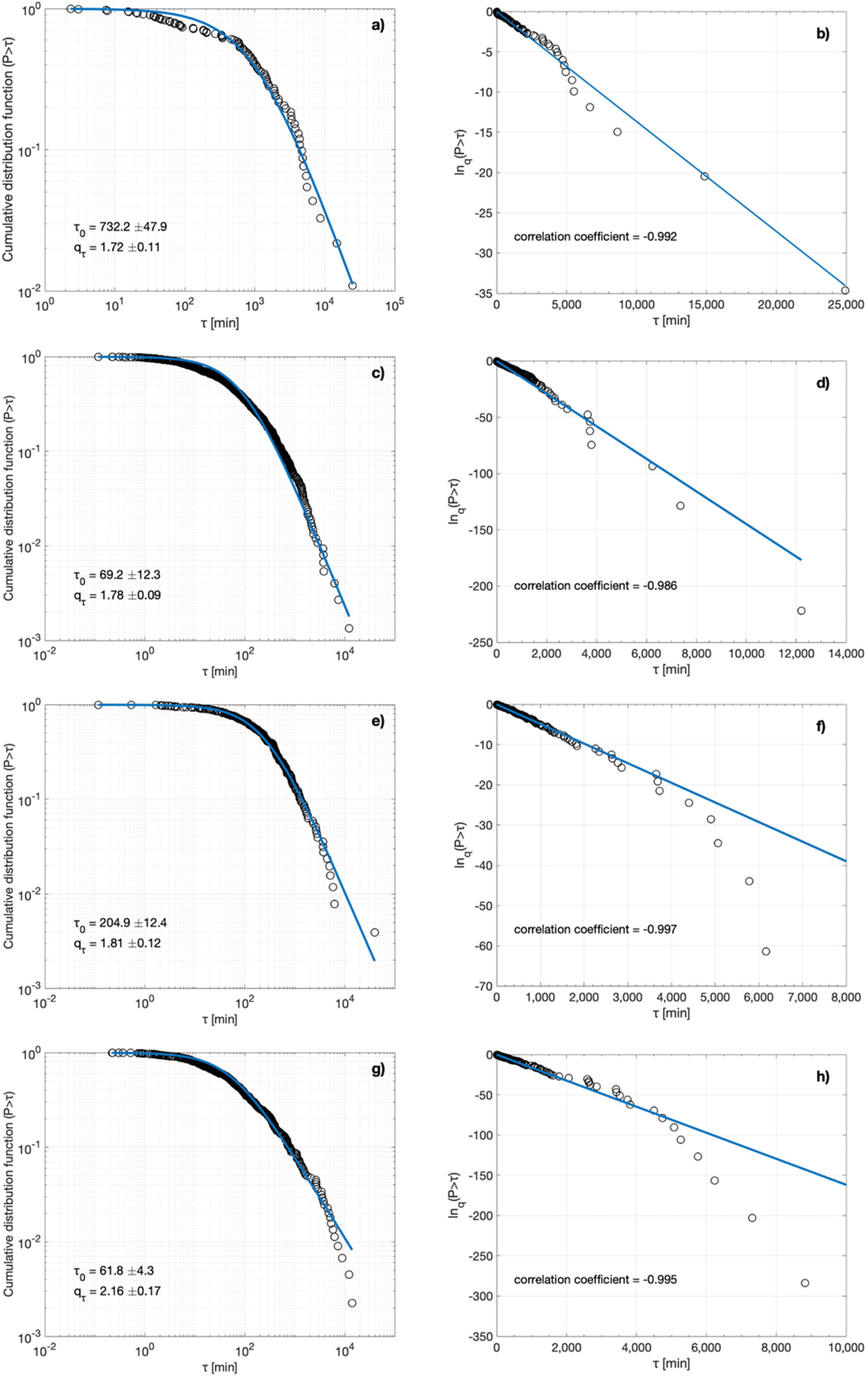
| N | Mc | αm | qm | τ0 | qτ | |
|---|---|---|---|---|---|---|
| Foreshocks | 410 | 2.8 | 3005 ± 734 | 1.46 ± 0.02 | 732.2 ± 47.9 | 1.72 ± 0.11 |
| Aftershocks (both NE and SW clusters) | 4465 | 2.5 | 384 ± 99 | 1.50 ± 0.01 | 69.2 ± 12.3 | 1.78 ± 0.09 |
| NE cluster | 1815 | 2.5 | 518 ± 84 | 1.43 ± 0.01 | 204.9 ± 12.4 | 1.81 ± 0.12 |
| SW cluster | 2431 | 2.5 | 409 ± 101 | 1.53 ± 0.01 | 61.8 ± 4.3 | 2.16 ± 0.17 |
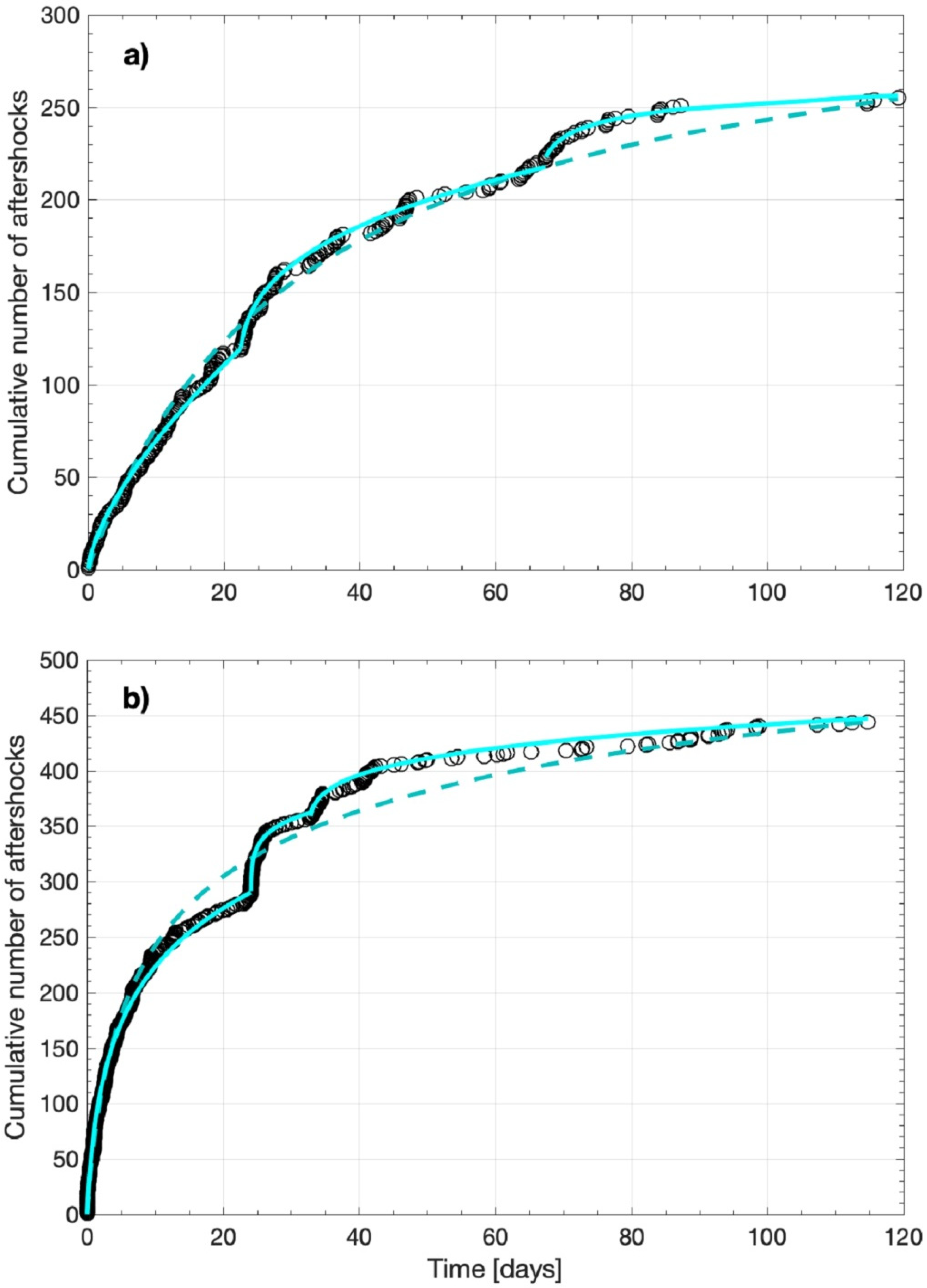
| Cluster | Model | Mainshock | Duration (Days) | N | K | c (Days) | p | AIC |
|---|---|---|---|---|---|---|---|---|
| NE cluster | Single model | M5.8 27/09/21 | 119.3 | 256 | 71.02 ± 14.45 | 28.35 ± 0.57 | 1.85 ± 0.08 | –72.4 |
| Composite model | M5.8 27/09/21 | 22.8 | 120 | 10.57 ± 7.18 | 0.01 ± 1.63 | 0.35 ± 0.12 | –125.7 | |
| M4.3 20/10/21 | 44.6 | 92 | 10.95 ± 3.98 | 0.24 ± 0.65 | 0.66 ± 0.06 | |||
| M3.7 03/12/21 | 51.9 | 44 | 11.57 ± 8.56 | 1.50 ± 1.63 | 1.10 ± 0.28 | |||
| SW cluster | Single model | M5.8 27/09/21 | 114.8 | 446 | 165.65 ± 126.80 | 1.76 ± 1.33 | 1.18 ± 0.16 | –1130 |
| Composite model | M5.8 27/09/21 | 24.1 | 290 | 81.09 ± 35.98 | 0.67 ± 1.15 | 1.01 ± 0.36 | –1304 | |
| M4.5 21/10/21 | 8.7 | 68 | 12.00 ± 4.66 | 0.01 ± 0.11 | 0.86 ± 0.19 | |||
| M3.7 03/12/21 | 82.0 | 88 | 10.00 ± 4.55 | 0.26 ± 0.32 | 0.77 ± 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F.; Karakonstantis, A.; Michas, G.; Pavlou, K.; Kouli, M.; Sakkas, V. On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations. Appl. Sci. 2022, 12, 7716. https://doi.org/10.3390/app12157716
Vallianatos F, Karakonstantis A, Michas G, Pavlou K, Kouli M, Sakkas V. On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations. Applied Sciences. 2022; 12(15):7716. https://doi.org/10.3390/app12157716
Chicago/Turabian StyleVallianatos, Filippos, Andreas Karakonstantis, Georgios Michas, Kyriaki Pavlou, Maria Kouli, and Vassilis Sakkas. 2022. "On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations" Applied Sciences 12, no. 15: 7716. https://doi.org/10.3390/app12157716
APA StyleVallianatos, F., Karakonstantis, A., Michas, G., Pavlou, K., Kouli, M., & Sakkas, V. (2022). On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations. Applied Sciences, 12(15), 7716. https://doi.org/10.3390/app12157716









