Multiple-Image Reconstruction of a Fast Periodic Moving/State-Changed Object Based on Compressive Ghost Imaging
Abstract
:1. Introduction
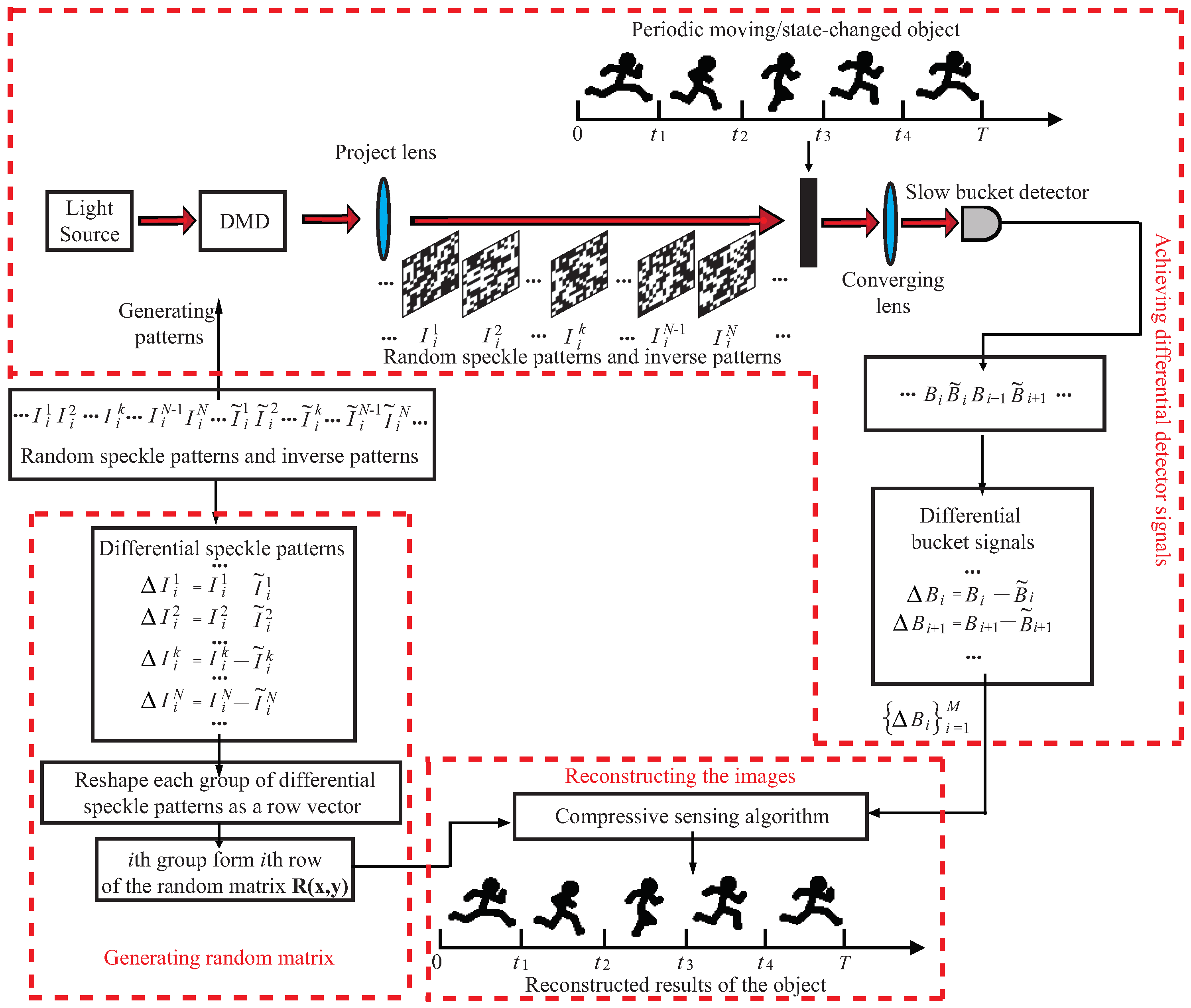
2. Theory and Methods
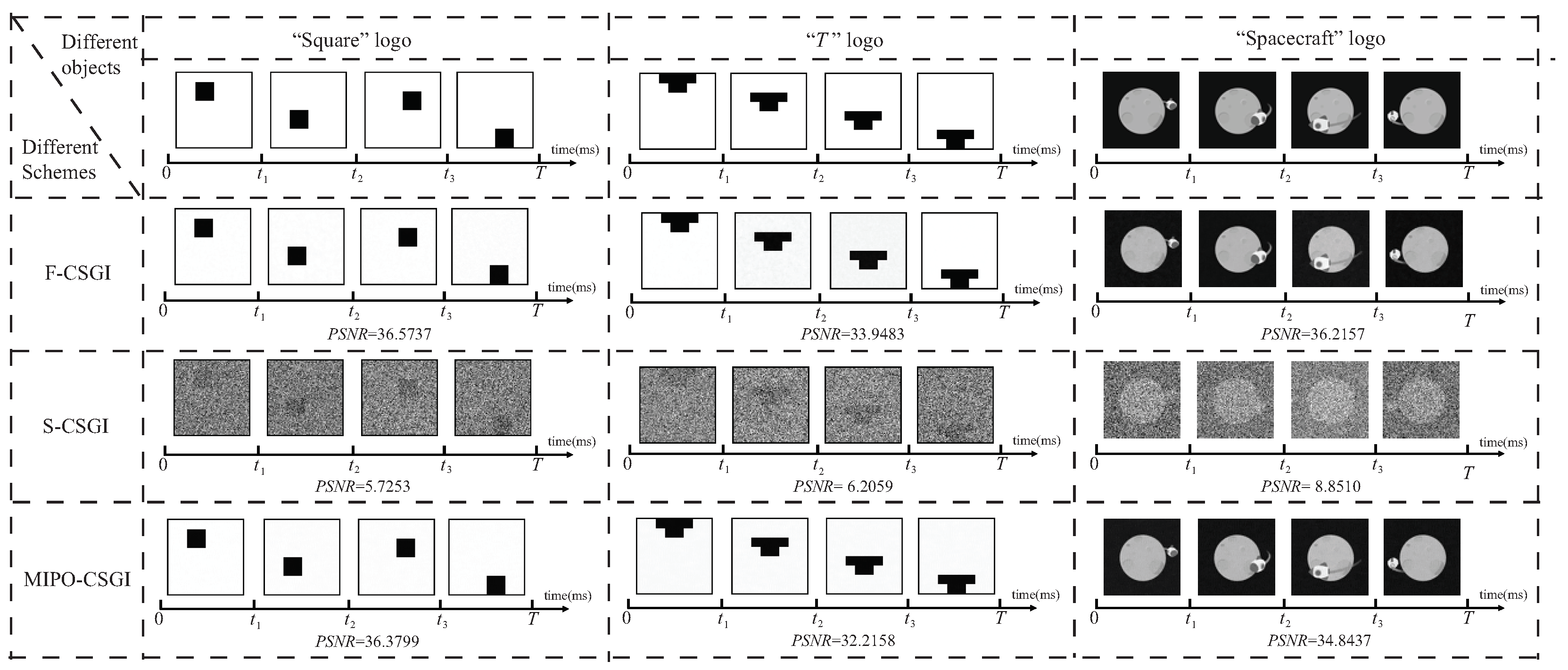
3. Numerical Verification
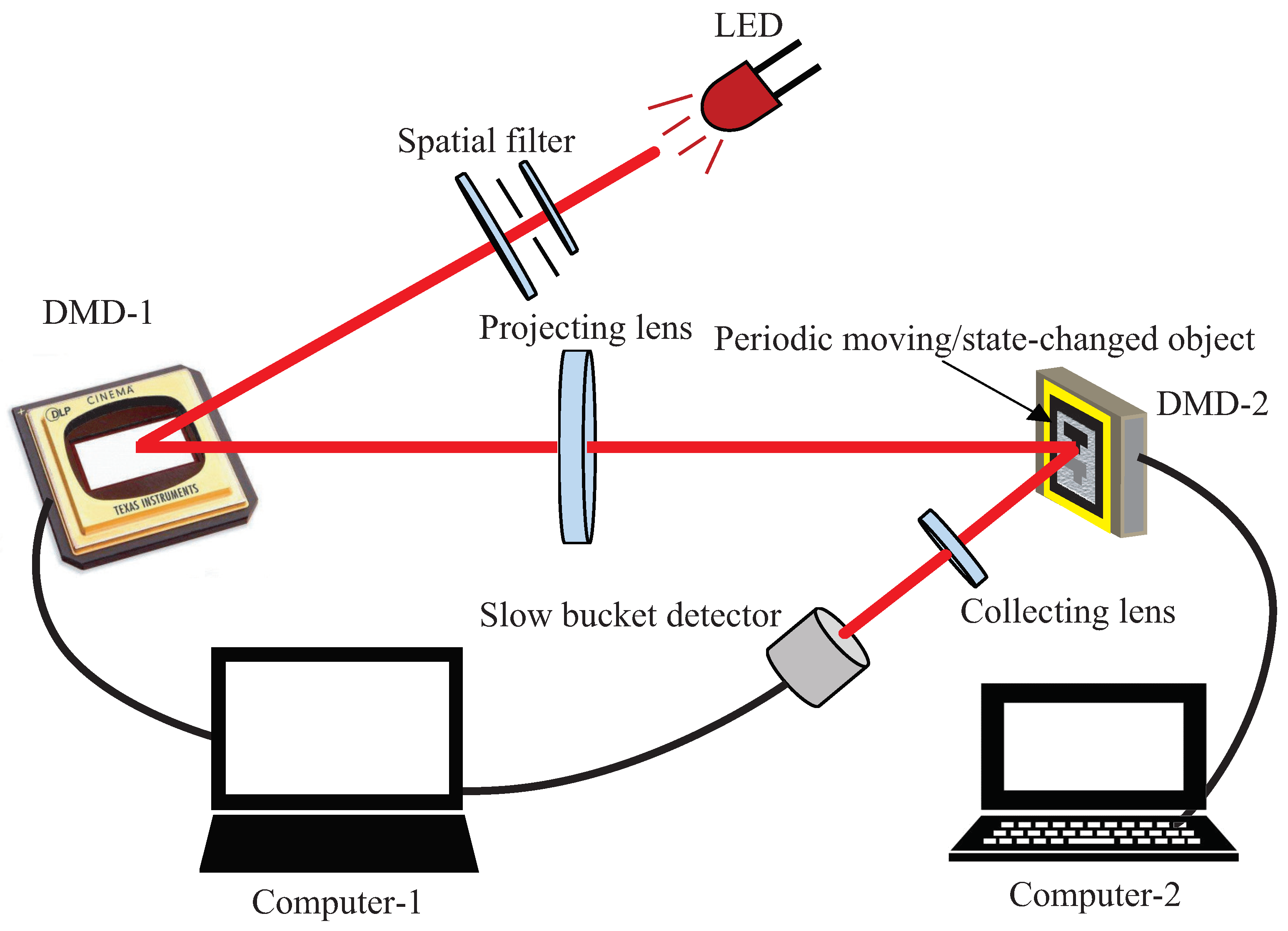
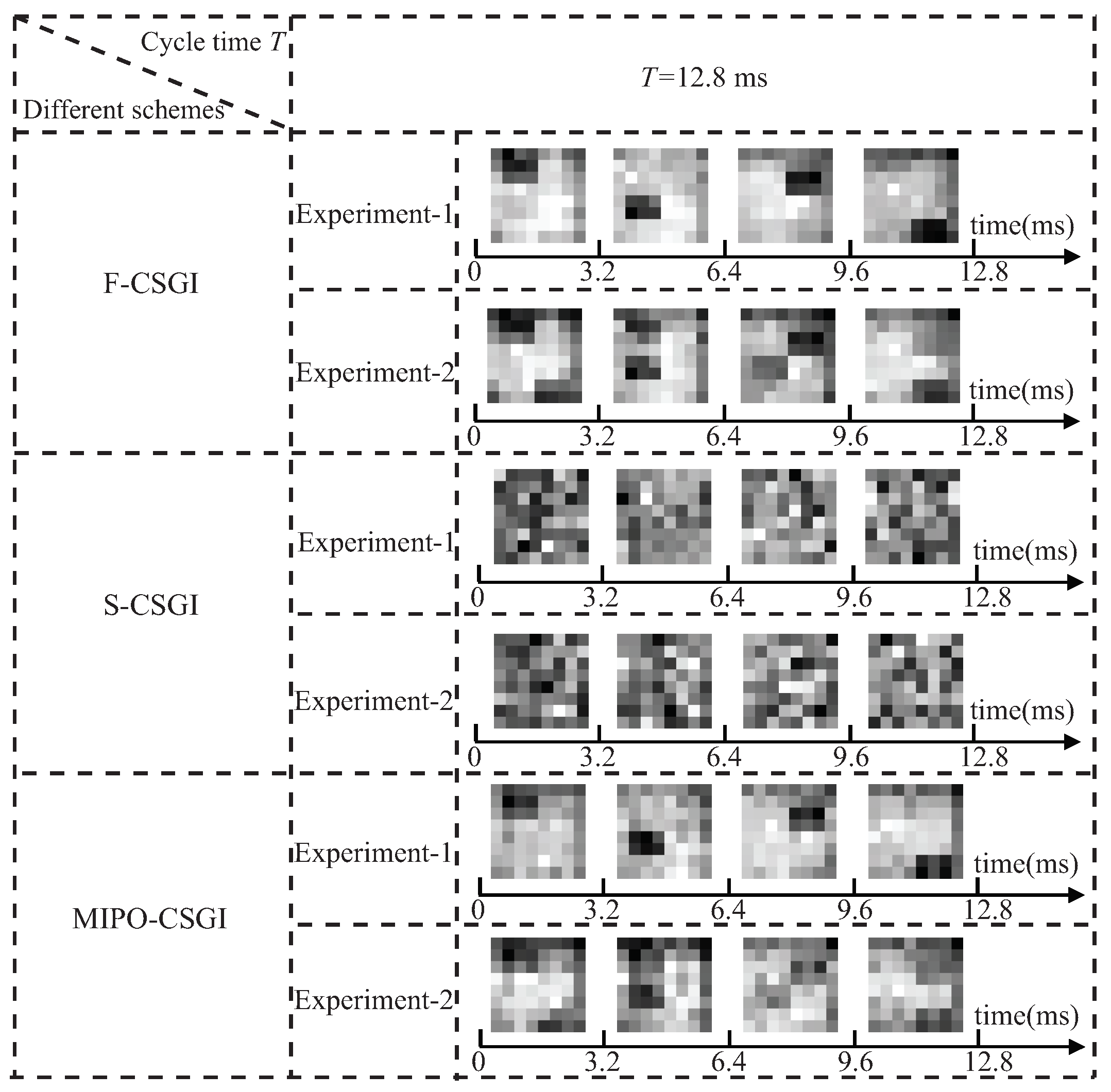
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost Imaging with Thermal Light: Comparing Entanglement and Classical Correlation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Zhao, S. Fast reconstructed and high-quality ghost imaging with fast Walsh–Hadamard transform. Photon. Res. 2016, 4, 240–244. [Google Scholar] [CrossRef]
- Zhang, H.; Duan, D. Computational ghost imaging with compressed sensing based on a convolutional neural network. Chin. Opt. Lett. 2021, 19, 101101. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, S. Super resolution ghost imaging based on Fourier spectrum acquisition. Opt. Lasers Eng. 2021, 139, 106473. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X. Optical authentication via photon-synthesized ghost imaging using optical nonlinear correlation. Opt. Lasers Eng. 2015, 73, 123–127. [Google Scholar] [CrossRef]
- Wang, L.; Zou, L.; Zhao, S. Edge detection based on subpixel-speckle-shifting ghost imaging. Opt. Commun. 2018, 407, 181–185. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Zhao, S. Spread spectrum ghost imaging. Opt. Express 2021, 29, 41485–41495. [Google Scholar] [CrossRef]
- Pittman, T.B.; Shih, Y.H.; Strekalov, D.V.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Sergienko, A.V.; Klyshko, D.N.; Shih, Y.H. Observation of Two-Photon “Ghost” Interference and Diffraction. Phys. Rev. Lett. 1995, 74, 3600–3603. [Google Scholar] [CrossRef]
- Cao, D.Z.; Xu, B.L.; Zhang, S.H.; Wang, K.G. Color Ghost Imaging with Pseudo-White-Thermal Light. Chin. Phys. Lett. 2015, 32, 114208. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Gatti, A.; Bache, M.; Brambilla, E.; Lugiato, L.A. High-Resolution Ghost Image and Ghost Diffraction Experiments with Thermal Light. Phys. Rev. Lett. 2005, 94, 183602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, D.Z.; Li, Q.C.; Zhuang, X.C.; Ren, C.; Zhang, S.H.; Song, X.B. Ghost images reconstructed from fractional-order moments with thermal light. Chin. Phys. B 2018, 27, 123401. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802(R). [Google Scholar] [CrossRef]
- Bromberg, Y.; Katz, O.; Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 2009, 79, 053840. [Google Scholar] [CrossRef] [Green Version]
- Jiao, S.; Feng, J.; Gao, Y.; Lei, T.; Yuan, X. Visual cryptography in single-pixel imaging. Opt. Express 2020, 28, 7301–7313. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhao, S. Full color single pixel imaging by using multiple input single output technology. Opt. Express 2021, 29, 24486–24499. [Google Scholar] [CrossRef]
- Li, H.; Xiong, J.; Zeng, G. Lensless ghost imaging for moving objects. Opt. Eng. 2011, 50, 127005. [Google Scholar] [CrossRef]
- Zhang, C.; Gong, W.; Han, S. Improving imaging resolution of shaking targets by Fourier-transform ghost diffraction. Appl. Phys. Lett. 2013, 102, 021111. [Google Scholar] [CrossRef] [Green Version]
- Li, E.; Bo, Z.; Chen, M.; Gong, W.; Han, S. Ghost imaging of a moving target with an unknown constant speed. Appl. Phys. Lett. 2014, 104, 251120. [Google Scholar] [CrossRef]
- Li, X.; Deng, C.; Chen, M.; Gong, W.; Han, S. Ghost imaging for an axially moving target with an unknown constant speed. Photon. Res. 2015, 3, 153–157. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.K.; Yao, X.R.; Liu, X.F.; Li, L.Z.; Zhai, G.J. Compressive moving target tracking with thermal light based on complementary sampling. Appl. Opt. 2015, 54, 4249–4254. [Google Scholar] [CrossRef]
- Sun, S.; Gu, J.H.; Lin, H.Z.; Jiang, L.; Liu, W.T. Gradual ghost imaging of moving objects by tracking based on cross correlation. Opt. Lett. 2019, 44, 5594–5597. [Google Scholar] [CrossRef]
- Yang, D.; Chang, C.; Wu, G.; Luo, B.; Yin, L. Compressive Ghost Imaging of the Moving Object Using the Low-Order Moments. Appl. Sci. 2020, 10, 7941. [Google Scholar] [CrossRef]
- Jiao, S.; Sun, M.; Gao, Y.; Lei, T.; Xie, Z.; Yuan, X. Motion estimation and quality enhancement for a single image in dynamic single-pixel imaging. Opt. Express 2019, 27, 12841–12854. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.H.; Chen, W.; Penuelas, J.; Padgett, M.; Sun, M.J. 1000 fps computational ghost imaging using LED-based structured illumination. Opt. Express 2018, 26, 2427–2434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; Chen, H.; Yuan, Y.; Zheng, H.; Liu, J.; Xu, Z.; Zhou, Y. Ultrahigh-Speed Color Imaging with Single-Pixel Detectors at Low Light Level. Phys. Rev. Appl. 2019, 12, 034049. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Wang, L.; Zhao, S.M. Imaging a periodic moving/state-changed object with Hadamard-based computational ghost imaging. Chin. Phys. B 2022, 31, 084201. [Google Scholar] [CrossRef]
- Katz, O.; Bromberg, Y.; Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 2009, 95, 131110. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhao, S.; Cheng, W.; Gong, L.; Chen, H. Optical image hiding based on computational ghost imaging. Opt. Commun. 2016, 366, 314–320. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, C.; Tian, T.; Liu, D.; Song, L. High-quality compressive ghost imaging. Opt. Commun. 2018, 412, 60–65. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, S. Compressed ghost imaging based on differential speckle patterns. Chin. Phys. B 2020, 29, 024204. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Jiang, H.; Zhang, Y. An efficient augmented Lagrangian method with applications to total variation minimization. Comput. Optim. Appl. 2013, 56, 507–530. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Wang, G.; Huang, H.; Song, L.; Xue, K. Edge detection based on joint iteration ghost imaging. Opt. Express 2019, 27, 27295–27307. [Google Scholar] [CrossRef] [PubMed] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Chen, Y.; Zhao, S. Multiple-Image Reconstruction of a Fast Periodic Moving/State-Changed Object Based on Compressive Ghost Imaging. Appl. Sci. 2022, 12, 7722. https://doi.org/10.3390/app12157722
Guo H, Chen Y, Zhao S. Multiple-Image Reconstruction of a Fast Periodic Moving/State-Changed Object Based on Compressive Ghost Imaging. Applied Sciences. 2022; 12(15):7722. https://doi.org/10.3390/app12157722
Chicago/Turabian StyleGuo, Hui, Yuxiang Chen, and Shengmei Zhao. 2022. "Multiple-Image Reconstruction of a Fast Periodic Moving/State-Changed Object Based on Compressive Ghost Imaging" Applied Sciences 12, no. 15: 7722. https://doi.org/10.3390/app12157722
APA StyleGuo, H., Chen, Y., & Zhao, S. (2022). Multiple-Image Reconstruction of a Fast Periodic Moving/State-Changed Object Based on Compressive Ghost Imaging. Applied Sciences, 12(15), 7722. https://doi.org/10.3390/app12157722



