Acoustic Roughness Measurement of Railway Tracks: Laboratory Investigation of External Disturbances on the Chord-Method with an Optical Measurement Approach
Abstract
:Featured Application
Abstract
1. Introduction
2. Experimental Approach and Optimization
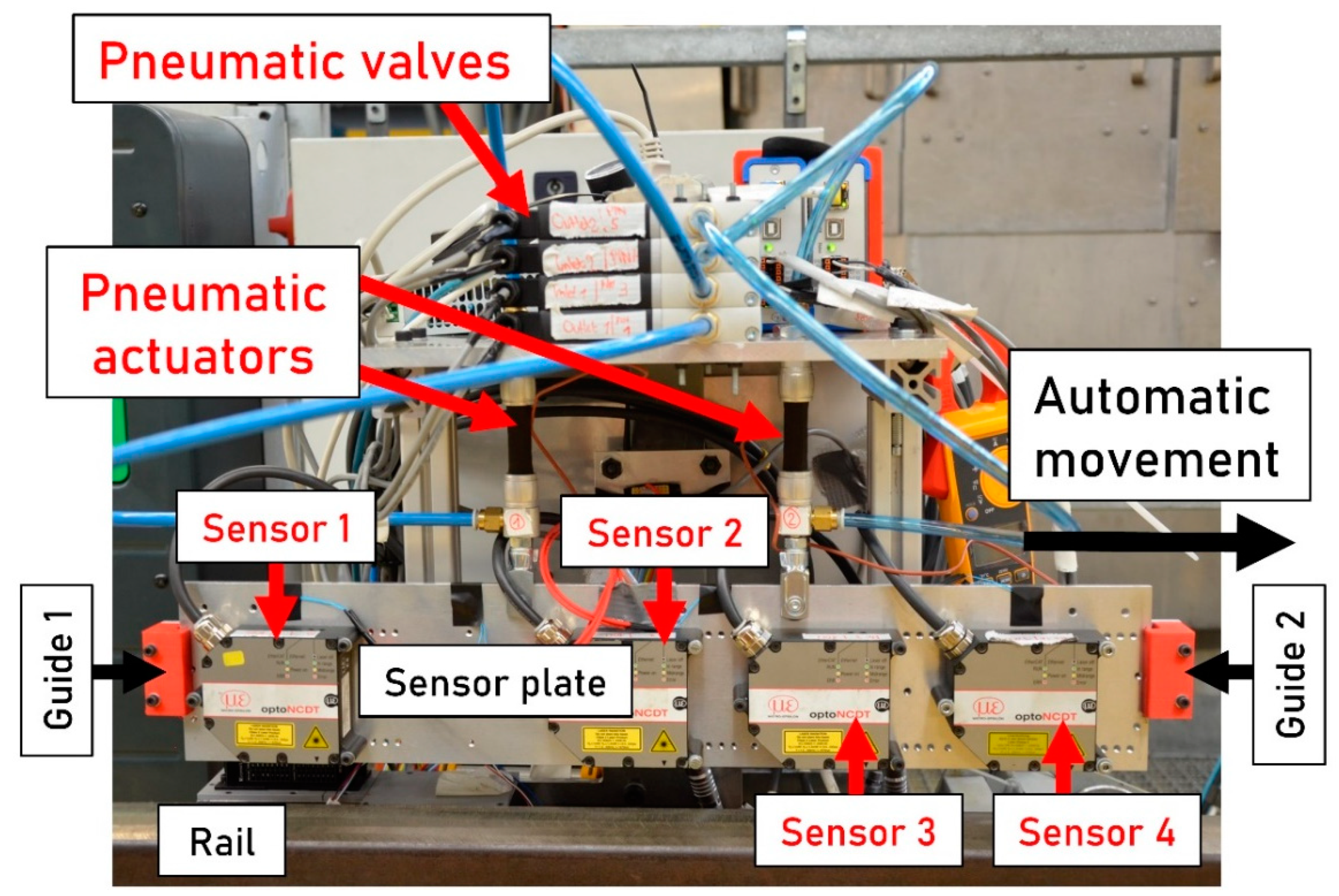
2.1. Setup
2.2. Experiments
- Constant velocity: A measurement at constant velocity and without further disturbances is modelled. All measurements, with the exception of the acceleration and deceleration measurements, are performed at constant speed.
- Acceleration & Deceleration: The situation of accelerating and braking is emulated. This should according to Grassie [21] not affect the chord method. For this purpose, the slider is stopped several times along the rail and then set in motion again.
- Heat: Additional heat flux affects the optical properties of the air between the rail and the sensor. For this purpose, a heat stream from a heat gun was directed towards the region between the sensor and the rail.
- Water: Wet track conditions occur in operation, for example during rainfall. Water or moisture on the rail will be rolled over, and will have no influence on the acoustic emission from the wheel-rail contact. Nevertheless, water can affect the optical measurement method, and must be considered in this study. Water is sprayed onto the surface of the rails. A uniform distribution is targeted, which is shown in Figure 2.
- Dust: Sand is applied to the rail near railway stations to achieve better adhesion. The sand would be overrun by following vehicles, and is therefore relevant for acoustic emissions resulting from the wheel-rail contact. In order to test the effect of the presence of particles on the rail surface, dust is applied to the rail. The particle distribution is kept identical for all tests with dust on the rail.
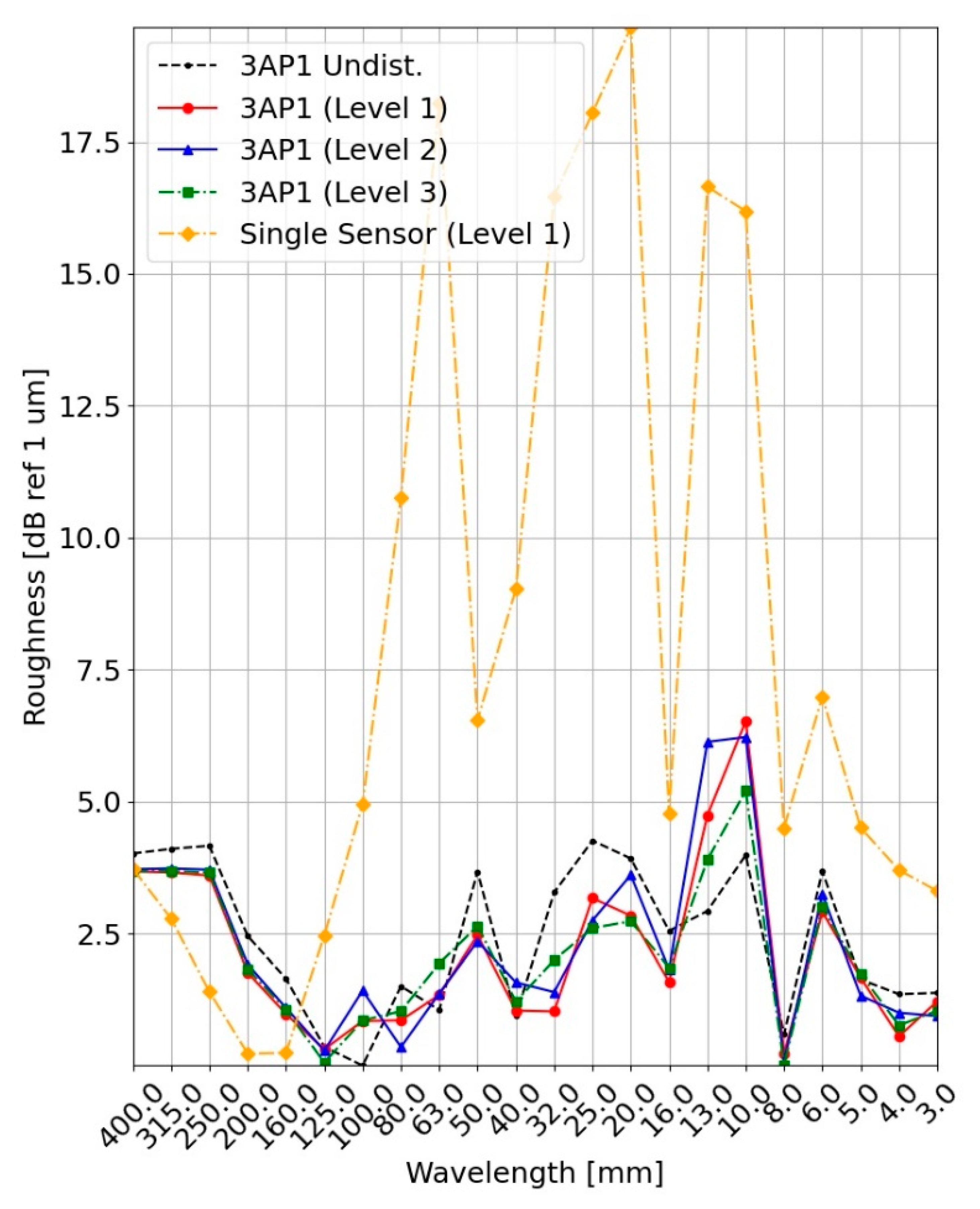
- Displacement & Tilting: Displacements of the entire measurement setup perpendicular to the rail surface occur because of the bogie suspension. A tilting of the measuring system can result, for example, from an inclined mounting position on the train. Both scenarios are artificially realized in the experimental setup by suspending the sensors from the pneumatic actuators. The degree of freedom to tilt in lateral direction is prevented by guides. The two pneumatic actuators are actuated at a frequency using rectangular pulses, either synchronously (displacement) or asynchronously (tilting). The amplitude represents the displacement at the location of each pneumatic actuator. Three different amplitudes are tested for displacement and tilting, respectively:
- ○
- Level 1:
- ○
- Level 2:
- ○
- Level 3:
- Vibration: Vibrations can originate from the train and its movement. Chen et al. [27] applied a simulation for a car body structure to determine modal frequencies up to . Therefore, three different and realistic frequencies are tested experimentally from to , by inducing small displacements with the pneumatic actuators, using identical pneumatic pressures for all frequencies.
- ○
- Level 1:
- ○
- Level 2:
- ○
- Level 3:
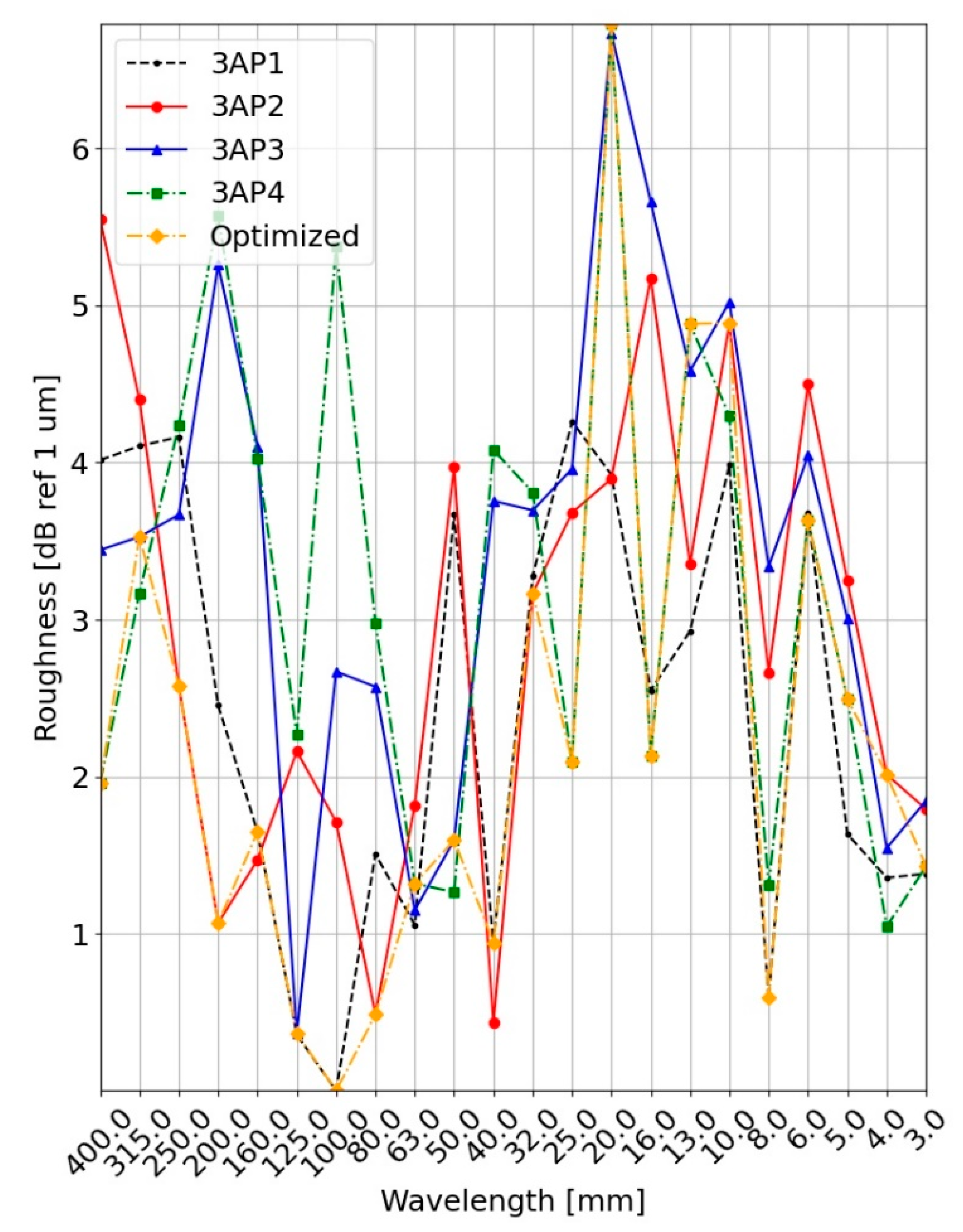
2.3. Chord Methods & Optimization
3. Results
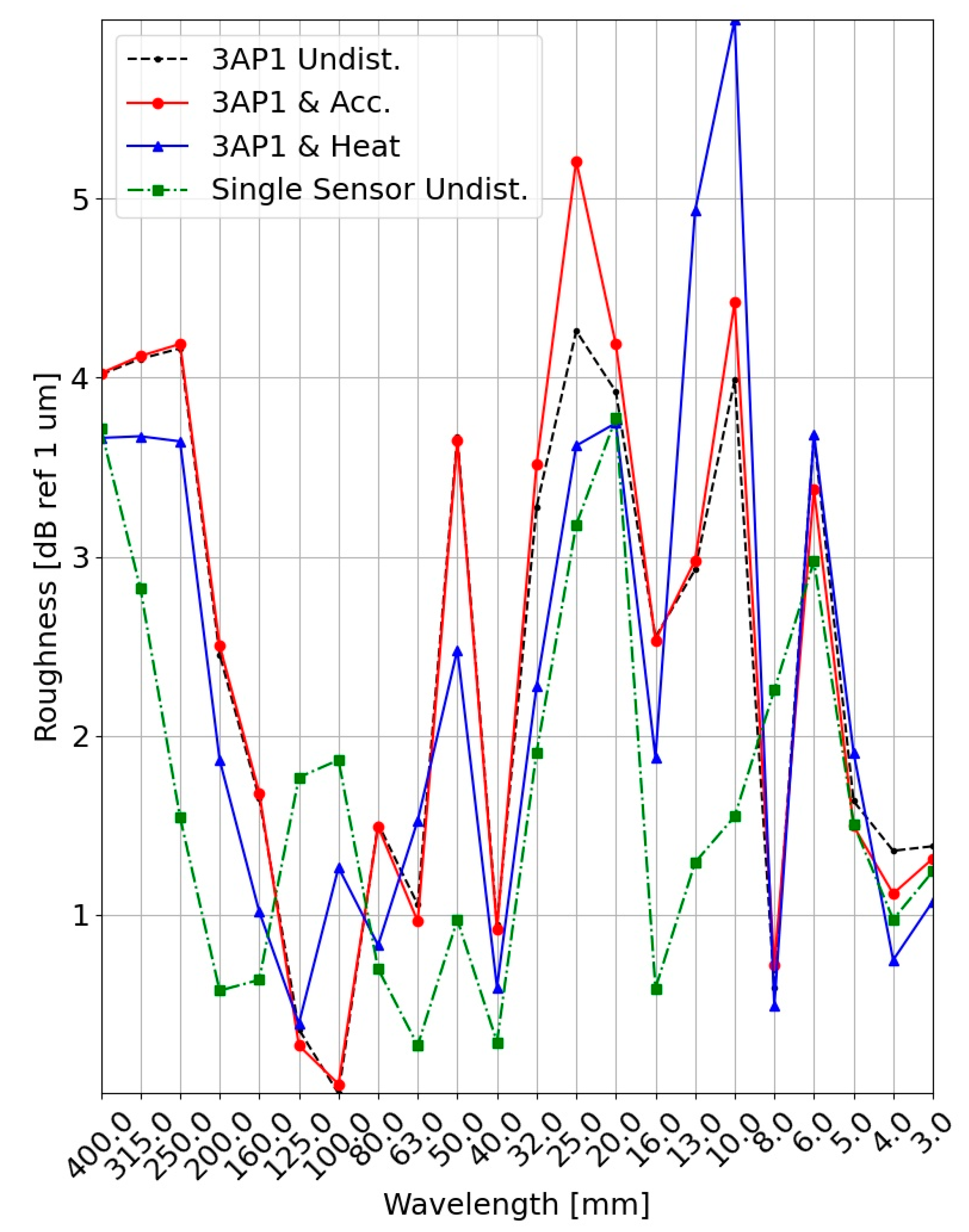
3.1. Constant Velocity, Acceleration & Heat
3.2. Water & Dust on the Rail
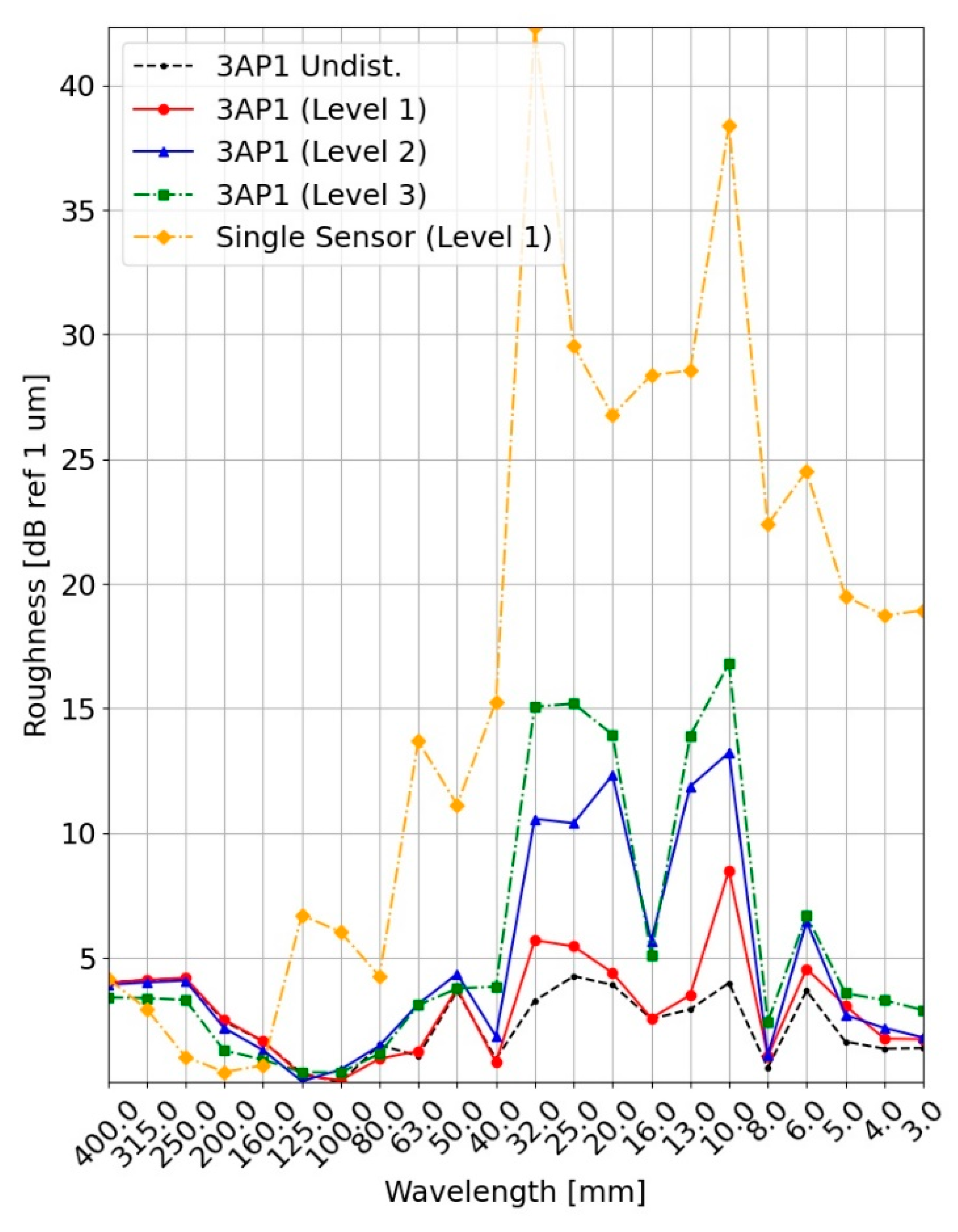
3.3. Displacement & Tilting
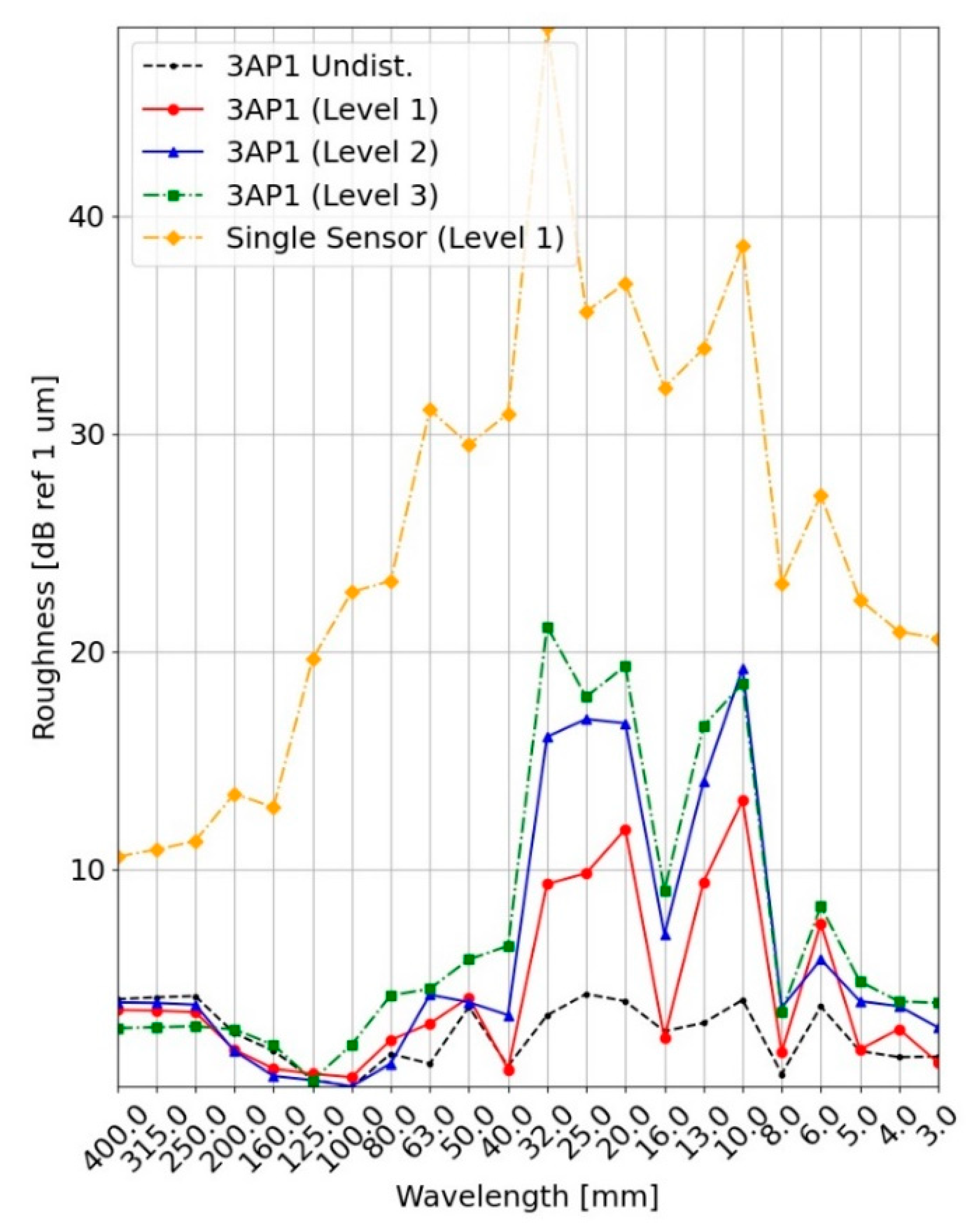
3.4. Vibration
3.5. Chord Methods & Optimization
4. Discussion
5. Conclusions & Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Veber, T.; Tamm, T.; Ründva, M.; Kriit, H.K.; Pyko, A.; Orru, H. Health impact assessment of transportation noise in two Estonian cities. Environ. Res. 2022, 204, 112319. [Google Scholar] [CrossRef] [PubMed]
- Vienneau, D.; Saucy, A.; Schäffer, B.; Flückiger, B.; Tangermann, L.; Stafoggia, M.; Wunderli, J.M.; Röösli, M. Transportation noise exposure and cardiovascular mortality: 15-years of follow-up in a nationwide prospective cohort in Switzerland. Environ. Int. 2022, 158, 106974. [Google Scholar] [CrossRef] [PubMed]
- Szwarc, M.; Kostek, B.; Kotus, J.; Szczodrak, M.; Czyżewski, A. Problems of Railway Noise-A Case Study. Int. J. Occup. Saf. Ergon. 2011, 17, 309–325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, D.J.; Fodiman, P.; Mahé, H. Experimental validation of the twins prediction program for rolling noise, part 2: Results. J. Sound Vib. 1996, 193, 137–147. [Google Scholar] [CrossRef]
- Miri, A.; Mohammadzadeh, S.; Salek, H. A finite element approach to develop track geometrical irregularity thresholds from the safety aspect. J. Theor. Appl. Mech. 2017, 55, 695. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2021, 151, 107336. [Google Scholar] [CrossRef]
- Kuffa, M.; Ziegler, D.; Peter, T.; Kuster, F.; Wegener, K. A new grinding strategy to improve the acoustic properties of railway tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 214–221. [Google Scholar] [CrossRef]
- Grassie, S.L. Rail irregularities, corrugation and acoustic roughness: Characteristics, significance and effects of reprofiling. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2012, 226, 542–557. [Google Scholar] [CrossRef]
- DIN EN 15610; Bahnanwendungen—Akustik—Messung der Schienen-und Radrauheit im Hinblick auf die Entstehung von Rollgeräuschen. Deutsche Fassung EN 15610:2019; Beuth Verlag: Berlin, Germany, 2021. [CrossRef]
- Mauz, F.; Wigger, R.; Wahl, T.; Kuffa, M.; Wegener, K. Acoustic roughness measurement of railway tracks: Implementation of an optical measurement approach & possible improvements to the standard. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 2022, 095440972210864. [Google Scholar] [CrossRef]
- Höjer, M.; Almgren, M. Monitoring system for track roughness. Euronoise 2015, 2015, 2007–2011. [Google Scholar]
- Valigi, M.C.; Logozzo, S.; Meli, E.; Rindi, A. New instrumented trolleys and a procedure for automatic 3d optical inspection of railways. Sensors 2020, 20, 2927. [Google Scholar] [CrossRef]
- Kuijpers, A.H.W.M.; Schwanen, W.; Bongini, E. Indirect Rail Roughness Measurement: The ARRoW System within the LECAV Project. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer: Tokyo, Japan, 2012; Volume 118, pp. 563–570. [Google Scholar]
- Kendl, F.; Heckelmüller, H.; Krump, G. Korrelation des Schallmesswagen-Pegels mit akustischer Schienenrauheit und Gleisabklingraten. In Proceedings of the DAGA 2016, Aachen, Germany, 14–17 March 2016. [Google Scholar]
- Lewis, R.B. Track-recording techniques used on British Rail. IEEE Proc. B Electr. Power Appl. 1984, 131, 73–81. [Google Scholar] [CrossRef]
- Bocciolone, M.; Caprioli, A.; Cigada, A.; Collina, A. A measurement system for quick rail inspection and effective track maintenance strategy. Mech. Syst. Signal Process. 2007, 21, 1242–1254. [Google Scholar] [CrossRef]
- Bongini, E.; Grassie, S.L.; Saxon, M.J. “Noise mapping” of a railway network: Validation and use of a system based on measurement of axlebox vibration. Notes Numer. Fluid Mech. Multidiscip. Des. 2012, 118, 505–513. [Google Scholar] [CrossRef]
- Dittrich, M.G.; Janssens, M.H.A. Improved measurement methods for railway rolling noise. J. Sound Vib. 2000, 231, 595–609. [Google Scholar] [CrossRef]
- Phamová, L.; Bauer, P.; Malinský, J.; Richter, M. Indirect method of rail roughness measurement—VUKV implementation and initial results. Notes Numer. Fluid Mech. Multidiscip. Des. 2015, 126, 189–196. [Google Scholar] [CrossRef]
- Tufano, A.R.; Chiello, O.; Pallas, M.A.; Faure, B.; Chaufour, C.; Reynaud, E.; Vincent, N. On-board indirect measurements of the acoustic quality of railway track: State-of-the art and simulations. In Proceedings of the Inter-Noise 2019 Madrid—48th International Congrress Exhibition on Noise Control Engineering, Madrid, Spain, 6–19 June 2019. [Google Scholar]
- Grassie, S.L. Measurement of railhead longitudinal profiles: A comparison of different techniques. WEAR An Int. J. Sci. Technol. Frict. Lubr. Wear 1996, 191, 245–251. [Google Scholar] [CrossRef]
- Tanaka, H.; Shimizu, A.; Sano, K. Development and verification of monitoring tools for realizing effective maintenance of rail corrugation. In Proceedings of the 6th IET Conference on Railway Condition Monitoring (RCM), Birmingham, UK, 17–18 September 2014; Volume 2014, pp. 1–6. [Google Scholar] [CrossRef]
- Naganuma, Y.; Tanaka, M.; Ichikawa, K. High-Speed Track Inspection Car in New Dr. Yellow. In Proceedings of the World Congress on Railway Research (WCRR), Cologne, Germany, 25–29 November 2001. [Google Scholar]
- Wang, C.; Zeng, J. Combination-Chord Measurement of Rail Corrugation Using Triple-Line Structured-Light Vision: Rectification and Optimization. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7256–7265. [Google Scholar] [CrossRef]
- Jeong, D.; Choi, H.S.; Choi, Y.J.; Jeong, W. Measuring acoustic roughness of a longitudinal railhead profile using a multi-sensor integration technique. Sensors 2019, 19, 1610. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, H.; Ma, Z.; Wang, C.; Zhong, X. Rail Corrugation Broadband Measurement Based on Combination-Chord Model and LS. IEEE Trans. Instrum. Meas. 2018, 67, 938–949. [Google Scholar] [CrossRef]
- Chen, T.L.; Yao-Hui, L.; Zeng, J.; Zhang, L.M. Modal and local modal analysis of high speed train car-body. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2012; Volume 215, pp. 800–803. [Google Scholar]
- DIN EN 13848-1; Bahnanwendungen—Oberbau—Gleislagequalität—Teil 1: Beschreibung der Gleisgeometrie. Deutsche Fassung EN 13848-1:2019; Beuth Verlag: Berlin, Germany, 2019.
- Dumitriu, M. Influence of the Longitudinal and Lateral Suspension Damping on the Vibration Behaviour in the Railway Vehicles. Arch. Mech. Eng. 2015, 62, 115–140. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Verlinden, O. Railway-induced ground vibrations—A review of vehicle effects. Int. J. Rail Transp. 2014, 2, 69–110. [Google Scholar] [CrossRef] [Green Version]




| Designation | [mm] | [mm] | [mm] | [-] |
|---|---|---|---|---|
| 3AP1 (Three-Point Asymmetrical 1) | 168 | 113 | 281 | 0.598 |
| 3AP2 (Three-Point Asymmetrical 2) | 168 | 218 | 386 | 0.435 |
| 3AP3 (Three-Point Asymmetrical 3) | 281 | 105 | 386 | 0.728 |
| 3AP4 (Three-Point Asymmetrical 4) | 113 | 105 | 218 | 0.518 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauz, F.; Wigger, R.; Wahl, T.; Kuffa, M.; Wegener, K. Acoustic Roughness Measurement of Railway Tracks: Laboratory Investigation of External Disturbances on the Chord-Method with an Optical Measurement Approach. Appl. Sci. 2022, 12, 7732. https://doi.org/10.3390/app12157732
Mauz F, Wigger R, Wahl T, Kuffa M, Wegener K. Acoustic Roughness Measurement of Railway Tracks: Laboratory Investigation of External Disturbances on the Chord-Method with an Optical Measurement Approach. Applied Sciences. 2022; 12(15):7732. https://doi.org/10.3390/app12157732
Chicago/Turabian StyleMauz, Florian, Remo Wigger, Tobias Wahl, Michal Kuffa, and Konrad Wegener. 2022. "Acoustic Roughness Measurement of Railway Tracks: Laboratory Investigation of External Disturbances on the Chord-Method with an Optical Measurement Approach" Applied Sciences 12, no. 15: 7732. https://doi.org/10.3390/app12157732
APA StyleMauz, F., Wigger, R., Wahl, T., Kuffa, M., & Wegener, K. (2022). Acoustic Roughness Measurement of Railway Tracks: Laboratory Investigation of External Disturbances on the Chord-Method with an Optical Measurement Approach. Applied Sciences, 12(15), 7732. https://doi.org/10.3390/app12157732






