Abstract
In this article, a novel and efficient collocation method based on Fibonacci wavelets is proposed for the numerical solution of the non-linear Hunter–Saxton equation. Firstly, the operational matrices of integration associated with the Fibonacci wavelets are constructed by following the strategy of Chen and Hsiao. The operational matrices merged with the collocation method are used to convert the given problem into a system of algebraic equations that can be solved by any classical method, such as Newton’s method. Moreover, the non-linearity arising in the Hunter–Saxton equation is handled by invoking the quasi-linearization technique. To show the efficiency and accuracy of the Fibonacci-wavelet-based numerical technique, the approximate solutions of the non-linear Hunter–Saxton equation with other numerical methods including the Haar wavelet, trigonometric B-spline, and Laguerre wavelet methods are compared. The numerical outcomes demonstrate that the proposed method yields a much more stable solution and a better approximation than the existing ones.
1. Introduction
Non-linear partial differential equations play a vital role in modeling real-life phenomena, especially in the field of applied sciences such as meteorology, aerospace engineering, oceanography, geology, astronomy, and many other disciplines. For the realistic treatment of these non-linear models, several numerical techniques such as the barycentric interpolation collocation method [], Fourier spectral method [], and reproducing kernel method [] have been adopted for the numerical treatment of these non-linear partial differential equations, such as the Klein–Gordon–Zakharov equations, Schrödinger equation, Duffing systems, and many more. The Hunter–Saxton equation is one among those non-linear partial differential equations that describe waves of a nematic liquid crystal in an enormous director field and arise at the short-wave limit of the Camassa–Holm equation—an integrable model of shallow-water waves propagating uni-directionally across a flat bottom []. This equation has both the bi-Hamiltonian and bi-variational structure of integrable partial differential equations, often referred to as the Hunter–Saxton equation, which re-expresses the geodesic flow in the diffeomorphism group of a circle. Formally, the non-linear Hunter–Saxton equation is given by
Equation (1) can also be redrafted as
where and denote the space and time coordinates, respectively, with initial and boundary conditions:
In practice, it is more appropriate to impose a boundary condition of the form:
or even the initial and boundary conditions:
where
, and are sufficiently smooth functions.
Keeping in view the prolificacy of the Hunter–Saxton equation governed by the differential Equation (2), a substantial amount of research has been carried out in the quest to obtain numerical solutions via several analytical and numerical techniques. For instance, Behzadi [] employed the homotopy analysis method (HAM) for the approximate solution of the non-linear Hunter–Saxton equation and showed that the HAM is more rapidly convergent than certain other iterative methods such as the variational iteration method, Adomian decomposition method, modified variational iteration method, and modified Adomian decomposition method, whereas Wei et al. [] established the global solutions of the periodic Hunter–Saxton equation with weak dissipation. Aratyn et al. [] obtained exact rational solutions of the generalized Hunter–Saxton equation by using the Padé approximation. Besides, Rouhparvar [] proposed the reduced differential transform method for obtaining the solution of the non-linear Hunter–Saxton equation, which does not require linearization, discretization, nor perturbation of the underlying non-linear differential equation. Hashmi et al. [] examined the efficiency of the cubic trigonometric B-spline method for obtaining the numerical solution of the non-linear Hunter–Saxton equation. Karaagac et al. [] applied the finite element method by reducing the governing non-linear partial differential equation to a system of ordinary differential equations in terms of shape functions. Sato [] formulated a stable and convergent finite difference method for the modified Hunter–Saxton equation on a periodic domain. Nonetheless, very recently, Ahmad et al. [] demonstrated a highly applicable aspect of the Hunter–Saxton equation while undertaking the numerical treatment of the liquid crystal model described through the Hunter–Saxton equation by employing the Sinc collocation method via the theta weighted scheme.
Over the last couple of decades, wavelet theory has seen unprecedented progress in the form of innovative and efficient numerical algorithms. Wavelet-based numerical schemes have dethroned the usual numerical methods and have received much attention from researchers working in various disciplines of science and engineering [,]. In particular, the wavelet-based matrix methods have acquired a respectable status in numerical analysis due to their easy implementation, simple procedure, and rapid convergence. Moreover, they are computer-oriented and do not require calculating the inverse of the wavelet matrix, and less CPU time is needed as the major blocks of the wavelet operational matrix are computed once and reused in subsequent computations. As of now, numerous linear and non-linear differential equations have been solved by employing various wavelet families, including the Haar wavelets, Euler wavelets, Bernoulli wavelets, Chebyshev wavelets, Legendre wavelets, Hermite wavelets, Gegenbauer wavelets, and ultraspherical wavelets [,,,,,,,]. To harness the advantages of wavelet-based numerical methods in the context of the non-linear Hunter–Saxton equation, many wavelet-based methods have been employed for obtaining the numerical solution. To mention a few, Arbabi et al. [] utilized the Haar wavelet quasi-linearization approach to obtain the approximate solution of the Hunter–Saxton equation. Recently, Srinivasa et al. [] developed a collocation technique based on the Laguerre wavelet for the numerical solution of the Hunter–Saxton equation and exhibited the uniform convergence of the employed method.
The origin of the Fibonacci numbers dates back to the early 1200s with the seminal work of Italian mathematician Fibonacci studying the famous rabbit problem. The Fibonacci numbers with initial values are the terms of the sequence . Using the Fibonacci-like recurrence relations, Catalan and Jacobsthal introduced a large class of polynomials commonly known as Fibonacci polynomials. The polynomials introduced by Catalan are defined by the recurrence relation with , whereas the polynomials introduced by Jacobsthal have the general form , with . Later on, Byrd defined another class of Fibonacci polynomials of the form , where . Over a couple of decades, some prominent offshoots of the Fibonacci polynomials have appeared in the open literature. For instance, Falcon and Plaza [] introduced the notion of h-Fibonacci polynomials and studied the derivatives of these polynomials in terms of the convolution of h-Fibonacci polynomials. Mathematically, the -Fibonacci polynomials are defined by the recurrence relation , where , , and is a polynomial with real coefficients. It is pertinent to mention that for and , one can obtain the Fibonacci polynomials of the Catalan and Byrd type, respectively []. Lee and Asci [] define another novel generalization of Fibonacci polynomials coined as -Fibonacci polynomials and obtained several results regarding the factorization of the Pascal matrix involving these polynomials. Such polynomials are defined by the recurrence relation , where , and and are polynomials with real coefficients. Subsequently, Catarino [] defined a quaternion analogue of the h-Fibonacci polynomials of the form where is the -Fibonacci polynomial. Recently, Strzałka et al. [] introduced a new class of Fibonacci polynomials coined as distance Fibonacci polynomials, which embodies the classical Fibonacci, Jacobsthal, and Narayana polynomials simultaneously. Owing to the nice characteristics of the Fibonacci polynomials, they have been extensively employed for solving differential equations [], integro-differential equations [], fractional delay differential equations [], fractional differential equations [], and many more.
Fibonacci wavelets are a novel addition to the class of compactly supported wavelets, having the main advantage of being polynomial-based and, as such, enjoying smoothness at the expense of having compact support. In fact, these wavelets are not generated by the orthogonal polynomials; however, the Fibonacci polynomials can be represented in terms of orthogonal Chebychev orthogonal polynomials of the second kind. Unlike the shifted Legendre polynomials, the Fibonacci polynomials possess fewer terms, resulting in faster computation, thus minimizing the computational errors. The Fibonacci wavelets are dependent on two parameters k and M, which increases the rate convergence of the Fibonacci wavelet series. Indeed, the convergence of the Fibonacci wavelet method is faster than the orthogonal wavelet methods and many other numerical methods. Motivated and inspired by the nice characteristics of the Fibonacci wavelets, our goal is to introduce a new numerical technique based on Fibonacci wavelets for obtaining the solution of the non-linear Hunter–Saxton Equation (2). At the outset, the operational matrices of integration associated with Fibonacci wavelets are constructed by following the strategy of Chen and Hsiao [], then the quasi-linearization technique is implemented to convert the underlying non-linear equation into the linearized form. Finally, the operational matrices of integration are employed to convert the problem under consideration into a system of algebraic equations, which are then solved with any conventional method, such as the Newton method.
The remainder of the article is organized as follows: Section 2 is completely devoted to an elucidation of the Fibonacci wavelet method, including the construction of operational matrices. In Section 3, the proposed method is implemented for solving the non-linear Hunter–Saxton equation. The error and convergence of the proposed method are briefly illustrated in Section 4. In Section 5, the validity and efficiency of the proposed wavelet scheme are demonstrated on certain test problems. The article ends with an epilogue in Section 6.
2. Fibonacci Wavelets and Operational Matrices
In the present section, we first construct the Fibonacci wavelets using the Fibonacci polynomials of degree M, and then, the corresponding operational matrices of integration are formulated by following the strategy of Chen and Hsiao []. Towards the end of the section, we shall also discuss the quasi-linearization technique, which plays a vital role in transforming the given non-linear problem into a linear differential equation.
2.1. Fibonacci Wavelets and Function Approximation
For any positive real number , the Fibonacci polynomials are defined by the recurrence formula:
with initial conditions . Generally, the Fibonacci polynomials are defined by
Wavelets constitute an orthonormal family of functions generated from dilations and translations of a fixed function called the “mother wavelet” . When the dilation and translation parameter vary continuously, one can obtain the following family of continuous wavelets []:
If we restrict the parameters and to discrete values, say , for positive integers n and k, we obtain the following family of discrete wavelets:
The discrete wavelet family forms a wavelet basis for . Motivated by the above construction, we define the Fibonacci wavelets on the interval as []:
where k and n, respectively, denote the level of resolution and translation with , . The Fibonacci polynomial of degree m can also be computed as []
where is the usual floor function with normalization factor
If we take , we obtain the following family of Fibonacci wavelets:
Any square integrable function can be approximated via Fibonacci wavelets as
where represents the Fibonacci wavelet coefficients, given by
The matrix appearing in Equation (16) represents the Fibonacci wavelet matrix of order and is given by
The wavelet coefficient vector can be attained as:
where
The following collocation points are considered for obtaining the Fibonacci wavelet approximations:
2.2. Operational Matrices of Integration via Fibonacci Wavelets
This subsection is committed to the construction of the operational matrices of integration associated with Fibonacci wavelets (10) by adopting the Chen and Hsiao technique []:
where denotes the Fibonacci wavelet operational matrix of integration with order .
2.3. Quasi-Linearization Technique
First introduced by Bellman and Kalaba [], quasi-linearization is a technique that is essentially a new variant of the well-known Newton–Raphson method, for facilitating the approximate solutions of the non-linear differential equations of degree m. For a clear understanding of this technique, we consider the following differential equation:
subject to
Implementing the quasi-linearization technique leads (24) to the recurrence relations:
with condition .
Subsequently, the recurrence relation for the nth-order non-linear differential equations can be obtained as:
with the same conditions. Equation (26) is the desired linear differential equation, which can be recursively solved for from .
3. Method of Solution
In this section, we shall employ the operational matrices of integration based on Fibonacci wavelets as discussed in Section 2 for the numerical treatment of the non-linear Hunter–Saxton Equation (2). To begin with, we recall the non-linear Hunter–Saxton equation:
with initial condition and boundary conditions:
where , and possess second-order continuous derivative and belong to . Following the quasi-linearization technique as discussed in the previous section, Relation (27) is transformed to a linear differential equation as
with initial guess . In order to solve (31), we approximate the highest partial derivative appearing in (29) by the Fibonacci wavelet basis as
where is the unknown wavelet coefficient vector given by (17) to be determined. Integrating (30) with respect to between limits and yields
Integrating (31) with respect to between the limits 0 and , we obtain
Again, integrating (32) with respect to between the limits 0 and yields
Differentiating (33) with respect to , we have
Next, we differentiate (34) with respect to to obtain
By implementing (36), we obtain the following system of algebraic equations:
Solving the system of algebraic Equation (38) at the collocation points (20) with the avail of Newton’s method in the MATLAB software, we can ascertain the Fibonacci coefficients, and thereafter, superseding the unknown coefficients in (37) yields the approximate solution of the Hunter–Saxton Equation (27) via the Fibonacci wavelet method.
4. Error Estimation and Convergence Analysis
This section is entirely devoted to study the error bounds and convergence results associated with the Fibonacci wavelet method.
Theorem 1.
Let be the Fibonacci wavelet expansion of any sufficiently smooth real-valued function belonging to the space . Then, the norm truncated error is given by
where
Proof.
constitute a basis for the polynomial space of degree M. Therefore, the Taylor expansion of any can be expressed as
From the above expansion, one can obtain
As the interval can be divided into sub-intervals of the form , therefore, by virtue of (40), we obtain
where and . Hence, . This completes the proof of Theorem 1. □
Theorem 2.
Let be a bounded continuous function in with bound . Then, the Fibonacci wavelet expansion given by (14) converges uniformly to with
Proof.
can be approximated by the Fibonacci wavelets as
where
By taking , we obtain
Consequently, we obtain
Applying the property of Fibonacci polynomials, we have
Thus, we conclude that converges absolutely provided , and hence, the Fibonacci wavelet series given by (14) converges uniformly to . □
Towards the culmination, we provide an Algorithm 1 of the Fibonacci wavelet method to obtain a numerical solution of the Hunter-Saxton Equation (27).
| Algorithm 1: Algorithm for the proposed Fibonacci wavelet method |
|
5. Numerical Examples and Discussion
This section constitutes the centerpiece of this article: the operational matrices of integration as constructed in Section 2 based on the Fibonacci wavelets are utilized for obtaining the approximate solution of the non-linear Hunter–Saxton Equation (27) under certain initial and boundary conditions. To facilitate the narrative, we take into account some examples whose exact solutions are available in the open literature. This allows us to compare the obtained results with exact solutions and the solutions acquired through other numerical techniques. The accuracy of the proposed method is determined by the absolute error:
where and , respectively, denote the exact and approximate solutions.
Example 1.



Consider Equation (29) subject to the initial condition:
and the boundary condition:
The analytic solution of the problem (29) with respect to the initial and boundary conditions (45) and (46) is
The initial guess is given by
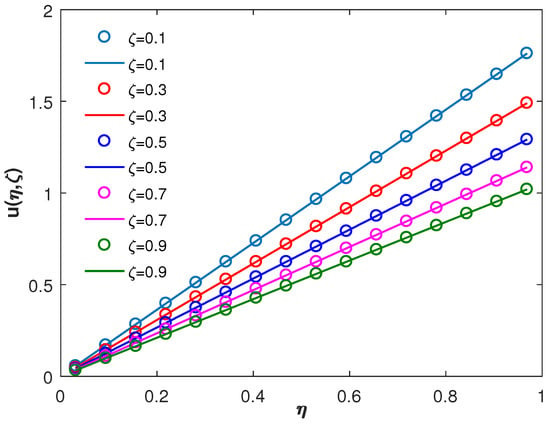
The comparison of the exact solution and the approximate solution for and is depicted in Figure 1 and Figure 2, respectively. From Figure 3, the absolute error for and is represented via three-dimensional plots, from which we infer that as we increase the wavelet parameters k and M, the absolute error decreases. To show the legitimacy of the proposed method, we compare the obtained absolute error with the absolute error of the trigonometric B-spline [] and the Haar wavelet methods [] in Table 1, Table 2 and Table 3 for different values of ζ, from which one can easily infer that the results achieved through the Fibonacci wavelets are reasonably effective in comparison to the other existing numerical methods.

Figure 1.
Comparison of analytic and FWM solutions of Example 1 at for different .

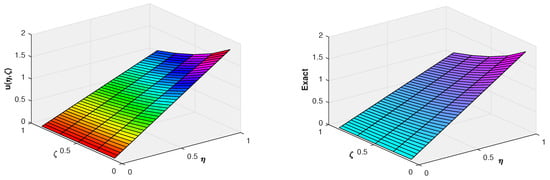
Figure 2.
Three-dimensional comparison of the approximate and exact solution at of Example 1.

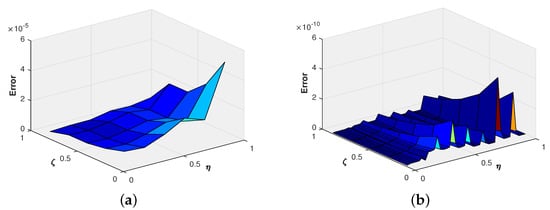
Figure 3.
(a) Absolute error at ; (b) absolute error at of Example 1.

Table 1.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for = 0.1.

Table 2.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for = 0.01.

Table 3.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 1 for = 0.001.
Example 2.



Consider Equation (29) subject to the initial conditions:
and the boundary conditions:
The analytic solution of the problem (29) together with the initial and boundary conditions (49) and (50) is
The initial guess is given by
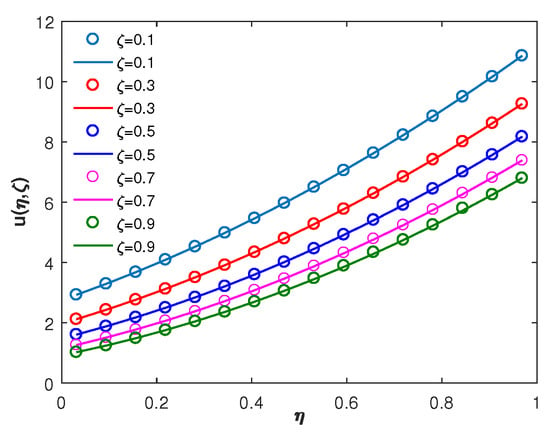
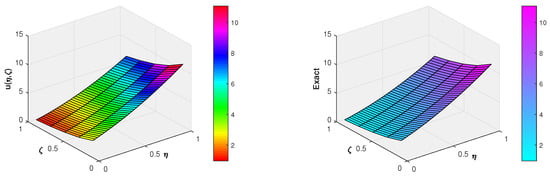
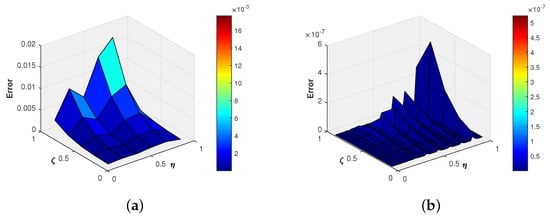
Figure 4 and Figure 5 depict the graphical comparison of the proposed method with the exact solution for and , respectively, which suggests that the Fibonacci wavelets are in good agreement with the analytic solution of the problem. Moreover, in Figure 6, the absolute error for different and is shown via a three-dimensional plot, which elucidates that, upon increasing the wavelet parameters k and M, the absolute error decreases. Finally, a comparison of the absolute error of the proposed method with the trigonometric B-spline [] and the Laguerre wavelet methods [] is given in Table 4, Table 5 and Table 6 for different values of ζ. From these tables, we conclude that the proposed method is more accurate than the other existing numerical methods.

Figure 4.
Comparison of analytic and FWM solutions of Example 2 at , for different .

Figure 5.
Three-dimensional comparison of the approximate and exact solutions at of Example 2.

Figure 6.
(a) Absolute error at ; (b) absolute error at of Example 2.

Table 4.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for = 0.1.

Table 5.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for = 0.01.

Table 6.
Comparison of the proposed method’s absolute error with the HWM and B-spline methods of Example 2 for = 0.001.
6. Conclusions and Future Work
In the present paper, we formulated a new and efficient collocation method based on the Fibonacci wavelets for obtaining the numerical solution of the non-linear Hunter–Saxton equation. The efficacy of the proposed method was demonstrated via certain test problems. The absolute error due to the proposed scheme was compared with the absolute error of the trigonometric B-spline method, Laguerre wavelet method, and Haar wavelet method. In conclusion, we inferred that the proposed wavelet-based numerical technique yields a much more stable solution and a better approximation than the existing ones. The present work can be extended across diverse fields of physical and biological sciences, in particular obtaining the solution of higher-dimensional time-fractional differential equations.
Author Contributions
Formal analysis, H.M.S. and F.A.S.; Investigation, F.A.S.; Methodology, N.A.N.; Project administration, H.M.S.; Software, N.A.N.; Supervision, H.M.S.; Validation, N.A.N.; Writing—original draft, F.A.S. and N.A.N.; Writing—review & editing, H.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are included within manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Oruç, O. Numerical simulation of two-dimensional and three-dimensional generalized Klein–Gordon–Zakharov equations with power law nonlinearity via a meshless collocation method based on barycentric rational interpolation. Numer. Methods Partial Differ. Equ. 2022, 38, 1068–1089. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, W.O.; Liu, X.; Qu, H. Fourier Spectral Method for a Class of Nonlinear Schrödinger Models. Adv. Math. Phys. 2021, 2021, 9934858. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, W.; Du, H. A new reproducing kernel method for Duffing equations. Int. J. Comput. Math. 2021, 98, 2341–2354. [Google Scholar] [CrossRef]
- Hunter, J.K.; Saxton, R. Dynamics of director fields. SIAM J. Appl. Math. 1991, 51, 1498–1521. [Google Scholar] [CrossRef]
- Behzadi, S.S. Numerical solution of Hunter–Saxton equation by using iterative methods. Int. J. Math. Math. Sci. 2011, 3, 127–143. [Google Scholar]
- Wei, X.; Yin, Z. Global existence and blow-up phenomena for the periodic Hunter–Saxton equation with weak dissipation. J. Nonlinear Math. Phys. 2011, 18, 139–149. [Google Scholar] [CrossRef]
- Aratyn, H.; Gomes, J.F.; Ruy, D.V.; Zimerman, A.H. Rational solutions from Padé approximants for the generalized Hunter–Saxton equation. J. Phys. Conf. Ser. 2013, 474, 012006. [Google Scholar] [CrossRef] [Green Version]
- Rouhparvar, H. Analytical solution of the Hunter–Saxton equation using the reduced differential transform method. J. Approx. Theory 2016, 10, 61–73. [Google Scholar]
- Hashmi, M.S.; Awais, M.; Waheed, A.; Ali, Q. Numerical treatment of Hunter–Saxton equation using cubic trigonometric B-spline collocation method. AIP Adv. 2017, 7, 095124. [Google Scholar] [CrossRef] [Green Version]
- Karaagac, B.; Esen, A. The Hunter–Saxton Equation: A numerical approach using collocation method. Numer. Methods Partial. Differ. Equ. 2018, 34, 1637–1644. [Google Scholar] [CrossRef]
- Sato, S. Stability and convergence of a conservative finite difference scheme for the modified Hunter–Saxton equation. BIT Numer. Math. 2019, 59, 213–241. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, I.; Ilyas, H.; Kutlu, K.; Anam, V.; Hussain, S.I.; Guirao, J.L.G. Numerical computing approach for solving Hunter–Saxton equation arising in liquid crystal model through sinc collocation method. Heliyon 2021, 7, E07600. [Google Scholar] [CrossRef] [PubMed]
- Debnath, L.; Shah, F.A. Wavelet Transforms and Their Applications; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Lepik, U.; Hein, H. Haar Wavelets with Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Shah, F.A.; Irfan, M.; Nisar, K.S.; Matoog, R.T.; Mahmoud, E.E. Fibonacci wavelet method for solving time-fractional telegraph equations with Dirichlet boundary conditions. Results Phys. 2021, 24, 104–123. [Google Scholar] [CrossRef]
- Shah, F.A.; Irfan, M. Generalized wavelet method for solving fractional bioheat transfer model during hyperthermia treatment. Int. J. Wavelets Multiresolut. Inf. Process. 2021, 19, 2050090. [Google Scholar] [CrossRef]
- Irfan, M.; Shah, F.A.; Nisar, K.S. Gegenbauer wavelet quasi-linearization method for solving fractional population growth model in a closed system. Math. Methods. Appl. Sci. 2022, 45, 3605–3623. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, F.A.; Abass, R. An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation. Russ. J. Math. Phys. 2019, 26, 77–93. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, F.A.; Irfan, M. Generalized wavelet quasi-linearization method for solving population growth model of fractional order. Math. Methods Appl. Sci. 2020, 43, 8753–8762. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Irfan, M.; Shah, F.A. A Fibonacci Wavelet method for solving dual-phase-lag heat transfer model in multi-layer skin tissue during hyperthermia treatment. Energies 2021, 14, 2254. [Google Scholar] [CrossRef]
- Chouhan, D.; Mishra, V.; Srivastava, H.M. Bernoulli wavelet method for numerical solution of anomalous infiltration and diffusion modeling by nonlinear fractional differential equations of variable order. Results Appl. Math. 2021, 10, 1–13. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, Y.; Yousefi, S.A. Fibonacci wavelets and their applications for solving two classes of time-varying delay problems. Optim. Control Appl. Meth. 2019, 41, 395–416. [Google Scholar] [CrossRef]
- Arbabi, S.; Nazari, A.; Darvishi, M.T. A semi-analytical solution of Hunter–Saxton equation. Optik 2016, 127, 5255–5258. [Google Scholar] [CrossRef]
- Srinivasa, K.; Rezazadeh, H.; Adel, W. Numerical investigation based on Laguerre wavelet for solving the Hunter Saxton equation. Int. J. Appl. Comput. Math. 2020, 6, 139. [Google Scholar] [CrossRef]
- Falcon, S.; Plaza, A. On k-Fibonacci sequences and polynomials and their derivatives. Chaos Soliton Fract. 2009, 39, 1005–1019. [Google Scholar] [CrossRef]
- Nalli, A.; Haukkanen, P. On generalized Fibonacci and Lucas polynomials. Chaos Soliton Fract. 2009, 42, 3179–3186. [Google Scholar] [CrossRef]
- Lee, S.; Asci, M. Some Properties of the (p,q)-Fibonacci and (p,q)-Lucas Polynomials. J. Appl. Math. 2012, 2012, 264842. [Google Scholar] [CrossRef] [Green Version]
- Catarino, P. A note on h(x)-Fibonacci quaternion polynomials. Chaos Soliton Fract. 2015, 77, 1–5. [Google Scholar] [CrossRef]
- Strzałka, D.; Wolski, S.; Wioch, A. Distance Fibonacci polynomials by graph methods. Symmetry. 2021, 13, 2075. [Google Scholar] [CrossRef]
- Koç, A.B.; Çakmak, M.; Kurnaz, A. A matrix method based on the Fibonacci polynomials to the generalized pantograph equations with functional arguments. Adv. Math. Phys. 2014, 2014, 694580. [Google Scholar] [CrossRef]
- Seifi, A.; Lotfi, T.; Allahviranloo, T. A new efficient method using Fibonacci polynomials for solving of first-order fuzzy Fredholm-Volterra integro-differential equations. Soft Comput. 2019, 23, 9777–9791. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, O.; Yousefi, S.A. Fractional-order Fibonacci-hybrid functions approach for solving fractional delay differential equations. Eng. Comput. 2020, 36, 795–806. [Google Scholar] [CrossRef]
- Mohamed, A.S. Fibonacci collocation pseudo-spectral method of variable-order space-fractional diffusion equations with error analysis. AIMS Math. 2022, 7, 14323–14337. [Google Scholar] [CrossRef]
- Chen, C.F.; Hsiao, C.H. Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc. Control Theory Appl. 1997, 144, 87–94. [Google Scholar] [CrossRef] [Green Version]
- Falcon, S.; Plaza, A. The k-Fibonacci sequence and the Pascal 2-triangle. Chaos Solitons Fract. 2007, 33, 38–49. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasi-linearization and Non-linear Boundary-Value Problems; Elsevier: New York, NY, USA, 1965. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).