Application of Three-Dimensional Direct Least Square Method for Ellipsoid Anisotropy Fitting Model of Highly Irregular Drill Hole Patterns

Abstract

Ellipsoid or geometric anisotropy is a widely used method in geostatistical analysis to obtain variograms with different ranges in different directions (azimuth) and relatively similar sill variance. Ellipsoid anisotropy is indispensable in mining when a resource geologist intends to understand the spatial continuity of variables related to any geological controls of the mineralization. For example, when dealing with mineralization related to tabular deposits, a porphyritic deposit with an irregular drill hole pattern (fan drilling), three-dimensional ellipsoid anisotropy is quite challenging to model. We assume that the variables’ spatial continuity is isotropic, and we model it using a three-dimensional omnidirectional variogram. However, if the actual spatial continuity of the variables has a three-dimensional anisotropy, then assuming a three-dimensional omnidirectional variogram will generate imprecise resource estimations. This study presents a new practical three-dimensional ellipsoid model-fitting method using a three-dimensional direct least square method. We investigated a zinc (Zn) dataset from thousands of irregular drill hole patterns from a porphyritic system associated with skarn orebodies for the case study.

1. Introduction

Ellipsoid anisotropy, also known as geometric anisotropy, is widely used in the variogram analysis of any type of mineral deposit. Ellipsoid anisotropy can indicate metal grade continuities in different directions. Typically, we perform variogram modeling in a three-dimensional (3D) dataset for at least four directions on the horizontal axis (i.e., north–south (N–S), northeast–southwest (NE–SW), east–west (E–W), and southeast–northwest (SE-NW)), and one direction on the vertical axis or in the downhole direction. For regular drill hole patterns, the searching direction of an experimental variogram follows the azimuth or the direction of the drill hole or sample pattern. A problem arises when the drill hole or sample pattern is highly irregular for a specific mineral deposit (e.g., a fan drilling pattern in a porphyritic deposit). In such drill hole patterns, simply assuming an anisotropy model is very common in experimental variograms.

Some researchers have studied two-dimensional anisotropy or ellipsoid anisotropy modeling in the horizontal direction [1,2,3,4]. Nakaya et al. [5] addressed the determination of the anisotropy of the spatial correlation structure in three-dimensional datasets, and Borgman and Chao [6] studied an estimation of a multidimensional covariance function in the case of anisotropy. Two papers [7] and [8] presented a two-dimensional direct least square method for fitting the two-dimensional ellipsoid anisotropy from a coal and laterite nickel dataset with a relatively regular drill hole pattern. A paper [9] explained a generalization of the three-dimensional ellipsoid fitting using a three-dimensional direct least square method to obtain hyperboloids.

This paper proposes a new approach for the three-dimensional model fitting of ellipsoid anisotropy by modifying the three-dimensional direct least square method [9]. For the case study, we examined a dataset of zinc grades from highly irregular drill hole patterns in the contact zone between a porphyritic system and a skarn deposit. This three-dimensional ellipsoid model can signify the three-dimensional area of influence for investigating the spatial distribution of metal grades (i.e., the maximum searching windows of three-dimensional estimation or interpolation). We obtain the input for three-dimensional ellipsoid fitting derived from the variogram ranges for each direction in three-dimensional space. The more precise mineral resource estimation results obtained by this new practical approach can produce more confidence in ore reserves in mining industries.

2. Material and Method

2.1. Dataset

We adopted the dataset used in this study from [10]. It contains zinc (Zn) grades in % weight from an irregular drill hole pattern in the contact zone between porphyritic systems and skarn orebodies with various structural and stratigraphic settings. The dataset comprised 11,773 zinc assay data derived from thousands of mostly fan drilling patterns (Figure 1). These composited data with average length of 15 m were used for variogram construction and kriging estimation.

We depict the statistical distribution of Zn grades in Figure 2, where it is transformed into the lognormal scale with a mean of 0.019% and a variance of 0.014%.

Experimental variograms are sensitive to the data pattern when we mainly derive the stationary variogram from data with a relatively regular pattern. We should perform a strategy for setting the parameters for experimental variogram construction to obtain a relatively robust variogram when we derive the dataset from an irregular drill hole pattern, as shown in Figure 1.

In this study, because the drill hole patterns did not show any specific orientation, we constructed an experimental variogram in the horizontal direction following the four principal directions (i.e., N–S, NE–SW, E–W, SE–NW). A lag distance of 100 m was used following the average drill hole spacing. Meanwhile, an experimental variogram was constructed for the downhole direction with azimuth (bearing) following the eight principal directions (N, NE, E, SE, S, SW, W, NW) with azimuth tolerance of 45° for each direction, and bandwidth was set to be the same as lag distance. At the same time, we determined the dip or inclination arbitrarily (trial for each 10° from horizontal to vertical) using a lag distance of 15 m following the sample interval in the downhole with azimuth tolerance of 45° for each direction, and bandwidth was set to be the same as lag distance. Among them, we chose the relatively most robust experimental variogram for a specific dip, as downhole patterns are highly irregular in any direction in three-dimensional (3D) space.

Four horizontal and eight inclined variogram fittings were performed using a spherical model to obtain the variogram model parameters, mainly the range (see Figure 3). For the fitting model of 3D ellipsoid anisotropy, we set the total sill of all variograms (nugget plus sill variances) to be the same as the statistical variance (i.e., 0.014%).

Table 1. Result of 3D variogram fitting parameters and their position in q Cartesian coordinate system.

3D Variogram of Zn Grade					Result of Conversion into 3D Coordinate Points
No.	Azimuth (N°E)	Dip (°)	Range (m)	Orientation	No.	x	y	z
1	0	0	1000	horizontal	1	0	1000	0
2	45	0	550	horizontal	2	388.91	388.91	0
3	90	0	500	horizontal	3	500	0	0
4	135	0	950	horizontal	4	671.75	−671.75	0
5	180	0	1000	horizontal	5	0	−1000	0
6	225	0	550	horizontal	6	−388.91	−388.91	0
7	270	0	500	horizontal	7	−500	0	0
8	315	0	950	horizontal	8	−671.75	671.75	0
9	0	20	65	inclined	9	0	22.23	−22.23
10	45	20	45	inclined	10	29.90	−42.29	10.88
11	90	40	40	inclined	11	30.64	0	−25.71
12	135	20	90	inclined	12	−59.80	−30.78	59.80
13	180	40	180	inclined	13	−137.89	0	−115.70
14	225	30	225	inclined	14	−137.78	−137.78	−112.50
15	270	30	115	inclined	15	−99.59	0	−57.50
16	315	40	50	inclined	16	−27.08	−32.14	−27.08

summarizes the variograms’ ranges and their position in the Cartesian coordinate system in 3D space.

If we plot the range of a variogram in 3D space, it likely shows a 3D ellipsoid anisotropy, which we fitted using the 3D direct least square method (Figure 4). The direct least square method is a procedure to find the best fit for data points. This method aims to minimize the sum of the square of the difference between an observed value and the fitted value provided by a model. In several studies, a linear or a non-linear equation in a two-dimensional (2D) space has been shown to be able to fit scattered data. However, in this paper, we develop the 3D direct least square method to fit a quadratic surface equation to variogram ranges in this research.

A significant challenge for this method is that the ranges and inclinations varied for each downhole direction (see Table 1). We explain the method in the following sub-section.

2.2. Method

This study uses the principle of the least square method described in [9]. In Rahmadiantri et al. [9], the fittings of data points can be hyperboloid. So that the three-dimensional ellipsoid anisotropy modeling remains relevant in the real world, the data fitting has been successfully limited to an ellipsoid shape in this research. Fikri et al. [8] demonstrated the application of the direct least square method for fitting the two-dimensional (2D) ellipsoid anisotropy of some coal deposit parameters (see Figure 5). The fitting method would be more complicated in 3D ellipsoid anisotropy because there is additional range data in the downhole direction.

First, to fit the data into three-dimensional shapes, the following general form of the quadratic surface equation is used:

$$f\left(x,y,z\right)≔a_{11}{x}^2+2a_{12}xy+2a_{13}xz+2a_{23}yz+a_{22}{y}^2+a_{33}{z}^2+b_{1}x+b_{2}y+b_{3}z+c=\mathit{u}·\mathit{x}=0$$

with:

$$\mathit{u}={\left(a_{11} 2a_{12} 2a_{13} 2a_{23} a_{22} a_{33} b_1 b_2 b_3 c\right)}^T$$

$$\mathit{x}={\left(\begin{array}{cccccccccc}{x}^2& xy& xz& yz& y^2& z^2& x& y& z& 1\end{array}\right)}^T.$$

Furthermore, to obtain the coefficients of the general equation, the following steps are performed:

• Step 1. From the data, build the following matrix:

  $$\mathit{S}=\left(\begin{array}{cccccccccc}{x}_1& y_1& z_1& 1& x_1{}^2& \sqrt{2}{x}_1{y}_1& \sqrt{2}{x}_1{z}_1& \sqrt{2}{y}_1{z}_1& y_1{}^2& z_1{}^2\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_n& y_n& z_n& 1& x_n{}^2& \sqrt{2}{x}_n{y}_n& \sqrt{2}{x}_n{z}_n& \sqrt{2}{y}_n{z}_n& y_n{}^2& z_n{}^2\end{array}\right)$$

  where $n$ is the number of data.
• Step 2. Use $QR$ factorization to get $\mathit{S}=\mathit{Q}\mathit{R}$, where Q is an orthogonal matrix and R is an upper triangular matrix.
• Step 3. Write $\mathit{R}$ as $=\left(\begin{array}{cc}{\mathit{R}}_{\mathbf{11}}& {\mathit{R}}_{\mathbf{12}}\\ \mathbf{0}& {\mathit{R}}_{\mathbf{22}}\end{array}\right)$ and define the vectors $\mathit{v}={\left(\begin{array}{ccc}{b}_1& b_2& b_{3}c\end{array}\right)}^T$ and $\mathit{w}={\left(\begin{array}{ccc}{a}_{11}& \sqrt{2}{a}_{12}& \sqrt{2}{a}_{13}\sqrt{2}{a}_{23}{a}_{22}{a}_{33}\end{array}\right)}^T$.
• Step 4. Write $\Vert \mathit{S}\left(\begin{array}{c}\mathit{v}\\ \mathit{w}\end{array}\right)\Vert =\Vert \mathit{Q}\mathit{R}\left(\begin{array}{c}\mathit{v}\\ \mathit{w}\end{array}\right)\Vert =\Vert \mathit{R}\left(\begin{array}{c}\mathit{v}\\ \mathit{w}\end{array}\right)\Vert$. The problem is to solve $min\Vert {\mathit{R}}_{\mathbf{22}}\mathit{w}\Vert$ with constraint $\Vert \mathit{w}\Vert =1$.
• Step 5. Use singular value decomposition (SVD) on ${\mathit{R}}_{\mathbf{22}}$ to get ${\mathit{R}}_{\mathbf{22}}=\mathit{U}\Sigma {\mathit{V}}^T$.
• Step 6. By the SVD theorem, the solution of $\min \Vert {\mathit{R}}_{\mathbf{22}}\mathit{w}\Vert$ with constraint $\Vert \mathit{w}\Vert =1$ is $\mathit{w}={\mathit{v}}_{\mathit{n}}$, where ${\mathit{v}}_{\mathit{n}}$ is the last column of $\mathit{V}$.
• Step 7. Get $\mathit{v}=-R_{11}{}^{-1}{R}_{12}\mathit{w}$. Then $\mathit{u}$ is obtained by substituting the vectors v and w. Use $QR$ factorization to get $\mathit{S}=\mathit{Q}\mathit{R}$, where Q is an orthogonal matrix and R is an upper triangular matrix.

Next, substitute the coefficients in vector $\mathit{u}$ into the general equation $f\left(x,y,z\right)$ to obtain ellipsoid or hyperboloid fitting. To obtain the ellipsoid form dataset, two steps are done: (1) if the obtained equation $f\left(x,y,z\right)$ is an ellipsoid equation, then the desired result has been obtained; (2) if the obtained result is a hyperboloid equation, then continue the fitting process using the following steps:

1.

From the calculation result, ${\mathit{w}}^{\prime }$ and ${\mathit{v}}^{\prime }$ coefficients are set as follows:

$${\mathit{w}}^{\prime }=\left(\begin{array}{c}{a}_{11}^{\prime }\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 0\end{array}\\ {a^{\prime }}_{22}\end{array}\\ {a^{\prime }}_{33}\end{array}\right)\mathrm{and}{\mathit{v}}^{\prime }=\left(\begin{array}{c}{b}_1\\ \begin{array}{c}{b}_2\\ b_3\end{array}\\ c\end{array}\right)$$

• with the following conditions:
• if $c>0,$ then ${{\mathit{a}}^{\prime }}_{\mathbf{11}}=-\left|{\mathit{a}}_{\mathbf{11}}\right|$, ${{\mathit{a}}^{\prime }}_{\mathbf{22}}=-\left|{\mathit{a}}_{\mathbf{22}}\right|$, ${{\mathit{a}}^{\prime }}_{\mathbf{33}}=-\left|{\mathit{a}}_{\mathbf{33}}\right|$; and
• if $c<0$, then ${{\mathit{a}}^{\prime }}_{\mathbf{11}}=\left|{\mathit{a}}_{\mathbf{11}}\right|$, ${{\mathit{a}}^{\prime }}_{\mathbf{22}}=\left|{\mathit{a}}_{\mathbf{22}}\right|$, ${{\mathit{a}}^{\prime }}_{\mathbf{33}}=\left|{\mathit{a}}_{\mathbf{33}}\right|$.

2.

Hence, the following equation is obtained:

$${a^{\prime }}_{11}{x}^2+{a^{\prime }}_{22}{y}^2+{a^{\prime }}_{33}{z}^2+b_{1}x+b_{2}y+b_{3}z+c=0.$$

The equation can be simplified as follows:

$${a^{\prime }}_{11}{x}^2+b_{1}x+{a^{\prime }}_{22}{y}^2+b_{2}y+{a^{\prime }}_{33}{z}^2+b_{3}z+c=0$$

$$\begin{array}{c}\iff a_{11}^{\prime }{\left(x+\frac{b_1}{2a^{\prime }{}_{11}}\right)}^2-\frac{b_1^2}{4{a^{\prime }}_{11}^2}+{a^{\prime }}_{22}{\left(y+\frac{b_2}{2a^{\prime }{}_{22}}\right)}^2-\hfill \\ \frac{b_2^2}{4a^{\prime }{}_{22}^2}+a_{33}^{\prime }{\left(z+\frac{b_3}{2a^{\prime }{}_{33}}\right)}^2-\frac{b_3^2}{4a^{\prime }{}_{33}^2}+c=0\iff \hfill \\ {a^{\prime }}_{11}{\left(x+\frac{b_1}{{2a^{\prime }}_{11}}\right)}^2+{a^{\prime }}_{22}{\left(y+\frac{b_2}{2a^{\prime }{}_{22}}\right)}^2+{a^{\prime }}_{33}(z+\hfill \\ {\left.\frac{b_3}{2{a^{\prime }}_{33}}\right)}^2=\frac{b_1^2}{4{a^{\prime }}_{11}^2}+\frac{b_2^2}{4{a^{\prime }}_{22}^2}+\frac{b_3^2}{4{a^{\prime }}_{33}^2}-c.\hfill \end{array}$$

3.

Suppose $\frac{b_1}{2{a^{\prime }}_{11}}=\alpha$, $\frac{b_2}{2{a^{\prime }}_{22}}=\beta ,\frac{b_3}{2{a^{\prime }}_{33}}=\gamma$, $\frac{b_1^2}{4{a^{\prime }}_{11}^2}+\frac{b_2^2}{4{a^{\prime }}_{22}^2}+\frac{b_3^2}{4{a^{\prime }}_{33}^2}-c=p$, then,

$$\begin{gathered} {a^{\prime }}_{11}{(x+\alpha )}^2+{a^{\prime }}_{22}{\left(y+\beta \right)}^2+{a^{\prime }}_{33}{(z+\gamma )}^2=p \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⟺ \frac{{a^{\prime }}_{11}{(x+\alpha )}^2}{p}+\frac{{a^{\prime }}_{22}{\left(y+\beta \right)}^2}{p}+\frac{{a^{\prime }}_{33}{(z+\gamma )}^2}{p}=1. \end{gathered}$$

4.

Suppose $\frac{{a^{\prime }}_{11}}{p}=q, \frac{{a^{\prime }}_{22}}{p}=r, \frac{{a^{\prime }}_{33}}{p}=s$, then the following general ellipsoid equation is obtained as follows:

$$\frac{{(x+\alpha )}^2}{q}+\frac{{\left(y+\beta \right)}^2}{r}+\frac{{(z+\gamma )}^2}{s}=1.$$

2.3. Computer Code Availability

There are two open-source software used in this study:

• The Stanford Geostatistical Modeling Software (SGeMS) is an open-source computer package for solving problems involving spatially related variables. In this study, SGeMS was used to plot the 3D data point, provide the primary statistical analysis, construct the experimental variogram, and make a fitting model of the 3D variogram. One can access the software through the following site: http://sgems.sourceforge.net/ (accessed on 22 June 2022).
• GeoGebra is a free online math tool for graphing, geometry, 3D, and more. In this study, GeoGebra was used to plot the 3D ellipsoid model. One can access the software through the following site: https://www.geogebra.org/?lang=en (accessed on 22 June 2022).

3. Results and Discussion

3.1. Three-Dimensional Ellipsoid Anisotropy of Zn Grade

To obtain the fitting model for 3D ellipsoid anisotropy, a curve fitting was performed by the following steps, as described above. We obtain the w and v coefficients as follows:

$$\mathit{w}=\left(\begin{array}{c}0.005\\ 0.002\\ -0.675\\ -0.003\\ 0.001\\ 0.737\end{array}\right)\mathrm{and}\mathit{v}=\left(\begin{array}{c}-0.028\\ 0.013\\ 60.557\\ 1405.264\end{array}\right)$$

with matrix S, the QR decomposition of S, matrix R, and the SVD of R₂₂ written in Appendix A.

Hence, the hyperboloid curve equation is obtained as follows:

$$\begin{gathered} f\left(x,y,z\right):=0.005x^2+\left(2\right)\left(0.002\right)xy+\left(2\right)\left(-0.675\right)xz+ \\ \left(2\right)\left(-0.003\right)yz+0.001y^2+0.737z^2-0.028x+0.013y+60.557z+ \\ 1405.264=0. \end{gathered}$$

Because the obtained equation was nevertheless a hyperboloid equation, we follow the steps that have been described before to produce the following coefficients:

$${\mathit{w}}^{\prime }=\left(\begin{array}{c}-0.005\\ 0\\ 0\\ 0\\ -0.001\\ -0.737\end{array}\right)\mathrm{and}{\mathit{v}}^{\prime }=\left(\begin{array}{c}-0.028\\ 0.013\\ 60.557\\ 1405.264\end{array}\right).$$

Therefore, the required ellipsoid equation is as follows:

$$\begin{gathered} f\left(x,y,z\right)≔-0.005x^2-0.001y^2-0.737z^2-0.028x+0.013y+60.557z+ \\ 1405.264=0. \end{gathered}$$

Furthermore, by means of the GeoGebra application, the 3D images of the ellipsoid equation with 24 data points of Zn grade were obtained, as depicted in Figure 6.

Next, we will see the area of influence of Zn grade from the result of the 3D ellipsoid modeling. First, the above equation can be written in the form of the general equation of ellipsoid as follows:

$$\frac{{\left(x+2.688\right)}^2}{514582.228}+\frac{{\left(y-4.875\right)}^2}{1922922.530}+\frac{{\left(z-41.053\right)}^2}{3590.741}=1.$$

Hence, the ellipsoid center coordinate is (−2.688, 4.875, 41.053), and the area of influence of Zn grade from the center is 717 m on the x-axis, 1386 m on the y-axis, and 59 m on the z-axis.

3.2. Calculating the Error of the 3D Fitting Model

We also computed the error value resulting from the fitting. We used Lagrange multipliers to find the shortest distance between the data points and the ellipsoid. We set the square distance function $d\left(x,y,z\right)={\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2$ as the objective function, where $\left(a,b,c\right)$ is each data point in Table 1 and the ellipsoid equation $f\left(x,y,z\right)≔-0.005x^2-0.001y^2-0.737z^2-0.028x+0.013y+60.557z+1405.264=0$ as the constraint. Our target is to solve the system of equations $\nabla d\left(x,y,z\right)=\lambda \nabla f\left(x,y,z\right)$ and $f\left(x,y,z\right)=0$, where $\nabla f\left(x,y,z\right)$ is the vector gradient of $f$, $\nabla d\left(x,y,z\right)$ is the vector gradient of $d$, and $\lambda$ is the Lagrange multiplier. Afterward, we obtain the minimum square of the distance for each data point. The previous distance was compared with the distance from the ellipsoid surface to the center for calculating the error. Only 8 of 16 data points were beyond the ellipsoid, and 2 of them are outliers. The fitting error result of six data points of the 3D ellipsoid anisotropy and the respected variogram parameters are summarized in

Table 2. Result of error calculation for the 3D fitting model of ellipsoid anisotropy.

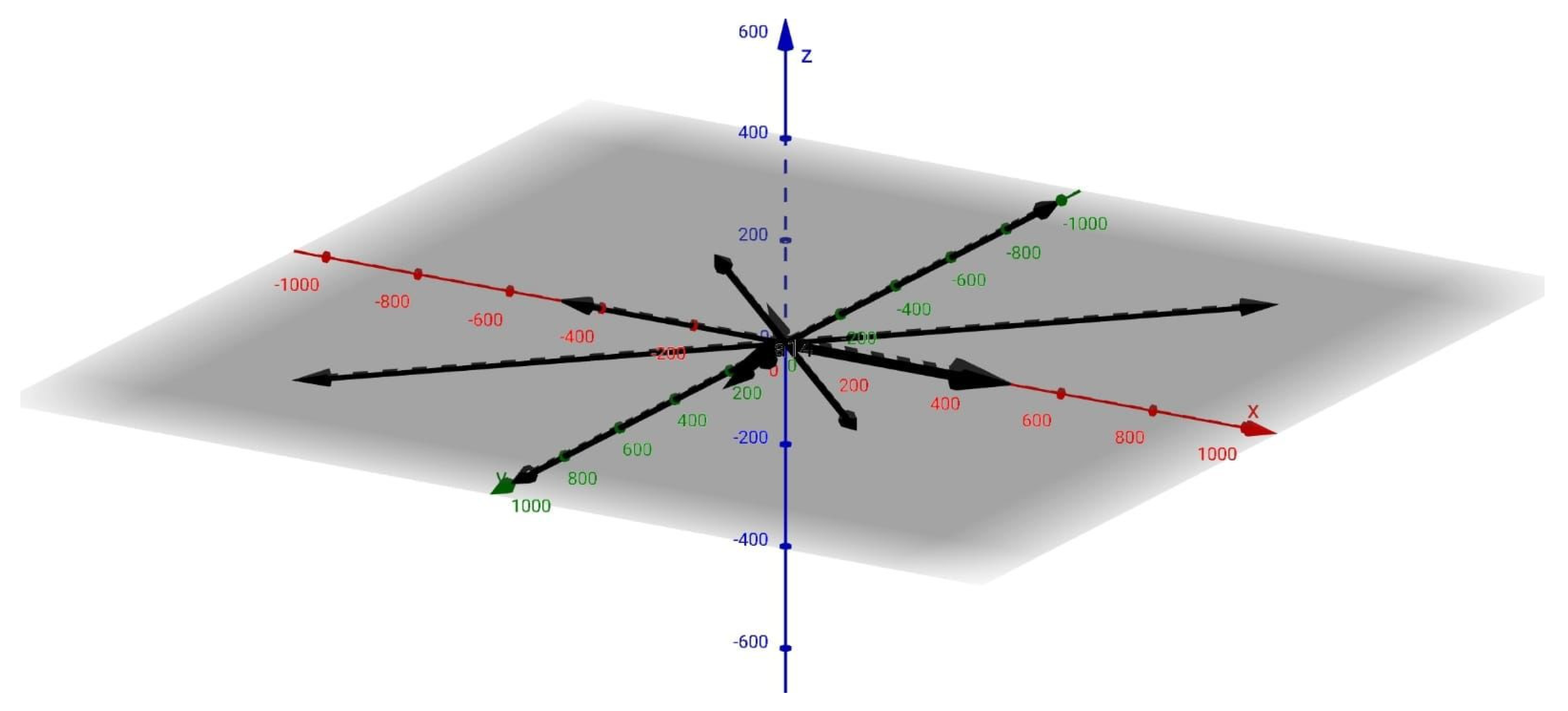
3D Variogram of Zn Grade				Result of Conversion into 3D Coordinate Points			% Error
Azimuth (N°E)	Dip (°)	Range (m)	Orientation	x	y	z
135	0	950	horizontal	671.75	−671.75	0	26.15%
315	0	950	horizontal	−671.75	671.75	0	25.32%
0	20	65	inclined	0	22.23	−22.23	5.62%
90	40	40	inclined	30.64	0	−25.71	11.51%
270	30	115	inclined	−99.59	0	−57.50	65.02%
315	40	50	inclined	−27.08	−32.14	−27.08	13.79%
Error Average							24.57%

.

For comparison, we constructed a 3D omnidirectional variogram of Zn grade with a lag distance of 50 m. One commonly uses 3D omnidirectional variograms for irregular drill hole patterns. We depict the experimental variogram and its manual fitting model using spherical in Figure 7, where the obtained range or area of influence was 800 m for the x, y, and z directions.

Meanwhile, the area of influence obtained from the least square method was approximately 720 m, 1390 m, and 60 m, respectively, in the x, y, and z directions. The area of influence obtained from manual fitting of the 3D omnidirectional variogram (i.e., 800 m) likely only represents the area of influence in the x-direction in terms of the result from the 3D ellipsoid anisotropy.

3.3. Comparing Isotropy and Anisotropy 3D Ellipsoid

The isotropy model of variogram is the simpler and faster model to be produced for any kind of ore deposit related to the porphyry copper deposit. Due to the tabular geometrical ore deposit shape, the drill hole pattern for this deposit is commonly irregular. Practically, the isotropy experimental variogram is constructed to obtain the model of the spatial structure of any variable (i.e., grade) related to this kind of deposit (see Figure 7). If the detailed spatial structure should be considered, we could construct a directional experimental variogram following the direction (azimuth and dip) of each drill hole pattern to check if the anisotropy exists (see Figure 3). The model of the spatial structure produced from variogram modeling should represent the geometry of the mineral deposit. When this model is used for geostatistical estimation parameters (i.e., as searching radius), then it may influence the result of the estimated grade as well as the accuracy, which is indicated by the kriging variance, because the different search ellipsoids will cover different neighborhood data (different numbers and directions) needed for the estimation process. This study compared the 3D kriging block model using two different searching radii (i.e., isotropy (spherical) and anisotropy (ellipsoid)). The block size is 15 m, 15 m, 15 m and number of blocks is 134, 174, 121, respectively, in x, y, z directions. The minimum and maximum number of data is 3 and 10, respectively, while the searching radius is following the respected range of variograms.

The 3D kriging block model produced for Zn grade and their kriging variance using the isotropy model and anisotropy model of search ellipsoid is depicted in Figure 8a–d, respectively. We can see the difference between Figure 8a–c, which relatively shows a columnar or tabular distribution model compared to Figure 8b–d, which shows lenses or a layering distribution model. Based on the typical mineralization or deposit model, a Pb-Zn skarn mineralization associated with porphyritic mineralization has lenses or a layering model because they could be originally formed as vein type. Therefore, the 3D kriging block model shown in Figure 8b–d is a more realistic representation of the vein type of Zn skarn mineralization. The difference in the mineralization model between porphyritic, which typically shows columnar or tabular, and skarn, which typically shows lenses or layering, can be seen in Figure 9. The result of kriging estimation on Zn grade using both search ellipsoids can be seen in Figure 10. The mean of estimated Zn grade shows a lower grade in Figure 10b (i.e., 0.04%) compared to Figure 10a (i.e., 0.11%), which seems to indicate that the isotropy model tends to be overestimated (i.e., almost three times higher on average). However, the mean of kriging variance is not so different (i.e., 0.024%² in Figure 10c and 0.021%² in Figure 10d).

4. Conclusions

A highly irregular 3D drill hole pattern in a porphyritic system associated with skarn orebodies generated a complex spatial characterization of metal grades. In such cases, the problem with the experimental variogram construction is how to set the parameters in order to obtain a robust variogram model (i.e., azimuth and dip), particularly for the inclined directions. We used the 3D direct least square method for fitting the 3D ellipsoid anisotropy of zinc (Zn) grade associated with highly irregular drill hole patterns with a fitting error of less than 25% on average. The anisotropy model of the search radius was more realistically applied for the 3D geostatistical estimation of Zn skarn mineralization, which typically shows lenses or a layering model. While the isotropy model of the search radius (i.e., a spherical model, which is commonly used for a porphyritic system) was less realistic for the skarn orebodies, as the 3D geostatistical estimation tends to generate a columnar or tabular model.

For future research, the methodology can be incorporated into a geostatistical software application to accommodate the 3D variogram construction and fitting model, particularly in cases involving a highly irregular 3D drill hole pattern. Apart from the ellipsoid anisotropy, a hyperboloid anisotropy can also be considered in the spatial continuity modeling of mineral resources.