Contribution to Excitonic Linewidth from Free Carrier–Exciton Scattering in Layered Materials: The Example of hBN
Abstract
:1. Introduction
2. Free Carrier–Exciton Scattering
Differential Scattering Cross Section
3. Total Cross Section
3.1. Elastic Scattering
3.2. Inelastic Scattering
3.2.1. Transitions
3.2.2. Transitions
3.3. Joint Elastic and Inelastic Scattering
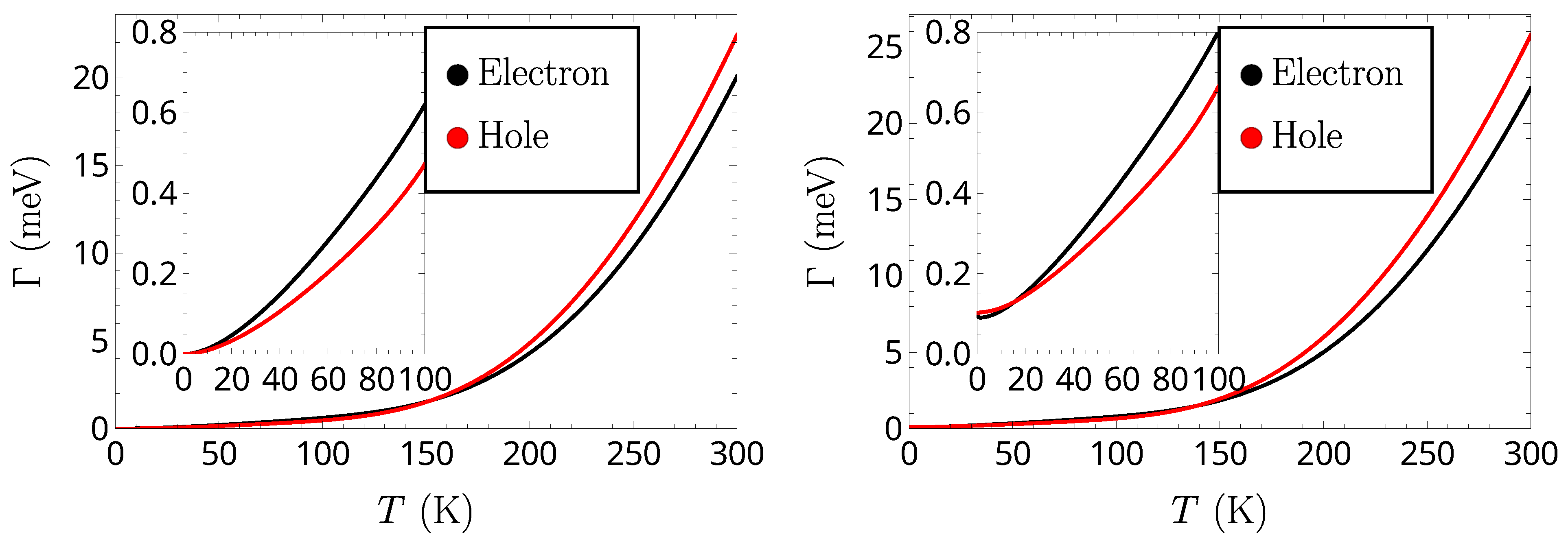
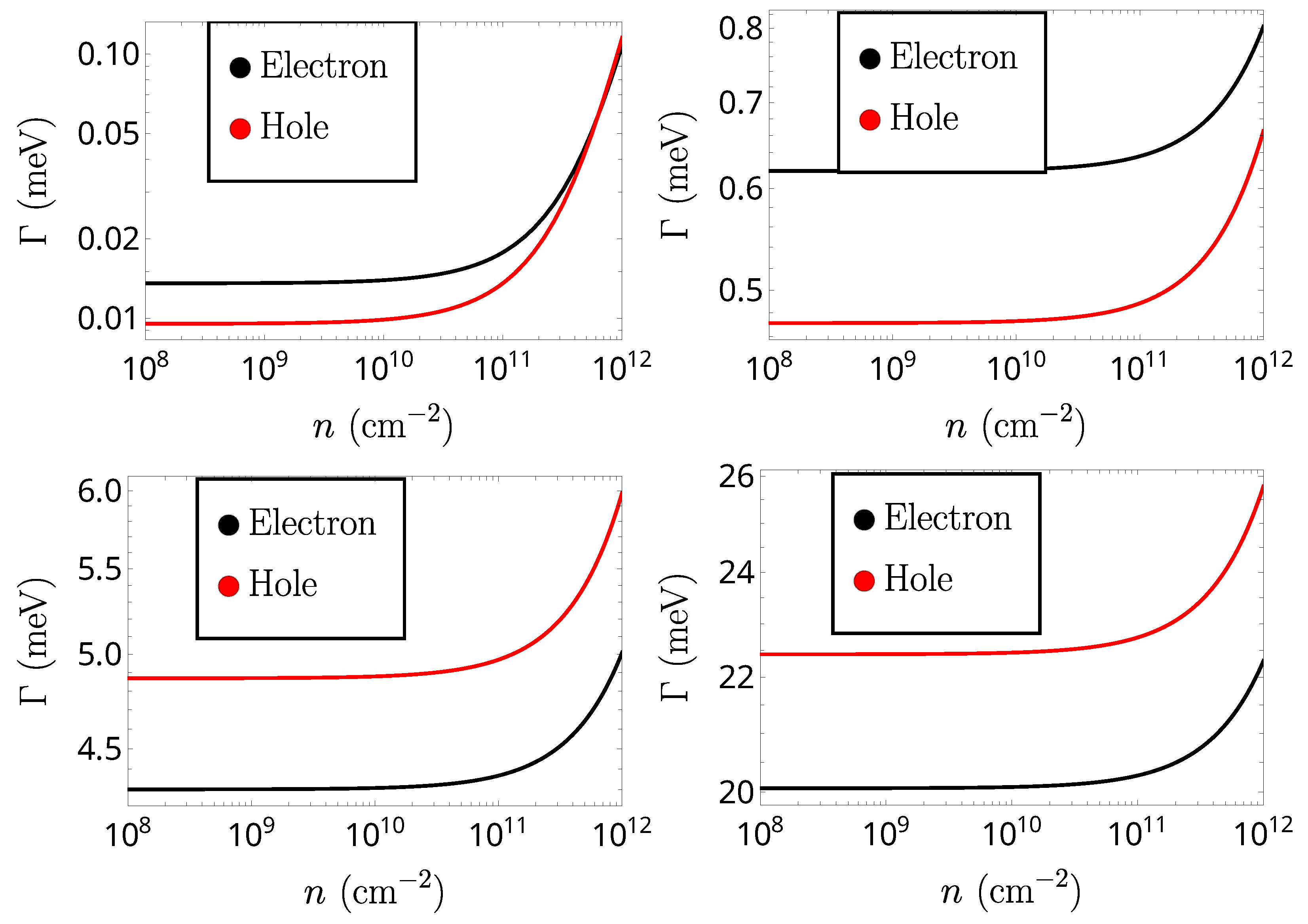
4. Scattering Contribution to Exciton Linewidth
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| hBN | hexagonal boron nitride |
| RMS | root mean squared |
Appendix A. Derivation of Differential Scattering Cross Section
Appendix B. Computation of Scattering Contribution to Excitonic Linewidth
References
- Àla Guillaume, C.B.; Debever, J.M.; Salvan, F. Radiative Recombination in Highly Excited CdS. Phys. Rev. 1969, 177, 567–580. [Google Scholar] [CrossRef]
- Iwai, S.; Namba, S. Emission Spectra in CdS under High Excitation by Electron Beam. Appl. Phys. Lett. 1971, 19, 41–43. [Google Scholar] [CrossRef]
- In Yu, C.; Goto, T.; Ueta, M. Emission of Cuprous Halide Crystals at High Density Excitation. J. Phys. Soc. Jpn. 1973, 34, 693–698. [Google Scholar] [CrossRef]
- Braun, W.; Bille, J.; Fischer, T.; Huber, G. Laser Emission in CdSe Due to Exciton—Exciton and Exciton—Electron Interaction. Phys. Status Solidi (B) 1973, 58, 759–765. [Google Scholar] [CrossRef]
- Levy, R.; Grun, J.B. Optical properties of strongly excited direct band gap materials. Phys. Status Solidi (A) 1974, 22, 11–38. [Google Scholar] [CrossRef]
- Klingshirn, C. The Luminescence of ZnO under High One- and Two-Quantum Excitation. Phys. Status Solidi (B) 1975, 71, 547–556. [Google Scholar] [CrossRef]
- Hönerlage, B.; Klingshirn, C.; Grun, J.B. Spontaneous emission due to exciton—Electron scattering in semiconductors. Phys. Status Solidi (B) 1976, 78, 599–608. [Google Scholar] [CrossRef]
- Levy, R.; Grun, J.B.; Nikitine, S. Experimental investigation of the competition of stimulated emissions involving exciton. Excit. High Density 1975, 73, 211–219. [Google Scholar]
- Elkomoss, S.G.; Munschy, G. Electron-exciton elastic scattering cross sections in the central field and the exchange approximations. J. Phys. Chem. Solids 1977, 38, 557–563. [Google Scholar] [CrossRef]
- Elkomoss, S.G.; Munschy, G. Electron-exciton inelastic collision cross sections for different semiconductors. J. Phys. Chem. Solids 1979, 40, 431–438. [Google Scholar] [CrossRef]
- Reynolds, D.C.; Bajaj, K.K.; Litton, C.W.; Singh, J.; Yu, P.W.; Pearah, P.; Klem, J.; Morkoc, H. High-resolution photoluminescence and reflection studies of GaAs-AlxGa1−xAs multi-quantum-well structures grown by molecular-beam epitaxy: Determination of microscopic structural quality of interfaces. Phys. Rev. B 1986, 33, 5931–5934. [Google Scholar] [CrossRef] [PubMed]
- Museur, L.; Feldbach, E.; Kanaev, A. Defect-related photoluminescence of hexagonal boron nitride. Phys. Rev. B 2008, 78, 155204. [Google Scholar] [CrossRef] [Green Version]
- Cadiz, F.; Courtade, E.; Robert, C.; Wang, G.; Shen, Y.; Cai, H.; Taniguchi, T.; Watanabe, K.; Carrere, H.; Lagarde, D.; et al. Excitonic Linewidth Approaching the Homogeneous Limit in MoS2-Based van der Waals Heterostructures. Phys. Rev. X 2017, 7, 021026. [Google Scholar] [CrossRef] [Green Version]
- Elias, C.; Valvin, P.; Pelini, T.; Summerfield, A.; Mellor, C.J.; Cheng, T.S.; Eaves, L.; Foxon, C.T.; Beton, P.H.; Novikov, S.V.; et al. Direct band-gap crossover in epitaxial monolayer boron nitride. Nat. Commun. 2019, 10, 2639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Wang, J.; Zhang, X.; Elias, C.; Ye, G.; Evans, D.; Eda, G.; Redwing, J.M.; Cassabois, G.; Gil, B.; et al. Hexagonal Boron Nitride Crystal Growth from Iron, a Single Component Flux. ACS Nano 2021, 15, 7032–7039. [Google Scholar] [CrossRef]
- Vuong, T.Q.P.; Cassabois, G.; Valvin, P.; Rousseau, E.; Summerfield, A.; Mellor, C.J.; Cho, Y.; Cheng, T.S.; Albar, J.D.; Eaves, L.; et al. Deep ultraviolet emission in hexagonal boron nitride grown by high-temperature molecular beam epitaxy. 2D Materials 2017, 4, 021023. [Google Scholar] [CrossRef]
- Kim, S.M.; Hsu, A.; Park, M.H.; Chae, S.H.; Yun, S.J.; Lee, J.S.; Cho, D.H.; Fang, W.; Lee, C.; Palacios, T.; et al. Synthesis of large-area multilayer hexagonal boron nitride for high material performance. Nat. Commun. 2015, 6, 8662. [Google Scholar] [CrossRef] [Green Version]
- Yano, M.; Yap, Y.K.; Okamoto, M.; Onda, M.; Yoshimura, M.; Mori, Y.; Sasaki, T. Na: A New Flux for Growing Hexagonal Boron Nitride Crystals at Low Temperature. Jpn. J. Appl. Phys. 2000, 39, L300–L302. [Google Scholar] [CrossRef]
- Dingle, R.; Wiegmann, W.; Henry, C.H. Quantum States of Confined Carriers in Very Thin AlxGa1−xAs-GaAs-AlxGa1−xAs Heterostructures. Phys. Rev. Lett. 1974, 33, 827–830. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S.; Eilenberger, D.J.; Smith, P.W.; Gossard, A.C.; Tsang, W.T. Large room-temperature optical nonlinearity in GaAs/Ga1−xAlxAs multiple quantum well structures. Appl. Phys. Lett. 1982, 41, 679–681. [Google Scholar] [CrossRef]
- Poellmann, C.; Steinleitner, P.; Leierseder, U.; Nagler, P.; Plechinger, G.; Porer, M.; Bratschitsch, R.; Schüller, C.; Korn, T.; Huber, R. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 2015, 14, 889–893. [Google Scholar] [CrossRef]
- Merkl, P.; Mooshammer, F.; Steinleitner, P.; Girnghuber, A.; Lin, K.Q.; Nagler, P.; Holler, J.; Schüller, C.; Lupton, J.M.; Korn, T.; et al. Ultrafast transition between exciton phases in van der Waals heterostructures. Nat. Mater. 2019, 18, 691–696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.; Koteles, E.S.; Vassell, M.O. Luminescence linewidths of excitons in GaAs quantum wells below 150 K. Phys. Rev. B 1986, 33, 5512–5516. [Google Scholar] [CrossRef] [PubMed]
- Spector, H.N.; Lee, J.; Melman, P. Exciton linewidth in semiconducting quantum-well structures. Phys. Rev. B 1986, 34, 2554–2560. [Google Scholar] [CrossRef]
- Henriques, J.C.G.; Mortensen, N.A.; Peres, N.M.R. Analytical description of the 1s exciton linewidth temperature dependence in transition metal dichalcogenides. Phys. Rev. B 2021, 103, 235402. [Google Scholar] [CrossRef]
- Cingolani, R.; Ploog, K. Frequency and density dependent radiative recombination processes in III–V semiconductor quantum wells and superlattices. Adv. Phys. 1991, 40, 535–623. [Google Scholar] [CrossRef]
- Palummo, M.; Bernardi, M.; Grossman, J.C. Exciton Radiative Lifetimes in Two-Dimensional Transition Metal Dichalcogenides. Nano Lett. 2015, 15, 2794–2800. [Google Scholar] [CrossRef] [Green Version]
- Singh, J.; Bajaj, K.K. Theory of excitonic photoluminescence linewidth in semiconductor alloys. Appl. Phys. Lett. 1984, 44, 1075–1077. [Google Scholar] [CrossRef]
- Basu, P.K. Linewidth of free excitons in quantum wells: Contribution by alloy disorder scattering. Appl. Phys. Lett. 1990, 56, 1110–1112. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Song, A.; Liang, J.; Xu, B.; Zhu, Z.; Zheng, W.; Liao, Q.; Yang, B. Photoluminescence studies on very high-density quasi-two-dimensional electron gases in pseudomorphic modulation-doped quantum wells. J. Appl. Phys. 1995, 78, 593–595. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Kwok, W.M.; Leung, Y.H.; Chan, W.K.; Phillips, D.L.; Lin, M.S.; Gwo, S. Ultrafast spectroscopy of stimulated emission in single ZnO tetrapod nanowires. Nanotechnology 2005, 17, 244–249. [Google Scholar] [CrossRef]
- Young, J.F.; Wood, B.M.; Charbonneau, S. Optical Probes of Resonant Tunneling Structures. In Electronic Properties of Multilayers and Low-Dimensional Semiconductor Structures; Springer: Boston, MA, USA, 1990; pp. 331–349. [Google Scholar] [CrossRef]
- Teran, F.J.; Martín, M.D.; Calleja, J.M.; Viña, L.; Eaves, L.; Henini, M. Carrier injection effects on exciton dynamics in GaAs/AlAs resonant-tunneling diodes. EPL (Europhys. Lett.) 2009, 85, 67010. [Google Scholar] [CrossRef]
- Koh, T.S.; Feng, Y.P.; Spector, H.N. Effect of an electric field on the scattering of excitons by free carriers in semiconducting quantum-well structures. J. Appl. Phys. 1997, 81, 2704–2708. [Google Scholar] [CrossRef]
- Vella, D.; Barbosa, M.B.; Trevisanutto, P.E.; Verzhbitskiy, I.; Zhou, J.Y.; Watanabe, K.; Taniguchi, T.; Kajikawa, K.; Eda, G. In-Plane Field-Driven Excitonic Electro-Optic Modulation in Monolayer Semiconductor. Adv. Opt. Mater. 2022, 10, 2102132. [Google Scholar] [CrossRef]
- Efimkin, D.K.; Laird, E.K.; Levinsen, J.; Parish, M.M.; MacDonald, A.H. Electron-exciton interactions in the exciton-polaron problem. Phys. Rev. B 2021, 103, 075417. [Google Scholar] [CrossRef]
- Feng, Y.P.; Spector, H.N. Scattering of excitons by free carriers in semiconducting quantum well structures. J. Phys. Chem. Solids 1987, 48, 593–601. [Google Scholar] [CrossRef]
- Massey, H.S.W.; Moiseiwitsch, B.L. The application of variational methods to atomic scattering problems—I. The elastic scattering of electrons by hydrogen atoms. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1951, 205, 483–496. [Google Scholar] [CrossRef]
- Bates, D.R.; Griffing, G. Inelastic Collisions between Heavy Particles I: Excitation and Ionization of Hydrogen Atoms in Fast Encounters with Protons and with other Hydrogen Atoms. Proc. Phys. Soc. Sect. A 1953, 66, 961–971. [Google Scholar] [CrossRef]
- Mott, N.F.; Massey, H.S.W. Theory of Atomic Collisions, 3rd ed.; Monographs on Physics; Oxford University Press: London, UK, 1965. [Google Scholar]
- Feng, Y.P.; Spector, H. Scattering of screened excitons by free carriers in semiconducting quantum well structures. IEEE J. Quantum Electron. 1988, 24, 1659–1663. [Google Scholar] [CrossRef]
- Rytova, S.N. The Screened Potential of a Point Charge in a Thin Film. arXiv 2018, arXiv:1806.00976. [Google Scholar]
- Keldysh, L.V. Coulomb interaction in thin semiconductor and semimetal films. Sov. J. Exp. Theor. Phys. Lett. 1979, 29, 658. [Google Scholar]
- Li, P.; Appelbaum, I. Excitons without effective mass: Biased bilayer graphene. Phys. Rev. B 2019, 99, 035429. [Google Scholar] [CrossRef] [Green Version]
- Versteegh, M.A.M.; Kuis, T.; Stoof, H.T.C.; Dijkhuis, J.I. Ultrafast screening and carrier dynamics in ZnO: Theory and experiment. Phys. Rev. B 2011, 84, 035207. [Google Scholar] [CrossRef] [Green Version]
- Quintela, M.F.C.M.; Henriques, J.C.G.; Tenório, L.G.M.; Peres, N.M.R. Theoretical Methods for Excitonic Physics in 2D Materials. Phys. Status Solidi (B) 2022, 259, 2200097. [Google Scholar] [CrossRef]
- Gomes, J.N.S.; Trallero-Giner, C.; Vasilevskiy, M.I. Variational calculation of the lowest exciton states in phosphorene and transition metal dichalcogenides. J. Phys. Condens. Matter 2021, 34, 045702. [Google Scholar] [CrossRef]
- Lee, Y.C.; Lin, D.L. Wannier excitons in a thin crystal film. Phys. Rev. B 1979, 19, 1982–1989. [Google Scholar] [CrossRef]
- Yang, X.L.; Guo, S.H.; Chan, F.T.; Wong, K.W.; Ching, W.Y. Analytic solution of a two-dimensional hydrogen atom. I. Nonrelativistic theory. Phys. Rev. A 1991, 43, 1186–1196. [Google Scholar] [CrossRef]
- Wannier, G.H. The Structure of Electronic Excitation Levels in Insulating Crystals. Phys. Rev. 1937, 52, 191–197. [Google Scholar] [CrossRef]
- Serway, R.A.; Faughn, J.S.; Moses, C.J. College Physics; Number Volume 1 in College Physics; Brooks/Cole: Devon, UK, 2003. [Google Scholar]
- Ferreira, F.; Chaves, A.J.; Peres, N.M.R.; Ribeiro, R.M. Excitons in hexagonal boron nitride single-layer: A new platform for polaritonics in the ultraviolet. J. Opt. Soc. Am. B 2019, 36, 674–683. [Google Scholar] [CrossRef] [Green Version]
- Henriques, J.C.G.; Ventura, G.B.; Fernandes, C.D.M.; Peres, N.M.R. Optical absorption of single-layer hexagonal boron nitride in the ultraviolet. J. Phys. Cond. Matter 2020, 32, 025304. [Google Scholar] [CrossRef] [Green Version]
- Selig, M.; Berghäuser, G.; Raja, A.; Nagler, P.; Schüller, C.; Heinz, T.F.; Korn, T.; Chernikov, A.; Malic, E.; Knorr, A. Excitonic linewidth and coherence lifetime in monolayer transition metal dichalcogenides. Nat. Commun. 2016, 7, 13279. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, W. Controlling the Functionalizations of Hexagonal Boron Nitride Structures by Carrier Doping. J. Phys. Chem. Lett. 2011, 2, 2168–2173. [Google Scholar] [CrossRef]
- Majety, S.; Doan, T.C.; Li, J.; Lin, J.Y.; Jiang, H.X. Electrical transport properties of Si-doped hexagonal boron nitride epilayers. AIP Adv. 2013, 3, 122116. [Google Scholar] [CrossRef]
- He, B.; Qiu, M.; Yuen, M.F.; Zhang, W.J. Electrical properties and electronic structure of Si-implanted hexagonal boron nitride films. Appl. Phys. Lett. 2014, 105, 012104. [Google Scholar] [CrossRef]
- Sun, F.; Hao, Z.; Liu, G.; Wu, C.; Lu, S.; Huang, S.; Liu, C.; Hong, Q.; Chen, X.; Cai, D.; et al. p-Type conductivity of hexagonal boron nitride as a dielectrically tunable monolayer: Modulation doping with magnesium. Nanoscale 2018, 10, 4361–4369. [Google Scholar] [CrossRef]
- Feng, Y.P.; Spector, H.N. Exciton linewidth due to scattering from free carriers in semiconducting quantum well structures. Superlattices Microstruct. 1987, 3, 459–461. [Google Scholar] [CrossRef]
- Feng, Y.P. Excitons in Semiconducting Quantum Well Structures. Ph.D. Thesis, Illinois Institute of Technology, Chicago, IL, USA, 1989. [Google Scholar]
- Koh, T.S.; Feng, Y.P.; Spector, H.N. Exciton linewidth due to scattering by free carriers in semiconducting quantum well structures: Finite confining potential model. J. Appl. Phys. 1997, 81, 2236–2240. [Google Scholar] [CrossRef]
- Kythe, P.K.; Puri, P. Computational Methods for Linear Integral Equations; Birkhäuser: Boston, MA, USA, 2002. [Google Scholar]
- Du, Y.; Neal, A.T.; Zhou, H.; Ye, P.D. Transport studies in 2D transition metal dichalcogenides and black phosphorus. J. Phys. Condens. Matter 2016, 28, 263002. [Google Scholar] [CrossRef] [Green Version]
- Kuiri, M.; Srivastav, S.K.; Ray, S.; Watanabe, K.; Taniguchi, T.; Das, T.; Das, A. Enhanced electron-phonon coupling in doubly aligned hexagonal boron nitride bilayer graphene heterostructure. Phys. Rev. B 2021, 103, 115419. [Google Scholar] [CrossRef]
- Li, J.; Goryca, M.; Yumigeta, K.; Li, H.; Tongay, S.; Crooker, S.A. Valley relaxation of resident electrons and holes in a monolayer semiconductor: Dependence on carrier density and the role of substrate-induced disorder. Phys. Rev. Mater. 2021, 5, 044001. [Google Scholar] [CrossRef]
- Lampert, M.A. Mobile and Immobile Effective-Mass-Particle Complexes in Nonmetallic Solids. Phys. Rev. Lett. 1958, 1, 450–453. [Google Scholar] [CrossRef]
- Kheng, K.; Cox, R.T.; d’Aubigné, M.Y.; Bassani, F.; Saminadayar, K.; Tatarenko, S. Observation of negatively charged excitons X− in semiconductor quantum wells. Phys. Rev. Lett. 1993, 71, 1752–1755. [Google Scholar] [CrossRef]
- Chen, G.; Stievater, T.H.; Batteh, E.T.; Li, X.; Steel, D.G.; Gammon, D.; Katzer, D.S.; Park, D.; Sham, L.J. Biexciton Quantum Coherence in a Single Quantum Dot. Phys. Rev. Lett. 2002, 88, 117901. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y.; Steel, D.; Gammon, D.; Stievater, T.H.; Katzer, D.S.; Park, D.; Piermarocchi, C.; Sham, L.J. An All-Optical Quantum Gate in a Semiconductor Quantum Dot. Science 2003, 301, 809–811. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintela, M.F.C.M.; Peres, N.M.R. Contribution to Excitonic Linewidth from Free Carrier–Exciton Scattering in Layered Materials: The Example of hBN. Appl. Sci. 2022, 12, 7872. https://doi.org/10.3390/app12157872
Quintela MFCM, Peres NMR. Contribution to Excitonic Linewidth from Free Carrier–Exciton Scattering in Layered Materials: The Example of hBN. Applied Sciences. 2022; 12(15):7872. https://doi.org/10.3390/app12157872
Chicago/Turabian StyleQuintela, Maurício F. C. Martins, and Nuno M. R. Peres. 2022. "Contribution to Excitonic Linewidth from Free Carrier–Exciton Scattering in Layered Materials: The Example of hBN" Applied Sciences 12, no. 15: 7872. https://doi.org/10.3390/app12157872
APA StyleQuintela, M. F. C. M., & Peres, N. M. R. (2022). Contribution to Excitonic Linewidth from Free Carrier–Exciton Scattering in Layered Materials: The Example of hBN. Applied Sciences, 12(15), 7872. https://doi.org/10.3390/app12157872






