Influence of Contact Surfaces’ Impact on the Gear Profile during Hobbing Process
Abstract
1. Introduction
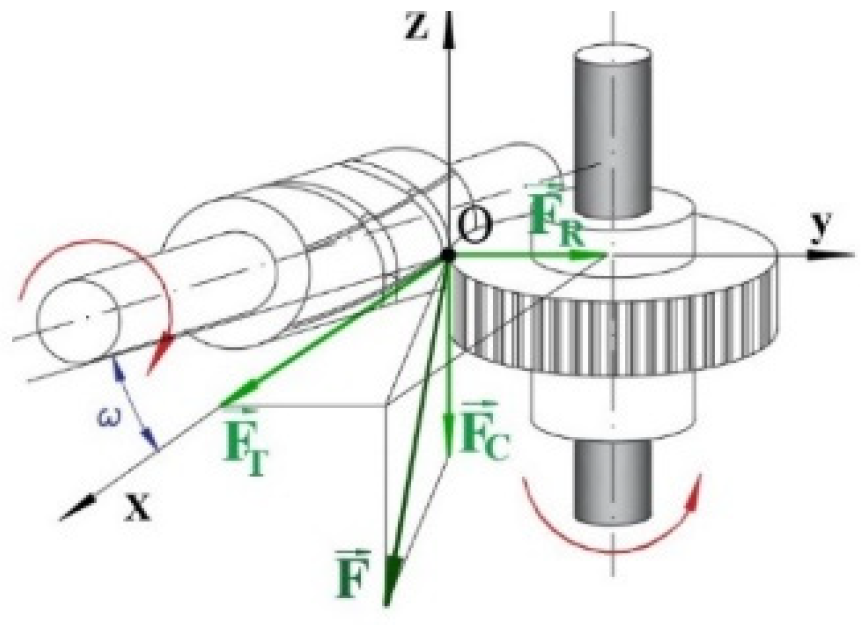
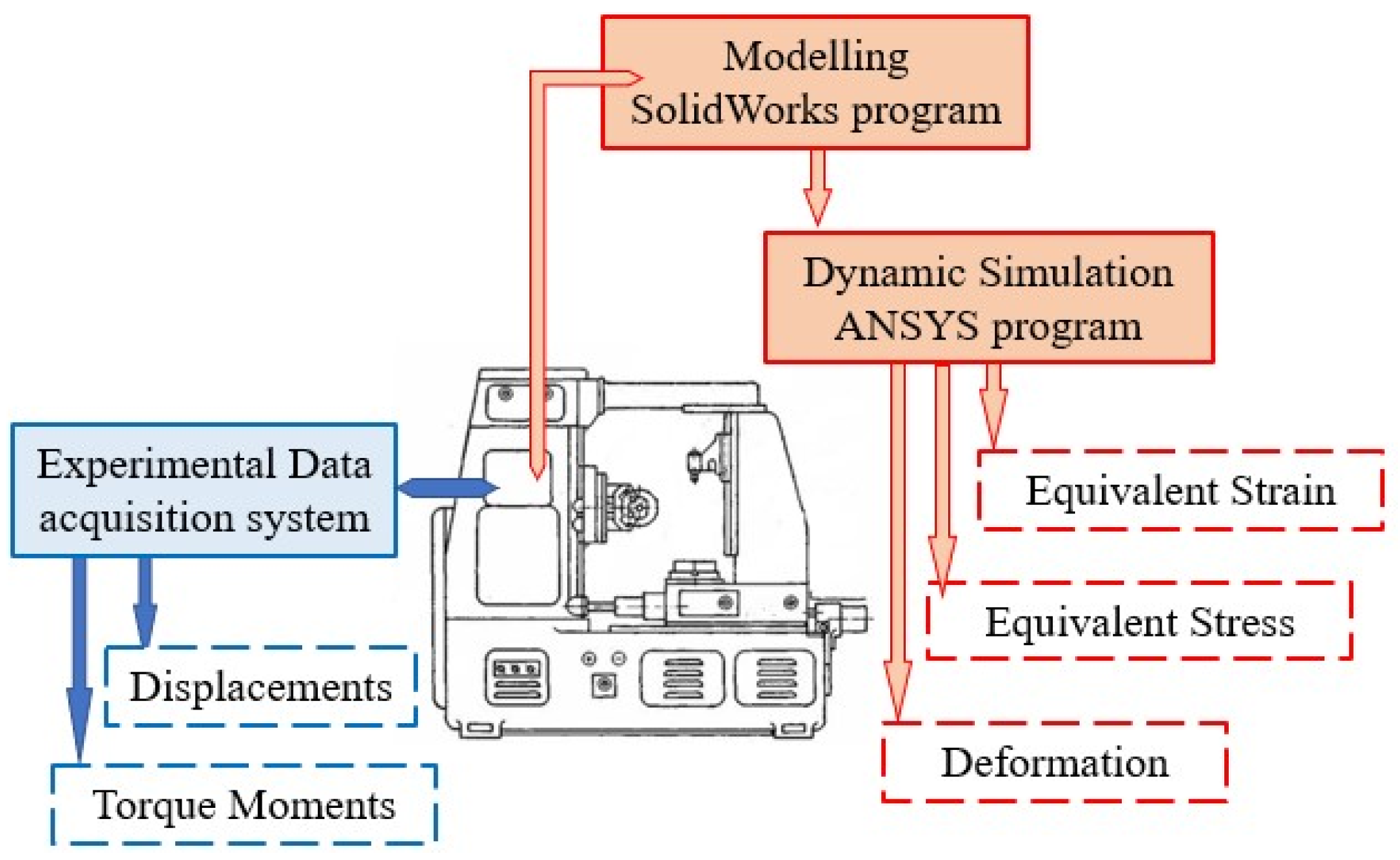
2. Research Methodology
3. Results and Discussion
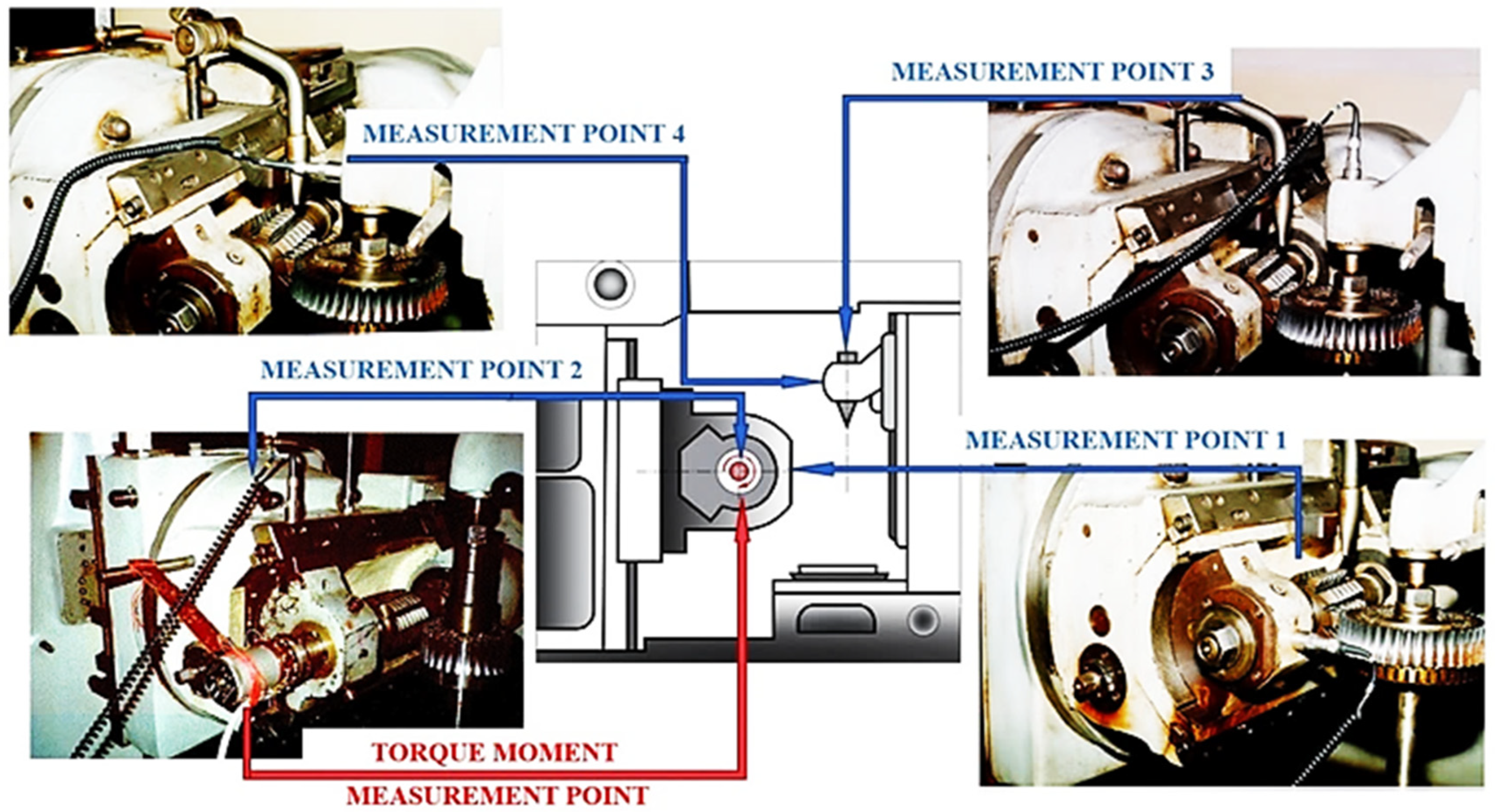
3.1. Experimental Results
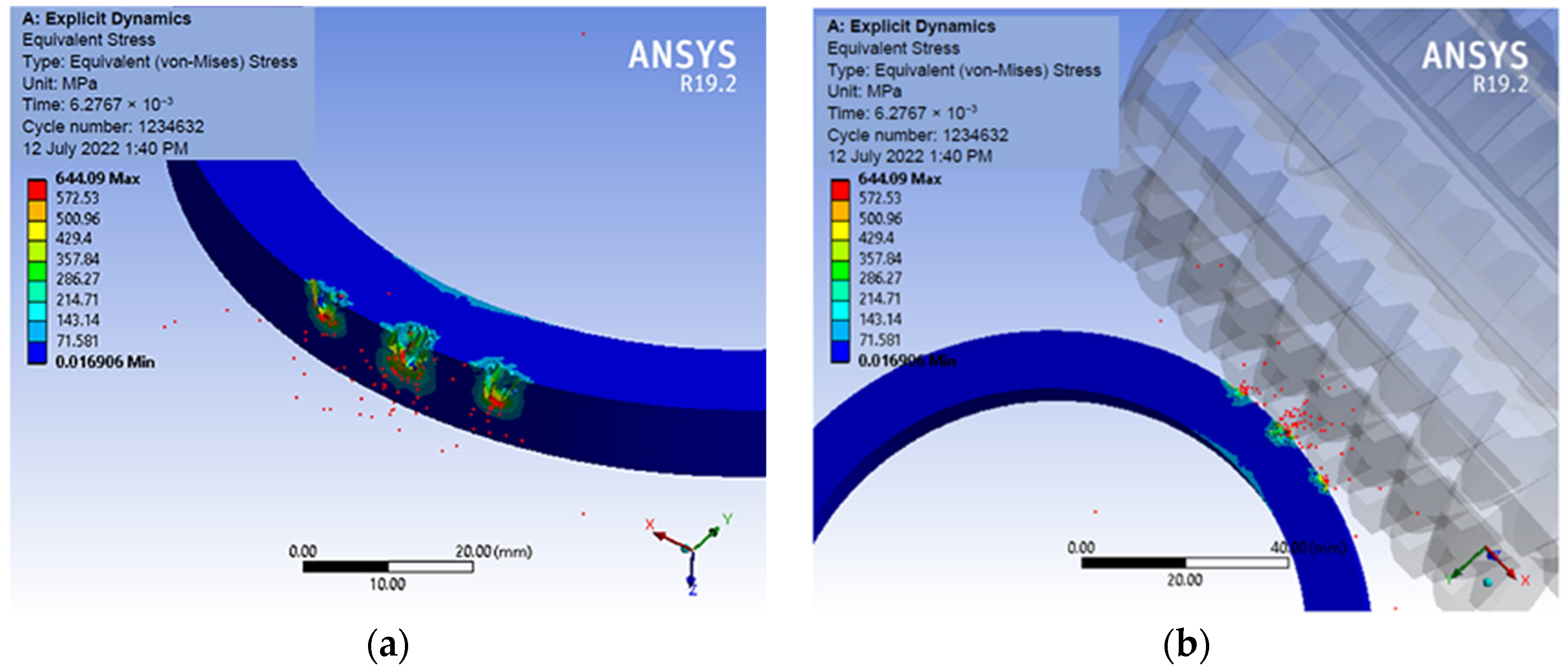
3.2. Numerical Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ciofu, C.D.; Mindru, T. Researches Concerning Shafts and Gears Milling Process. Int. J. Mod. Manuf. Technol. 2009, 1, 25–30. [Google Scholar]
- Liu, Z.; Yue, C.; Li, X.; Liu, X.; Liang, S.Y.; Wang, L. Research on Tool Wear Based on 3D FEM Simulation for Milling Process. J. Manuf. Mater. Process. 2020, 4, 121. [Google Scholar] [CrossRef]
- Litvin, F.L.; Gonzalez-Perez, I.; Yukishima, K.; Fuentes, A.; Hayasaka, K. Generation of planar and helical elliptical gears by application of rack-cutter, hob, and shaper. Comput. Methods Appl. Mech. Eng. 2007, 196, 4321–4336. [Google Scholar] [CrossRef]
- Mazuru, S.; Scaticailov, S. Tehnologii si Procedee de Danturare a Rotilor Dintate; Editura “Tehnica–UTM”: Chisinau, Republic of Moldavia, 2018. [Google Scholar]
- Radzevich, S. Practical Gear Design and Manufacture. In Dudley’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Claudin, C.; Rech, J. Development of a new rapid characterization method of hob’s wear resistance in gear manufacturing—Application to the evaluation of various cutting-edge preparations in high-speed dry gear hobbing. J. Mater. Process. Technol. 2009, 209, 5152–5160. [Google Scholar] [CrossRef]
- Pathan, N.; Singh, W.; Shrestha, P.P. Design and Modal Analysis of Spur Gear with Experimental Verification. Int. J. Eng. Sci. Res. Technol. IJESRT 2014, 3, 225–230. Available online: http://www.ijesrt.com (accessed on 25 April 2022).
- Zhao, M.X.; Balachandran, B. Dynamics and stability of milling process. Int. J. Solids Struct. 2001, 38, 2233–2248. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, W. Stability analysis in milling of the thin-walled part considering multiple variables of manufacturing systems. Int. J. Adv. Manuf. Technol. 2017, 89, 515–527. Available online: https://link.springer.com/article/10.1007/s00170-016-9072-8 (accessed on 25 April 2022). [CrossRef]
- Radzevich, S. Investigation of the Tooth Geometry of a Hob for Machining of Involute Gears (in the Tool-in-Use Reference System). Trans. ASME J. Manuf. Sci. Eng. 2007, 129, 750–759. [Google Scholar] [CrossRef]
- Smith, S.; Tlusty, J. An Overview of Modeling and Simulation of the Milling Process. J. Manuf. Sci. Eng. 1991, 113, 169–175. [Google Scholar] [CrossRef]
- Voronov, S.A.; Ivanov, I.I.; Kiselev, I.A. Investigation of the Milling Process Based on a Reduced Dynamic Model of Cutting Tool. J. Mach. Manuf. Reliab. 2015, 44, 70–78. [Google Scholar] [CrossRef]
- Belis, T.; Antoniadis, A. Hobbing Wear Prediction Model Based on 3D Chips Determination. In Proceedings of the International Conference on Design, Technology and Management in Manufacturing, Beijing, China, 23–25 November 2010. [Google Scholar]
- Karpuschewski, B.; Beutner, M.; Köchig, M.; Härtling, C. Influence of the tool profile on the wear behaviour in gear hobbing. CIRP J. Manuf. Sci. Technol. 2017, 18, 128–134. [Google Scholar] [CrossRef]
- Dong, X.; Liao, C.; Shin, Y.C.; Zhang, H.H. Machinability Improvement of Gear Hobbing via Process Simulation and Tool Wear Predictions. 2016. Available online: https://link.springer.com/content/pdf/10.1007/s00170-016-8400-3.pdf (accessed on 25 April 2022).
- Liu, W.; Rena, D.; Usuia, S.; Wadella, J.; Marusicha, T.D. A Gear Cutting Predictive Model Using the Finite Element Method. In Proceedings of the 14th CIRP Conference on Modeling of Machining Operations, Turin, Italy, 13–14 June 2013. [Google Scholar] [CrossRef][Green Version]
- Tapoglou, N.; Antoniadis, A. Hob3D: A Novel Gear Hobbing Simulation Software. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011; Volume 1. [Google Scholar]
- Antoniadis, A. Gear skiving—CAD simulation approach. Comput.-Aided Des. 2012, 44, 611–616. [Google Scholar] [CrossRef]
- Vasilis, D.; Nectarios, V.; Aristomenis, A. Advanced Computer Aided Design Simulation of Gear Hobbing by Means of Three-Dimensional Kinematics Modeling. J. Manuf. Sci. Eng.-Trans. ASME 2006, 129, 911–918. [Google Scholar] [CrossRef]
- Tapoglou, N.; Belis, T.; Vakondios, D.; Antoniadis, A. CAD-Based Simulation of Gear hobbing. In Proceedings of the Symposium on Mechanics and Materials, Agia Marina, Greece, 9–14 May 2010. [Google Scholar]
- Jani, S.; Jinesh, B.; Shah Vala, K. Design and Analysis of Helical Gear Pair using ANSYS, FEM and AGMA Standards for Calculating a Bending and Contact Stress on Gear Profiles: A Review. IJARIIE 2017, 3, 3813–3821, ISSN(O)-2395-4396. [Google Scholar]
- Bouzakis, K.; Friderikos, O.; Tsiafis, I. FEM-supported simulation of chip formation and flow in gear hobbing of spur and helical gears. CIRP J. Manuf. Sci. Technol. 2008, 1, 18–26. [Google Scholar] [CrossRef]
- Bouzakis, K.; Lili, E.; Michailidis, N.; Friderikos, O. Manufacturing of cylindrical gears by generating cutting processes: A critical synthesis of analysis methods. CIRP Ann.-Manuf. Technol. 2008, 57, 676–696. [Google Scholar] [CrossRef]
- Klocke, F.; Gorgels, C.; Schalaster, R.; Stuckenberg, A. An Innovative Way of Designing Gear Hobbing Processes. 2012. Available online: Geartechnology.com (accessed on 15 February 2022).
- Bergs, T.; Brimmers, J.; Georgoussis, A.; Kromer, M. Investigation of the chip formation during hobbing by means of an analytical approach. CIRP ICME’20 2021, 99, 226–231. [Google Scholar] [CrossRef]
- Duta, A.; Ozyilmaz, E.; Raicu, L.; Sass, L.; Stanescu, G. Aspects of Dynamic Analysis for FD320A Milling Machine. In Proceedings of the Annals of DAAAM for 2010 & Proceedings of the 21st International DAAAM Symposium, Zadar, Croatia, 20–23 October 2010; ISBN 978-3-901509-73-5. ISSN 1726-9679. [Google Scholar]
- Duta, A.; Minciu, C. A Model of Dynamic Calculus of the Main Kinematic Chain and of the Roller Chain. Ph.D. Thesis, Politechnica University of Bucharest, Bucharest, Rome, 1998. [Google Scholar]
- Geradin, M.; Rixen, D.J. Mechanical Vibrations: Theory and Application to Structural Dynamics, 3rd ed.; Wiley: Chichester, UK, 2015; ISBN1 9781118900208. ISBN2 978-1-118-90020-8. [Google Scholar]
- Ispas, C.; Simion, F.P. Vibratiile Masinilor-Unelte, Teorie si Aplicatii (Vibrations for Tools-Machines. Theory and Application); Editura Academiei, R.S.R., Ed.; Romanian Academy Publishing House: Bucharest, Romania, 1986. [Google Scholar]
- Azvar, M.; Katz, A.; Erkorkmaz, K. Chip geometry and cutting force prediction in gear. Mater. Sci. CIRP Ann. 2021, 70, 95–98. [Google Scholar] [CrossRef]
- Yagishita, H. Method for measuring the dynamic transmission error in large gear hobbing machines. Precis. Eng. 1990, 12, 144–150. [Google Scholar] [CrossRef]
- Abood, A.M. Dynamic Analysis of The Cutting Forces in Gear Hobbing. Ph.D. Thesis, School of Mechanical and Systems Engineering, University of Newcastle upon Tyne, Newcastle upon Tyne, UK, 2002. [Google Scholar]
- Tapoglou, N.; Mammas, A.; Antoniadis, A. Influence of machining data on developed cutting forces in gear hobbing. Int. J. Mach. Mach. Mater. 2013, 14, 66. [Google Scholar] [CrossRef]
- ANSYS Engineering Simulation Software; ANSYS: Canonsburg, PA, USA, 2022.
- Available online: https://www.bksv.com/en/analysis-software/data-acquisition-software (accessed on 18 February 2022).
- Xia, C.; Wang, S.; Long, T.; Ma, C.; Wang, S. Transmission chain error elimination for gear hobbing machines based on classified compensation theory and frequency response identification. Measurement 2020, 156, 107596. [Google Scholar] [CrossRef]
- Picos, C.; Pruteanu, O.; Bohosievici, C.; Coman, G.; Braha, V.; Paraschiv, D.; Slatineanu, L.; Gramescu, T.; Marin, A.; Ionesii, V.; et al. Proiectarea Tehnologiilor de Prelucrare Mecanica prin Aschiere. In Manual de Proiectare (The Design of Mechanical Processing Technologies, Design Manual); Universitas: Chisinau, Moldova, 1992; Volume 2. [Google Scholar]





| Name | Symbol | Value | Units |
|---|---|---|---|
| Module | m | 3.5 | mm |
| Pressure angle | α | 20 | deg |
| Teeth no. | z | 14 | μL |
| Number of origins | z1 | 1 | μL |
| Tooth height | h | 7.875 | mm |
| Outside diameter | dh | 90 | mm |
| Pitch diameter | d | 83 | mm |
| Chanel angle | ω | 2°31′24″ | deg |
| Chanel pitch | Cp | 6575.43 | mm |
| Relieving angle | δ | 25 | deg |
| Hob Module m (mm) | Rotational Speed nh (rpm) | Feed Rate vf (mm/min) | Point 1 Displacements shy (μm) | Point 2 Displacements shz (μm) | Point 3 Displacements sgz (μm) | Point 4 Displacements sgy (μm) |
|---|---|---|---|---|---|---|
| 3.5 | 95 | 4 | −1.29 … 2.44 | −1.31 … 1.01 | −1.71 … 1.29 | −1.17 … 1.02 |
| Module m (mm) | Rotational Speed nh (rpm) | Feed Rate vf (mm/min) | Maximum Torque Moment Mtmax (Nm) | Torque Moment Expression Mt (Nm) |
|---|---|---|---|---|
| 3.5 | 95 | 4 | 52.96 | 18.207 + 9.224 sin 0.233t + 4.955 sin 2.623t |
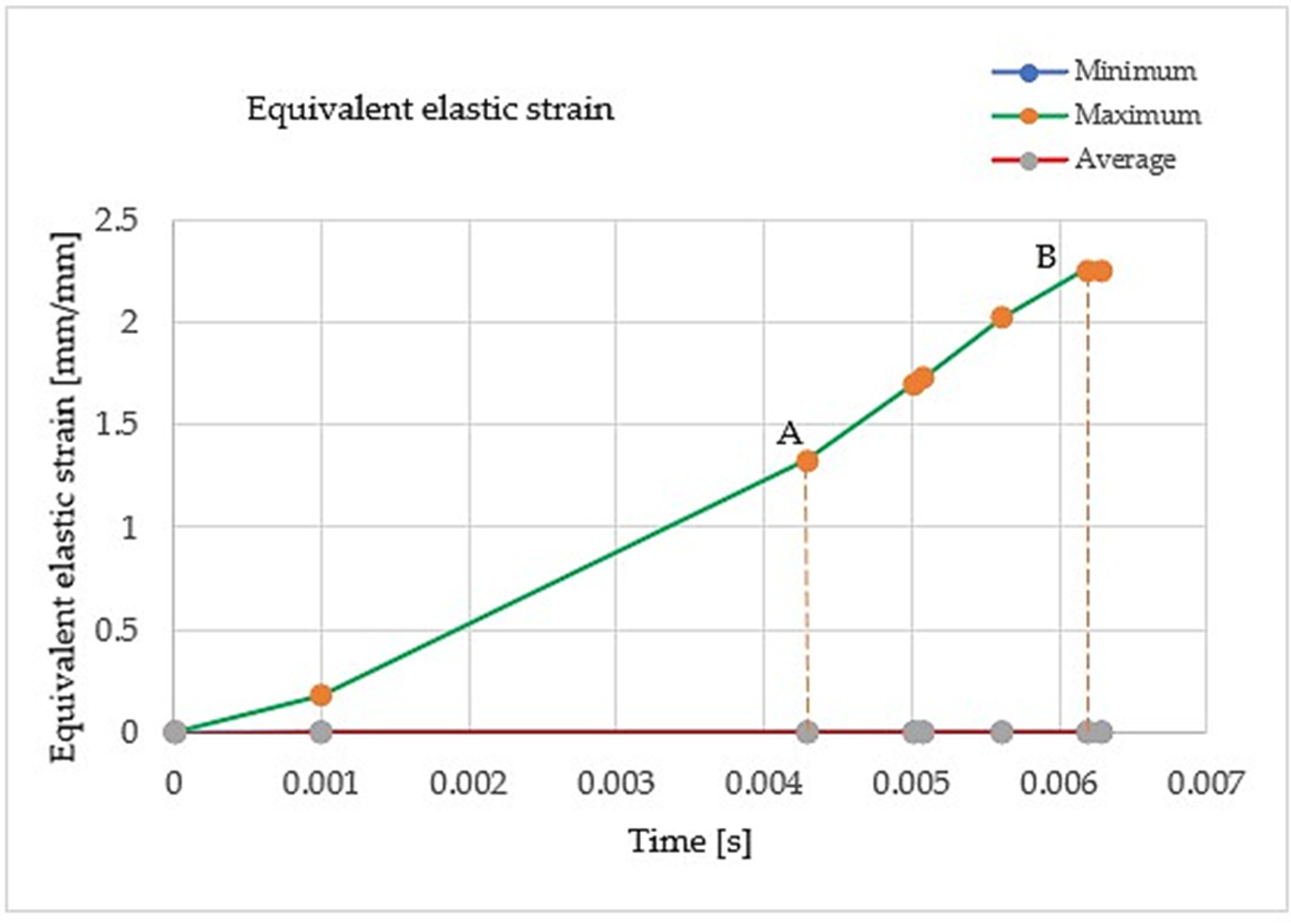
| Time t (s) | Minimum Equivalent Elastic Strain εmin (mm/mm) | Maximum Equivalent Elastic Strain εmax (mm/mm) | Average Equivalent Elastic Strain |
|---|---|---|---|
| 1.1755 × 10−38 | 0 | - | |
| 9.9221× 10−4 | 0 | 0.17969 | 2.4293 × 10−5 |
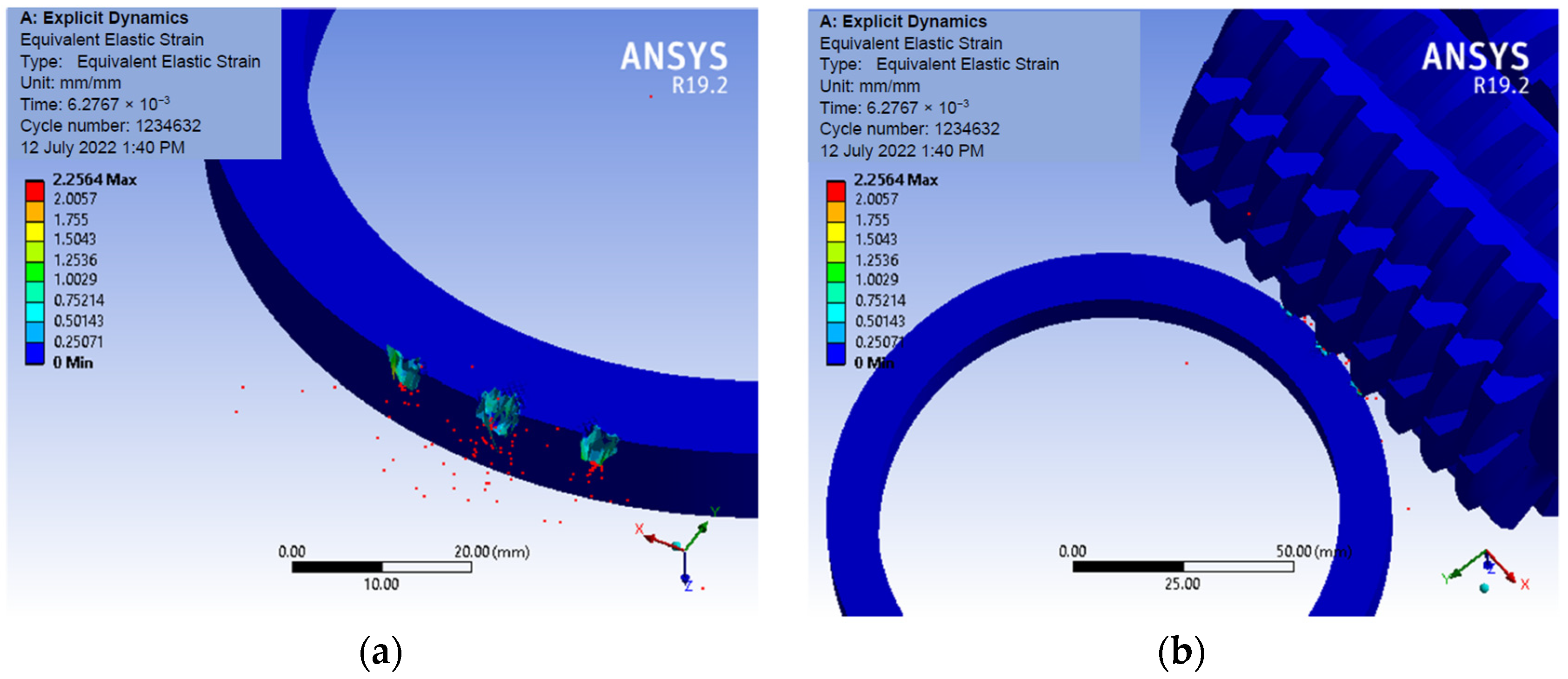
| 4.2896 × 10−3 (point A, Figure 11) | 0 | 1.3295 (point A, Figure 11) | 3.0552 × 10−4 |
| 5.0076 × 10−3 | 0 | 1.6974 | 3.6991 × 10−4 |
| 5.0749 × 10−3 | 0 | 1.7331 | 3.7898 × 10−4 |
| 5.6075 × 10−3 | 0 | 2.0255 | 4.2279 × 10−4 |
| 6.1808 × 10−3 (point B, Figure 11) | 0 | 2.2548 (point B, Figure 11) | 4.6702 × 10−4 |
| 6.2767 × 10−3 | 0 | 2.2564 | 4.7281 × 10−4 |
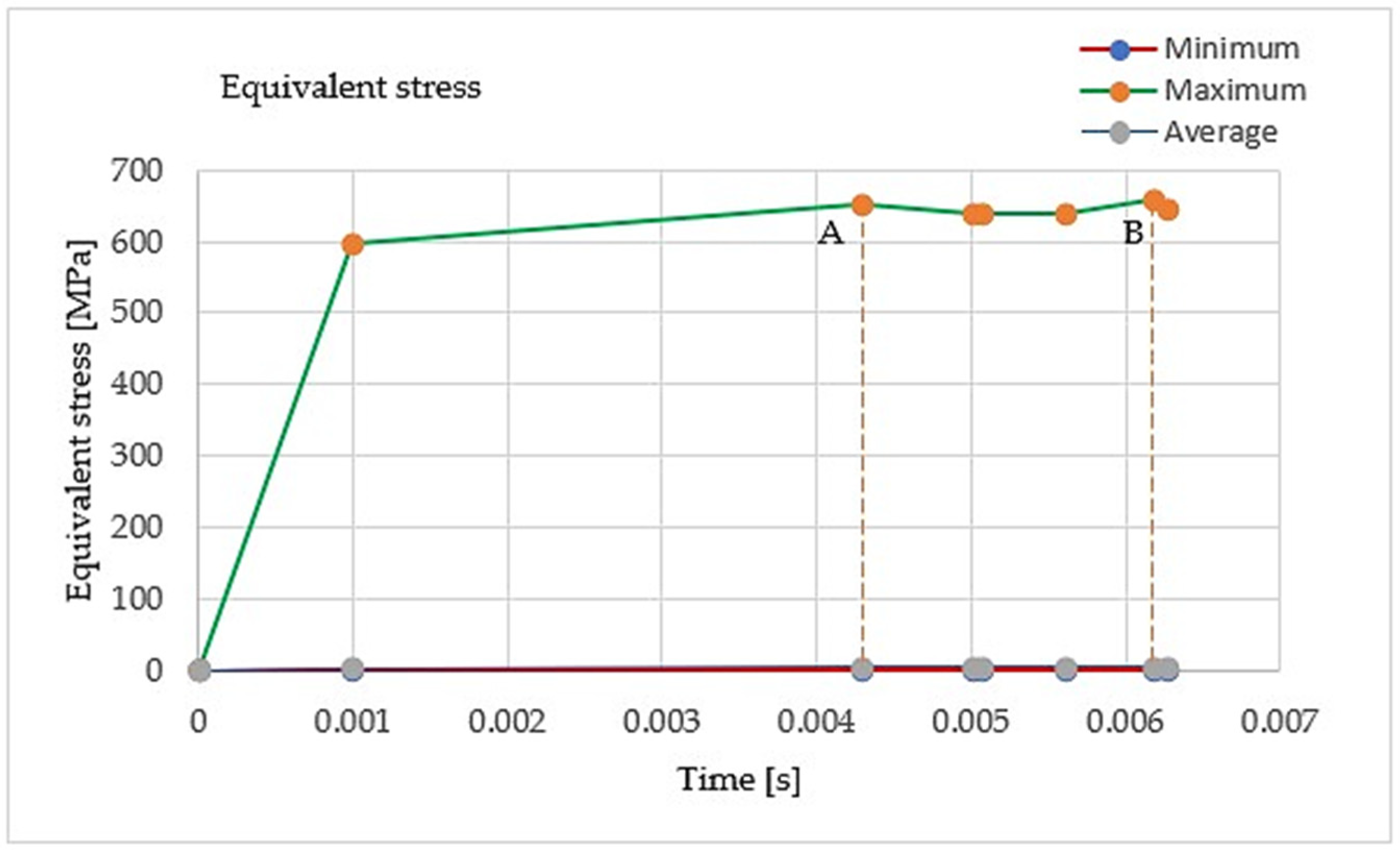
| Time t (s) | Minimum Equivalent Stress σv min (MPa) | Maximum Equivalent Stress σv max (MPa) | Average Equivalent Stress |
|---|---|---|---|
| 1.1755 × 10−38 | - | - | - |
| 9.9221 × 10−4 | 1.5649 × 10−2 | 596.63 | 3.0684 |
| 4.2896 × 10−3 (point A, Figure 12) | 3.0400 × 10−2 | 651.79 (point A, Figure 12) | 6.0913 |
| 5.0076 × 10−3 | 1.5193 × 10−2 | 639.94 | 5.8218 |
| 5.0749 × 10−3 | 1.7860 × 10−2 | 640.14 | 5.9126 |
| 5.6075 × 10−3 | 3.8187 × 10−2 | 640.10 | 4.8760 |
| 6.1808 × 10−3 (point B, Figure 12) | 1.9844 × 10−2 | 656.97 (point B, Figure 12) | 4.8431 |
| 6.2767 × 10−3 | 1.6906 × 10−2 | 644.09 | 4.6169 |
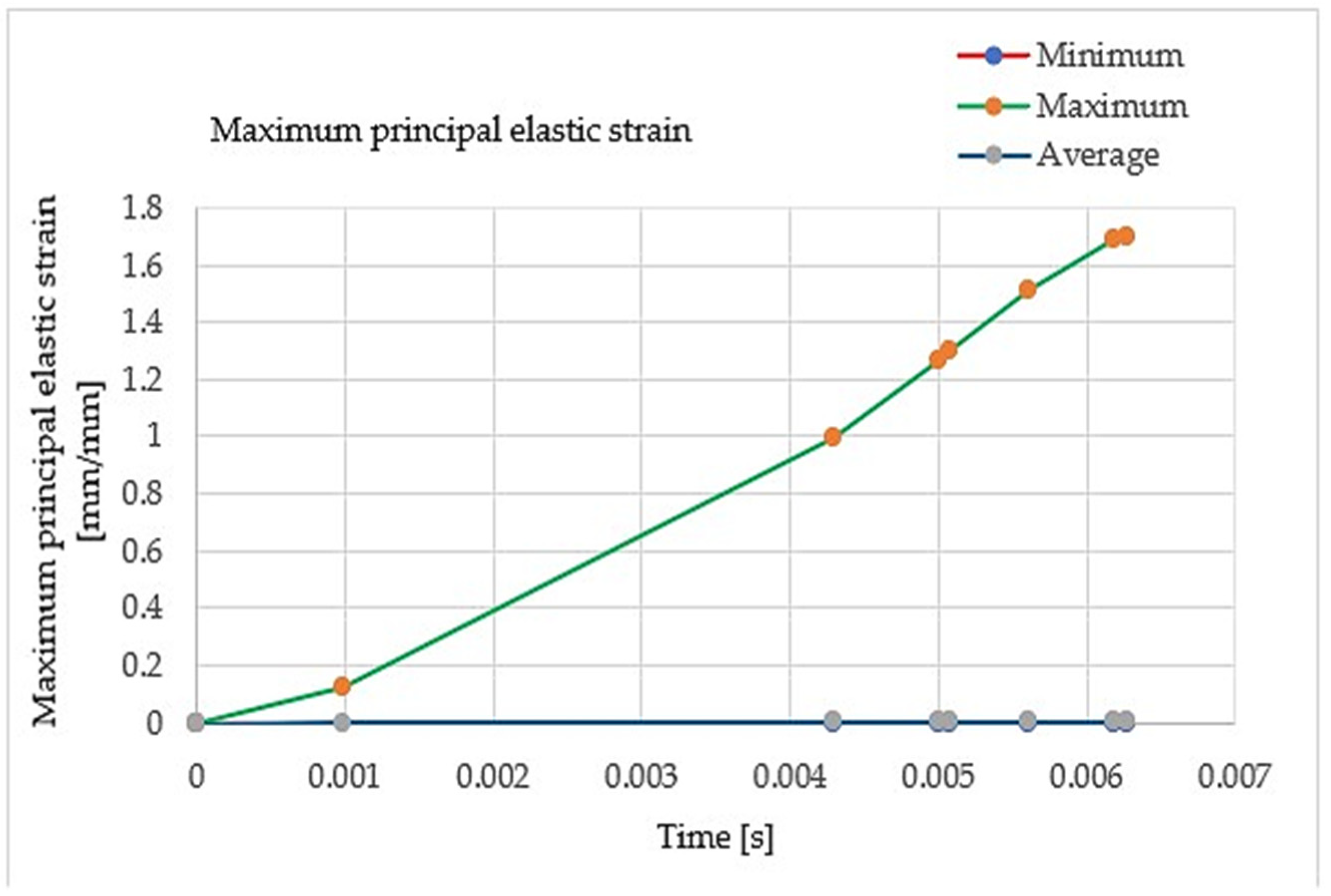
| Time t (s) | Minimum ε1 min (mm/mm) | Maximum ε1 max (mm/mm) | Average |
|---|---|---|---|
| 1.1755 × 10−38 | - | - | - |
| 9.9221 × 10−4 | −6.6972 × 10−4 | 0.12717 | 1.6845 × 10−5 |
| 4.2896 × 10−3 | −7.8338 × 10−8 | 0.9956 | 2.3802 × 10−4 |
| 5.0076 × 10−3 | −4.8383 × 10−8 | 1.2695 | 2.8779 × 10−4 |
| 5.0749 × 10−3 | −9.6818 × 10−8 | 1.2963 | 2.9485 × 10−4 |
| 5.6075 × 10−3 | −2.7392 × 10−7 | 1.5132 | 3.2678 × 10−4 |
| 6.1808 × 10−3 | 4.1564 × 10−9 | 1.6921 | 3.5890 × 10−4 |
| 6.2767 × 10−3 | −2.0218 × 10−7 | 1.6938 | 3.6272 × 10−4 |
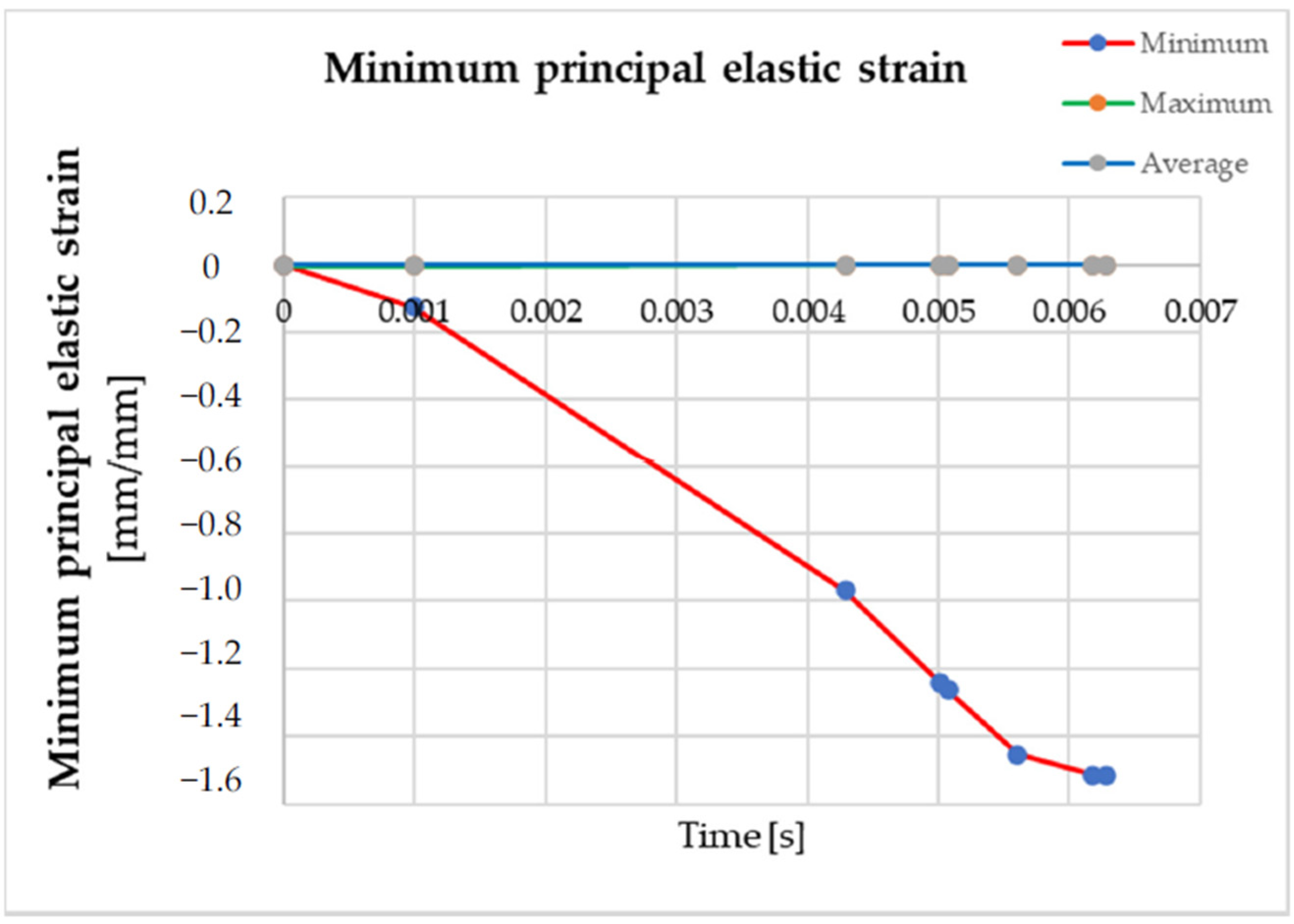
| Time t (s) | Minimum ε3 min (mm/mm) | Maximum ε3 max (mm/mm) | Average |
|---|---|---|---|
| 1.1755 × 10−38 | - | - | - |
| 9.9221 × 10−4 | −0.12521 | 4.2826 × 10−8 | −1.7264 × 10−5 |
| 4.2896 × 10−3 | −0.96972 | 1.1543 × 10−4 | −2.2078 × 10−4 |
| 5.0076 × 10−3 | −1.2395 | 3.3848 × 10−5 | −2.6823 × 10−4 |
| 5.0749 × 10−3 | −1.2643 | 2.5838 × 10−5 | −2.7514 × 10−4 |
| 5.6075 × 10−3 | −1.4533 | 1.5112 × 10−4 | −3.0484 × 10−4 |
| 6.1808 × 10−3 | −1.5139 | 6.9237 × 10−5 | −3.3336 × 10−4 |
| 6.2767 × 10−3 | −1.5149 | 1.1148 × 10−4 | −3.3702 × 10−4 |
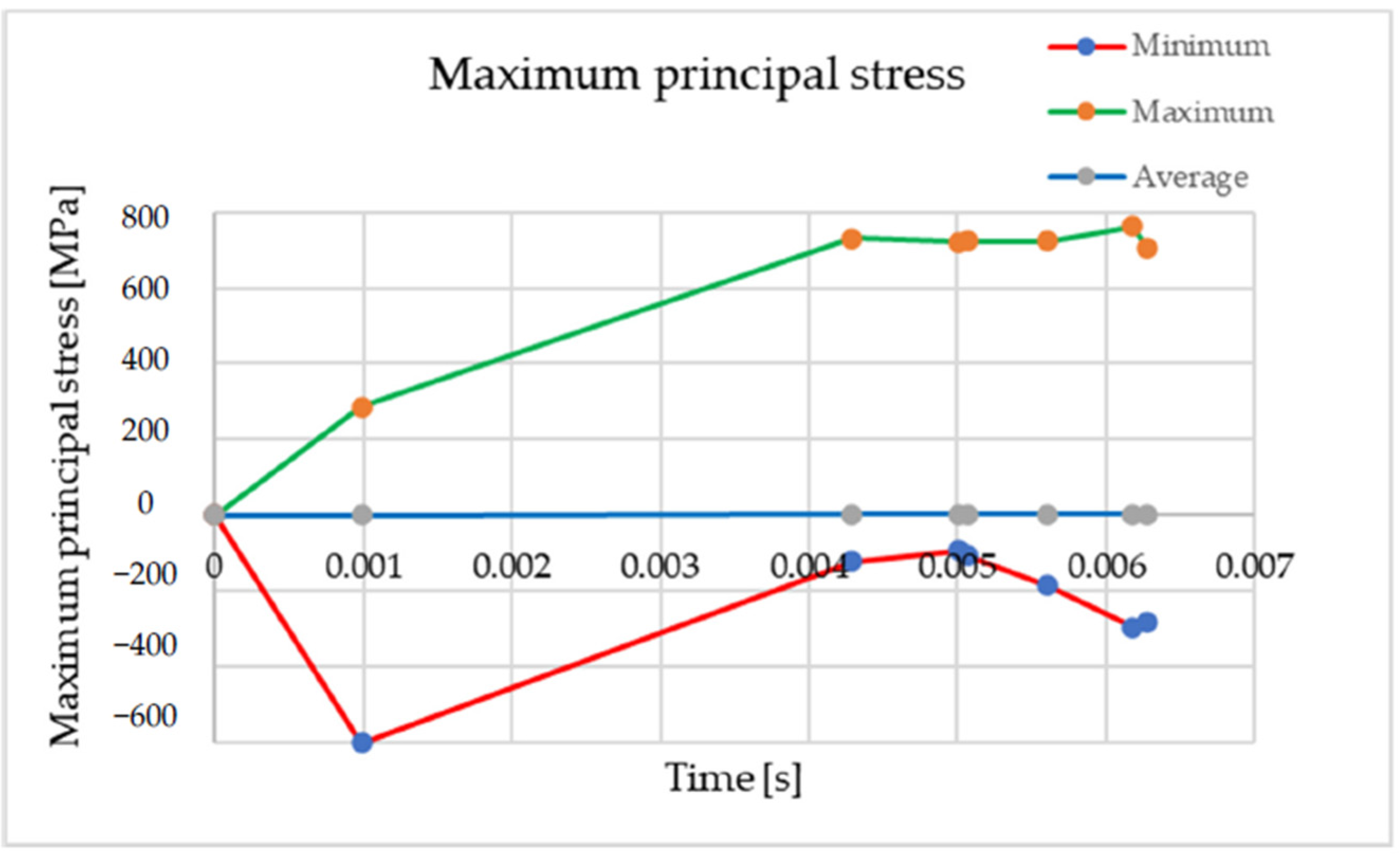
| Time t (s) | Minimum σ1 min (MPa) | Maximum σ 1 max (MPa) | Average |
|---|---|---|---|
| 1.1755 × 10−38 | - | - | - |
| 9.9221 × 10−4 | −599.08 | 286.3 | 1.5373 |
| 4.2896 × 10−3 | −120.35 | 729.74 | 3.2888 |
| 5.0076 × 10−3 | −91.411 | 720.88 | 3.1674 |
| 5.0749 × 10−3 | −105.46 | 724.08 | 3.2223 |
| 5.6075 × 10−3 | −183.68 | 722.13 | 2.6878 |
| 6.1808 × 10−3 | −293.7 | 762.69 | 2.7075 |
| 6.2767 × 10−3 | −278.74 | 704.82 | 2.5722 |
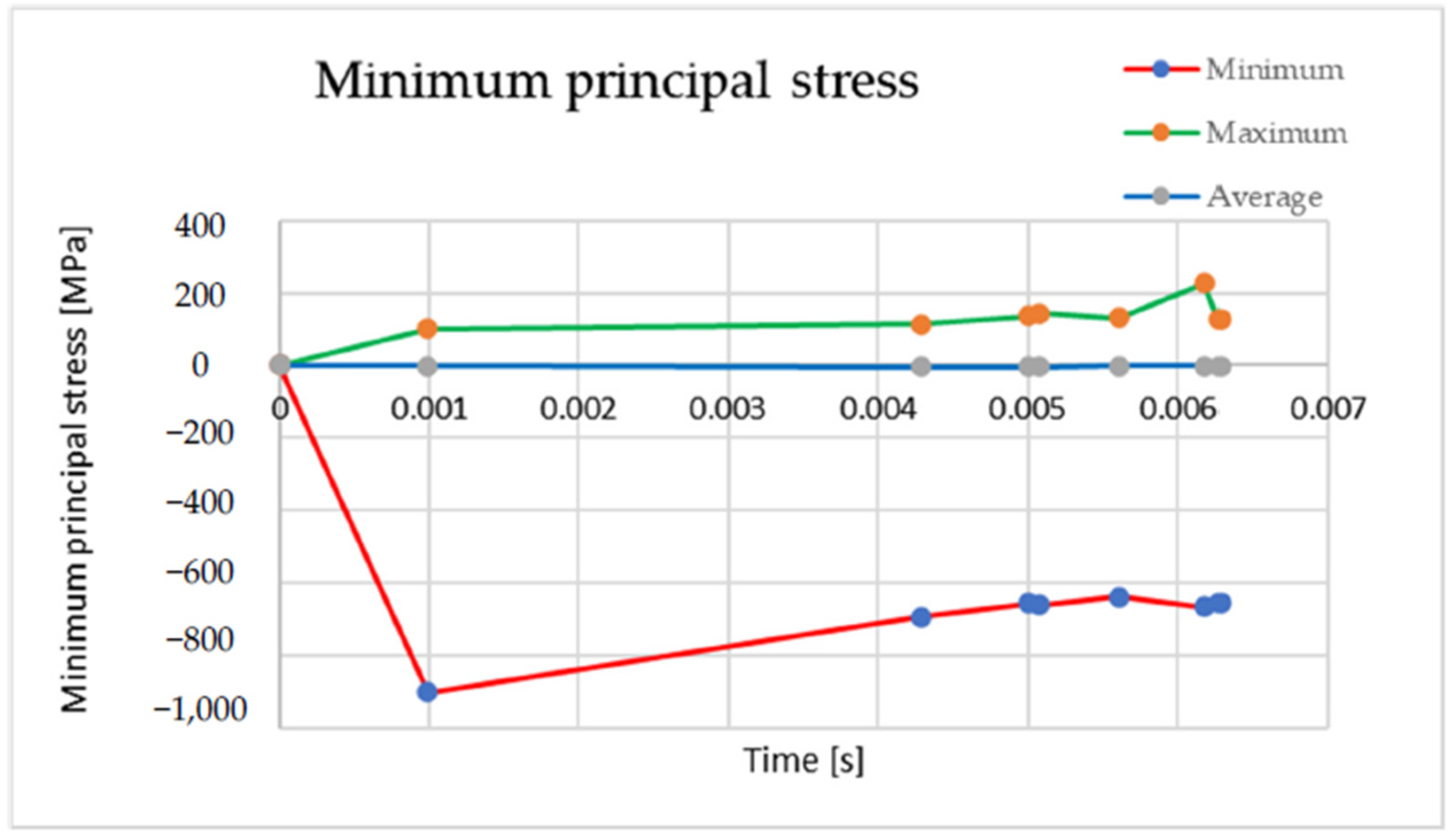
| Time t (s) | Minimum σ 3 min (MPa) | Maximum σ 3 max (MPa) | Average |
|---|---|---|---|
| 1.1755 × 10−38 | - | - | - |
| 9.9221 × 10−4 | −902.82 | 100.31 | −1.8632 |
| 4.2896 × 10−3 | −696.26 | 114.68 | −3.4724 |
| 5.0076 × 10−3 | −656.76 | 135.43 | −3.2939 |
| 5.0749 × 10−3 | −662.87 | 145.14 | −3.3447 |
| 5.6075 × 10−3 | −639.07 | 131.42 | −2.7467 |
| 6.1808 × 10−3 | −668.44 | 226.54 | −2.6771 |
| 6.2767 × 10−3 | −657.54 | 125.58 | −2.5576 |
| Type | Equivalent Elastic Strain ε (mm/mm) | Equivalent (von Mises) Stress σv (MPa) | Total Deformation δ (mm) | Maximum Principal Elastic Strain ε1 (mm/mm) | Minimum Principal Elastic Strain ε3 (mm/mm) | Middle Principal Elastic Strain ε2 (mm/mm) | Maximum Shear Elastic Strain τmax (mm/mm) | Maximum Principal Stress σ1 (MPa) |
|---|---|---|---|---|---|---|---|---|
| Minimum | 0, | 1.6906 × 10−2 | 5.123 × 10−2 | −2.0218 × 10−7 | −1.5149 | −0.24722 | 1.1954 × 10−7 | −278.74 |
| Maximum | 2.2564 | 644.09 | 714.66 | 1.6938 | 1.1148 × 10−4 | 0.12853 | 3.2087 | 704.82 |
| Average | 4.7281 × 10−4 | 4.6169 | 0.40745 | 3.6272 × 10−4 | −3.3702 × 10−4 | −1.6867 × 10−5 | 6.9974 × 10−4 | 2.5722 |
| Time | 6.2767 × 10−3 s | |||||||
| Set | 14 | |||||||
| Cycle Number | 1,234,632 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duta, A.; Geonea, I.-D.; Popa, D.-L.; Sass, L. Influence of Contact Surfaces’ Impact on the Gear Profile during Hobbing Process. Appl. Sci. 2022, 12, 8027. https://doi.org/10.3390/app12168027
Duta A, Geonea I-D, Popa D-L, Sass L. Influence of Contact Surfaces’ Impact on the Gear Profile during Hobbing Process. Applied Sciences. 2022; 12(16):8027. https://doi.org/10.3390/app12168027
Chicago/Turabian StyleDuta, Alina, Ionut-Daniel Geonea, Dragos-Laurentiu Popa, and Ludmila Sass. 2022. "Influence of Contact Surfaces’ Impact on the Gear Profile during Hobbing Process" Applied Sciences 12, no. 16: 8027. https://doi.org/10.3390/app12168027
APA StyleDuta, A., Geonea, I.-D., Popa, D.-L., & Sass, L. (2022). Influence of Contact Surfaces’ Impact on the Gear Profile during Hobbing Process. Applied Sciences, 12(16), 8027. https://doi.org/10.3390/app12168027







