Rapid Temperature Control in Melt Extrusion Additive Manufacturing Using Induction Heated Lightweight Nozzle
Abstract
1. Introduction
- Location of the temperature sensor at a distance from the mentioned heater and the nozzle leads to an error in measuring the temperature of the nozzle and polymer in 10–20 °C [12,13,14,15] (without extrusion). With an increase in the extrusion speed to the level of 30–40 mm/s, the accuracy of measuring the nozzle temperature decreases by another ~10 °C [16], and the accuracy of measuring the polymer temperature decreases to ±30 °C [14,15,16,17,18] or more with a further increase in the extrusion speed [17];
- The large mass (from 20 g onwards) of the heater block and the low speed of the thermistors and thermocouples used (response time of 100–140 ms, not ideal thermal contact with the heater block) do not allow heating or cooling of the nozzle to adjust the polymer temperature during the deposition process with a speed adequate to the deposition speed when filling the layer.
2. Materials and Methods
3. Results and Discussion
3.1. FEM Modelling of HF Induction Heating of the Nozzle during Extrusion of a Thermoplastic
3.2. Numerical Implementation of the Coupled Model of Induction Heating of the Nozzle during Extrusion of a Thermoplastic
3.3. Phase-Amplitude Resonant Measurement Method
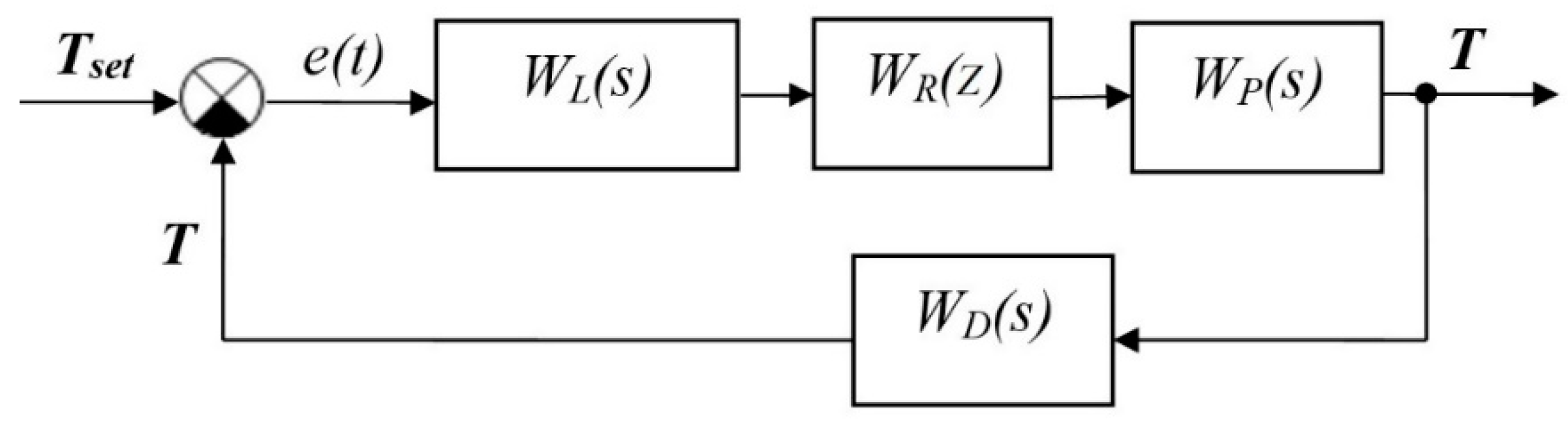
3.4. Development of a Method for Controlling the Temperature of the Lightweight Nozzle
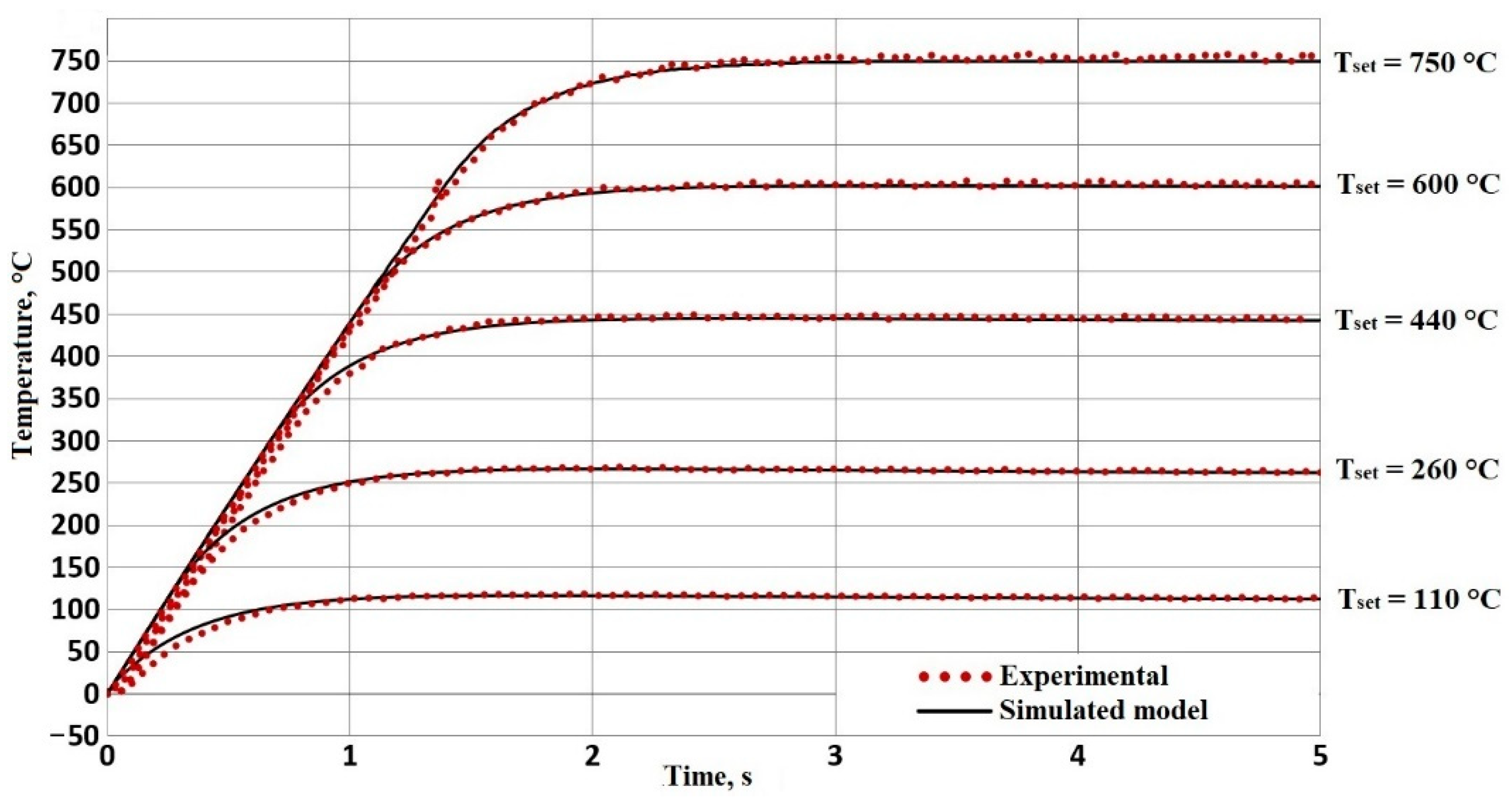
3.5. Experimental Verification of the Proposed Control Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Zhao, K.; Li, Y.; Chen, F. Mechanical characterization of biocompatible PEEK by FDM. J. Manuf. Process. 2020, 56, 28–42. [Google Scholar] [CrossRef]
- Honigmann, P.; Sharma, N.; Okolo, B.; Popp, U.; Msallem, B.; Thieringer, F.M. Patient-specific surgical implants made of 3D printed PEEK: Material, technology, and scope of surgical application. BioMed Res. Int. 2018, 2018, 4520636. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Müller, W.D.; Rumjahn, A.; Schwitalla, A. Parameters influencing the outcome of additive manufacturing of tiny medical devices based on PEEK. Materials 2020, 13, 466. [Google Scholar] [CrossRef] [PubMed]
- Pikkarainen, A.; Piili, H.; Salminen, A. The design process of an occupationally safe and functional 3d printing learning environment for engineering education. Eur. J. Educ. Stud. 2020, 7, 80–105. [Google Scholar]
- Yang, C.; Tian, X.; Li, D.; Cao, Y.; Zhao, F.; Shi, C. Influence of thermal processing conditions in 3D printing on the crystallinity and mechanical properties of PEEK material. J. Mater. Process. Technol. 2017, 248, 1–7. [Google Scholar] [CrossRef]
- Gardner, J.M.; Stelter, C.J.; Yashin, E.A.; Siochi, E.J. High Temperature Thermoplastic Additive Manufacturing Using Low-Cost, Open-Source Hardware; National Aeronautics and Space Administration; Langley Research Center: Hampton, VA, USA, 2016. [Google Scholar]
- Wang, P.; Zou, B.; Xiao, H.; Ding, S.; Huang, C. Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK. J. Mater. Process. Technol. 2019, 271, 62–74. [Google Scholar] [CrossRef]
- Syrlybayev, D.; Zharylkassyn, B.; Seisekulova, A.; Akhmetov, M.; Perveen, A.; Talamona, D. Optimisation of strength properties of FDM printed parts—A critical review. Polymers 2021, 13, 1587. [Google Scholar] [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of nozzle temperature and building orientation on mechanical properties and microstructure of PEEK and PEI printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Costanzo, A.; Croce, U.; Spotorno, R.; Fenni, S.E.; Cavallo, D. Fused deposition modeling of polyamides: Crystallization and weld formation. Polymers 2020, 12, 2980. [Google Scholar] [CrossRef]
- Jiang, S.; Liao, G.; Xu, D.; Liu, F.; Li, W.; Cheng, Y.; Li, Z.; Xu, G. Mechanical properties analysis of polyetherimide parts fabricated by fused deposition modeling. High Perform. Polym. 2019, 31, 97–106. [Google Scholar] [CrossRef]
- Sukindar, N.A.; Mohd Ariffin, M.K.A.; Baharuddin, B.T.; Jaafar, C.N.A.; Ismail, M.I.S. Analysis on temperature setting for extruding polylactic acid using open-source 3D printer. ARPN J. Eng. Appl. Sci. 2017, 12, 1348–1353. [Google Scholar]
- Shukla, V.V.; Kulkarni, A.K.; Pingle, A.K.; Oza, S. Thermal analysis of 3-D printer liquefier indicates a probable cause of nozzle clogging. Int. J. Mech. Prod. Eng. Res. Dev. 2019, 9, 176–182. [Google Scholar]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Experimental and analytical study of the polymer melt flow through the hot-end in material extrusion additive manufacturing. Addit. Manuf. 2020, 32, 100997. [Google Scholar] [CrossRef]
- Pollard, D.; Ward, C.; Herrmann, G.; Etches, J. Filament temperature dynamics in fused deposition modelling and outlook for control. Procedia Manuf. 2017, 11, 536–544. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the polymer flow through the hot-end in filament-based material extrusion additive manufacturing. Addit. Manuf. 2020, 36, 101454. [Google Scholar] [CrossRef]
- Anderegg, D.A.; Bryant, H.A.; Ruffin, D.C.; Skrip, S.M., Jr.; Fallon, J.J.; Gilmer, E.L.; Bortner, M.J. In-situ monitoring of polymer flow temperature and pressure in extrusion based additive manufacturing. Addit. Manuf. 2019, 26, 76–83. [Google Scholar] [CrossRef]
- Maidin, S.; Muhamad, M.K.; Pei, E. Experimental setup for ultrasonic-assisted desktop fused deposition modeling system. Appl. Mech. Mater. 2015, 761, 324–328. [Google Scholar] [CrossRef]
- Nigmetzyanov, R.I.; Sundukov, S.K.; Fatyukhin, D.S.; Grib, V.V.; Kartsov, S.K. Additive Manufacturing with Ultrasound. Russ. Eng. Res. 2017, 37, 1070–1073. [Google Scholar] [CrossRef]
- Tofangchi, A.; Han, P.; Izquierdo, J.; Iyengar, A.; Hsu, K. Effect of ultrasonic vibration on interlayer adhesion in fused filament fabrication 3D printed ABS. Polymers 2019, 11, 315. [Google Scholar] [CrossRef]
- Li, G.; Zhao, J.; Jiang, J.; Jiang, H.; Wu, W.; Tang, M. Ultrasonic strengthening improves tensile mechanical performance of fused deposition modeling 3D printing. Int. J. Adv. Manuf. Technol. 2018, 96, 2747–2755. [Google Scholar] [CrossRef]
- Li, G.; Zhao, J.; Wu, W.; Jiang, J.; Wang, B.; Jiang, H.; Fuh, J.Y.H. Effect of ultrasonic vibration on mechanical properties of 3D printing non-crystalline and semi-crystalline polymers. Materials 2018, 11, 826. [Google Scholar] [CrossRef]
- Watson, N.J.; Johal, R.K.; Glover, Z.; Reinwald, Y.; White, L.J.; Ghaemmaghami, A.M.; Morgan, S.P.; Rose, F.R.A.J.; Povey, M.J.W.; Parker, N.G. Post-processing of polymer foam tissue scaffolds with high power ultrasound: A route to increased pore interconnectivity, pore size and fluid transport. Mater. Sci. Eng. 2013, 33, 4825–4832. [Google Scholar] [CrossRef][Green Version]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Kishore, V.; Ajinjeru, C.; Nycz, A.; Post, B.; Lindahl, J.; Kunc, V.; Duty, C. Infrared preheating to improve interlayer strength of big area additive manufacturing (BAAM) components. Addit. Manuf. 2017, 14, 7–12. [Google Scholar] [CrossRef]
- Sabyrov, N.; Abilgaziyev, A.; Ali, M. Enhancing interlayer bonding strength of FDM 3D printing technology by diode laser-assisted system. Int. J. Adv. Manuf. Technol. 2020, 108, 603–611. [Google Scholar] [CrossRef]
- Fang, L.; Yan, Y.; Agarwal, O.; Yao, S.; Seppala, J.E.; Kang, S.H. Effects of environmental temperature and humidity on the geometry and strength of polycarbonate specimens prepared by fused filament fabrication. Materials 2020, 13, 4414. [Google Scholar] [CrossRef]
- Casavola, C.; Cazzato, A.; Karalekas, D.; Moramarco, V.; Pappalettera, G. The effect of chamber temperature on residual stresses of FDM parts. In Residual Stress, Thermomechanics & Infrared Imaging, Hybrid Techniques and Inverse Problems; Springer: Cham, Switzerland, 2019; Volume 7, pp. 87–92. [Google Scholar]
- Zhou, Y.; Lu, H.; Wang, G.; Wang, J.; Li, W. Voxelization modelling based finite element simulation and process parameter optimization for Fused Filament Fabrication. Mater. Des. 2020, 187, 108409. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Li, H.; Feng, H. Simulation of Temperature Field in FDM Process. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 032080. [Google Scholar] [CrossRef]
- El Moumen, A.; Tarfaoui, M.; Lafdi, K. Modelling of the temperature and residual stress fields during 3D printing of polymer composites. Int. J. Adv. Manuf. Technol. 2019, 104, 1661–1676. [Google Scholar] [CrossRef]
- Zhou, Y.; Nyberg, T.; Xiong, G.; Liu, D. Temperature analysis in the fused deposition modeling process. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; pp. 678–682. [Google Scholar]
- Verma, A.; Vishnoi, P.; Sukhotskiy, V.; Furlani, E.P. Numerical simulation of extrusion additive manufacturing: Fused deposition modeling. TechConnect Briefs 2018, 4, 118–121. [Google Scholar]
- Xia, H.; Lu, J.; Dabiri, S.; Tryggvason, G. Fully resolved numerical simulations of fused deposition modeling. Part I: Fluid flow. Rapid Prototyp. J. 2018, 24, 463–476. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Sheoran, A.J.; Kumar, H. Fused Deposition modeling process parameters optimization and effect on mechanical properties and part quality: Review and reflection on present research. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- Lee, B.H.; Abdullah, J.; Khan, Z.A. Optimization of rapid prototyping parameters for production of flexible ABS object. J. Mater. Process. Technol. 2005, 169, 54–61. [Google Scholar] [CrossRef]
- Srivastava, M.; Rathee, S. Optimisation of FDM process parameters by Taguchi method for imparting customised properties to components. Virtual Phys. Prototyp. 2018, 13, 203–210. [Google Scholar] [CrossRef]
- Raju, M.; Gupta, M.K.; Bhanot, N.; Sharma, V.S. A hybrid PSO–BFO evolutionary algorithm for optimization of fused deposition modelling process parameters. J. Intell. Manuf. 2019, 30, 2743–2758. [Google Scholar] [CrossRef]
- Dong, G.; Wijaya, G.; Tang, Y.; Zhao, Y.F. Optimizing process parameters of fused deposition modeling by Taguchi method for the fabrication of lattice structures. Addit. Manuf. 2018, 19, 62–72. [Google Scholar] [CrossRef]
- Hikmat, M.; Rostam, S.; Ahmed, Y.M. Investigation of tensile property-based Taguchi method of PLA parts fabricated by FDM 3D printing technology. Results Eng. 2021, 11, 100264. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Li, S.; Si, L.; Peng, J.; Hu, Y. Mechanical property parametric appraisal of fused deposition modeling parts based on the gray Taguchi method. Int. J. Adv. Manuf. Technol. 2017, 89, 2387–2397. [Google Scholar] [CrossRef]
- Cho, E.E.; Hein, H.H.; Lynn, Z.; Hla, S.J.; Tran, T. Investigation on influence of infill pattern and layer thickness on mechanical strength of PLA material in 3D printing technology. J. Eng. Sci. Res. 2019, 3, 27–37. [Google Scholar]
- Tan, W.S. Application of Induction Heating to 3D Print Low Melting Point Metal Alloy: Final Project Summary Report 2015, UNSW@ADFA; IOP: Bristol, UK, 2015; p. 13. [Google Scholar]
- Hemang, J.; Manish, A. Induction Heating Based 3D Metal Printing of Eutectic Alloy Using Vibrating Nozzle. In Advances in Additive Manufacturing, Modeling Systems and 3D Prototyping; Springer: Cham, Switzerland, 2020; pp. 71–80. [Google Scholar]
- Carter, W.G.; Rios, O.; Akers, R.R.; Morrison, W.A. Low-Cost Electromagnetic Heating Technology for Polymer Extrusion-Based Additive Manufacturing; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016. [Google Scholar]
- Seppala, J.E.; Han, S.H.; Hillgartner, K.E.; Davis, C.S.; Migler, K.B. Weld formation during material extrusion additive manufacturing. Soft Matter 2017, 13, 6761–6769. [Google Scholar] [CrossRef]
- Franco, C.; Acero, J.; Alonso, R.; Sagues, C.; Paesa, D. Inductive sensor for temperature measurement in induction heating applications. IEEE Sens. J. 2012, 12, 996–1003. [Google Scholar] [CrossRef]
- Lang, S. Temperature Measurement in a Cooking Vessel. U.S. Patent 9544947B2, 10 January 2017. [Google Scholar]
- Cojuhari, I.; Fiodorov, I.; Izvoreanu, B.; Moraru, D.; Botnaru, S. Automatic temperature control in 3D printing of the polymer details. In Proceedings of the 2017 International Conference on Electromechanical and Power Systems (SIELMEN), Iasi, Romania, 11–13 October 2017; pp. 31–35. [Google Scholar]
- Mir-Nasiri, N.; Ali, M.H.; Kurokawa, S. Development of 3D printer with integrated temperature control system. In Proceedings of the 2015 International Conference on Informatics, Electronics & Vision (ICIEV), Fukuoka, Japan, 15–18 June 2015; pp. 1–6. [Google Scholar]
- Oskolkov, A.; Bezukladnikov, I.; Trushnikov, D. Indirect Temperature Measurement in High Frequency Heating Systems. Sensors 2021, 21, 2561. [Google Scholar] [CrossRef]
- Mohan, N. Power Electronics. A First Course, 1st ed.; John Wiley & Sons: New York, NY, USA, 2011; p. 288. [Google Scholar]
- Texas Instruments. Phase-Shifted Full Bridge DC/DC Power Converter Design Guide; Texas Instruments: Dallas, TX, USA, 2015. [Google Scholar]
- Texas Instruments. INA240 High- and Low-Side, Bidirectional, Zero-Drift, Current-Sense Amplifier with Enhanced PWM Rejection; Texas Instruments: Dallas, TX, USA, 2018. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 1st ed.; John Wiley & Sons: New York, NY, USA, 1962; p. 641. [Google Scholar]
- Serdeczny, M.P. Numerical and Experimental Analysis of Filament-Based Material Extrusion Additive Manufacturing. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2020. [Google Scholar]
- Coogan, T.J.; Kazmer, D.O. In-line rheological monitoring of fused deposition modeling. J. Rheol. 2019, 63, 141–155. [Google Scholar] [CrossRef]
- Phan, D.D.; Swain, Z.R.; Mackay, M.E. Rheological and heat transfer effects in fused filament fabrication. J. Rheol. 2018, 62, 1097–1107. [Google Scholar] [CrossRef]
- Pigeonneau, F.; Xu, D.; Vincent, M.; Agassant, J.F. Heating and flow computations of an amorphous polymer in the liquefier of a material extrusion 3D printer. Addit. Manuf. 2020, 32, 101001. [Google Scholar] [CrossRef]
- Dieckerhoff, S.; Ruan, M.J.; De Doncker, R.W. Design of an IGBT-based LCL-resonant inverter for high-frequency induction heating. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference, Thirty-Forth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999; Volume 3, pp. 2039–2045. [Google Scholar]
- Silicon Laboratories Inc. Improving ADC Resolution by Oversampling and Averaging; Silicon Laboratories Inc.: Austin, TX, USA, 2015. [Google Scholar]
- Atmel Corporation. AVR121: Enhancing ADC Resolution by Oversampling; Atmel Corporation: San Jose, CA, USA, 2005. [Google Scholar]
- Fischer, G.L.; Doht, H. An inverter system for inductive tube welding utilizing resonance transformation. In Proceedings of the Conference Record of the 1994 IEEE Industry Applications Society Annual Meeting, Denver, CO, USA, 2–6 October 1994; Volume 2, pp. 833–840. [Google Scholar]
- RM0364. Reference Manual. STM32F334xx Advanced Arm//STMicroelectronics. 2017. 1124p. Available online: https://www.st.com/resource/en/reference_manual/dm00093941-stm32f334xx-advanced-arm-based-32-bit-mcus-stmicroelectronics.pdf (accessed on 10 July 2022).
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 11th ed.; Prentice Hall: Hoboken, NJ, USA, 2008; p. 1022. [Google Scholar]
- Astrom, K.J. PID Controllers, Theory, Design and Tuning, 2nd ed.; Instrument Society of America: Pittsburgh, PA, USA, 1995; p. 354. [Google Scholar]
- Standartinform. State All-Union Standard 11262-2017. PLASTICS. Tensile Test Method; Standartinform: Moscow, Russia, 2017. [Google Scholar]
- Ahn, S.H.; Montero, M.; Odell, D.; Roundy, S.; Wright, P.K. Anisotropic material properties of fused deposition modeling ABS. Rapid Prototyp. J. 2002, 8, 248–257. [Google Scholar] [CrossRef]
- Wang, J.Y.; Xu, D.D.; Sun, W.; Du, S.M.; Guo, J.J.; Xu, G.J. Effects of nozzle-bed distance on the surface quality and mechanical properties of fused filament fabrication parts. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bristol, UK, 1 February 2019; Volume 479, p. 012094. [Google Scholar]
- Cantrell, J.T.; Rohde, S.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, C.; et al. Experimental characterization of the mechanical properties of 3D-printed ABS and polycarbonate parts. Rapid Prototyp. J. 2017, 23, 811–824. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Sun, J.; Yu, Z. The effect of process parameters in fused deposition modelling on bonding degree and mechanical properties. Rapid Prototyp. J. 2018, 24, 80–92. [Google Scholar] [CrossRef]
- Guo, Z.; Peng, X.; Sang, L. Enhancement of Mechanical Properties of PA6 Blending with Talcum for Fused Deposition Modeling. Macromol. Mater. Eng. 2020, 305, 2000355. [Google Scholar] [CrossRef]
- Masood, S.H.; Mau, K.; Song, W.Q. Tensile properties of processed FDM polycarbonate material. Mater. Sci. Forum 2010, 654, 2556–2559. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical property characterization and simulation of fused deposition modeling Polycarbonate parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Deng, X.; Zeng, Z.; Peng, B.; Yan, S.; Ke, W. Mechanical properties optimization of poly-ether-ether-ketone via fused deposition modeling. Materials 2018, 11, 216. [Google Scholar] [CrossRef]

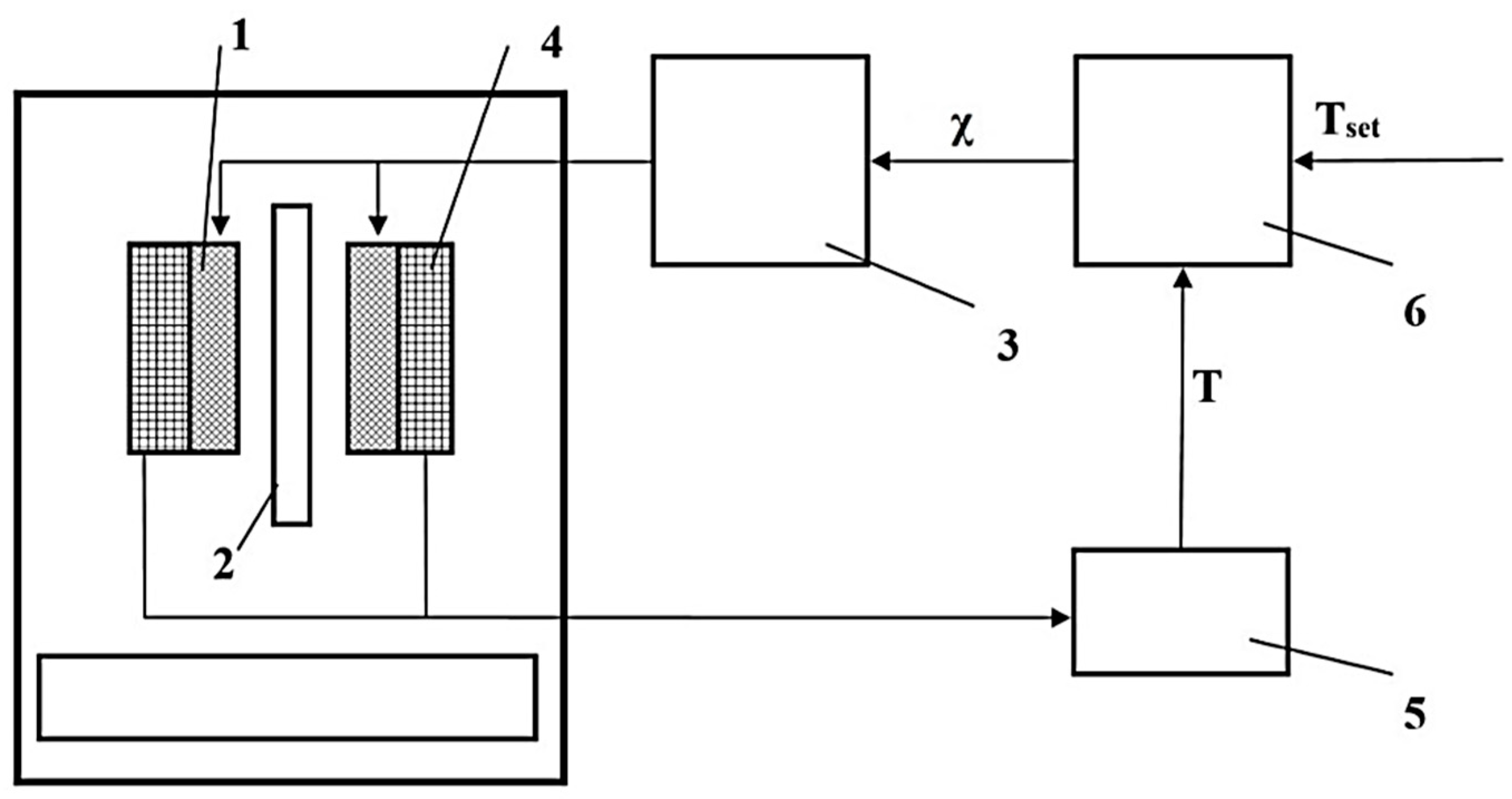
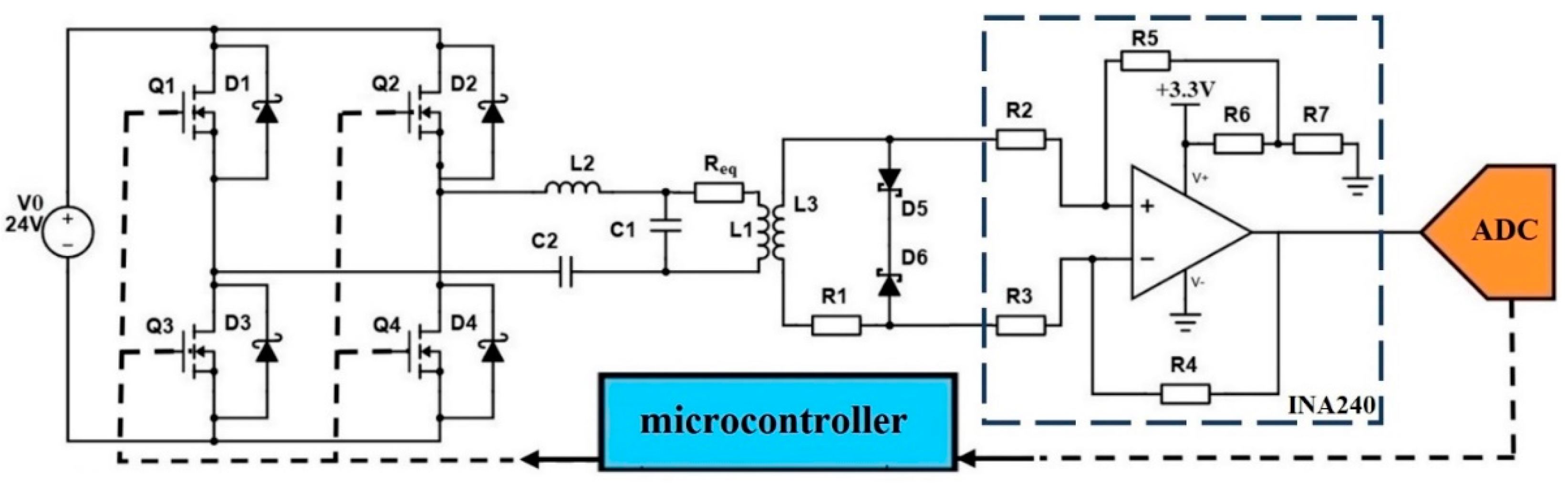
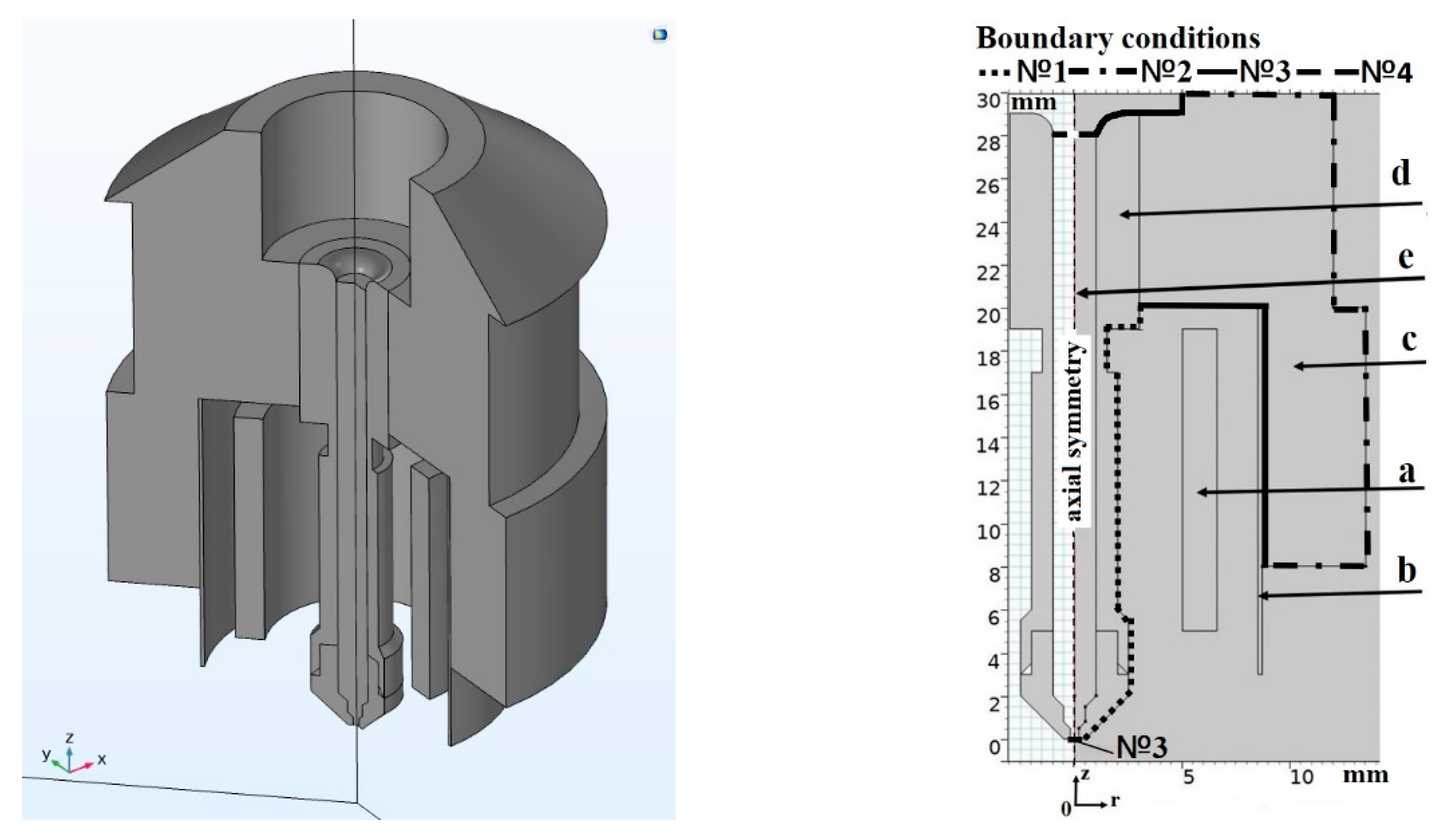
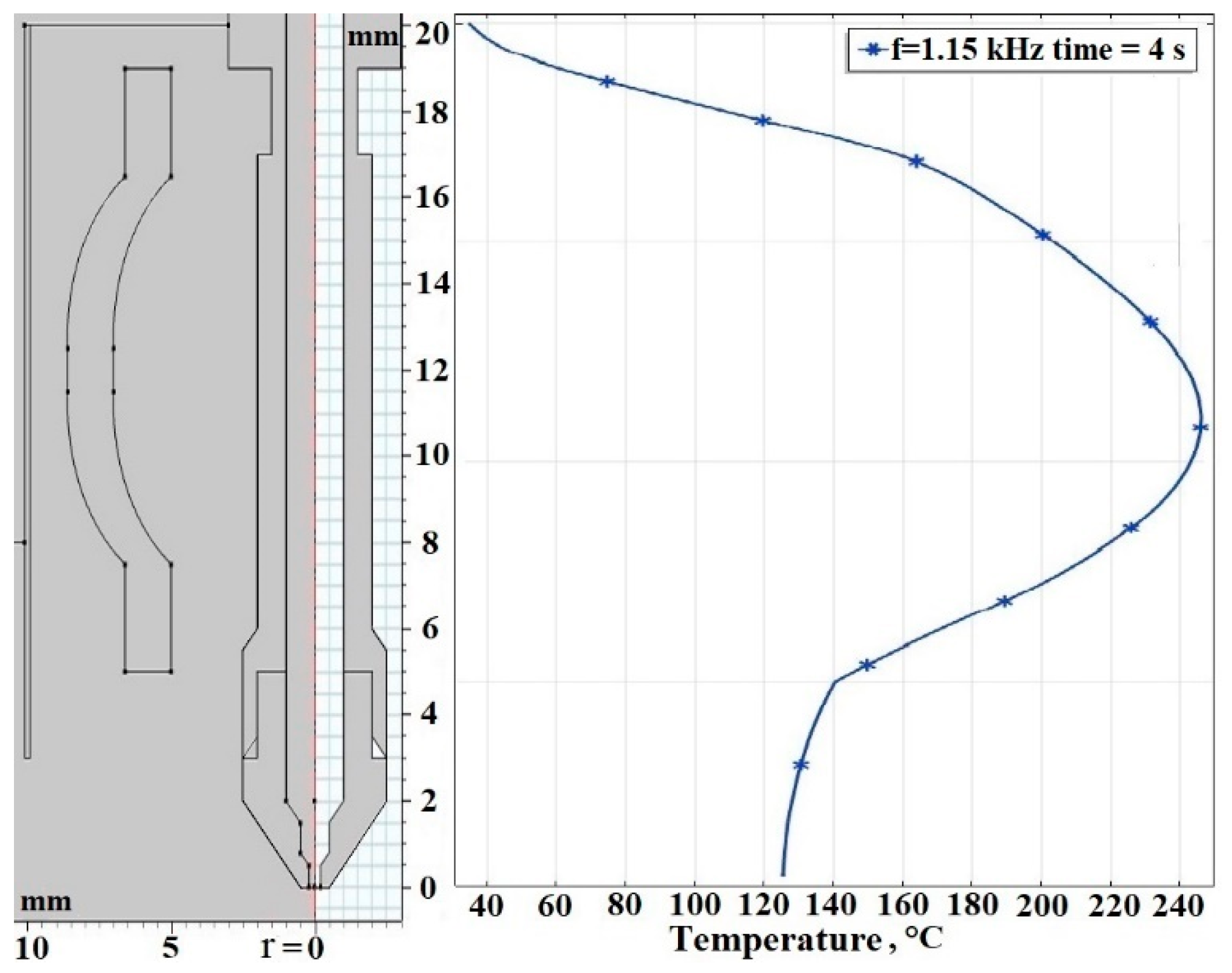
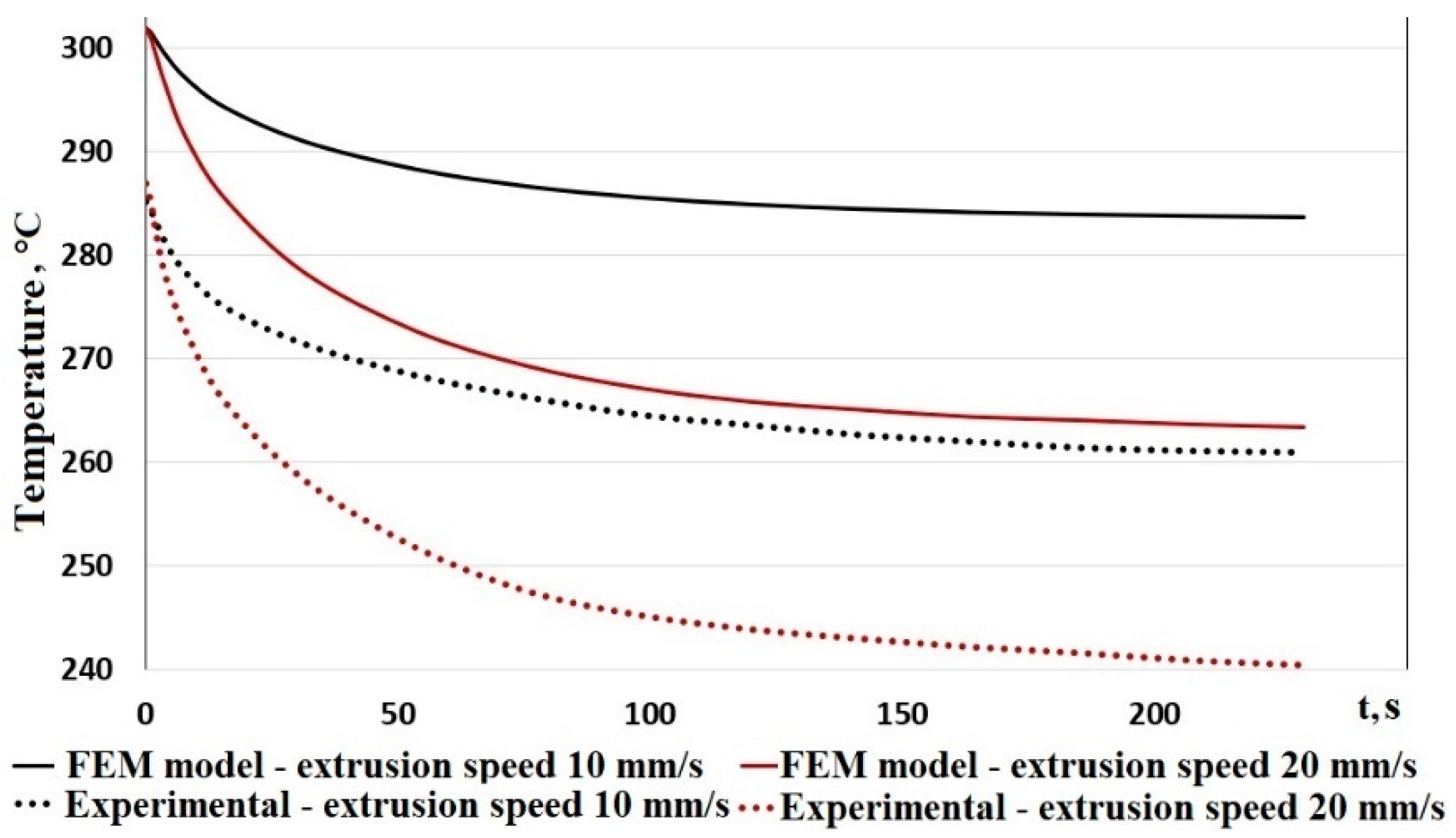
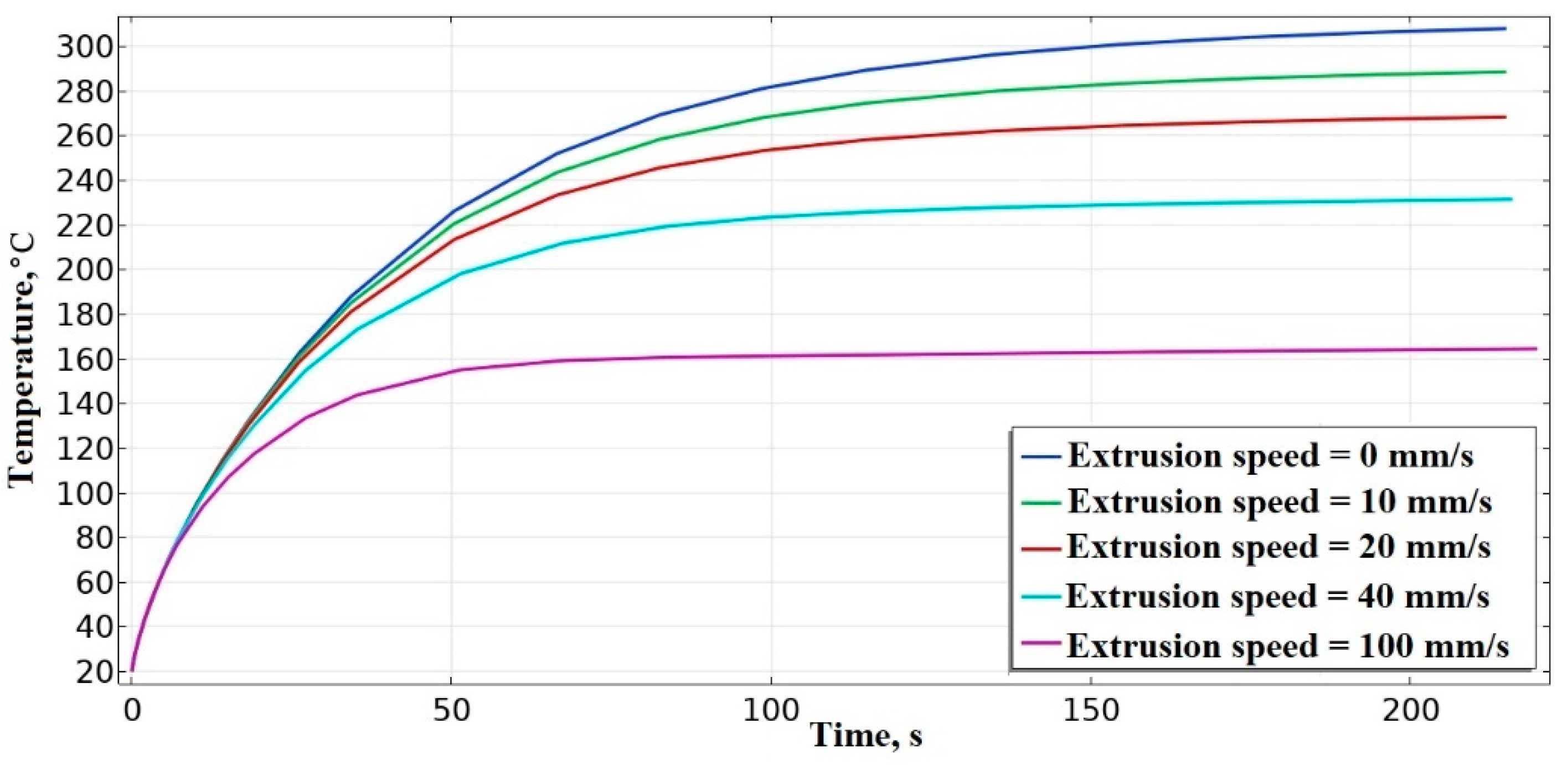

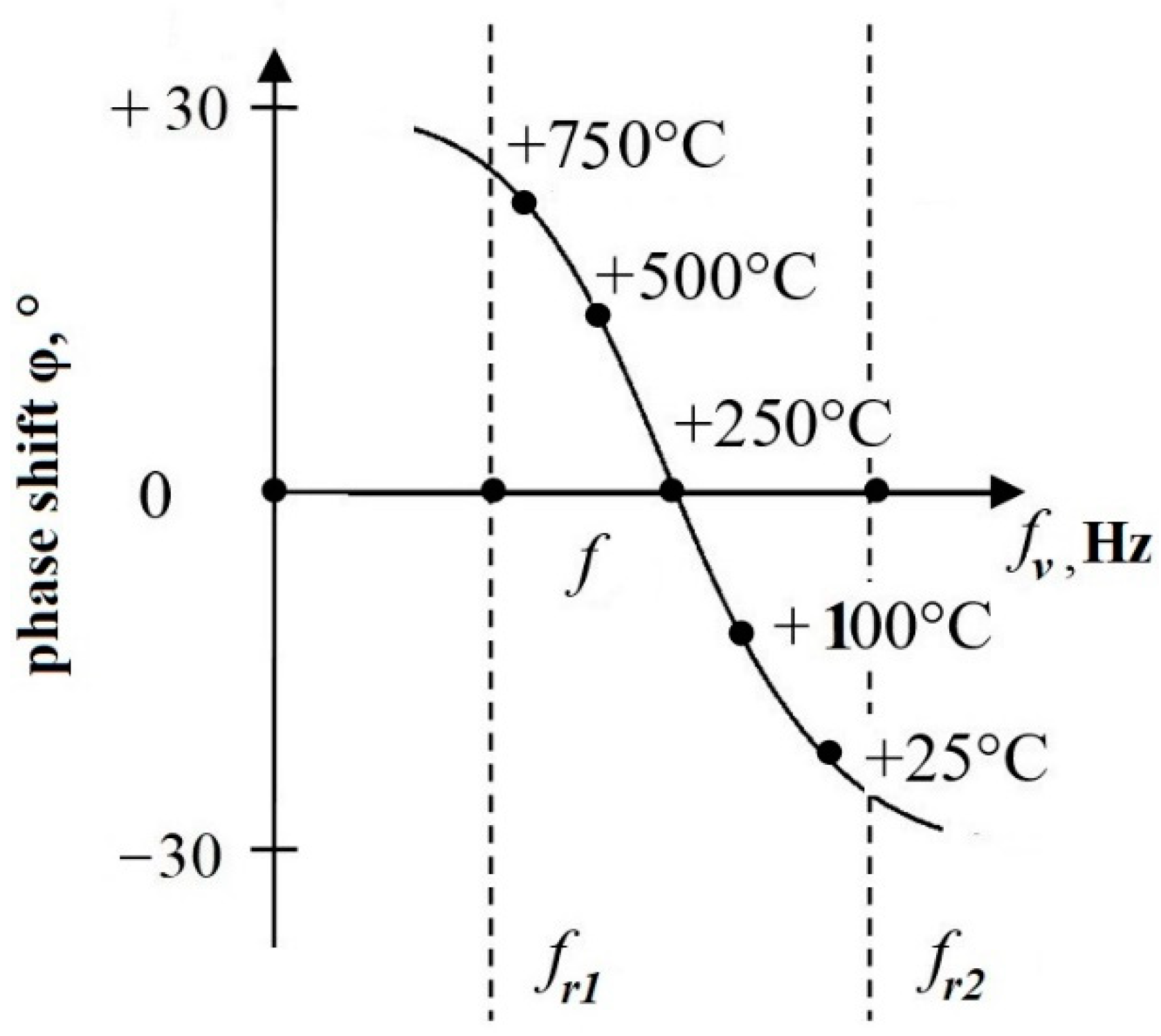
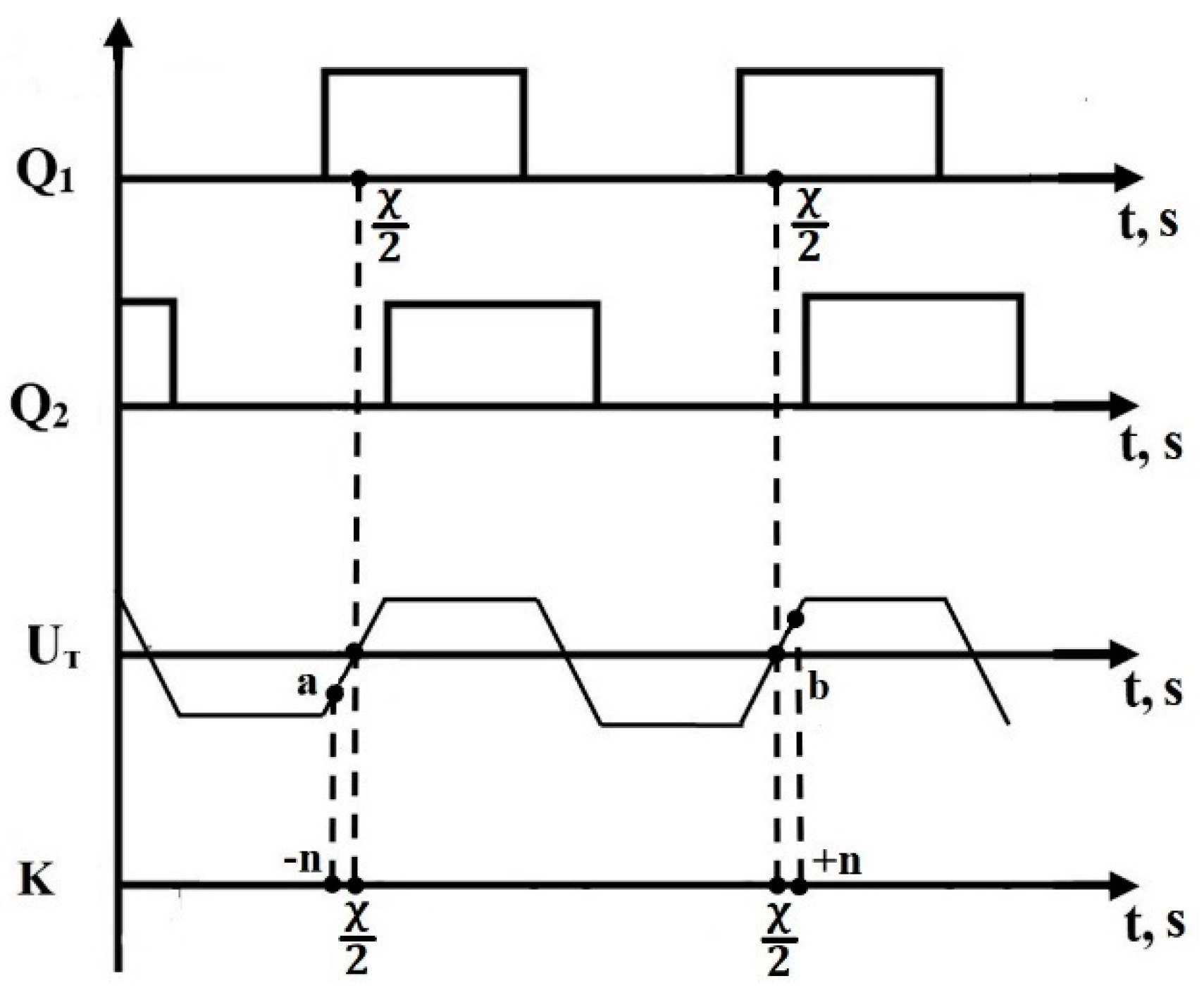
| Material | ρ, kg·m–3 | σ, Sm/m | µ | ε | Cp, J·kg –1·K–1 | λ, W·m–1·K–1 |
|---|---|---|---|---|---|---|
| Steel AISI420 | 7650 | 1.02·107 | 1500 | 1 | 482 | 25 |
| Copper | 8700 | 5.998·107 | 1 | 1 | 385 | 400 |
| Supermalloy 79NM | 8600 | 0.001 | 20,000 | 4.5 | 1369 | 1.2 |
| Polyamide PA 6 | 1050 | 0.001 | 1 | 4 | 2000 | 0.33 |
| Aluminium alloy | 2800 | 3.774·107 | 1 | 1 | 920 | 130 |
| Setpoint Tset, °C | Steady-State (after 30 s, Averaged over 5 s), °C | Value Fluctuations (10 Consecutive Measurements after 30 s, in 5 s Intervals, No Averaging), °C | Settling Time after Disabling Heater, s | Max Overshoot, °C | |
|---|---|---|---|---|---|
| Developed method | 250 | 249.5 | 249.4–249.6 | 0.32 | 0.9 |
| Thermocouple inside, 10% | 236.3 | 236.2–236.3 | 12.8 | 26 | |
| Thermocouple inside, 50% (reference) | 250.1 | 250.0–250.2 | 6.3 | 11 | |
| Thermocouple inside, 90% | 221.4 | 221.3–221.6 | 18.5 | 38 | |
| Thermocouple on the surface, 10% | 235.4 | 235.3–235.5 | 3.2 | 6 | |
| Thermocouple on the surface, 50% | 250.0 | 249.9–250.1 | 2.5 | 4 | |
| Thermocouple on the surface, 90% | 216.5 | 216.4–216.7 | 4.8 | 8 |
| Setpoint, °C | PID Controller Optimized for 260 °C | PID Controller Optimized for 440 °C | PID Controller Optimized for 750 °C | |||
|---|---|---|---|---|---|---|
| Max Overshoot, % | Settling Time, s | Max Overshoot, % | Settling Time, s | Max Overshoot, % | Settling Time, s | |
| 260 | 0.9 | 3.8 | 5 | 3.3 | 8 | 4.8 |
| 440 | 1.5 | 7.2 | 1.1 | 4.2 | 5.5 | 5.8 |
| 750 | 2.3 | 9.6 | 0.7 | 6.6 | 0.4 | 7.1 |
| Power Level of HF Generator, % | Phase Shift χ, ° | Power Consumed by the Inductor, W | Source Voltage V1 and V2, V | Estimated Currents I of the Inductor, A | Estimated Steady-State Temperatures of the Nozzle T, °C |
|---|---|---|---|---|---|
| 1 | 18 | 3.3 | 2.4 | 2.6 | 59 |
| 10 | 56 | 32.2 | 7.5 | 8.1 | 548 |
| 20 | 80 | 65.2 | 10.66 | 11.5 | 1086 |
| 30 | 98 | 97 | 13 | 14 | 1608 |
| 100 | 180 | 331 | 24 | 26 | 5549 |
| Material | Nozzle Temperature, °C | Bed Temperature, °C | Raster Angle/No. | Deposition Speed, mm/s | Nozzle Diameter, mm | Layer Thickness, mm | |
|---|---|---|---|---|---|---|---|
| −45°: 45° | 0°: 90° | ||||||
| PA 6 | 250 | 130 | 1 | 2 | 40 | 0.6 | 0.2 |
| 260 | 3 | 4 | |||||
| PC | 240 | 120 | 1 | 2 | 40 | ||
| 250 | 3 | 4 | |||||
| PEEK | 440 | 140 | 1 | 2 | 25 | ||
| 450 | 3 | 4 | |||||
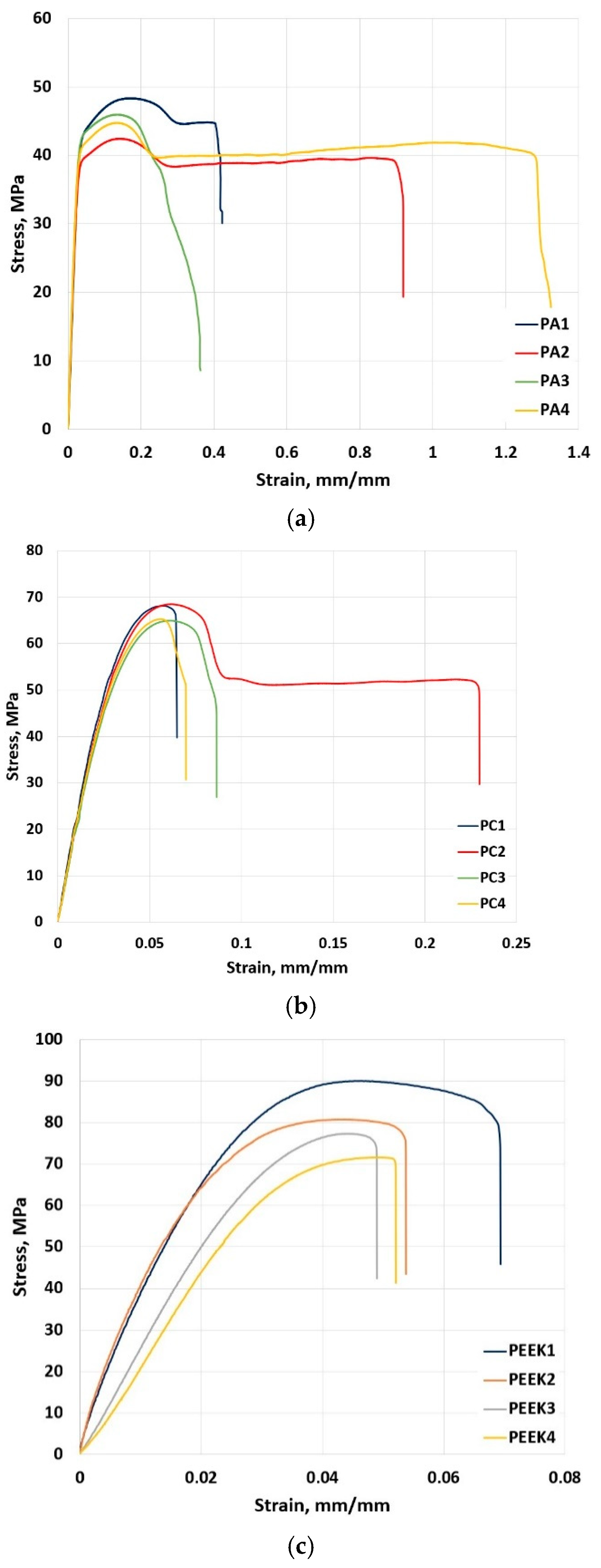
| Material | No. | Tensile Strength, MPa | Elongation at Maximum Tensile Stress, % |
|---|---|---|---|
| PA 6 | 1 | 48.37 | 17.1 |
| 2 | 42.42 | 14.5 | |
| 3 | 45.95 | 13.3 | |
| 4 | 44.73 | 13.5 | |
| PC | 1 | 68.13 | 5.7 |
| 2 | 68.48 | 6.2 | |
| 3 | 64.94 | 6.1 | |
| 4 | 65.24 | 5.6 | |
| PEEK | 1 | 89.91 | 4.7 |
| 2 | 80.72 | 4.3 | |
| 3 | 77.34 | 4.4 | |
| 4 | 71.56 | 4.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oskolkov, A.A.; Bezukladnikov, I.I.; Trushnikov, D.N. Rapid Temperature Control in Melt Extrusion Additive Manufacturing Using Induction Heated Lightweight Nozzle. Appl. Sci. 2022, 12, 8064. https://doi.org/10.3390/app12168064
Oskolkov AA, Bezukladnikov II, Trushnikov DN. Rapid Temperature Control in Melt Extrusion Additive Manufacturing Using Induction Heated Lightweight Nozzle. Applied Sciences. 2022; 12(16):8064. https://doi.org/10.3390/app12168064
Chicago/Turabian StyleOskolkov, Alexander A., Igor I. Bezukladnikov, and Dmitriy N. Trushnikov. 2022. "Rapid Temperature Control in Melt Extrusion Additive Manufacturing Using Induction Heated Lightweight Nozzle" Applied Sciences 12, no. 16: 8064. https://doi.org/10.3390/app12168064
APA StyleOskolkov, A. A., Bezukladnikov, I. I., & Trushnikov, D. N. (2022). Rapid Temperature Control in Melt Extrusion Additive Manufacturing Using Induction Heated Lightweight Nozzle. Applied Sciences, 12(16), 8064. https://doi.org/10.3390/app12168064






