Empirical Correlation between Standard Penetration Resistance (SPT-N) and Shear Wave Velocity (Vs) for Soils in Metro Manila, Philippines
Abstract
:1. Introduction
2. The Study Area
3. Field Investigations
3.1. Geotechnical Investigations
3.2. Geophysical Investigations
4. Methodology
5. Results and Discussion
5.1. All Soils
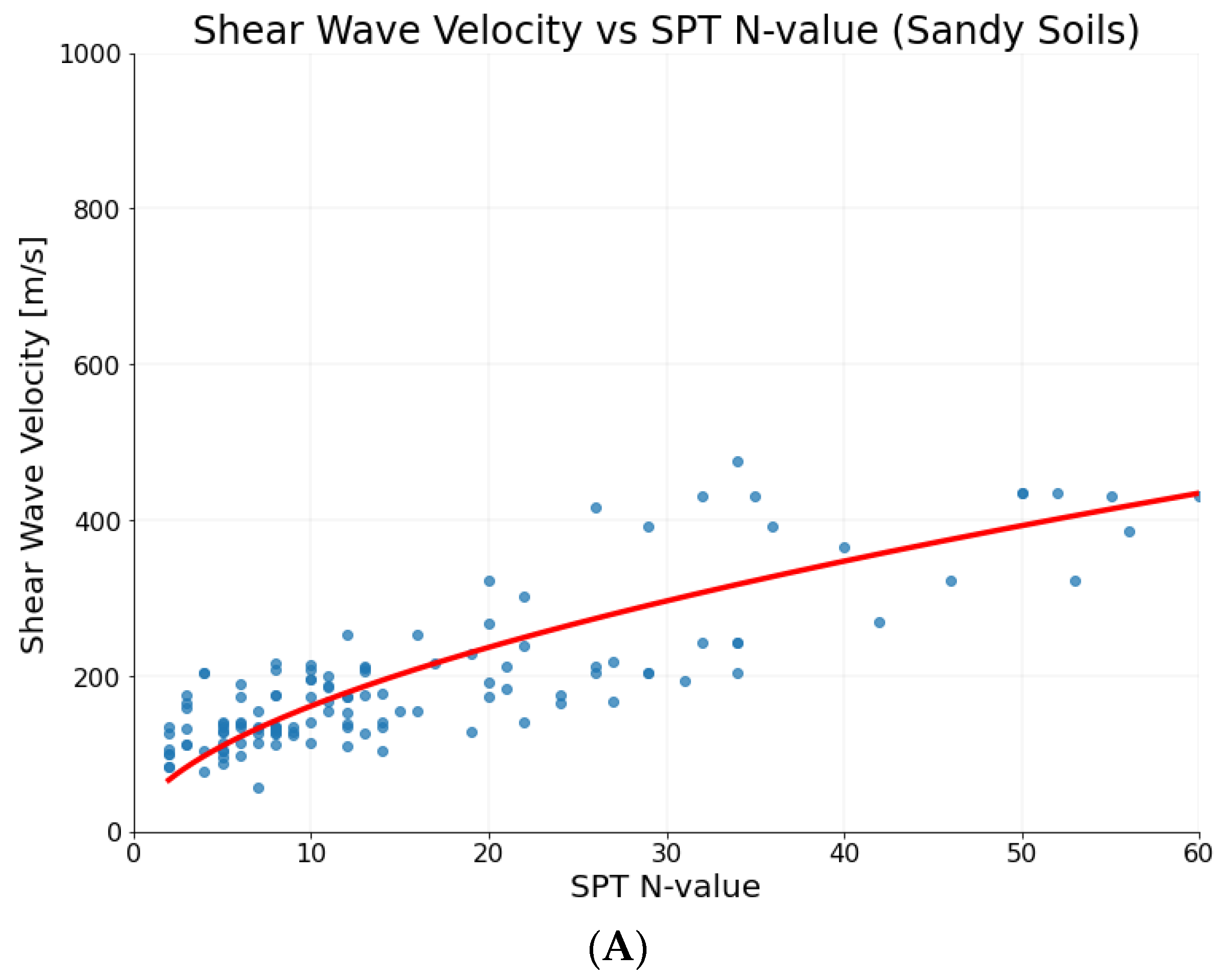
5.2. Sandy Soils
5.3. Clayey Soils
5.4. Statistical Evaluation
5.5. Application for Site-Specific Characterization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, W.; Cai, G.; Liu, S.; Puppala, A.J. Correlations between Shear Wave Velocity and Geotechnical Parameters for Jiangsu Clays of China. Pure Appl. Geophys. 2019, 176, 669–684. [Google Scholar] [CrossRef]
- Gautam, D. Empirical Correlation between Uncorrected Standard Penetration Resistance (N) and Shear Wave Velocity (VS) for Kathmandu Valley, Nepal. Geomat. Nat. Hazards Risk 2017, 8, 496–508. [Google Scholar] [CrossRef]
- Andrus, R.D.; Stokoe, K.H.; Hsein Juang, C. Guide for Shear-Wave-Based Liquefaction Potential Evaluation. Earthq. Spectra 2004, 20, 285–308. [Google Scholar] [CrossRef]
- Kayen, R.; Moss, R.E.S.; Thompson, E.M.; Seed, R.B.; Cetin, K.O.; Kiureghian, A.D.; Tanaka, Y.; Tokimatsu, K. Shear-Wave Velocity–Based Probabilistic and Deterministic Assessment of Seismic Soil Liquefaction Potential. J. Geotech. Geoenviron. Eng. 2013, 139, 407–419. [Google Scholar] [CrossRef]
- Mohamed, A.M.E.; Abu El Ata, A.S.A.; Abdel Azim, F.; Taha, M.A. Site-Specific Shear Wave Velocity Investigation for Geotechnical Engineering Applications Using Seismic Refraction and 2D Multi-Channel Analysis of Surface Waves. NRIAG J. Astron. Geophys. 2013, 2, 88–101. [Google Scholar] [CrossRef]
- Sasitharan, S.; Robertson, P.K.; Sego, D.C. Sample Disturbance from Shear Wave Velocity Measurements. Can. Geotech. J. 1994, 31, 119–124. [Google Scholar] [CrossRef]
- Ghazi, A.; Moghadas, N.H.; Sadeghi, H.; Ghafoori, M.; Lashkaripur, G.R. Empirical Relationships of Shear Wave Velocity, SPT-N Value and Vertical Effective Stress for Different Soils in Mashhad, Iran. Ann. Geophys. 2015, 58, 2. [Google Scholar] [CrossRef]
- Imai, T.; Yoshimura, Y. Elastic Wave Velocity and Soil Properties in Soft Soil. Tsuchi-ToKiso 1970, 18, 17–22. (In Japanese) [Google Scholar]
- Ohba, S.; Toriumi, I. Dynamic Response Characteristics of Osaka Plain. In Proceedings of the Annual Meeting, Architectural Institure of Japan, Tokyo, Japan, 5 October 1970. [Google Scholar]
- Shibata, T. The Relationship between the N-Value and S-Wave Velocity in the Soil Layer; Disaster Prevention Research Laboratory, Kyoto University: Kyoto, Japan, 1970. [Google Scholar]
- Ohta, T.; Hara, A.; Niwa, M.; Sakano, T. Elastic Shear Moduli as Estimated from N-Value. In Proceedings of the 7th Annual Convention of Japan Society of Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1972; pp. 265–268. [Google Scholar]
- Fujiwara, T. Estimation of Ground Movements in Actual Destructive Earthquakes. In Proceedings of the Fourth European Symposium on Earthquake Engineering, London, UK, 5–7 September 1972; pp. 125–132. [Google Scholar]
- Ohsaki, Y.; Iwasaki, R. On Dynamic Shear Moduli and Poisson’s Ratios of Soil Deposits. Soils Found. 1973, 13, 61–73. [Google Scholar] [CrossRef]
- Imai, T. P and S Wave Velocities of the Ground in Japan. In Proceedings of the IX International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1977; pp. 127–132. [Google Scholar]
- Imai, T.; Tonouchi, K. Correlation of N-Value with S-Wave Velocity and Shear Modulus. In Proceedings of the 2nd European Symposium of Penetration Testing, Amsterdam, The Netherlands, 24–27 May 1982; pp. 57–72. [Google Scholar]
- Seed, H.B.; Idriss, I.M. Evaluation of Liquefaction Potential Sand Deposits Based on Observation of Performance in Previous Earthquakes. In Proceedings of the ASCE National Convention 1981, St. Louis, MO, USA, 26–30 October 1981; pp. 481–544. [Google Scholar]
- Seed, H.; Tokimatsu, K.; Harder, L.F.; Chung, R.M. Influence of SPT Procedures in Soil Liquefaction Resistance Evaluations. J. Geotech. Eng. 1985, 111, 1425–1445. [Google Scholar] [CrossRef]
- Sykora, D.E.; Stokoe, K.H. Correlations of In-Situ Measurements in Sands of Shear Wave Velocity. Soil Dyn. Earthq. Eng. 1983, 20, 125–136. [Google Scholar]
- Rollins, K.M.; Evans, M.D.; Diehl, N.B.; Iii, W.D.D. Shear Modulus and Damping Relationships for Gravels. J. Geotech. Geoenviron. Eng. 1998, 124, 396–405. [Google Scholar] [CrossRef]
- Brandenberg, S.J.; Bellana, N.; Shantz, T. Shear Wave Velocity as Function of Standard Penetration Test Resistance and Vertical Effective Stress at California Bridge Sites. Soil Dyn. Earthq. Eng. 2010, 30, 1026–1035. [Google Scholar] [CrossRef]
- Kalteziotis, N.; Sabatakakis, N.; Vassiliou, J. Evaluation of Dynamic Characteristicsof Greek Soil Formations. In Proceedings of the 2nd Hellenic Conference on Geotechnical Engineering, Thessaloniki, Greece, 28 September–1 October 1992; pp. 239–246. [Google Scholar]
- Pitilakis, K.; Raptakis, D.; Lontzetidis, K.; Tika-Vassilikou, T.; Jongmans, D. Geotechnical and Geophysical Description of Euro-Seistest Using Field, Laboratory Tests and Moderate Strong Motion Recordings. J. Earthq. Eng. 1999, 3, 381–409. [Google Scholar] [CrossRef]
- Athanasopoulos, G. Empirical Correlations Vs-N SPT for Soils of Greece: A Comparative Study of Reliability. In Proceedings of the 7th International Conference on Soil Dynamics and Earthquake Engineering, Crete, Greece, 7 May 1995; pp. 19–36. [Google Scholar]
- Raptakis, D.G.; Anastasiadis, S.A.J.; Pitilakis, K.D.; Lontzetidis, K.S. Shear Wave Velocities and Damping of Greek Natural Soils. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; pp. 477–482. [Google Scholar]
- Tsiambaos, G.; Sabatakakis, N. Empirical Estimation of Shear Wave Velocity from in Situ Tests on Soil Formations in Greece. Bull. Eng. Geol. Environ. 2011, 70, 291–297. [Google Scholar] [CrossRef]
- Iyisan, R. Correlations between Shear Wave Velocity and In-Situ Penetration Test Results. Chamb. Civ. Eng. Turk. Tek. Dergi 1996, 7, 1187–1199. [Google Scholar]
- Kayabali, K. Soil Liquefaction Evaluation Using Shear Wave Velocity. Eng. Geol. 1996, 44, 121–127. [Google Scholar] [CrossRef]
- Hasancebi, N.; Ulusay, R. Empirical Correlations between Shear Wave Velocity and Penetration Resistance for Ground Shaking Assessments. Bull. Eng. Geol. Environ. 2007, 66, 203–213. [Google Scholar] [CrossRef]
- Koçkar, M.K.; Akgün, H. Development of a Geotechnical and Geophysical Database for Seismic Zonation of the Ankara Basin, Turkey. Env. Geol. 2008, 55, 165–176. [Google Scholar] [CrossRef]
- Dikmen, Ü. Statistical Correlations of Shear Wave Velocity and Penetration Resistance for Soils. J. Geophys. Eng. 2009, 6, 61–72. [Google Scholar] [CrossRef]
- Akin, M.K.; Kramer, S.L.; Topal, T. Empirical Correlations of Shear Wave Velocity (Vs) and Penetration Resistance (SPT-N) for Different Soils in an Earthquake-Prone Area (Erbaa-Turkey). Eng. Geol. 2011, 119, 1–17. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Sitharam, T.G. Relationship between Low Strain Shear Modulus and Standard Penetration Test N Values. Geotech. Test. J. 2010, 33, 102278. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Kumar, A.; Sitharam, T.G. Seismic Site Classification and Correlation between Standard Penetration Test N Value and Shear Wave Velocity for Lucknow City in Indo-Gangetic Basin. Pure Appl. Geophys. 2013, 170, 299–318. [Google Scholar] [CrossRef]
- Hanumantharao, C.; Ramana, G.V. Dynamic Soil Properties for Microzonation of Delhi, India. J. Earth Syst. Sci. 2008, 117, 719–730. [Google Scholar] [CrossRef]
- Uma Maheswari, R.; Boominathan, A.; Dodagoudar, G.R. Use of Surface Waves in Statistical Correlations of Shear Wave Velocity and Penetration Resistance of Chennai Soils. Geotech. Geol. Eng. 2010, 28, 119–137. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Wen, K.-L.; Hsieh, H.-H.; Chang, T.-M.; Lin, C.-M.; Chen, C.-T. Evaluating Empirical Regression Equations for Vs and Estimating Vs30 in Northeastern Taiwan. Soil Dyn. Earthq. Eng. 2011, 31, 431–439. [Google Scholar] [CrossRef]
- Gervacio, F. The Geology, Structures, and Landscape Development of Manila and Suburbs. Philipp. Geol. 1968, 21, 178–192. [Google Scholar]
- Bureau of Mines and Geosciences. Geological Map of Manila and Quezon City Quadrangle—Sheet 3263-IV [Map]; Bureau of Mines and Geosciences: Quezon City, Philippines, 1983.
- Japan International Cooperation Agency; Metropolitan Manila Development Agency; Philippine Institute of Volcanology and Seismology. Earthquake Impact Reduction Study for Metro Manila, Republic of the Philippines; Japan International Cooperation Agency: Makati City, Philippines, 2004.
- Miura, H.; Midorikawa, S.; Fujimoto, K.; Pacheco, B.M.; Yamanaka, H. Earthquake Damage Estimation in Metro Manila, Philippines Based on Seismic Performance of Buildings Evaluated by Local Experts’ Judgments. Soil Dyn. Earthq. Eng. 2008, 28, 764–777. [Google Scholar] [CrossRef]
- Teves, J.S.; Gonzales, M.L. The Geology of the University Site, Balara Area, Quezon City. Phil. Geol. 1950, 4, 1–10. [Google Scholar]
- Rimando, R.E.; Knuepfer, P.L.K. Neotectonics of the Marikina Valley Fault System (MVFS) and Tectonic Framework of Structures in Northern and Central Luzon, Philippines. Tectonophysics 2006, 415, 17–38. [Google Scholar] [CrossRef]
- Tan, R.C. Engineering Properties of Manila Subsoils; University of the Philippines: Quezon City, Philippines, 1983. [Google Scholar]
- Association of Structural Engineers of the Philippines, Inc. National Structural Code of the Philippines, 7th ed.; Association of Structural Engineers of the Philippines, Inc.: Quezon City, Philippines, 2015; Volume 1. [Google Scholar]
- ASTM D1586/D1586M-18e1; Test Method for Standard Penetration Test (SPT) and Split-Barrel Sampling of Soils. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM D2487-17e1; Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2022.
- Louie, J.N. Faster, Better: Shear-Wave Velocity to 100 Meters Depth from Refraction Microtremor Arrays. Bull. Seismol. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Philippine Institute of Volcanology and Seismology. The Philippine Earthquake Model; Philippine Institute of Volcanology and Seismology: Quezon City, Philippines, 2017.
- Chatterjee, K.; Choudhury, D. Variations in Shear Wave Velocity and Soil Site Class in Kolkata City Using Regression and Sensitivity Analysis. Nat. Hazards 2013, 69, 2057–2082. [Google Scholar] [CrossRef]
- Rezaei, S.; Shooshpasha, I.; Rezaei, H. Empirical Correlation between Geotechnical and Geophysical Parameters in a Landslide Zone (Case Study: Nargeschal Landslide). Earth Sci. Res. J. 2018, 22, 195–204. [Google Scholar] [CrossRef]
- Lin, J.; Cai, G.; Liu, S.; Puppala, A.J.; Zou, H. Correlations Between Electrical Resistivity and Geotechnical Parameters for Jiangsu Marine Clay Using Spearman’s Coefficient Test. Int. J. Civ. Eng. 2017, 15, 419–429. [Google Scholar] [CrossRef]
- Kanai, K. Conference on Cone Penetrometer; The Ministry of Public Works and Settlement: Ankara, Turkey, 1966.
- Imai, T.; Fumoto, H.; Yokota, K. The Relation of Mechanical Properties of Soil to Pand S-Wave Velocities in Japan. In Proceedings of the 4th Japan Earthquake Engineering Symposium, Tokyo, Japan, 6 September 1975. [Google Scholar]
- Ohta, Y.; Goto, N.; Kagami, H.; Shiono, K. Shear Wave Velocity Measurement during a Standard Penetration Test. Earthq. Eng. Struct. Dyn. 1978, 6, 43–50. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of Liquefaction Potential Using Field Performance Data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Fumal, T.E.; Tinsley, J.C. Predicting Area Limits of Earthquake Induced Land Sliding Based on Seismological Parameters. In Evaluation of Earthquake Hazards in the Los Angeles Region–An Earth Science Prospective; U.S. Geological Survey: Los Angeles, CA, USA, 1985; pp. 127–150. [Google Scholar]
- Tonouchi, K.; Sakayama, T.; Imai, T. S Wave Velocity in the Ground and the Damping Factor. Bull. Int. Assoc. Eng. Geol. 1983, 26–27, 327–333. [Google Scholar]
- Jinan, Z. Correlation between Seismic Wave Velocity and the Number of Blow of SPT and Depth. Sel. Pap. Chin. J. Geotech. Eng. 1987, 1, 92–100. [Google Scholar]
- Okamoto, T.; Kokusho, T.; Yoshida, Y.; Kusuonoki, K. Comparison of Surface versus Subsurface Wave Source for P–Slogging in Sand Layer. In Proceedings of the 44th Annal Conference JSCE, October 1989; Volume 3, pp. 996–997. [Google Scholar]
- Lee, S.H. Regression Models of Shear Wave Velocities in Taipei Basin. J. Chin. Inst. Eng. 1990, 13, 519–532. [Google Scholar] [CrossRef]
- Yokota, K.; Imai, T.; Konno, M. Dynamic Deformation Characteristics of Soils Determined by Laboratory Tests. OYO Technical Report. 1981, p. 26. Available online: https://www.oyo.co.jp/oyocms_hq/wp-content/uploads/2014/12/1981_03.pdf (accessed on 20 June 2022).
- Pitilakis, K.D.; Anastasiadis, A.; Raptakis, D. Field and Laboratory Determination of Dynamic Properties of Natural Soil Deposits. In Proceedings of the 10th World Conference Earthquake Engineering, Rotherdam, The Netherlands, 19 July 1992; pp. 1275–1280. [Google Scholar]
- Sisman, H. An Investigation on Relationships between Shear Wave Velocity, and SPT and Pressuremeter Test Results. Master’s Thesis, Ankara University, Geophysical Engineering Department, Ankara, Turkey, 1995. [Google Scholar]
- Jafari, M.K.; Asghari, A.; Rahmani, I. Empirical Correlation between Shear Wave Velocity (Vs) and SPT-N Value for South Tehran Soils. In Proceedings of the 4th International Conference on Civil Engineering, Tehran, Iran, 4–6 May 1997. [Google Scholar]
- Kiku, H.; Yoshida, N.; Yasuda, S.; Irisawa, T.; Nakazawa, H.; Shimizu, Y.; Ansal, A.; Erkan, A. In-Situ Penetration Tests and Soil Profiling in Adapazari, Turkey. In Proceedings of the ICSMGE/TC4 Satellite Conference on Lessons Learned From Recent Strong Earthquakes, Istanbul, Turkey, 25 August 2001; pp. 259–265. [Google Scholar]
- Jafari, M.K.; Shafiee, A.; Razmkhah, A. Dynamic Properties of Fine Grained Soils in South of Tehran. J. Seismol. Earthq. Eng. 2002, 4, 25–35. [Google Scholar]
- Fauzi, A. Empirical Correlation of Shear Wave Velocity and N-SPT Value for Jakarta. Geomate 2014, 7, 980–984. [Google Scholar] [CrossRef]
- Moore, D.S.; Notz, W.; Fligner, M.A. The Basic Practice of Statistics, 6th ed.; W.H. Freeman: New York, NY, USA, 2013; ISBN 978-1-4641-0254-7. [Google Scholar]
- Kayen, R.E.; Mitchell, J.K.; Seed, R.B.; Lodge, A.; Nishio, S.; Coutinho, R. Evaluation of SPT-, CPT-, and Shear Wave-Based Methods for Liquefaction Potential Assessment Using Loma Prieta Data. In Proceedings of the 4th Japan-U.S. Workshop on Earthquake Resistant Design of Lifeline Facilities and Countermeasures for Soil Liquefaction, Honolulu, Hawaii, 27–29 May 1992; Volume 1, pp. 117–204. [Google Scholar]
- Youd, T.L.; Idriss, I.M.; Andrus, R.D.; Arango, I.; Castro, G.; Christian, J.T.; Dobry, R.; Finn, W.D.L.; Harder, L.F.; Hynes, M.E.; et al. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Skempton, A.W. Standard Penetration Test Procedures and the Effects in Sands of Overburden Pressure, Relative Density, Particle Size, Ageing and Overconsolidation. Géotechnique 1986, 36, 425–447. [Google Scholar] [CrossRef]
- Ohta, Y.; Goto, N. Empirical Shear Wave Velocity Equations in Terms of Characteristic Soil Indexes. Earthquake Engng. Struct. Dyn. 1978, 6, 167–187. [Google Scholar] [CrossRef]
- Pancha, A.; Apperley, R.A. Multidisciplinary Site Investigations: Refraction Microtremor Surveys. J. Seism. 2021, 1–14. [Google Scholar] [CrossRef]










| Site No. | Name | City | Long. (°) | Lat. (°) | Water Table Depth (m) | Depth (m) | Soil Type (USCS) |
|---|---|---|---|---|---|---|---|
| 1 | Wawang Pulo Elementary School | Valenzuela | 120.928018 | 14.733015 | 0.2 | 0–1 1–2 2–5 5–6 6–15 | SM GM SM ML CL |
| 2 | Pio Valenzuela Elementary School | Valenzuela | 120.946090 | 14.707048 | 0.3 | 0.5 0.5–4.5 4.5–10 10–11.5 11.5–13 13–15 | GM SM CL ML SM CL |
| 3 | Tagalag Elementary School | Valenzuela | 120.938120 | 14.724660 | 0.7 | 0–15 | SM |
| 4 | Coloong Elementary School | Valenzuela | 120.944549 | 14.725007 | 4.0 | 0–10.0 10–15 | ML SM |
| 5 | San Roque Elementary School | Navotas | 120.938040 | 14.669389 | 0.8 | 0–6 6–12 12–25 | SM MH ML |
| 6 | Tangos National High School | Navotas | 120.932246 | 14.674792 | 0.6 | 0–1 1–2 2–3 3–6 6–7.5 7.5–10.5 10.5–12 12–13.5 13.5–22.5 22.5–25 | SM SC SM SP-SM SC MH ML SC MH SM |
| 7 | Kapitbahayan Elementary School | Navotas | 120.957491 | 14.643937 | 0.6 | 0–4.5 4.5–9 9–15 | SM CL SC |
| 8 | Tanza Elementary School | Navotas | 120.933461 | 14.679129 | 2.0 | 0–3 3–4.5 4.5–6 6–7.5 7.5–9 9–10.5 10.5–12 12–13.5 13.5–15 15–18 18–20 | SC ML GP CL SC MH CL ML CL SM GC-GM |
| 9 | Dagat-Dagatan Elementary School | Navotas | 120.956282 | 14.651251 | 0.3 | 0–1.5 1.5–6 6–12 | CH SC-SM CH |
| 10 | Malabon Elementary School | Malabon | 120.940551 | 14.677009 | 1.0 | 0–4.5 4.5–12 12–15 | SP-SM ML CL |
| 11 | Panghulo Elementary School | Malabon | 120.957800 | 14.684380 | 0.5 | 0–1.5 1.5–6 6–7.5 7.5–9 9–10.5 10.5–13.5 13.5–16.5 16.5–18 18–20 | SP-SM SM CH CL CH MH CH MH CH |
| 12 | Imelda Elementary School | Malabon | 120.960990 | 14.648665 | 1.2 | 0–3 3–9 9–15 | SM CL CH |
| 13 | Ninoy Aquino Elementary School | Malabon | 120.960700 | 14.654450 | 0.2 | 0–3 3–7.5 7.5–15 | SC SM SC |
| 14 | Epifanio Delos Santos Elementary School | Malabon | 120.992414 | 14.575557 | 3.0 | 0–4.5 4.5–6 | SC SM |
| 15 | Manuel A. Roxas High School | Manila | 120.999027 | 14.582204 | 0.9 | 0–1.5 1.5–4.5 4.5–6 6–10.5 10.5–12 12–13.5 13.5–15 | SP-SM CH ML SM CH SM CH |
| 16 | Rafael Palma Elementary School | Manila | 121.005917 | 14.567431 | 2.5 | 0–3 3–4.5 4.5–7.5 7.5–9 9–10.5 10.5–12 12–13.5 13.5–15 | CL SC SM SC SW-SM SM SW-SM SP-SM |
| 17 | Jose Rizal Elementary School | Pasay | 120.997418 | 14.543973 | 3.5 | 0–1.5 1.5–3 3–6 6–7.5 7.5–12 12–13.5 13.5–16.5 16.5–18 18–19.5 19.5–21 21–22.5 22.5–24 24–25.5 25.5–30 | GC SP SW SP-SM SM SC CH SM ML MH CH MH CH MH |
| 18 | Paranaque Science High School | Parańaque | 120.994677 | 14.500793 | 0.7 | 0–1.5 1.5–3 3–4.5 4.5–6 6–7.5 7.5–12 12–13.5 13.5–15 | GM GP SP-SM SM MH SM CL MH |
| 19 | Sto. Nino Elementary School | Parańaque | 120.996088 | 14.503082 | No data | 0–1.5 1.5–3 3–4.5 4.5–6 6–7.5 7.5–9 9–10.5 10.5–12 12–13.5 13.5–15 | SC SP-SM SM ML MH GC ML MH CL CH |
| 20 | Manuyo Elementary School | Las Pińas | 120.985444 | 14.482353 | 1.0 | 0–1.5 1.5–4.5 4.5–6 6–7.5 7.5–9 9–10.5 10.5–12 12–13.5 13.5–15 | SP-SM SW-SM SP SM SP-SM CL MH CL SC |
| Author | All Soils | Sand | Silt | Clay |
|---|---|---|---|---|
| Kanai (1966) [52] | Vs = 19N0.6 | - | - | - |
| Shibata (1970) [10] | - | Vs = 31.7N0.54 | - | - |
| Imai and Yoshimura (1970) [8] | Vs = 76N0.33 | - | - | - |
| Ohba and Toriumi (1970) [9] | Vs = 84N0.31 | - | - | - |
| Ohta et al. (1972) [11] | - | Vs = 87.2N0.36 | - | - |
| Fujiwara (1972) [12] | Vs = 92.1N0.337 | - | - | - |
| Ohsaki and Iwasaki (1973) [13] | Vs = 81.4N0.39 | - | - | - |
| Imai et al. (1975) [53] | Vs = 89.9N0.341 | - | - | - |
| Imai (1977) [14] | Vs = 91N0.337 | Vs = 80.6N0.331 | - | Vs = 80.2N0.292 |
| Ohta et al. (1978) [54] | Vs = 85.35N0.348 | - | - | - |
| Seed and Idriss (1981) [16] | Vs = 61.4N0.5 | - | - | - |
| Imai and Tonouchi (1982) [15] | Vs = 96.9N0.314 | - | - | - |
| Seed et al. (1983) [55] | - | Vs = 56.4N0.5 | - | - |
| Sykora and Stokoe (1983) [18] | - | Vs = 100.5N0.29 | - | - |
| Fumal and Tinsley (1985) [56] | - | Vs = 152 + 51N0.27 | - | - |
| Tonouchi et al. (1983) [57] | Vs = 97N0.314 | - | - | - |
| Jinan (1987) [58] | Vs = 116 (N + 0.3185)0.6 | - | - | - |
| Okamoto et al. (1989) [59] | - | Vs = 125N0.3 | - | - |
| Lee (1990) [60] | - | Vs = 57.4N0.49 | Vs = 105.64N0.319 | Vs = 114.43N0.31 |
| Athanasopoulos (1995) [23] | Vs = 107.6N0.36 | - | - | Vs = 76.55N0.445 |
| Yokota et al. (1981) [61] | Vs = 121N0.27 | - | - | Vs = 114N0.31 |
| Kalteziotis et al. (1992) [21] | Vs = 76.2N0.24 | - | - | - |
| Pitilakis et al. (1992) [62] | - | Vs = 162N0.17 | - | - |
| Raptakis et al. (1995) [24] | - | Vs = 100.7N0.24 | - | - |
| Sisman (1995) [63] | Vs = 32.8N0.51 | - | - | - |
| Iyisan (1996) [26] | Vs = 51.5N0.516 | - | - | - |
| Kayabali (1996) [27] | - | Vs = 175 + (3.75N) | - | - |
| Jafari et al. (1997) [64] | Vs = 22N0.85 | - | - | - |
| Pitilakis et al. (1999) [22] | - | Vs = 145 (N60)0.178 | - | Vs = 132 (N60)0.271 |
| Kiku et al. (2001) [65] | Vs = 68.3N0.292 | - | - | - |
| Jafari et al. (2002) [66] | - | - | Vs = 22N0.77 | Vs = 27N0.73 |
| Hasancebi and Ulusay (2007) [28] | Vs = 90N0.309 | Vs = 90.82N0.319 | - | Vs = 97.89N0.269 |
| Hasancebi and Ulusay (2007) [28] | Vs = 104.8 (N60)0.26 | Vs = 131 (N60)0.205 | - | Vs = 107.6 (N60)0.237 |
| Dikmen (2009) [30] | Vs = 58N0.39 | Vs = 73N0.33 | Vs = 60N0.36 | Vs = 44N0.48 |
| Uma Maheswari et al. (2010) [35] | Vs = 95.64N0.301 | Vs = 100.53N0.265 | - | Vs = 89.3N0.358 |
| Fauzi (2014) [67] | Vs = 105.03N0.286 | - | - | - |
| Soil Type | Proposed Correlation | Coefficient of Regression (R2) | Coefficient of Correlation(r) | Spearman Rank Correlation (rs) |
|---|---|---|---|---|
| All soils | Vs = 56.82N0.4861 | 0.7515 | 0.8767 | 0.8424 |
| Sandy soil | Vs = 45.07N0.5534 | 0.7922 | 0.9050 | 0.8192 |
| Clayey soil | Vs = 70.26N0.4220 | 0.7334 | 0.8453 | 0.8493 |
| Soil Profile Type | Soil Profile Description | Shear Wave Velocity, Vs, (m/s) | SPT-N (Blows/30 cm) |
|---|---|---|---|
| SA | Hard Rock | >1500 | - |
| SB | Rock | 760–1500 | - |
| SC | Very Dense Soil and Soft Rock | 360–760 | >50 |
| SD | Stiff Soil | 180–360 | 15–50 |
| SE 1 | Soft Soil | <180 | <15 |
| SF | Soil requiring site-specific evaluation | ||
| Location | Coordinates | Generalized Soil Profile Description | Vs30 Using Proposed Correlation for All Soil Types | Site Class Per NSCP (2015) |
|---|---|---|---|---|
| J. A. Santos High School, Manila City | 120.972674° E, 14.597179° N | poorly graded to silty sand, silt | 187.30 | Class D |
| T. Paez Elementary School, Manila City | 120.966613° E 14.630679° N | silt, well-graded and silty sand | 243.10 | Class D |
| Amang Rodriguez Elementary School, Malabon City | 120.949242° E 14.671821° N | silty gravel, silty sand, clays | 320.08 | Class D |
| Tangos I Elementary School, Navotas City | 120.932371° E 14.673729° N | poorly graded to silty sand, silt | 274.71 | Class D |
| Jose Rizal Elementary School, Pasay City | 120.997418° E 14.543973° N | well graded to silty sand, silt | 330.05 | Class D |
| V.E. Fugoso Memorial Elementary School, Marikina City | 121.118325° E 14.666042° N | high plasticity silt, low plasticity clay | 225.04 | Class D |
| Soil Description | Vs (m/s) | SPT N-value |
|---|---|---|
| Very soft to soft soils | <180 m/s | <10 |
| Stiff soils | 180–360 m/s | 10–45 |
| Very dense soils | 360–760 m/s | >45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daag, A.S.; Halasan, O.P.C.; Magnaye, A.A.T.; Grutas, R.N.; Solidum, R.U., Jr. Empirical Correlation between Standard Penetration Resistance (SPT-N) and Shear Wave Velocity (Vs) for Soils in Metro Manila, Philippines. Appl. Sci. 2022, 12, 8067. https://doi.org/10.3390/app12168067
Daag AS, Halasan OPC, Magnaye AAT, Grutas RN, Solidum RU Jr. Empirical Correlation between Standard Penetration Resistance (SPT-N) and Shear Wave Velocity (Vs) for Soils in Metro Manila, Philippines. Applied Sciences. 2022; 12(16):8067. https://doi.org/10.3390/app12168067
Chicago/Turabian StyleDaag, Arturo S., Oliver Paul C. Halasan, Arielle Anne T. Magnaye, Rhommel N. Grutas, and Renato U. Solidum, Jr. 2022. "Empirical Correlation between Standard Penetration Resistance (SPT-N) and Shear Wave Velocity (Vs) for Soils in Metro Manila, Philippines" Applied Sciences 12, no. 16: 8067. https://doi.org/10.3390/app12168067
APA StyleDaag, A. S., Halasan, O. P. C., Magnaye, A. A. T., Grutas, R. N., & Solidum, R. U., Jr. (2022). Empirical Correlation between Standard Penetration Resistance (SPT-N) and Shear Wave Velocity (Vs) for Soils in Metro Manila, Philippines. Applied Sciences, 12(16), 8067. https://doi.org/10.3390/app12168067






