BDS/IMU Integrated Auto-Navigation System of Orchard Spraying Robot
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
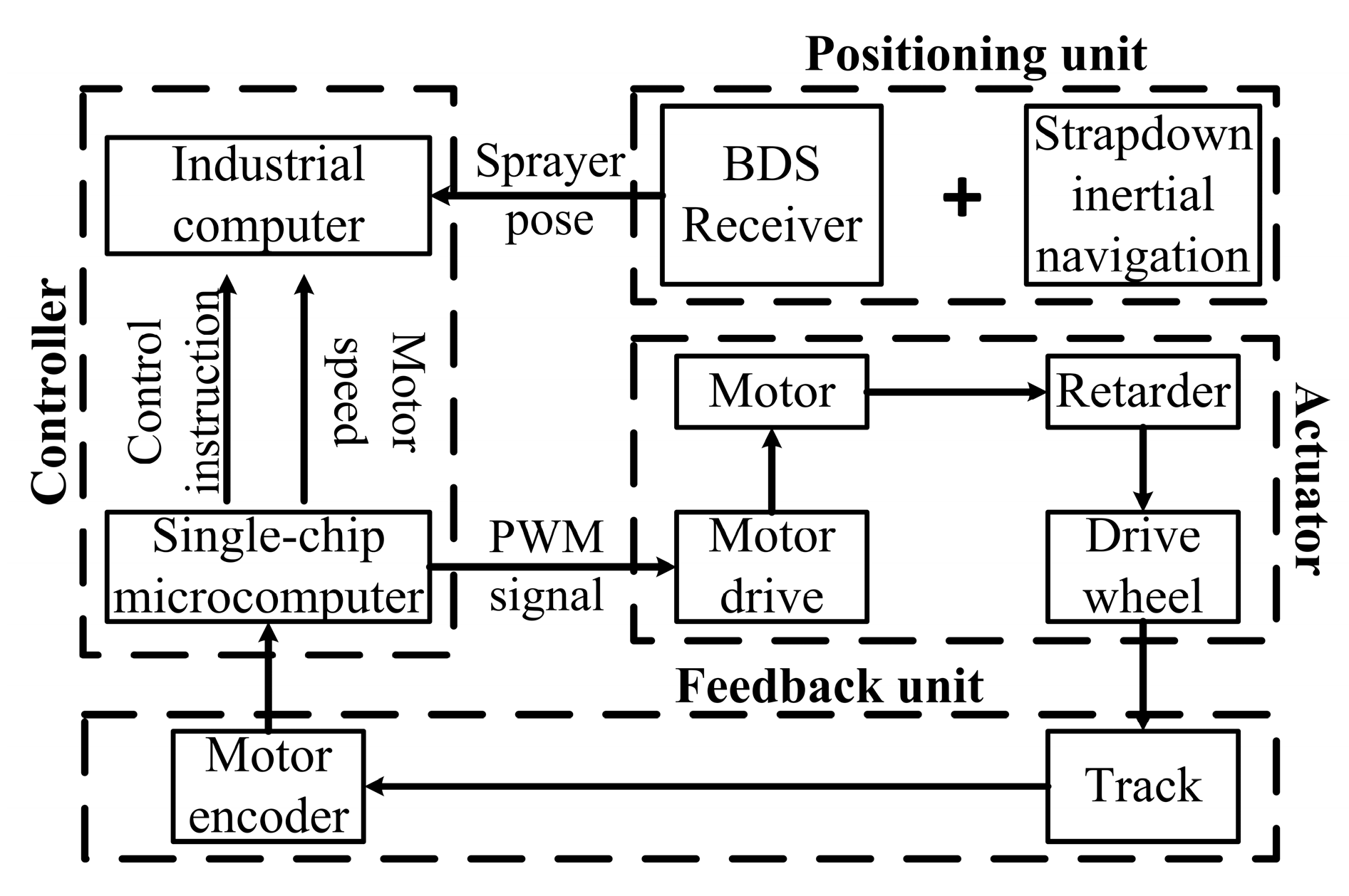
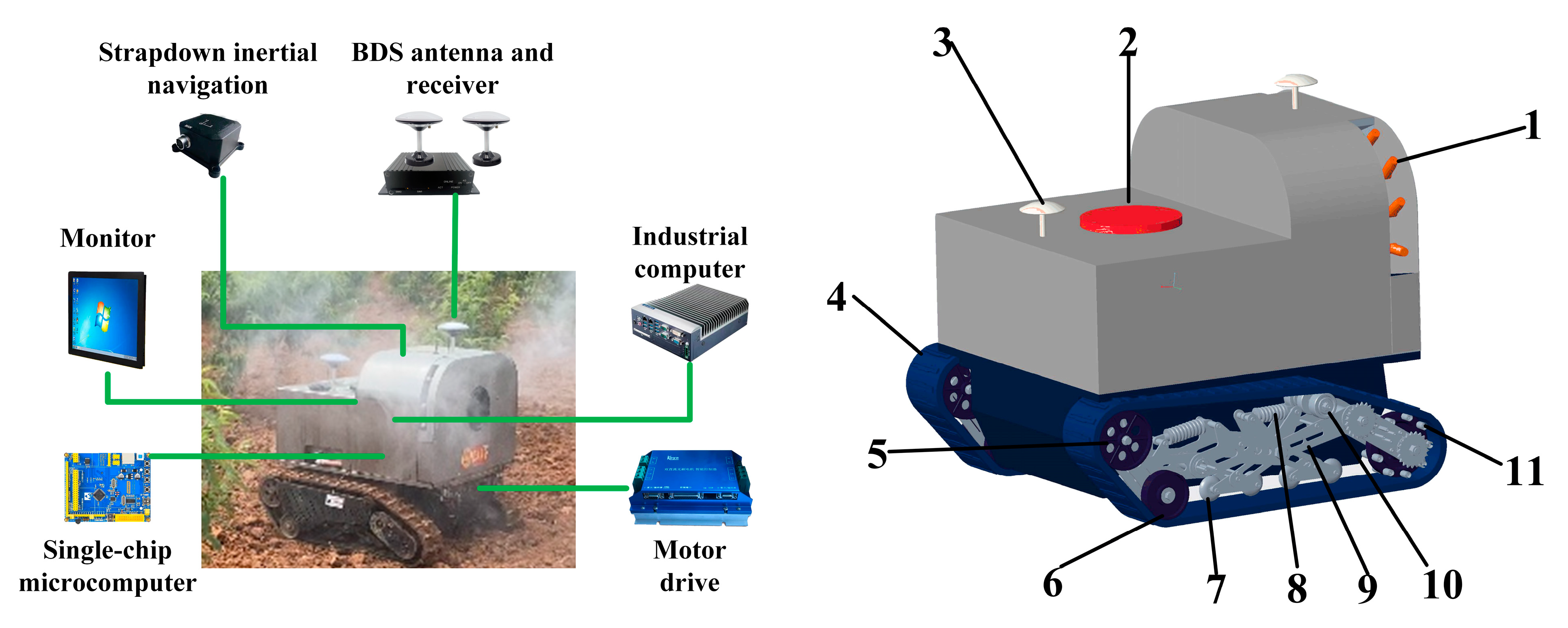
2.1. Overall Design of the System
2.2. Error Kalman Filter Integrated Navigation Algorithm Based on the Measurement of Position and Heading Angle
2.2.1. IMU Solution
2.2.2. BDS/IMU Integrated Navigation Model
- Continuous-time error Kalman filter equation for BDS/IMU integrated navigation;
- 2.
- Discrete error Kalman filter equation for BDS/IMU integrated navigation;
- 3.
- The error Kalman filter equation;
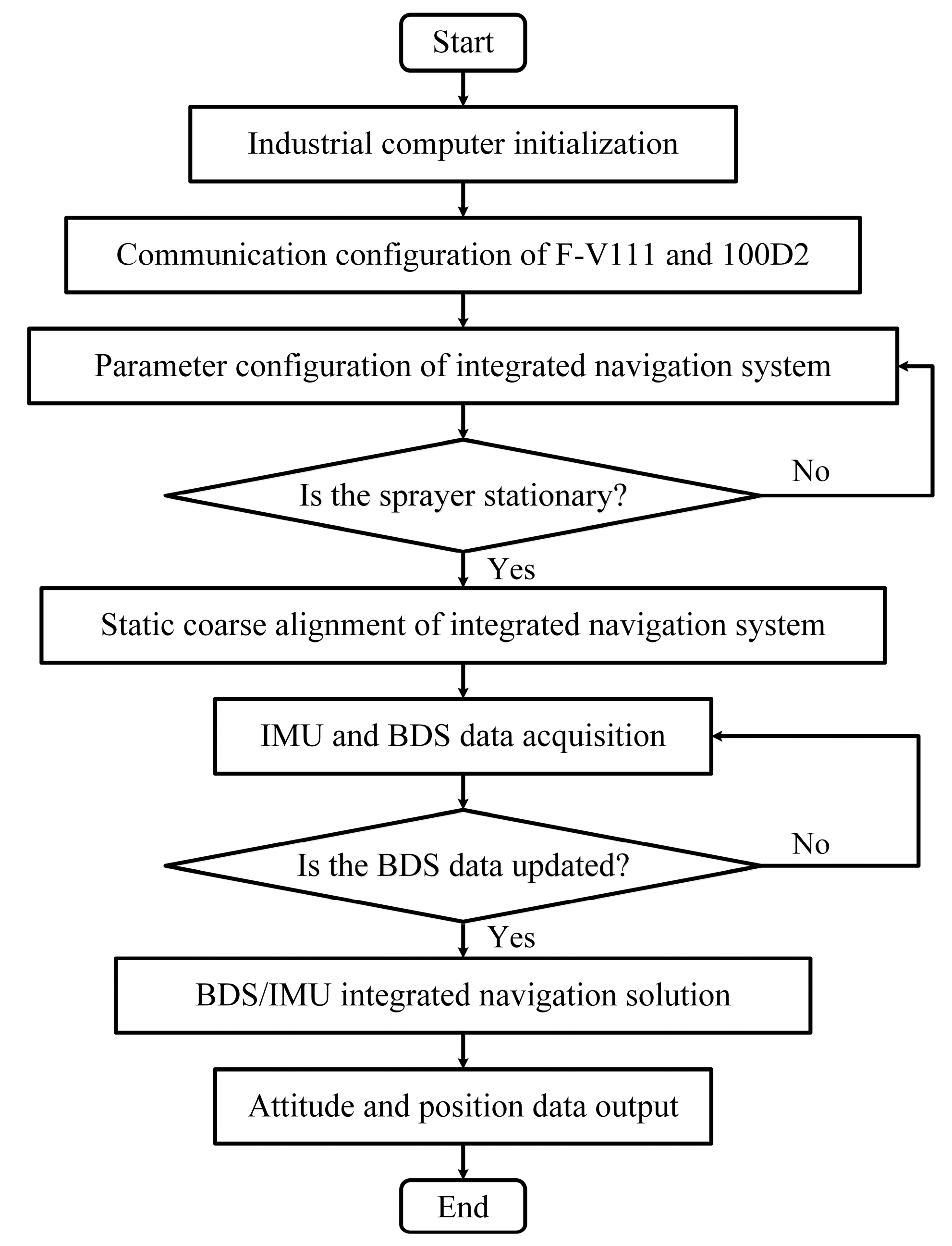
2.2.3. Design of the BDS/IMU Integrated Navigation Program
2.3. Control Model of the System
2.3.1. Navigation Control Principle of the Spraying Robot
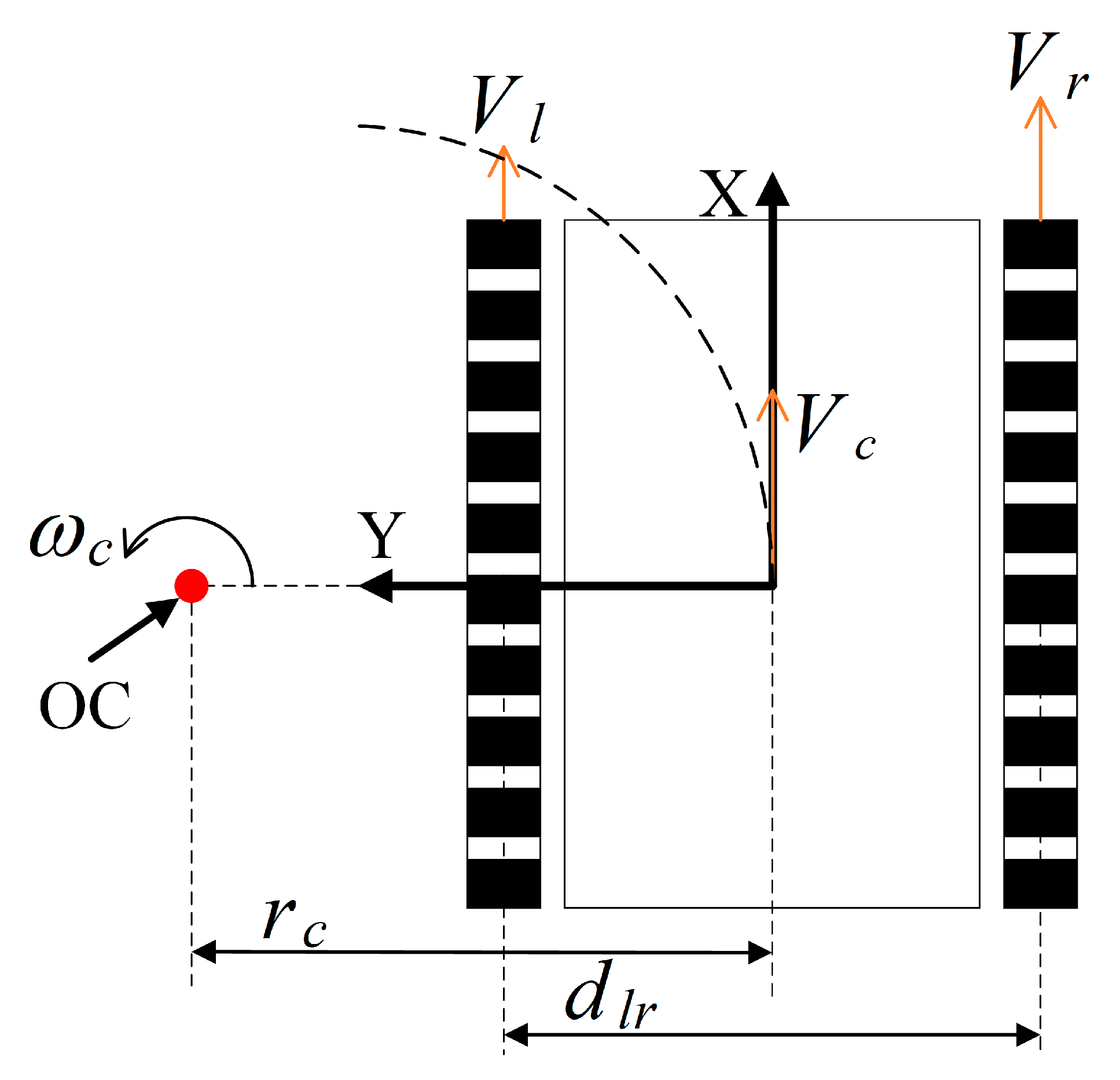
2.3.2. Kinematic Model of the Spraying Robot
2.3.3. Pure Pursuit Model
2.3.4. Path Planning
3. Results
3.1. Static Positioning
3.2. Dynamic Positioning
3.3. Auto-Navigation Performances in Orchard
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.; Xiao, H.; Mei, S.; Song, Z.; Ding, W.; Jing, Y. Current status and development strategies of orchard mechanization production in China. J. China Agric. Univ. 2017, 22, 116–127. [Google Scholar]
- Zheng, Y.; Chen, B.; Lyu, H.; Kang, F.; Jiang, S. Research progress of orchard plant protection mechanization technology and equipment in China. Trans. Chin. Soc. Agric. Eng. 2020, 36, 110–124. [Google Scholar]
- Shamshiri, R.R.; Weltzien, C.; Hameed, I.A.; Yule, I.J.; Grift, T.E.; Balasundram, S.K.; Pitonakova, L.; Ahmad, D.; Chowdhary, G. Research and development in agricultural robotics: A perspective of digital farming. Int. J. Agric. Biol. Eng. 2018, 11, 1–14. [Google Scholar] [CrossRef]
- Malavazi, F.B.; Guyonneau, R.; Fasquel, J.-B.; Lagrange, S.; Mercier, F. LiDAR-only based navigation algorithm for an autonomous agricultural robot. Comput. Electron. Agric. 2018, 154, 71–79. [Google Scholar] [CrossRef]
- Yang, Q.; Qu, D.; Xu, F.; Zou, F.; He, G.; Sun, M. Mobile robot motion control and autonomous navigation in GPS-denied outdoor environments using 3D laser scanning. Assem. Autom. 2018, 15439, 469–478. [Google Scholar] [CrossRef]
- Jones, M.H.; Bell, J.; Dredge, D.; Seabright, M.; Scarfe, A.; Duke, M.; MacDonald, B. Design and testing of a heavy-duty platform for autonomous navigation in kiwifruit orchards. Biosyst. Eng. 2019, 187, 129–146. [Google Scholar] [CrossRef]
- Opiyo, S.; Okinda, C.; Zhou, J.; Mwangi, E.; Makange, N. Medial axis-based machine-vision system for orchard robot navigation. Comput. Electron. Agric. 2021, 185, 106153. [Google Scholar] [CrossRef]
- Ponnambalam, V.R.; Bakken, M.; Moore, R.J.; Glenn Omholt Gjevestad, J.; Johan From, P. Autonomous crop row guidance using adaptive multi-roi in strawberry fields. Sensors 2020, 20, 5249. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhang, W.; Qureshi, W.S.; Gao, C.; Zhang, C.; Li, W. Autonomous navigation for a wolfberry picking robot using visual cues and fuzzy control. Inf. Process. Agric. 2021, 8, 15–26. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Z.; Hu, Y.; Chu, D. Integration of vision and topological self-localization for intelligent vehicles. Mechatronics 2018, 51, 46–58. [Google Scholar] [CrossRef]
- Tu, X.; Gai, J.; Tang, L. Robust navigation control of a 4WD/4WS agricultural robotic vehicle. Comput. Electron. Agric. 2019, 164, 104892. [Google Scholar] [CrossRef]
- Yin, X.; Wang, Y.; Chen, Y.; Jin, C.; Du, J. Development of autonomous navigation controller for agricultural vehicles. Int. J. Agric. Biol. Eng. 2020, 13, 70–76. [Google Scholar] [CrossRef]
- Barawid, O.C., Jr.; Mizushima, A.; Ishii, K.; Noguchi, N. Development of an autonomous navigation system using a two-dimensional laser scanner in an orchard application. Biosyst. Eng. 2007, 96, 139–149. [Google Scholar] [CrossRef]
- Thanpattranon, P.; Ahamed, T.; Takigawa, T. Navigation of autonomous tractor for orchards and plantations using a laser range finder: Automatic control of trailer position with tractor. Biosyst. Eng. 2016, 147, 90–103. [Google Scholar] [CrossRef]
- Ai, C.; Lin, H.; Wu, D.; Feng, Z. Path planning algorithm for plant protection robots in vineyard. Trans. Chin. Soc. Agric. Eng. 2018, 34, 77–85. [Google Scholar]
- Guo, C.; Fan, Y.; Zhang, S.; Chen, J. Progress on vehicle automatic navigation in orchard. J. Northeast. Agric. Univ. 2019, 50, 87–96. [Google Scholar]
- Han, Z.; Li, J.; Yuan, Y.; Fang, X.; Zhao, B.; Zhu, L. Path Recognition of Orchard Visual Navigation Based on U-Net. Trans. Chin. Soc. Agric. Mach. 2021, 52, 30–39. [Google Scholar]
- Li, W. Research on the Method of Generating Visual Navigation Path of Kiwi Picking Robot. Master’s Thesis, Northwest A&F University, Xianyang, China, 1 May 2017. [Google Scholar]
- Wang, Y.; Liu, B.; Xiong, L.; Wang, Z.; Yang, C. Research on generating algorithm of orchard road navigation line based on deep learning. J. Hunan Agric. Univ. 2019, 45, 674–678. [Google Scholar]
- Ma, C.; Dong, Z.; Chen, Z.; Zhu, Y.; Shi, F. Research on navigation line generation of kiwi orchard between rows based on root point substitution. Agric. Res. Arid. Areas 2021, 39, 222–230. [Google Scholar]
- Radcliffe, J.; Cox, J.; Bulanon, D.M. Machine vision for orchard navigation. Comput. Ind. 2018, 98, 165–171. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, Z.; Zhao, Z.; Chen, B.; Hu, L.; Wu, X. Design of DGPS navigation control system for Dongfanghong X-804 tractor. Trans. CSAE 2009, 25, 139–145. [Google Scholar]
- Nagasaka, Y.; Umeda, N.; Kanetai, Y.; Taniwaki, K.; Sasaki, Y. Autonomous guidance for rice transplanting using global positioning and gyroscopes. Comput. Electron. Agric. 2004, 43, 223–234. [Google Scholar] [CrossRef]
- Xiong, B.; Zhang, J.; Qu, F.; Fan, Z.; Wang, D.; Li, W. Navigation Control System for Orchard Spraying Machine Based on Beidou Navigation Satellite System. Trans. Chin. Soc. Agric. Mach. 2017, 48, 45–50. [Google Scholar]
- Zhang, S.; Guo, C.; Gao, Z.; Sugirbay, A.; Chen, J.; Chen, Y. Research on 2D Laser Automatic Navigation Control for Standardized Orchard. Appl. Sci. 2020, 10, 2763. [Google Scholar] [CrossRef]
- Chen, J.Q.; Qiang, H.; Wu, J.; Xu, G.; Wang, Z.; Liu, X. Extracting the navigation path of a tomato-cucumber greenhouse robot based on a median point Hough transform. Comput. Electron. Agric. 2020, 174, 105472. [Google Scholar] [CrossRef]
- Inoue, K.; Kaizu, Y.; Igarashi, S.; Imou, K. The development of autonomous navigation and obstacle avoidance for a robotic mower using machine vision technique. IFAC-PapersOnLine 2019, 52, 173–177. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, Y.; Chen, P.; Wu, Y. Application of a Gaussian processes based central difference Kalman filter in the BDS/IMS integrated system. J. Chin. Inert. Technol. 2020, 28, 192–198. [Google Scholar]
- Gao, W.; Zhang, Y.; Wang, J. A strapdown interial navigation system/beidou/doppler velocity log integrated navigation algorithm based on a cubature kalman filter. Sensors 2014, 14, 1511–1527. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, W.; Huang, F.; Wang, Y.; Chen, X.; Hsu, L.-T. GNSS-RTK Adaptively Integrated with LiDAR/IMU Odometry for Continuously Global Positioning in Urban Canyons. Appl. Sci. 2022, 12, 5193. [Google Scholar] [CrossRef]
- Karaim, M.; Tamazin, M.; Noureldin, A. An Efficient Ultra-Tight GPS/RISS Integrated System for Challenging Navigation Environments. Appl. Sci. 2020, 10, 3613. [Google Scholar] [CrossRef]




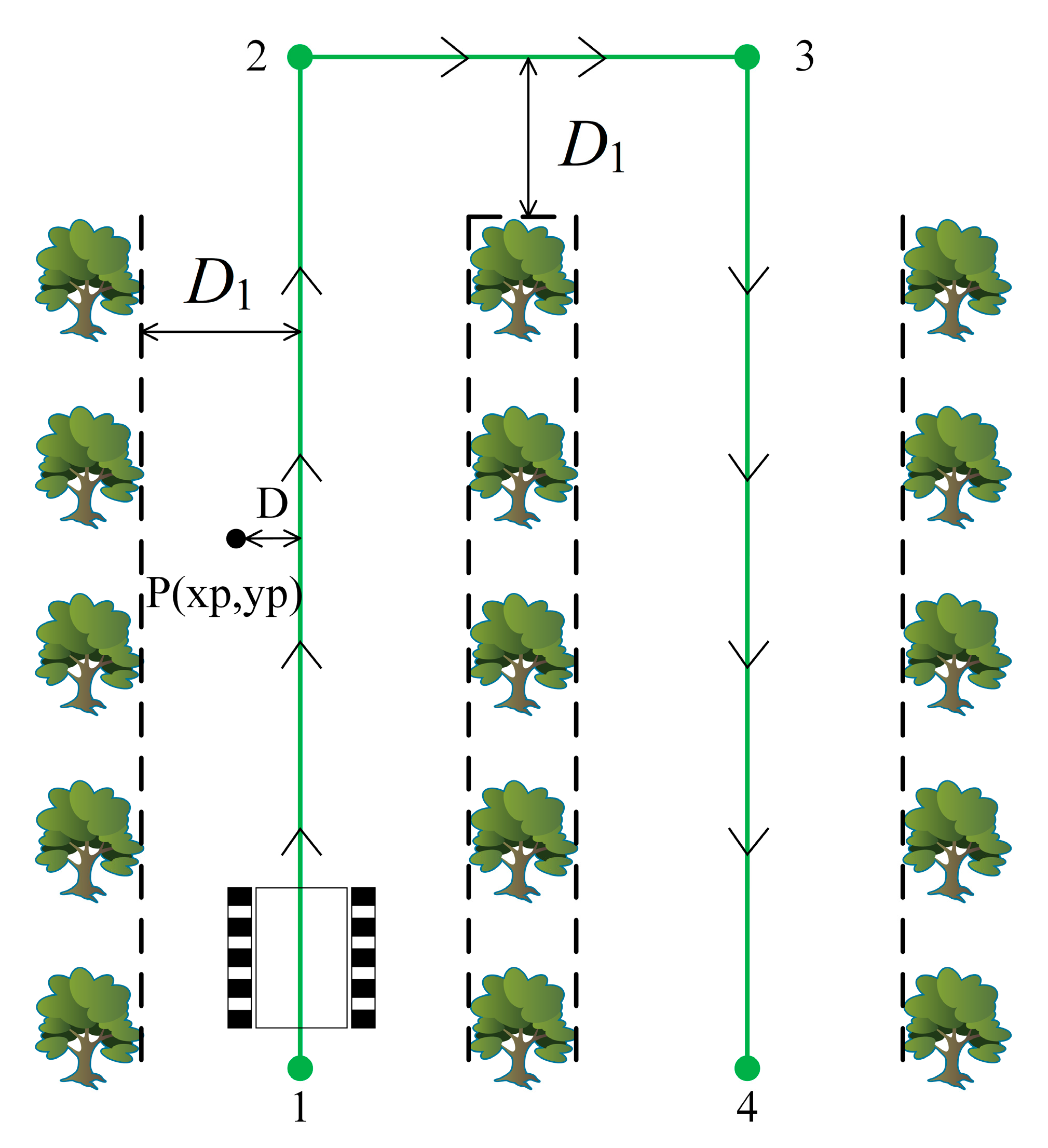



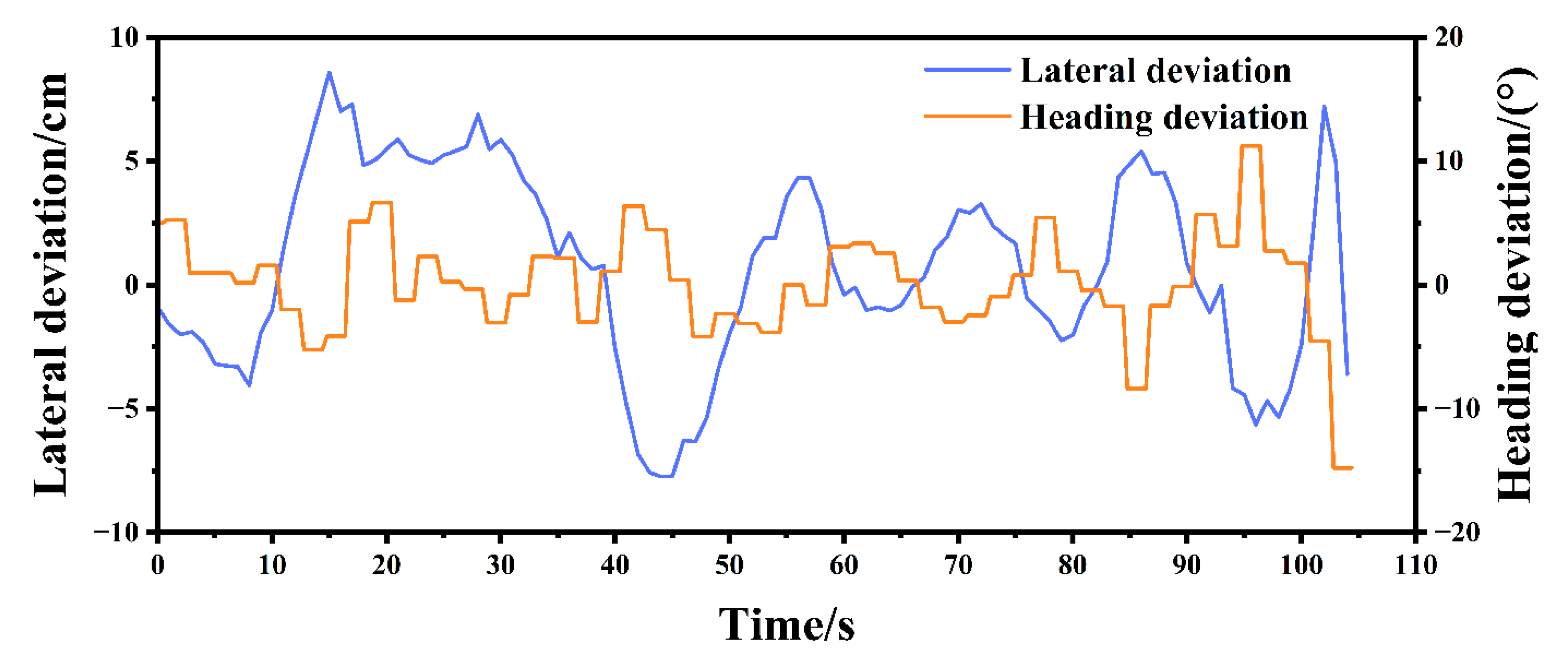

| Line Number | Time/s | Maximum Error/cm | Minimum Error/cm | Average Absolute Error/cm | Root Mean Square Error/cm |
|---|---|---|---|---|---|
| 1 | 109.00 | 8.58 | 0.01 | 3.23 | 1.21 |
| 2 | 108.01 | 9.36 | 0.06 | 2.96 | 0.35 |
| 3 | 108.01 | 10.77 | 0.06 | 3.93 | 1.73 |
| 4 | 108.01 | 9.98 | 0.11 | 4.16 | 2.37 |
| 5 | 110.00 | 9.32 | 0.01 | 3.48 | 0.29 |
| Overall | / | / | / | 3.55 | 1.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhu, X.; Huang, J.; Huang, J.; Xie, J.; Xiao, X.; Yin, G.; Wang, X.; Li, M.; Fang, K. BDS/IMU Integrated Auto-Navigation System of Orchard Spraying Robot. Appl. Sci. 2022, 12, 8173. https://doi.org/10.3390/app12168173
Zhang L, Zhu X, Huang J, Huang J, Xie J, Xiao X, Yin G, Wang X, Li M, Fang K. BDS/IMU Integrated Auto-Navigation System of Orchard Spraying Robot. Applied Sciences. 2022; 12(16):8173. https://doi.org/10.3390/app12168173
Chicago/Turabian StyleZhang, Liang, Xinghui Zhu, Jingjing Huang, Jinqi Huang, Jingxin Xie, Xu Xiao, Gang Yin, Xiayu Wang, Ming Li, and Kui Fang. 2022. "BDS/IMU Integrated Auto-Navigation System of Orchard Spraying Robot" Applied Sciences 12, no. 16: 8173. https://doi.org/10.3390/app12168173
APA StyleZhang, L., Zhu, X., Huang, J., Huang, J., Xie, J., Xiao, X., Yin, G., Wang, X., Li, M., & Fang, K. (2022). BDS/IMU Integrated Auto-Navigation System of Orchard Spraying Robot. Applied Sciences, 12(16), 8173. https://doi.org/10.3390/app12168173






