The Effect of Cr Substitution on the Anomalous Hall Effect of Co3−xCrxAl (x = 0, 1, 2, 3) Heusler Compounds: An Ab Initio Study
Abstract
Featured Application
Abstract
1. Introduction
2. Theory and Computational Methods
3. Results and Discussion
3.1. Crystal Structure and Magnetic Properties
3.2. Mechanical Properties
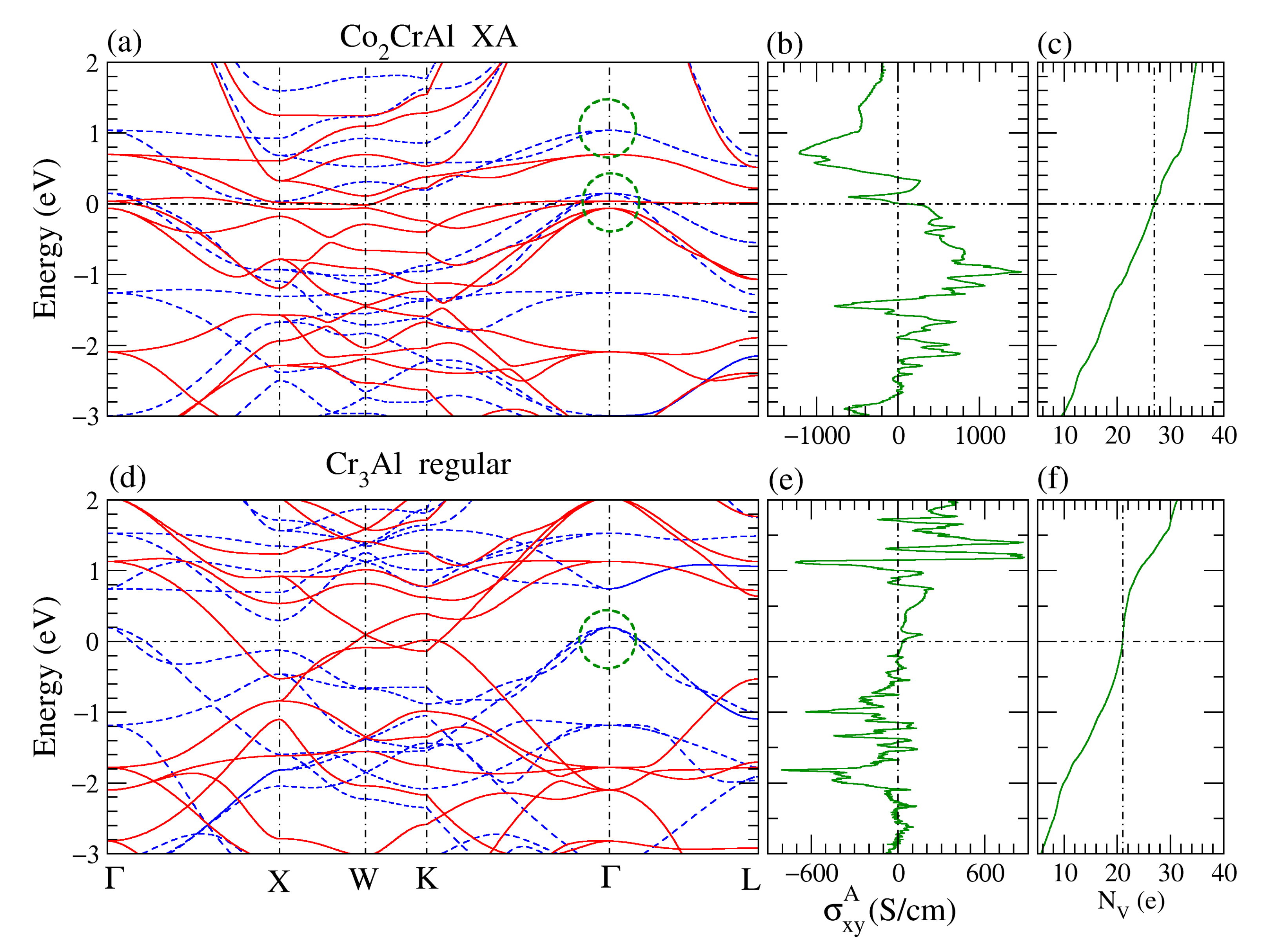
3.3. Spin and Anomalous Hall Conductivities
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- De Groot, R.A.; Mueller, F.M.; Van Engen, P.G.; Buschow, K.H.J. New Class of Materials: Half-Metallic Ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; Von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.M.; De Wijis, G.A.; De Groot, R.A. Spin-polarization in half-metals (invited). J. Appl. Phys. 2002, 91, 8340. [Google Scholar] [CrossRef]
- Jin, Y.; Kharel, P.; Lukashev, P.; Valloppilly, S.; Staten, B.; Herran, J.; Tutic, I.; Mitrakumar, M.; Bhusal, B.; O’Connell, A.; et al. Magnetism and electronic structure of CoFeCrX (X = Si, Ge) Heusler alloys. J. Appl. Phys. 2016, 120, 053903. [Google Scholar] [CrossRef]
- Ram, M.; Saxena, A.; Aly, A.E.; Shankar, A. Half-metallicity in new Heusler alloys Mn2ScZ (Z = Si, Ge, Sn). RSC Adv. 2020, 10, 7661. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Venkatesan, M. Half-metallic ferromagnetism: Example of CrO2 (invited). J. Appl. Phys. 2002, 91, 8345. [Google Scholar] [CrossRef]
- Lewis, S.P.; Allen, P.B.; Sasaki, T. Band structure and transport properties of CrO2. Phys. Rev. B 1997, 55, 10253. [Google Scholar] [CrossRef]
- Fujii, S.; Ishida, S.; Asano, S. A half-metallic band structure and Fe2MnZ (Z = Al, Si, P). J. Phys. Soc. Jpn. 1995, 64, 185–191. [Google Scholar] [CrossRef]
- Ishida, S.; Mizutani, S.; Fujii, S.; Asano, S. Theoretical prediction of materials to preserve high spin polarization against chemical disorder. Mater. Trans. 2006, 47, 31–37. [Google Scholar] [CrossRef][Green Version]
- Luo, H.; Zhu, Z.; Li, M.; Xu, S.; Liu, H.; Qu, J.; Wu, G. Electronic structure and magnetic properties of Fe2YSi (Y = Cr, Mn, Fe, Co, Ni) Heusler alloys: A theoretical and experimental study. J. Phys. D Appl. Phys. 2007, 40, 7121. [Google Scholar] [CrossRef]
- Zhang, X.J.; Liu, Z.H.; Zhang, Y.J.; Liu, H.Y.; Liu, G.D.; Cui, Y.T.; Ma, X.Q. Theoretical and experimental study of the phase formation for Ti2YAl and Ti2Y’Ga (Y = Co, Fe; Y’ = Cr, Fe). Intermetallics 2016, 73, 26–30. [Google Scholar] [CrossRef]
- Tung, J.-C.; Guo, G.-Y. High spin polarization of the anomalous Hall current in Co-based Heusler compounds. New J. Phys. 2013, 15, 033014. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; Van Engen, P.G.; Jongebreur, R. Magneto-optical Properties of Metallic Ferromagnetic Materials. J. Magn. Magn. Mater. 1983, 38, 1–22. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, A.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-initio Total Energy Calculations for Metals and Semiconductors using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab initio Total-Energy Calculations using a Plane-Wave basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements. J. Phys. Condens. Matter 1997, 6, 8245–8257. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation. Phys. Rev. B 1986, 3, 8800–8802. [Google Scholar] [CrossRef]
- Pizzi, G.; Vitale, V.; Arita, R.; Blügel, S.; Freimuth, F.; Géranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]
- Fuh, H.-R.; Guo, G.-Y. Intrinsic anomalous Hall effect in nickel: A GGA+U study. Phys. Rev. B 2011, 84, 144427. [Google Scholar] [CrossRef]
- Tung, J.-C.; Fuh, H.-R.; Guo, G.-Y. Anomalous and spin Hall effects in hcp cobalt from GGA+U calculations. Phys. Rev. B 2012, 86, 024435. [Google Scholar] [CrossRef]
- Huang, H.-L.; Tung, J.-C.; Guo, G.-Y. Anomalous Hall effect and current spin polarization in Co2FeX Heusler compounds (X = Al, Ga, In, Si, Ge, and Sn): A systematic ab initio study. Phys. Rev. B 2015, 91, 134409. [Google Scholar] [CrossRef]
- Husmann, A.; Singh, L.J. Temperature dependence of the anomalous Hall conductivity in the Heusler alloy Co2CrAl. Phys. Rev. B 2006, 73, 172417. [Google Scholar] [CrossRef]
- Luo, H.; Ma, L.; Zhu, Z.; Wu, G.; Liu, H.; Qu, J.; Li, Y. Ab initio study of Cr substitution for Co in the Heusler alloy Co2CrAl: Half-metallicity and adjustable magnetic moments. Phys. B Condens. Matter. 2008, 403, 1797–1802. [Google Scholar] [CrossRef]
- Luo, H.; Zhu, Z.; Ma, L.; Xu, S.; Wu, G.; Liu, H.; Qu, J.; Li, Y.; Zhu, X.; Jiang, C.; et al. Effect of Cr on the electronic structure of Co3Al intermetallic compound: A first-principles study. J. Magn. Magn. Mater. 2008, 320, 1345. [Google Scholar] [CrossRef]
- Zhao, W.Q.; Dai, X.F.; Zhang, X.M.; Mo, Z.J.; Wang, X.T.; Chen, G.F.; Cheng, Z.X.; Liu, G.D. Preparation and physical properties of a Cr3Al film with a DO3 structure. IUCrJ 2019, 6, 552–557. [Google Scholar] [CrossRef]
- Mohanta, S.K.; Tao, Y.; Yan, X.; Qin, G.; Chandragiri, V.; Li, X.; Jing, C.; Cao, S.; Zhang, J.; Qiao, Z.; et al. First principles electronic structure and magnetic properties of inverse Heusler alloys X2YZ(X = Cr; Y = Co, Ni; Z = Al, Ga, In, Si, Ge, Sn, Sb). J. Magn. Magn. Mater. 2017, 430, 65–69. [Google Scholar] [CrossRef]
- Jamer, M.E.; Marshall, L.G.; Sterbinsky, G.E.; Lewis, L.H.; Heiman, D. Low-moment ferrimagnetic phase of the Heusler compound Cr2CoAl. J. Magn. Magn. Mater. 2015, 394, 32–36. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal Elastic Anisotropy Index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef]
- Lee, C.-H.; Tung, J.-C. Large Bandgap Topological Insulator in Oxide APoO3 (A = Be, Mg, Ca, Sr, Ba, and Ra) Perovskite: An Ab Initio Study. Appl. Sci. 2021, 11, 1143. [Google Scholar] [CrossRef]
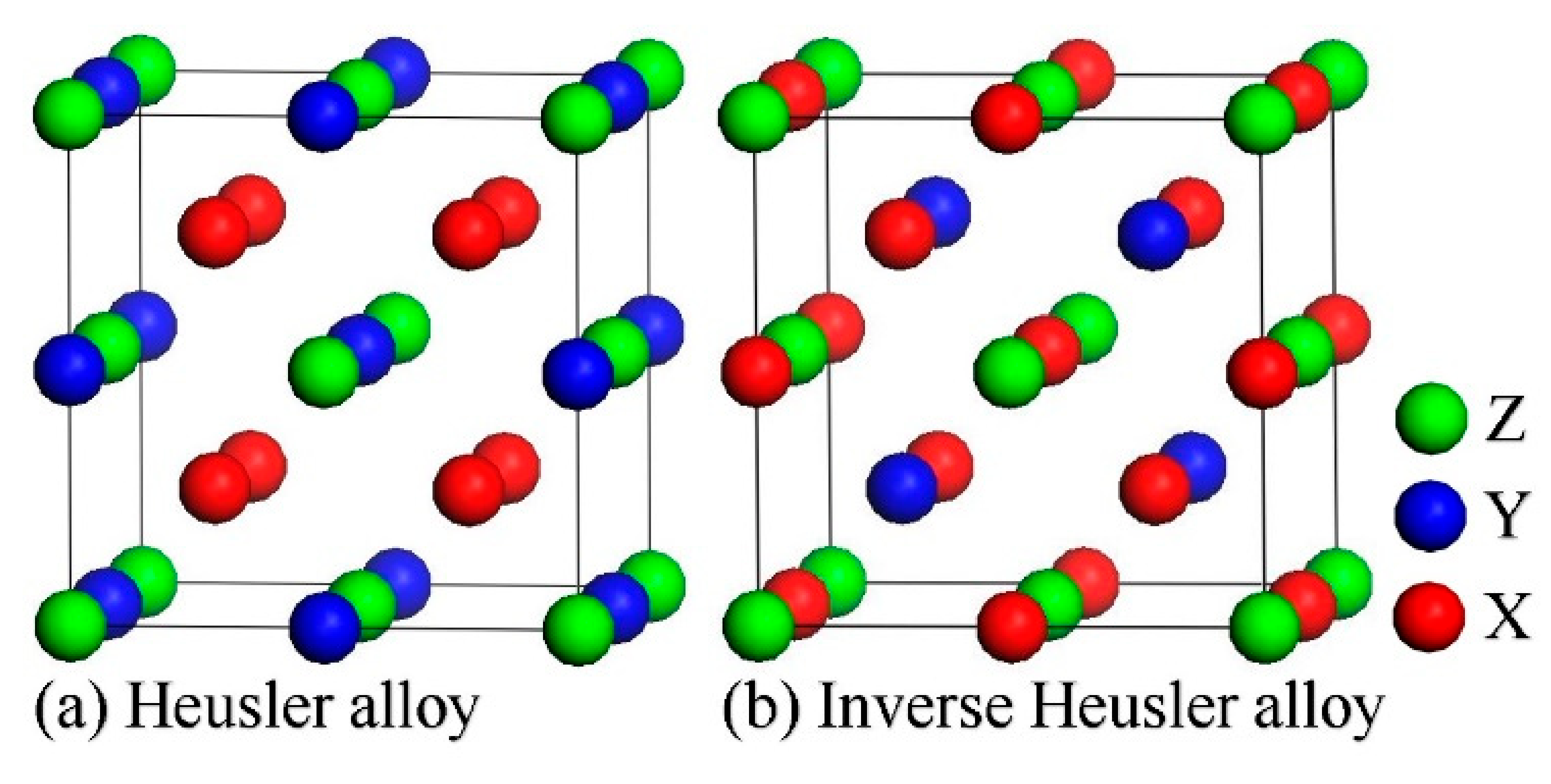


| X2YZ | Structure | a | |||||
|---|---|---|---|---|---|---|---|
| Co3Al | regular | 5.672 | 4.00, 3.90 1 | 1.25 | 1.25 | 1.71 | −0.087 |
| Co2CrAl | regular | 5.701, 5.727 2 | 3.00, 1.55 2 | 0.77 | 0.77 | 1.58 | −0.093 |
| XA | 5.723 | 0.82 | 0.93 | 1.33 | −1.32 | −0.035 | |
| Cr2CoAl | regular | 5.885 | 5.75 | 2.18 | 2.18 | 1.17 | 0.020 |
| XA | 5.721, 5.79 3 | 0.00 | - | - | - | ||
| Cr3Al | regular | 5.908, 5.83 4 | 2.92, 2.88 4 | −1.60 | 2.16 | 2.16 | 0.033 |
| X2YZ | Structure | B | G | E | B/G | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (GPa) | arb. Unit | |||||||||||
| Co3Al | regular | 214 | 160 | 132 | 178 | 90 | 52 | 71 | 188 | 4.89 | 0.32 | 2.51 |
| Co2CrAl | regular | 268 | 166 | 145 | 200 | 107 | 83 | 95 | 247 | 2.86 | 0.30 | 2.11 |
| XA | 191 | 150 | 135 | 164 | 90 | 42 | 66 | 174 | 6.59 | 0.32 | 2.48 | |
| Cr2CoAl | regular | 133 | 141 | 135 | 138 | 80 | −11 | 34 | 95 | - | 0.39 | 4.06 |
| XA | 326 | 153 | 109 | 211 | 102 | 101 | 100 | 258 | 1.26 | 0.30 | 2.11 | |
| Cr3Al | regular | 254 | 72.4 | 122 | 133 | 110 | 107 | 107 | 256 | 1.35 | 0.18 | 1.24 |
| X2YZ | Structure | ρ | ||||
|---|---|---|---|---|---|---|
| g/cm3 | (m/s) | K | ||||
| Co3Al | regular | 4.397 | 6069 | 3099 | 3472 | 459 |
| Co2CrAl | regular | 4.182 | 6816 | 3678 | 4106 | 540 |
| XA | 4.135 | 6013 | 3075 | 3445 | 451 | |
| Cr2CoAl | regular | 3.668 | 8115 | 3502 | 3956 | 504 |
| XA | 3.993 | 7164 | 3882 | 4332 | 568 | |
| Cr3Al | regular | 3.492 | 6866 | 4293 | 4729 | 600 |
| X2YZ | Structure | |||||||
|---|---|---|---|---|---|---|---|---|
| (S/cm) | % | % | ||||||
| Co3Al | regular | 434 | 182 | 35 | 399 | 69 | −84 | 0.84 |
| Co2CrAl | regular | 155 | 63.3 | 14.2 | 140.8 | 100 | 63 | 0.82 |
| XA | 104 | 370 | −318 | 440 | 81 | −621 | 7.12 | |
| Cr2CoAl | regular | 490 | 34.2 | 211 | 279 | 75 | −14 | 0.14 |
| XA | - | - | - | - | 0 | - | ||
| Cr3Al | regular | 30.4 | −24.0 | 39.2 | −8.8 | 57 | 158 | 1.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tung, J.-C.; Huang, S.-W.; Wu, B.-E.; Chang, C.-C.; Liu, P.-L. The Effect of Cr Substitution on the Anomalous Hall Effect of Co3−xCrxAl (x = 0, 1, 2, 3) Heusler Compounds: An Ab Initio Study. Appl. Sci. 2022, 12, 8303. https://doi.org/10.3390/app12168303
Tung J-C, Huang S-W, Wu B-E, Chang C-C, Liu P-L. The Effect of Cr Substitution on the Anomalous Hall Effect of Co3−xCrxAl (x = 0, 1, 2, 3) Heusler Compounds: An Ab Initio Study. Applied Sciences. 2022; 12(16):8303. https://doi.org/10.3390/app12168303
Chicago/Turabian StyleTung, Jen-Chuan, Shih-Wei Huang, Bo-En Wu, Cheng-Chung Chang, and Po-Liang Liu. 2022. "The Effect of Cr Substitution on the Anomalous Hall Effect of Co3−xCrxAl (x = 0, 1, 2, 3) Heusler Compounds: An Ab Initio Study" Applied Sciences 12, no. 16: 8303. https://doi.org/10.3390/app12168303
APA StyleTung, J.-C., Huang, S.-W., Wu, B.-E., Chang, C.-C., & Liu, P.-L. (2022). The Effect of Cr Substitution on the Anomalous Hall Effect of Co3−xCrxAl (x = 0, 1, 2, 3) Heusler Compounds: An Ab Initio Study. Applied Sciences, 12(16), 8303. https://doi.org/10.3390/app12168303








