Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs
Abstract
:Featured Application
Abstract
1. Introduction
2. Design Concepts and Features
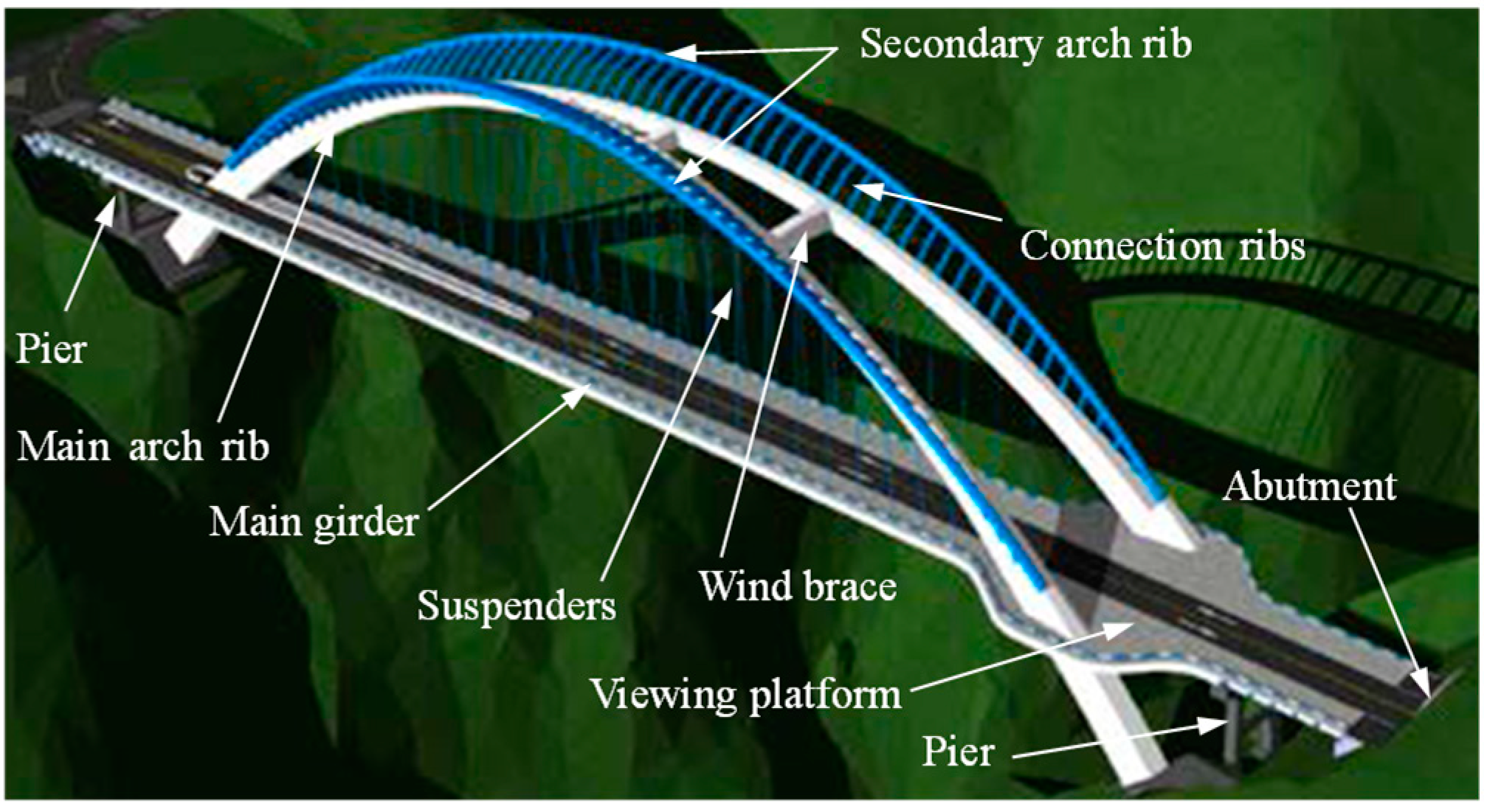
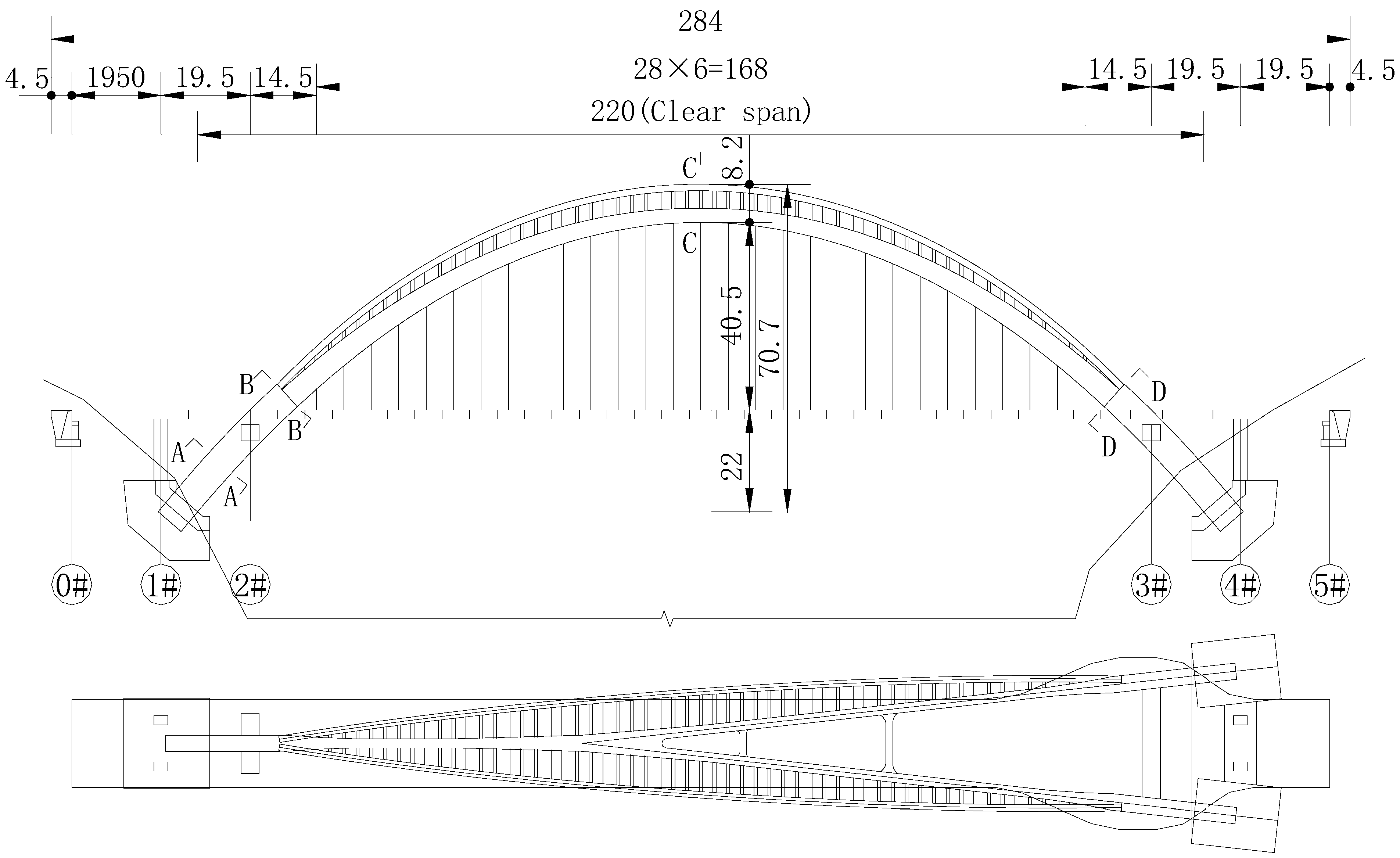
2.1. Target Bridge
2.2. Innovative Design Concepts
2.3. Design Features and Details
3. Numerical Model
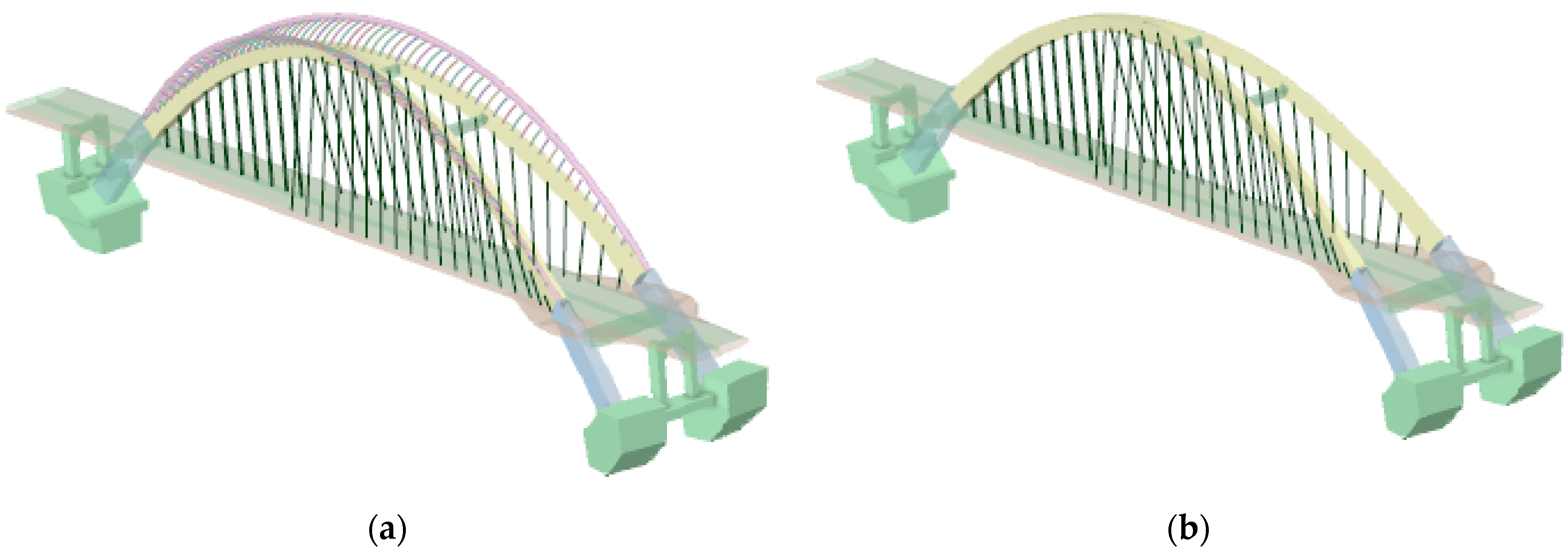
3.1. Establishment of Numerical Model
3.2. Material Parameters
4. Numerical Verification of Innovative Designs
4.1. Load-Carrying Capacity
4.2. Axial Force Distribution of Main and Secondary Arch Ribs
4.3. Deformation Analysis
4.4. Dynamic Characteristic Analysis
5. Bifurcation Segment Shear Lag Effect and Stress Distribution
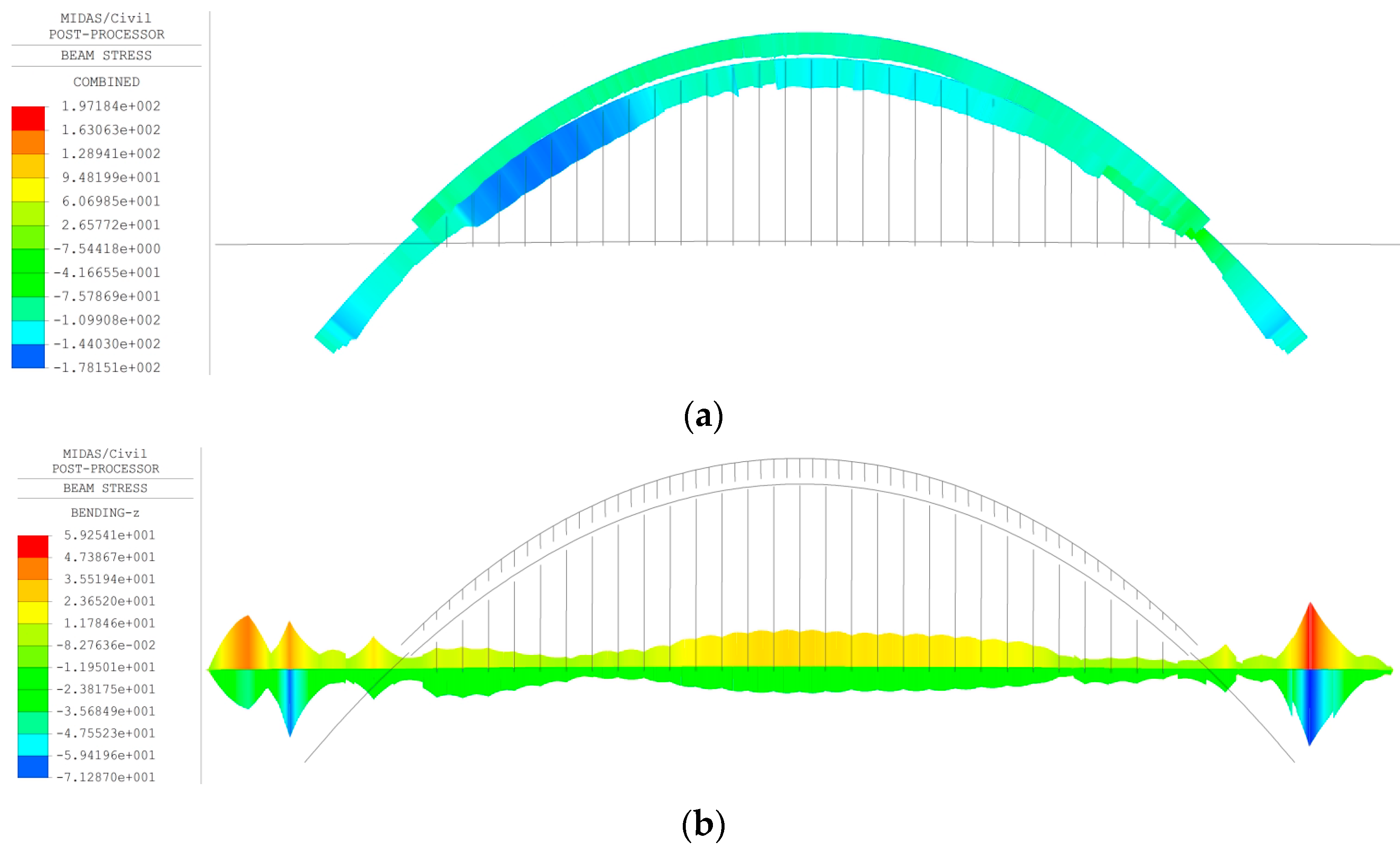
5.1. Analysis of Shear Lag Effect
5.2. Stress Distribution Analysis of Single and Double Arch Rib Bifurcation Segment
6. Conclusions
- The innovative design concept and design details have been discussed and verified by numerical calculations, showing that the structure meets the design requirements in terms of mechanical performance and has certain advantages in terms of static stability.
- The traditional single arch rib design is mechanically and aesthetically slightly worse than the main and secondary arch collaborative system. The secondary arch rib bears a certain proportion of the load with a smaller cross-sectional area, which not only plays the role of structural bearing, but also meets the aesthetic needs of the landscape; therefore, the synergistic effect of the main and secondary arch rib collaborative system is outstanding and reasonably designed.
- The maximum tensile and compressive stresses in the main girder all occur at 3/8 of the span; the maximum tensile stress in the arch ribs occurs at the main arch end of the main and sub-arch connecting ribs, and the maximum compressive stress occurs at the position of 1/4 arch rib on the single arch side.
- As the shape of the arch rib is spatially Y-shaped, the vertical deformation of the structure is special, and the maximum vertical deformation of the arch rib is not in the middle of the span, but in the vicinity of 3 L/8 and 5 L/8, and the deformation trend is similar to a “W” shape.
- The structural mode is mainly manifested as deflection and drift, and special attention should be paid to the deflection vibration problem in the design. The relatively good torsional stability performance of the structure is mainly due to the innovative design of the three-part bifurcated arch ribs and the stiffness contribution of the secondary arch ribs and connecting ribs, and these design measures can be referred to by future bridge designs.
- The shear lag effect was observed in any cross-section of unconventional thin-walled steel box arch ribs, and the shear lag effect was more noticeable in single arch ribs than double arch ribs. The shear lag coefficient decreased with the decrease in arch rib width, and the maximum shear lag coefficient was 1.4 under the design load combination.
- In future bridge construction, the main and secondary arch collaborative Y-shaped steel box arch design may be widely used in urban landscape bridges, and the design concept and method presented in this paper may provide an effective reference for the construction of similar projects in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Zhang, X.G. Thoughts on the Development of Bridge Technology in China. Engineering 2019, 5, 1120–1130. [Google Scholar] [CrossRef]
- Chen, B.C.; Liu, J.P. Review of construction and technology development of arch bridges in the world. J. Traffic Transp. Eng. 2020, 20, 27–41. (In Chinese) [Google Scholar] [CrossRef]
- Liang, Y.; He, W.; Tang, M.L. State-of-the-art review of bridge aesthetics in 2019. J. Civ. Environ. Eng. 2020, 42, 213–222. [Google Scholar] [CrossRef]
- Kossakowski, P.G.; Wcislik, W. Fiber-Reinforced Polymer Composites in the Construction of Bridges: Opportunities, Problems and Challenges. Fibers 2022, 10, 37. [Google Scholar] [CrossRef]
- Ma, B.; Lin, Y.P.; Zhang, J.J.; Xu, Y. Decade Review: Bridge Type Selection and Challenges of Lupu Bridge. Struct. Eng. Int. 2013, 23, 317–322. [Google Scholar] [CrossRef]
- Qin, S.Q.; Hu, J.; Cao, H.Y.; Kang, J.T.; Pu, Q.H. Finite Element Model Updating of Large-span Arch Bridge Based on Experimental Data. China J. Highw. Transp. 2019, 32, 66–76. (In Chinese) [Google Scholar] [CrossRef]
- Wang, F. Comparison and Selection of Erection Scheme for Steel Box Basket Handle Arch or Xijiang River Bridge on Newly-Built Nanning-Guangzhou Railway. Bridge Constr. 2013, 43, 117–121. (In Chinese) [Google Scholar]
- Cheng, K.M.; Ketchum, M.A.; Drouillard, F. Nanning Butterfly Tied Arch Bridge Over the Yong River in China. Struct. Eng. Int. 2010, 20, 308–311. [Google Scholar] [CrossRef]
- Ni, Z. Key Techniques in the Fabrication Process of the Steel Structure for Lupu Bridge. China Railw. Sci. 2005, 26, 134–140. (In Chinese) [Google Scholar] [CrossRef]
- Quan, J. Study on Theory and Model Experiment of Steel-Concrete Compound Arch Support for Ningbo Mingzhou Bridge. Urban Roads Bridges Flood Control 2016, 5, 90–94. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, P.J.; Ma, B. An Analysis of Construction Key Points in Mingzhou Bridge with Large Span Steel Arch Bridge Type. China Munic. Eng. 2015, 3, 25–29, 111. (In Chinese) [Google Scholar] [CrossRef]
- Cai, S.Y.; Chen, W.Z.; Xu, J. Full-scale fatigue tests on a novel box-shaped steel rod of a spatial arch bridge for fatigue assessment. Adv. Struct. Eng. 2018, 21, 694–706. [Google Scholar] [CrossRef]
- Lin, Y.Z. Structure Analysis and Construction Control of Special-shaped Arch Bridge. Master’s Thesis, Dalian University of Technology, Dalian, China, May 2016. (In Chinese). [Google Scholar]
- Bozyigit, B.; Acikgoz, S. Determination of free vibration properties of masonry arch bridges using the dynamic stiffness method. Eng. Struct. 2022, 250, 18. [Google Scholar] [CrossRef]
- Wu, G.; Ren, W.X.; Zhu, Y.F.; Hussain, S.M. Static and dynamic evaluation of a butterfly-shaped concrete-filled steel tube arch bridge through numerical analysis and field tests. Adv. Mech. Eng. 2021, 13, 13. [Google Scholar] [CrossRef]
- Li, S.Y.; Hong, Y.; Gou, H.Y.; Pu, Q.H. An improved method for analyzing shear-lag in thin-walled girders with rectangular ribs. J. Constr. Steel. Res. 2021, 177, 12. [Google Scholar] [CrossRef]
- Mazinani, I.; Jumaat, M.Z.; Ismail, Z.; Chao, O.Z. Comparison of shear lag in structural steel building with framed tube and braced tube. Struct. Eng. Mech. 2014, 49, 297–309. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, Z. Research on the Effect of Seismic Isolation on Shear Lag Effect of High Rise Tube Structure. J. Disaster Prev. Mitig. Eng. 2017, 37, 981–986. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Bao, L.; Dong, L.; Wang, Q. Numerical and theoretical analysis of spatial shear lag effect in through wide box bowstring arch bridge main girder. Structures 2021, 33, 141–151. [Google Scholar] [CrossRef]
- Zhang, K.; Lei, J.Q.; Cao, S.S. Influence of Damage of Suspenders on Static Performances of Steel-Box Stacked Arch Bridge. Adv. Mater. Res. 2013, 655–657, 1864–1867. [Google Scholar] [CrossRef]
- Gao, Z.S.; Huang, Y.; Liu, Y.; Qi, L.K. Stability Analysis of Xiwu Road Steel Box Arch Bridge in Zibo City. Adv. Mater. Res. 2011, 255–260, 1012–1016. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, H.; Zheng, W. Experimental modal analysis of steel box basket-handle arch bridge. J. Vib. Shock 2004, 23, 43–47. (In Chinese) [Google Scholar] [CrossRef]
- He, X.H.; Wei, B.; Zou, Y.F.; Hu, D.Y.; Linzell, D.G. Dynamic characteristics and seismic response analysis of a long-span steel-box basket-handle railway arch bridge. J. Vibroeng. 2015, 17, 2422–2432. [Google Scholar]
- Su, Q.T.; Ren, F.; Liu, Y.W. Study on Stresses Distribution Pattern of Wide Box Steel Girder of Arch Bridge. Appl. Mech. Mater. 2013, 275–277, 1158–1162. [Google Scholar] [CrossRef]
- Ma, H.J.; Chen, X.C. Space Stability Analysis of Inclined Thin-Walled Steel Box Ribs. Appl. Mech. Mater. 2014, 578–579, 954–959. [Google Scholar] [CrossRef]
- Liu, A.-R.; Zhang, J.-P.; Yu, Q.-C. Study on detail constructions and shear lag effect of a new type space-combined tied arch bridge. Acta Sci. Nat. Univ. Sunyatseni 2007, 46, 30–34. (In Chinese) [Google Scholar] [CrossRef]
- Xie, X.; Zhuge, H.; Tang, Z.; Wang, T.; Liao, Y. Damage characteristics of thin-walled steel arch bridges subjected to in-plane earthquake action. J. Constr. Steel. Res. 2018, 151, 70–82. [Google Scholar] [CrossRef]
- Xuhui, H.E.; Zhouquan, F.; Zhengqing, C.; Zhiwu, Y.U. Interactive stability analysis of steel box arch based on mixed finite element method. J. Rail. Sci. Eng. 2007, 4, 7–11. (In Chinese) [Google Scholar] [CrossRef]
- Lu, P.; Zhang, J.; Zhao, R. Study on the mechanical performance of Butterfly Arch Bridge. Struct. Des. Tall Spec. Build. 2009, 18, 469–483. [Google Scholar] [CrossRef]
- Chen, K.; Wu, Q.; Nakamura, S.; Chen, B. Experimental and numerical study on compressive behavior of convex steel box section for arch rib. Eng. Struct. 2016, 114, 35–47. [Google Scholar] [CrossRef]
- Huang, Q.; Wu, X.G.; Hu, K.J.; Xu, N. Design of Cable Suspension System for Spatial Y-shaped Steel Box Arch Bridge in V-shaped Canyon Area. In Proceedings of the World Forum on Transport Engineering and Technology (WTC2021), Xi’an, China, 16–18 June 2021. (In Chinese). [Google Scholar] [CrossRef]
- JTG D60-2015; Industry Standard of the People’s Republic of China; General Specifications for Design of Highway Bridges and Culverts. Industry Standard of the People’s Republic of China: Beijing, China, 2015.
- JTG D64-2015; Industry Standard of the People’s Republic of China; Specification for Design of Highway Steel bridge. Industry Standard of the People’s Republic of China: Beijing, China, 2015.
- JTG/T D65-06-2015; Industry Standard of the People’s Republic of China; Specifications for Design of Highway Concrete-filled Steel Tubular Arch Bridges. Industry Standard of the People’s Republic of China: Beijing, China, 2015.















| No. | Bridge Name | Country of Affiliation | Build Year | Span (m) |
|---|---|---|---|---|
| 1 | Rainbow Bridge | USA | 1942 | 290 |
| 2 | Fremont Bridge | USA | 1973 | 383 |
| 3 | Roosevelt Lake Bridge | USA | 1990 | 329 |
| 4 | Kizugawa Bridge | Japan | 1993 | 305 |
| 5 | Lupu Bridge | China | 2003 | 550 |
| 6 | Wuyuan Bridge | China | 2004 | 208 |
| 7 | Caiyuanba Bridge | China | 2008 | 400 |
| 8 | Nanning Bridge | China | 2009 | 300 |
| 9 | Mingzhou Bridge | China | 2011 | 450 |
| 10 | Nan-Guang Railroad Xijiang Bridge | China | 2014 | 450 |
| 11 | Yibin Jinsha River Highway–Railway Dual-Use Bridge | China | 2017 | 336 |
| Bearing Type | Bearing Capacity (kN) | Design Displacement (mm) | Yield Force (kN) | Pre-Yield Strength (kN/mm) | Post-Yield Strength (kN/mm) | Horizontal Equivalent Stiffness (kN/mm) |
|---|---|---|---|---|---|---|
| SHDR620 × 620 × 223 | 3500 | ±100 | 179 | 9.6 | 1.7 | 2.8 |
| SHDR770 × 770 × 256 | 5500 | ±125 | 279 | 12.1 | 2.2 | 3.6 |
| Brand | Thickness (mm) | Lower Yield Strength (MPa) | Tensile Strength (MPa) | Elongation at Fracture (A/%) | Impact Absorbed Energy (KV2/J) |
|---|---|---|---|---|---|
| Q420qDNH | ≤50 | 420 | 540 | 19 | 120 |
| Brand | Thickness (mm) | Lower Yield Strength (MPa) | Tensile Strength(MPa) | Elongation at Fracture (A/%) | Impact Test | |
|---|---|---|---|---|---|---|
| Temperature (°C) | Absorption Power (J) | |||||
| Q235B | ≤16 | ≥235 | 370~500 | ≥26 | +20 | 27 |
| >16–40 | ≥225 | ≥26 | ||||
| >40–60 | ≥215 | ≥25 | ||||
| Brand | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio | Coefficient of Linear Expansion (1/°C) |
|---|---|---|---|---|
| Q420qDNH | 7850 | 206,000.00 | 0.30 | 1.2 × 10−5 |
| Q235B | 7850 | 206,000.00 | 0.30 | 1.2 × 10−5 |
| Steel Stranded Wires | 7850 | 205,000.00 | 0.30 | 1.2 × 10−5 |
| Number | Cable Tension (kN) | Breaking Force (kN) | Number | Cable Tension (kN) | Breaking Force (kN) | Number | Cable Tension (kN) | Breaking Force (kN) |
|---|---|---|---|---|---|---|---|---|
| 1#(1′#) | 1468 | 4972 | 11#(11′#) | 670 | 3746 | 21#(21′#) | 912 | 3746 |
| 2#(2′#) | 1250 | 4155 | 12#(12′#) | 1046 | 3746 | 22#(22′#) | 969 | 3746 |
| 3#(3′#) | 1171 | 4155 | 13#(13′#) | 792 | 3746 | 23#(23′#) | 883 | 3746 |
| 4#(4′#) | 802 | 3746 | 14#(14′#) | 914 | 3746 | 24#(24′#) | 750 | 3746 |
| 5#(5′#) | 901 | 3746 | 15#(15′#) | 898 | 3746 | 25#(25′#) | 1158 | 3746 |
| 6#(6′#) | 872 | 3746 | 16#(16′#) | 908 | 3746 | 26#(26′#) | 1198 | 3746 |
| 7#(7′#) | 692 | 3746 | 17#(17′#) | 1078 | 3746 | 27#(27′#) | 1102 | 3746 |
| 8#(8′#) | 831 | 3746 | 18#(18′#) | 777 | 3746 | 28#(28′#) | 1409 | 3746 |
| 9#(9′#) | 1076 | 3746 | 19#(19′#) | 967 | 3746 | 29#(29′#) | 1359 | 3746 |
| 10#(10′#) | 783 | 3746 | 20#(20′#) | 883 | 3746 | — | — | — |
| Location | Total Axial Force (kN) | Secondary Arch Rib | Main Arch Rib | ||
|---|---|---|---|---|---|
| Axial Force (kN) | Share Percentage (%) | Axial Force (kN) | Share Percentage (%) | ||
| 1—1 | −28,763.56 | −3470.34 | 12.07 | −25,293.22 | 87.93 |
| 2—2 | −24,516.02 | −3498.39 | 14.27 | −21,017.63 | 85.73 |
| 3—3 | −21,117.33 | −3544.81 | 16.79 | −17,572.52 | 83.21 |
| 4—4 | −11,881.99 | −3571.70 | 30.06 | −8310.29 | 69.94 |
| 5—5 | −12,405.42 | −3549.76 | 28.61 | −8855.66 | 71.39 |
| 6—6 | −13,355.12 | −3544.85 | 26.54 | −9810.27 | 73.46 |
| 7—7 | −16,641.71 | −3183.11 | 19.13 | −13,458.6 | 80.87 |
| Vibration Mode Serial Number | Frequency (Hz) | Vibration Mode Characteristics |
|---|---|---|
| 1 | 0.53 | Arch rib flexure in cross-bridge direction |
| 2 | 0.65 | Arch rib flexure in vertical direction Main girder drift in along-bridge direction |
| 3 | 0.72 | Main girder drift in cross-bridge direction |
| 4 | 0.73 | Antisymmetric flexure of main girder in vertical direction |
| 5 | 0.95 | Antisymmetric bending and twisting of arch ribs in cross-bridge direction |
| 6 | 1.12 | Arch rib flexure in vertical direction Symmetrical flexure of main girder in vertical direction |
| Section | σ (MPa) | σ0 (MPa) | λ |
|---|---|---|---|
| A-A | 73.1 | 59.0 | 1.24 |
| B-B | 73.0 | 60.3 | 1.21 |
| C-C | 60.1 | 61.7 | 0.97 |
| D-D | 77.2 | 68.9 | 1.12 |
| E-E | 78.4 | 70.0 | 1.12 |
| F-F | 71.4 | 72.3 | 0.99 |
| Load Combination | Allowable Stress | Single Arch Rib | Double Arch Ribs | ||||
|---|---|---|---|---|---|---|---|
| Top Slab | Bottom Slab | Web | Top Slab | Bottom Slab | Web | ||
| (1) | 320 | 0–128 | 0–117 | 0–128 | 0–151 | 0–137 | 0–151 |
| (2) | 320 | 0–155 | 0–172 | 0–172 | 0–173 | 0–192 | 0–192 |
| (3) | 320 | 0–144 | 0–104 | 0–144 | 0–167 | 0–122 | 0–167 |
| (4) | 320 | 0–151 | 0–164 | 0–164 | 0–169 | 0–186 | 0–186 |
| (5) | 320 | 0–137 | 0–197 | 0–197 | 0–169 | 0–124 | 0–169 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Wu, X.; Wei, H.; Chen, Q. Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs. Appl. Sci. 2022, 12, 8370. https://doi.org/10.3390/app12168370
Huang Q, Wu X, Wei H, Chen Q. Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs. Applied Sciences. 2022; 12(16):8370. https://doi.org/10.3390/app12168370
Chicago/Turabian StyleHuang, Qian, Xiaoguang Wu, Hui Wei, and Qida Chen. 2022. "Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs" Applied Sciences 12, no. 16: 8370. https://doi.org/10.3390/app12168370
APA StyleHuang, Q., Wu, X., Wei, H., & Chen, Q. (2022). Innovative Design of Novel Main and Secondary Arch Collaborative Y-Shaped Arch Bridge and Research on Shear Lag Effect of Its Unconventional Thin-Walled Steel Box Arch Ribs. Applied Sciences, 12(16), 8370. https://doi.org/10.3390/app12168370






