An Overview of Variants and Advancements of PSO Algorithm
Abstract
:1. Introduction
2. Concept of Particle Swarm Optimization (PSO) Technique
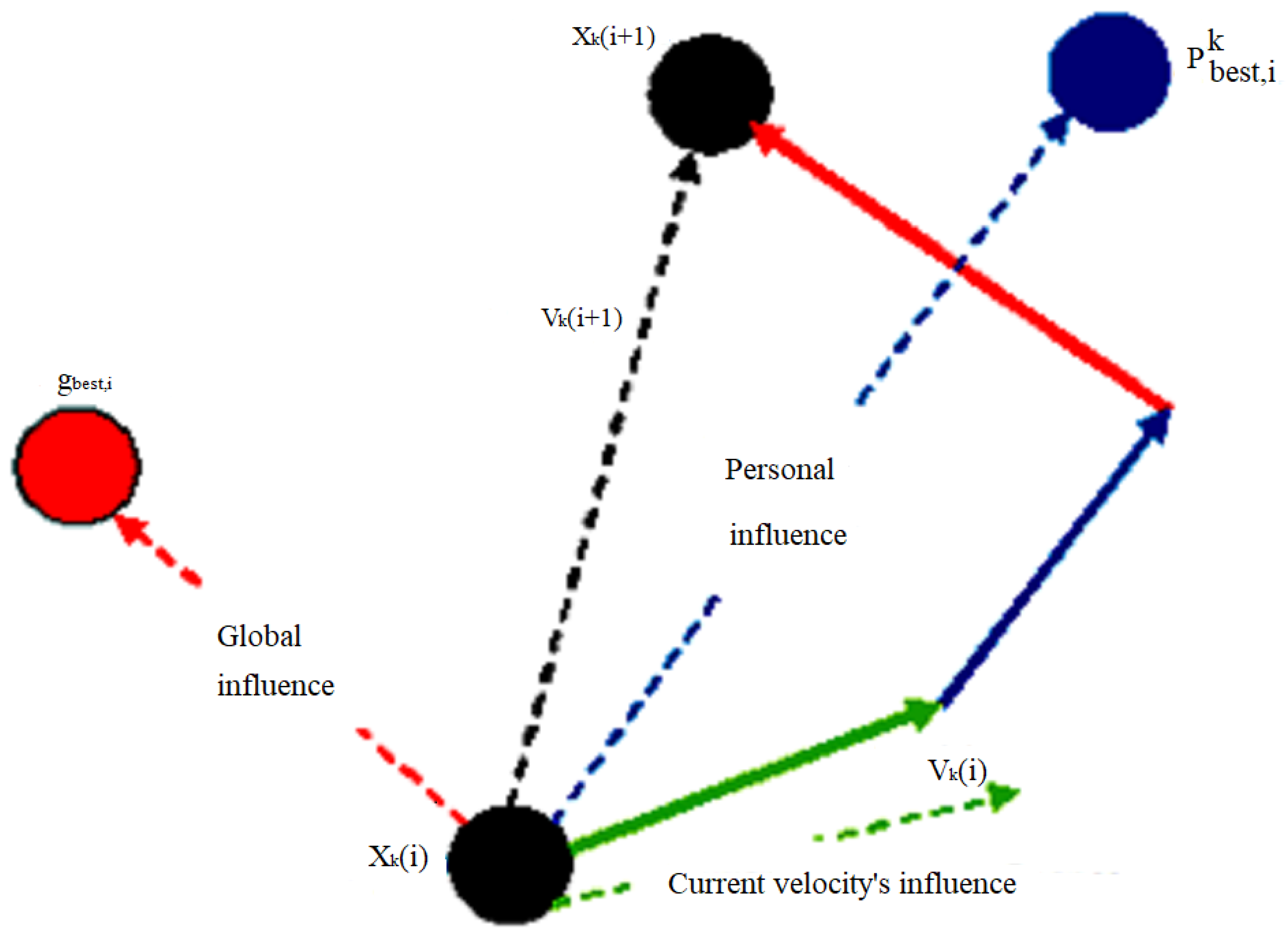
2.1. Updating of Velocity and Position of Particle in the Swarm
2.1.1. Updating of Velocity
- Momentum part;
- Cognitive part;
- Social part.
2.1.2. Updating the Position of Particle
2.2. Standard Particle Swarm Optimization (SPSO)
2.3. Pseudocode of PSO Algorithm
| Algorithm 1: The Pseudocde of the algorithm is as follows |
INPUT: Fitness function, lower bound, upper bound is the part of problem i.e., it will be given in the problem. Np (Population Size), I (No. of iteration), ω, are to be chosen by the user.
For iteration:- for i = 1 to I for k = 1 to Np Determine the velocity () of kth particle; Determine the new position () of kth particle; Bound ; Evaluate the objective function value of kth particle; Update the population by including and ; Update ; Update . end end |
2.4. Working Example of PSO
3. Parameters of PSO
3.1. Population Size
3.2. Number of Iterations
3.3. Neighborhood Size
3.4. Acceleration Coefficients
3.5. Velocity Clamping
3.6. Constriction Coefficient
3.7. Inertia Weight
4. Advances on Particle Swarm Optimization (PSO) Algorithm
- Modifications of original PSO;
- Extensions of applications of PSO;
- Theoretical analysis on PSO;
- Hybridization of PSO.
4.1. Modifications of Original PSO
4.2. Extensions of Applications of PSO
4.3. Theoretical Analysis on PSO
4.4. Hybridization of PSO Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Jia, H.; Sun, K.; Zhang, W.; Leng, X. An enhanced chimp optimization algorithm for continuous optimization domains. Complex Intell. Syst. 2022, 8, 65–82. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat Swarm Optimizer. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 8457–8482. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Kim, D.-S. Dragonfly-based swarm system model for node identification in ultra-reliable low-latency communication. Neural Comput. Appl. 2021, 33, 1837–1880. [Google Scholar] [CrossRef]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse herd optimization algorithm: A nature-inspired algorithm for high-dimensional optimization problems. Knowl. Based Syst. 2021, 213, 106711. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar] [CrossRef]
- Martínez-Álvarez, F.; Asencio-Cortés, G.; Torres, J.F.; Gutiérrez-Avilés, D.; Melgar-García, L.; Pérez-Chacón, R.; Rubio-Escudero, C.; Riquelme, J.C.; Troncoso, A. Coronavirus optimization algorithm: A bioinspired metaheuristic based on the COVID-19 propagation model. Big Data 2020, 8, 308–322. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Odili, J.B.; Kahar, M.N.M.; Anwar, S. African Buffalo Optimization: A Swarm-Intelligence Technique. Procedia Comput. Sci. 2015, 76, 443–448. [Google Scholar] [CrossRef] [Green Version]
- Eiben, A.E.; Schippers, C.A. On evolutionary exploration and exploitation. Fundam. Inform. 1998, 35, 35–50. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE Press: Piscataway, NJ, USA, 1995; pp. 1942–1947. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A Modified Particle Swarm Optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; IEEE Press: Piscataway, NJ, USA, 1998; pp. 69–73. [Google Scholar]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley and Sons: Hoboken, NJ, USA, 2007; Chapter 16; pp. 289–357. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Particle Swarm Optimization: Developments, Applications and Resources. In Proceedings of the IEEE Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 27–30. [Google Scholar]
- Clerc, M. The Swarm and the Queen: Towards a Deterministic and Adaptive Particle Swarm Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1951–1957. [Google Scholar]
- Clerc, M.; Kennedy, J. The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Eberhart, R.C.; Shi, Y. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 84–88. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. A Study of Particle Swarm Optimization Particle Trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory analysis and application. Swarm Evol. Comput. 2001, 63, 100868. [Google Scholar] [CrossRef]
- Krohling, R.A. Gaussian Swarm: A Novel Particle Swarm Optimization Algorithm. In Proceedings of the Cybernetics and Intelligent systems IEEE, Singapore, 1–3 December 2004; Volume 1, pp. 372–376. [Google Scholar]
- Baskar, S.; Suganthan, P.N. A Novel Concurrent Particle Swarm Optimization. In Proceedings of the Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 1, pp. 792–796. [Google Scholar]
- Kennedy, J.; Eberhart, R. A Discrete Binary Version of the Particle Swarm Optimization. In Proceedings of the International Conference on Neural Network, Perth, Australia, 12–15 October 1997; Volume 4, pp. 4104–4107. [Google Scholar]
- Kennedy, J. Bare Bones Particle Swarms. In Proceedings of the IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 26 April 2003; IEEE Press: Piscataway, NJ, USA, 2003; pp. 80–87. [Google Scholar]
- Mendes, R.; Kennedy, J.; Neves, J. The Fully Informed Particle Swarm: Simpler, maybe Better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Cervantes, A.; lsasi, P.; Galvan, I. Binary Particle Swarm Optimization in Classification. Neural Netw. World 2005, 15, 229–241. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation CEC2001, Seoul, Korea, 27–30 May 2001; IEEE Press Los Alamitos, COEX, World Trade Center: Seoul, Korea, 2001; pp. 101–106. [Google Scholar]
- Ghandi Bashir, M.; Nagarajan, R.; Desa, H. Classification of Facial Emotions using Guided Particle Swarm Optimization I. Int. J. Comput. Commun. Technol. 2009, 1, 36–46. [Google Scholar]
- Tanweer, M.R.; Suresh, S.; Sundararajan, N. Self regulating particle swarm optimization algorithm. Inf. Sci. 2015, 294, 182–202. [Google Scholar] [CrossRef]
- Hwang, S.K.; Koo, K.; Lee, J.S. Homogeneous Particle Swarm Optimizer for Multi-Objective Optimization Problem. 2001. Available online: www.icgst.com (accessed on 21 September 2021).
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization. In Proceedings of the Congress on Evolutionary Computation (CEC’2002), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Mohamed, A.W.; Zaher, H.; Korshid, M. A particle swarm approach for solving stochastic optimization problems. Applied. Math. Inf. Sci. 2011, 5, 379–401. [Google Scholar]
- Bansal, J.C.; Deep, K. A Modified Binary Particle Swarm Optimization for Knapsack Problems. Appl. Math. Comput. 2012, 218, 11042–11061. [Google Scholar] [CrossRef]
- Rahmani, R.; Othman, M.F.; Yusof, R.; Khalid, M. Solving Economic Dispatch Problem using Particle Swarm Optimization by an Evolutionary Technique for Initializing Particles. J. Theor. Appl. Inf. Technol. 2012, 46, 526–536. [Google Scholar]
- Neshat, M.; Yazdi, S.F. A New Cooperative Algorithm Based on PSO and K-Means for Data Clustering. J. Comput. Sci. 2012, 8, 188–194. [Google Scholar]
- Kanoh, H.; Chen, S. Particle Swarm Optimization with Transition Probability for Timetabling Problems. In Adaptive and Natural Computing Algorithms; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7824, pp. 256–264. [Google Scholar]
- Garsva, G.; Danenas, P. Particle Swarm Optimization for Linear Support Vector Machines Based Classifier Selection. Nonlinear Anal.: Model. Control 2014, 19, 26–42. [Google Scholar] [CrossRef]
- Li, X.; Wu, D.; He, J.; Bashir, M.; Liping, M. An Improved Method of Particle Swarm Optimization for Path Planning of Mobile Robot. J. Control. Sci. Eng. 2020, 2020, 3857894. [Google Scholar] [CrossRef]
- Hoang, T.T.; Cho, M.-Y.; Alam, M.N.; Vu, Q.T. A novel differential particle swarm optimization for parameter selection of support vector machines for monitoring metal-oxide surge arrester conditions. Swarm Evol. Comput. 2018, 38, 120–126. [Google Scholar] [CrossRef]
- Karakuzu, C.; Karakaya, F.; Çavuşlu, M.A. FPGA implementation of neuro-fuzzy system with improved PSO learning. Neural Netw. 2016, 79, 128–140. [Google Scholar] [CrossRef]
- Liao, C.-L.; Lee, S.-J.; Chiou, Y.-S.; Lee, C.-R.; Lee, C.-H. Power consumption minimization by distributive particle swarm optimization for luminance control and its parallel implementations. Expert Syst. Appl. 2018, 96, 479–491. [Google Scholar] [CrossRef]
- Li, J.; Sun, Y.; Hou, S. Particle Swarm Optimization Algorithm with Multiple Phases for Solving Continuous Optimization Problems. Discret. Dyn. Nat. Soc. 2021, 2021, 8378579. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. Empirical Study of Particle Swarm Optimization. In Proceedings of the Congress on Evolutionary Computation, CEC 99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Krohling, R.A.; Coelho, L.D.S. PSO-E: Particle Swarm with Exponential Distribution. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1428–1433. [Google Scholar]
- Feng, C.S.; Cong, S.; Feng, X.Y. A New Adaptive Inertia Weight Strategy in Particle Swarm Optimization. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Singapore, 25–28 September 2007; pp. 4186–4190. [Google Scholar]
- Qin, Z.; Yu, F.; Shi, Z.; Wang, Y. Adaptive Inertia Weight Particle Swarm Optimization. In Artificial Intelligence and Soft Computing—ICAISC; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4029, pp. 450–459. [Google Scholar]
- Jiao, B.; Lian, Z.; Gu, X. A Dynamic Inertia Weight Particle Swarm Optimization Algorithm. Chaos Solut. Fractals 2008, 37, 698–706. [Google Scholar] [CrossRef]
- Deep, K.; Arya, M.; Bansal, J.C. A non-deterministic adaptive inertia weight in PSO. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; pp. 1155–1162. [Google Scholar]
- Deep, K.; Chauhan, P.; Pant, M. A New Fine Grained Inertia Weight Particle Swarm Optimization. In Proceedings of the IEEE, World Congress on Information and Communication Technologies (WICT-2011), Mumbai, India, 11–14 December 2011; pp. 430–435. [Google Scholar]
- Isiet, M.; Gadala, M. Sensitivity analysis of control parameters in particle swarm optimization. J. Comput. Sci. 2020, 41, 101086. [Google Scholar] [CrossRef]
- Deep, K.; Bansal, J.C. Hybridization of Particle Swarm Optimization with Quadratic Approximation. Opsearch 2009, 46, 3–24. [Google Scholar] [CrossRef]
- Bao, M.; Zhang, H.; Wu, H.; Zhang, C.; Wang, Z.; Zhang, X. Multiobjective Optimal Dispatching of Smart Grid Based on PSO and SVM. Mob. Inf. Syst. 2022, 2022, 2051773. [Google Scholar] [CrossRef]
- Liua, H.; Caia, Z.; Wang, Y. Hybridizing Particle Swarm Optimization with Differential Evolution for Constrained Numerical and Engineering Optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Pu, Q.; Gan, J.; Qiu, L.; Duan, J.; Wang, H. An efficient hybrid approach based on PSO, ABC and k-means for cluster analysis. Multimed. Tools Appl. 2021, 81, 19321–19339. [Google Scholar] [CrossRef]
- Mao, Y.; Qin, G.; Ni, P.; Liu, Q. Analysis of road traffic speed in Kunming plateau mountains: A fusion PSO-LSTM algorithm. Int. J. Urban Sci. 2022, 26, 87–107. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.; Singh, S.B. HPSO: A New Version of Particle Swarm Optimization Algorithm. J. Artif. Intell. 2012, 3, 123–134. [Google Scholar]
- Ankita; Sahana, S.K. Ba-PSO: A Balanced PSO to solve multi-objective grid scheduling problem. Appl. Intell. 2022, 52, 4015–4027. [Google Scholar] [CrossRef]
- Song, Y.; Zhu, M.; Wei, N.; Deng, L. Regression analysis of friction resistance coefficient under different support methods of roadway based on PSO-SVM. J. Phys. Conf. Ser. 2021, 1941, 012046. [Google Scholar] [CrossRef]
- Yang, P. Forecasting Model of Number of Entrepreneurs in Colleges and Universities Based on PSO Algorithm. Cyber Secur. Intell. Anal. 2022, 123, 351–358. [Google Scholar] [CrossRef]
- Pozna, C.; Precup, R.-E.; Horvath, E.; Petriu, E.M. Hybrid Particle Filter-Particle Swarm Optimization Algorithm and Application to Fuzzy Controlled Servo Systems. IEEE Trans. Fuzzy Syst. 2022, 1. [Google Scholar] [CrossRef]
- Nasab, H.H.; Emami, L. A Hybrid Particle Swarm Optimization for Dynamic Facility Layout Problem. Int. J. Prod. Res. 2013, 51, 4325–4334. [Google Scholar] [CrossRef]
- Esmin, A.A.A.; Matwin, S. HPSOM: A Hybrid Particle Swarm Optimization Algorithm with Genetic Mutation. Int. J. Innov. Comput. Inf. Control. 2013, 9, 1919–1934, ISSN 1349-4198. [Google Scholar]
- Abd-Elazim, S.M.; Ali, E.S. A Hybrid Particle Swarm Optimization and Bacterial Foraging for Power System Stability Enhancement. Complexity 2014, 21, 245–255. [Google Scholar] [CrossRef]
- Enireddy, V.; Kumar, R.K. Improved cuckoo search with particle swarm optimization for classification of compressed images. Sadhana 2015, 40, 2271–2285. [Google Scholar] [CrossRef] [Green Version]
- Garg, H. A Hybrid PSO-GA Algorithm for Constrained Optimization Problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.B. Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer for Improving Convergence Performance. J. Appl. Math. 2017, 2017, 2030489. [Google Scholar] [CrossRef]
- Al-Thanoon, N.A.; Qasim, O.S.; Algamal, Z.Y. A new hybrid firefly algorithm andparticle swarm optimization for tuning parameter estimation in penalized supportvector machine with application in chemometrics. Chemom. Intell. Lab. Syst. 2019, 184, 142–152. [Google Scholar] [CrossRef]
- Khan, A.; Hizam, H.; Bin Abdul Wahab, N.I.; Lutfi Othman, M. Optimal power flow using hybrid firefly and particle swarm optimization algorithm. PLoS ONE 2020, 15, e0235668. [Google Scholar] [CrossRef]
- Bai, Q. Analysis of Particle Swarm Optimization Algorithm. Comput. Inf. Sci. 2010, 3, 180–184. [Google Scholar] [CrossRef] [Green Version]
| Name of Algorithm | Year | Description | Ref. No. |
|---|---|---|---|
| Artificial hummingbird algorithm | 2022 | Zhao et al. proposed an artificial hummingbird algorithm (AHA) to tackle optimization problems and proved its effectiveness over other metaheuristics with experimental results. | [1] |
| Chimp Optimization Algorithm (Khishe and Mosavi (2020a)) | 2022 | Jia et al. presented an enhanced chimp optimization algorithm (EChOA) and analyzed its performance on 12 classical benchmark functions and 15 CEC2017 benchmark functions. | [2] |
| Rat swarm optimization (Dhiman et al. (2021)) | 2021 | Dhiman et al. presents swarm-based rat swarm optimization and tested its performance on unimodal, multimodal and CEC-15 special session benchmark functions. | [3] |
| African Vulture’s Optimization Algorithm (Abdollahzadeh et al. (2021) | 2021 | A new metaheuristics, namely African Vulture’s Optimization Algorithm (AVOA) is proposed by Abdollahzadeh et al. They proved it as a best algorithm on 30 out of 36 benchmark functions. | [4] |
| Dragonfly optimization | 2021 | Bhardwaj and Kim proposed dragonfly node identification algorithm (DNIA) and evaluated its robustness and efficiency using statistical analysis, convergence rate analysis, Wilcoxon test, Friedman rank test, and analysis of variance on classical as well as modern IEEE CEC 2014 benchmark functions. | [5] |
| Horse herd optimization algorithm | 2021 | In order to solve high dimensional optimization techniques, MiarNaeimi et al. developed a new meta-heuristic algorithm called the Horse herd Optimization Algorithm (HOA).Through statistical results, they demonstrated the merits of their proposed algorithm. | [6] |
| Gaining-sharing knowledge-based algorithm | 2020 | Mohamed et al. proposed a gaining-sharing knowledge-based algorithm and proved it was better by completing experiments on various problems, along with CEC 2017 benchmark functions. | [7] |
| Coronavirus optimization algorithm | 2020 | Martinez-Alvarez et al. introduced a novel bio-inspired metaheuristic, based on the coronavirus behavior. They elaborated major advantages of coronavirus optimization algorithm compared to other similar strategies. | [8] |
| Harris Hawks Optimization | 2019 | Heidari et al. proposed a novel paradigm called Harris Hawks Optimizer (HHO), and tested it on 29 benchmark problems and several real-world engineering problems | [9] |
| African Buffalo Optimization | 2015 | Odili et al. developed a novel optimization technique, namely the African Buffalo Optimization (ABO) and checked its validation on a number of benchmark Traveling Salesman Problems. Authors recommended to use ABO to solve knapsack problems. | [10] |
| Notation | Name of Component | Contribution of the Component in Updating the Velocity |
|---|---|---|
| Momentum part | It serves as a memory of the immediate past flight as it uses the previous velocity. It is also taken to be inertia component that makes a balance between the exploration and exploitation of each particle in search space. | |
| Cognitive part | This cognitive part drives the particles to their own best position and is equivalent to the distance of the particle from its personal best position till now. | |
| Social Part | This is the social component of the velocity equation that drives the particle to the best position determined by the swarm. |
| Values of Acceleration Coefficients | Impact of Acceleration Coefficients | Corresponding Change in Velocity Update Equation (1) |
|---|---|---|
| c1 = c2 = 0 | In this case, the particle moves on with the same current speed till it reaches the boundary of the search space as its velocity is independent from the impact of personal best and global best position. | |
| c1 > 0 and c2 = 0 | Here, the social component of the velocity does not influence the particle’s velocity and particle will move in the global search space according to its own best position. | |
| c1 = 0 and c2 > 0 | Here, the cognitive component of the velocity does not influence the particle’s velocity and particle will move in the global search space according to its neighbor’s best position. | |
| c1 = c2 | The particle is attracted towards the average of both pbest and gbest position. | |
| c1 >> c2 | Here, the personal best position will generally effect the particle’s velocity more, that leads to excessive wandering in the search space. | |
| c1 << c2 | Here, the best position of other members of the swarm has more impact on particle’s velocity that leads to pre mature convergence. | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. https://doi.org/10.3390/app12178392
Jain M, Saihjpal V, Singh N, Singh SB. An Overview of Variants and Advancements of PSO Algorithm. Applied Sciences. 2022; 12(17):8392. https://doi.org/10.3390/app12178392
Chicago/Turabian StyleJain, Meetu, Vibha Saihjpal, Narinder Singh, and Satya Bir Singh. 2022. "An Overview of Variants and Advancements of PSO Algorithm" Applied Sciences 12, no. 17: 8392. https://doi.org/10.3390/app12178392
APA StyleJain, M., Saihjpal, V., Singh, N., & Singh, S. B. (2022). An Overview of Variants and Advancements of PSO Algorithm. Applied Sciences, 12(17), 8392. https://doi.org/10.3390/app12178392






