Regional Analysis of Hotspot and Coldspot Areas Undergoing Nonstationary Drought Characteristics in a Changing Climate
Abstract
:1. Introduction
2. Materials and Methods
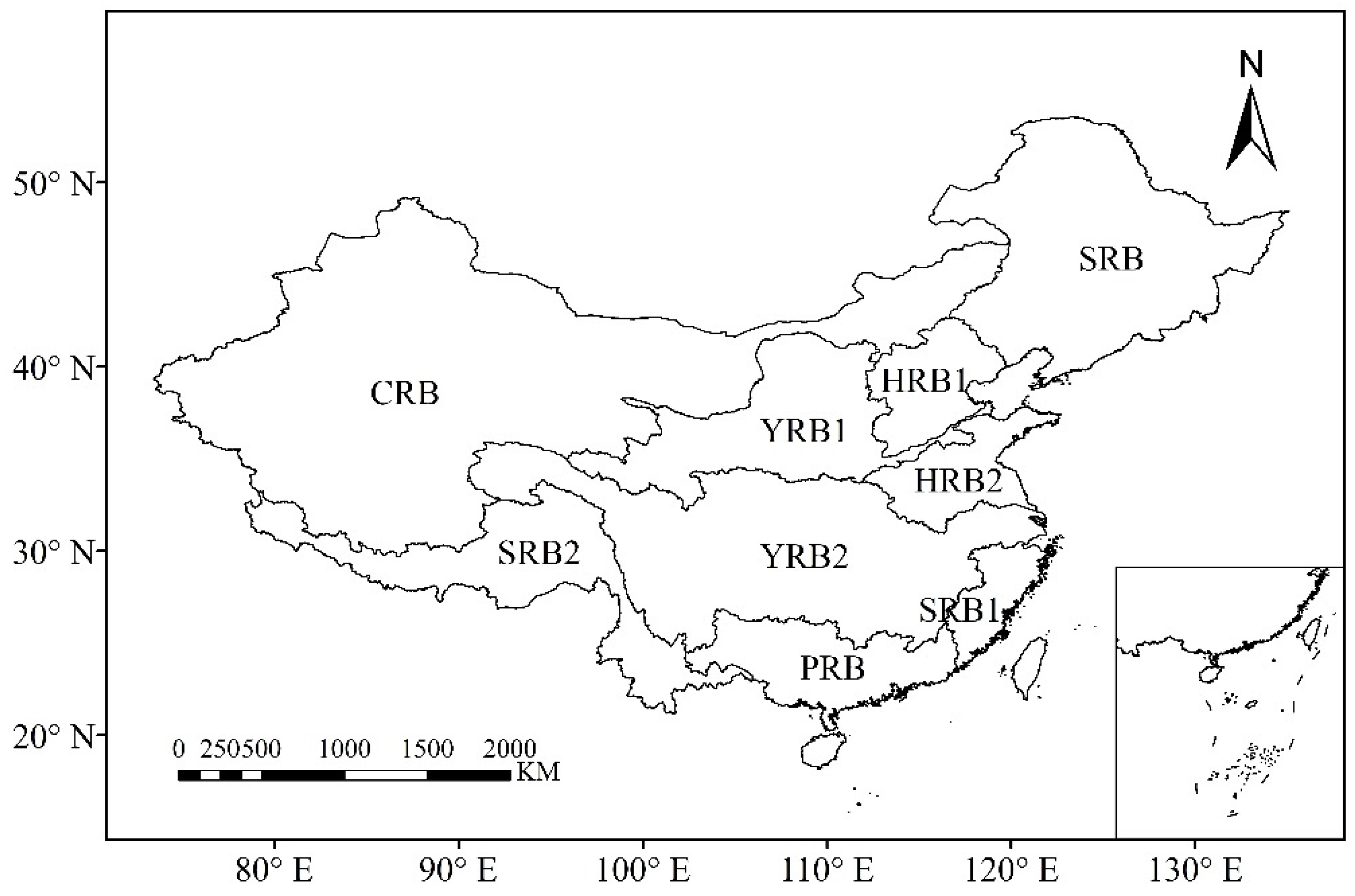
2.1. Study Area
2.2. Meteorological Data
2.3. Trend Analysis
2.4. Standardized Precipitation Evapotranspiration Index (SPEI)
- (a)
- Calculation of the PET; the monthly PET (mm) is obtained by;
- (b)
- (Calculation of the water balance Di, which is the difference between the monthly total precipitation and monthly PET:
- (c)
- Calculation of the cumulative difference in the mth month (January, February, and December) in n years is calculated:
- (d)
- Fitting of the cumulative D series using a probability density function. The general optimal distribution of the SPEI has not been specified [50]. To fit the GAMLSS model in R, a two-parameter distribution in the GAMLSS family in R, called logistic distribution, was used in this study ()).
- (e)
- Fitting of the cumulative probability of the D series under a particular time-scale is fitted. By transforming the cumulative probability density into a standard normal distribution with a mean of zero and variance of one, the SPEI can be obtained.
2.5. GAMLSS Approach
2.6. Nonstationary Standardized Precipitation Evapotranspiration Index (NSPEI)
3. Results
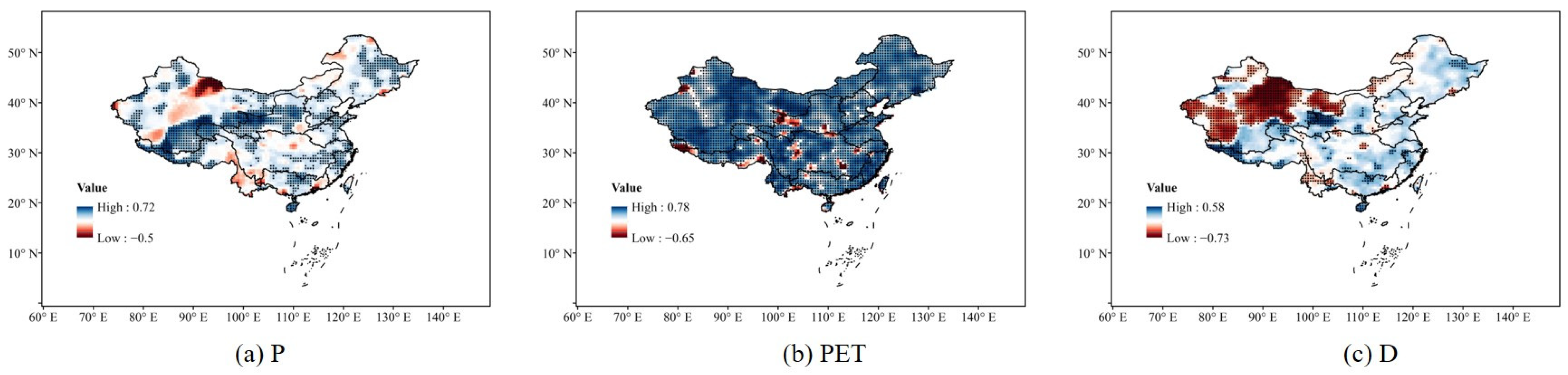
3.1. Spatial and Temporal Distribution of Long-Term Trends in Meteorological Variables
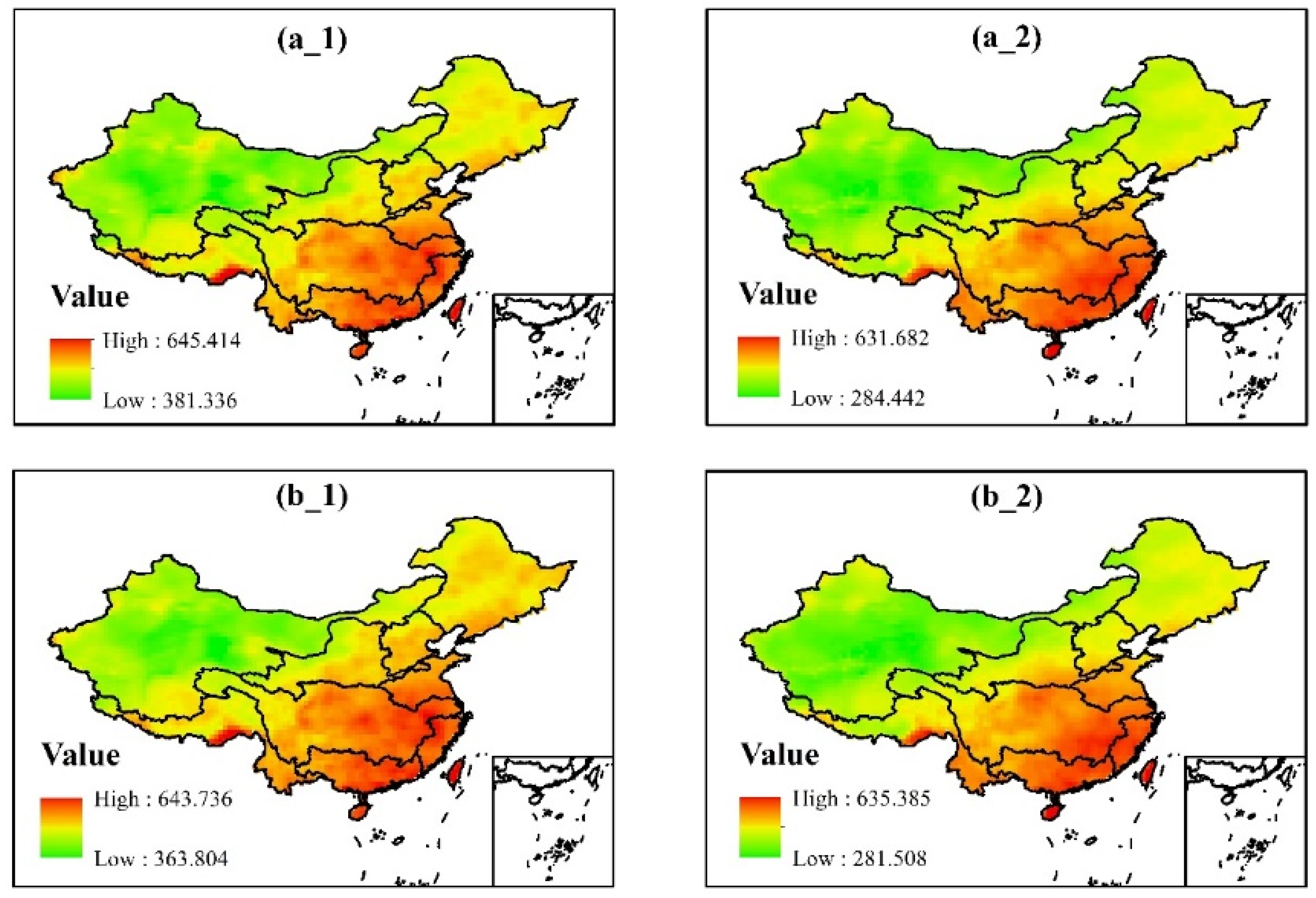
3.2. Performances of Nonstationary and Stationary Models
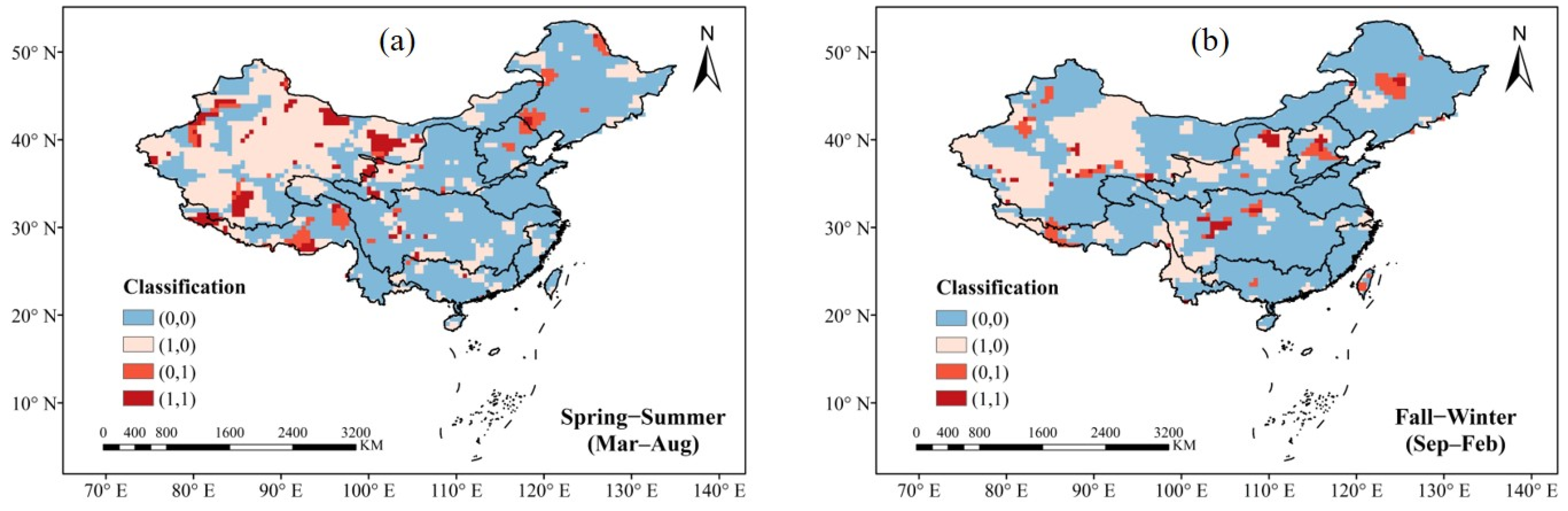
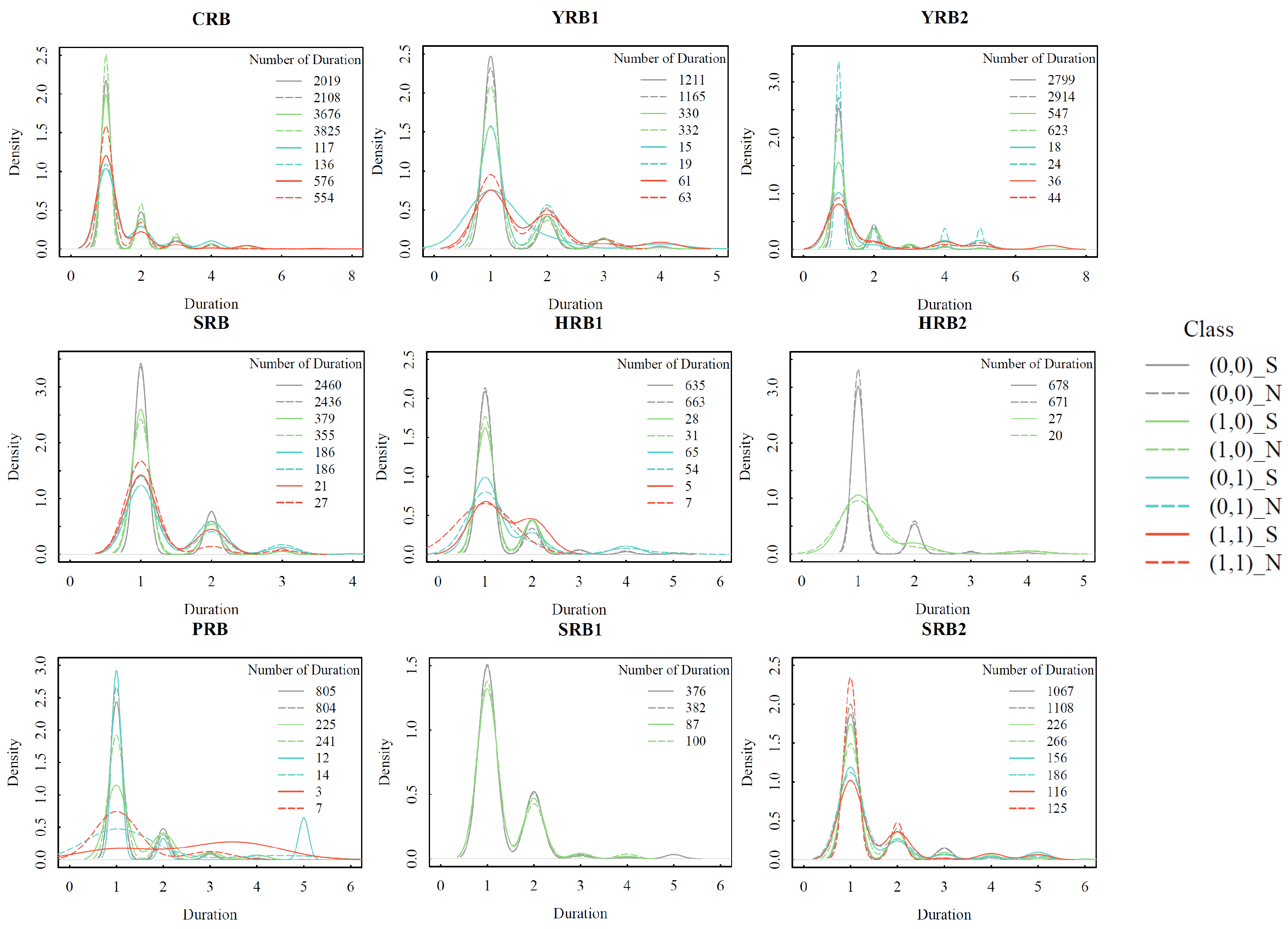
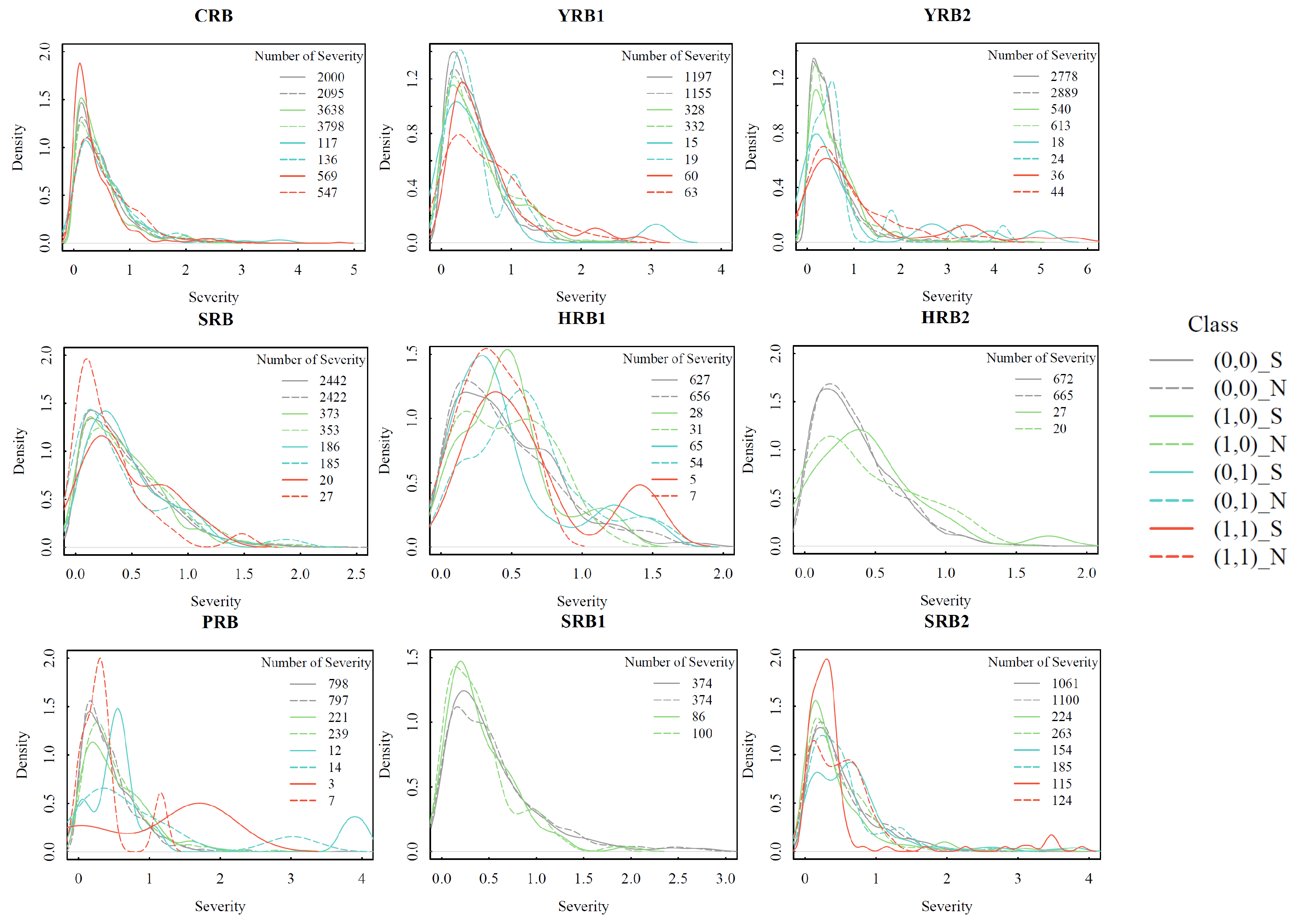
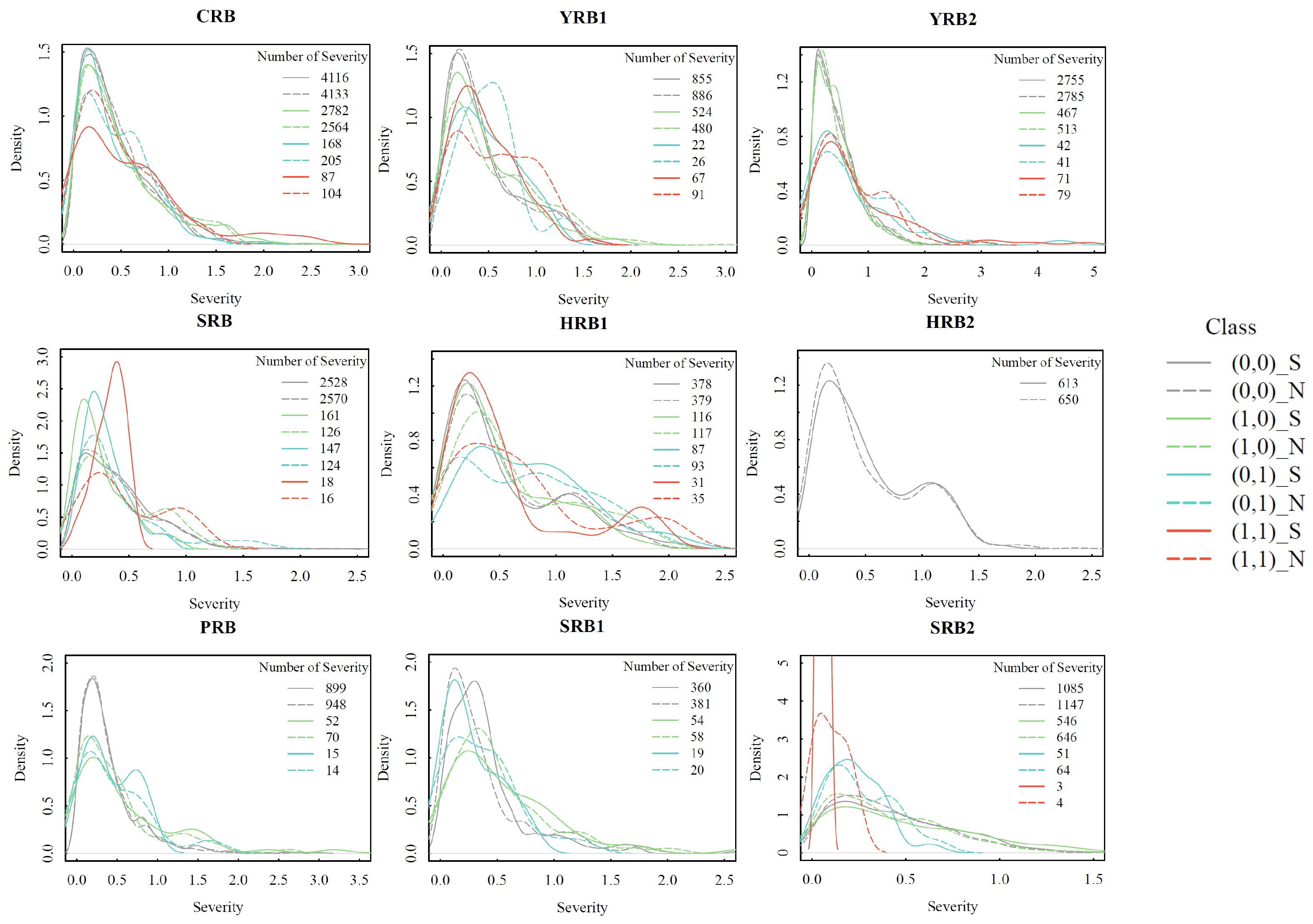
3.3. Nonstationary Hotspot Response Areas
3.4. Comparison of Nonstationary and Stationary Drought Characteristics in China
4. Discussion and Conclusions
- (1)
- During the period 1979–2020, both precipitation and evapotranspiration showed an increasing trend. The results of the D series showed that a drier tendency in Northwest China can be found;
- (2)
- Northwest China (CRB) was the main nonstationary hotspot response areas with changes in distribution parameters;
- (3)
- The stationary SPEI incorrectly identified more severe droughts as less severe, which caused the under-estimation of the severity of droughts in a changing climate;
- (4)
- Drought warnings should focus on Northwest and Southwest China; the former and latter were under-estimated in the spring–summer and the fall–winter seasons, respectively, under the current stationary drought index assessment system.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, T. Drought over East Asia: A review. J. Clim. 2015, 28, 3375–3399. [Google Scholar] [CrossRef]
- Yang, J.; Gong, D.; Wang, W.; Hu, M.; Mao, R. Extreme drought event of 2009/2010 over southwestern China. Meteorol. Atmos. Phys. 2012, 115, 173–184. [Google Scholar] [CrossRef]
- Guo, E.; Liu, X.; Zhang, J.; Wang, Y.; Wang, C.; Wang, R.; Li, D. Assessing spatiotemporal variation of drought and its impact on maize yield in Northeast China. J. Hydrol. 2017, 553, 231–247. [Google Scholar] [CrossRef]
- Das, S.; Das, J.; Umamahesh, N.V. Nonstationary modeling of meteorological droughts: Application to a region in India. J. Hydrol. Eng. 2021, 26, 05020048. [Google Scholar] [CrossRef]
- Soľáková, T.; De Michele, C.; Vezzoli, R. Comparison between parametric and nonparametric approaches for the calculation of two drought indices: SPI and SSI. J. Hydrol. Eng. 2014, 19, 04014010. [Google Scholar] [CrossRef]
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 8, 1149–1166. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Huang, S.; Li, P.; Huang, Q.; Leng, G.; Hou, B.; Ma, L. The propagation from meteorological to hydrological drought and its potential influence factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Cai, H.; Zhou, Z.; Sun, Y.; Shi, H. Propagation of meteorological to hydrological drought for different climate regions in China. J. Environ. Manag. 2021, 283, 111980. [Google Scholar] [CrossRef]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Mannocchi, F.; Todisco, F.; Vergni, L. Agricultural drought: Indices, definition and analysis. In International Symposium on Basis of Civilization—Water Science; International Association of Hydrological Science: Rome, Italy, 2004. [Google Scholar]
- Edwards, B.; Gray, M.; Hunter, B. The social and economic impacts of drought. Aust. J. Soc. Issues 2019, 54, 22–31. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Silver Sprin, MD, USA, 1965; Volume 30.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Zarch, M.A.A.; Sivakumar, B.; Sharma, A. Droughts in a warming climate: A global assessment of Standardized Precipitation Index (SPI) and Reconnaissance Drought Index (RDI). J. Hydrol. 2015, 526, 183–195. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Tang, X.; Duan, Q.; He, X. A nonparametric standardized runoff index for characterizing hydrological drought on the Loess Plateau, China. Glob. Planet. Chang. 2018, 161, 53–65. [Google Scholar] [CrossRef]
- Shafer, B.A.; Dezman, L.E. Development of surface water supply index (SWSI) to assess the severity of drought condition in snowpack runoff areas. In Proceedings of the Western Snow Conference, Reno, Nevada, 19–23 April 1982. [Google Scholar]
- Palmer, W.C. Keeping track of crop moisture conditions, nationwide: The new crop moisture index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Sohrabi, M.M.; Ryu, J.H.; Abatzoglou, J.; Tracy, J. Development of soil moisture drought index to characterize droughts. J. Hydrol. Eng. 2015, 20, 04015025. [Google Scholar] [CrossRef]
- Bushra, N.; Rohli, R.V.; Lam, N.S.N.; Zou, L.; Mostafiz, R.B.; Mihunov, V. The relationship between the normalized difference vegetation index and drought indices in the South Central United States. Nat. Hazards 2019, 96, 791–808. [Google Scholar] [CrossRef]
- Guo, X.; Gao, W.; Richard, P.; Lu, Y.; Zheng, Y.; Pietroniro, E. Canadian prairie drought assessment through MODIS vegetation indices. In Remote Sensing and Modeling of Ecosystems for Sustainability; SPIE: Bellingham, WA, USA, 2004; Volume 5544, pp. 149–158. [Google Scholar]
- Yan, X.; Lin, M.; Chen, X.; Yao, H.; Liu, C.; Lin, B. A new method to restore the impact of land-use change on flood frequency based on the Hydrologic Engineering Center-Hydrologic Modelling System model. Land Degrad. Dev. 2020, 31, 1520–1532. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, S.; Ren, L.; Xu, C.; Wei, L.; Cui, H.; Yuan, F.; Liu, Y.; Yang, X. The development of a nonstationary standardised streamflow index using climate and reservoir indices as covariates. Water Resour. Manag. 2022, 36, 1377–1392. [Google Scholar] [CrossRef]
- Zhang, T.; Su, X.; Feng, K. The development of a novel nonstationary meteorological and hydrological drought index using the climatic and anthropogenic indices as covariates. Sci. Total Environ. 2021, 786, 147385. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. C Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Song, Z.; Xia, J.; She, D.; Zhang, L.; Hu, C.; Zhao, L. The development of a Nonstationary Standardized Precipitation Index using climate covariates: A case study in the middle and lower reaches of Yangtze River Basin, China. J. Hydrol. 2020, 588, 125115. [Google Scholar] [CrossRef]
- Sun, X.; Li, Z.; Tian, Q. Assessment of hydrological drought based on nonstationary runoff data. Hydrol. Res. 2020, 51, 894–910. [Google Scholar] [CrossRef]
- Russo, S.; Dosio, A.; Sterl, A.; Barbosa, P.; Vogt, J. Projection of occurrence of extreme dry-wet years and seasons in Europe with stationary and nonstationary Standardized Precipitation Indices. J. Geophys. Res. Atmos. 2013, 118, 7628–7639. [Google Scholar] [CrossRef]
- Shiau, J. Effects of gamma-distribution variations on SPI-Based stationary and nonstationary drought analyses. Water Resour. Manag. 2020, 34, 2081–2095. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Feng, P.; Hu, R. A time-dependent drought index for non-stationary precipitation series. Water Resour. Manag. 2015, 29, 5631–5647. [Google Scholar] [CrossRef]
- Ju, X.; Wang, Y.; Wang, D.; Singh, V.P.; Xu, P.; Wu, J.; Ma, T.; Liu, J.; Zhang, J. A time-varying drought identification and frequency analyzation method: A case study of Jinsha River Basin. J. Hydrol. 2021, 603, 126864. [Google Scholar] [CrossRef]
- Zou, L.; Xia, J.; Ning, L.; She, D.; Zhan, C. Identification of hydrological drought in Eastern China using a time-dependent drought index. Water 2018, 10, 315. [Google Scholar] [CrossRef]
- Kang, L.; Jiang, S. Bivariate frequency analysis of hydrological drought using a nonstationary standardized streamflow index in the Yangtze river. J. Hydrol. Eng. 2019, 24, 05018031. [Google Scholar] [CrossRef]
- Bazrafshan, J.; Hejabi, S. A non-stationary reconnaissance drought index (NRDI) for drought monitoring in a changing climate. Water Resour. Manag. 2018, 32, 2611–2624. [Google Scholar] [CrossRef]
- Li, J.Z.; Wang, Y.X.; Li, S.F.; Hu, R. A nonstationary standardized precipitation index incorporating climate indices as covariates. J. Geophys. Res. Atmos. 2015, 120, 12082–12095. [Google Scholar] [CrossRef]
- Masanta, S.K.; Srinivas, V.V. Proposal and evaluation of nonstationary versions of SPEI and SDDI based on climate covariates for regional drought analysis. J. Hydrol. 2022, 610, 127808. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, L.; Liu, T.; Li, J.; Feng, P. A non-stationary standardized streamflow index for hydrological drought using climate and human-induced indices as covariates. Sci. Total Environ. 2020, 699, 134278. [Google Scholar] [CrossRef]
- CPC Global Unified Gauge-Based Analysis of Daily Precipitation. Available online: https://psl.noaa.gov/data/gridded/data.cpc.globalprecip.html (accessed on 9 August 2020).
- CPC Global Unified Temperature. Available online: https://psl.noaa.gov/data/gridded/data.cpc.globaltemp.html (accessed on 9 August 2020).
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin Charles: London, UK, 1975; Volume 120. [Google Scholar]
- Gu, X.; Zhang, Q.; Singh, V.P.; Shi, P. Nonstationarity in timing of extreme precipitation across China and impact of tropical cyclones. Glob. Planet. Chang. 2017, 149, 153–165. [Google Scholar] [CrossRef]
- Oliveira, P.T.; Santos e Silva, C.M.; Lima, K.C. Climatology and trend analysis of extreme precipitation in subregions of Northeast Brazil. Theor. Appl. Climatol. 2017, 130, 77–90. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Yimer, E.A.; Van Schaeybroeck, B.; Van de Vyver, H.; Van Griensven, A. Evaluating probability distribution functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere 2022, 13, 364. [Google Scholar] [CrossRef]
- Cole, T.J.; Green, P.J. Smoothing reference centile curves: The LMS method and penalized likelihood. Stat. Med. 1992, 11, 1305–1319. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. A semi-parametric additive model for variance heterogeneity. Stat. Comput. 1996, 6, 57–65. [Google Scholar] [CrossRef]
- Rigby, B.S.; Harley, R.G. The development of an advanced series compensator based on a single voltage source inverter. In Proceedings of the IEEE AFRICON′96, Stellenbosch, South Africa, 27 September 1996; pp. 215–220. [Google Scholar]
- Akaike, H. Citation classic—A new look at the statistical-model identification. Curr. Contents/Eng. Technol. Appl. Sci. 1981, 51, 22. [Google Scholar]
- Sun, J.; Ao, J. Changes in precipitation and extreme precipitation in a warming environment in China. Sci. Bull. 2013, 58, 1395–1401. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.; Wen, J.; Xu, M.; Tan, J. Changing characteristics of precipitation in China during 1960–2012. Int. J. Climatol. 2016, 36, 1387–1402. [Google Scholar] [CrossRef]
- Mavromatis, T. Drought index evaluation for assessing future wheat production in Greece. Int. J. Climatol. 2007, 27, 911–924. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Changes in drought characteristics over China using the standardized precipitation evapotranspiration index. J. Clim. 2015, 28, 5430–5447. [Google Scholar] [CrossRef]


| Threshold Value | Description |
|---|---|
| SPEI > −0.50 | Normal |
| −1.00 < SPEI ≤ −0.50 | Mild drought |
| −1.50 < SPEI ≤ −1.00 | Moderate drought |
| −2.00 < SPEI ≤ −1.50 | Severe drought |
| SPEI ≤ −2.00 | Extreme drought |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Yoon, H.-C.; Lee, J.-H.; Kim, J.-S. Regional Analysis of Hotspot and Coldspot Areas Undergoing Nonstationary Drought Characteristics in a Changing Climate. Appl. Sci. 2022, 12, 8479. https://doi.org/10.3390/app12178479
Wu D, Yoon H-C, Lee J-H, Kim J-S. Regional Analysis of Hotspot and Coldspot Areas Undergoing Nonstationary Drought Characteristics in a Changing Climate. Applied Sciences. 2022; 12(17):8479. https://doi.org/10.3390/app12178479
Chicago/Turabian StyleWu, Dian, Hyeon-Cheol Yoon, Joo-Heon Lee, and Jong-Suk Kim. 2022. "Regional Analysis of Hotspot and Coldspot Areas Undergoing Nonstationary Drought Characteristics in a Changing Climate" Applied Sciences 12, no. 17: 8479. https://doi.org/10.3390/app12178479
APA StyleWu, D., Yoon, H.-C., Lee, J.-H., & Kim, J.-S. (2022). Regional Analysis of Hotspot and Coldspot Areas Undergoing Nonstationary Drought Characteristics in a Changing Climate. Applied Sciences, 12(17), 8479. https://doi.org/10.3390/app12178479








