A Differential Subgrid Stress Model and Its Assessment in Large Eddy Simulations of Non-Premixed Turbulent Combustion
Abstract
:1. Introduction
2. Subgrid Stress Tensor Equation Closure and Calibration
2.1. Subgrid Stress Tensor Equation
2.2. Closure
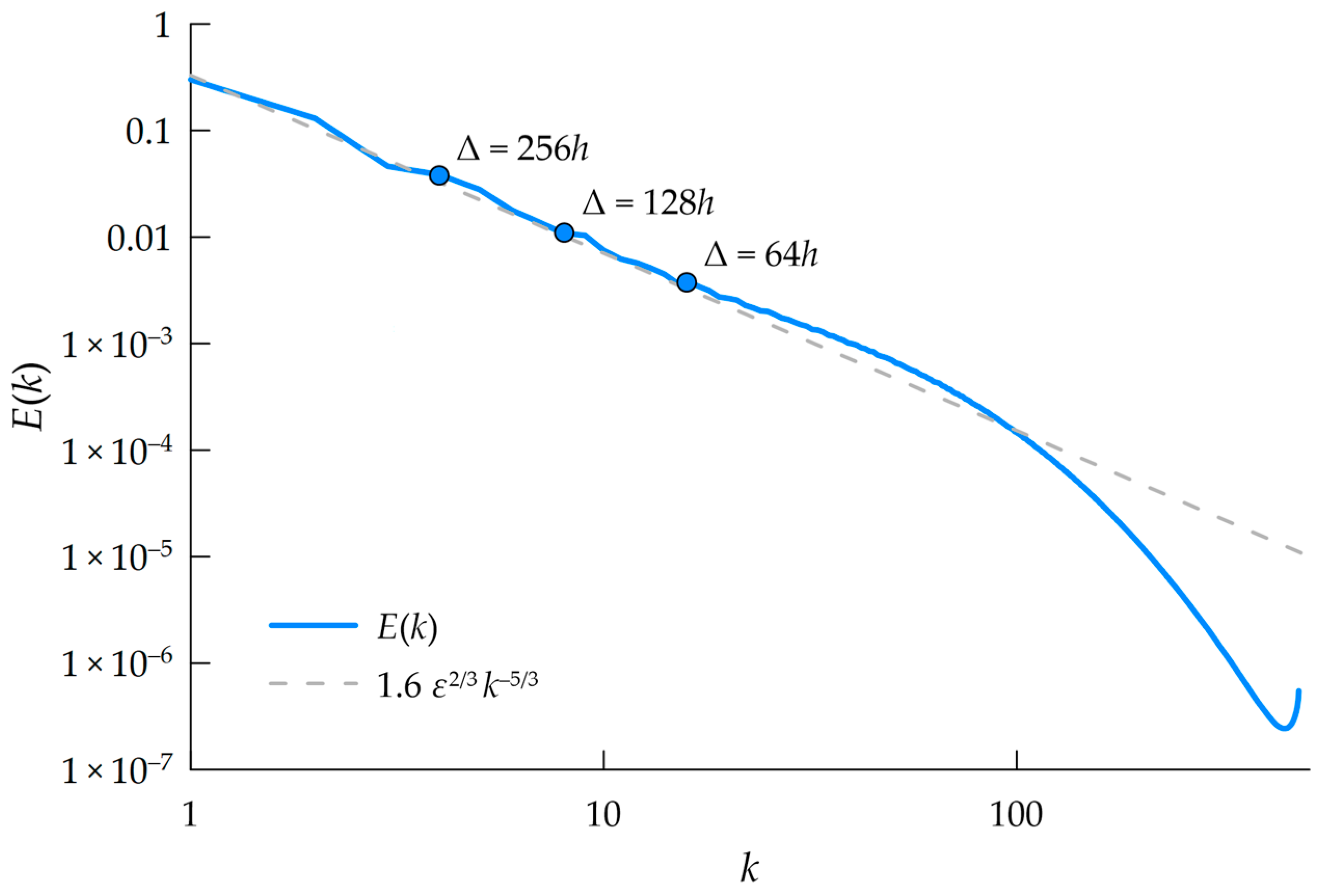
2.3. DNS Database and Filtering
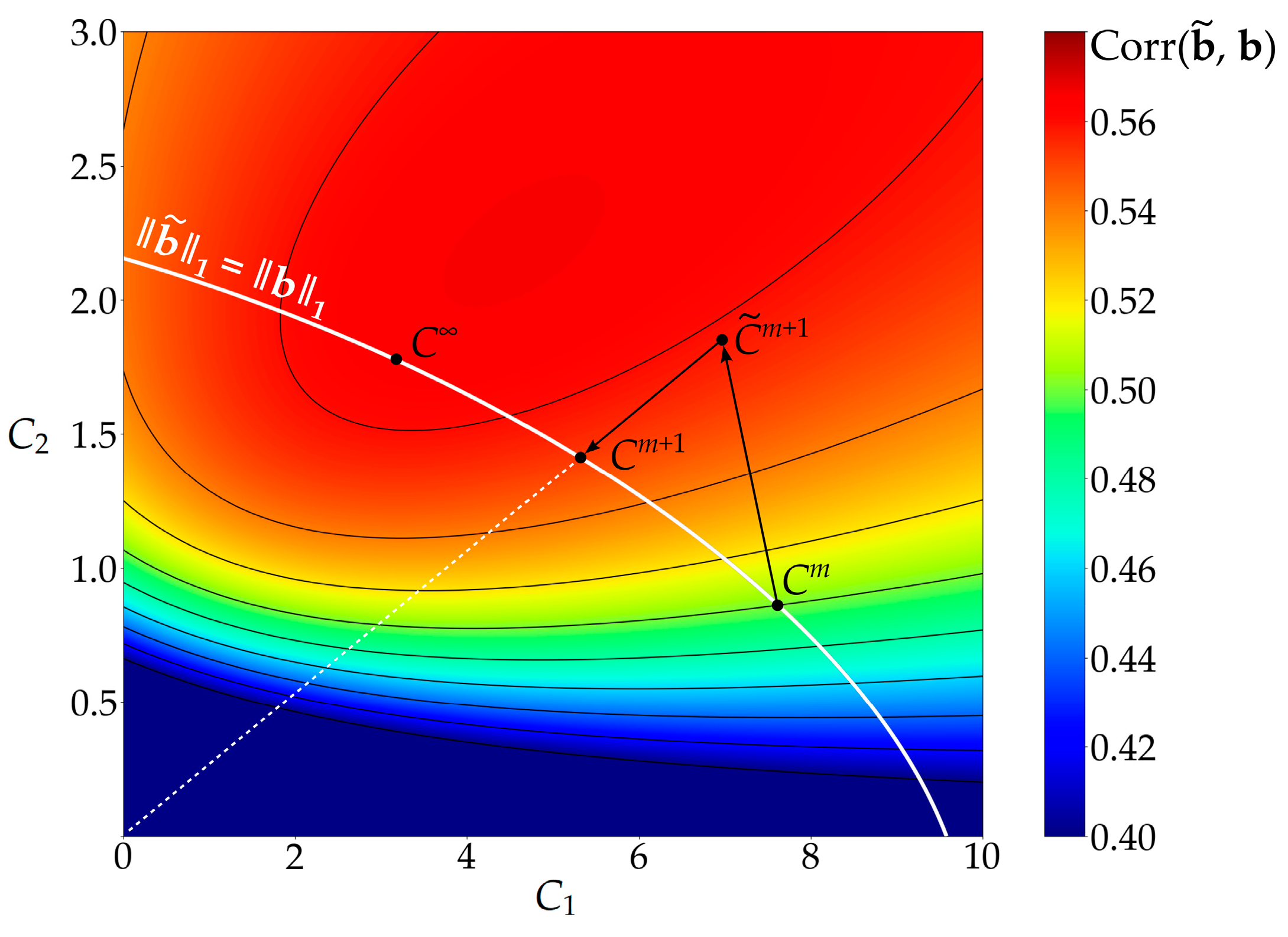
2.4. Calibration Method
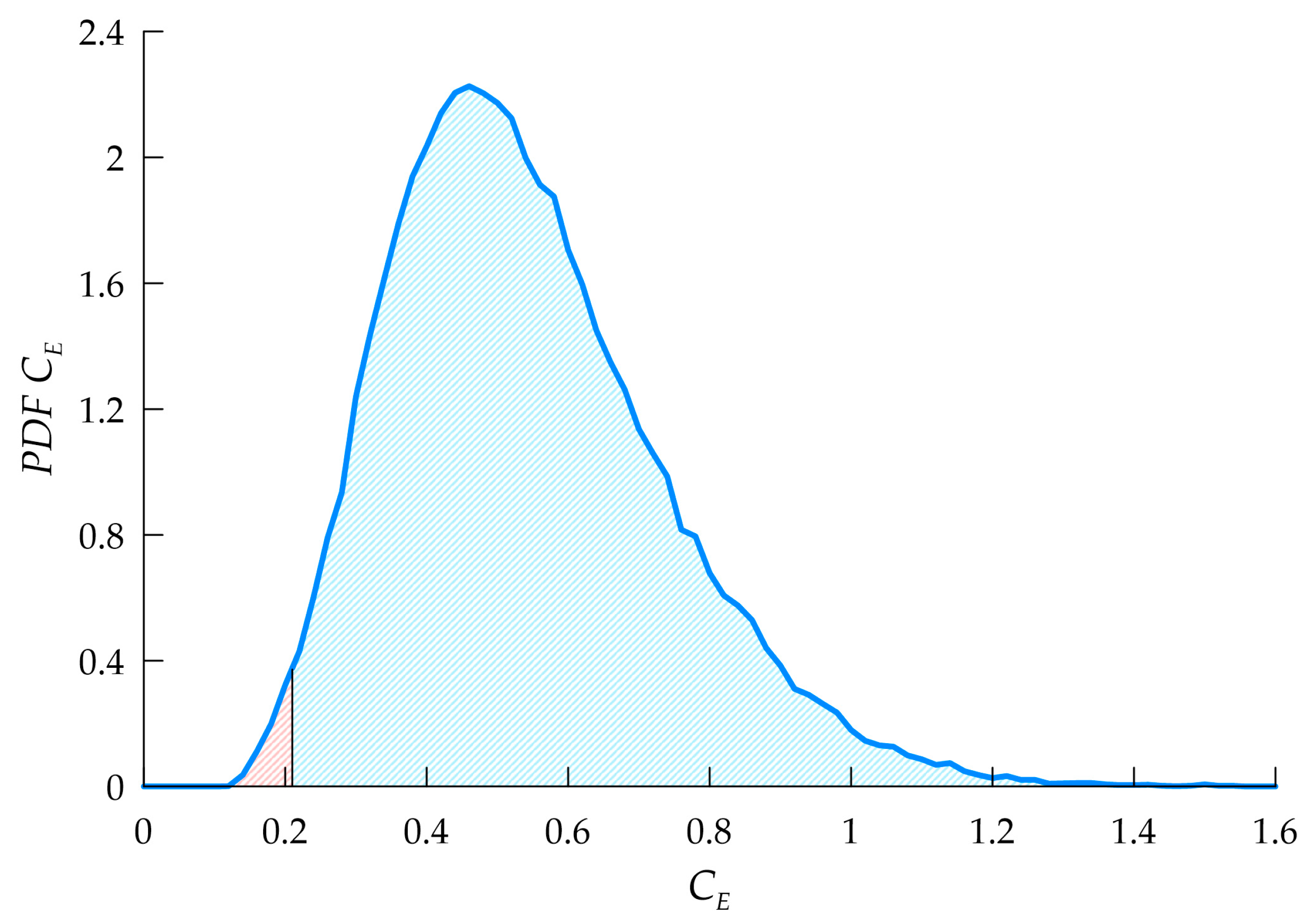
2.5. Calibration Results
2.6. Standard Subgrid Viscosity Models
3. Large Eddy Simulations of Isothermal Combustion
3.1. Problem Statement and Numerical Setup
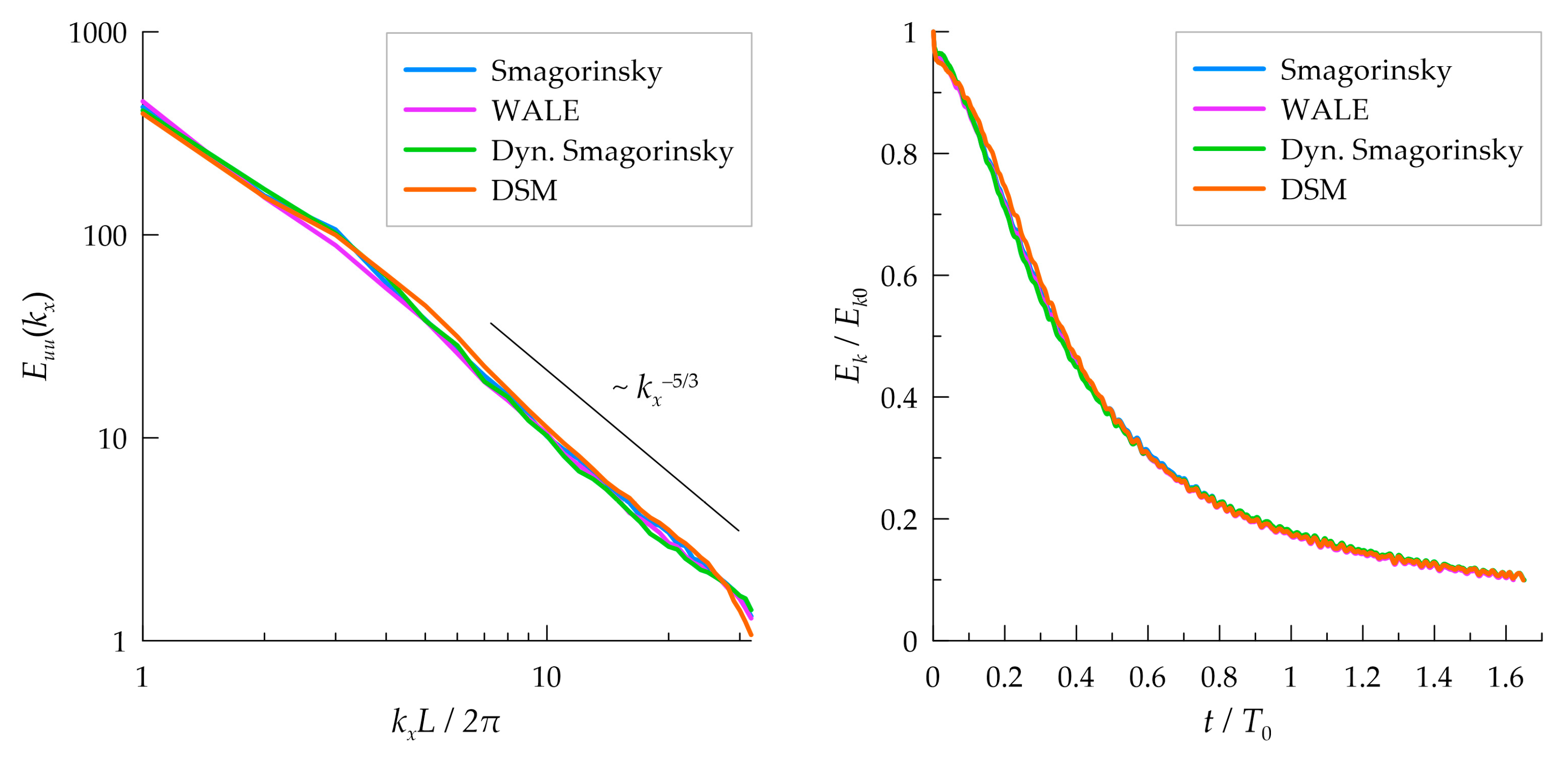
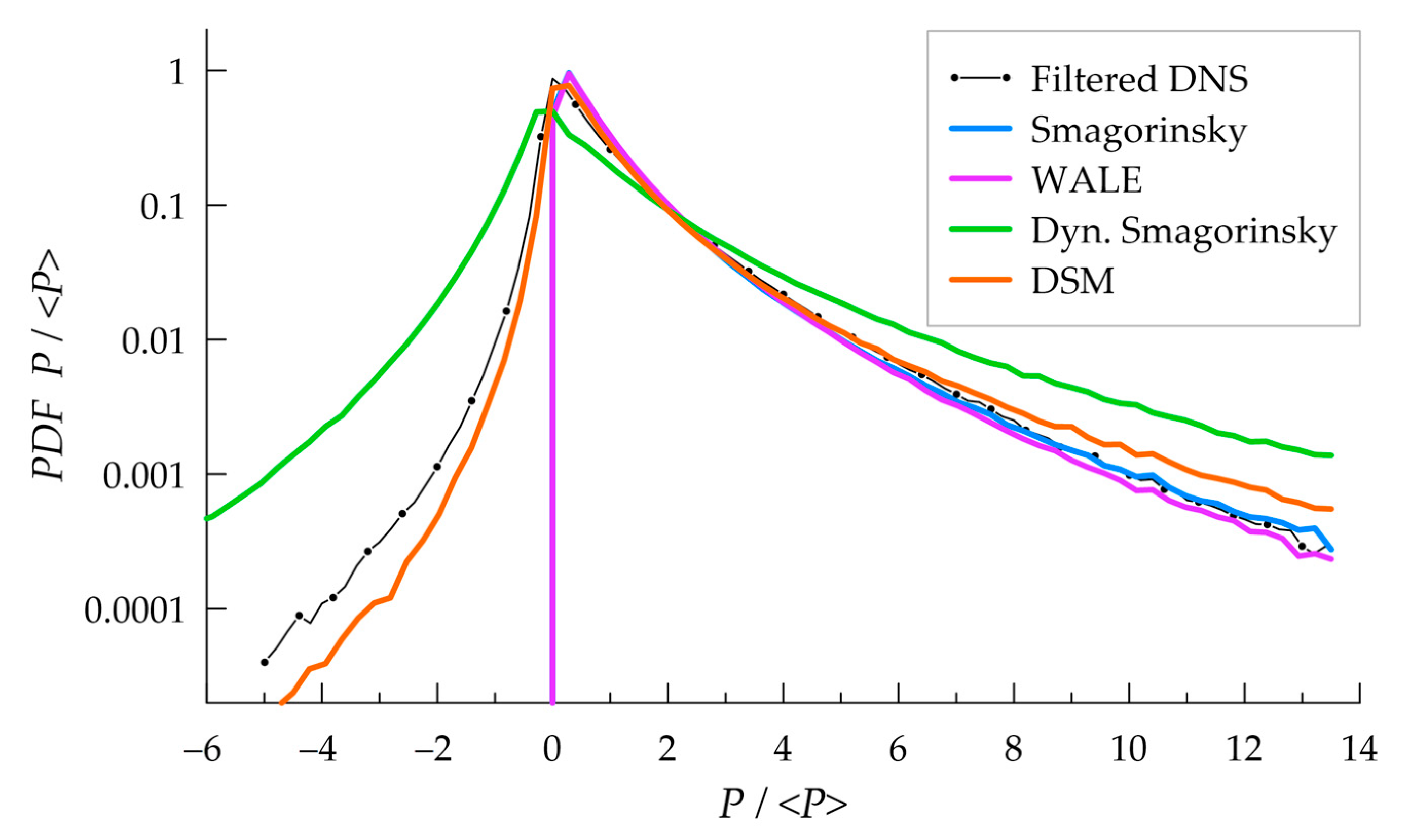
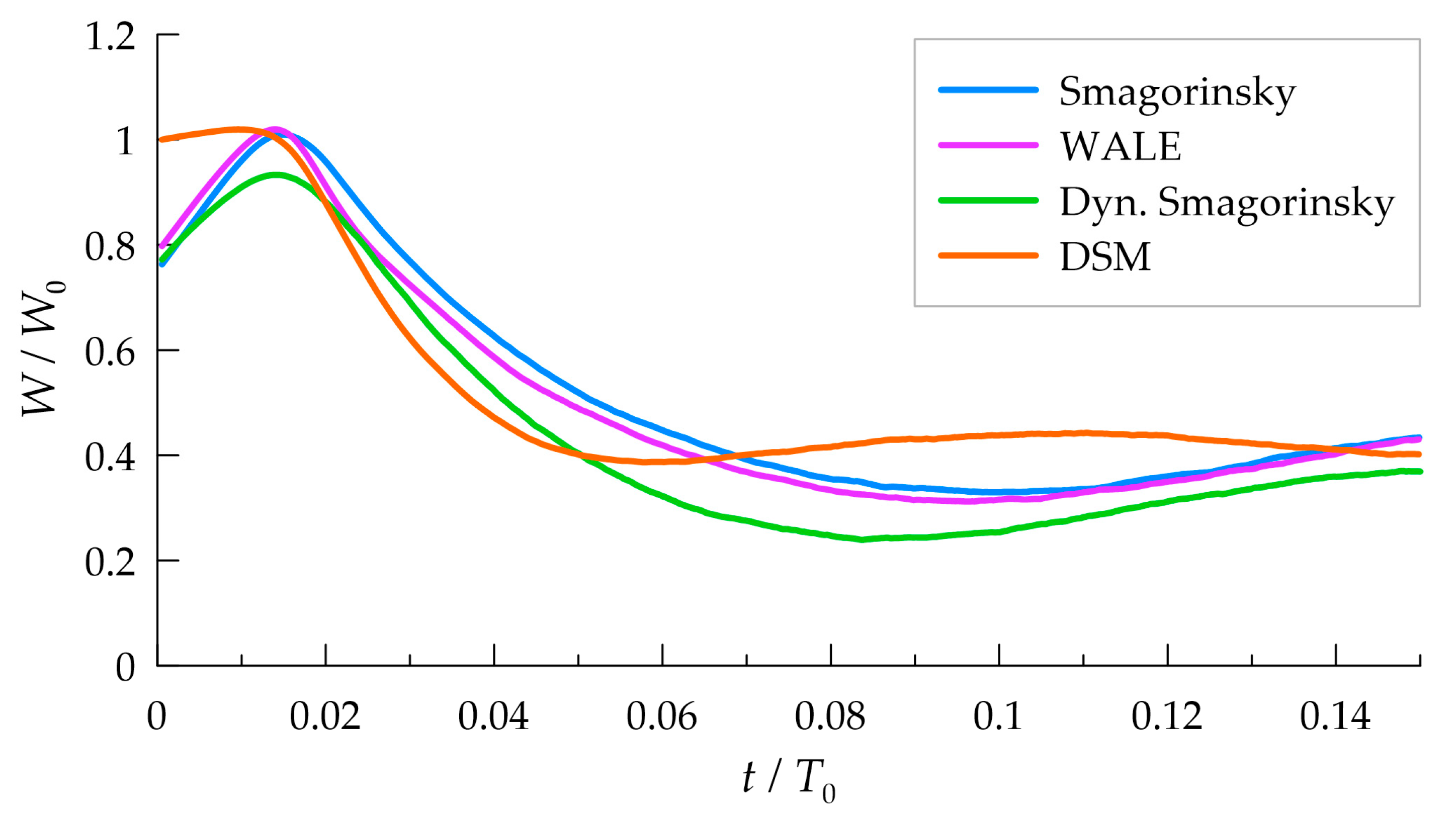
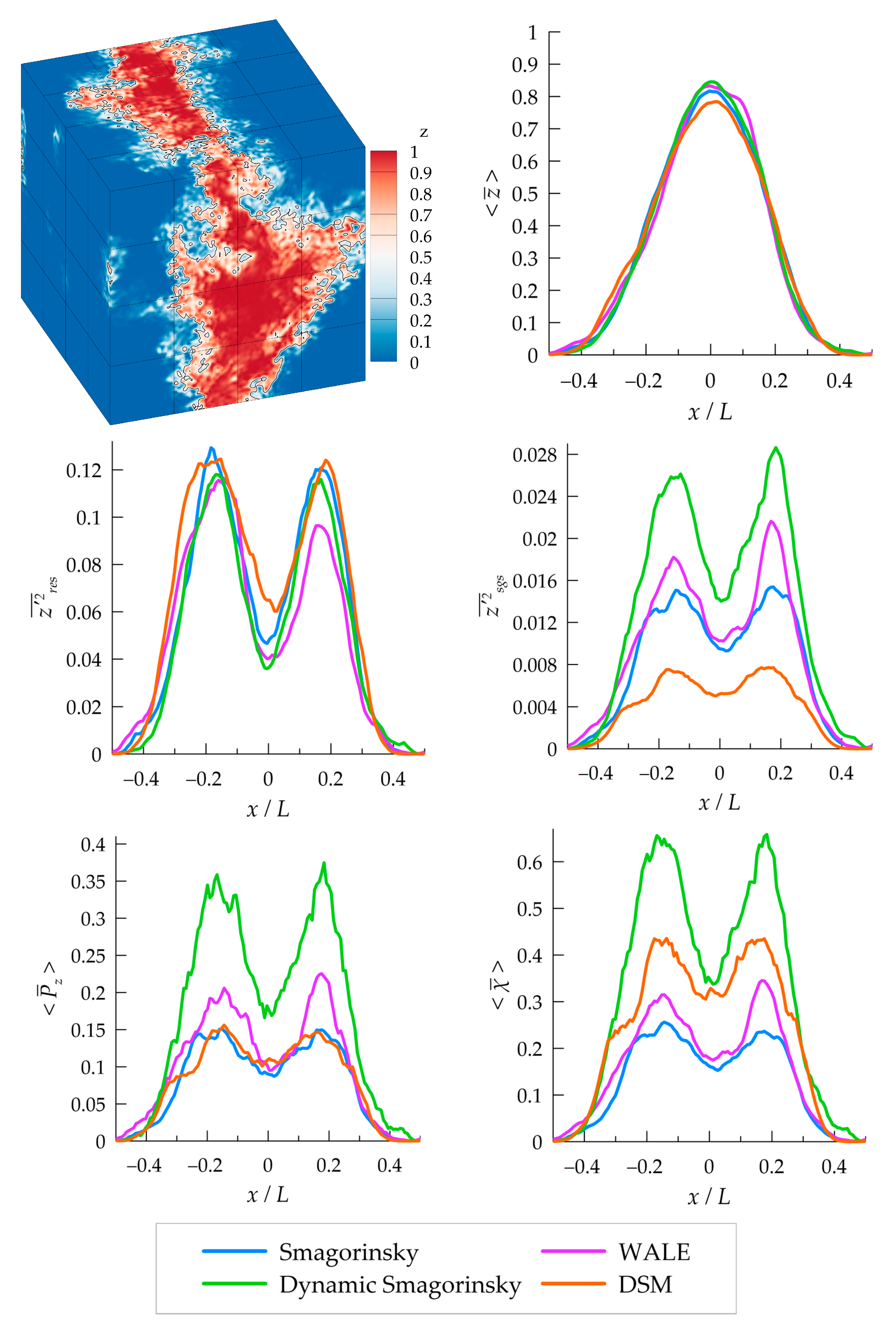
3.2. Subgrid Model Performance
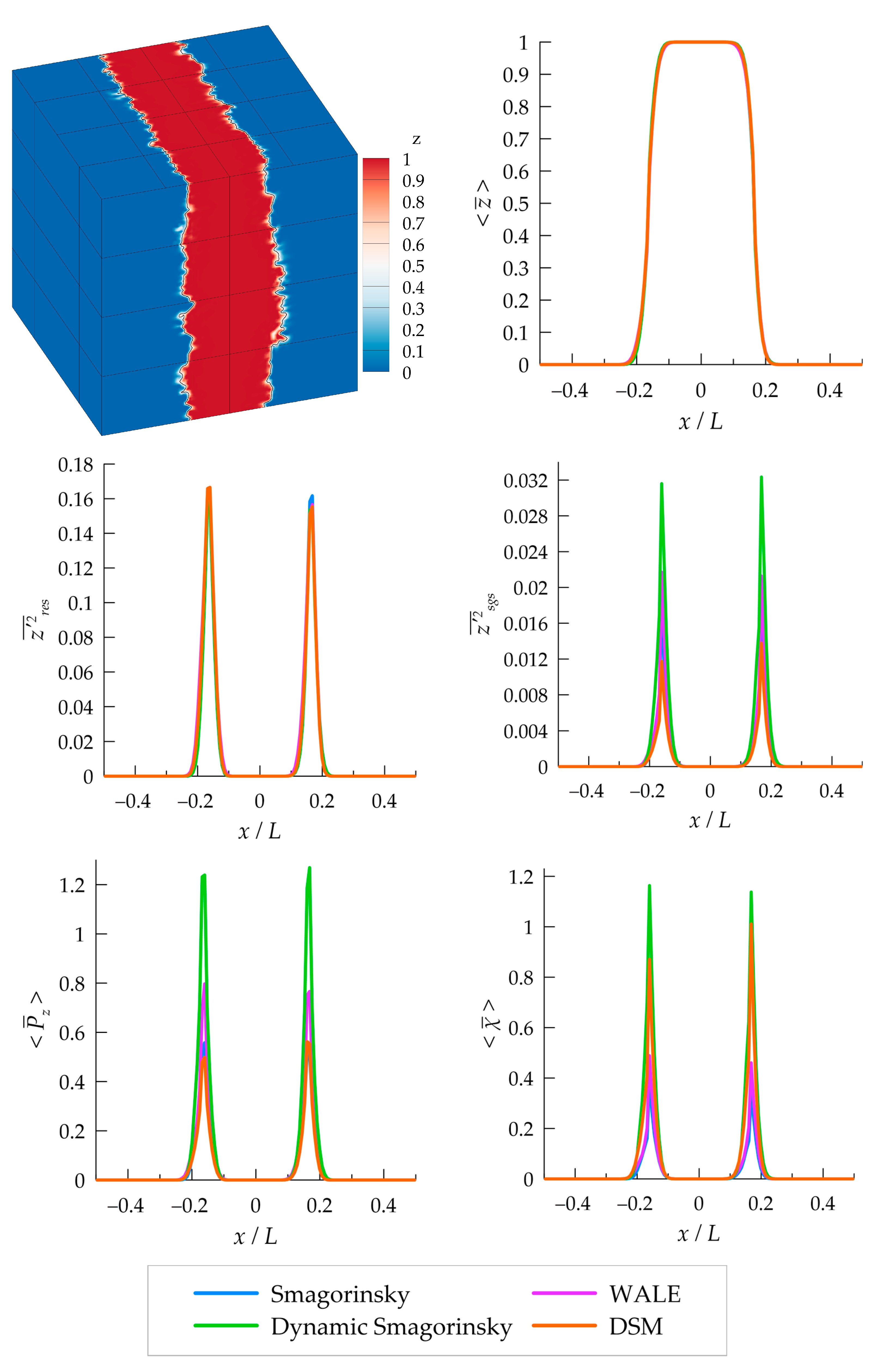
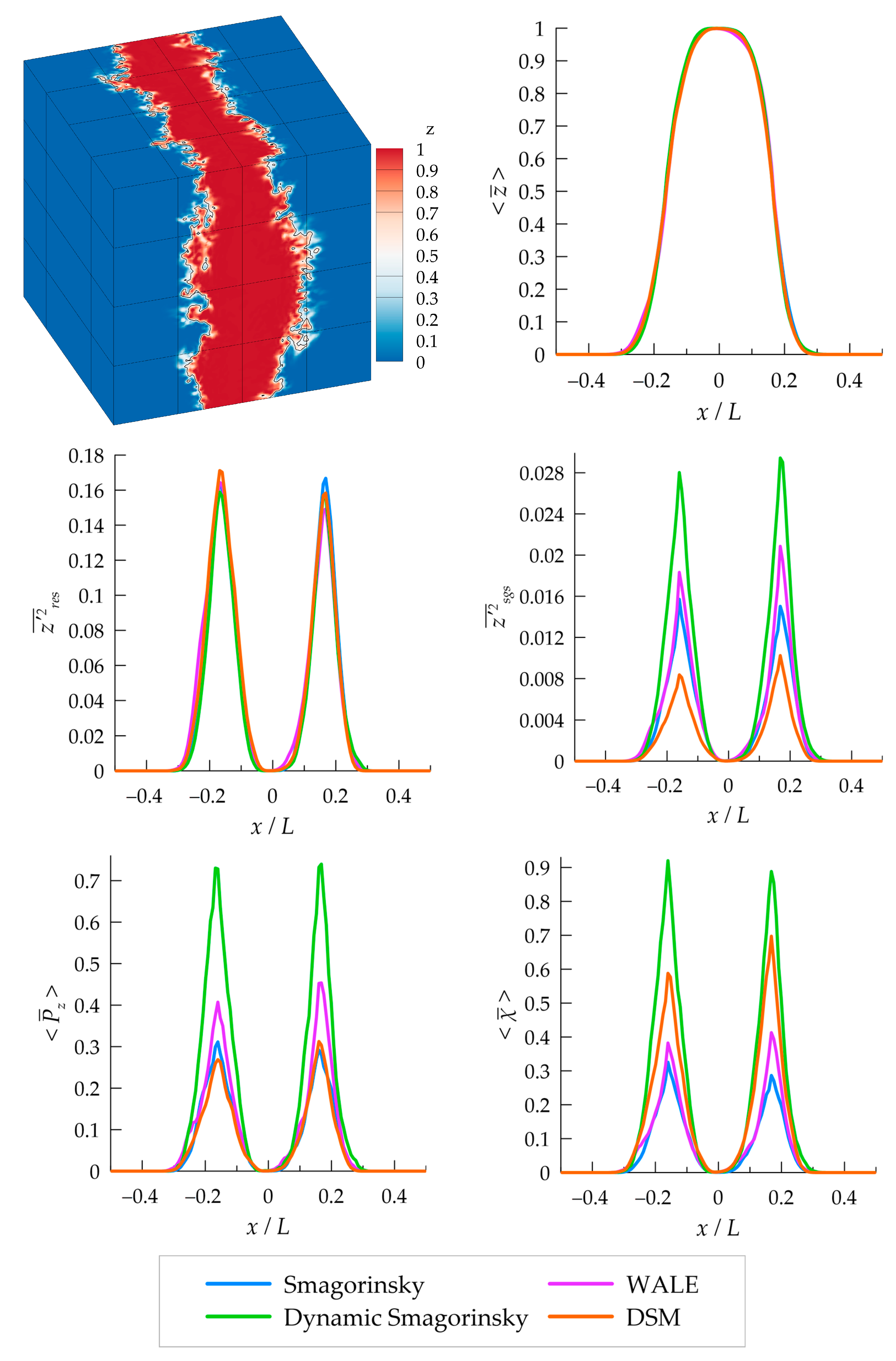
3.3. Mixture Fraction Statistics
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sagaut, P. Large Eddy Simulations of Incompressible Flows, 3rd ed.; Springer: Berlin, Germany, 2008; 558p. [Google Scholar]
- Higgins, C.W.; Parlange, M.B.; Meneveau, C. Alignment trends of velocity gradients and subgrid-scale fluxes in the turbulent atmospheric boundary layer. Bound.-Layer Meteorol. 2003, 109, 59–83. [Google Scholar] [CrossRef]
- Ballouz, J.G.; Ouellette, N.T. Tensor geometry in the turbulent cascade. J. Fluid Mech. 2018, 835, 1048–1064. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Zang, Y.; Street, R.L.; Koseff, J.R. A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows. Phys. Fluids A 1993, 5, 3186–3196. [Google Scholar] [CrossRef]
- Zhao, H.; Voke, P.R. A dynamic subgrid-scale model for low-Reynolds-number channel flow. Int. J. Numer. Methods Fluids 1996, 23, 19–27. [Google Scholar] [CrossRef]
- Montecchia, M.; Brethouwer, G.; Johansson, A.V.; Wallin, S. Taking large-eddy simulation of wall-bounded flows to higher Reynolds numbers by use of anisotropy-resolving subgrid models. Phys. Rev. Fluids 2017, 2, 034601. [Google Scholar] [CrossRef]
- Troshin, A.; Bakhne, S.; Sabelnikov, V. Numerical and physical aspects of large-eddy simulation of turbulent mixing in a helium-air supersonic co-flowing jet. In Progress in Turbulence IX. iTi 2021; Örlü, R., Talamelli, A., Peinke, J., Oberlack, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 297–302. [Google Scholar] [CrossRef]
- Deardorff, J.W. The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. J. Fluids Eng. 1973, 95, 429–438. [Google Scholar] [CrossRef]
- Fureby, C.; Tabor, G.; Weller, H.G.; Gosman, A.D. Differential subgrid stress models in large eddy simulations. Phys. Fluids 1997, 9, 3578–3580. [Google Scholar] [CrossRef]
- Zhuchkov, R.N.; Utkina, A.A. Combining the SSG/LRR-ω differential Reynolds stress model with the detached eddy and laminar-turbulent transition models. Fluid Dyn. 2016, 51, 733–744. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Z.; Zhu, L.; Wang, S. Numerical investigation of flows around an axisymmetric body of revolution by using Reynolds-stress model based hybrid Reynolds-averaged Navier–Stokes/large eddy simulation. Phys. Fluids 2021, 33, 085115. [Google Scholar] [CrossRef]
- Wang, G.; Wang, S.; Li, H.; Fu, X.; Liu, W. Comparative assessment of SAS, IDDES and hybrid filtering RANS/LES models based on second-moment closure. Adv. Mech. Eng. 2021, 13, 1–14. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Cook, A.W.; Riley, J.J.; Kosály, G. A laminar flamelet approach to subgrid-scale chemistry in turbulent flows. Combust. Flame 1997, 109, 332–341. [Google Scholar] [CrossRef]
- Williams, F.A. Combustion Theory, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018; 708p. [Google Scholar]
- Peters, N. Laminar diffusion flamelet models in non-premixed turbulent combustion. Prog. Energy Combust. Sci. 1984, 10, 319–339. [Google Scholar] [CrossRef]
- Rota, G.-C. On the combinatorics of cumulants. J. Comb. Theory Ser. A 2000, 91, 283–304. [Google Scholar] [CrossRef]
- Germano, M. A proposal for a redefinition of the turbulent stresses in the filtered Navier–Stokes equations. Phys. Fluids 1986, 29, 2323–2324. [Google Scholar] [CrossRef]
- Hanjalić, K.; Launder, B. Modelling Turbulence in Engineering and the Environment; Cambridge University Press: Cambridge, UK, 2011; 402p. [Google Scholar]
- Younis, B.A.; Gatski, T.B.; Speziale, C.G. Towards a rational model for the triple velocity correlations of turbulence. Proc. R. Soc. Lond. A 2002, 456, 909–920. [Google Scholar] [CrossRef]
- Lumley, J.L. Computational modeling of turbulent flows. Adv. Appl. Mech. 1979, 18, 123–176. [Google Scholar] [CrossRef]
- Li, Y.; Perlman, E.; Wan, M.; Yang, Y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A.; Eyink, G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 2008, 9, N31. [Google Scholar] [CrossRef]
- Available online: http://turbulence.pha.jhu.edu/ (accessed on 4 July 2022).
- Menter, F.R.; Garbaruk, A.V.; Egorov, Y. Explicit algebraic Reynolds stress models for anisotropic wall-bounded flows. In Proceedings of the 3rd European Conference for Aero-Space Sciences, Versailles, France, 6–9 July 2009. [Google Scholar]
- Lily, D.K. The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, Yorktown Heights, NY, USA, 14–16 November 1966; IBM Form No. 320-1951. pp. 195–210. [Google Scholar]
- Canuto, V.M.; Cheng, Y. Determination of the Smagorinsky–Lilly constant CS. Phys. Fluids 1997, 9, 1368–1378. [Google Scholar] [CrossRef]
- Jameson, A. Formulation of kinetic energy preserving conservative schemes for gas dynamics and direct numerical simulation of one-dimensional viscous compressible flow in a shock tube using entropy and kinetic energy preserving schemes. J. Sci. Comput. 2008, 34, 188–208. [Google Scholar] [CrossRef]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations (Introductory Mathematics for Scientists and Engineers); John Wiley & Sons: Hoboken, NJ, USA, 1973; 278p. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. Synthetic turbulence generators for RANS-LES interfaces in zonal simulations of aerodynamic and aeroacoustic problems. Flow Turbul. Combust. 2014, 93, 63–92. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000; 324p. [Google Scholar]
- NIST/SEMATECH e-Handbook of Statistical Methods. Available online: https://itl.nist.gov/div898/handbook/eda/section3/eda366h.htm (accessed on 4 July 2022).
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; RT Edwards: Philadelphia, PA, USA, 2005; 538p. [Google Scholar]
- Lien, F.S.; Liu, H.; Chui, E.; McCartney, C.J. Development of an analytical β-function pdf integration algorithm for simulation of non-premixed turbulent combustion. Flow Turbul. Combust. 2009, 83, 205–226. [Google Scholar] [CrossRef]
- Available online: https://www.boost.org/ (accessed on 4 July 2022).
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure–strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]

| Correlation Coefficient | ||||
| 64 | 0.823 | –1.308 | 1.848 | 0.861 |
| 128 | 0.804 | –1.380 | 2.103 | 0.808 |
| 256 | 0.783 | –1.421 | 2.305 | 0.717 |
| Correlation Coefficient | |||||
|---|---|---|---|---|---|
| 64 | 2.020 | 1.364 | 0.449 | 0.791 | 0.590 |
| 128 | 1.850 | 1.283 | 0.384 | 0.681 | 0.664 |
| 256 | 1.630 | 1.222 | 0.324 | 0.587 | 0.747 |
| Correlation Coefficient | ||||||||
|---|---|---|---|---|---|---|---|---|
| 64 | 3.305 | 1.060 | –0.134 | –0.044 | –0.269 | 0.356 | 1.335 | 0.604 |
| 128 | 3.046 | 1.030 | –0.137 | –0.061 | –0.233 | 0.359 | 1.202 | 0.684 |
| 256 | 2.740 | 1.029 | –0.137 | –0.069 | –0.191 | 0.313 | 1.014 | 0.760 |
| Correlation Coefficient | ||||
|---|---|---|---|---|
| 64 | 0.0178 | 0.0084 | 0.0615 | 0.869 |
| 128 | 0.0176 | 0.0042 | 0.0617 | 0.868 |
| 256 | 0.0207 | 0.0094 | 0.0665 | 0.844 |
| Correlation Coefficient | |||
|---|---|---|---|
| 64 | 0.0185 | 0.0619 | 0.869 |
| 128 | 0.0179 | 0.0619 | 0.868 |
| 256 | 0.0211 | 0.0669 | 0.844 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balabanov, R.; Usov, L.; Troshin, A.; Vlasenko, V.; Sabelnikov, V. A Differential Subgrid Stress Model and Its Assessment in Large Eddy Simulations of Non-Premixed Turbulent Combustion. Appl. Sci. 2022, 12, 8491. https://doi.org/10.3390/app12178491
Balabanov R, Usov L, Troshin A, Vlasenko V, Sabelnikov V. A Differential Subgrid Stress Model and Its Assessment in Large Eddy Simulations of Non-Premixed Turbulent Combustion. Applied Sciences. 2022; 12(17):8491. https://doi.org/10.3390/app12178491
Chicago/Turabian StyleBalabanov, Roman, Lev Usov, Alexei Troshin, Vladimir Vlasenko, and Vladimir Sabelnikov. 2022. "A Differential Subgrid Stress Model and Its Assessment in Large Eddy Simulations of Non-Premixed Turbulent Combustion" Applied Sciences 12, no. 17: 8491. https://doi.org/10.3390/app12178491






