Study on Static Analytical Method of Multi-Tower Self-Anchored Suspension Bridge
Abstract
:1. Introduction
2. Establishment of Basic Differential Equation
2.1. Basic Assumption
- (1)
- The main cable is only in tension, but does not bear the bending moment. The geometric shape of the main cable is a quadratic parabola due to the horizontal uniform load along the span.
- (2)
- The slings are densely distributed vertically along the whole bridge span, which is regarded as a “membrane” that only provides vertical resistance, regardless of its elongation and inclination under live load; that is, the deformation of the main cable and the stiffening beam is the same.
- (3)
- In each span, the stiffened beam is a straight beam with equal cross section; that is, the cross section characteristics and material parameters are constant.
- (4)
- Ignore the shear deformation of stiffened beams.
- (5)
- Consider the longitudinal stiffness of the main tower and the influence of unbalanced horizontal forces of main cables on both sides of the tower top on the horizontal displacement of the main tower.
2.2. Derivation of Basic Equation
2.3. Equilibrium Differential Equation
2.4. Deformation Compatibility Equation
2.5. Expansion of the Equation
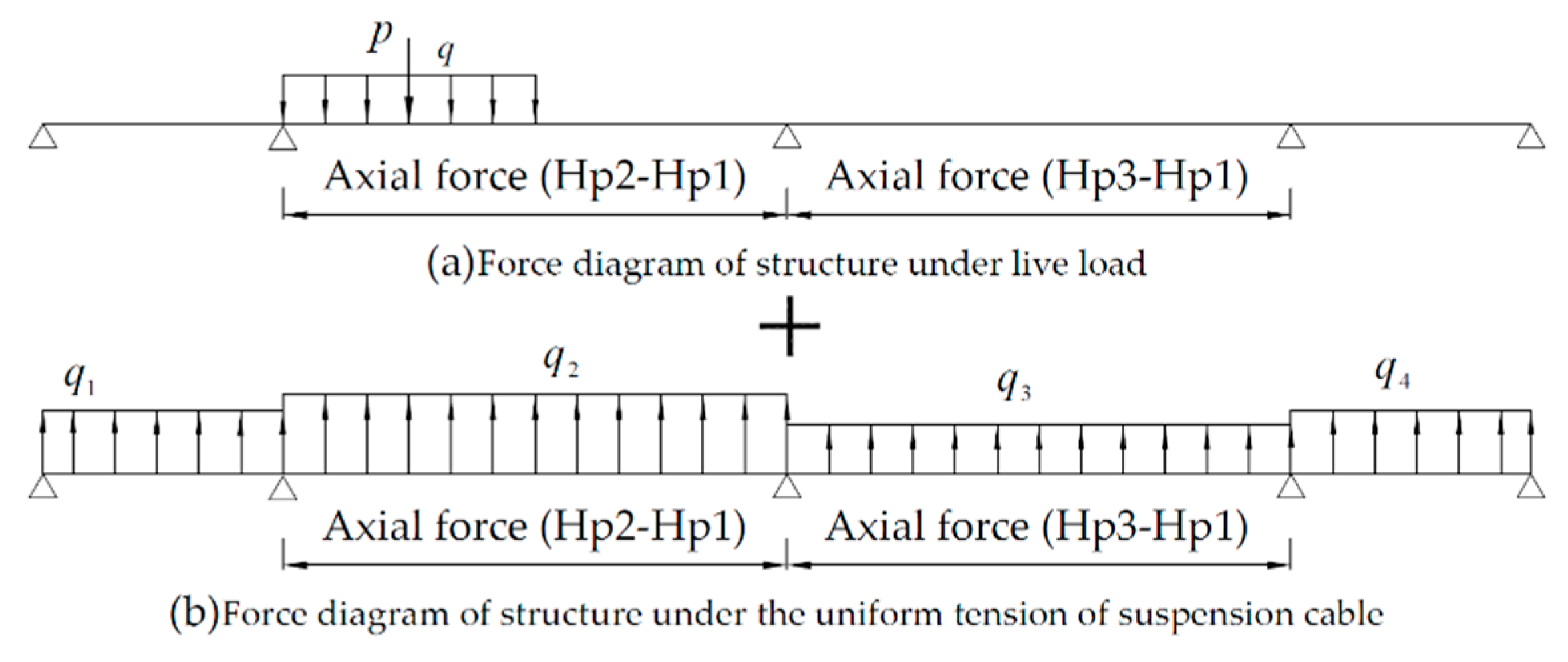
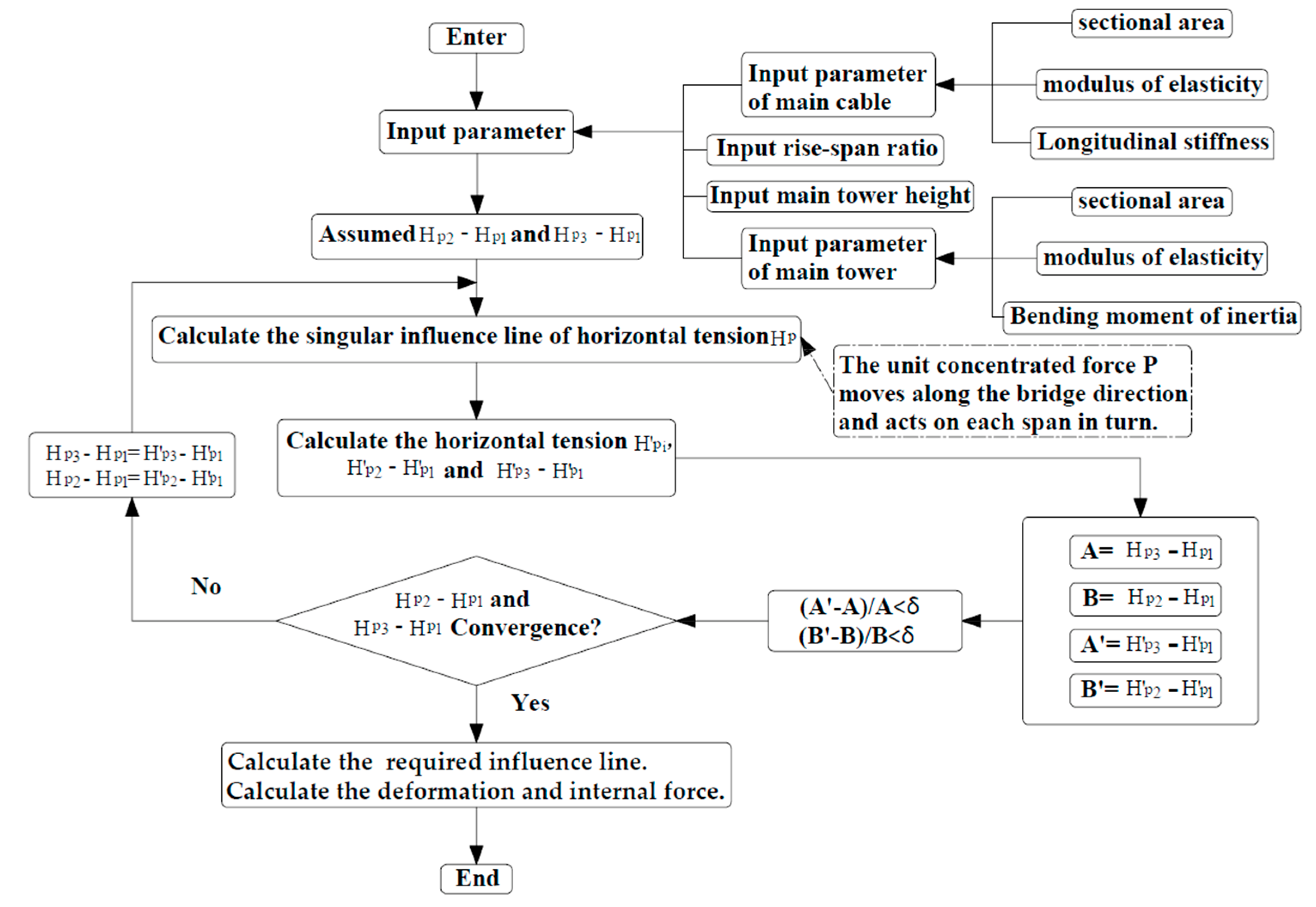
3. Solution of Differential Equation
3.1. Ideas of Solving Equations
3.2. Matlab Calculation Flow
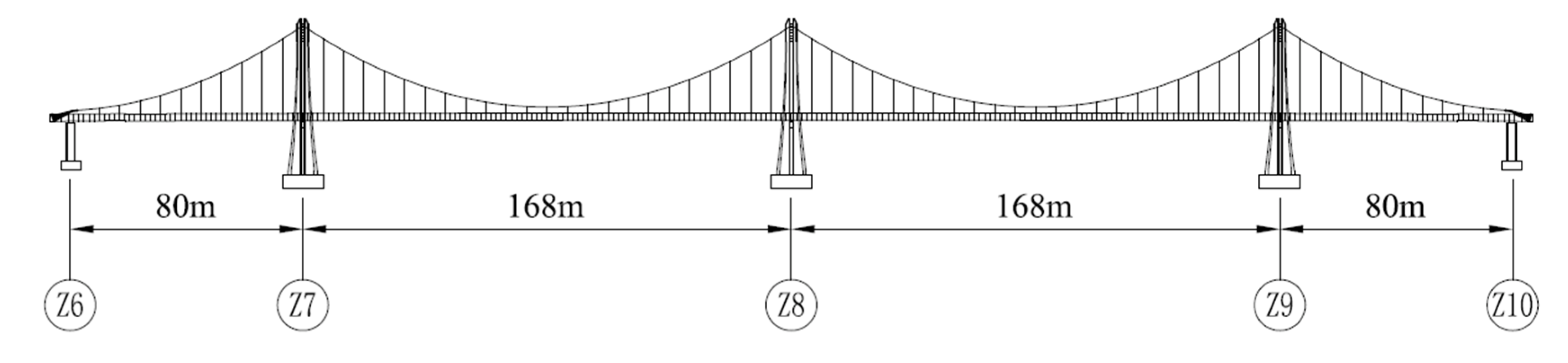
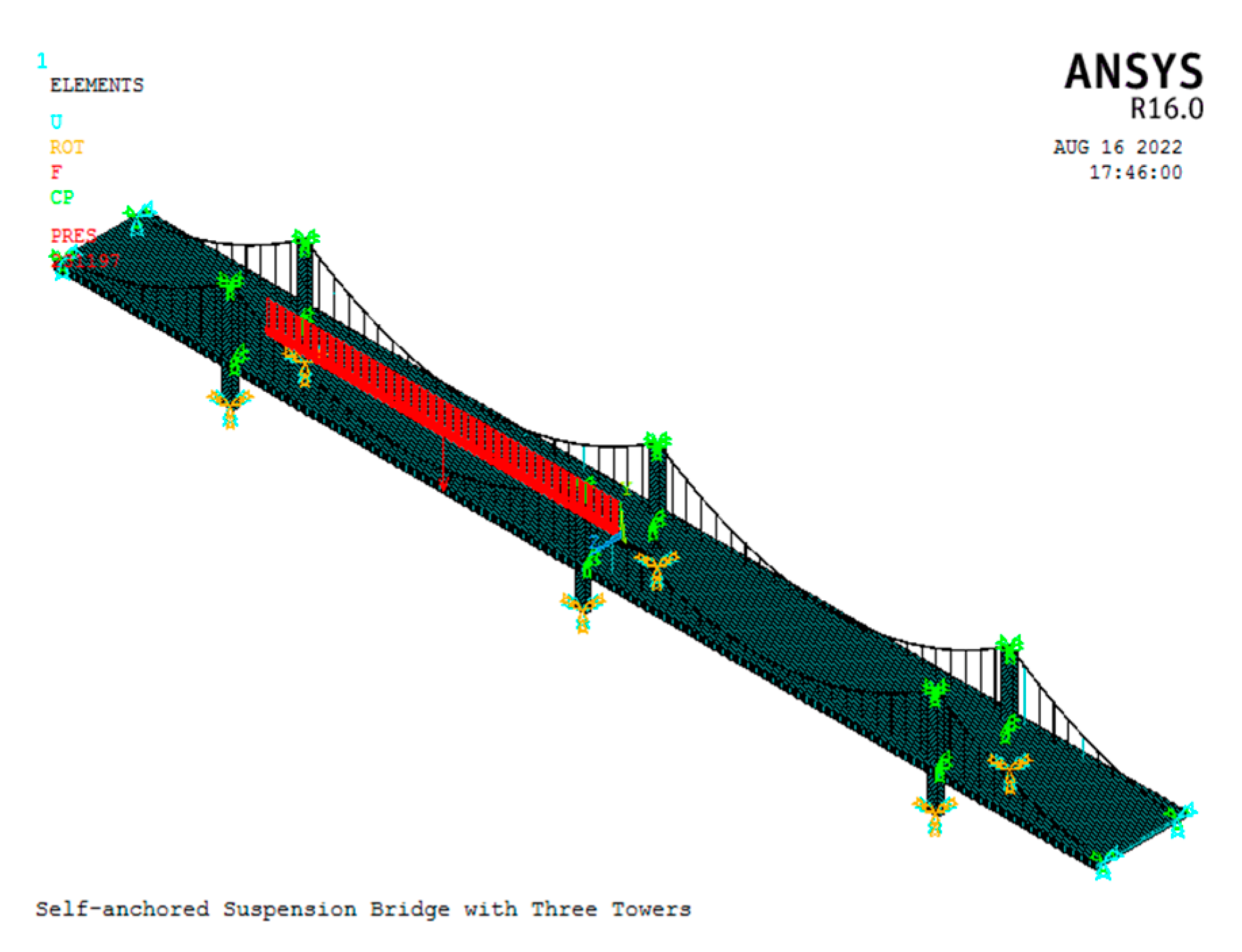
4. Application Example
4.1. Finite Element Model
4.2. Comparison of Calculation Results
5. Conclusions
- (1)
- Based on the deflection theory, for a multi-tower self-anchored suspension bridge, there is a nonlinear term in the balance differential equation established by adding the influence of the stiffness of the main tower. The nonlinearity is mainly manifested in the coupling term between the horizontal tension difference of the live load of the adjacent main cable and the corresponding deformation in the main span balance equation.
- (2)
- Different from the previous theoretical analysis of deflection of ground-anchored suspension bridge, the axial compression deformation of stiffening beam should be considered when establishing the deformation coordination equation of multi-tower self-anchored suspension bridge. Meanwhile, whether the longitudinal horizontal displacement of the top of the main tower is considered has great influence on the internal force and deformation of the multi-tower self-anchored suspension bridge.
- (3)
- The practical calculation formula of internal force and deformation of multi-tower self-anchored suspension bridge derived in this paper has a clear mechanical concept, which can theoretically explain the mechanical characteristics of the structure. In addition, it can be applied to single-tower and double-tower self-anchored suspension bridges and ground-anchored suspension bridges only by appropriately modifying the static analysis calculation formula and the MATLAB calculation program of the multi-tower self-anchored suspension bridge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Latimer, M.; Hindle, B.; Kranzberg, M. Bridge to the Future: A Centennial Celebration of the Brooklyn Bridge-introduction. Ann. N. Y. Acad. Sci. 1984, 424, 9–12. [Google Scholar]
- Ochsendorf, J.A.; Billington, D.P. Self-anchored suspension bridges. J. Bridge Eng. 1999, 4, 151–156. [Google Scholar] [CrossRef]
- Kim, H.-K.; Lee, M.-J.; Chang, S.-P. Non-linear shape-finding analysis of a self-anchored suspension bridge. Eng. Struct. 2002, 24, 1547–1559. [Google Scholar] [CrossRef]
- Gil, H.; Choi, Y. Cable Erection Test at Splay Band for Spatial Suspension Bridge. J. Bridge Eng. 2002, 7, 300–307. [Google Scholar] [CrossRef]
- Sun, J.; Manzanarez, R.; Nader, M. Design of Looping Cable Anchorage System for New San Francisco-Oakland Bay Bridge Main Suspension Span. J. Bridge Eng. 2002, 7, 315–324. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, M.; Wang, L.; Zhang, Z. Self-Anchored suspension bridges in China. Pract. Period. Struct. Des. Constr. 2017, 22, 1–10. [Google Scholar] [CrossRef]
- Tao Song, T.; Wang, B.; Song, Y. A Simplified Calculation Method for Multi-Tower Self-Anchored Suspension Bridges Based on Frame Structure Theory Model. Int. J. Steel Struct. 2022, 22, 373–388. [Google Scholar] [CrossRef]
- Chang, F.; Chen, L.; Shao, C.; Lu, D. Design of Main Bridge of Fenghuang Yellow River Bridge in Jinan. Bridge Constr. 2021, 51, 101–107. (In Chinese) [Google Scholar]
- Lei, S.; Liu, C.; Zhang, Z. Basic differential equation deductive of the self-anchored suspension bridge. J. Harbin Inst. Technol. 2004, 36, 1733–1735. (In Chinese) [Google Scholar]
- Shen, R.; Wang, Z. Study on mechanical property of self-anchored suspension bridge based upon deflection theory. J. Highw. Transp. Res. Dev. 2008, 25, 94–98. (In Chinese) [Google Scholar]
- Tang, M. The Static and Dynamic Performance Study of Long-Span Self-Anchored Suspension Bridges and Parameter Sensitivity Analysis. Ph.D. Thesis, Central South University, Changsha, China, March 2007. [Google Scholar]
- Huang, Q.; Ye, M. Study on Simplified Calculation Method of Self-anchored Suspension Bridge. J. China Railw. Soc. 2008, 30, 122–126. (In Chinese) [Google Scholar]
- Zhang, W.; Yang, C.; Wang, Z.; Liu, Z. An analytical algorithm for reasonable central tower stiffness in the three-tower suspension bridge with unequal-length main spans. Eng. Struct. 2019, 199, 109595. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, H.-P.; Xu, D. New Method for Shape Finding of Self-Anchored Suspension Bridges with Three Dimensionally Curved Cables. J. Bridge Eng. 2015, 20, 1–22. [Google Scholar] [CrossRef]
- Buonopane, S.G.; Billington, D.P. Theory and history of suspension bridge design from 1823 to 1940. J. Struct. Eng. (United States) 1993, 119, 954–977. [Google Scholar] [CrossRef]
- Jung, M.-R.; Shin, S.-U.; Attard, M.M.; Kim, M.-Y. The flection Theory for Self-Anchored Suspension Bridges under Live Load. J. Bridge Eng. 2015, 20, 1–19. [Google Scholar] [CrossRef]
- Zhang, Z. Self-Anchored Concrete Suspension Bridge; People’s Communications Publishing House: Beijing, China, 2005. [Google Scholar]
- Pang, H.; Wang, J.; Li, X. Static analysis of suspension bridges based on deflection theory. J. Hefei Univ. Technol. Nat. Sci. Ed. 2010, 33, 261–265. (In Chinese) [Google Scholar]
- Lee, B. Research on Bridge and Structure Theory; Shanghai Science and Technology Literature Publishing House: Shanghai, China, 1983; pp. 1–12. [Google Scholar]
- Professional Standard of the People’s Republic of China, JTG T60-2015; General Code for Design of Highway Bridges and Culverts. Communications Press: Beijing, China, 2015.


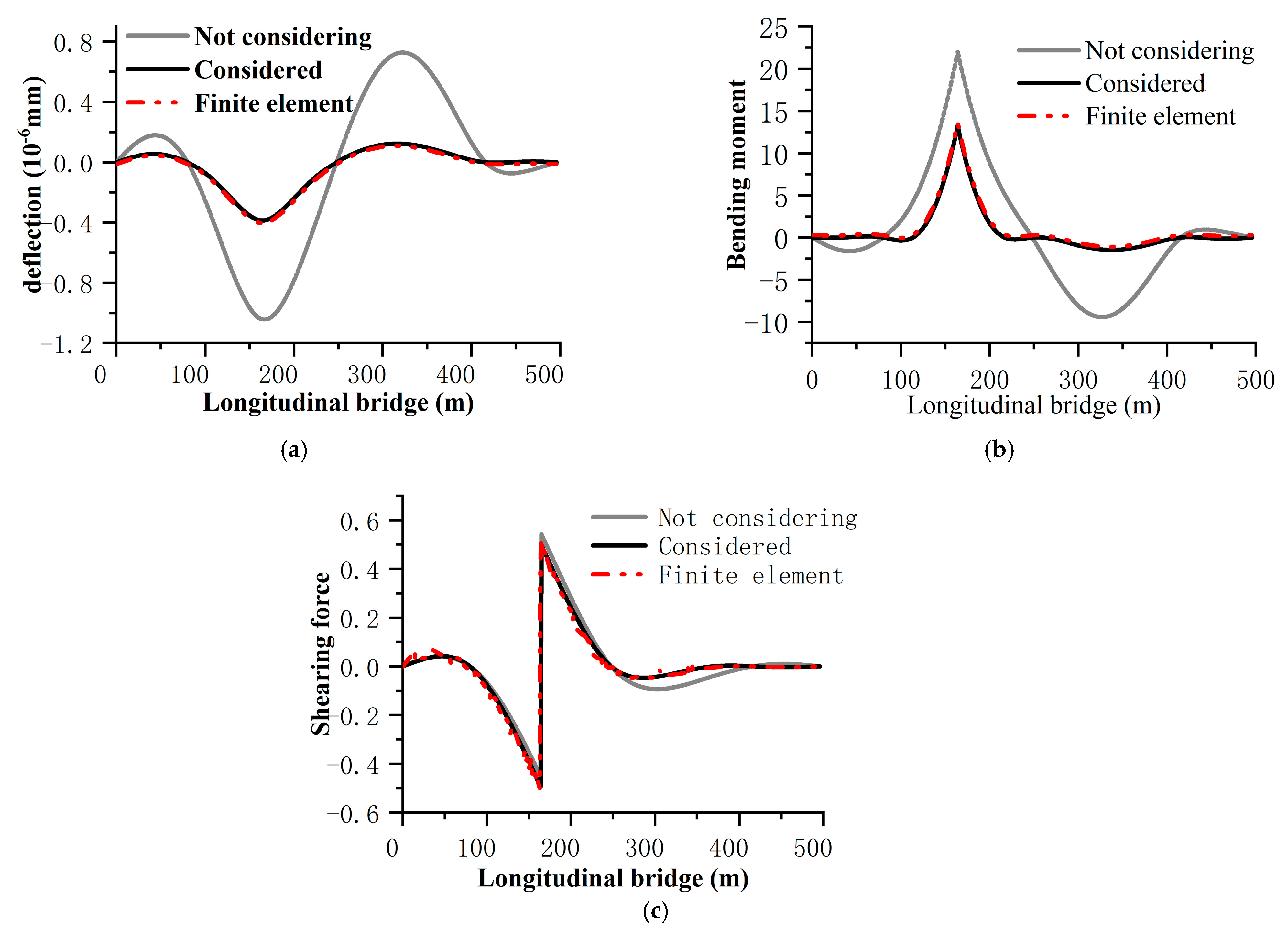
| Section Position | Finite Element Results (m) | Without Considering the Stiffness of the Main Tower | Considering Stiffness of Main Tower | ||
|---|---|---|---|---|---|
| Computed Value (m) | Error | Computed Value (m) | Error | ||
| Mid-span section of the left span | 0.038 | 0.057 | 50.00% | 0.035 | −7.89% |
| Mid-span section of the left main span | −0.194 | −0.361 | 86.08% | −0.189 | −2.58% |
| Mid-span section of the right main span | 0.065 | 0.104 | 60.00% | 0.070 | 7.69% |
| Mid-span section of the right span | 0.007 | 0.019 | −23.59% | 0.006 | −14.29% |
| Section Position | Finite Element Results (KN·m) | Without Considering the Stiffness of the Main Tower | Considering Stiffness of Main Tower | ||
|---|---|---|---|---|---|
| Computed Value (KN·m) | Error | Computed Value (KN·m) | Error | ||
| Mid-span of the left span | −17,955 | −29,394 | 63.71% | −16,567 | −7.73% |
| Support of left tower | −20,472 | −35,899 | 75.36% | −19,381 | −5.33% |
| Mid-span of the left main span | 38,131 | 56,832 | 49.04% | 36,987 | −3.00% |
| Support of middle tower | −16,920 | −20,182 | 19.28% | −14,820 | −12.41% |
| Mid-span of the right main span | −7051 | −11,980 | 69.90% | −7711 | 9.36% |
| Support of right tower | 10,708 | 21,269 | 98.63% | 11,534 | −7.71% |
| Mid-span of the right span | −1630 | −2319 | 42.27% | −1809 | 10.98% |
| Section Position | Finite Element Results (KN) | Without Considering the Stiffness of the Main Tower | Considering Stiffness of Main Tower | ||
|---|---|---|---|---|---|
| Computed Value (KN) | Error | Computed Value (KN) | Error | ||
| Support of left tower | 85 | 22 | −74.12% | 116 | 36.47% |
| Mid-span of the left main span | 585 | 447 | −23.59% | 692 | 36.47% |
| Support of middle tower | 850 | 1322 | 55.53% | 588 | −30.82% |
| Support of right tower | 383 | 588 | 53.52% | 523 | 36.55% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-j.; Wang, S.; Zhong, J.-w.; Lian, F. Study on Static Analytical Method of Multi-Tower Self-Anchored Suspension Bridge. Appl. Sci. 2022, 12, 8499. https://doi.org/10.3390/app12178499
Chen Y-j, Wang S, Zhong J-w, Lian F. Study on Static Analytical Method of Multi-Tower Self-Anchored Suspension Bridge. Applied Sciences. 2022; 12(17):8499. https://doi.org/10.3390/app12178499
Chicago/Turabian StyleChen, Yong-jian, Song Wang, Ji-wei Zhong, and Fei Lian. 2022. "Study on Static Analytical Method of Multi-Tower Self-Anchored Suspension Bridge" Applied Sciences 12, no. 17: 8499. https://doi.org/10.3390/app12178499






