The Bearing Capacity of Dam Body Structure with Cemented and Weathered Materials: A Constitutive Model
Abstract
:1. Introduction
2. The Constitutive Model of Weathered Material
2.1. Improvement of Saenz’s Constitutive Model
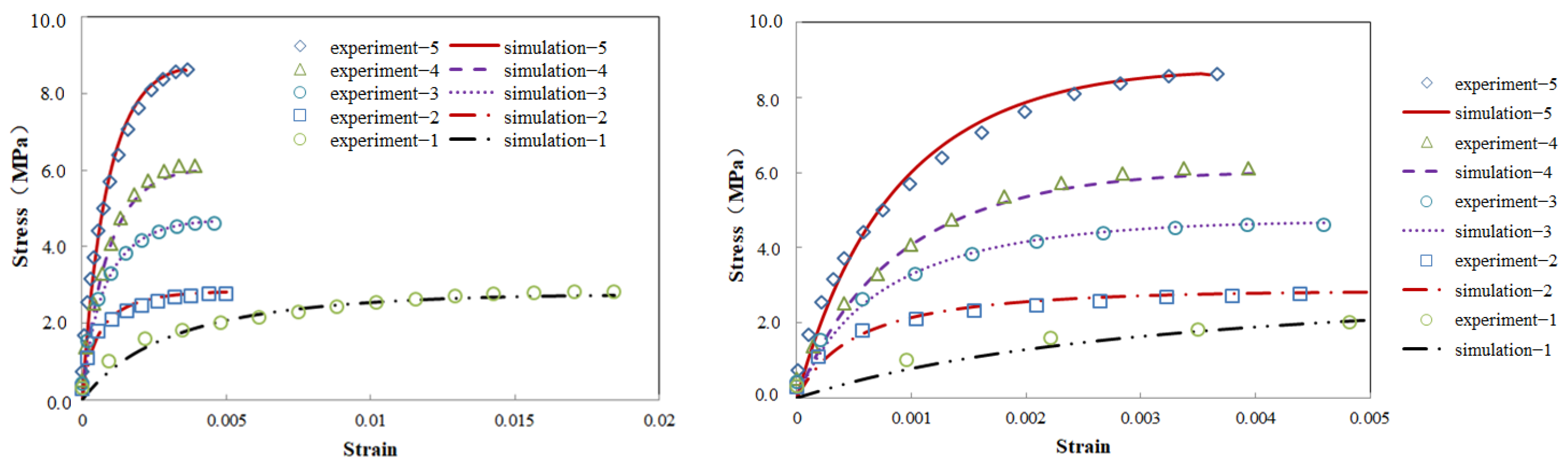
2.2. Validity Analysis of Constitutive Model
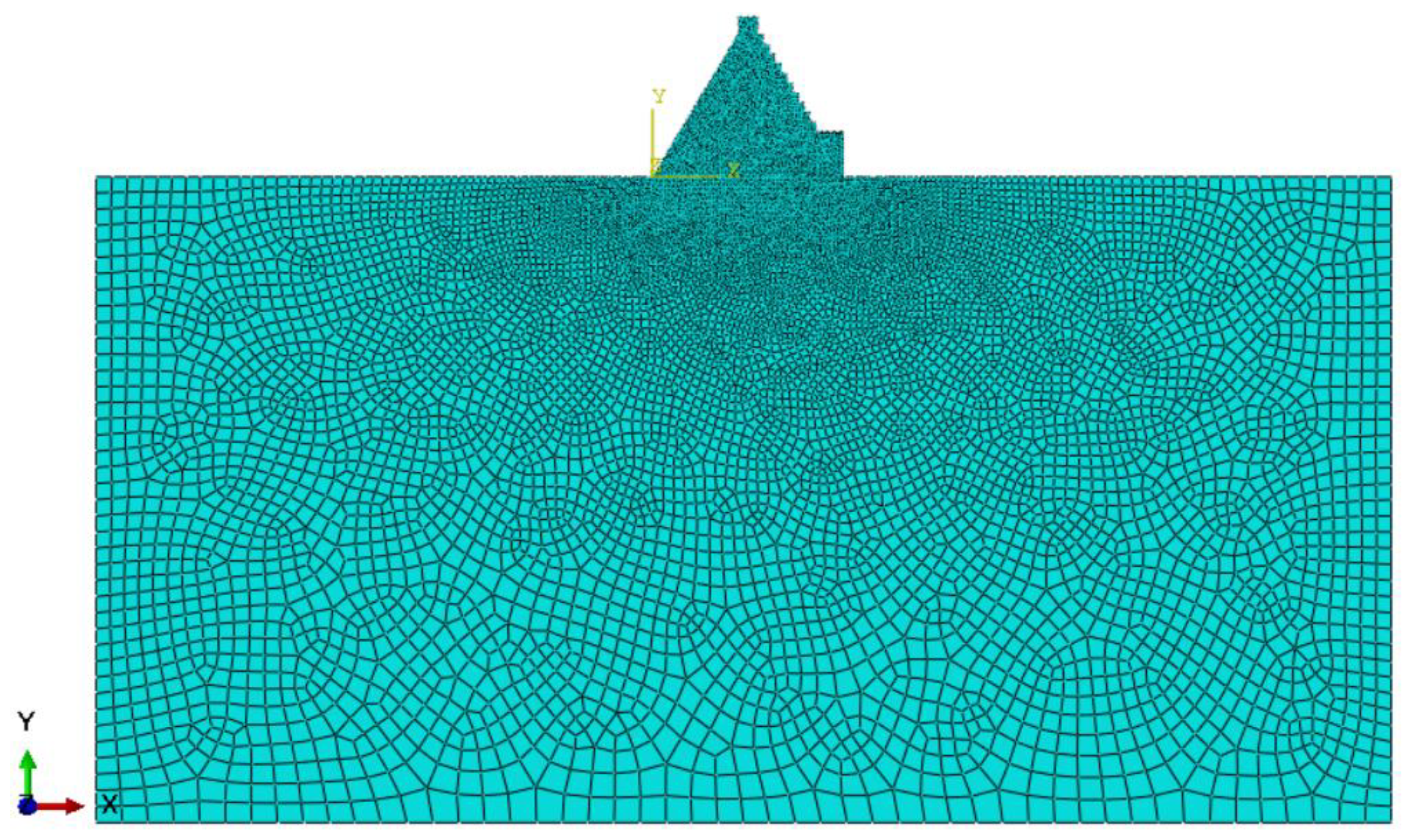
3. Engineering Overview and Model Establishment
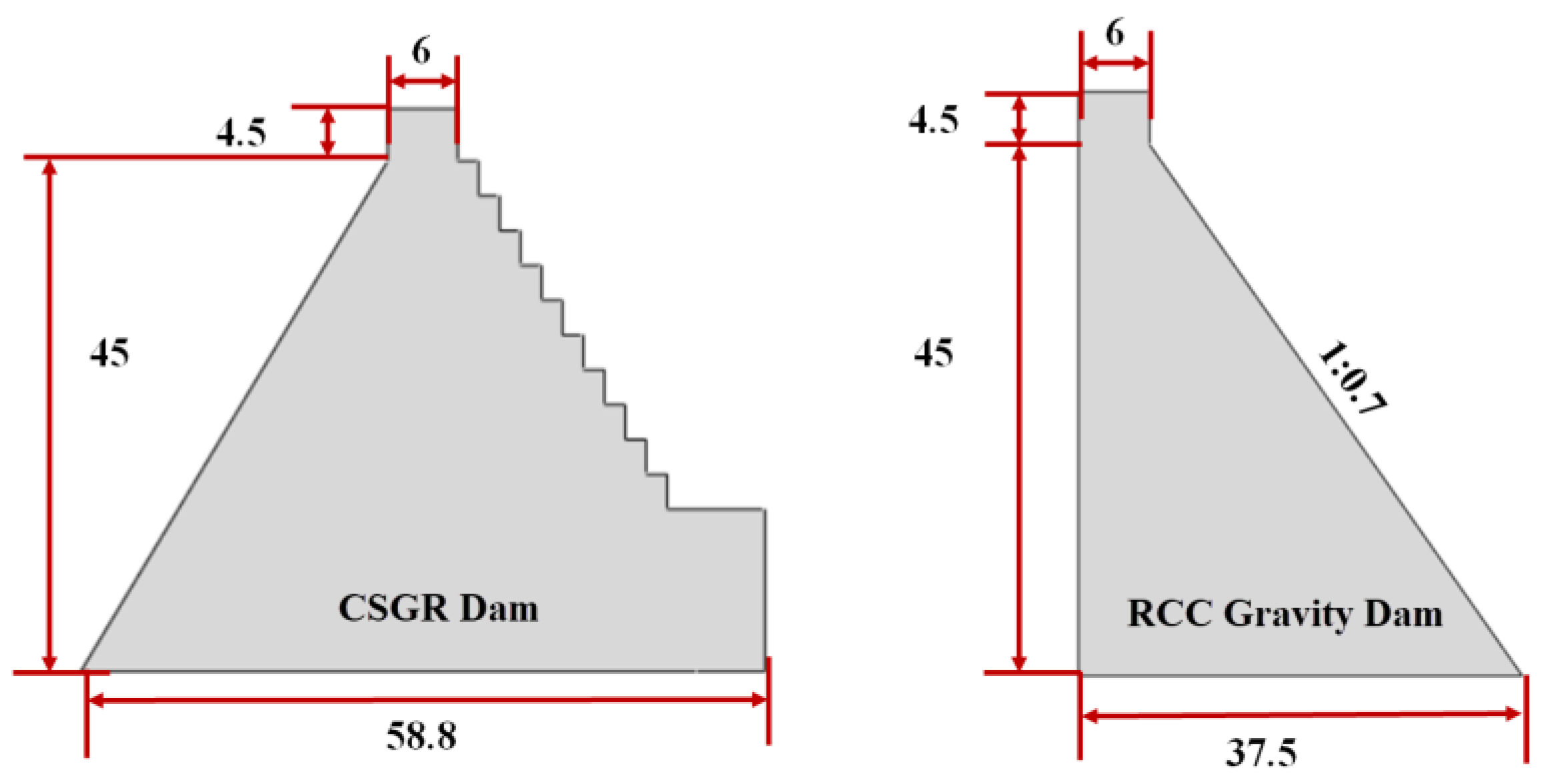
3.1. Basic Engineering Information
3.2. Mechanical Calculation Model and Its Parameters of Dam Structure
3.3. Calculation Model and Parameters of Bearing Capacity of Dam Body
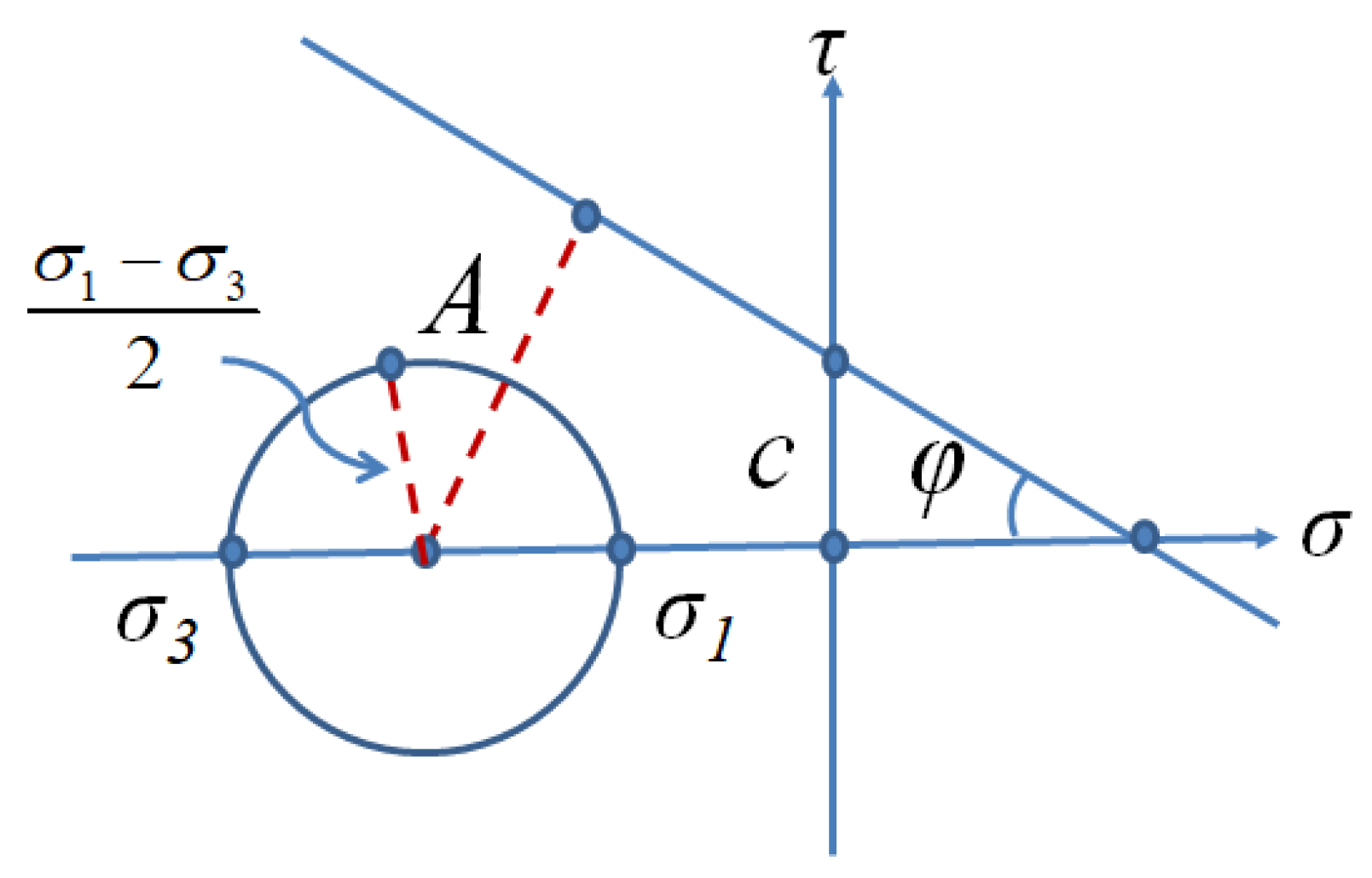
3.3.1. Yield Criteria
3.3.2. Model and Parameters
3.4. Calculation Model and Its Parameters of Dam Structure with Hydraulic Fracturing
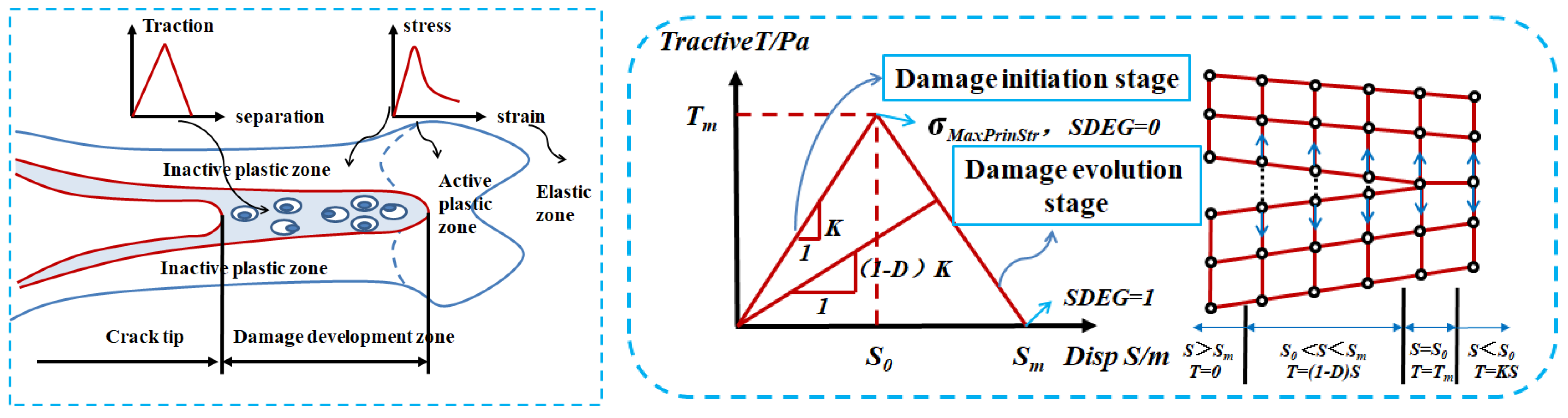
3.4.1. Failure Criterion
3.4.2. Model and Parameters
4. Analysis of the Results
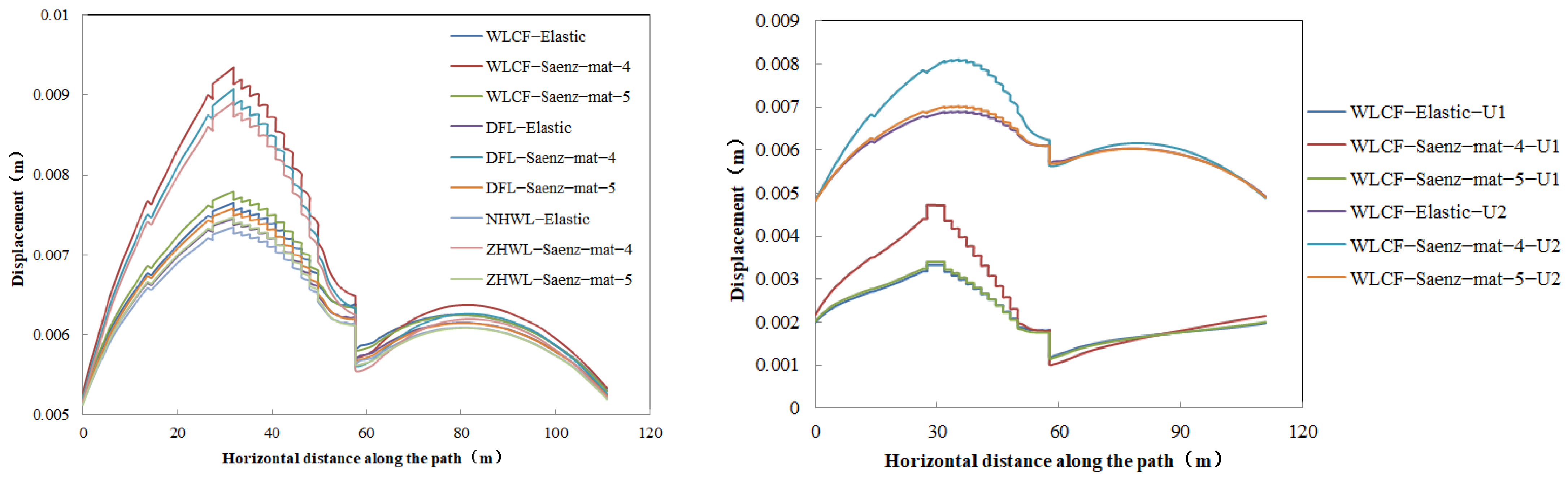
4.1. Mechanical Behavior of Dam Structure with Different Constitutive Models
4.2. Analysis on Bearing Capacity of Dam Structure
4.2.1. Calculation of Overload Capacity of Dam Body by Overload Method
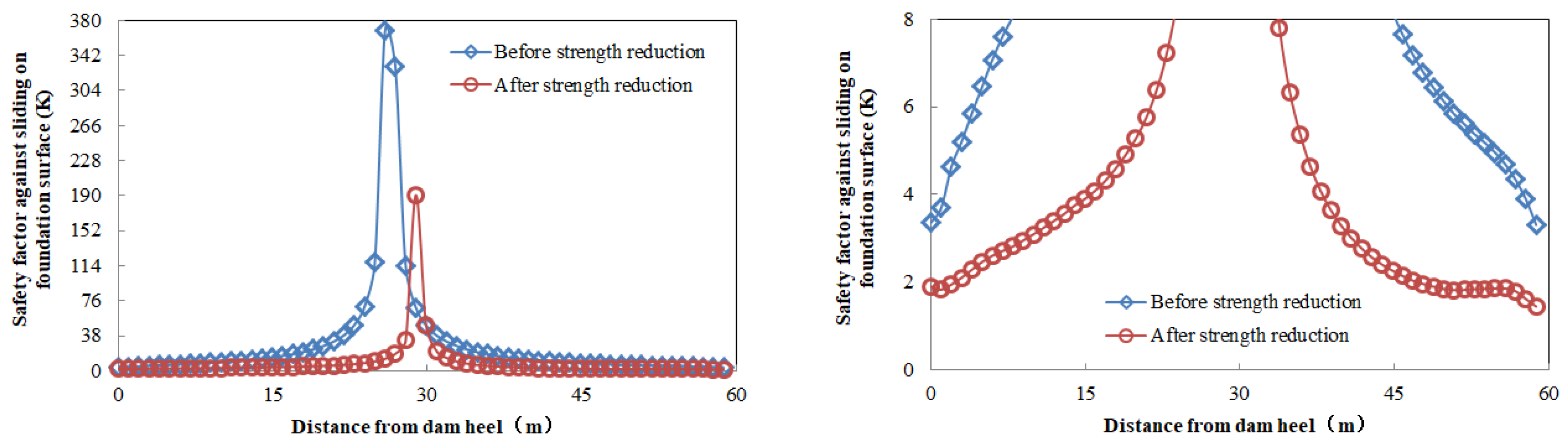
4.2.2. Calculation of Dam Body Safety Margin by Strength-Reduction Method
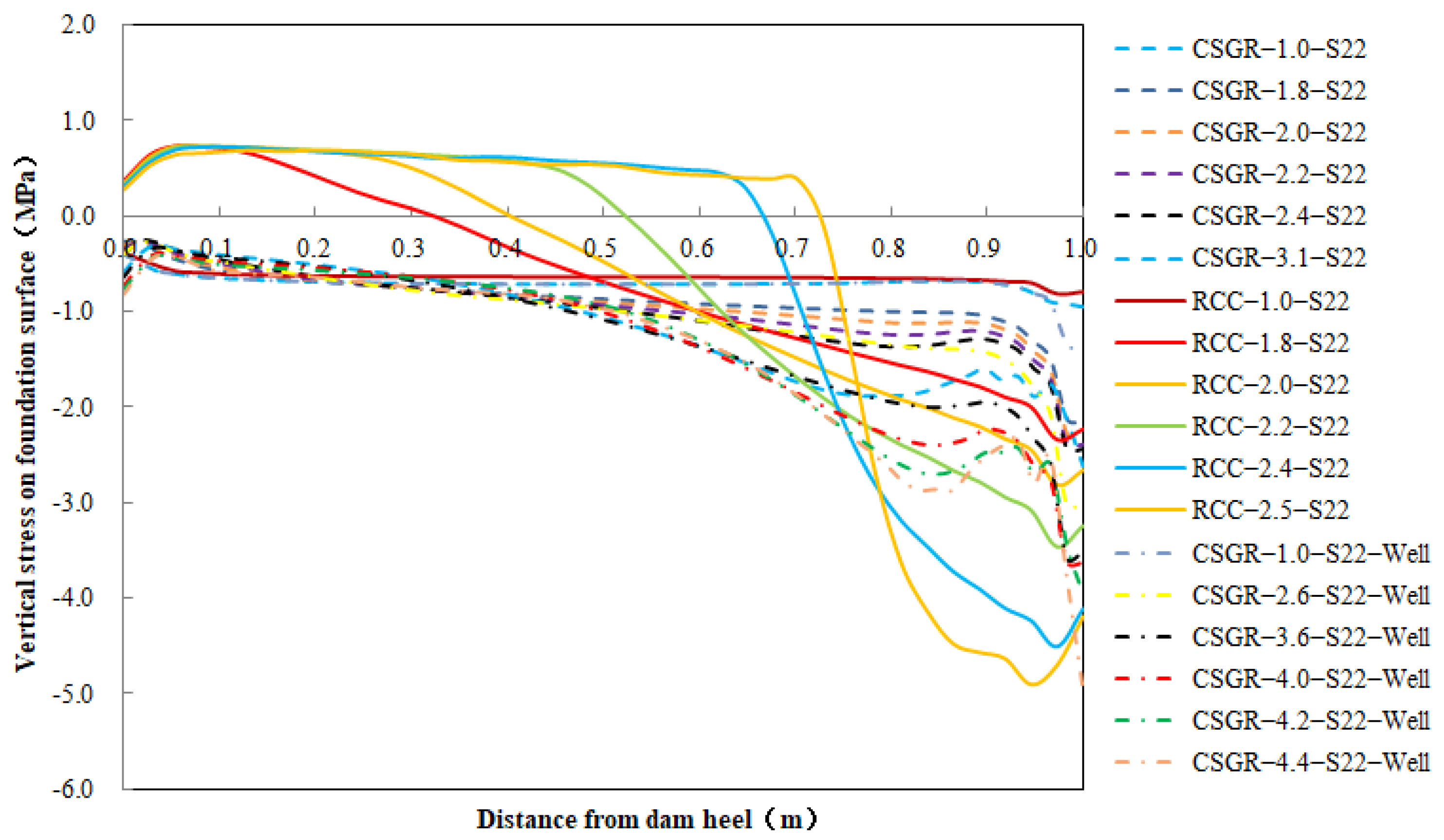
4.3. Bearing Capacity of Dam Body with Hydraulic Fracturing
4.3.1. Overloading Capacity of Dam Body with Hydraulic Fracturing
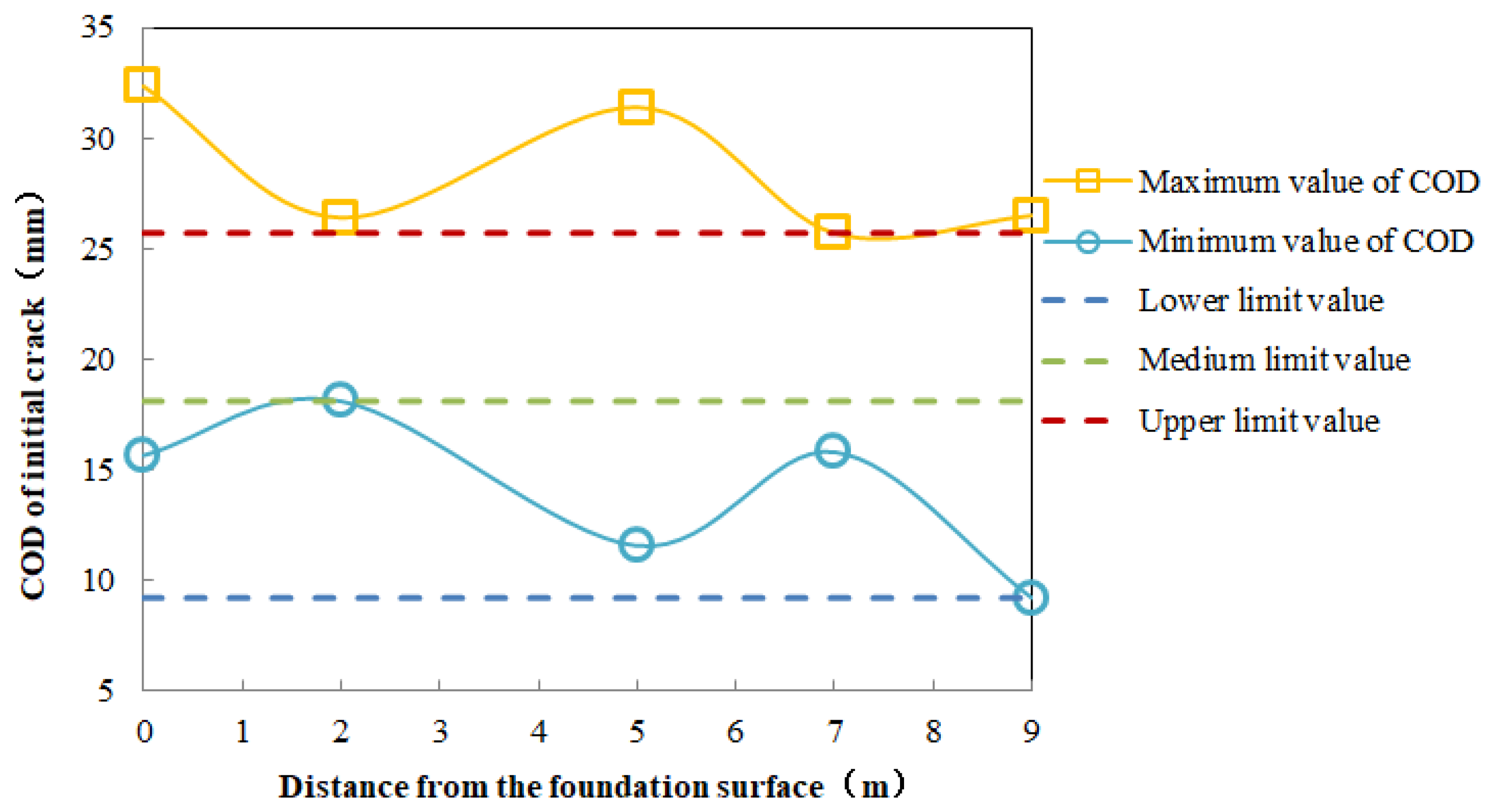
4.3.2. Suggestions on Dam Crack Propagation Treatment
5. Summary and Conclusions
- (1)
- The improved Saenz’s model can be used as a constitutive model in the structural calculation of CSGR with weathered material, and the dam stress may enter the nonlinear elastic stage.
- (2)
- The CSGR with weathered material features larger displacement of the dam body and slightly changed distribution of the stress contour, despite increased maximum principal stress on the downstream surface and intensified fluctuation. It is recommended to increase the material strength and structural thickness of the stepped protective layer on the downstream surface.
- (3)
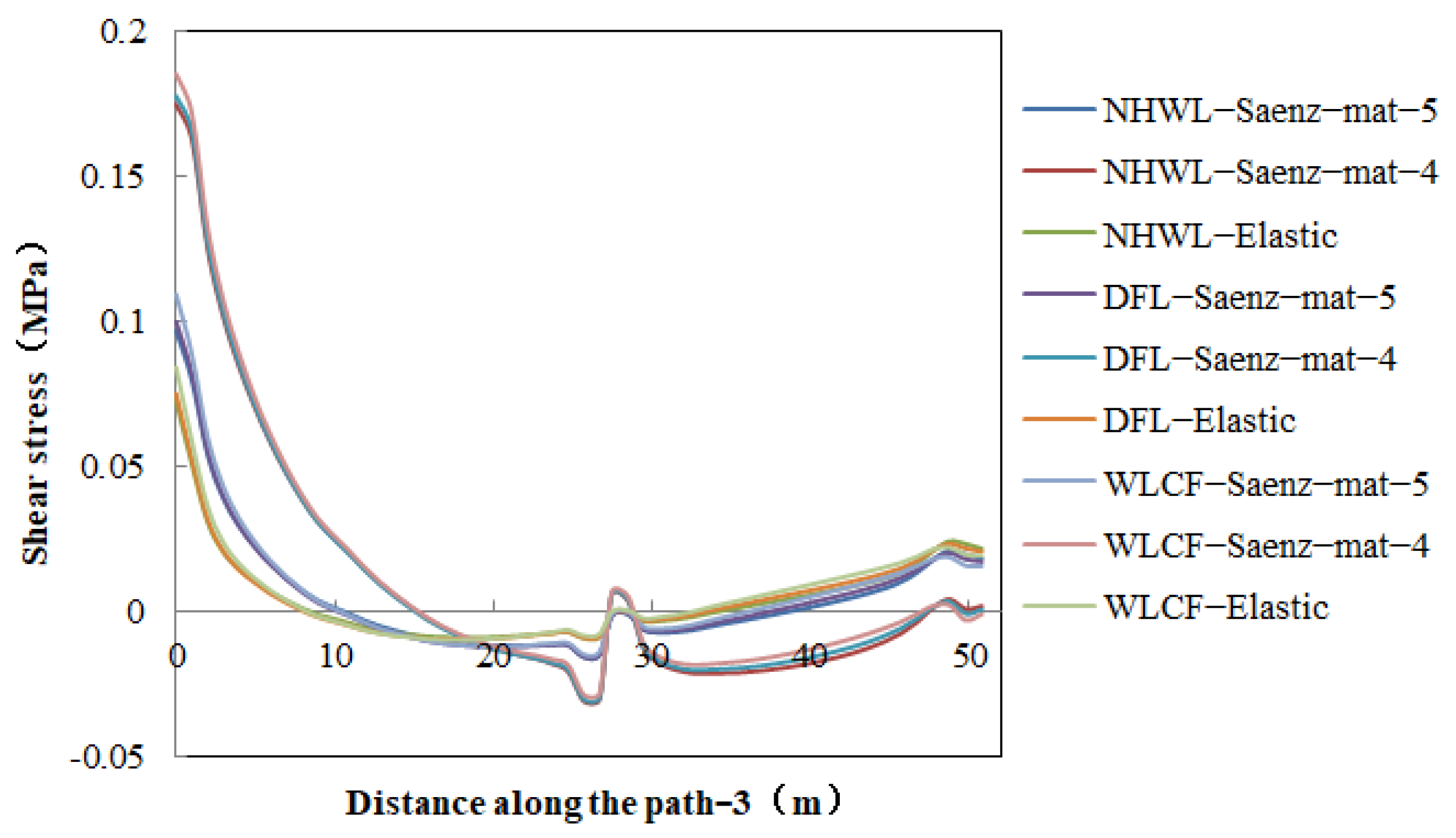
- On the upstream surface, the influence of CSGR with weathered material on the seepage prevention and protection function can be ignored. However, the shear stress on the joint surface between C15 rich-mix CSGR and internal CSGR increases significantly and should be closely monitored during construction.
- (4)
- With the overload safety factor being 2.4, the comprehensive overload capacity of the CSGR dam with weathered material is stronger than that of the RCC gravity dam, while the overload safety factor of the CSGR dam without weathered material is 26.2% higher than that of CSGR dam with weathered material. The safety margin of the dam is 2.75.
- (5)
- According to results on the influence of cracks with different depths and heights, hydraulic fracturing will significantly undermine the safety of the dam body and ensure greater safety. Suggestions on the treatment of dam cracks are given with the COD.
Author Contributions
Funding
Conflicts of Interest
References
- Jia, J.S.; Liu, N.; Zheng, C.Y.; Ma, F.L.; Du, Z.K.; Wang, Y. Studies on cemented material dams and its application. J. Hydraul. Eng. 2016, 3, 315–323. [Google Scholar]
- Jia, J.S.; Lino, M.; Jin, F.; Zheng, C.Y. The Cemented Material Dam: A New, Environmentally Friendly Type of Dam. Engineering 2016, 4, 490–497. [Google Scholar] [CrossRef]
- Jia, J.S.; Zheng, C.Y.; Wang, Y.; Feng, W.; Wang, S. Theoretical discussion and practical progress of cemented material dam construction. Sci. Sin. Tech. 2018, 10, 1049–1056. [Google Scholar] [CrossRef]
- Jiang, M.M.; Li, W.W.; Xiang, X.; Guo, X.W.; Cai, X. Elastoplastic constitutive model with the double-yield surface of cement-sand-gravel material. Water Resour. Hydropower Eng. 2022, 53, 73–87. [Google Scholar]
- Guo, L.; Li, M.R.; Guo, L.X.; Zhang, F.F.; Wang, L.Y. Study on constitutive model of cement sand and gravel material. Yangtze River 2022, 53, 165–168. [Google Scholar]
- Wu, M.X.; Du, B.; Yao, Y.C.; He, X.F. Triaxial tests and a new constitutive model of hardfill material. Rock Soil Mech. 2011, 32, 2241–2250. [Google Scholar]
- Sun, M.Q.; Yang, S.F.; Zhang, J.J. Study on constitutive model for over lean cemented material. Adv. Sci. Technol. Water Resour. 2007, 3, 35–37. [Google Scholar]
- Yang, A.Y.; Zuo, B.J.; Wang, W.Q.; Cao, S.Y.; Zheng, F.; Wang, L.L.; Lin, X. Study on dilatancy equation of cement-sand-gravel materials. Yellow River 2022, 44, 121–124. [Google Scholar]
- Hirose, T. Design Criteria for Trapezoid-Shaped CSG Dams. In Proceedings of the 69th ICOLD Annual Meeting, Dresden, Germany, 3–6 August 2001. [Google Scholar]
- Fujisawa, T.; Nakamura, A.; Kawasaki, H.; Hirayama, D.; Yamaguchi, Y.; Sasaki, T. Material Properties of CSG for the Seismic Design of Trapezoid-Shaped CSG dam. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2001. [Google Scholar]
- Liu, J.L.; He, Y.L.; Xiong, K. Study on nonlinear elasticity constitutive model of Hardfill material. J. Hydraul. Eng. 2013, 44, 451–461. [Google Scholar]
- Lija, R.L.; Beulah, G.A.G.; Krishanu, R.; James, B.P.L. Effect of super absorbent polymer on microstructural and mechanical properties of concrete blends using granite pulver. Struct. Concr. 2020, 22 (Suppl. S1), 898–915. [Google Scholar]
- Lija, R.L.; Beulah, G.A.G.; Krishanu, R.; James, B.P.L. Influence of super absorbent polymer on mechanical, rheological, durability, and microstructural properties of self-compacting concrete using non-biodegradable granite pulver. Struct. Concr. 2020, 22 (Suppl. S1), 1093–1116. [Google Scholar]
- Jiang, J.J.; Liu, X.Z. Finite Element Analysis of Concrete Structures; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Yang, H.C. Structural Design Research on Cemented Sand and Gravel Dam and Engineering Application; China Institute of Water Resources and Hydropower Research: Beijing, China, 2013. [Google Scholar]
- Sun, M.Q.; Yue, P.Z.; Zheng, C.Y. Mechanical characteristics and overload capacity of cement-sand-gravel dam. J. N. China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2012, 33, 56–58. [Google Scholar]
- Xiong, K.; Weng, Y.H.; He, Y.L. Seismic failure modes and seismic safety of Hardfill dam. Water Sci. Eng. 2013, 2, 199–214. [Google Scholar]
- Arefian, A.; Noorzad, A.; Ghaemian, M.; Hosseini, A. Seismic evaluation of cemented material dams–A case study of Tobetsu dam in Japan. J. Earthq. Struct. 2016, 10, 717–733. [Google Scholar] [CrossRef]
- Sun, Y.P. Study on Hydraulic Fracturing Mechanism; Tsinghua University: Beijing, China, 1985. [Google Scholar]
- Jin, F.; Hu, W.; Zhang, C.H.; Wang, J.T. Analogical project comparative study of safety evaluation for xiaowan arch dam. Chin. J. Rock Mech. Eng. 2008, 203, 2027–2033. [Google Scholar]
- Pan, J.W.; Zhang, C.H.; Jin, F. Failure analysis of gravity dams with existing cracks based on extended finite element method. J. Hydroelectr. Eng. 2011, 30, 138–144. [Google Scholar]
- Gan, L.; Wu, J.; Ma, Z.K. Analysis of hydraulic fracturing characteristics of cracks in a high concrete gravity dam heel. Adv. Sci. Technol. Water Resour. 2020, 40, 23–27. [Google Scholar]
- ABAQUS 6.14 Documentation; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- Darwin, D.; Pecknold, A. Nonlinear biaxial stress-strain law for concrete. ASCE J. Eng. Mech. 1977, 103 (EM2), 229–241. [Google Scholar] [CrossRef]
- SL 678-2014; Technical Guideline for Cemented Granular Material Dams; China Water & Power Press: Beijing, China, 2014.
- T/CHINCOLD 002-2021; Specifications for Test Methods for Mechanical Properties of Cemented Sand Gravel and Rock; China Water & Power Press: Beijing, China, 2021.
- Wang, S. Quality Control and Reliability Analysis of Cemented Sand, Gravel, and Rock (CSGR) Dam; China Institute of Water Resources and Hydropower Research: Beijing, China, 2019. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures; China Architecture & Building Press: Beijing, China, 2015.
- Zhu, B.F. The Finite Element Method Theory and Application; China Water & Power Press: Beijing, China, 1998. [Google Scholar]
- SL319-2018; Design Specification for Concrete Gravity Dams; China Water & Power Press: Beijing, China, 2018.
- Jia, B.Z.; Jia, J.S.; Zheng, C.Y.; Li, S.G.; Ding, L.Y. Experimental study of in-situ shear of cemented sand and gravel rocks layers. J. China Inst. Water Resour. Hydropower Res. 2021, 19, 1–7. [Google Scholar]
- Yang, H.C.; Jia, J.S.; Zheng, C.Y. Study and application of the improved finite element equivalent stress method to analyze the strength of gravity dams. J. China Inst. Water Resour. Hydropower Res. 2013, 11, 112–116. [Google Scholar]









| Numbers | Proportion of Weathered Material | Cement | Fly Ash | Total Amounts | Water | Sand Percentage % | Water Reducer % | Water- Binder Ratio |
|---|---|---|---|---|---|---|---|---|
| kg/m3 | ||||||||
| mat-1 | B50% + C50% | 60 | 60 | 120 | 200 | 35 | 0.7 | 1.67 |
| mat-2 | B50% + C50% | 60 | 60 | 120 | 160 | 35 | 0.7 | 1.33 |
| mat-3 | B50% + C50% | 60 | 60 | 120 | 140 | 35 | 0.7 | 1.17 |
| mat-4 | B50% + C50% | 60 | 60 | 120 | 120 | 35 | 0.7 | 1.0 |
| mat-5 | B50% + C50% | 60 | 60 | 120 | 108 | 35 | 0.7 | 0.9 |
| Numbers | E0 (Pa) | Ec (Pa) | εc | ν | Error with Test Curve |
|---|---|---|---|---|---|
| mat-1 | 938,205,008 | 131,327,778 | 0.018445 | 0.2 | 13.5% |
| mat-2 | 5,761,383,766 | 496,744,182.3 | 0.00500392 | 0.2 | 4.79% |
| mat-3 | 6,911,107,832 | 906,005,363.9 | 0.00460222 | 0.2 | 10.47% |
| mat-4 | 7,273,588,265 | 1,361,842,139 | 0.00394821 | 0.2 | 3.29% |
| mat-5 | 13,758,971,722 | 2,126,195,556 | 0.00367616 | 0.2 | 10.93% |
| Numbers | Linear Elastic Limit (MPa) | Elastic Limit (MPa) | Peak Stress (MPa) | Peak Strain |
|---|---|---|---|---|
| mat-1 | 0.83 | 1.97 | 2.82 | 0.018445 |
| mat-2 | 1.07 | 1.93 | 2.75 | 0.00500392 |
| mat-3 | 1.22 | 3.22 | 4.6 | 0.00460222 |
| mat-4 | 1.45 | 4.27 | 6.1 | 0.00394821 |
| mat-5 | 2.69 | 6.02 | 8.6 | 0.00367616 |
| Region | Density (kg/m3) | E (GPa) | ν |
|---|---|---|---|
| CSGR | 2400 | Saenz’s model Linear elastic model is 15 | 0.2 |
| Foundation | 2690 | 10 | 0.25 |
| C20 Concrete | 2400 | 25.5 | 0.2 |
| C15 Concrete | 2400 | 22 | 0.2 |
| C15 rich-mix CSGR | 2400 | 22 | 0.25 |
| C10 rich-mix CSGR | 2400 | 17.5 | 0.25 |
| Calculation Conditions | Content |
|---|---|
| Normal high water level (NHWL) | Dam weight + upstream water level (44 m) + downstream water level (0 m) + uplift pressure |
| Design flood level (DFL) | Dam weight + upstream water level (45.39 m) + downstream water level (7.33 m) + uplift pressure |
| Water level of check flood (WLCF) | Dam weight + upstream water level (47.28 m) + downstream water level (9.58 m) + uplift pressure |
| Type | Region | Density (kg/m3) | E (GPa) | ν | Friction Coefficient | Cohesion (MPa) |
|---|---|---|---|---|---|---|
| CSGR (weathered material) | Dam body | 2400 | mat-5 | 0.2 | 0.75 | 0.8 |
| Foundation | 2690 | 10 | 0.25 | 0.87 | 0.6 | |
| CSGR (unweathered material) | Dam body | 2400 | mat-5 | 0.2 | 1.0 | 0.9 |
| Foundation | 2690 | 10 | 0.25 | 0.87 | 0.6 | |
| RCC gravity dam | Dam body | 2400 | 28 | 0.167 | 1.3 | 1.2 |
| Foundation | 2400 | 20 | 0.2 | 1.0 | 0.9 |
| Type | Region | Density (kg/m3) | E (GPa) | ν | Maximum Principle Stress (MPa) | Failure Displacement (m) |
|---|---|---|---|---|---|---|
| CSGR | Dam body | 2400 | mat-5 | 0.2 | 0.86 | 0.0026 |
| Foundation | 2690 | 10 | 0.25 | 0.7 | 0.0023 |
| Calculation Conditions | Constitutive Model | Displacement (mm) | Dam Heel Stress (MPa) | Dam Toe Stress (MPa) | Maximum Principal Stress (MPa) | Position | Minimum Principal Stress (MPa) | Position |
|---|---|---|---|---|---|---|---|---|
| Normal high water level | Elastic | 7.352 | −0.852 | −1.72 | 0.089 | C10 rich-mix CSGR for the first step downstream | −2.376 | C15 rich-mix CSGR at dam toe |
| Saenz-mat-5 | 7.482 | −0.802 | −1.921 | 0.0564 | −2.285 | |||
| Saenz-mat-4 | 8.937 | −0.716 | −2.214 | 0.1442 | −2.304 | |||
| Design flood level | Elastic | 7.462 | −0.849 | −1.771 | 0.0919 | −2.4 | ||
| Saenz-mat-5 | 7.596 | −0.798 | −1.973 | 0.054 | −2.306 | |||
| Saenz-mat-4 | 9.205 | −0.704 | −2.258 | 0.1517 | −2.343 | |||
| Water level of check flood | Elastic | 7.663 | −0.828 | −1.831 | 0.096 | −2.472 | ||
| Saenz-mat-5 | 7.803 | −0.777 | −2.037 | 0.0569 | −2.374 | |||
| Saenz-mat-4 | 9.371 | −0.674 | −2.328 | 0.1595 | −2.413 |
| Constitutive Model | Displacement Contour | Vertical Stress Contour | Maximum Principal Stress Contour | Minimum Principal Stress Contour |
|---|---|---|---|---|
| Elastic |  |  |  | 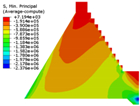 |
| Saenz-mat-5 | 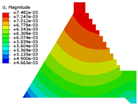 | 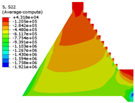 | 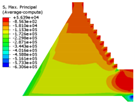 | 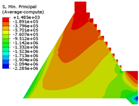 |
| Saenz-mat-4 | 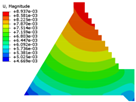 | 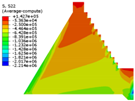 | 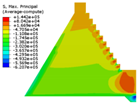 | 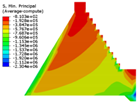 |
| Numbers | Content |
|---|---|
| Path-1 | Outside upstream + dam crest + outside downstream + outside cushion |
| Path-2 | Joint surface between C20 reinforced concrete panel and C15 rich-mix CSGR + dam crest+ joint surface between C10 rich-mix CSGR and internal CSGR + joint surface between cushion and internal CSGR |
| Path-3 | Joint surface between C15 rich-mix CSGR and internal CSGR + dam crest + joint surface between C10 rich-mix CSGR and internal CSGR + joint surface between cushion and internal CSGR |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Jia, J.; Zheng, C.; Wu, Y. The Bearing Capacity of Dam Body Structure with Cemented and Weathered Materials: A Constitutive Model. Appl. Sci. 2022, 12, 8572. https://doi.org/10.3390/app12178572
Zhao L, Jia J, Zheng C, Wu Y. The Bearing Capacity of Dam Body Structure with Cemented and Weathered Materials: A Constitutive Model. Applied Sciences. 2022; 12(17):8572. https://doi.org/10.3390/app12178572
Chicago/Turabian StyleZhao, Lei, Jinsheng Jia, Cuiying Zheng, and Yangfeng Wu. 2022. "The Bearing Capacity of Dam Body Structure with Cemented and Weathered Materials: A Constitutive Model" Applied Sciences 12, no. 17: 8572. https://doi.org/10.3390/app12178572
APA StyleZhao, L., Jia, J., Zheng, C., & Wu, Y. (2022). The Bearing Capacity of Dam Body Structure with Cemented and Weathered Materials: A Constitutive Model. Applied Sciences, 12(17), 8572. https://doi.org/10.3390/app12178572






