A Hybrid Method for Structural Modal Parameter Identification Based on IEMD/ARMA: A Numerical Study and Experimental Model Validation
Abstract
:1. Introduction
2. Theoretical Background of Proposed Method
2.1. EMD
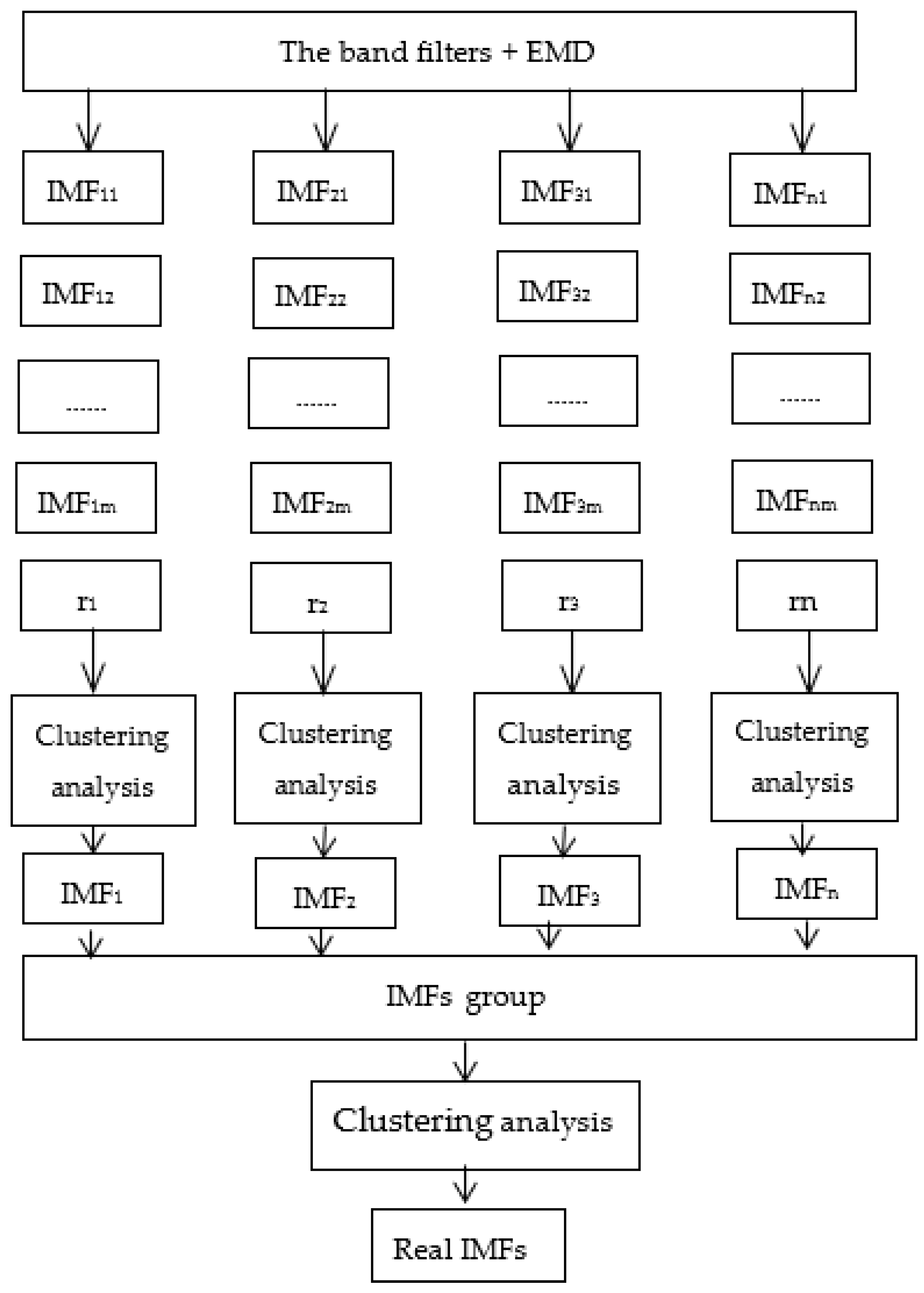
2.2. IEMD
- (1)
- Use fast Fourier transform (FFT) to obtain the spectrum of the acceleration response signal, seeking each peak frequency as the center frequency of the band-pass filter, and then let the signal go through to the specific frequency-band filter. Namely, using FFT to analyze the acceleration signal , utilizing the frequency spectrum of FFT to choose the peak frequency, and then roughly estimate each frequency range, for example, , then let the signal pass the band-pass filter with specific bandwidth , (here , ) eventually, the signal will be differentiated into limited sub-band acceleration signals.
- (2)
- After filtering, each sub-band signal is processed by EMD, and IMFs component of each sub-signal are obtained successively.
- (3)
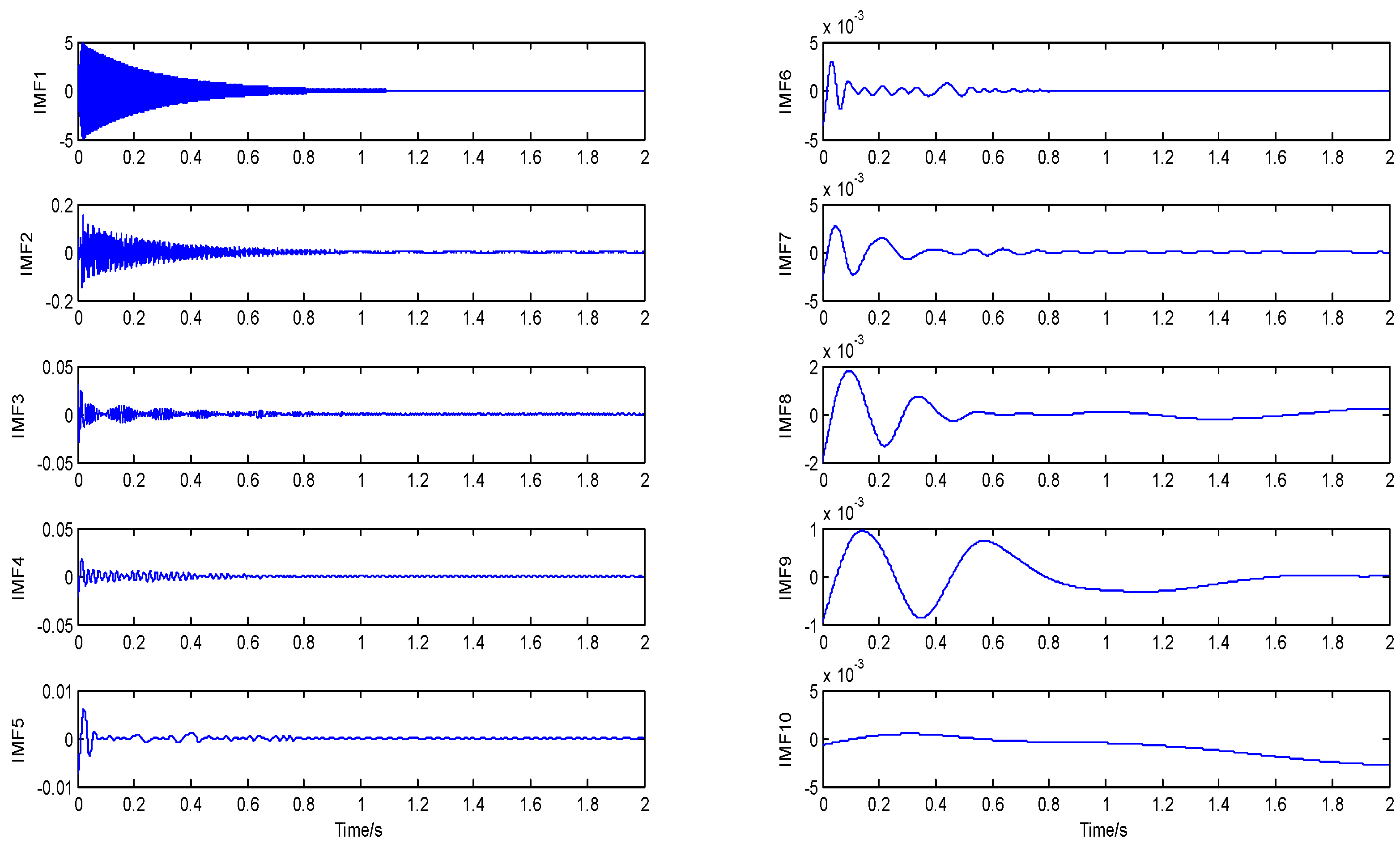
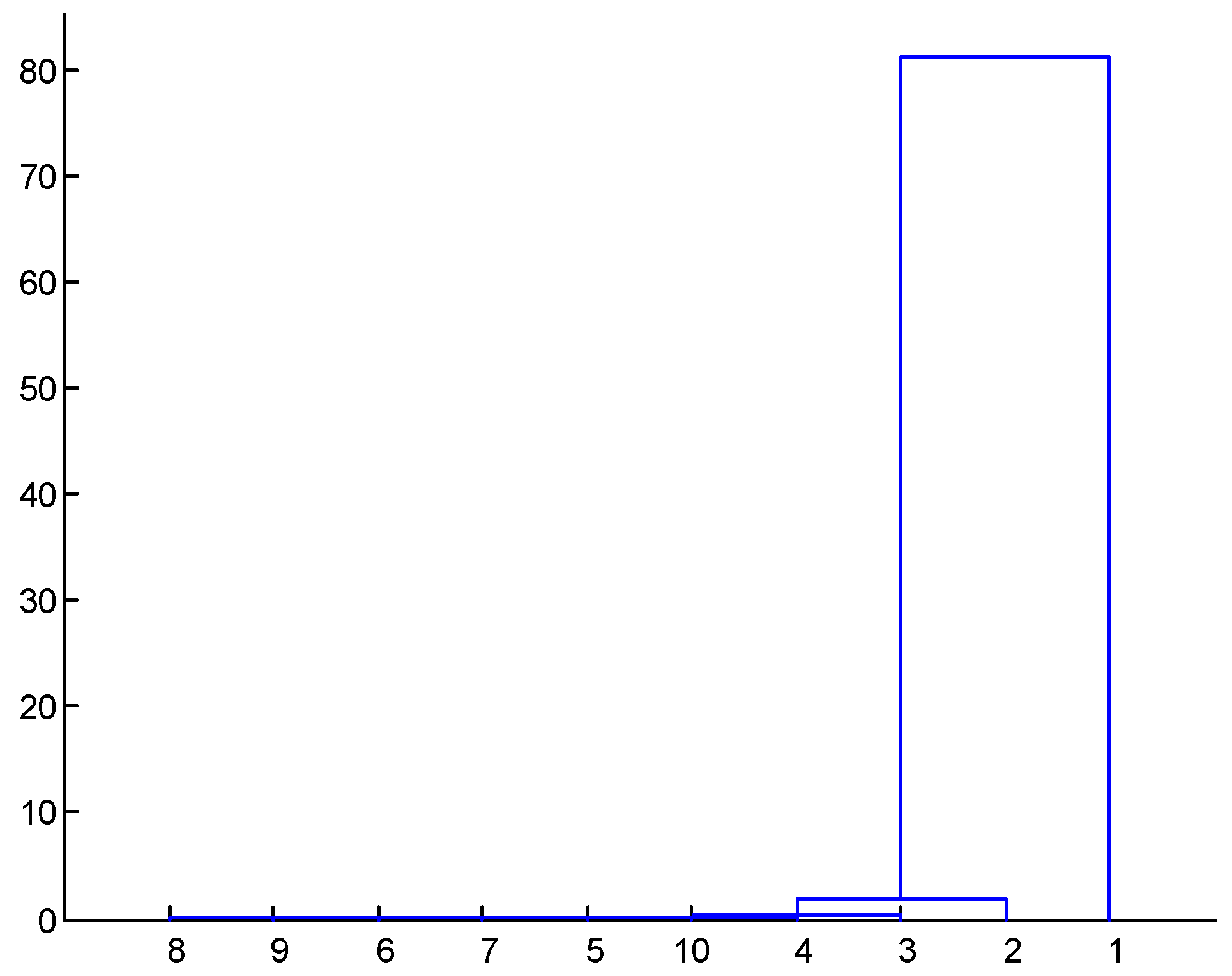
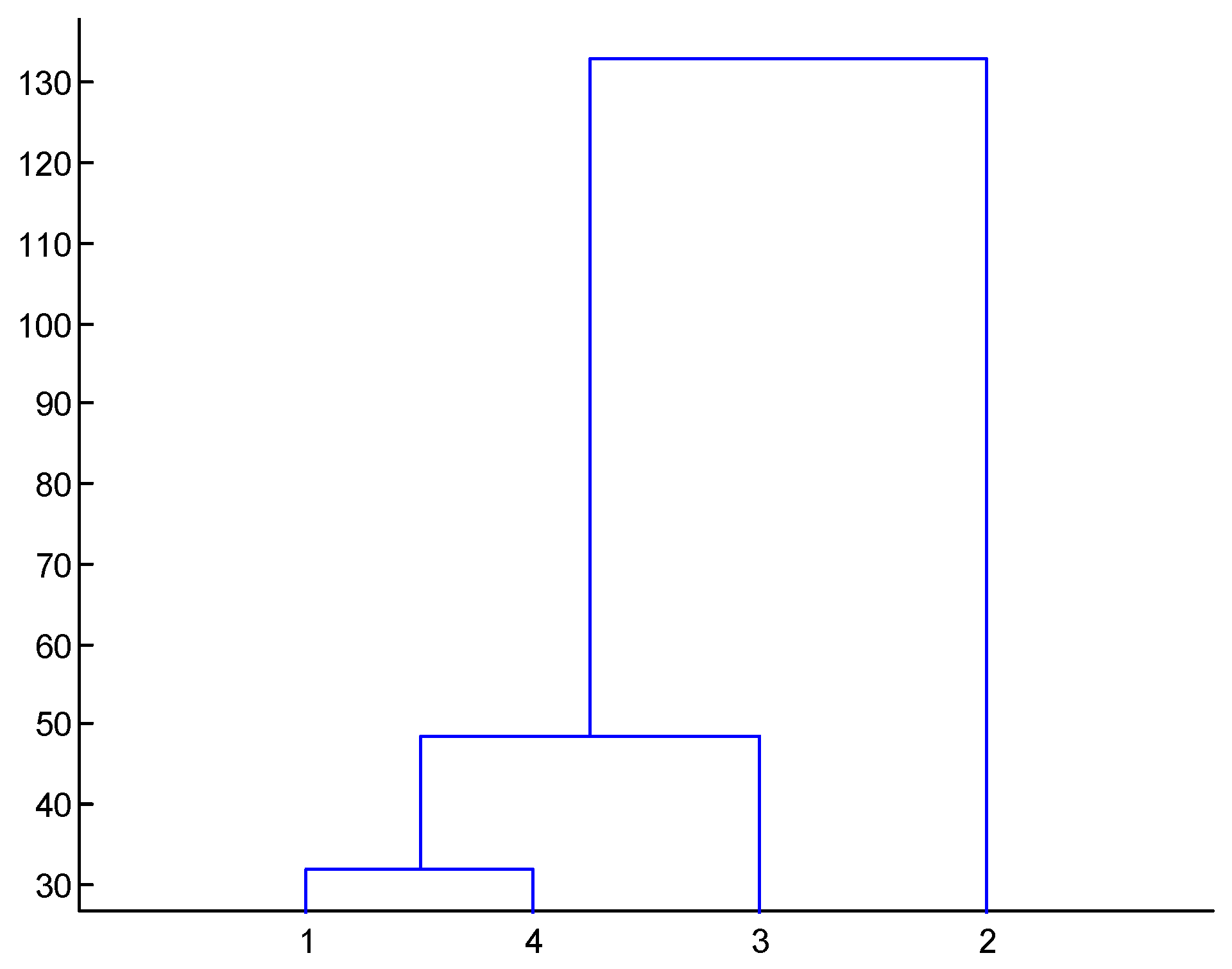
- After the signal is processed according to the two steps mentioned above, multiple IMF groups are obtained. The key problem is how to identify the real IMFs from multiple IMF groups. In view of this, cluster analysis [26] using the multivariate data analysis method is introduced in this paper to solve the problem of the determination of the real IMF. Through a two-time cluster analysis, the screened IMF can be guaranteed to be the real IMF, and there is no mode mixing among the IMFs.
2.3. ARMA
- (1)
- In a practical application, a high-order differential equation can be used to describe the relationship between an incentive and response for the N degrees of freedom linear system in a discrete time domain, which is composed of a series of time series in different times; namely, the ARMA time-series model in Equation (2), this equation can be used to represent specific relations between xt (response data sequence) and xt−k (history value).
- (2)
- According to the generalized Yule–Walker equation (Equation (3)), the least squares solution (Equation (4)) of the system can be obtained using the pseudo-inverse method, and the autoregressive coefficient ak (k = 1, 2, …, 2N) can be obtained.
- (3)
- The sliding average model coefficient bk (1, 2, …, 2N) can be obtained by using the nonlinear equations (Equation (5)).
- (4)
- ak and bk can be obtained from Equations (4) and (5), and the modal parameters of the system can be calculated through the transfer function expression of the ARMA model. The transfer function of the ARMA model is shown in Equation (6):
- (5)
- Modal frequency and damping ratio obtained using Equation (7), as shown in Equation (8):
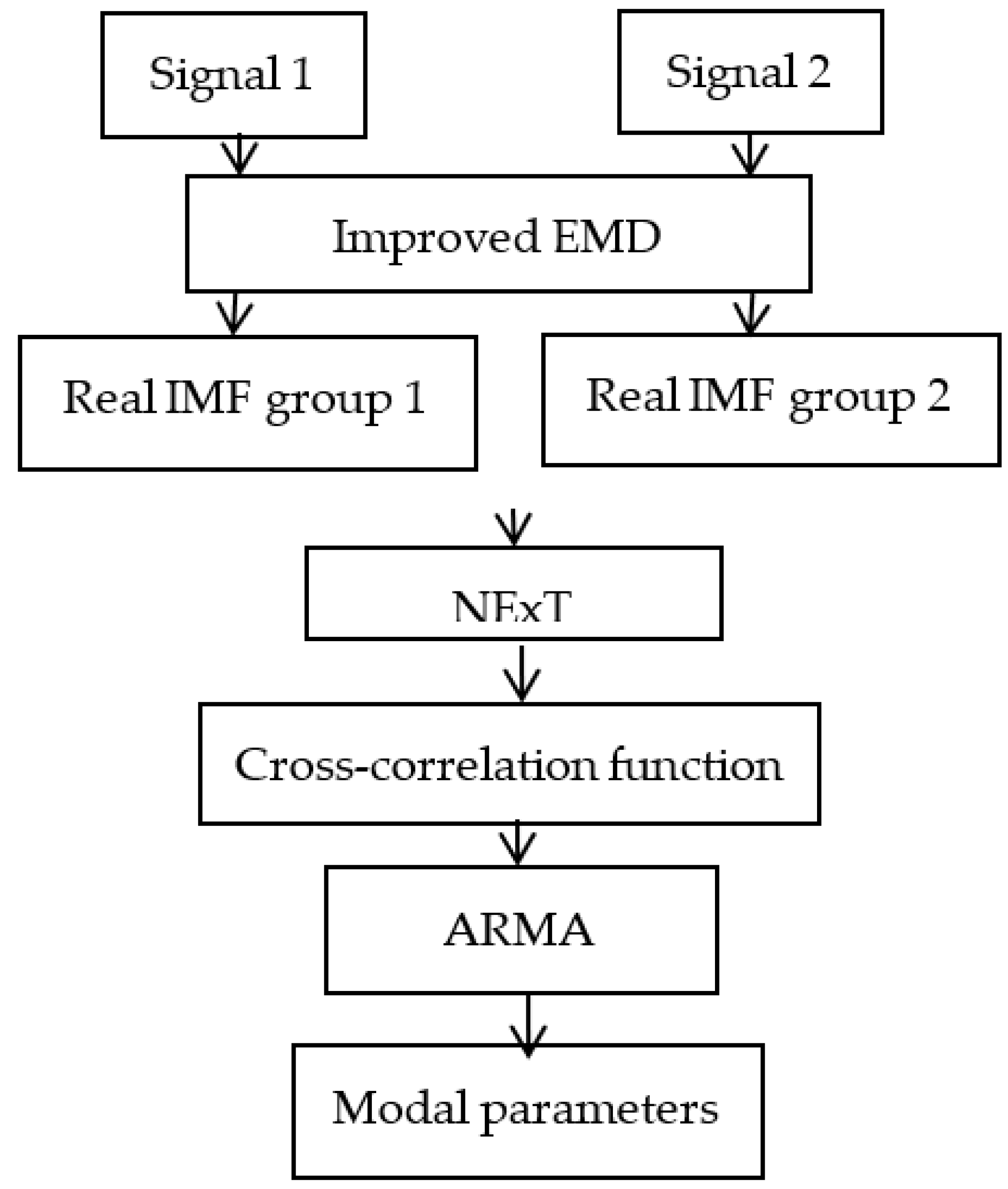
3. The Principle of IEMD and ARMA
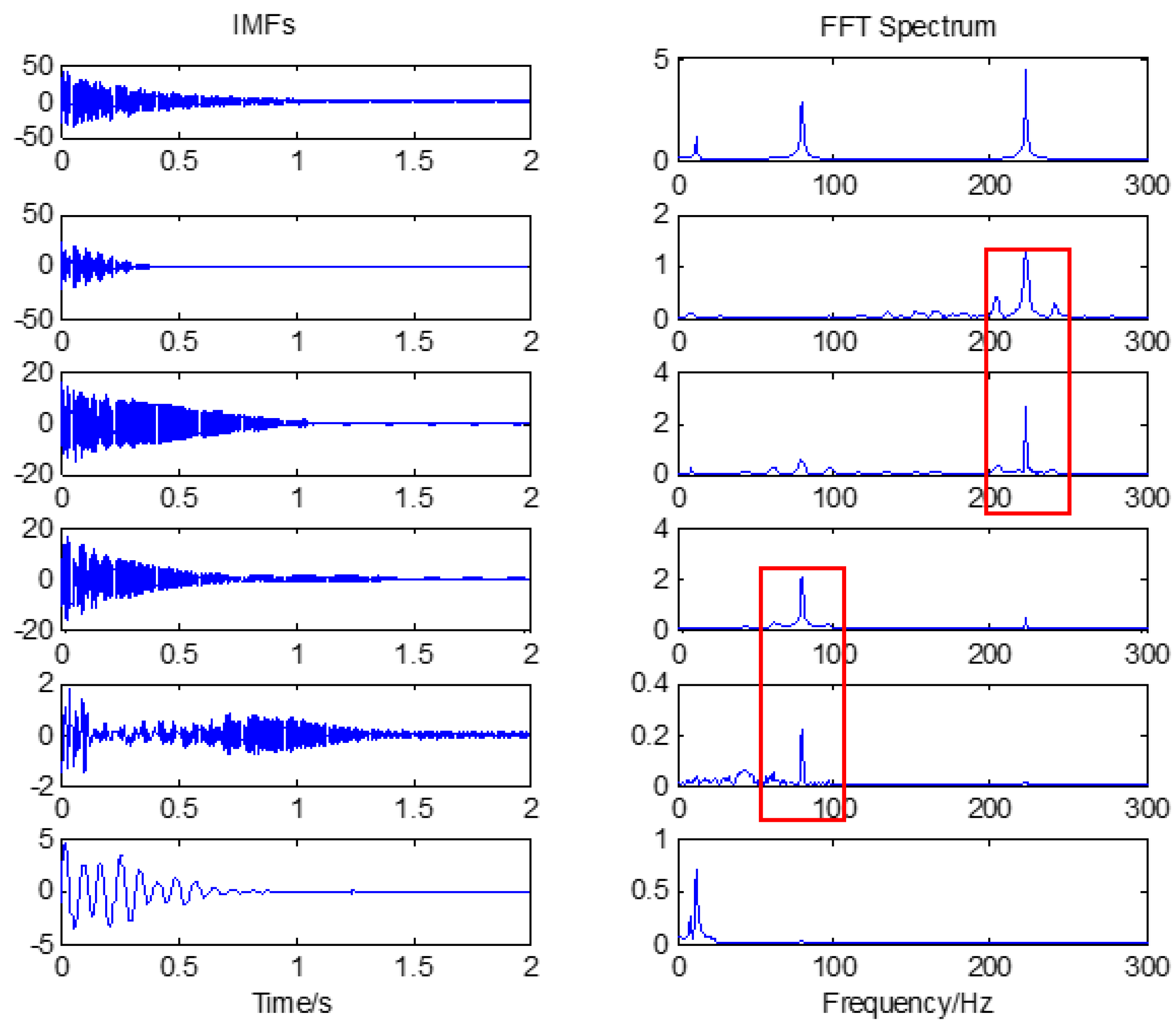
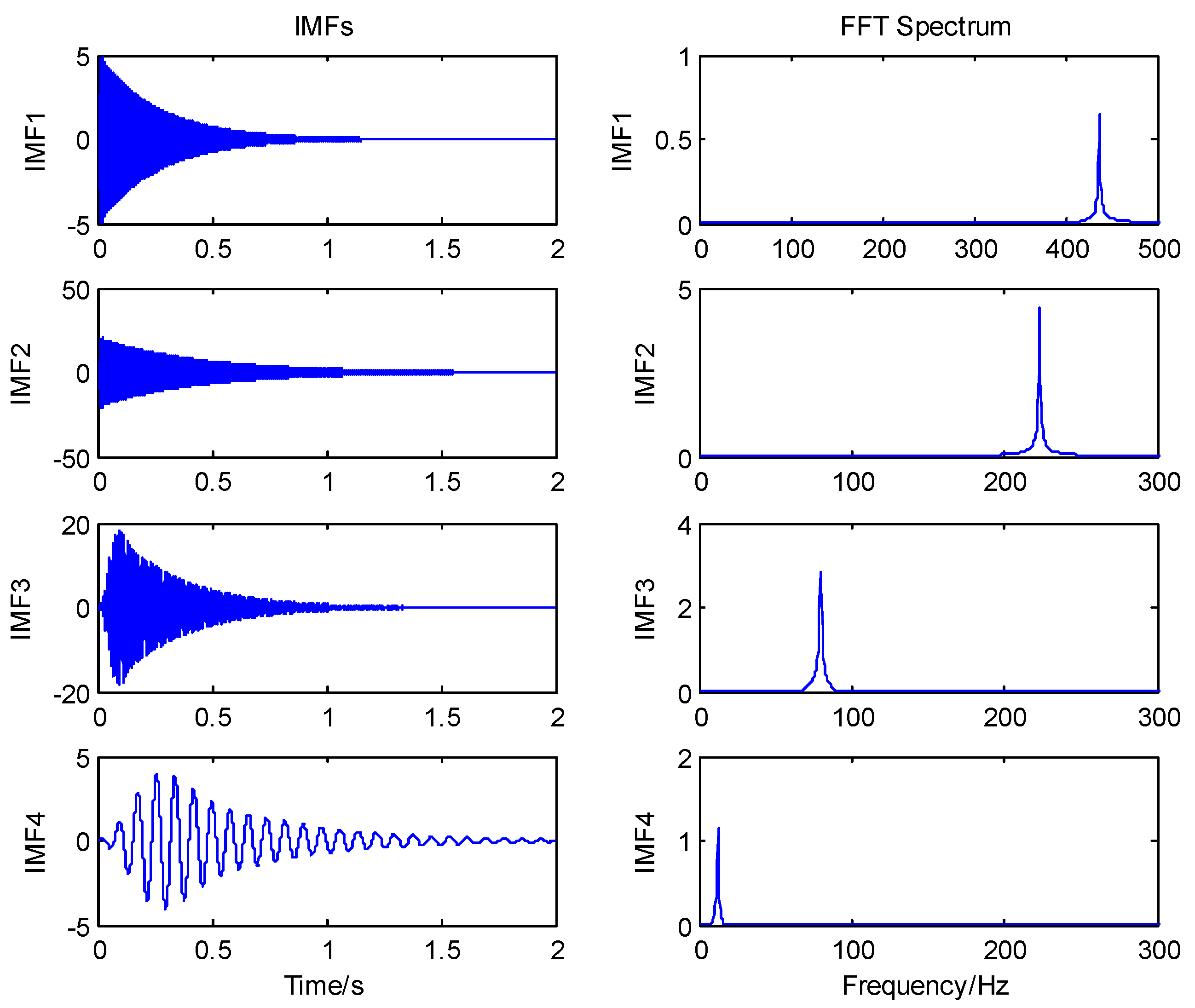
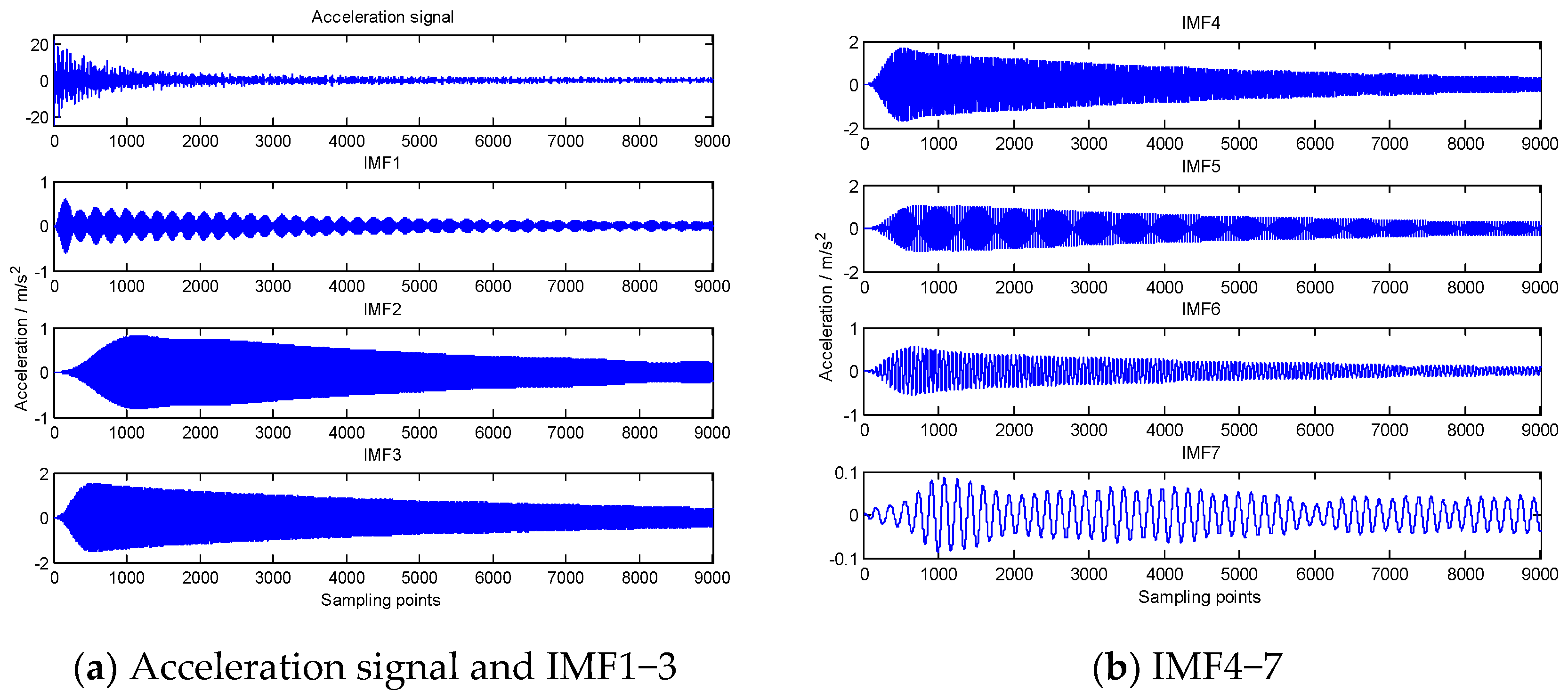
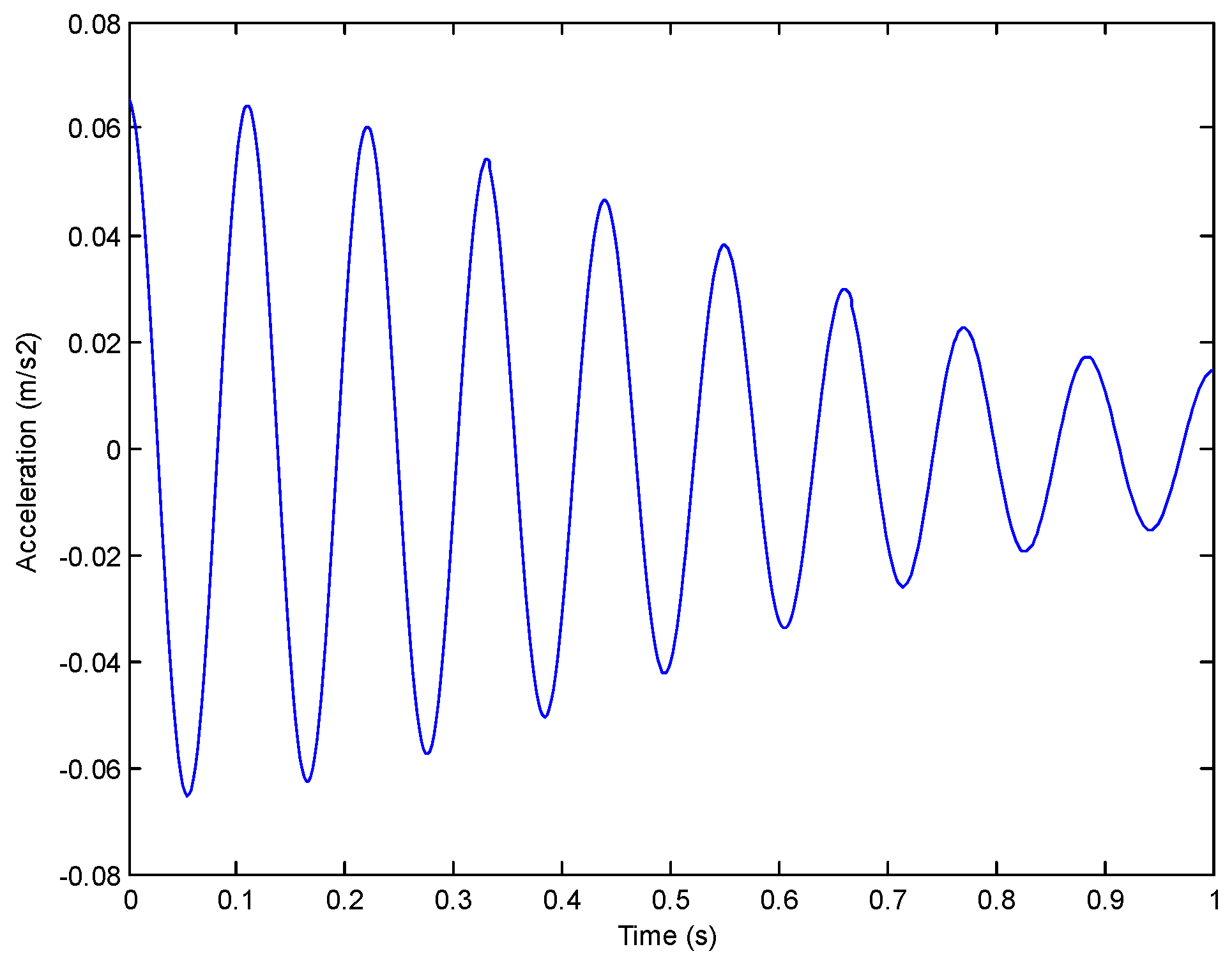
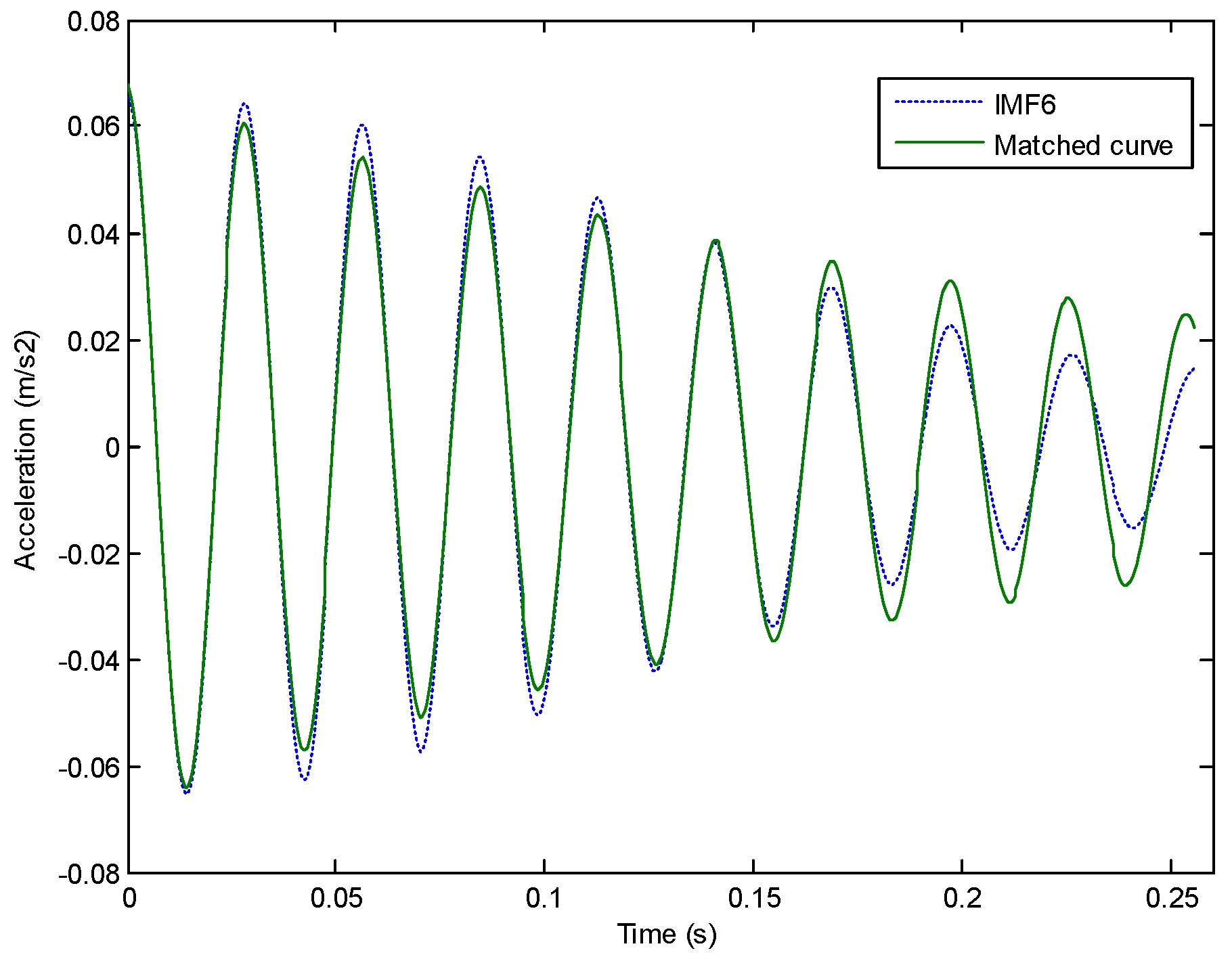
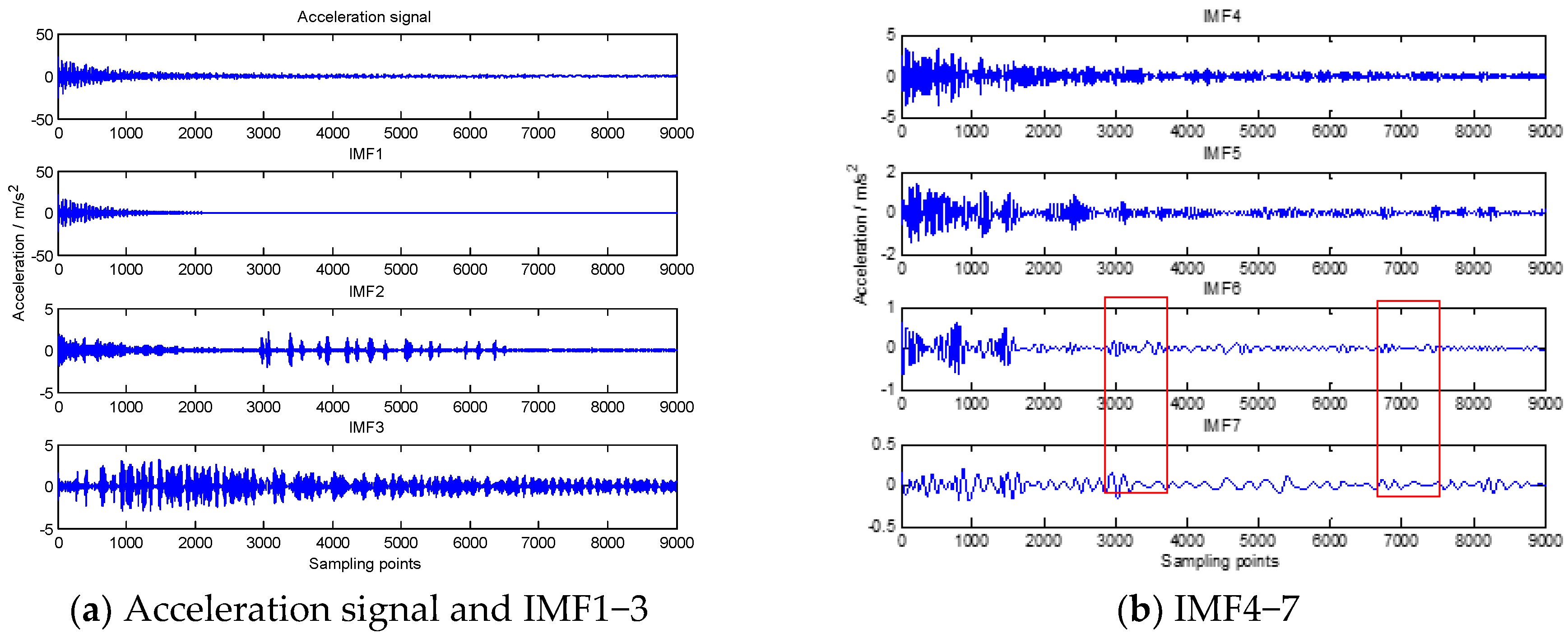
4. Numerical Validation
5. Test Verification
5.1. Experiment
5.2. Identification Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Jiang, X.; Zhang, M.; Zhang, J.; Sun, H.; Li, X. Modal parameters identification of bridge by improved stochastic subspace identification method with Grubbs criterion. Meas. Control 2021, 54, 457–464. [Google Scholar] [CrossRef]
- Mao, J.; Yang, C.; Wang, H.; Zhang, Y.; Lu, H. Bayesian Operational Modal Analysis with Genetic Optimization for Structural Health Monitoring of the Long-Span Bridge. Int. J. Struct. Stab. Dyn. 2022, 22, 225001. [Google Scholar] [CrossRef]
- Ahmed, B.; Dinu, F.; Marginean, I. Structural health monitoring of steel frame structure by experimental modal parameter identification. Adv. Eng. Forum. 2020, 37, 1–13. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G.; Pollet, T.; Schueremans, L. Stochastic subspace techniques applied to parameter identification of civil engineering structures. In New Advances in Modal Synthesis of Large Structures: Nonlinear, Damped and Nondeterministic Cases; Katholieke Universiteit Leuven: Leuven, Belgium, 1995. [Google Scholar]
- Clemente, P.; Bongiovanni, G.; Buffarini, G.; Saitta, F. Structural health status assessment of a cable-stayed bridge by means of experimental vibration analysis. J. Civ. Struct. Health Monit. 2019, 9, 655–669. [Google Scholar] [CrossRef]
- Nicoletti, V.; Arezzo, D.; Carbonari, S.; Gara, F. Dynamic monitoring of buildings as a diagnostic tool during construction phases. J. Build. Eng. 2022, 46, 103764. [Google Scholar] [CrossRef]
- Pereira, S.; Magalhães, F.; Gomes, J.P.; Cunha, Á.; Lemos, J.V. Vibration-based damage detection of a concrete arch dam. Eng. Struct. 2021, 235, 112032. [Google Scholar] [CrossRef]
- Peeters, B.; Roeck, G.D. Reference-based stochastic subspace identification in civil engineering. In Proceedings of the Second International Conference on Identification in Engineering System, Swansea, UK, 29–31 March 1999; pp. 639–648. [Google Scholar]
- James, G.H.; Carne, T.G.; Lauffer, J.P. The Natural Excitation Technique for Modal Parameter Extraction from Operating Wind Turbines; No. SAND92-1666, UC-261; Sandia National Laboratories: Albuquerque, NM, USA, 1993. [Google Scholar]
- Yao, X.J.; Yi, T.H.; Qu, C.X. Autoregressive spectrum-guided variational mode decomposition for time-varying modal identification under nonstationary conditions. Eng. Struct. 2022, 251, 113543. [Google Scholar] [CrossRef]
- Yuan, Q.; He, J. Modal parameter identification of large cable-stayed bridge based on IEEMD and ARMA algorithm. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2016, 35, 121. [Google Scholar]
- Akaike, H. Power spectrum estimation through autoregressive model fitting. Ann. Inst. Stat. Math. 1969, 21, 407–419. [Google Scholar] [CrossRef]
- Xu, S.D.; Wang, F.Q. Mode parameter identification of engineering structure based on ARMA model. Ind. Archit. 2007, 37, 20–22. [Google Scholar]
- Neto, A.C.; Faria, T. Boostrap for order identification ARMA(p,q) structures. Indep. J. Manag. Prod. 2015, 6, 169–181. [Google Scholar]
- Abo-Hammour, Z.S.; Alsmadi, M.K.; Al-Smadi, A.M. A Novel Technique for ARMA Modelling with Order and Parameter Estimation Using Genetic Algorithms. In Proceedings of the NDT 2010—Second International Conference, Prague, Czech Republic, 7–9 July 2010. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Yang, J.N.; Lei, Y.; Lin, S.; Huang, N. Hilbert-Huang Based Approach for Structural Damage Detection. J. Eng. Mech. 2004, 130, 85–95. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Mean-optimized mode decomposition: An improved EMD approach for non-stationary signal processing. ISA Trans. 2020, 106, 392–401. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-Khah, M.; Catalao, J.P.S. Improved EMD-Based Complex Prediction Model for Wind Power Forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Cai, J.H.; Hu, W.W.; Wang, X.C. Fault diagnosis of rolling bearing based on EMD-ICA de-noising. J. Mach. Des. 2015, 32, 17–23. [Google Scholar]
- Yuan, Y.; Li, B.; Yao, S. Improved Empirical Mode Decomposition Denoised by Singular Value Decomposition. J. Vib. Meas. Diag. 2010, 30, 325–338. [Google Scholar]
- Wu, Z.H.; Huang, N.E. Ensemble Empirical mode decomposition-a noise assisted data analysis method. Adv. Adap. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Charbonnel, P. Fuzzy-driven strategy for fully automated modal analysis: Application to the SMART2013 shaking-table test campaign. Mech. Syst. Signal Process. 2020, 152, 107388. [Google Scholar] [CrossRef]
- Tronci, E.; de Angelis, M.; Betti, R.; Altomare, V. Multi-stage semi-automated methodology for modal parameters estimation adopting parametric system identification algorithms. Mech. Syst. Signal Pract. 2022, 165, 108317. [Google Scholar] [CrossRef]
- Yao, X.-J.; Yi, T.-H.; Zhao, S.-W.; Qu, C.-X.; Liu, H. Fully Automated Operational Modal Identification Using Continuously Monitoring Data of Bridge Structures. J. Perform. Constr. Facil. 2021, 35, 04021041. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, X.; Liu, L.; Yang, W. Fuzzy-clustering-based All Factor Automatous Validation Approach of Modal Parameters of Structures. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 811–816. [Google Scholar]
- Liu, J.L.; Yu, A.H.; Wu, C.; Sheng, Y.; Luo, Y.P. A New Method for Modal Parameter Identification of Civil Engineering Structures under Unknown Excitation. Noise Vib. Control 2019, 39, 6–12. [Google Scholar]
- Fu, C.; Jiang, S. A Hybrid Data-Fusion System by Integrating CFD and PNN for Structural Damage Identification. Appl. Sci. 2021, 11, 8272. [Google Scholar] [CrossRef]

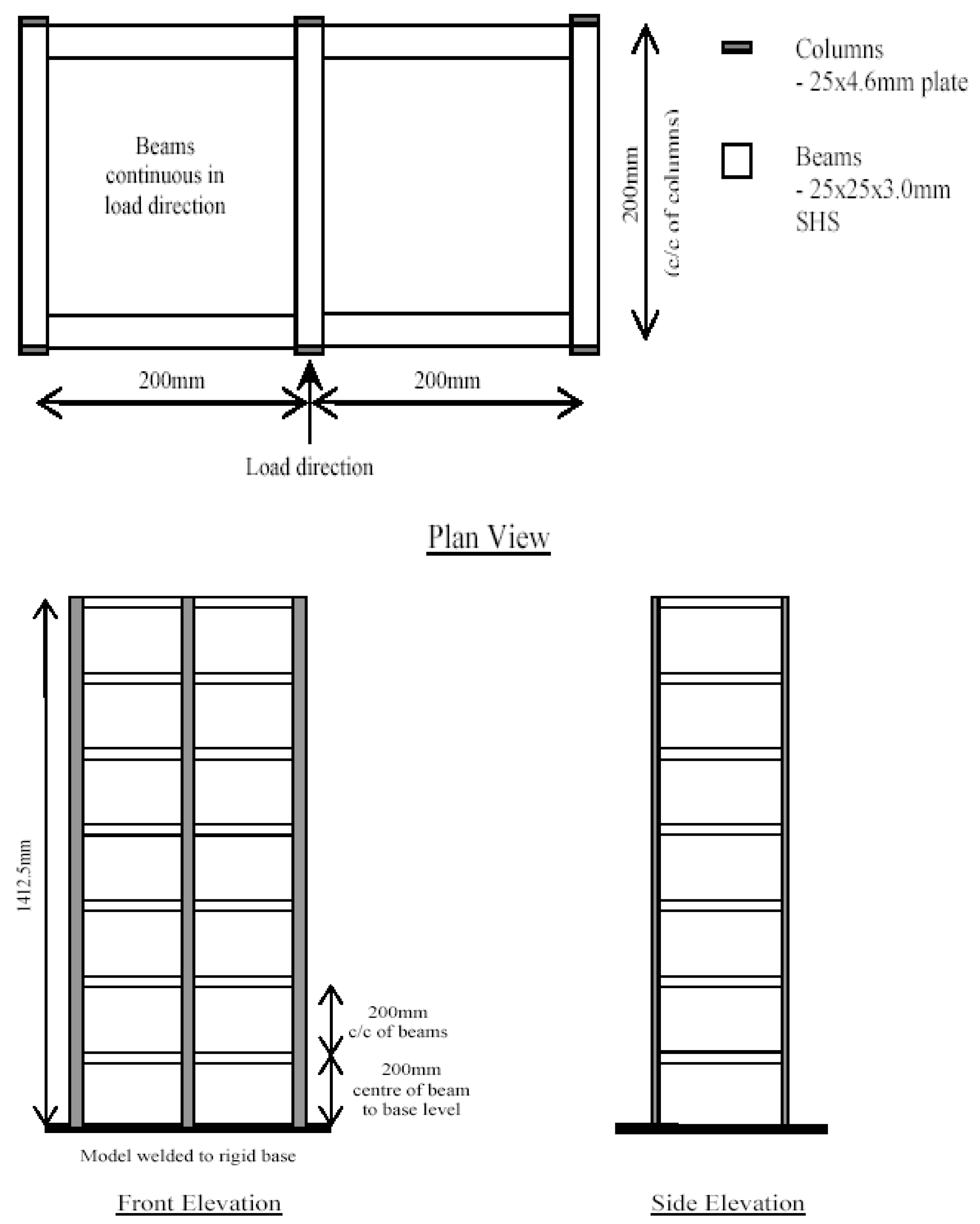



| Geometrical Features | Beam | Column |
|---|---|---|
| Sectional dimension | 25 mm × 25 mm × 3 mm (SHS) | 25 mm × 4.6 mm |
| Sectional area A/m2 | 286 × 10−6 | 115 × 10−6 |
| Inertia moment I/m4 | 2.41 × 10−8 | 7.78 × 10−10 |
| Young modulus E/Pa | 206 × 109 | 206 × 109 |
| Volume density ρ [kg/m3] | 7850 | 7850 |
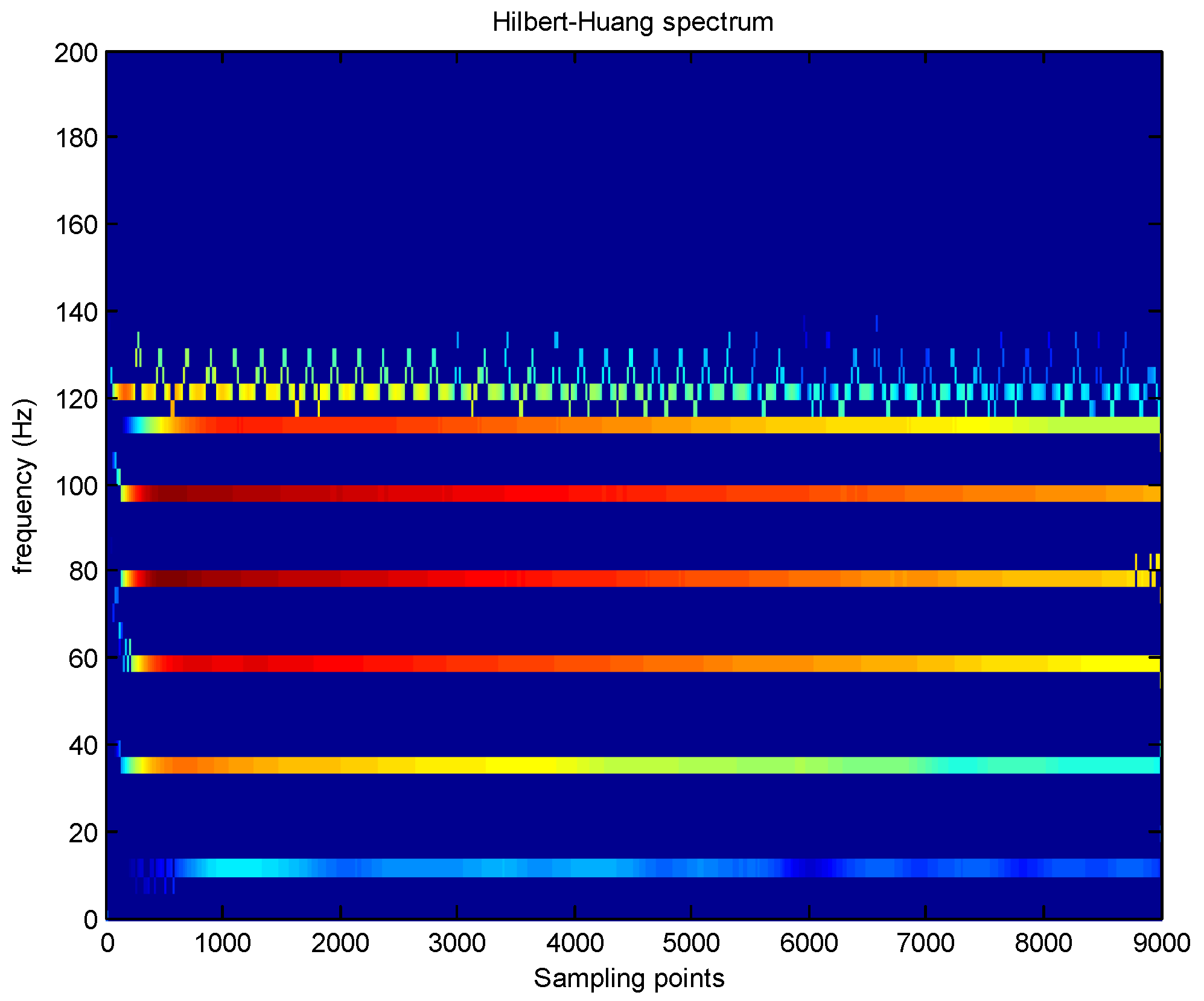
| Mode | Theoretical Value [28] | Proposed Method | HHT | NExT/ARMA |
|---|---|---|---|---|
| 1 | 11.7 | 11.86 | 13.35 | -- |
| 2 | 35.2 | 35.5 | 8.96 | 35.6 |
| 3 | 58.6 | 58.58 | 35.56 | 58.54 |
| 4 | 80.1 | 79.94 | 58.30 | 80.75 |
| 5 | 99.6 | 98.71 | 99.48 | 98.76 |
| 6 | 113.3 | 113.4 | 67.92 | 113.27 |
| 7 | 123.0 | 122.84 | 293.22 | 122.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Jiang, S.-F. A Hybrid Method for Structural Modal Parameter Identification Based on IEMD/ARMA: A Numerical Study and Experimental Model Validation. Appl. Sci. 2022, 12, 8573. https://doi.org/10.3390/app12178573
Fu C, Jiang S-F. A Hybrid Method for Structural Modal Parameter Identification Based on IEMD/ARMA: A Numerical Study and Experimental Model Validation. Applied Sciences. 2022; 12(17):8573. https://doi.org/10.3390/app12178573
Chicago/Turabian StyleFu, Chun, and Shao-Fei Jiang. 2022. "A Hybrid Method for Structural Modal Parameter Identification Based on IEMD/ARMA: A Numerical Study and Experimental Model Validation" Applied Sciences 12, no. 17: 8573. https://doi.org/10.3390/app12178573
APA StyleFu, C., & Jiang, S.-F. (2022). A Hybrid Method for Structural Modal Parameter Identification Based on IEMD/ARMA: A Numerical Study and Experimental Model Validation. Applied Sciences, 12(17), 8573. https://doi.org/10.3390/app12178573






