A Framework for Assessing the Performance Capabilities of Rock Fall Protections for Hazard Analysis and Zoning
Abstract
:1. Introduction
2. Rock Fall Hazard Zoning and Protection Measures
3. Methodology for Evaluating the Effectiveness of Rock Fall Protections
- (a)
- An initial phase of field survey and data collection, which includes information on the current hazard scenario threatening a site and the actual conditions of existing protection measures;
- (b)
- A central phase of evaluation of the actual effectiveness of the protections against the current hazard;
- (c)
- A final phase, in which the hazard zoning at the study site is possibly re-evaluated, based on the results of the previous phase (i.e., according to the influence that the protections in their actual state have on the hazard affecting the site), and suggestions are given for possible further actions to be taken.
3.1. Hazard Scenario and Existing Protection Measures
- Environmental factors—they are related to the site where the protection is installed and account for issues in connection with the interaction between the environment and the measure, such as: the presence of spring or torrents, which could generate erosion around the foundations of certain protections and make them unstable and/or expose them to other physical/chemical agents; possible frequent snow, which could fill up the nets of a barrier fence or reduce the effective height of an embankment; freezing and thawing cycles, which could affect the behaviour of some materials used for the protections, etc. A list of all factors of this type included so far in the methodology is shown in Table 1;
- Factors related to the concept of the protection (general design and installation)—they represent potential issues generally common to most (or all) types of protections included in the methodology and consider effects such as: the possibility for structural measures of undergoing plastic deformations (e.g., barrier fences), possible redundancy of main structural elements which might help redistributing the efforts after an impact, consistency in the structure of the protection (e.g., such as in an embankment) as opposed to the presence of potential weak points (i.e., posts of a barrier fence rather than the steel wire mesh), respect of current norms, etc. These factors are also listed in Table 1.
- Category 1: flaws/faults due to lack of maintenance, e.g., posts of barrier fences damaged by impacts of blocks, barrier fences or embankments, or ditches partially filled up by blocks from previous events, nets of barrier fences or wire meshes loosened and/or damaged, corrosion on metal elements of the protections, etc.
- Category 2: issues related to the original design of a given type of protection, including potential stability problems of embankments or barrier fences, inadequate protection against corrosion of the metallic elements of the protection, differences in the original positioning of the protection measure compared to the position required at present, as a consequence of the possible evolution of the events to be mitigated, etc.;
- Category 3: causes of malfunctioning of the measures due to installation problems, such as sealing injections for anchors/nails, control of the applied stress in the anchors, etc.
- Category 4: causes of malfunctioning originated by the fact that the measure has attained (or passed) its life span.
3.2. Analysis of the Effectiveness of the Protection Measures
- 0 means the corresponding factor has such a high influence on the behaviour of the protection that it makes it totally unserviceable (associated to highest severity);
- 1 corresponds to null or negligible influence of the factor on the performance of the protection measure (associated to lowest severity), i.e., the protection can work as per design.
- A reduction in the capacity of the protection in terms of energy and return period retention all over the threatened areas (coefficients rn), the energy and return period retention capacity being hereby defined as the capacity of a protection measure of preventing a given location on the slope from being affected by values of energy E > Em and return period T < Tm, which is not compatible with the desired mitigation effect H(Em, Tm);
- A reduction of the nominal energy absorption capacity Eopt established at the time of the design (coefficients en);
- A reduction of the nominal effective height Dopt established at the time of the design, preventing a given location on the slope—and, possibly, beyond—from being affected by a value of frequency of reach Pr higher than a desired value (coefficients tn).
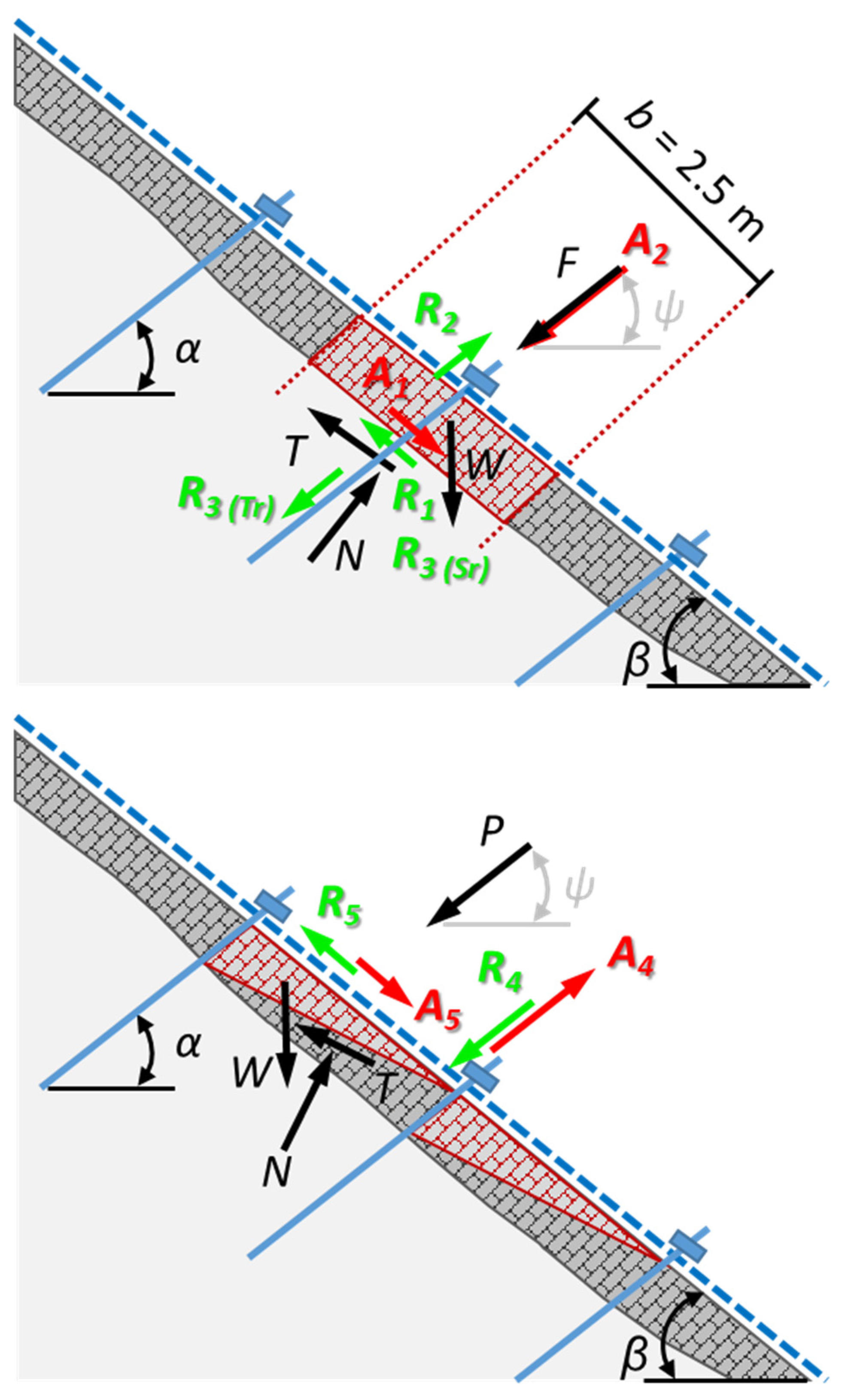
3.2.1. Types of Protections, Performance Capacity and Penalty Coefficients
Protection Measures at the Rock Fall Source Area
Protection Measures in the Propagation Zone
3.2.2. Evaluation of the Actual Performance Capacity
- Very low 1.00–0.95
- Low 0.95–0.90
- Moderate 0.90–0.80
- High 0.80–0.70
- Very high <0.70
Effective Performance Capacity: Condition 0
Reduced Performance Capacity: Conditions 1 to 4
3.3. Re-Evaluation of Hazard at the Study Site
3.3.1. Protection Measures at the Rock Fall Source Area
3.3.2. Protection Measures in the Propagation Zone
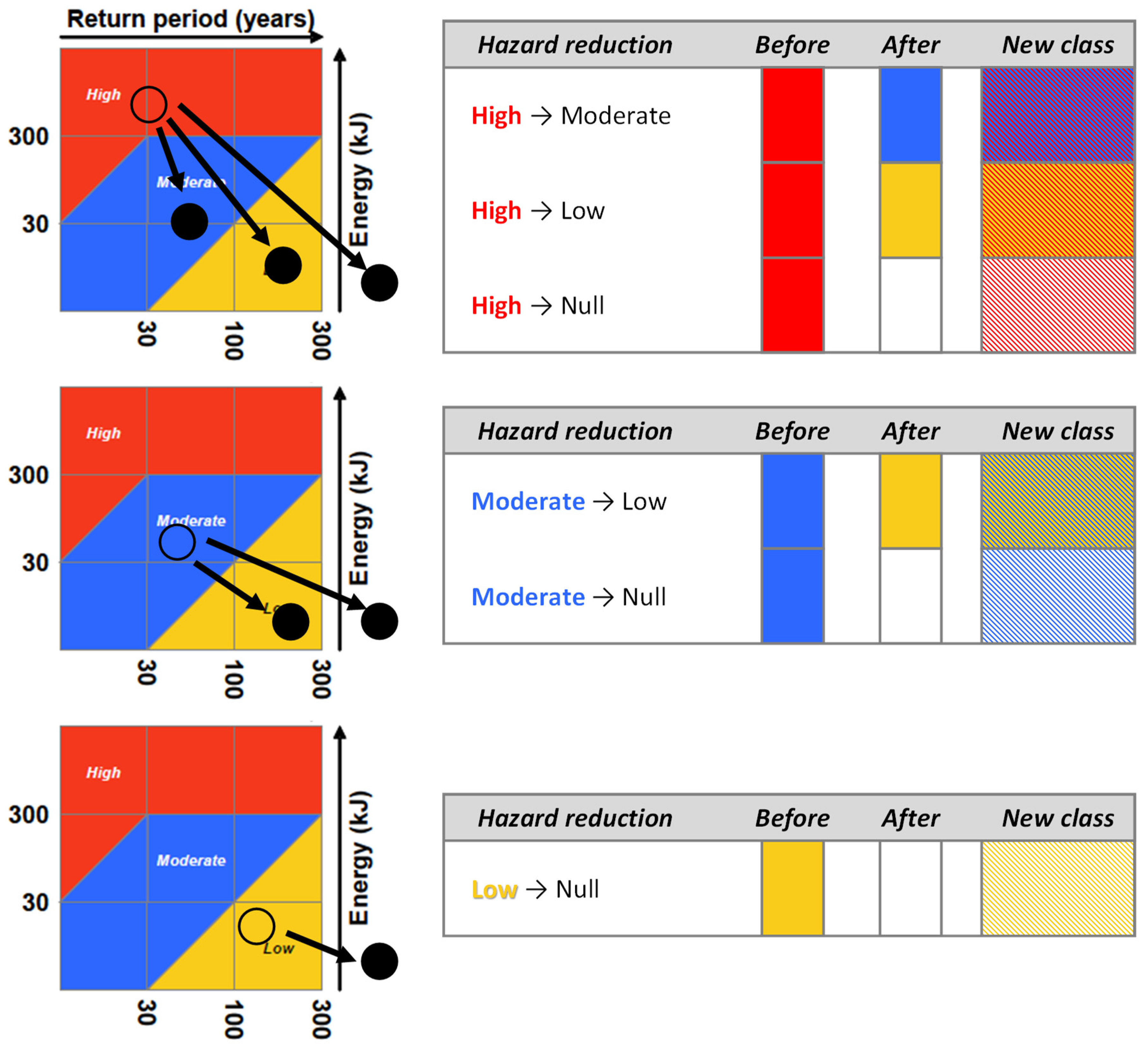
3.3.3. Account for the Effect of Protection Measures in Hazard Zoning
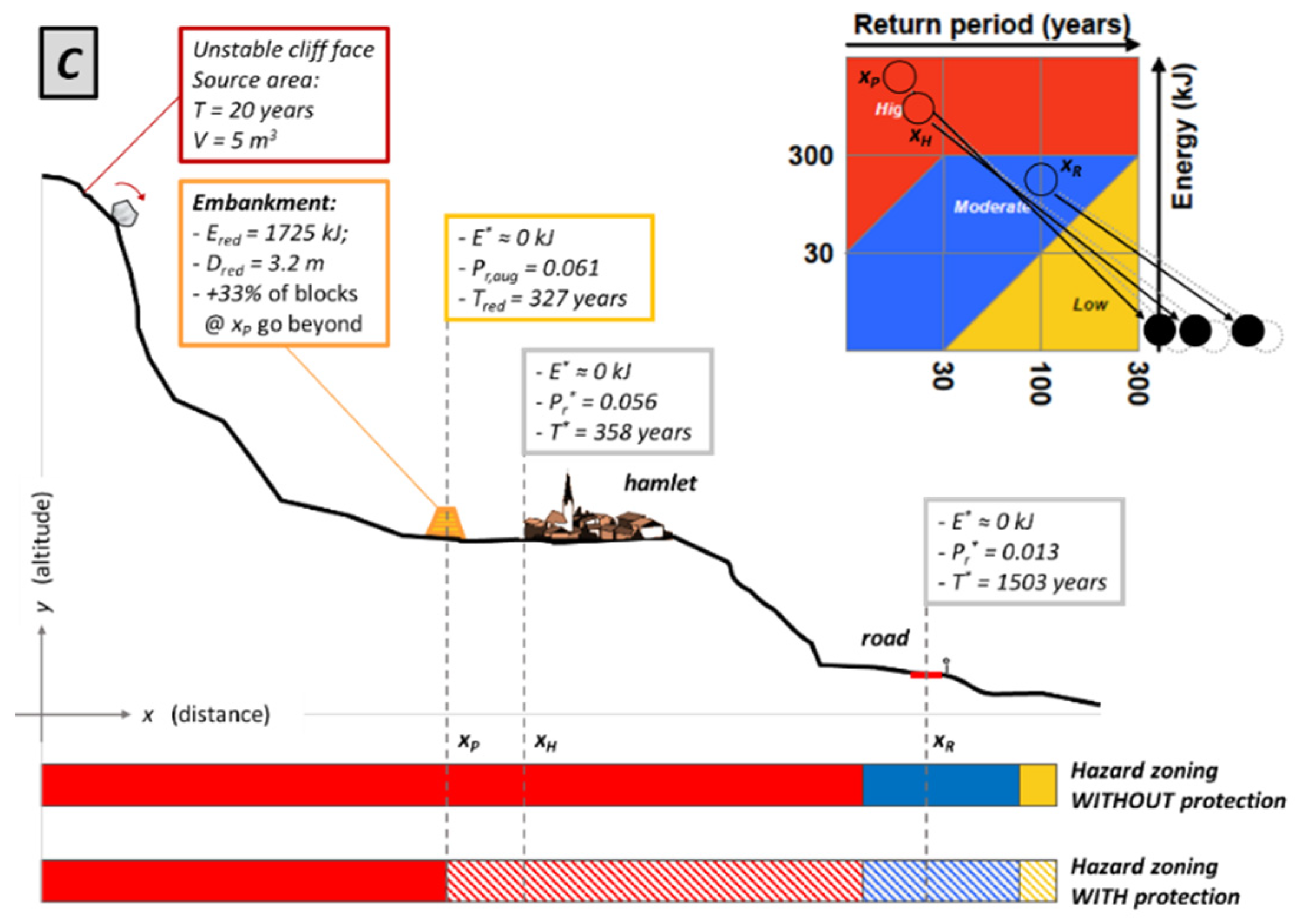
4. Applications
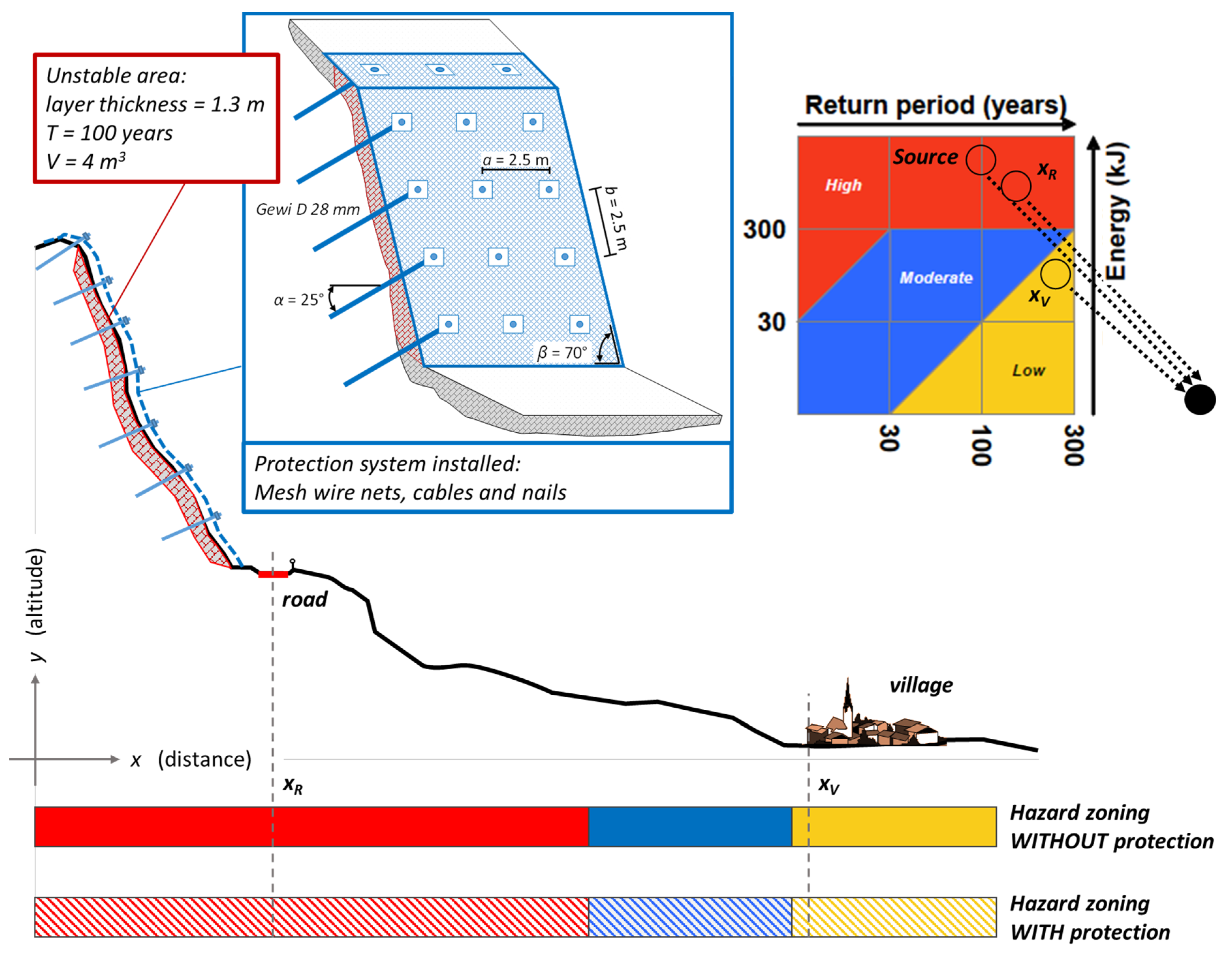
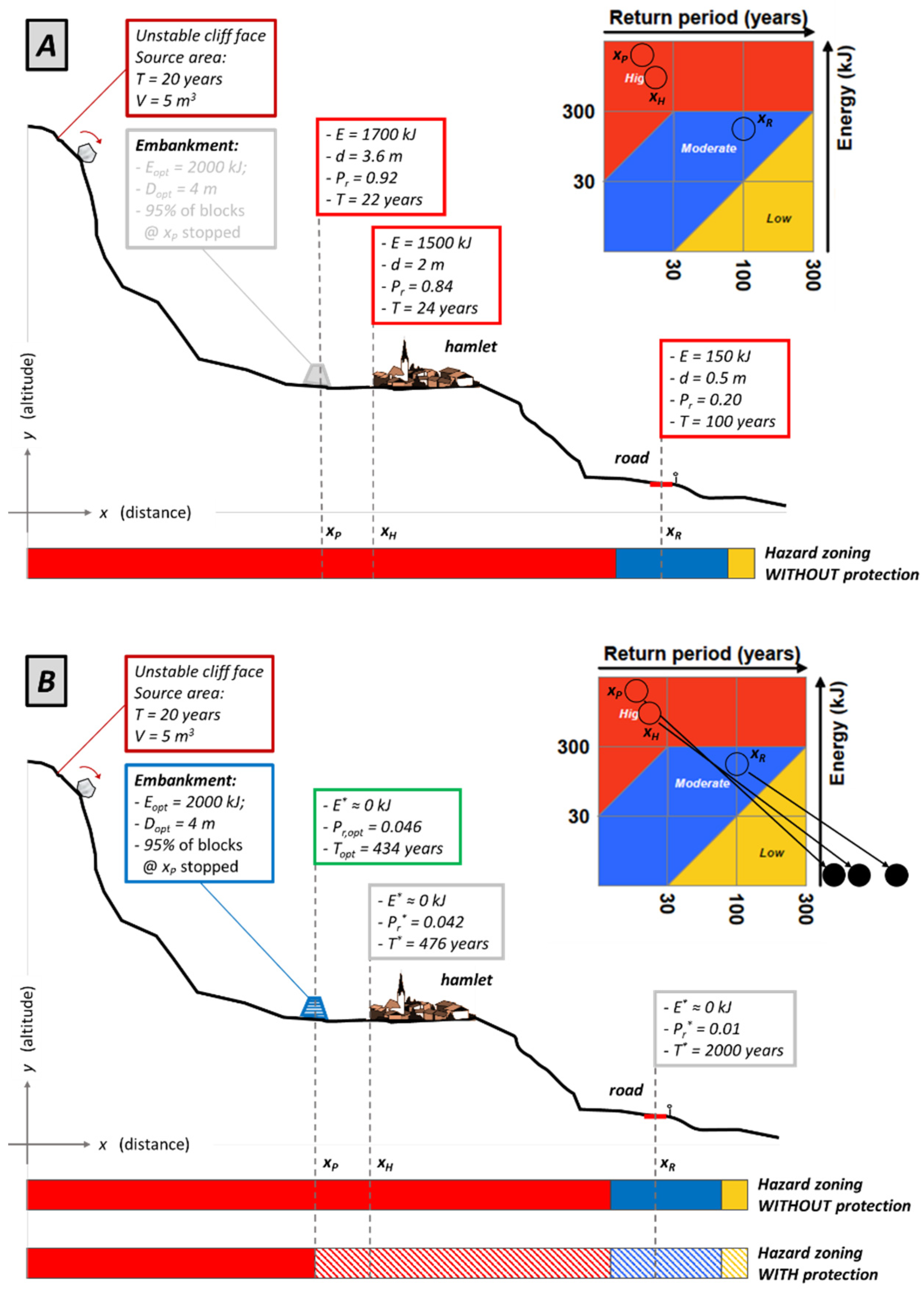
4.1. Example 1: Effectiveness of Rock Fall Protection at the Source Area
- -
- Corrosion of mesh: low r21 = 0.93;
- -
- Corrosion of nails: moderate → r28 = 0.85;
- -
- Damages to the mesh: low to very low r12 = 0.95.
4.2. Example 2: Effectiveness of Rock Fall Protection in the Propagation Zone
- -
- Frequent snow: moderate (Condition 0) → t03 = 0.85;
- -
- Lack of purge: moderate to low (Condition 1) → t15 = 0.90;
- -
- Deformations due to previous impacts: moderate (Condition 1) e11 = 0.88;
- -
- Stability issues of upslope face: very low (Condition 2) e23 = 0.98 t23 = 0.98.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cascini, L.; Bonnard, C.; Corominas, J.; Jibson, R.; Montero-Olarte, J. Landslide hazard and risk zoning for urban planning and development. In Proceedings of the International Conference on Landslide Risk Management, Vancouver, BC, Canada, 31 May–3 June 2005; Balkema: Rotterdam, The Netherlands, 2005; pp. 199–235. [Google Scholar]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z.; on behalf of the JTC-1 Joint Technical Committee on Landslides and Engineered Slopes. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Labiouse, V.; Abbruzzese, J.M. Rockfall hazard zoning for land use planning. In Rockfall Engineering; Lambert, S., Nicot, F., Eds.; John Wiley & Sons: New York, NY, USA, 2011; pp. 211–253. [Google Scholar]
- Corominas, J.; Copons, R.; Vilaplana, J.M.; Altimir, J.; Amigó, J. Integrated landslide susceptibility analysis and hazard assessment in the Principality of Andorra. Nat. Hazards 2003, 30, 421–435. [Google Scholar] [CrossRef]
- Ministere De L’amenagement Du Territoire Et De L’environnement; Ministere De L’equipement, Des Transports Et Du Logement. Plans de Prévention des Risques Naturels (PPR), Risques de Mouvements de Terrain, Guide Méthodologique; La documentation Française: Paris, France, 1999. [Google Scholar]
- Raetzo, H.; Lateltin, O.; Bollinger, D.; Tripet, J.P. Hazard assessment in Switzerland—Codes of Practice for mass movements. Bull. Eng. Geol. Environ. 2002, 61, 263–268. [Google Scholar]
- Lateltin, O.; Haemmig, C.; Raetzo, H.; Bonnard, C. Landslide risk management in Switzerland. Landslides 2005, 2, 313–320. [Google Scholar] [CrossRef]
- Volkwein, A.; Melis, L.; Haller, B.; Pfeifer, R. Protection from Landslides and High Speed Rockfall Events–Reconstruction of Chapman’s Peak Drive. In Proceedings of the IABSE Symposium “Structures and Extreme Events”, Lisbon, Portugal, 14–17 September 2005; IABSE Reports. pp. 47–54. [Google Scholar]
- Muhunthan, B.; Shu, S.; Sasiharan, N.; Hattamleh, O.A.; Badger, T.C.; Lowell, S.M.; Duffy, J.D. Design Guidelines for Wire Mesh/Cable Net Slope Protection; Report N. WA-RD 612.2; Washington State Transportation Center (TRAC); University of Washington: Washington, DC, USA, 2005. [Google Scholar]
- Peila, D.; Oggeri, C.; Castiglia, C. Ground reinforced embankments for rockfall protection: Design and evaluation of full scale tests. Landslides 2007, 4, 255–265. [Google Scholar] [CrossRef]
- Peila, D.; Ronco, C. Technical Note: Design of rockfall net fences and the new ETAG 027 European guideline. Nat. Hazards Earth Syst. Sci. 2009, 9, 1291–1298. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- CCC (Christchurch City Council). Technical Guideline for Rockfall Protection Structures; Australian Geomechanics: Perth, Australia, 2013; p. 42. [Google Scholar]
- Lambert, S.; Kister, B. Analysis of Existing Rockfall Embankments of Switzerland (AERES), Part A: State of Knowledge; Federal Office for the Environment: Bern, Switzerland, 2017. [Google Scholar]
- Prina Howald, E.; Abbruzzese, J.M.; Grisanti, C. An approach for evaluating the role of protection measures in rockfall hazard zoning based on the Swiss experience. Nat. Hazards Earth Syst. Sci. 2017, 17, 1127–1144. [Google Scholar] [CrossRef]
- Ronco, C.; Oggeri, C.; Peila, D. Design of reinforced ground embankments used for rockfall protection. Nat. Hazards Earth Syst. Sci. 2009, 9, 1189–1199. [Google Scholar] [CrossRef]
- Marchelli, M.; De Biagi, V.; Peila, D. A quick-assessment procedure to evaluate the degree of conservation of rockfall drapery meshes. Frattura ed Integrità Strutturale 2019, 47, 437–450. [Google Scholar] [CrossRef]
- Fell, R.; Ho, K.K.S.; Lacasse, S.; Leroi, E. A framework for landslide risk assessment and management. In Landslide Risk Management; Hungr, O., Fell, R., Couture, R., Eberhardt, E., Eds.; Taylor & Francis Group: London, UK, 2005; pp. 3–25. [Google Scholar]
- Keusen, H.; Gerber, W.; Rovina, H. Partie C: Processus de Chute—Évaluation de L’effet des Mesures de Protection Contre les Dangers Naturels pour Fonder leur Prise en Compte dans L’amenagement du Territoire; PLANAT: Bern, Switzerland, 2008. [Google Scholar]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating Rockfall Risk: Some Critical Aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef] [Green Version]
- Grisanti, C.; Prina Howald, E. Methodology for analyzing the effects of protective measures for falling blocks in the Canton of Vaud, Switzerland. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015; ISRM: Salzburg, Austria, 2015. [Google Scholar]
- Geobrugg. Tecco System—Publications 1998–2019. Technical Documentation (03/19). 2020. Available online: http://www.geobrugg.com (accessed on 22 June 2020).
- Interreg Iic. Prévention des Mouvements de Versants et des Instabilités de Falaises: Confrontation des Méthodes D’étude D’éboulements Rocheux dans l’arc Alpin; Interreg Communauté Européenne, 2001. [Google Scholar]
- AGS (Australian Geomechanics Society). Landslide Risk Management Concepts and Guidelines; Australian Geomechanics Society Sub-Committee on Landslide Risk Management, 2007; pp. 51–70. Available online: http://www.australiangeomechanics.org/resources/downloads (accessed on 24 June 2020).
- Crosta, G.B.; Agliardi, F. A methodology for physically based rockfall hazard assessment. Nat. Hazards Earth Syst. Sci. 2003, 3, 407–422. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.-P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Abbruzzese, J.M.; Labiouse, V. New Cadanav methodology for quantitative rock fall hazard assessment and zoning at the local scale. Landslides 2013, 11, 551–564. [Google Scholar] [CrossRef]
- Alejano, L.R.; Pons, B.; Bastante, F.G.; Alonso, E.; Stockhausen, H.W. Slope geometry design as a means of rockfall control in quarries. Int. J. Rock Mech. Min. Sci. 2007, 44, 903–921. [Google Scholar] [CrossRef]
- Alejano, L.R.; Stockhausen, H.; Bastante, F.G.; Alonso, E.; Ramírez-Oyanguren, P. ROFRAQ: A statistics-based empirical method for assessing accident risk from rockfalls in quarries. Int. J. Rock Mech. Min. Sci. 2008, 45, 1252–1272. [Google Scholar] [CrossRef]
- Thoeni, K.; Giacomini, A.; Sloan, S.W.; Lambert, C.; Casagrande, D. Numerical analysis of rockfall hazard in open pit coal mines. In Proceedings of the 13th International Conference of the International Association for Computer methods and Advances in Geomechanics (IACMAG 13), Melbourne, Australia, 9–11 May 2011; pp. 1151–1156. [Google Scholar]

| n. | Factor | Type |
|---|---|---|
| 1 | Proximity of a stream and/or action of rainwater | Environment |
| 2 | Freezing/thawing | Environment |
| 3 | Frequent snow | Environment |
| 4 | Presence of outcropping rock before the measure | Environment |
| 5 | Damages due to animals | Environment |
| 6 | Manufacturing faults | Protection measure |
| 7 | Possibility of plastic deformations | Protection measure |
| 8 | Redundancy of load-bearing elements | Protection measure |
| 9 | Consistency of the structure/points of weakness | Protection measure |
| 10 | Respect of current norms | Protection measure |
| 11 | Resistance to cyclic loading | Protection measure |
| (1) Mesh Wire/Cable Nets | |||
| n. | Factors | Type | Category |
| General | |||
| 1 | Corrosion of the mesh | Maintenance, design, life span | 1, 2, 4 |
| 2 | Damages to mesh | Maintenance, life span | 1, 4 |
| 3 | Excessive deformation of the mesh | Maintenance, design, life span | 1, 2, 4 |
| 4 | Lack of connectors between mesh drapes (clips, knots) | Maintenance, installation | 1, 3 |
| 5 | Damages to cables | Maintenance, design, life span | 1, 2, 4 |
| 6 | Loosening or loss of connection of cables | Maintenance, installation | 1, 3 |
| 7 | Lack of connectors cable/mesh (clips, knots) | Maintenance, installation | 1, 3 |
| Mesh wire nets with shotcrete/mesh wire with shotcrete and nails—Sub-type specific | |||
| 6 | Corrosion of the mesh | Maintenance, design, life span | 1, 2, 4 |
| 7 | Faults of injection (sealing) | Installation | 3 |
| Mesh wire nets, plated, with nails—Sub-type specific | |||
| 8 | Corrosion of nails (uniform or localised) | Maintenance, design, life span | 1, 2, 4 |
| 9 | Faults of injection (sealing of nails) | Installation | 3 |
| (2) Nails | |||
| n. | Factors | Type | Category |
| 1 | Corrosion (uniform or localised) | Maintenance, design, life span | 1, 2, 4 |
| 2 | Faults of injection (sealing) | Installation | 3 |
| (3) Anchors | |||
| n. | Factors | Factors | Category |
| 1 | Corrosion | Maintenance, design, life span | 1, 2, 4 |
| 2 | Rupture of the anchor | Maintenance, design, installation, life span | 1, 2, 3, 4 |
| 3 | Rupture of the head plate | Design, installation | 2, 3 |
| 4 | Faults of injection (sealing) | Installation | 3 |
| 5 | Flaws in controlling applied stress | Maintenance, design, installation | 1, 2, 3 |
| (4) Barrier Fences | |||
| n. | Factors | Type | Category |
| General (low and high energy vertical barrier fences) | |||
| 1 | Points of weakness along rock fall preferential paths | Design | 2 |
| 2 | Homologation of the structural measure | Design | 2 |
| 3 | Corrosion of supporting elements | Maintenance, design, life span | 1, 2, 4 |
| 4 | Corrosion of the net | Maintenance, design, life span | 1, 2, 4 |
| 5 | Loss of effective height due to partially filled net | Maintenance | 1 |
| 6 | Damages to supports after impacts | Maintenance, life span | 1, 4 |
| High energy vertical barrier fences—Sub-type specific | |||
| 7 | Loss of galvanisation of the net | Maintenance, design, life span | 1, 2, 4 |
| 8 | Loss of the torque wrench locking of cables | Installation | 3 |
| 9 | Fissures on the tubes of the energy dissipating devices | Maintenance, design, life span | 1, 2, 4 |
| 10 | Deformed or loosened cables | Maintenance, life span | 1, 4 |
| (5) Embankments | |||
| n. | Factors | Type | Category |
| General (earth and masonry embankments) | |||
| 1 | Significant deformations due to previous impacts | Maintenance, design, installation, life span | 1, 2, 3, 4 |
| 2 | Instability after impact | Design, life span | 2, 4 |
| 3 | Instability of any of the faces of the embankment | Maintenance, design, installation | 1, 2, 3 |
| 4 | Penetration by blocks | Maintenance, life span | 1, 4 |
| 5 | Loss of effective height due to blocks cumulated behind | Maintenance | 1 |
| 6 | Possibility of fragments thrown over the structure | Maintenance, life span | 1, 4 |
| 7 | Possibility of blocks rolling over the upslope face | Life span | 4 |
| (6) Retaining Walls | |||
| n. | Factors | Type | Category |
| General (concrete, masonry, gabion, anchored and wooden walls) | |||
| 1 | Loss of effective height due to blocks cumulated behind | Maintenance | 1 |
| Concrete wall—Sub-type specific | |||
| 2 | Corrosion of reinforcement rebars | Maintenance, design, life span | 1, 2, 4 |
| Gabion wall—Sub-type specific | |||
| 3 | Corrosion | Maintenance, design, life span | 1, 2, 4 |
| Anchored wall—Sub-type specific | |||
| 4 | Corrosion | Maintenance, design, life span | 1, 2, 4 |
| 5 | Rupture of the anchor | Maintenance, design, installation, life span | 1, 2, 3, 4 |
| 6 | Rupture of the head plate | Design, installation | 2, 3 |
| 7 | Faults of injection (sealing) | Installation | 3 |
| 8 | Flaws in controlling applied stress | Maintenance, design, installation | 1, 2, 3 |
| Wooden wall—Sub-type specific | |||
| 9 | Corrosion of metal elements | Maintenance, design, life span | 1, 2, 4 |
| 10 | Fire | Maintenance, design | 1, 4 |
| 11 | Penetration by blocks | Maintenance, life span | 1, 4 |
| 12 | Rupture of components | Maintenance, life span | 1, 4 |
| (7) Ditches and berms | |||
| n. | Factors | Type | Category |
| Ditches | |||
| 1 | “Springboard” effect due to filling | Maintenance, design | 1, 2 |
| 2 | Instability of any of the faces of the ditch | Maintenance, design, installation | 1, 2, 3 |
| 3 | Loss of effective depth due to blocks cumulated inside | Maintenance | 1 |
| Berms | |||
| 4 | Loss of effective height due to blocks cumulated behind | Maintenance | 1 |
| 5 | Possibility of blocks rolling over the downslope face | Life span | 4 |
| 6 | Instability of any of the faces of the berm | Maintenance, design, installation | 1, 2, 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prina Howald, E.; Abbruzzese, J.M. A Framework for Assessing the Performance Capabilities of Rock Fall Protections for Hazard Analysis and Zoning. Appl. Sci. 2022, 12, 8834. https://doi.org/10.3390/app12178834
Prina Howald E, Abbruzzese JM. A Framework for Assessing the Performance Capabilities of Rock Fall Protections for Hazard Analysis and Zoning. Applied Sciences. 2022; 12(17):8834. https://doi.org/10.3390/app12178834
Chicago/Turabian StylePrina Howald, Erika, and Jacopo Maria Abbruzzese. 2022. "A Framework for Assessing the Performance Capabilities of Rock Fall Protections for Hazard Analysis and Zoning" Applied Sciences 12, no. 17: 8834. https://doi.org/10.3390/app12178834
APA StylePrina Howald, E., & Abbruzzese, J. M. (2022). A Framework for Assessing the Performance Capabilities of Rock Fall Protections for Hazard Analysis and Zoning. Applied Sciences, 12(17), 8834. https://doi.org/10.3390/app12178834





