1. Introduction
An Electromagnetic Launcher (EML) is a device that converts electromagnetic force into kinetic energy to accelerate a projectile. Hence, the EML can replace the chemical energy of liquid or solid fuel or explosives such as gunpowder. Additionally, it does not cause any environmental problems and could launch multiple times in the presence of a charging environment. Therefore, the EML is actively studied in various countries as an accelerator for defense or space launchers [
1,
2]. A coil gun is an electromagnetic launch system and projectile accelerator that uses electromagnetic force. Coil guns are emerging as an important study subject among various electromagnetic launch systems because, unlike rail guns, coil guns are not greatly damaged by the friction between the launch tube and projectile. Moreover, they have high energy conversion efficiency and a long operating life [
3,
4]. Particularly in a coil gun system, the kinetic energy converted from the electromagnetic force generated in a solenoid coil accelerates the projectile. Here, the generated electromagnetic force is proportional to the coil’s number of turns and the supplied current’s magnitude. Accordingly, many studies have been conducted on the solenoid coil design elements [
5] and on the used copper wire’s diameter to improve the gun’s performance. Jang, J.H and Lee, S.J analyzed a coil gun with a mathematical model in 2015 to derive a projectile’s maximum velocity in a single-stage coil gun [
6]. A relevant study was also conducted on the electromagnetic force generated upon supplying the maximum current to the coil. However, these studies did not consider the distribution of the magnetic energy supplied to the projectile in a coil gun circuit. In a coil gun system, due to the solenoid coil’s characteristics, when a projectile passes through the coil’s center, it is subjected to a force opposing it, consequently decreasing its velocity. Therefore, merely increasing the number of turns and the supplied current may decrease the energy distribution efficiency, even if the electromagnetic force generated in the coil is high, potentially decreasing the projectile’s acceleration efficiency. Therefore, in this research, we designed the solenoid coil and capacitance to improve the projectile acceleration performance and the electrical to kinetic energy conversion efficiency. Notably, in this research, not only did we set the used copper wire’s diameter as a design variable, but also the number of turns of the solenoid coil was set as well. Accordingly, we selected the suitable capacitance depending on the coil’s shape to efficiently convert the generated electromagnetic force into kinetic energy. Additionally, not only do the coil gun’s electric circuit components act as important design factors, but also the projectile’s location during operation [
7]. This is because the force received by the projectile continuously varies according to the distance and time between it and the solenoid coil. For this reason, it is difficult to directly calculate the projectile velocity [
8,
9]. Therefore, using a computation program might be the best idea for efficient designs. Moreover, we simulated the designed coil gun model by FEA using ANSYS Maxwell, an electromagnetic analysis FEA software [
10]. Based on the simulation results, a prototype was fabricated and the projectile velocity was measured for the prototype. Since a single-coil gun’s acceleration performance is limited due to its solenoid’s magnetic saturation point, multi-stage coil guns are studied to increase the projectile velocity [
11,
12]. Therefore, we also considered in this study a situation where the projectile had an initial velocity at each stage, except for the first and last ones. A multi-stage coil gun (with 9 stages) was designed, and the design method, which was based on that of a single-coil gun, was presented.
2. The Coil Gun’s Circuit Configuration and Projectile Selection
A coil gun system consists of a solenoid coil that generates an electromagnetic force and a power supply that supplies current to the coil. High voltages and currents are usually applied/supplied using a charged capacitor. Typically, a high-voltage DC power supply, such as a booster converter, is required to charge the capacitor, and devices such as the SCR, IGBT, and FET are required to stably supply the stored electric charge. In this study, we used a DC power supply boosted up to 400 V using a booster converter boost circuit. Additionally, for the sake of circuit configuration convenience, we configured a coil gun circuit using an SCR thyristor device. Furthermore, in this study, we designed a multi-stage coil gun targeting a projectile velocity of 100 m/s with nine stages. We chose the projectile before designing and experimenting with any circuit. In the coil gun, a projectile accelerates by promptly receiving an electromagnetic force. Hence, it should be composed of a magnetic material. If its volume increases, the electromagnetic force required for acceleration increases. Therefore, upon deciding the projectile’s shape, a coil gun circuit that will generate the appropriate electromagnetic force should be designed.
Figure 1 shows an image of the projectile used in this experiment. The projectile was composed of a piece of S45 C steel with a 7.5 mm diameter and a length of 35 mm. Its weight was 11.35 g. Even though we chose steel, which is advantageous when it comes to its material availability and ease of fabrication, using a high-permeability metal, such as permalloy, can help increase the projectile’s velocity.
3. Establishment of the Coil Gun Design Problems
As shown in
Figure 2, the solenoid coil’s winding shape is generally determined by the number of turns in its radial (M) and axial directions (N), respectively. Additionally, in this study, we also included the diameter (d) of the copper wire used to manufacture the coil in the coil design variables. In addition to the coil shape, the capacitance and capacitor charging voltage also act as design variables.
Furthermore, not only does the coil gun’s circuit configuration act as an important design variable but so does the distance (x) between the solenoid coil and the projectile upon launching, i.e., when the coil gun’s capacitor discharges. This importance sprouts from the supplied current’s variability. Moreover, the magnitude of the electromagnetic force received by the projectile continuously varies according to the latter’s location and the passage of time. Hence, to further understand the magnitude of the electromagnetic force generated in the coil, the circuit’s current waveform must be calculated.
The electromagnetic force generated in the solenoid coil is determined by the coil’s number of turns and the used copper wire’s diameter. Likewise, the current’s waveform flowing in it is determined by the resistance (
R), according to the coil’s shape and inductance (
L), and the capacitance (
C). Generally, the coil gun’s circuit is composed of a solenoid coil and a capacitor. Due to the coil’s self-resistance, the shape of the current flowing in the circuit takes the form of an RLC function and the shape of an underdamped system. Three sub-systems, namely the mechanical, magnetic, and electrical sub-systems, are coupled in a coil gun system. This coupled system can be expressed using the following governing equation:
Additionally, the magnetic force received by the projectile from the coil gun is affected by the magnetic flux density, magnetic permeability, etc. The magnetic flux density continuously varies according to the projectile’s position, and the force received by the projectile at position
x is expressed as follows:
where
u is the magnetic field energy in a certain space, expressed as the product of the volume (
v) and the magnetic flux density (
B). The variation of energy, Δ
u, is expressed as:
where
µ0 and
µm respectively represent the magnetic permeability of air and the material occupying the space. We can obtain the force F received by the projectile using Equations (2) and (3). We can express the magnetic flux density (
B) as an integral value with respect to the distance as follows, where
r is the projectile’s radius and
L is the solenoid coil’s length:
The magnetic field B also changes according to the projectile’s distance x. Therefore, simulating the coil gun system expressed above using analytical methods is difficult.
Figure 3 is a graph showing the projectile velocity’s shape, the electromagnetic force received by it, and the coil gun circuit’s current waveform in a system that uses a 7000 uF capacitor on a solenoid coil wound with 24(M) × 9(N) turns, using a 1.7 mm diameter copper wire. Upon operating the coil gun, the distance between it and the projectile was 7 mm. Notably, as shown in
Figure 3, the projectile received a force in the direction opposing that of its launching while its center of gravity passed through the coil’s center at 3.4 ms. Additionally, the received electromagnetic force was proportional to the current’s magnitude. The current peaked at 3.8 ms and decreased when the projectile passed through the coil’s center. The projectile received 70 and 30% of the total generated electromagnetic force in the projectile motion’s forward and reverse directions, respectively. Therefore, the current must be cut off during the coil gun’s operation using a device, such as the IGBT, to improve its performance. Otherwise, analyzing the circuit’s RLC-function waveform and comparing it with the projectile’s acceleration shape is important for designing the coil gun’s components, such that the energy is distributed and most of the generated electromagnetic force is transmitted in the projectile motion’s forward direction.
However, in a multi-stage coil gun, the RLC function’s period in the coil gun’s circuit should be shorter than that of a single-coil gun because the projectile’s acceleration time in the multi-stage coil gun is reduced due to its initial velocity. Therefore, it is necessary to analyze the electromagnetic force generated in the coil based on the RLC period that can properly accelerate the projectile. For example, the magnetic field in a circular coil is given by:
where H is the magnetic field intensity (AT/m),
N is the number of turns,
I is the supplied current (A), and a is the coil’s radius (m). Therefore, the electromagnetic force is proportional to the solenoid coil’s number of turns and the supplied current’s magnitude. In cases where a solenoid coil is constructed using a copper wire with a large diameter since the corresponding self-resistance and inductance of the coil are low, a capacitance of at least 7000 uF is required to match the RLC function’s period. However, the corresponding supplied current’s magnitude increases. Furthermore, merely increasing the number of turns to reduce the capacitance increases the coil’s overall volume, potentially reducing the magnitude of the electromagnetic force transmitted to the projectile. Therefore, in this study, the shape of the coil suitable for the coil gun was proposed by comparing coil gun systems with different copper wire diameters.
4. Finite Element Analysis
We conducted the coil gun model’s finite element analysis using ANSYS Maxwell, a commercial electromagnetic analysis FEA software. Particularly, three coil gun systems using a copper wire diameter of 1.3, 1.7, and 2.0 mm, respectively, were analyzed and compared. Their respective analysis models were configured according to the design variables shown in
Table 1, and the maximum projectile velocity of each was derived.
Additionally, to shorten the analysis time, we only analyzed the respective 2D models of the coil guns.
Figure 4 shows the coil gun’s 2D finite element analysis model. In the model, the design variables were set such that the RLC function’s period was sufficiently long for the projectile to receive at least 70% of the electrical energy while moving in the launch direction. Moreover, the values of the design variables at which the optimal projectile velocity was achieved were set as reference values. Notably, coil guns that accelerated at a stopped projectile were simulated and compared based on the final projectile velocity when the projectile was completely ejected out of the solenoid coil’s magnetic field. The optimal values of the coil gun design elements were derived using the experiment method’s design, which is the most efficient method because the design elements of the coil gun are independent of each other.
Table 1 shows the ranges of design variables according to the diameters of individual copper wires. A table of orthogonal arrays was created with the set ranges of design variables to compose the test points, and the design variables with the highest velocity were summarized.
Table 2 shows the optimal coil gun shapes according to respective copper wire diameters obtained from the finite element analysis.
Furthermore, the respective energy conversion efficiencies of the coil guns were compared using simple equations. Assuming that there was no loss during conversions, the energy conversion efficiency was calculated by comparing the electric energy stored in the capacitor and the projectile’s kinetic energy. In electric energy, C is the capacitance and V is the charging voltage. In kinetic energy,
m and
v are the projectile’s mass and velocity, respectively.
For the chosen values of the coil gun variables in the analysis, between the coil gun systems using 1.3 and 1.7 mm diameter copper wires, respectively, the kinetic energy of the projectile was 9% higher. However, the used electrical energy for energy conversion was 133% higher for the system using a 1.7 mm diameter copper wire. Generally, for high energy conversion efficiency, it is good to use a copper wire with a small diameter to increase the solenoid coil’s number of turns and lower the capacitance to match the coil gun circuit’s RLC function’s period. However, if a coil is manufactured using a copper wire with a large diameter, it has the advantage of being able to set a shorter RLC period in the circuit due to the low self-resistance and inductance. Thus, if the goal is to derive maximum projectile velocity from a limited number of stages in a multi-stage coil gun, it is recommended to fabricate a solenoid coil using a large diameter copper wire and construct an RLC function suitable for the circuit using a high-capacity capacitor.
Notably, in this study’s coil gun system using a 1.7 mm diameter copper wire, the maximum current was 1400 A. This required a high specification SCR, potentially affecting the coil gun circuit’s life and durability. Due to the characteristics of the circuit using a solenoid coil, a freewheeling diode may be additionally required in the circuit for stable operation. Functionally, a freewheeling diode is used to avoid damaging the circuit by the inductor’s charging current by connecting the diode with the load in parallel.
Based on the analysis, we considered that it would be appropriate to configure the coil gun system using a 1.3 mm diameter copper wire. Therefore, we constructed a multi-stage coil gun system using a 1.3 mm diameter copper wire. We also determined its number of turns and capacitance through finite element analysis. We simulated the multi-stage coil gun system using the same coil gun analysis model by inputting the projectile velocity at the end of the previous stage as the initial projectile velocity of the current stage (except for a current, first stage).
Table 3 shows the number of turns and capacitance of the respective solenoid coils of the 9 stages (total).
We further optimized the nine-stage coil gun using the design of the experiment method. We designed the multi-stage coil gun by setting the projectile’s final velocity derived in the relevant stage as the projectile’s initial velocity in the next stage.
Table 3 shows the velocities of the projectile calculated using simulations. The coil gun was designed to have a projectile velocity of at least 100 m/s. In the simulation, 107 m/s was finally derived from the nine-stage coil gun. Considering the errors that may have occurred during the experiment, we decided to manufacture a prototype of the nine-stage coil gun.
Generally, as the stage number increases, the time for the projectile to accelerate decreases, so the period of the RLC function of the coil gun circuit also becomes shorter.
5. Prototype Fabrication and Measurement
We fabricated a prototype based on the results of the FEA and design. We further measured its projectile velocity.
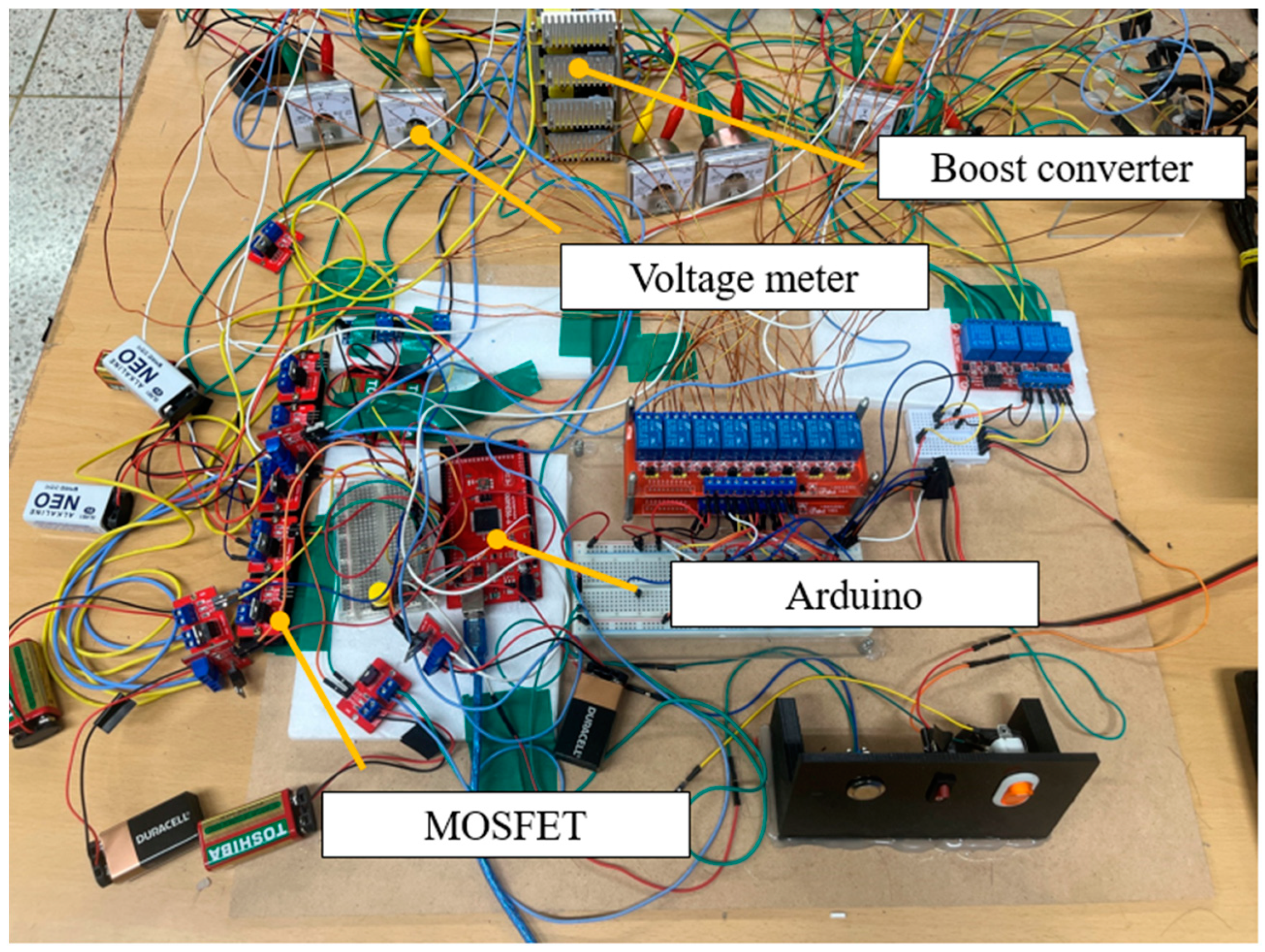
Figure 5 shows the overall view of the nine-stage coil gun prototype used in the measurement experiment and the experimental setup. Particularly, non-metallic materials were used to prevent projectile velocity variation arising from eddy currents. Considering their durability, we constructed the launch tube using carbon pipes.
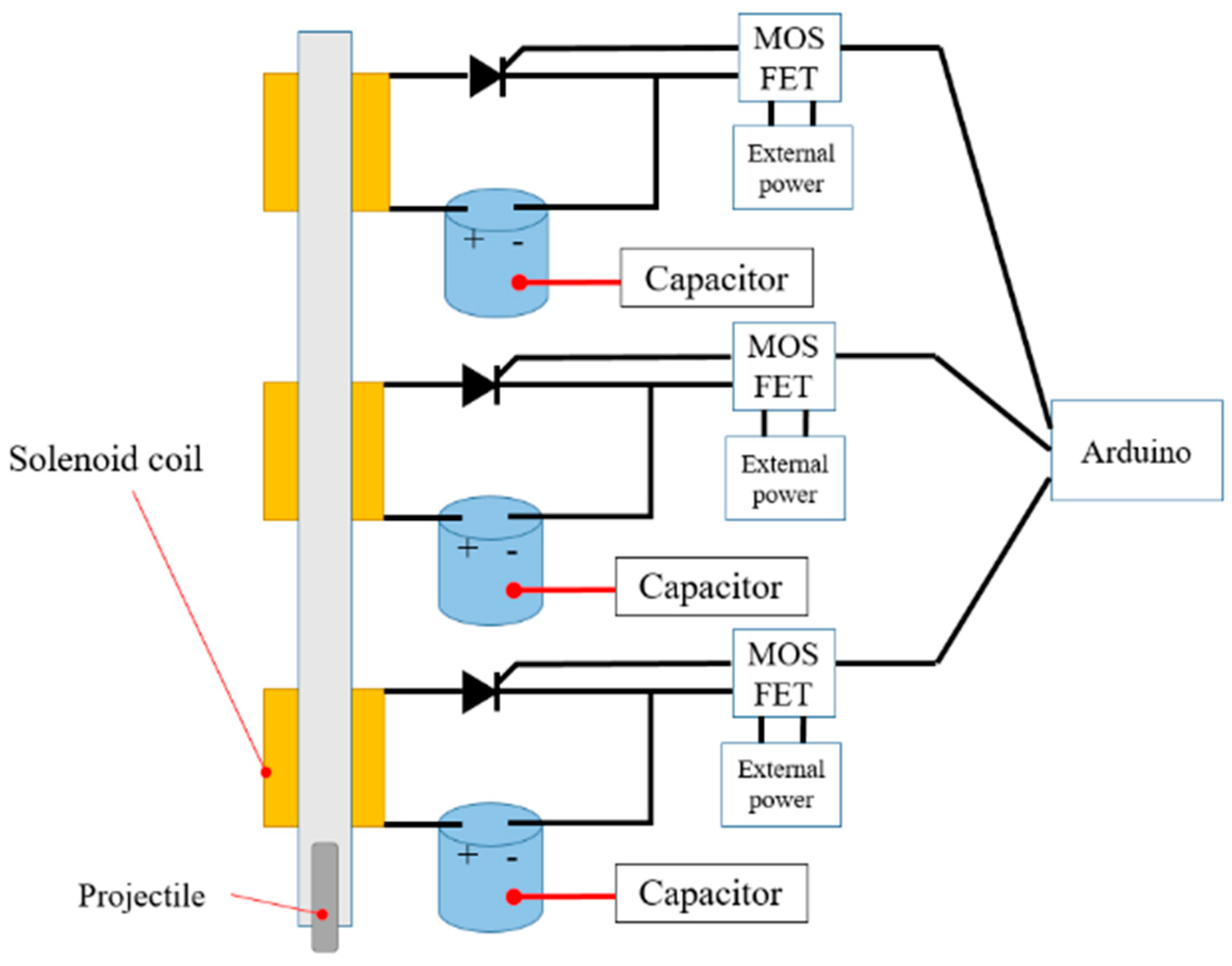
We configured the coil gun system’s circuit such that the charging and discharging of the nine stages could be controlled. The capacitor was also charged by boosting a 12 V DC power to 400 V with a booster converter. We also developed and used a charging device to charge the nine-stage capacitors without errors. The projectile’s position when the coil gun discharges acts as one of the most important design variables. In a multi-stage coil gun, a discharge system that can operate the circuit when the moving projectile has reached a certain position is needed. Here, we used an SCR thyristor for the discharge circuit, and the discharge control signals were outputted using an Arduino, a commercial development platform. However, since the signals outputted from the Arduino were insufficient to operate the SCR, a method of amplifying the output signals with a MOSFET device and an external power source was used.
For the used SCR in the experiment, we configured the circuit using VS-80RIA80, a lead-type SCR manufactured by VISHAY. At room temperature, the relevant model’s operating current should be at least 6 mA; however, it should not exceed 120 mA. The operating voltage should be at least 0.25 V and should not exceed 3 V. The digital signal output of the Arduino Mega model is 5 V at 500 mA. Based on the figures, we can operate up to 4 SCRs with the Arduino’s own output. However, in this study, we must operate a total of 9 SCRs. Thus, we used the above method.
Figure 6 shows a schematic diagram of the discharge circuit’s connection.
The charging device’s 12 V DC power supply was boosted to 400 V, which is the capacitor’s charging capacity, using a booster converter boost circuit. Since a total of nine capacitors of the nine-stage coil gun should be charged, we developed a device that connects and disconnects the capacitors during charging using a relay to reduce the errors caused by the difference in the charging amounts of individual capacitors. We designed it to unite the capacitors before charging and separate them after it to separately discharge them.
Figure 7 shows a schematic diagram of the charge circuit.
The charging-discharging device used in the experiment is shown in
Figure 8.
As for the discharge control signals, a method of adding a delay between the discharge of each coil gun circuit was used. The discharge of the stage 1 coil gun was controlled via an external switch’s input. After outputting the first stage coil gun’s SCR operation signal, that of the second stage circuit was outputted after a 2900 us delay. The delay value was calculated considering the projectile velocity for the optimal position from the finite element analysis and was adjusted by conducting an experiment based on it.
6. Measurement Results
The projectile’s velocity was measured using the velocity measuring equipment shown in
Figure 5, which was the WST’s X01 model. Its measurement range and information are summarized in
Table 4. Particularly, we measured the projectile velocity by stage, namely from one to nine stages, to identify its velocity increment. The measured velocities are presented in
Table 5. To ensure high measurement accuracy, the projectile’s velocity was measured 10 times by stage and the average velocity was considered as the stage’s projectile velocity.
As for the projectile velocity’s error, the frequency of different velocity measurements increased as the number of stages increased. This correlation existed because the projectile position deviated from the intended one during discharge due to recoiling, and the corresponding error accumulated as the number of stages increased. In this study, the error was eliminated by completely fixing the launch tube. However, unlike this study’s discharge method, we recommend a method of directly recognizing the projectile’s position using an obstacle detection sensor, such as a photo-interrupter, to operate the discharge circuit. Although setting the projectile’s position during discharge is difficult, and the discharge control circuit’s configuration is complicated when using the recommended method, we can configure multi-stage coil gun systems with fewer errors than those found in this study’s discharge control method. This is because there is no reason for changing the set discharge position due to factors such as recoiling.
Additionally, we analyzed the manufactured prototype’s performance by studying its projectile acceleration shape and acceleration performance.
Figure 9a,b show the projectile velocity and projectile velocity increment by stage, respectively.
Notably, between the coil gun’s 6~9th stages, the projectile velocity increment converged to 5 m/s. We analyzed the RLC function’s period to fit the acceleration shape to improve the acceleration efficiency according to the projectile’s velocity by reducing the number of turns and capacitance. However, since there was a limit for adjusting the number of turns, for the cases of 4~5th and 6~9th stages of the coil gun, respectively, with small velocity increments, we recommend using copper wires with a diameter larger than 1.3 mm in the solenoid coil. Therefore, if the goal is to derive a projectile velocity of 100 m/s or higher, fabricating the solenoid coils of the multi-stage coil gun circuit by incrementally increasing the copper wire’s diameter is appropriate, especially if we were to consider the increase in the number of stages, the projectile’s initial velocity, and the acceleration time.
7. Conclusions
In this study, we added the diameter of the copper wire used to manufacture a coil gun’s solenoid coil as a design variable. Subsequently, the respective designed models of coil gun systems with varying copper wire diameters were simulated to compare the circuit’s acceleration performance and energy conversion efficiency. First, for the efficient conversion of the electromagnetic force generated in the circuit into kinetic energy, at least 70% of it should be transmitted to the projectile in the launch direction to reduce the force transmitted to it in the reverse direction after passing through the coil’s center. The period of the RLC function with the energy distribution shape suitable for the projectile’s initial velocity should be set by comparing the function’s shape and the projectile’s acceleration shape. Additionally, the electromagnetic force generated in the solenoid coil is proportional to the coil’s winding shape and the supplied current’s magnitude. Therefore, we can use two methods to increase the magnitude of the coil’s generated electromagnetic force. The first method is designing a low-capacitance coil using a small-diameter copper wire to increase the winding density and number of turns. The second is using a large-diameter copper wire to increase the capacitance by reducing the number of turns to increase the supplied current’s magnitude, thereby increasing the magnitude of the coil’s electromagnetic force. When we configured the coil gun system using a 1.3 mm diameter copper wire based on the experimented projectile in this study, the solenoid coil’s resistance and inductance were high. Therefore, a capacitance of 3000 uF, which is a capacity less than half of that of a coil gun system configured using a 1.7 mm diameter copper wire, was used to match the RLC period. However, the magnetic flux density transferred from the coil gun’s solenoid coil to the projectile increased. Thus, there was no significant velocity difference. When configuring the coil gun circuit using a small-diameter copper wire, we can increase the magnetic flux density by increasing the number of turns for the same volume of the solenoid coil. However, we should use a low-capacitance capacitor to set the RLC function’s period due to the coil’s high inductance and resistance. In the case of a multi-stage coil gun, setting this period is limited by the number of turns and capacitance because the acceleration time depends on the projectile’s initial velocity. This adjustment may be good for energy conversion efficiency because the circuit can be configured with a low-capacitance capacitor. On the other hand, when a coil gun circuit is configured using a large diameter copper wire, if the number of turns increases, the entire coil’s size increases compared to that of the projectile. This may decrease the efficiency of the electromagnetic force transmission to the projectile. Therefore, we should design a multi-stage coil gun to match the RLC function’s period using a high-capacitance capacitor and by increasing the supplied current’s magnitude. In this study, we identified the acceleration performance degradation in the five-stage and higher-stage coil gun systems. Despite optimally designing the values, acceleration performance degradation and increases in the number of stages were observable in the simulation. This was mainly because the solenoid coil’s generated electromagnetic force decreased proportionally to the reduction in the number of turns, even though we optimized the values by reducing the RLC function’s period by reducing the number of turns. Therefore, if one’s purpose is to improve the acceleration efficiency more than that in this study, the solenoid coil should be designed using a copper wire with a diameter larger than 1.5 mm to optimize the five-stage and higher-stage coil gun systems. Although this design method has low energy conversion efficiency due to high capacitance, its advantage is that the circuit’s RLC function’s period can be shortened due to the coil’s low self-resistance and inductance. Particularly, this design method is suitable for increasing the acceleration performance when the projectile’s initial velocity is high in a multi-stage coil gun system. Consequently, when designing a multi-stage coil gun, it is recommended to incrementally increase the copper wire’s diameter according to the projectile’s initial velocity.