SRRI Methodology to Quantify the Seismic Resilience of Road Infrastructures
Abstract
:1. Background
2. Loss Model (LM)
2.1. Prolongation of Travel (PT)
2.2. Connectivity Losses (CL)
3. SRRI Methodology
- t0E is the time of occurrence of the earthquake E;
- RT is the repair time (RT) that is necessary to recover the original functionality;
- Q(t) is the recovery function that describes the recovery process necessary to return to the pre-earthquake level of functionality (see Figure 1). It is important to note that the recovery function starts at the time of occurrence (idle time neglected).
- Im is the intensity measure used for the definition of the hazard;
- D(Im) are the direct losses as proportional as the sum of the RCR and of the repair time (RT) calculated by the PBEE methodology:
- I(Im) are the indirect losses, calculated as follows:
- n is the number of interdependent infrastructures that are present in the network;
- ri is the functionality ratio of the infrastructure (r = 1 means that the infrastructure is fully operational, r = 0 means that the infrastructure is closed);
- PTi are the losses connected with prolongation of travel (PT) for infrastructures i = 1…n:
- pi is a parameter that needs to be calibrated to calculate the PT for infrastructure i;
- CLi represents the losses connected with connectivity loss (CL) for infrastructures i = 1…n;
- ci is a parameter that needs to be calibrated to calculate the PT for infrastructure i;
4. Case Study
- n1 and n2 are the number of bridges for Infrastructure 1 and Infrastructure 2, respectively;
- r1 and r2 are the functionality ratios of Infrastructures 1 and 2, respectively.
4.1. Bridge Models
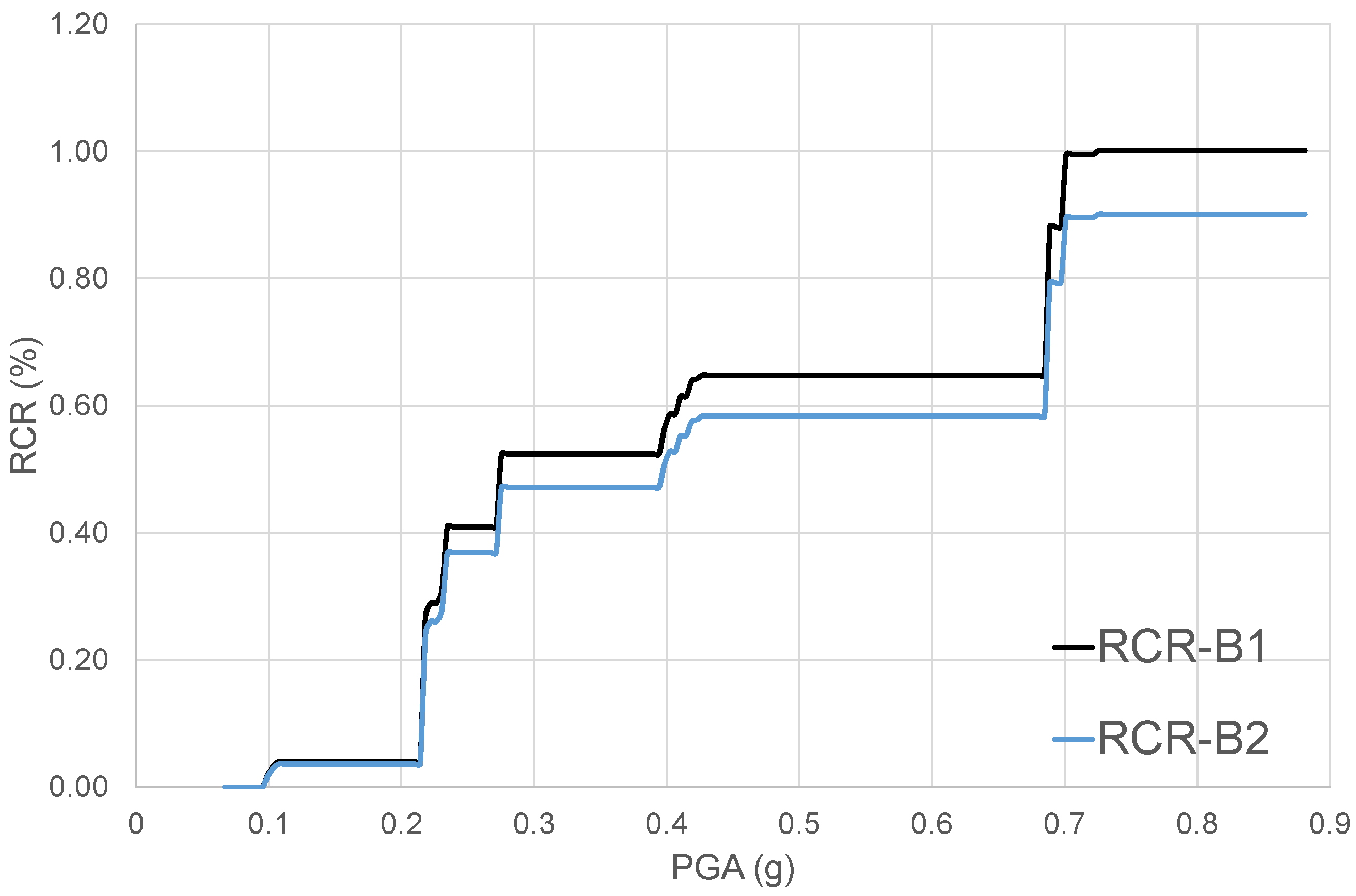
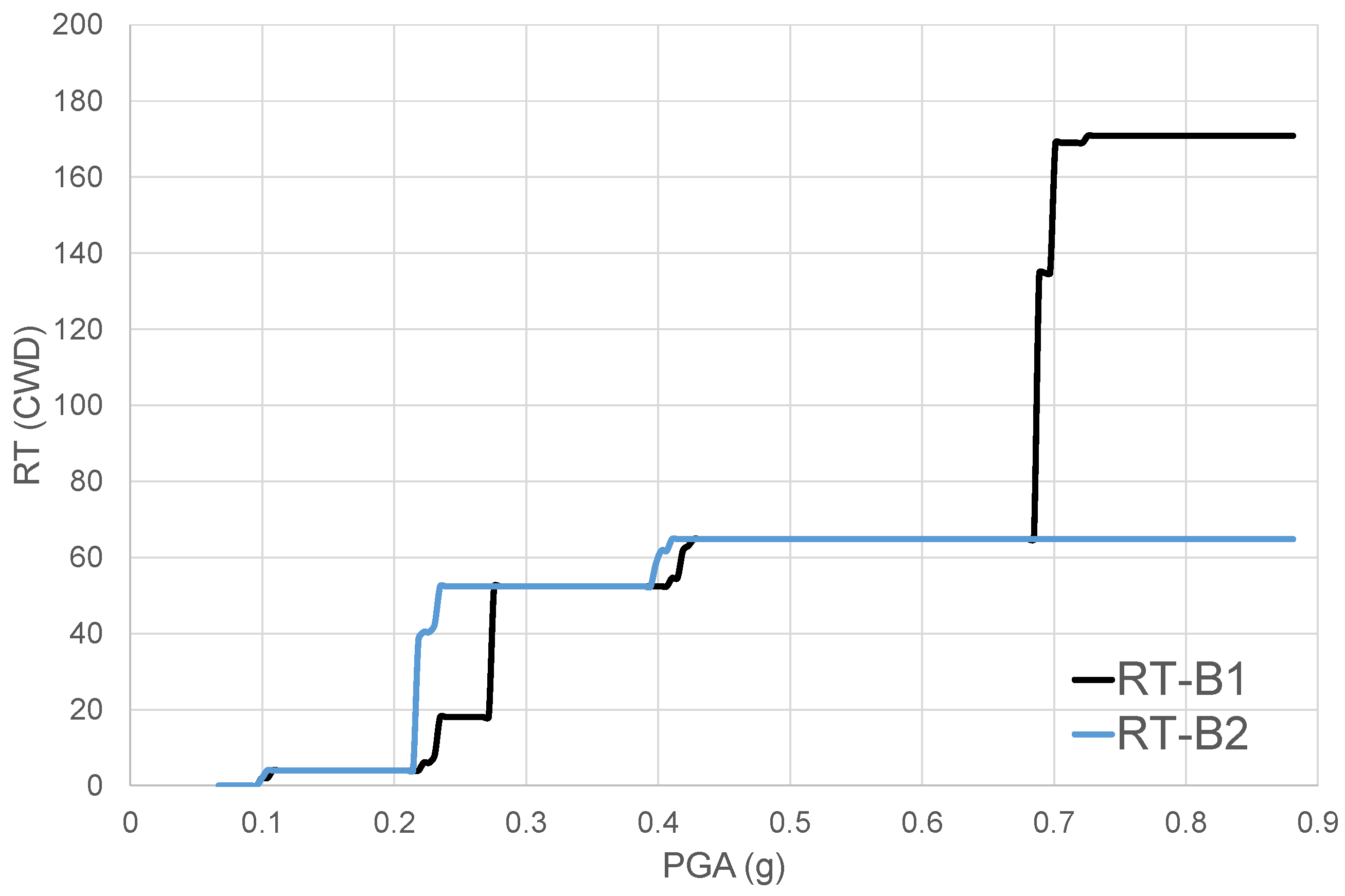
4.2. SRRI Calculation
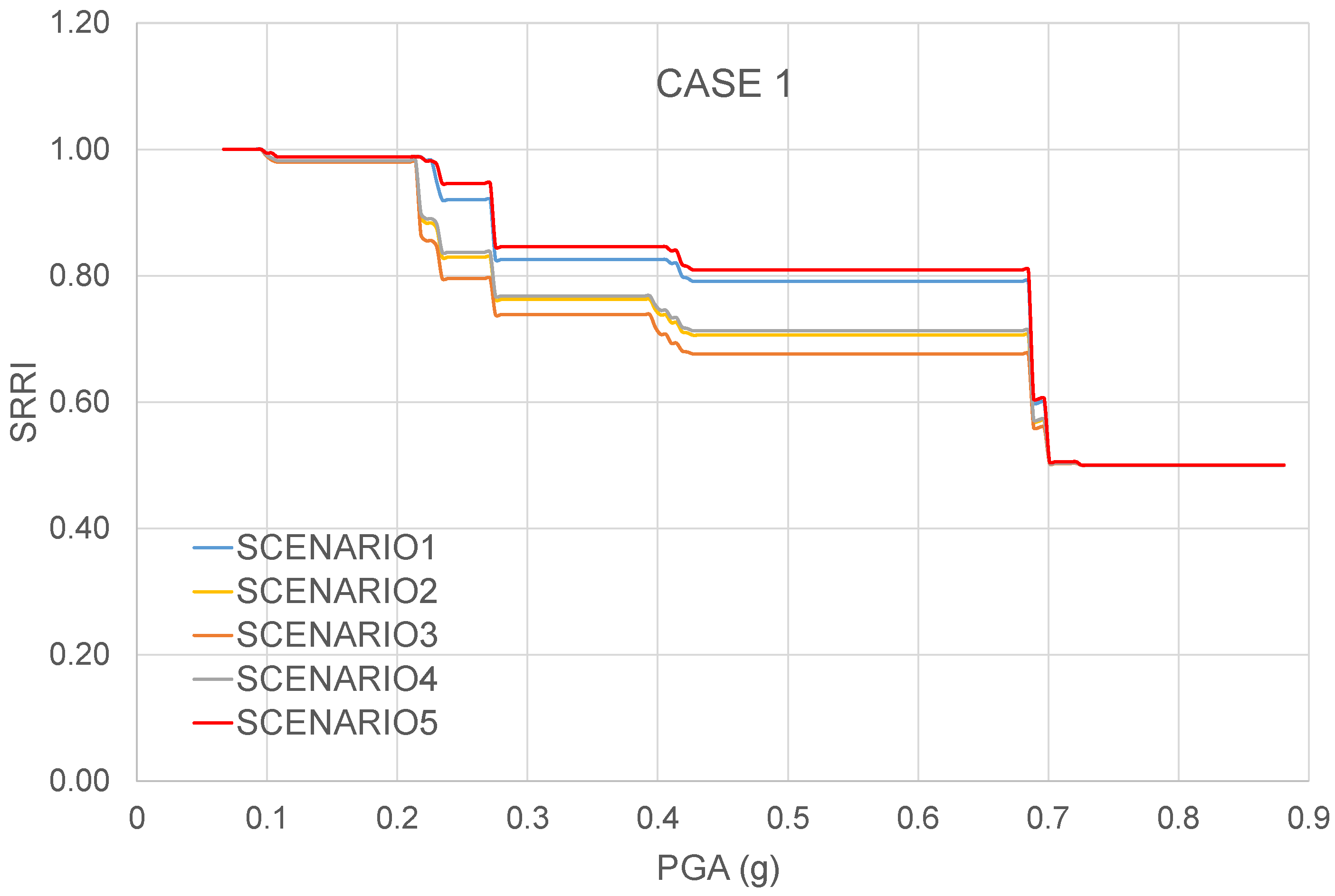
4.2.1. Case 1: n1 = 3, n2 = 6
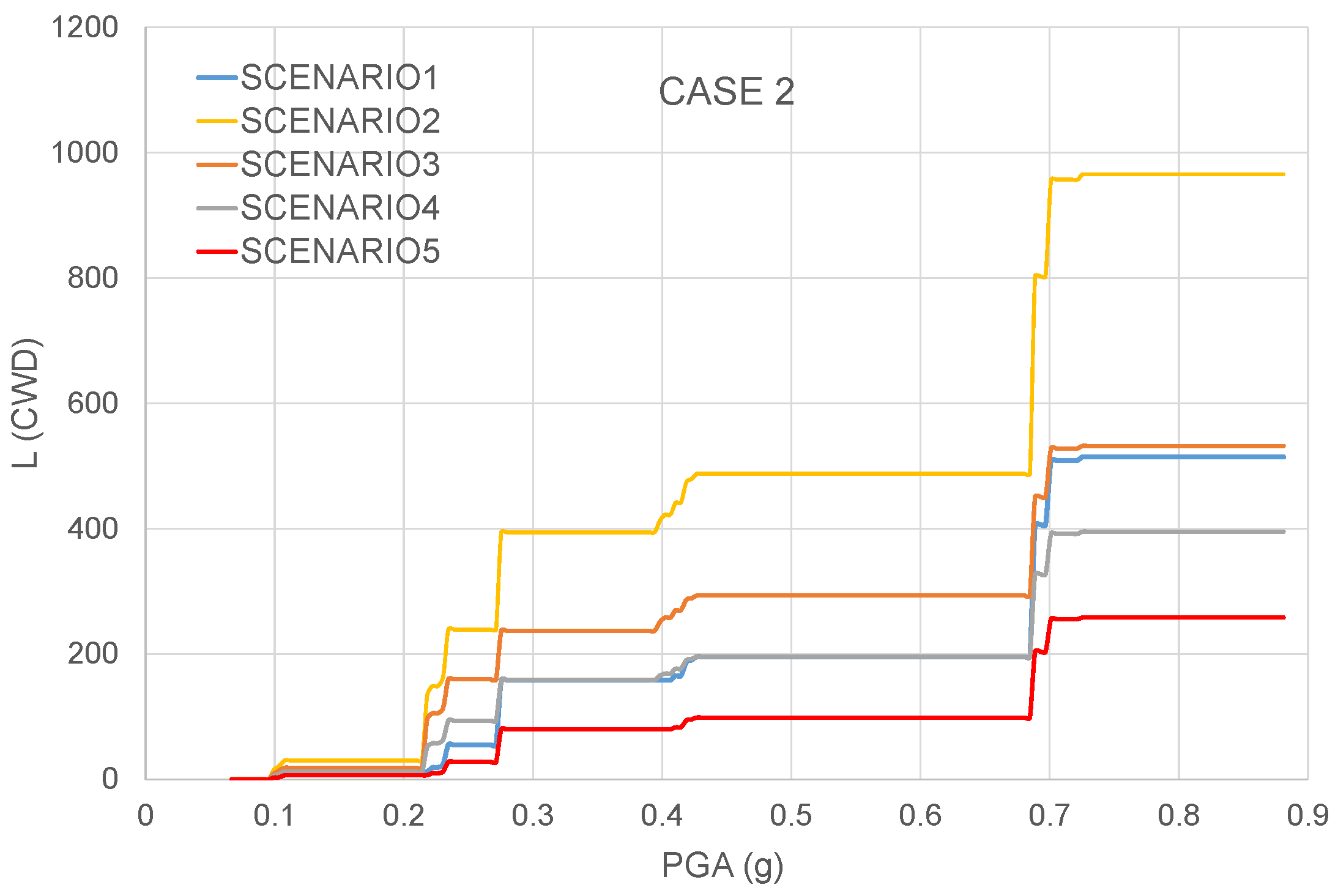
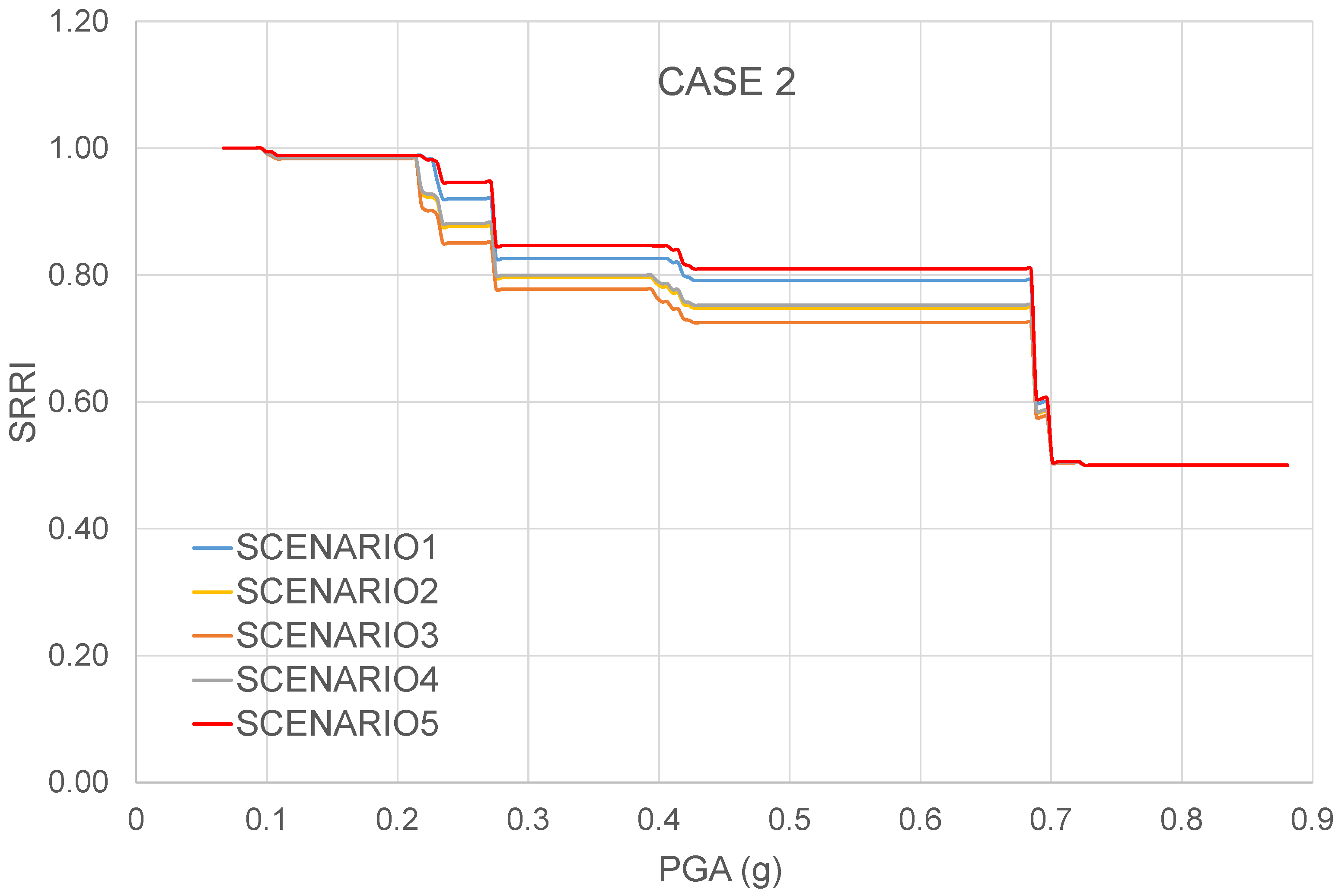
4.2.2. Case 2: n1 = n2 = 3
4.2.3. SRRI Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SRRI | Seismic resilience of road infrastructure |
| PGA | Peak ground acceleration |
| t0E | Time of occurrence of earthquake E |
| RT | Repair time (RT) |
| Q(t) | Recovery function |
| β | Ratio between the final functionality Q and the original functionality of the system before the earthquake |
| α | Exponent of the growth of the functionality curve |
| Im | Intensity measure used for the definition of the hazard |
| L | Losses |
| D | Direct losses |
| I | Indirect losses |
| PT | Prolongation time |
| CL | Connection losses |
| RCR | Repair cost ratio |
| RT | Repair time |
| n | Number of interdependent infrastructures present in the network |
| ri | Functionality ratio of the infrastructure |
References
- Dehgani, M.; FLintsch, G.; McNeil, S. Impact of road conditions and disruption uncertainties on network vulnerability. J. Infrastruct. Syst. ASCE 2014, 20, 04014015. [Google Scholar] [CrossRef]
- Moini, N. Modeling of Risks Threatening Critical Infrastructures: System Approach. J. Infrastruct. Syst. ASCE 2016, 22, 04015010. [Google Scholar] [CrossRef]
- Nourzad, S.H.H.; Pradhan, A. Vulnerability of Infrastructure Systems. Macroscopic Analysis of Critical Disruptions on Road Networks. J. Infrastruct. Syst. ASCE 2016, 22, 04015014. [Google Scholar] [CrossRef]
- Forcellini, D. A Resilience-Based (RB) Methodology to Assess Resilience of Health System Infrastructures to Epidemic Crisis. Appl. Sci. 2022, 12, 3032. [Google Scholar] [CrossRef]
- Adey, B.; Hajdin, R.; Brudwile, E. Effect of common cause failures on indirect costs. J. Bridge Eng. 2004, 9, 200–208. [Google Scholar] [CrossRef]
- Brookshire, D.S.; Chang, S.E.; Cochrane, H.; Olson, R.A.; Rose, A.; Steenson, J. Direct and indirect economic losses from earthquake damage. Earthq. Spectra. 1997, 14, 683–701. [Google Scholar] [CrossRef]
- Forcellini, D. A new methodology to assess Indirect Losses in Bridges subjected to multiple hazards. Innov. Infrastruct. Solut. 2019, 4, 1–9. [Google Scholar] [CrossRef]
- Forcellini, D. Resilience-Based Methodology to Assess Soil Structure Interaction on a Benchmark Bridge. Infrastructures 2020, 5, 90. [Google Scholar] [CrossRef]
- Quang, C.; Shen, J.J.; Zhou, M.; Lee, G.C. Force-based and displacement-based reliability assessment approaches for highway bridges under multiple hazard actions. J. Traffic Transp. Eng. 2015, 2, 223–232. [Google Scholar]
- Alipour, A.; Shafei, B.; Shinozuka, M. Reliability-based calibration of load and resistance factors for design of RC bridges under multiple extreme vents: Sour and earthquake. J. Bridge Eng. 2013, 18, 362–371. [Google Scholar] [CrossRef]
- Gelh, P.; D’Ayala, D. Development of a Bayesian Networks for the multi-hazard fragility assessment of bridge systems. Struct. Saf. 2016, 60, 37–46. [Google Scholar] [CrossRef]
- Andric, J.M.; Lu, D. Risk assessment of bridges under multiple hazards in operation period. Saf. Sci. 2016, 83, 80–92. [Google Scholar] [CrossRef]
- Gardoni, P.; LaFave, J.M. Multi-hazard approaches to civil infrastructure engineering: Mitigating risks and promoting resilience. In Multi-Hazard Approaches to Civil Infrastructure Engineering; Gardoni, P., LaFave, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–12. [Google Scholar]
- Gidaris, I.; Padgett, J.E.; Barbosa, A.R.; Chen, S. Multiple-hazard fragility and restoration models of highway bridges for regional risk and resilience assessment in the United States: State-of-the-art review. J. Struct. Eng. 2017, 143, 04016188. [Google Scholar] [CrossRef]
- Gautam, D.; Dong, Y. Multi-hazard vulnerability of structures and lifelines due to the 2015 Gorkha earthquake and 2017 central Nepal flash flood. J. Build. Eng. 2018, 17, 196–201. [Google Scholar] [CrossRef]
- Chang, S.E.; Shinozuka, M. Measuring improvements in the disaster resilience of communities. Eng. Struct. 2004, 20, 739–755. [Google Scholar] [CrossRef]
- Renschler, C.; Frazier, A.; Arendt, L.; Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for Defining and Measuring Resilience at the Community Scale: The PEOPLES Resilience Framework; Technical Report MCEER-10-006; University at Buffalo: Buffalo, NY, USA, 2010. [Google Scholar]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, D.; Pitilakis, K.; Tsinidis, G.; Huang, H.; Zhang, D.; Argyroudis, S. Resilience assessment of tunnels: Framework and application for tunnels in alluvial deposits exposed to seismic hazard. Soil Dyn. Earthq. Eng. 2022, 162, 107456, ISSN 0267–7261. [Google Scholar] [CrossRef]
- Mina, D.; Forcellini, D.; Karampour, H. Analytical fragility curves for assessment of the seismic vulnerability of HP/HT unburied subsea pipelines. Soil Dyn. Earthq. Eng. 2020, 137, 106308. [Google Scholar] [CrossRef]
- Forcellini, D.; Walsh, K.Q. Seismic resilience for recovery investments of bridges methodology. In Proceedings of the Institution of Civil Engineers—Bridge Engineering; ICE Publishing: London, UK, 2021. [Google Scholar] [CrossRef]
- Saydam, D.; Frangopol, D.M.; Dong, Y. Assessment of Risk Using Bridge Element Condition Ratings. J. Infrastruct. Syst. 2013, 19, 252–265. [Google Scholar] [CrossRef]
- Ranjbar, P.R.; Naderpour, H. Probabilistic evaluation of seismic resilience for typical vital buildings in terms of vulnerability curves. Structures 2020, 23, 314–323. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Nasiopoulos, G.; Mantadakis, N.; Mitoulis, S.A. Cost-based resilience assessment of bridges subjected to earthquake excitations including direct and indirect losses. Int. J. Disaster Resil. Built Environ. 2020, 12, 209–222. [Google Scholar] [CrossRef]
- Meyer, V.; Becker, N.; Markantonis, V.; Schwarze, R.; van den Bergh, J.C.J.M.; Bouwer, L.M.; Bubeck, P.; Ciavola, P.; Genovese, E.; Green, C.; et al. Assessing the costs of natural hazards—State of the art and knowledge gaps. Nat. Hazards Earth Syst. Sci. 2013, 13, 1351–1373. [Google Scholar] [CrossRef]
- Mechler, R.; Linnerooth-Bayer, J.; Peppiatt, D. Microinsurance for Natural Disasters in Developing Countries: Benefits, Limitations and Viability, ProVention Consortium, Geneva. 2006. Available online: http://www.proventionconsortium.org/themes/default/pdfs/Microinsurance study July06.pdf (accessed on 15 August 2022).
- Hallegatte, S.; Dumas, P. Can Natural Disasters Have Positive Consequences? Investigating the Role of Embodied Technical Change. Ecol. Econom. 2008, 68, 777–786. [Google Scholar] [CrossRef]
- Hallegatte, S.; Ghil, M. Natural Disasters Impacting a Macroeconomic Model with Endogenous Dynamics. Ecol. Econom. 2008, 68, 582–592. [Google Scholar] [CrossRef]
- Hackl, J.; Adey, B.T.; Lethanh, N. Determination of Near-Optimal Restorationprograms for Transportation networks following Natural Hazard Events Using Simulated Annealing. Comput. -Aided Civ. Infrastruct. Eng. 2018, 33, 618–637. [Google Scholar] [CrossRef]
- Mackie, K.R.; Wong, J.; Stojadinovic, B. Integrated Probabilistic Performance-Based Evaluation of Benchmark Reinforced Concrete Bridges; Report No. 2007/09; University of California Berkeley, Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2008. [Google Scholar]
- Mackie, K.R.; Wong, J.-M.; Stojadinovic, B. Post-earthquake bridge repair cost and repair time estimation methodology. Earthq. Eng. Struct. Dyn. 2010, 39, 281–301. [Google Scholar] [CrossRef]
- Mackie, K.R.; Stojadinovic, B. Fourway: A graphical tool for performance-based earthquake engineering. J. Struct. Eng. 2006, 132, 1274–1283. [Google Scholar] [CrossRef]
- Kröger, W.; Zio, E. Vulnerable Systems; Springer: London, UK, 2011. [Google Scholar] [CrossRef]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, understanding, and analysing critical infrastructure interdependencies. In IEE Control Systems Magazine; IEEE: Piscataway, NJ, USA, 2001; pp. 11–25. Available online: http://user.it.uu.se/~bc/Art.pdf (accessed on 2 October 2012).
- Ouyang, M. Review on modeling and simulation of interdependent critical infrastructure systems. Reliab. Eng. Syst. Saf. 2014, 121, 43–60. [Google Scholar] [CrossRef]
- Adey, B.; Lethanh, N.; Lepert, P. An impact hierarchy for the evaluation of intervention strategies for public roads. In Proceedings of the 4th European Pavament Asset Management Conference (EPAM), Malmo, Sweden, 5–7 September 2012. [Google Scholar]
- Luna, R.; Balakrishnan, N.; Dagli, C.H. Postearthquake recovery of a water distributionsystem: Discrete event simulation using colored Petri nets. J. Infrastruct. Syst. 2011, 17, 25–34. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Timothy, C.; Matisziw, T.C.; Murray, A.T.; Snediker, D. Comparative Approaches For Assessing Network Vulnerability. Int. Reg. Sci. Rev. 2008, 31, 88–112. [Google Scholar] [CrossRef]
- Duenas-Osorio, L.; Craig, J.I.; Goodno, B.J. Seismic response of critical interdependent networks. Earthq. Eng. Struct. Dyn. 2007, 36, 285–306. [Google Scholar] [CrossRef]
- Cimellaro, G.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Forcellini, D. Cost assessment of isolation technique applied to a benchmark bridge with soil structure interaction. Bull. Earthq. Eng. 2017, 15, 51–69. [Google Scholar] [CrossRef]
- Caltrans (California Department of Transportation). Seismic Design Criteria Version 1.3; Caltrans: Sacramento, CA, USA, 2003. [Google Scholar]
- Forcellini, D.; Kelly, J.M. The analysis of the large deformation stability of elastomeric bearings. J. Eng. Mech. ASCE 2014, 140, 04014036. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation, User Command-Language Manual; OpenSees Version 2.0; Pacifc Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2009. [Google Scholar]
- Spacone, E.; Filippou, F.C.; Taucer, F. Fibre beam-column model for non-linear analysis of r/c frames: Part I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
- Savvided, A.A.; Papadrakis, M. A computational study on the uncertainty quantification of failure of clays with a modified Cam-Clay yield criterion. SN Appl. Sci. 2021, 3, 659. [Google Scholar] [CrossRef]


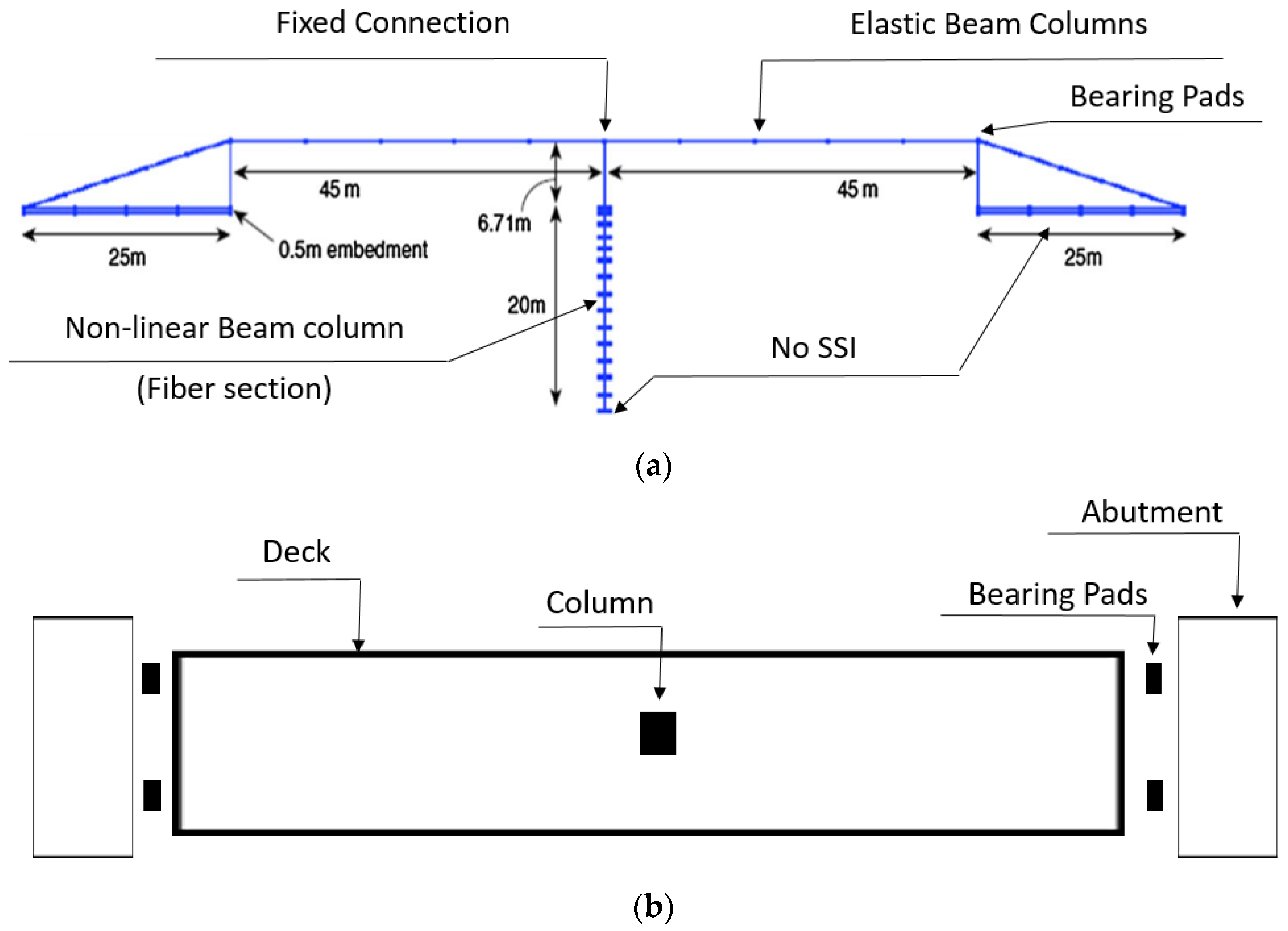

| Scenario | r1 | r2 |
|---|---|---|
| n.1 | 0 | 1.0 |
| n.2 | 0 | 0.5 |
| n.3 | 0.5 | 0.5 |
| n.4 | 0.5 | 0.75 |
| n.5 | 0.5 | 1.0 |
| Characteristic | |
|---|---|
| Length (m) | 90.00 |
| Width (m) | 11.90 |
| Depth (m) | 1.83 |
| E (MPa) | 2.80 × 105 |
| G (MPa) | 1.15 × 105 |
| Area (m2) | 5.72 |
| Itrasv (m4) | 2.81 |
| Ivert (m4) | 53.9 |
| Weight (kN/m) | 130.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forcellini, D. SRRI Methodology to Quantify the Seismic Resilience of Road Infrastructures. Appl. Sci. 2022, 12, 8945. https://doi.org/10.3390/app12188945
Forcellini D. SRRI Methodology to Quantify the Seismic Resilience of Road Infrastructures. Applied Sciences. 2022; 12(18):8945. https://doi.org/10.3390/app12188945
Chicago/Turabian StyleForcellini, Davide. 2022. "SRRI Methodology to Quantify the Seismic Resilience of Road Infrastructures" Applied Sciences 12, no. 18: 8945. https://doi.org/10.3390/app12188945
APA StyleForcellini, D. (2022). SRRI Methodology to Quantify the Seismic Resilience of Road Infrastructures. Applied Sciences, 12(18), 8945. https://doi.org/10.3390/app12188945






