Robust Backstepping Control Applied to UAVs for Pest Recognition in Maize Crops

Abstract

In this paper, a robust control technique is developed to achieve the quadrotor stabilization against unmodeled matching vanishing dynamics. The synthesis of the proposed robust control is based on the Lyapunov approach and the backstepping method allowing to construct an iterative control algorithm. To compare the performance of the proposed controller, a Proportional Derivative (PD) controller is used to obtain experimental results in an outdoor environment. To compare the closed-loop system responses with both controllers, the Integral Absolute Error is computed and several tests are conducted to calculate the error standard deviation. Ultimately, employing the robust backstepping control approach in pest recognition in maize crops, which is a specific task of precision agriculture, demonstrates its effectiveness in improving the trajectory tracking of the vehicle while it captures images of the crops.

1. Introduction

Today, the use of Unmanned Aerial Vehicles (UAVs) is growing, and multirotor systems are expected to replace manned aircraft in a variety of activities [1]. Examples of such activities include search and rescue missions, data collection, precision agriculture, and payload delivery [2,3,4,5]. Quadcopters can rapidly change direction and perform vertical takeoffs and landings, thus making them increasingly popular.

Small-scale UAVs typically suffer from the effects of outside wind gusts and unmodeled dynamics, effects that involve changes in mass and inertial moments causing parametric uncertainties. These effects also result from the coupling effect between the forces and moments produced by their actuators, which are commonly neglected in the practical designs [6]. Since an advanced control system is based on the nominal model, the uncertain parameters and unmodeled dynamics adversely affect its performance. Developing robust controllers to guarantee UAV stabilization has been a key topic that some authors have handled in different ways. For instance, on the basis of sliding mode algorithms and backstepping methods, [7] offers a robust backstepping sliding mode controller for attitude and position control; accordingly, smooth bounded disturbances and non-vanishing perturbations were considered for a quadrotor vehicle, and simulation results were presented. In [8], the attitude control of an eight-rotor UAV in the presence of model uncertainties and external disturbances was suggested; hence, a robust backstepping sliding mode controller with adaptive radial basis function neural network was employed, and simulation results were reported. According to [9], the adaptive backstepping sliding mode tracking control method for underactuated unmanned surface vehicle was employed to compensate for its model uncertainty, time-varying disturbances and input saturation, and a simulation study was introduced. Attitude and position tracking were performed using the backstepping technique and sliding mode control in [10]; in this case, the controller adapts to the mass changes to control the UAV, and the controller performance was evaluated through simulations. Furthermore, attitude regulation and translational movement of an aircraft using a backstepping approach was done in [11], and altitude control was performed with sliding mode control considering uncertainties. As a result of the presence of sinusoidal functions in the roll and pitch subsystems, the virtual input is always bounded, allowing the control input produced with backstepping to be smoother than the input provided by the sliding mode controller, exhibiting no implementation issues such as chattering; however, the controller robustness problem was not addressed. In [12], a backstepping control strategy was employed to decrease the wind disturbances that can impact the accuracy of image acquisition in the course of drone flight in an outdoor environment; in particular, the specific task involved estimating nitrogen in a rice crop using the aerial imagery.

As a result of adaptive backstepping control, several estimations of the non-vanishing external disturbance were employed for the proposed controller in [13]; in this case, the experimental results were obtained in an indoor environment using a VICON Bonita motion capture system and MATLAB software. Similarly, in [14], the same motion capture system was used to implement feedback linearization and an integral-backstepping-like controller to address the perturbation problems that appear in a quadrotor; in this sense, simulations and indoor environment experimental results were presented with slowly-varying wind conditions. To regulate quadrotors in the presence of constant and time-varying disturbances, a nonlinear controller based on backstepping was designed, and simulation results were presented in [15]; the non-vanishing disturbances were estimated by a nonlinear observer. A nonlinear robust and adaptive backstepping control strategy was proposed in [16] to solve the trajectory tracking problem of hexacopter UAVs. The nominal backstepping control approach was designed as the main controller, and simulations were performed considering non-vanishing bounded disturbances. In [17], the robust position and attitude tracking control problem of a quadrotor subject to nonlinearities, input coupling, aerodynamic uncertainties and external wind disturbances was presented, the control scheme was validated through simulations and experimental validation on a Quanser’s 3–DOF Hover setup. In [18], a robust landing algorithm onto a heaving platform, using an autonomous quadcopter DJI-F450, was presented. This algorithm addressed the altitude flight under the ground effect and external disturbances. In [19], a nonlinear robust Fast Terminal Sliding Mode Controller was designed to control and to stabilize a reconfigurable UAV in the presence of uncertain and variable parameters. The proposed controller was evaluated through a flight scenario. In [20], a hybrid control architecture that combines Deep Reinforcement Learning and Robust Linear Quadratic Regulator for vision-based lateral control of an autonomous vehicle was presented. The proposal was validated via simulation results. The robust control Lyapunov function approach is another control approach that has been used to tackle the rejecting bounded-matched disturbance problems in a Planar Vertical Take-Off and Landing (PVTOL) [21], presenting experimental results. Furthermore, using the command filtered backstepping approach with a parameter scheduling algorithm, an experimental flying test of a quadrotor with a nonlinear controller in an indoor environment was described in [22]; however, the robust design was not included in the controller synthesis. Simulation routines of a robust control based on a backstepping method was presented in [23] to drive the position and attitude of a unmanned mini aerial rotorcraft vehicle subjected to bounded uncertainties and bounded disturbances.

According to the specialized literature cited above, most of the robust backstepping or robust control algorithms were tested in simulations: [7,8,9,10,15,16,19,20,23]; advanced control in an outdoor environment: for nitrogen estimation with relative high-cost equipment was presented in [12], and robust landing algorithm onto a heaving platform in [18]; in an indoor environment in UAVs [13,14,17] and in a PVTOL [21]. In our opinion, a robust backstepping control algorithm has to be sufficiently simple to implement it on an autopilot for flying tests in a more realistic environment (outdoors and trajectory tracking in precision agriculture). In this sense, the embedded computing resources required by autonomous unmanned aircraft systems represented a challenge [24]. The backstepping algorithm allows to synthesize a recursive stabilizing controllers for nonlinear systems and it could be modified to obtain robust controllers. Moreover, unmodeled dynamics, external disturbances, actuators, and signal conditioner nonlinearities are latent in the real-time control loop. Under all these conditions, it is essential to assess the controller’s performance [25] by experimental evaluation of the control algorithms in meaningful environments to validate their robustness in a closed loop with a real plant.

In this contribution, based on the Lyapunov approach, a robust nonlinear controller solves the trajectory tracking problem for a quadrotor. Our proposal uses the backstepping method [26], allowing to construct an iterative control algorithm that rejects the effects of the unstructured dynamics in the quadrotor nonlinear model. For this purpose, the quadrotor model is divided into four subsystems related to the altitude, the yaw angle, the pitch-x and the roll-y, as in [11], and it considers the coupled nonlinear dynamics in the actuators. While these disturbances are unknown, they are assumed as bounded matched vanishing dynamics. The robustness is incorporated in the proposed controller to stabilize the drone in the presence of non-modeled dynamics, which improve the image capture system on board of the UAV as it flies over corn crops to detect dry leaves, providing clues to identify fungus such as Phyllachora maydis, Monographella maydis, and Coniothyrium phyllachorae on the corn leaves. These fungi are the cause of the tar spot in the corn [27], which causes crop losses.

Regarding the proposal mission in this paper, growing loss owing to disease is one of the most representative problem in agriculture. Crop growth inspecting and early identification of pest in the crops is still an important issue. In this regard, farmers are investing great efforts to conserve crops; however, they are mostly failing because they are not correctly monitoring the crops when they have been infested. Additionally, plagues in the crops are also difficult to detect due to it is not uniformly distributed. Hence, UAVs have a key role in crop disease surveillance and early detection [28,29,30]. This research attempts to provide experimental evidence of the implementation feasibility of the developed robust backstepping control in a PixHawk autopilot used in a pest detection task. An RGB GoPro Hero8 Black camera is mounted on the vehicle, and the video is processed off-line in the MATLAB software. This image processing provides the approximated location of the possibly affected crops. The overall system (UAV and camera) represents a relative low-cost (less than USD 450) alternative in precision agriculture.

The contributions of the article are as follows:

• A new robust backstepping approach-based control algorithm that considers matched vanishing disturbances is proposed. The proposed controller uses a virtual bounded input: the function $sin(.)$, which produces bounded control signals, and it is appropriate to the physical constrains of the UAV.
• Experimental results in trajectory tracking using a UAV in an outdoor environment are reported. A specific precision agriculture task is involved using a commercial camera system and MATLAB software.
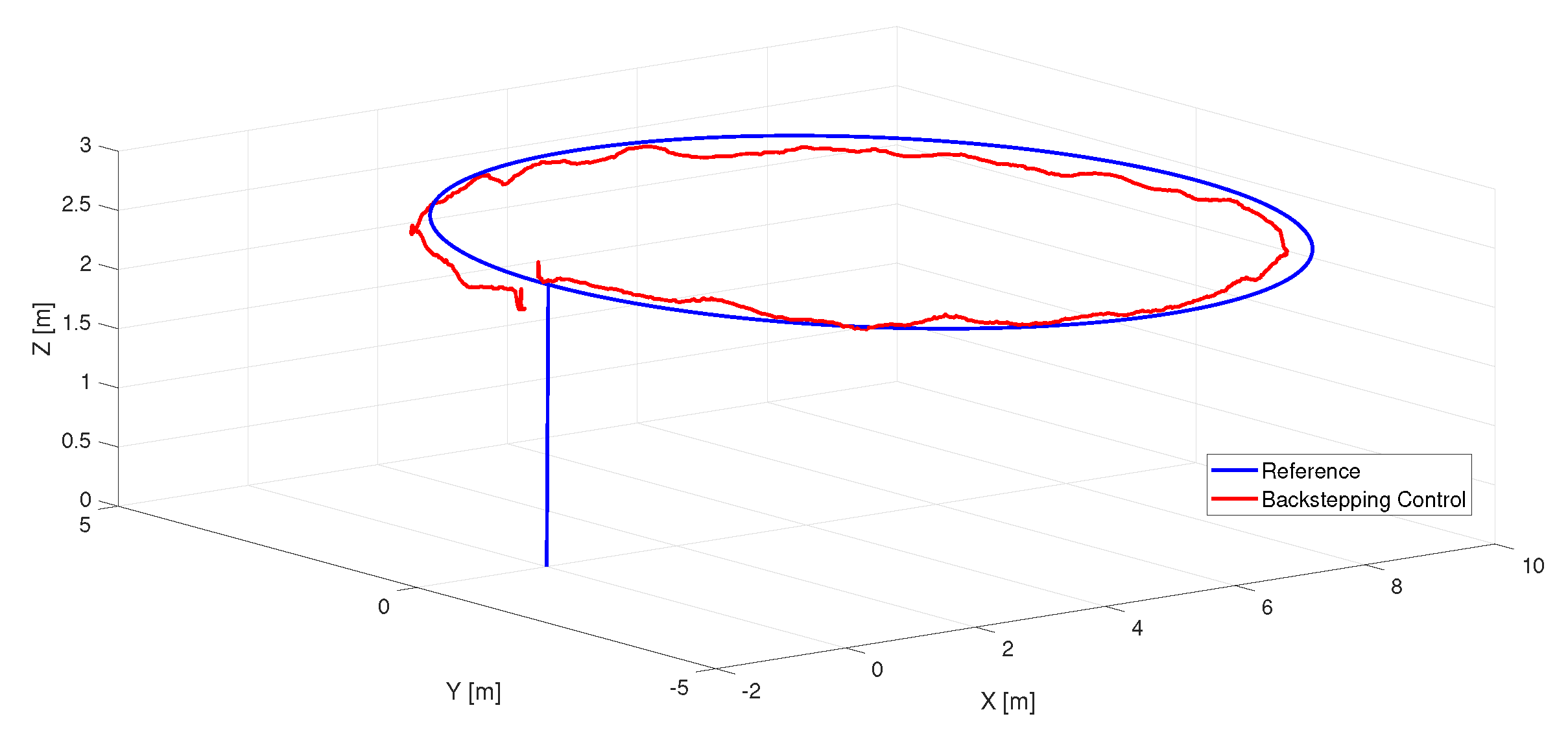
• The robustness provided to the proposed controller allows to reduce the capture of distorted crop images and it represents better performance when our proposal is compared to a PD controller, although a gimbal or additional software are not used.
• This article tries to fill the gap between the technological development with advanced control theory.

Accordingly, the paper is organized as follows: In Section 2, the problem formulation and the main result are presented. The quadrotor model is shown in Section 3, and the application of the control strategy is developed in Section 4. The description of the experimental platform and the experimental results are given in Section 5. Section 6 demonstrates how pests are detected in the field. Finally, concluding comments are enunciated in Section 7.

2. Problem Formulation and Main Results

In this part, the problem is stated and the theoretical main result is presented.

2.1. System Description

The following perturbed nonlinear system is addressed:

$$\begin{array}{ccc}\hfill \dot{\vartheta }& =& f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\zeta \hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \dot{\zeta }& =& u+\delta \left(t,\vartheta \right),\hfill \end{array}$$

(2)

where ${\left[{\vartheta }^T,\zeta \right]}^T\in {\mathbb{R}}^{n+1}$ is the state, and $u\in \mathbb{R}$ is the control input. It is considered that the next assumptions are fulfilled:

• The known functions $f_0:D\to {\mathbb{R}}^n$ and $f_1:D\to {\mathbb{R}}^n$ are continuously differentiable in a domain $D\subset {\mathbb{R}}^n$ that contains the origin $\vartheta =0$ and $f_0\left(0\right)=0$.
• The Equation (1) of the system can be stabilized with a state feedback $\zeta =\mu \left(\vartheta \right),$ with $\mu \left(0\right)=0$, then, there is a Lyapunov function that satisfies the following equation:

  $$\frac{\partial V\left(\vartheta \right)}{\partial \vartheta }\left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\mu \left(\vartheta \right)\right]\le -W\left(\vartheta \right),$$

  where $W\left(\vartheta \right)$ is a positive definite function, $\forall \vartheta \in D.$
• Function $\delta (t,\vartheta )$ is a bounded matched vanishing perturbation, i.e.,

  $$\delta \left(t,0\right)=0,\left|\delta (t,\vartheta )\right|\le \Delta ,\mathrm{and}\Delta >0.$$

  (3)

Problem statement: Design a control u that guarantees the closed-loop robust stability of the origin ($\vartheta =0,$ $\zeta =0$) of system (1) and (2) in the presence of unstructured matched disturbance $\delta (t,\vartheta )$. Then, compute the control laws for every subsystem of the quadrotor, guaranteeing its robust stabilization.

2.2. Main Result

The synthesis of the proposed control algorithm is stated as follows.

Theorem 1.

Consider the system (1) and (2), under the Assumptions 1–3, for $k>0$, and for a Lyapunov function of the form $V_1(\vartheta ,\overline{z})=V\left(\vartheta \right)+\frac{1}{2}{\overline{z}}^2$, with $\overline{z}=\zeta -\mu \left(\vartheta \right),$ then, the control law

$$u=\frac{\partial \mu \left(\vartheta \right)}{\partial \vartheta }\left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\zeta \right]-\frac{\partial V\left(\vartheta \right)}{\partial \vartheta }{f}_1\left(\vartheta \right)-k\overline{z}-sgn\left(\overline{z}\right)\Delta$$

(4)

robustly stabilizes the system.

Proof of Theorem 1.

The proof is inspired on the methodology given in [26]. Adding and subtracting $f_1\left(\vartheta \right)\mu \left(\vartheta \right)$ on the right-hand side of Equation (1), it yields to

$$\begin{array}{ccc}\hfill \dot{\vartheta }& =& \left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\mu \left(\vartheta \right)\right]+f_1\left(\vartheta \right)\left[\zeta -\mu \left(\vartheta \right)\right]\hfill \\ \hfill \dot{\zeta }& =& u+\delta \left(t,\vartheta \right).\hfill \end{array}$$

(5)

Define $\overline{f_0}\left(\vartheta \right)=f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\mu \left(\vartheta \right),$ $\overline{z}=\zeta -\mu \left(\vartheta \right),$ then its derivative is given by $\stackrel{\cdot }{\overline{z}}=\dot{\zeta }-\dot{\mu }\left(\vartheta \right)=\left(u+\delta \left(t,\vartheta \right)\right)-\dot{\mu }\left(\vartheta \right),$ and consider the change of variable

$$\overline{v}=u-\dot{\mu }\left(\vartheta \right),$$

(6)

where

$$\dot{\mu }\left(\vartheta \right)=\frac{\partial \mu \left(\vartheta \right)}{\partial \vartheta }\dot{\vartheta }=\frac{\partial \mu \left(\vartheta \right)}{\partial \vartheta }\left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\zeta \right].$$

(7)

Now, the system (5) is expressed in the classical backstepping form

$$\begin{array}{ccc}\hfill \dot{\vartheta }& =& \overline{f_0}\left(\vartheta \right)+f_1\left(\vartheta \right)\overline{z}\hfill \\ \hfill \stackrel{\cdot }{\overline{z}}& =& \overline{v}+\delta \left(t,\vartheta \right),\hfill \end{array}$$

(8)

when $\overline{z}=0$, it guarantees that the system (8) has an equilibrium point at the origin (according to Assumption 2).

A positive definite Lyapunov candidate function of the form $V_1\left(\vartheta ,\overline{z}\right)=V\left(\vartheta \right)+\frac{1}{2}{\overline{z}}^2$ is proposed, and its derivative along the trajectories of system (8), according to Assumption 2, is given by

$$\begin{array}{ccc}\hfill {\left.\dot{V_1}\left(\vartheta ,\overline{z}\right)\right|}_{\left(8\right)}& =& \frac{\partial V\left(\vartheta \right)}{\partial \vartheta }\overline{f_0}\left(\vartheta \right)+\frac{\partial V\left(\vartheta \right)}{\partial \vartheta }{f}_1\left(\vartheta \right)\overline{z}+\overline{z}\stackrel{\cdot }{\overline{z}}\hfill \\ & \le & -W\left(\vartheta \right)+\frac{\partial V\left(\vartheta \right)}{\partial \vartheta }{f}_1\left(\vartheta \right)\overline{z}+\overline{z}\stackrel{\cdot }{\overline{z}},\hfill \end{array}$$

where $\stackrel{\cdot }{\overline{z}}=\overline{v}+\delta (t,\vartheta )$, set

$$\overline{v}=-k\overline{z}-\frac{\partial V\left(\vartheta \right)}{\partial \vartheta }{f}_1\left(\vartheta \right)-sgn\left(\overline{z}\right)\Delta ,$$

(9)

with $k>0$; substituting into the previous equation, it yields

$${\left.\dot{V_1}\left(\vartheta ,\overline{z}\right)\right|}_{\left(8\right)}\le -W\left(\vartheta \right)-k{\overline{z}}^2+\overline{z}\delta (t,\vartheta )-\overline{z}sgn\left(\overline{z}\right)\Delta .$$

(10)

Majorizing the term

$$\overline{z}\delta (t,\vartheta )\le \left|\overline{z}\delta (t,\vartheta )\right|\le \left|\overline{z}\right|\left|\delta (t,\vartheta )\right|\le \left|\overline{z}\right|\Delta ,$$

and $\left|\overline{z}\right|\triangleq \overline{z}sgn\left(\overline{z}\right)$; so, $\left|\overline{z}\right|\Delta =\overline{z}sgn\left(\overline{z}\right)\Delta$; substituting into Equation (10), it yields

$${\left.\dot{V_1}\left(\vartheta ,\overline{z}\right)\right|}_{\left(8\right)}\le -W\left(\vartheta \right)-k{\overline{z}}^2<0,$$

so, the origin of the system (8) is robustly stable; since $\mu \left(0\right)=0$, the origin of system (1) and (2) is robustly stable too. The input $u=\overline{v}+\dot{\mu }\left(\vartheta \right)$ is obtained from Equation (6), and replacing Equations (7) and (9) into u, the result follows in Equation (4). □

The control action (4) is used to solve the trajectory tracking problem of a quadrotor whose model is shown in the following section.

3. Quadrotor Model

The quadrotor model (see Figure 1) is obtained by representing a solid body moving in 3D space and being subjected to one force and three moments [31]. The generalized coordinates of the four rotor helicopter $q=(\gamma ,\lambda )$, where $\gamma =(x,y,z)\in {\mathbb{R}}^3$ represents the relative position of the center of mass of the quadrotor with respect to an inertial reference, and $\lambda =(\varphi ,\theta ,\psi )\in {\mathbb{R}}^3$ are the Euler angles representing the orientation of the quadrotor, known as roll-pitch-yaw, respectively. The inertial moments in the flying robot are defined by $I_x,I_y,I_z$ ordered with respect to x, y and z axes, while m denotes its mass, l is the arm length, and ${\tau }_{\varphi }$, ${\tau }_{\theta }$ and ${\tau }_{\psi }$ are the input signals to be applied to the motors.

The following equations describe the movement of the quadcopter affected by collective throttle $u_s$ and torques ${\tau }_{\varphi }$, ${\tau }_{\theta }$ and ${\tau }_{\psi }$ [32]

$$\begin{array}{c}\ddot{x}=-\frac{1}{m}sin\theta u_s\hfill \\ \ddot{y}=\frac{u_s}{m}cos\theta sin\varphi \hfill \\ \ddot{z}=\frac{cos\theta cos\varphi }{m}{u}_s-g\hfill \\ \ddot{\varphi }=\dot{\theta }\dot{\psi }\frac{I_y-I_z}{I_x}+\frac{l}{I_x}{\tau }_{\varphi }\hfill \\ \ddot{\theta }=\dot{\varphi }\dot{\psi }\frac{I_x-I_z}{I_y}+\frac{l}{I_y}{\tau }_{\theta }\hfill \\ \ddot{\psi }=\dot{\varphi }\dot{\theta }\frac{I_y-I_x}{I_z}+\frac{l}{I_z}{\tau }_{\psi }.\hfill \end{array}$$

(11)

The following assumptions, proposed in [11], are considered:

• The UAV is considered as a rigid and symmetrical body.
• The center of gravity (CoG) of the quadrotor is in its origin.
• The blades are rigid bodies with fixed angle pitch.
• In the nominal model of the quadrotor, the aerodynamics effects have not been considered.
• The motor dynamic could be modeled as a first-order transfer function, and it is sufficient to reproduce the dynamics between the propeller’s speed set-point and its true speed. As the time constant of this transfer function is small, we can consider that the rotor dynamic is approximately equal to one [33]. This assumption is used to suppose additional dynamics (or uncertain parameters) that represent matched vanishing perturbations in the actuators.
• The attitude angles, pitch, roll and yaw are restricted in the interval [$-\frac{\pi }{4}$, $\frac{\pi }{4}$].

Remark 1.

Additionally to Assumption 5, the effects of the propellers are neglected [34]. However, a more accurate trust model of the vehicle is given in [34], which can be expressed as

$$\begin{array}{ccc}\hfill T_i& =& c_1{\omega }_i^2\left(c_2\left(1+\frac{3}{2}{\mu }_i^2\left(t\right)\right)-{\lambda }_i\left(t\right)\right)\hfill \\ & =& c_1{\omega }_i^2{c}_2+\underset{\delta }{\underbrace{c_1{\omega }_i^2\left[c_2\frac{3}{2}{\mu }_i^2\left(t\right)-{\lambda }_i\left(t\right)\right]}},\hfill \end{array}$$

where $T_i$ is the trust of motor $i^{th},$ ${\omega }_i$ is the angular velocity of the motor $i^{th},$ ${\mu }_i\left(t\right)$ and ${\lambda }_i\left(t\right)$ are the advance and inflow ratios respectively (nonlinear functions), $c_1$ and $c_2$ are positive constants. So, δ could be the second term of $T_i,$ among other unmodelled dynamics.

With the nominal model given by (11), the robust backstepping controller is synthesized in the next section.

4. Control Strategy Applied to the Quadrotor

In this section, the quadrotor mathematical model (11) is divided into subsystems as was done in [11,35]: the altitude subsystem z, the yaw subsystem $\psi$, the pitch subsystem $x-\theta$ and the roll subsystem $y-\varphi$. Then, the robust stabilizing controllers for each subsystem are obtained using the result of Theorem 1 while considering the presence of matched vanishing disturbances $\delta (t,\vartheta )$.

4.1. Altitude Controller

The subsystem z that describes the UAV dynamic of altitude is represented by

$$\ddot{z}=\frac{cos\theta cos\varphi }{m}{u}_s-g+\delta (\vartheta ,t),$$

(12)

where $\left|\delta \left(t,\vartheta \right)\right|\le {\Delta }_1$, ${\Delta }_1$ is the upper bound of the matched disturbances. Defining the state variables $x_1=z$ and $x_2=\dot{z}$, and

$$u_s=\frac{m}{cos\theta cos\varphi }\left[g+u_z\right],$$

(13)

and according to the backstepping methodology [26], $x_2=\mu \left(x_1\right)=-{\alpha }_6{x}_1$, for ${\alpha }_6>0$, the subsystem (12) is rewritten as follows:

$$\begin{array}{c}{\dot{x}}_1=-{\alpha }_6{x}_1\hfill \\ {\dot{x}}_2=u_z+\delta (\vartheta ,t).\hfill \end{array}$$

(14)

The Lyapunov function is $V_z\left(x_1\right)=\frac{1}{2}{x}_1^2,$ and following the result of Theorem 1, with $\zeta =x_2$, $f_0\left(\vartheta \right)=0$, $\vartheta =x_1$, $f_1\left(\vartheta \right)=1$, and $\overline{z}=x_2+{\alpha }_6{x}_1,$ the stabilizing control for subsystem (14) takes the following form:

$$u_z=-(1+k_z{\alpha }_6)x_1-({\alpha }_6+k_z)x_2-sgn(x_2+{\alpha }_6{x}_1){\Delta }_1.$$

4.2. Yaw Controller

The dynamic of the $\psi$ angle is given by

$$\ddot{\psi }=\dot{\varphi }\dot{\theta }{c}_1+c_2{\tau }_{\psi }+\delta (\vartheta ,t),$$

(15)

where $c_1=\frac{I_y-I_x}{I_z}$, $c_2=\frac{l}{I_z}$, $\left|\delta \left(t,\vartheta \right)\right|\le {\Delta }_2$; $I_x$, $I_y$, $I_z$ are parameters of the inertia matrix. Defining the state variables $x_3=\psi$, $x_4=\dot{\psi },$ and

$${\tau }_{\psi }=\frac{1}{c_2}\left(-\dot{\varphi }\dot{\theta }{c}_1+u_{\psi }\right),$$

(16)

then Equation (15) becomes as follows:

$$\ddot{\psi }=u_{\psi }+\delta (\vartheta ,t).$$

Following a similar procedure as in the altitude control, $x_4=\mu \left(x_3\right)=-{\alpha }_7{x}_3$, for ${\alpha }_7>$ 0, the subsystem (15) yields to

$$\begin{array}{c}\dot{x_3}=-{\alpha }_7{x}_3\hfill \\ \dot{x_4}=u_{\psi }+\delta (\vartheta ,t).\hfill \end{array}$$

(17)

Let $V_{\psi }\left(x_3\right)=\frac{1}{2}{x}_3^2$ the Lyapunov function and defining $\zeta =x_4$, $\vartheta =x_3$, $f_0\left(\vartheta \right)=0$, $f_1\left(\vartheta \right)=1,$ $\overline{z}=x_4+{\alpha }_7{x}_3,$ the control law for the subsystem (17) is given by

$$u_{\psi }=-(1+k_{\psi }{\alpha }_7)x_3-({\alpha }_7+k_{\psi })x_4-sgn(x_4+{\alpha }_7{x}_3){\Delta }_2.$$

(18)

4.3. Controller for Subsystem $x-\theta$

Dynamics related with translational motion along x-axis and the pitch angle $\theta$ around the y-axis are described by

$$\begin{array}{c}\ddot{x}=-\frac{1}{m}sin\theta u_s\hfill \\ \ddot{\theta }=\dot{\varphi }\dot{\psi }\frac{I_x-I_z}{I_y}+\frac{l}{I_y}{\tau }_{\theta }+\delta (\vartheta ,t),\hfill \end{array}$$

(19)

where $c_3=\frac{I_x-I_z}{I_y}$, $u_s\ne 0$, and $c_4=\frac{l}{I_y}$. Let $x_5=x$, $x_6=\dot{x}$, $x_7=\theta$ and $x_8=\dot{\theta }$. Then, the state space representation is given by

$$\begin{array}{c}\dot{x_5}=x_6\hfill \\ \dot{x_6}=-\frac{1}{m}sin{x}_7{u}_s\hfill \\ \dot{x_7}=x_8\hfill \\ \dot{x_8}=\dot{\varphi }\dot{\psi }{c}_3+c_4{\tau }_{\theta }+\delta (\vartheta ,t).\hfill \end{array}$$

(20)

Considering the first and second equations of the state space representation (20) and defining the virtual input as follows:

$$u_{1x}=sin{x}_7=-\frac{m}{u_s}{u}_x,$$

(21)

then, according to the backstepping methodology [26] $x_6=\mu \left(x_5\right)=-{\alpha }_5{x}_5$, for ${\alpha }_5>0$. Notice that the selected virtual input $sin\left(x_7\right)$ produces bounded control signals and it is appropriate to the physical constrains of the UAV: $x_7$∈$[\frac{-\pi }{4},\frac{\pi }{4}]$. These equations can be rewritten as follows:

$$\begin{array}{c}\dot{x_5}=-{\alpha }_5{x}_5\hfill \\ \dot{x_6}=u_x,\hfill \end{array}$$

where $u_x=-(1+{\alpha }_5{k}_5)x_5-({\alpha }_5+k_5)x_6$ is the control input, computed with the Lyapunov function $V_1\left(x_5\right)=\frac{1}{2}{x_5}^2.$ Replacing $u_x$ into Equation (21), it yields to

$$u_{1x}=\frac{m}{u_s}\left(d_1{x}_5+d_2{x}_6\right),$$

(22)

where $d_1=1+{\alpha }_5{k}_5$ and $d_2={\alpha }_5+k_5$.

Next, the iterative methodology of backstepping is applied; taking the first three equations of the state space representation (20), the subsystem is rewritten as

$$\begin{array}{c}\left[\begin{array}{c}{\dot{x}}_5\\ {\dot{x}}_6\end{array}\right]=\left[\begin{array}{c}{x}_6\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ -\frac{u_s}{m}\end{array}\right]sin{x}_7\hfill \\ {\dot{x}}_7=x_8=u_{2x},\hfill \end{array}$$

(23)

In this case, $\vartheta ={\left(x_5,x_6\right)}^T,$ and $\zeta =x_7$. The modified backstepping structure, proposed by [11], is applied for system (23) considering the Lyapunov function

$$V_2=V_2\left(x_5,x_6\right)=\frac{1}{2}{x}_5^2+\frac{{\beta }_1}{2}{\left(x_6+{\alpha }_5{x}_5\right)}^2.$$

The virtual input ${\mu }_1={\mu }_1\left(x_5,x_6\right)=\frac{m}{u_s}\left(d_1{x}_5+d_2{x}_6\right)$ is defined as $u_{1x},$ given in Equation (22); substituting Equation (13) in ${\mu }_1$

$${\mu }_1\left(x_5,x_6\right)=\frac{cos{x}_{7}cos{x}_{11}}{p}\left(d_1{x}_5+d_2{x}_6\right).$$

where $p=g+u_z$. Applying Proposition 1 of [11], the control $u_{2x}$ has the following form:

$$u_{2x}=\frac{\frac{\partial {\mu }_1}{\partial \vartheta }\left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)sin\zeta \right]-\frac{\partial V_2}{\partial \vartheta }{f}_1\left(\vartheta \right)-k_6(sin{x}_7-{\mu }_1)}{cos\zeta },$$

(24)

where

$$\begin{array}{ccc}\hfill \frac{\partial \left({\mu }_1\left(x_5,x_6\right)\right)}{\partial x_5}& =& \frac{cos{x}_{7}cos{x}_{11}{d}_1}{p},\hfill \\ \hfill \frac{\partial \left({\mu }_1\left(x_5,x_6\right)\right)}{\partial x_6}& =& \frac{cos{x}_{7}cos{x}_{11}{d}_2}{p},\hfill \\ \hfill \frac{\partial \left(V_2\left(x_5,x_6\right)\right)}{\partial x_6}& =& {\beta }_1{\alpha }_5{x}_5+{\beta }_1{x}_6,\hfill \end{array}$$

So, the virtual input $u_{2x}$ is

$$\begin{array}{ccc}\hfill u_{2x}& =& \left(\frac{k_6{d}_{1}cos{x}_{11}}{p}+\frac{{\beta }_1{\alpha }_{5}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)x_5\hfill \\ & +& \left(\frac{d_{1}cos{x}_{11}+k_6{d}_{2}cos{x}_{11}}{p}+\frac{{\beta }_{1}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)x_6-\left(d_2+k_6\right)tan{x}_7\hfill \end{array}$$

(25)

Finally, the whole state space representation (20) is considered with $\vartheta ={(x_5,x_6,x_7)}^T,$ $\zeta =x_8$, and for

$${\tau }_{\theta }=\frac{1}{c_4}\left[-\dot{\varphi }\dot{\psi }{c}_3+{\tau }_{\theta a}\right],$$

(26)

this subsystem can be rewritten as

$$\begin{array}{c}\left[\begin{array}{c}{\dot{x}}_5\\ {\dot{x}}_6\\ {\dot{x}}_7\end{array}\right]=\left[\begin{array}{c}{x}_6\\ -\frac{psin{x}_7}{cos{x}_{7}cos{x}_{11}}\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]x_8,\hfill \\ {\dot{x}}_8={\tau }_{\theta a}+\delta (\vartheta ,t)=u_{3x}+\delta (\vartheta ,t).\hfill \end{array}$$

(27)

The proposed Lyapunov function for subsystem (27) is

$$\begin{array}{c}{V}_3=V_3(x_5,x_6,x_7)=\frac{1}{2}{x}_5^2+\frac{{\beta }_1}{2}{\left(x_6+{\alpha }_5{x}_5\right)}^2+\frac{{\beta }_2}{2}{\left(sin{x}_7-\frac{cos{x}_{7}cos{x}_{11}}{p}\left(d_1{x}_5+d_2{x}_6\right)\right)}^2,\hfill \end{array}$$

and the virtual input ${\mu }_2$ is associated with $u_{2x},$ given in (25), as

$$\begin{array}{c}{\mu }_2=\left(\frac{k_6{d}_{1}cos{x}_{11}}{p}+\frac{{\beta }_1{\alpha }_{5}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)x_5+\left(\frac{(d_1+k_6{d}_2)cos{x}_{11}}{p}+\frac{{\beta }_{1}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)x_6-\left(d_2+k_6\right)tan{x}_7.\hfill \end{array}$$

According to Theorem 1, the controller is given by

$$\begin{array}{ccc}\hfill u_{3}x& =& -k_7{z}_3-\frac{\partial V_3\left(\vartheta \right)}{\partial \vartheta }{f}_1\left(\vartheta \right)-sgn\left(z_3\right){\Delta }_3+\frac{\partial {\mu }_2\left(\vartheta \right)}{\partial \vartheta }\left[f_0\left(\vartheta \right)+f_1\left(\vartheta \right)\zeta \right],\hfill \end{array}$$

where $z_3=x_8-{\mu }_2$, $k_7>0$, $\vartheta ={(x_5,x_6,x_7)}^T$, $f_1\left(\vartheta \right)={[0,0,1]}^T$, and

$$\begin{array}{c}\frac{\partial {\mu }_2}{\partial x_5}=\left(\frac{k_6{d}_{1}cos{x}_{11}}{p}+\frac{{\beta }_1{\alpha }_{5}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)\hfill \\ \frac{\partial {\mu }_2}{\partial x_6}=\left(\frac{d_{1}cos{x}_{11}}{p}+\frac{k_6{d}_{2}cos{x}_{11}}{p}+\frac{{\beta }_{1}p}{{cos}^2{x}_{7}cos{x}_{11}}\right)\hfill \\ \frac{\partial {\mu }_2}{\partial x_7}=\left(\frac{2{\beta }_1{\alpha }_{5}psin{x}_7}{{cos}^3{x}_{7}cos{x}_{11}}\right)x_5+\left(\frac{2{\beta }_{1}psin{x}_7}{{cos}^3{x}_{7}cos{x}_{11}}\right)x_6-(d_2+k_6){sec}^2{x}_7\hfill \\ \frac{\partial V_3}{\partial x_7}={\beta }_{2}sin{x}_{7}cos{x}_7-\left[\frac{{\beta }_{2}cos{x}_{11}(d_1{x}_5+d_2{x}_6)}{p}\right]\left(2{cos}^2{x}_7-1\right).\hfill \end{array}$$

Therefore, the input $u_{3x}$ is

$$\begin{array}{ccc}\hfill u_{3x}& =& \frac{\partial {\mu }_2}{\partial x_5}{x}_6-\frac{\partial {\mu }_2}{\partial x_6}\frac{psin{x}_7}{cos{x}_{7}cos{x}_{11}}+\frac{\partial {\mu }_2}{\partial x_7}{x}_8-\frac{\partial V_3}{\partial x_7}-sgn(x_8-{\mu }_2){\Delta }_3-k_7(x_8-{\mu }_2).\hfill \end{array}$$

4.4. Controller for Subsystem $y-\varphi$

The translational and rotational dynamics experienced by the flying robot along the y-axis and the roll angle $\varphi$ respectively are represented by

$$\begin{array}{c}\ddot{y}=\frac{u_s}{m}cos\theta sin\varphi \hfill \\ \ddot{\varphi }=\dot{\theta }\dot{\psi }{c}_5+c_6{\tau }_{\varphi }+\delta (t,\vartheta ),\hfill \end{array}$$

(28)

where $c_5=\frac{I_y-I_z}{I_x}$, $c_6=\frac{l}{I_x}$. Defining the variables $x_9=y$, $x_{10}=\dot{y}$, $x_{11}=\varphi$, $x_{12}=\dot{\varphi }$, the state space representation is given by

$$\begin{array}{c}\dot{x_9}=x_{10}\hfill \\ \dot{x_{10}}=\frac{cos{x}_7}{m}sin{x}_{11}{u}_s\hfill \\ \dot{x_{11}}=x_{12}\hfill \\ \dot{x_{12}}=\dot{\theta }\dot{\psi }{c}_5+c_6{\tau }_{\varphi }+\delta (t,\vartheta ).\hfill \end{array}$$

(29)

Considering the first two equations of (29), the virtual input

$$u_y=sin{x}_{11}=\frac{m}{u_{s}cos{x}_7}{u}_1,$$

(30)

and defining $x_{10}=\mu \left(x_9\right)=-{\alpha }_1{x}_9$, for ${\alpha }_1>0$; the subsystem is rewritten as $\dot{x_9}=-{\alpha }_1{x}_9$ and $\dot{x_{10}}=u_1.$ The Lyapunov function is $V_1\left(x_9\right)=\frac{1}{2}{x}_9^2,$ and according to the classic backstepping methodology, the input $u_1=-\left(k_1{\alpha }_1+1\right)x_9-\left(k_1+{\alpha }_1\right)x_{10}$ is substituted into Equation (30), which yields

$$u_y=\frac{m}{u_{s}cos{x}_7}\left[-b_1{x}_9-b_2{x}_{10}\right],$$

(31)

where $b_1=k_1{\alpha }_1+1$, $b_2=k_1+{\alpha }_1$; substituting (13) into (31)

$$u_y=\frac{cos{x}_{11}}{p}\left(-b_1{x}_9-b_2{x}_{10}\right).$$

In the next step, the third equation of the state space representation (29) is added, and the subsystem is rewritten as in [11], with $\vartheta ={\left(x_9,x_{10}\right)}^T,$ and $\zeta =x_{11},$ as follows:

$$\begin{array}{c}\left[\begin{array}{c}{\dot{x}}_9\\ {\dot{x}}_{10}\end{array}\right]=\left[\begin{array}{c}{x}_{10}\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ \frac{p}{cos{x}_{11}},\end{array}\right]sin{x}_{11}\hfill \\ {\dot{x}}_{11}=x_{12}=u_{y2}.\hfill \end{array}$$

(32)

Following a similar procedure applied to the previous subsystems, with $V_2(x_9,x_{10})=\frac{1}{2}{x}_9^2+\frac{{\beta }_3}{2}{\left(x_{10}+{\alpha }_1{x}_9\right)}^2,$ and ${\mu }_1=\frac{cos{x}_{11}}{p}\left(-b_1{x}_9-b_2{x}_{10}\right),$ a control is obtained as the given in the Equation (24), and it has the following structure:

$$\begin{array}{c}{u}_{y2}=-\left[\frac{k_2{b}_1}{p}+\frac{{\beta }_3{\alpha }_{1}p}{{cos}^2{x}_{11}}\right]x_9-\left[\frac{b_1+k_2{b}_2}{p}+\frac{{\beta }_{3}p}{{cos}^2{x}_{11}}\right]x_{10}-(b_2+k_2)tan{x}_{11}.\hfill \end{array}$$

(33)

In the last step, subsystem (29) is fully considered, with $\vartheta ={(x_9,x_{10},x_{11})}^T$, $\zeta =x_{12}$, and defining

$${\tau }_{\varphi }=\frac{1}{c_6}\left[-\dot{\theta }\dot{\psi }{c}_5+{\tau }_1\right],$$

(34)

it can be rewritten as follows:

$$\begin{array}{c}\left[\begin{array}{c}{\dot{x}}_9\\ {\dot{x}}_{10}\\ {\dot{x}}_{11}\end{array}\right]=\left[\begin{array}{c}{x}_{10}\\ \frac{psin{x}_{11}}{cos{x}_{11}}\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]x_{12}\hfill \\ {\dot{x}}_{12}={\tau }_1+\delta (t,\vartheta ),\hfill \end{array}$$

(35)

where ${\tau }_1=u_{y3}$, ${\mu }_2$ is associated with $u_{y2}$, given in Equation (33), and the Lyapunov function is defined by

$$\begin{array}{ccc}\hfill V_3(x_9,x_{10},x_{11})& =& \frac{1}{2}{x}_9^2+\frac{{\beta }_3}{2}{\left(x_{10}+{\alpha }_1{x}_9\right)}^2+\frac{{\beta }_4}{2}{\left[sin{x}_{11}+\frac{\left(b_1{x}_9+b_2{x}_{10}\right)cos{x}_{11}}{p}\right]}^2.\hfill \end{array}$$

From Theorem 1, the input $u_{y3}$ is computed as

$$\begin{array}{ccc}\hfill u_{y3}& =& \frac{\partial {\mu }_2}{\partial x_9}{x}_{10}+\frac{\partial {\mu }_2}{\partial x_{10}}\frac{psin{x}_{11}}{cos{x}_{11}}+\frac{\partial {\mu }_2}{\partial x_{11}}{x}_{12}-\frac{\partial V_3}{\partial x_{11}}-k_3\left(x_{12}-{\mu }_2\right)-sgn\left(x_{12}-{\mu }_2\right){\Delta }_4.\hfill \end{array}$$

where

$$\begin{array}{c}\frac{\partial {\mu }_2}{\partial x_9}=-\left(\frac{k_2{b}_1}{p}+\frac{{\beta }_3{\alpha }_{1}p}{{cos}^2{x}_{11}}\right)\hfill \\ \frac{\partial {\mu }_2}{\partial x_{10}}=-\left(\frac{b_1+k_2{b}_2}{p}+\frac{{\beta }_{3}p}{{cos}^2{x}_{11}}\right)\hfill \\ \frac{\partial {\mu }_2}{\partial x_{11}}=-\left(\frac{(k_2+b_2)}{{cos}^2{x}_{11}}+\frac{({\alpha }_1{x}_9+x_{10})2{\beta }_{3}psin{x}_7}{{cos}^3{x}_7}\right)\hfill \\ \frac{\partial V_3}{\partial x_{11}}=\left[\frac{{\beta }_4}{p}(b_1{x}_9+b_2{x}_{10})\right]\left(2{cos}^2{x}_{11}-1\right)\hfill \\ +\left({\beta }_4-\frac{{\beta }_4(b_1^2{x}_9^2+b_2^2{x}_{10}^2)}{p^2}-\frac{2{\beta }_4{b}_1{b}_2{x}_9{x}_{10}}{m^2{p}^2}\right)sin{x}_{11}cos{x}_{11}.\hfill \end{array}$$

To assess the effectiveness of the synthesized controllers (13), (16), (26) and (34) in the trajectory tracking task of a quadrotor UAV, experimental tests are conducted as described in the next section.

5. Experimental Results

5.1. Experimental Platform Description

The quadrotor is constructed on a plastic frame F450. An autopilot Pixhawk, version 2.4.8, is on board the F450 structure. The Pixhawk exhibits the following performance: a primary clock at 168 MHz, and with a 32-bit processor STM32F427 Cortex M4 core with a floating processor unit. The autopilot has two accelerometers, a gyroscope, and two magnetometers for attitude measurements of the UAV. The Pixhawk is equipped with radio signal input ports compatible with Futaba 10J radio. Furthermore, it has eight pulse width modulation main outputs that are used to control the motors. To pinpoint the longitudinal positions, an external module Ublox NEO-M8N GPS (accuracy of 0.6–0.9 m) is mounted. The yaw angle is estimated via an internal magnetometer located in the GPS. As power supply of the UAV, Lipo technology batteries are employed (capacity of 5200 mAh, discharge rate of 15 C). The quadrotor has four propellers of model 1045, four 2212 920 KV brushless motors and four electronic speed controllers of model SIMONK30A. The trajectory tracking reference was programmed into the Pixhawk (Figure 2).

5.2. Experimental Results Applying Synthesized Controllers

In this subsection, for comparison purposes, experimental tests in outdoor environment of UAV are presented for the proposed backstepping controller and a PD controller. For the trajectory tracking task on the spaces $(x;y;z)$ and $(\varphi ,\theta ,\psi )$, the UAV follows three paths: 1. The manual takeoff of the UAV, until the desired altitude is reached, and this altitude is defined by the pilot. 2. The quadrotor tracks parametric circle equations given by

$$\begin{array}{ccc}\hfill x_{ref}& =& \left(-5cos\left(\frac{\pi }{180}t\right)+5\right)m,\hfill \\ \hfill y_{ref}& =& -5sin\left(\frac{\pi }{180}t\right)m,\hfill \\ \hfill z_{ref}& =& 2.3m.\hfill \end{array}$$

3. At the end, when the trajectory is finished, the pilot regains control of the quadrotor and lands it. The programmed sampling time (T) is $T=0.01$ s, it was used in all experimental tests. The quadrotor parameters are as follows: mass m = 1.3 kg, distance from the motors to the centre of gravity l = 0.3 m, constant of gravity g = 9.81 m/s${}^2$ and inertia moments $I_x=I_y$ = 0.01567 kgm${}^2$, $I_z$ = 0.028346 kgm${}^2$. The gains of controllers (13), (16), (26) and (34) are heuristically proposed in

Table 1. Controller gains.

Subsystems
$\mathit{\psi }$	$\mathit{z}$	$\mathit{x}\mathbf{-}\mathit{\theta }$	$\mathit{y}\mathbf{-}\mathit{\varphi }$
$k_{\psi }=24.2$	$k_z=7.39$	$k_5=0.1$	$k_1=0.4$
${\alpha }_7=5.7$	${\alpha }_6=12.3$	$k_6=0.13$	$k_2=0.27$
${\Delta }_1=3.2$	${\Delta }_2=2.5$	$k_7=7.3$	$k_3=5.3$
		${\Delta }_3=5$	${\Delta }_4=2$
		${\alpha }_5=12$	${\alpha }_1=0.009$
		${\beta }_1=0.1$	${\beta }_3=5.2$
		${\beta }_2=0.25$	${\beta }_4=3.64$

. The delta values (${\Delta }_i,i=1,2,3,4$) are the maximum values for the matched disturbances that could be adjusted heuristically such that the closed-loop performance is satisfactory.

To compare the behavior of the proposed controller, a PD controller, which is tuned as is proposed in [35], is employed, obtaining the gains by proposing the following temporal parameters: the maximum overshoot and the settling time. Translational and attitude initial values of the drone are near to the origin.

Figure 3 displays the translational positions recorded during the experiment following the desired trajectory. The figure is divided in three figures: 1. The first shows the trajectory of the vehicle on the X axis, 2. The second displays the trajectory along the Y axis, 3. The last one illustrates the trajectory tracking task on the Z axis. As shown in Figure 3, the trajectory tracking task in ($X,Y,Z$) space, in the blue line, displays a reliable performance when it is compared with the reference values in the red line. The position performance of the drone in the ($X,Y$) space is displayed in Figure 4 and Figure 5. It is noteworthy that these experimental results were obtained in an outdoor environment.

Figure 6 shows the relative small errors during the trajectory tracking. During the trajectory tracking task, the references are subject to changes in the X, Y axes, then the errors may increase or decrease. Nevertheless, for the altitude, the Set Point is constant, then the error is relatively small. Furthermore, the measurements of the position, provided by the GPS device, present a relatively larger deviations (around 1.4 m to 1.6 m) than other devices employed for indoor environment. This explains the errors in the trajectory-tracking displacement task.

The four control input signals for roll, pitch, altitude and yaw, respectively, are presented in Figure 7. These control inputs are obtained with the proposed backstepping controllers and are sent to the motors in real-time during the tests for desired trajectory tracking.

Figure 8 shows the recorded translational positions, following the desired trajectory, for PD controllers. This figure is divided into three subfigures, representing the trajectory performance along the X, Y and Z axes.

Figure 9 shows the UAV’s trajectory performance in three-dimensional space, whereas Figure 10 displays it in two-dimensional space. Figure 11 and Figure 12 show the errors during the trajectory tracking and the control signals for PD controllers, respectively.

To compare the performances of both controllers, the Integral Absolute Error (IAE) is computed for the robust backstepping (BS) and PD, and these values are reported in

Table 2. Comparative analysis of the performance IAE for the trajectory tracking phase.

Trajectory Tracking
Performance Index	BS	PD	${\mathit{\sigma }}_{\mathit{BS}}$	${\mathit{\sigma }}_{\mathit{PD}}$
IAEx	674.0325	732.8948	0.3195	0.6095
IAEy	646.48	849.0646	0.5691	0.6949
IAEz	59.96	85.4140	0.06747	0.0678

.

Table 2 shows that the robust backstepping controller outperforms the PD controller in the trajectory-tracking phase of the quadrotor in the presence of disturbances; additionally, the standard deviation is calculated to analyze the error dispersion, and the mean value of the 10 conducted experimental tests is calculated and compared with the results obtained using the PD control.

Additionally,

Table 3. Comparison of absolute control values during the trajectory tracking phase.

Trajectory Tracking
Performance Index	BS	PD
$J_{{\tau }_{\varphi }}$	6051.2	6662
$J_{{\tau }_{\theta }}$	7337	8661
$J_{u_s}$	519.647	662.5175
$J_{{\tau }_{\psi }}$	802.8	848.2

shows the mean of the integral of the absolute value of the signal control, defined as

$$J_{control}=\sum _{i=0}^N\left|control\left(i\right)\right|,$$

where N is the number of samples. The index $J_{control}$ is related with the energy consumption of the actuators.

According to the results showed on Table 3, the energy consumption required by the Robust Backstepping Controller (RBC) is lower than the PD controller. It implies that the control signal of the RBC is smaller and softer than the control signal of PD, which allows the captured images to be less blurred and distorted.

6. Detection of Pest in Corn Leaves

In this section, the vision system and the offline images processing are presented, aiming to locate the tar spot complex [27] in the maize fields based on the images taken when the quadcopter flies over the corn crop.

6.1. Vision System

The modules of the vision system include the camera and the image processing (a PC and MATLAB software). The natural light illuminates the plants to be inspected. The GoPro HERO8 Black camera [36] is mounted under the UAV frame (see Figure 13).

While the quadrotor flies over the crops, the camera lens captures and sends images to the camera sensor in the form of light. This sensor converts this light to a digital image that is then stored in the camera’s memory for later analysis. For the image processing, the “Color Thresholding” toolbox is used (included in MATLAB Software), in which the interesting areas in the analyzed images are selected based on the color spaces: Red, Green, Blue (RGB); Hue, Saturation, Value (HSV); Luma, Blue and Red chromaticity (YCbCr) and Luminosity, Red/Green and Yellow/Blue chromaticity coordinates (CIE-Lab). This is done by applying segmentation methods on the images; in this regard, image segmentation is a processing technique that refers to the extraction of useful information from a frame to facilitate observation and analysis since the rest of the image content is not useful for the purpose, i.e., if within an image the red color is selected, everything that is not red is discriminated by the segmentation method. This toolbox is selected because it allows comparing the intensity level, pixel by pixel, with a certain threshold previously defined by the user. To establish this threshold, it is necessary to analyze the interest region to be isolated, finding a characteristic and exclusive color level.

6.2. Image Processing

In computer vision, segmentation processes are of vital importance when it comes to detecting objects in unstructured environments.

In this article, the segmentation process employs the method based on regions [37] due to the specific task (detecting color levels on affected leaves). Methods based on regions aim to determine the areas of an image that have homogeneous properties, and the border of these areas will delimit some objects from others. Regarding the segmentation methods, Figure 14 displays the process of application followed in this work.

Segmentation Method

The application process of the segmentation method starts with the images of the corn fields (Figure 15) where the dry leaves of the plants are detected, as this is a symptom that the plant could be ill. For this purpose, first, based on the photograph, the pixels of interest are selected to find the thresholds. Once the pixel values are obtained, a new image is loaded to search for dry leaves in the field.

Figure 16 shows the processed image using different segmentation methods where the dry leaves of the plant are highlighted. It should be mentioned that in the processed image, the areas that are not of interest are colored in black. For the RGB segmentation method, the threshold values are as follows: R > 126, G > 104, B < 80. As for the HSV method, the ranges are as follows: 0.096 < H < 0.153, 0.243 < S < 0.944, 0.222 < V < 0.944. In the YCbCr method, the following values are obtained: 70 < Y < 225, 72 < Cb < 109, 136 < Cr < 163. Finally, from the application of the CIE-Lab segmentation, the values are as follows: 38.49 < L < 100, −10.353 < a < 19.622, 19.622 < b < 55.531.

With the obtained thresholds, from the segmentation methods, a MATLAB code runs to analyze the images obtained from the flights made over the corn fields. First, an image is selected and then subjected to the thresholds of each method to identify dry leaves in the field.

Figure 17 displays the segmented images using the RGB, HSV, YCbCr and CIE-Lab methods. From the images obtained after applying the segmentation methods with the thresholds proposed in the previous section, it can be seen that using RGB segmentation to detect dry leaves is not very convenient as only some points were highlighted, while in the HSV segmentation method, a greater detection of dry leaves can be noted in the image of the crop; however, these highlighted points look like brush strokes, and the plant is not well distinguished. In the YCbCr segmentation, the dry leaves can be better identified in the plot; however, when it is compared with the original image, there are parts of the dry leaves of the plant that despite being dry, do not appear in the processed image. Finally, the best detection is obtained when the CIE-Lab segmentation method is applied to the image, although it also detects a little of the soil, which does not represent a relevant issue.

The robustness provided to the proposed controller is necessary to improve the closed loop performance of the vehicle in outdoor environment. This improved performance is a crucial issue to the image capturing while the trajectory tracking task is executed by the UAV, allowing reduce distorted capture of the crops. In fact, when a PD controller is used to control the vehicle in order to capture the crop images, from ten experiments only six were satisfactory to stabilize the drone with the mounted camera. In contrast, for the robust backstepping control approach, all the tests were satisfactory, despite a gimbal or extra software not being used.

Furthermore, each processed image has an $(x,y)$ coordinate, which is obtained with the real-time clock (’Time stamp’ function) of the Pixhawk autopilot. Then, when an image with affected leaves is detected, the user obtains the relative position $(x,y)$ of the chosen reference frame, and then the user can apply a corrective action, programming a trajectory whose final point corresponds to these coordinates.

7. Conclusions

The quadrotor trajectory tracking problem, in outdoor environment, is addressed by the proposed robust control scheme. The four controllers are synthesized using the robust backstepping approach, it uses virtual bounded inputs (the function sin(.)), which produce bounded control signals, and it is appropriate to the physical constrains of the UAV. The convergence for altitude, translational and rotational UAV variables is guaranteed when the vehicle is subjected to vanishing disturbances. The proposed control algorithm achieves a higher performance in closed loop when is compared to a linearized model-based PD controller. This improved performance is a crucial issue to the image capturing while a trajectory tracking task is executed by the UAV, allowing to reduce the wrong capture of the crops, despite a gimbal or extra software not being used. In fact, the experimental results validate and confirm the aforementioned higher performance level of the proposed control algorithm. Moreover, the proposal presents a potential advantage in precision agriculture as it can prevent crop losses by identifying crop areas with dry leaves. In contrast to the most of the reported works, our proposal was tested in a precision agriculture task on a real maize crop. Future work includes onboard image processing and to implement new image segmentation techniques.