Load Transfer Efficiency Assessment of Concrete Pavement Joints Using Distributed Optical Vibration Sensor
Abstract
1. Introduction
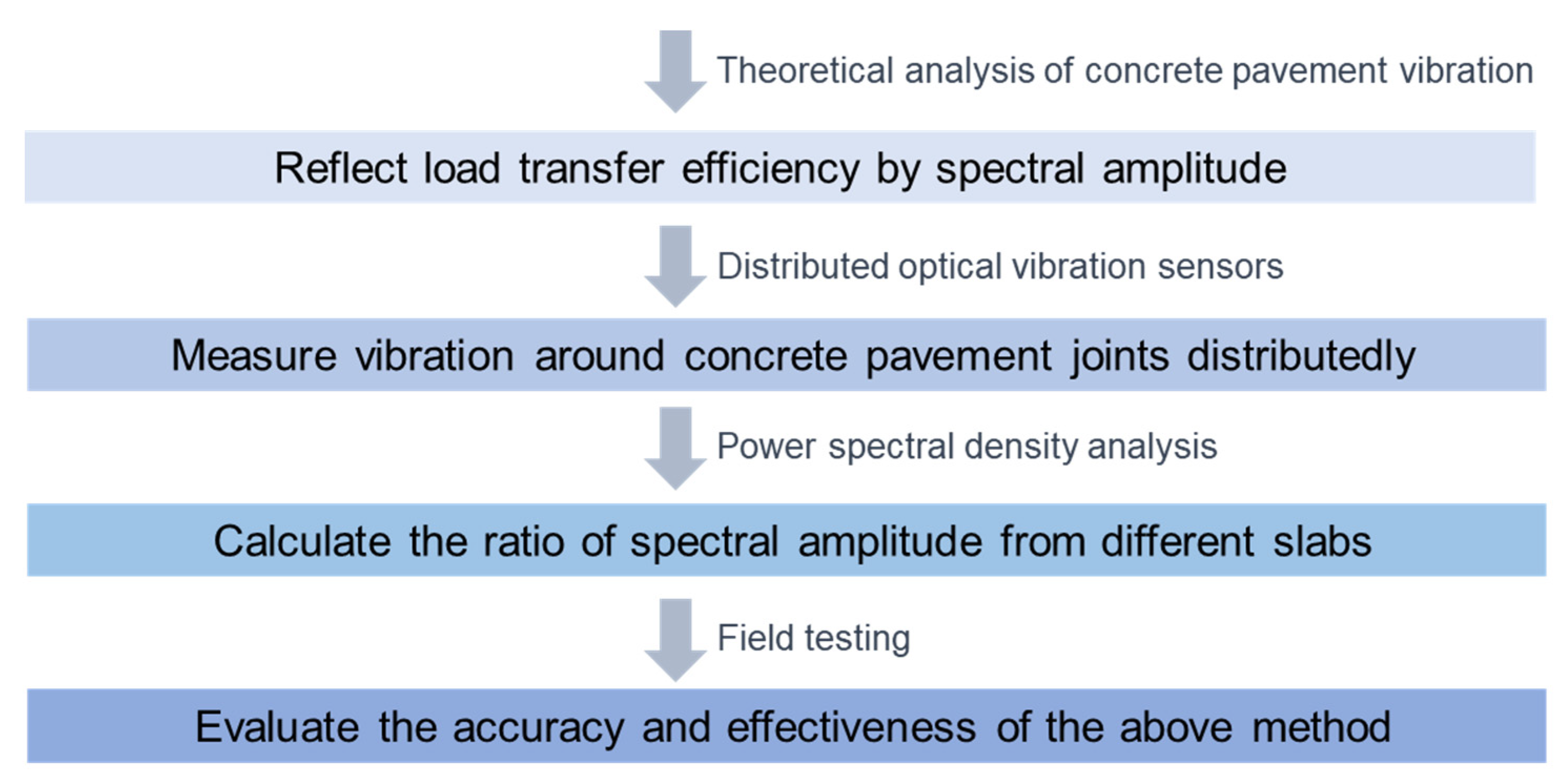
2. Methodology
- (1)
- theoretical analysis of concrete pavement vibration is conducted to investigate how to reflect LTE by spectral amplitude.
- (2)
- distributed optical vibration sensor (DOVS) is applied to measure vibration around joints distributedly.
- (3)
- the corresponding processing method for DOVS data was proposed to calculate the ratio of spectral amplitude from different slabs through power spectral density (PSD) analysis.
2.1. Theoretical Analysis of Concrete Pavement Vibration
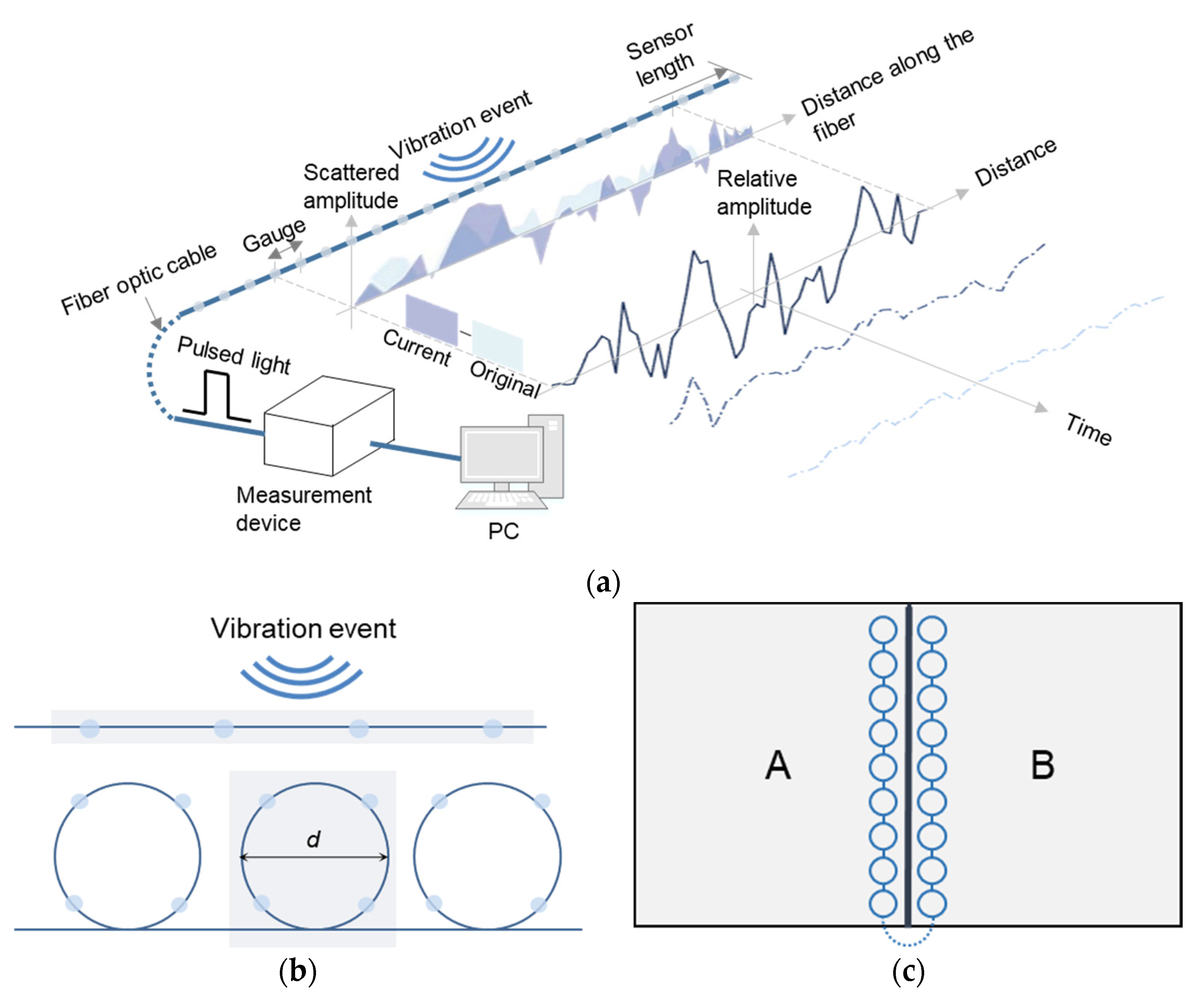
2.2. Measurement of Vibration around Concrete Pavement Joints
2.3. Calculation for the Ratio of Vibration Amplitude
- Denoise the original DOVS data:
- 2.
- Calculate the PSD of measurement point i:
- 3.
- Combine the PSD of all measurement points around the joint:
- 4.
- Extract the vector of PSD at mth natural frequency and divide it into two sets:
- 5.
- Calculate the ratio of PSDA(fm) and PSDB(fm):
- 6.
- Estimate the density distribution of elements in RPSDAB(fm) by kernel density estimation (KDE). The estimated probability density of RPSD at frequency f is calculated as:
3. Field Testing
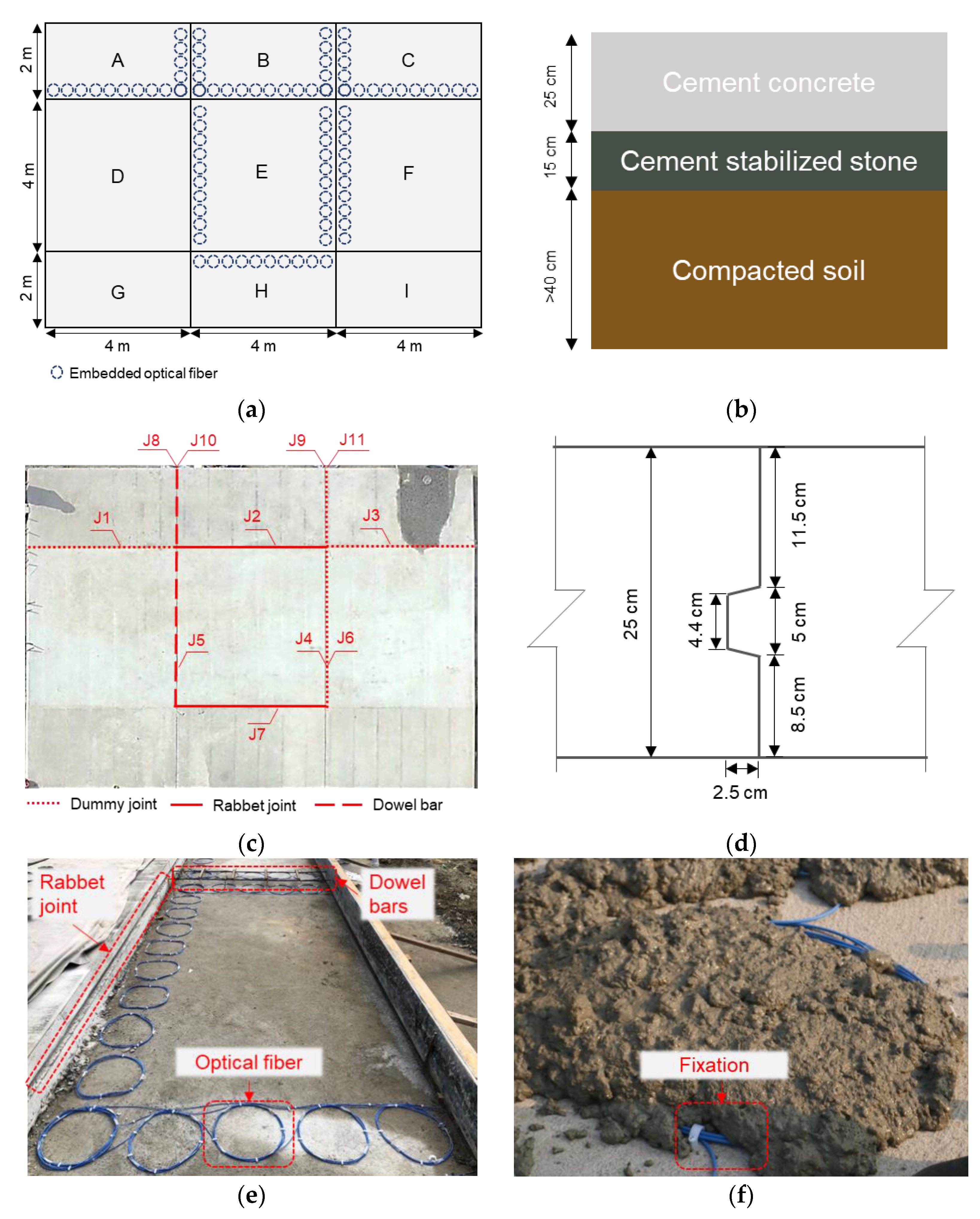
3.1. Test Set-Up
3.2. Data Collection
3.3. Results of Deflection-Based LTE (DLTE)
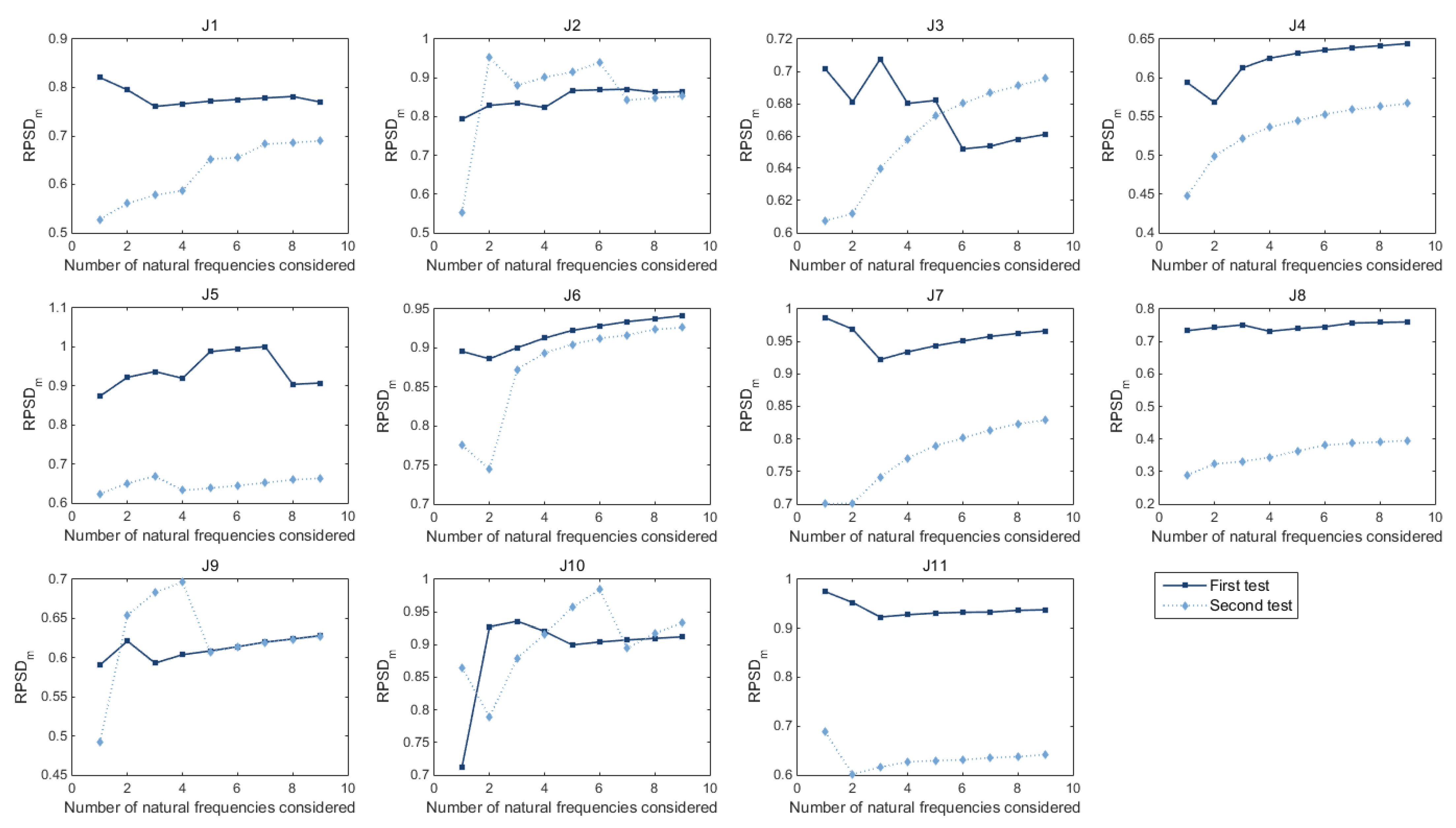
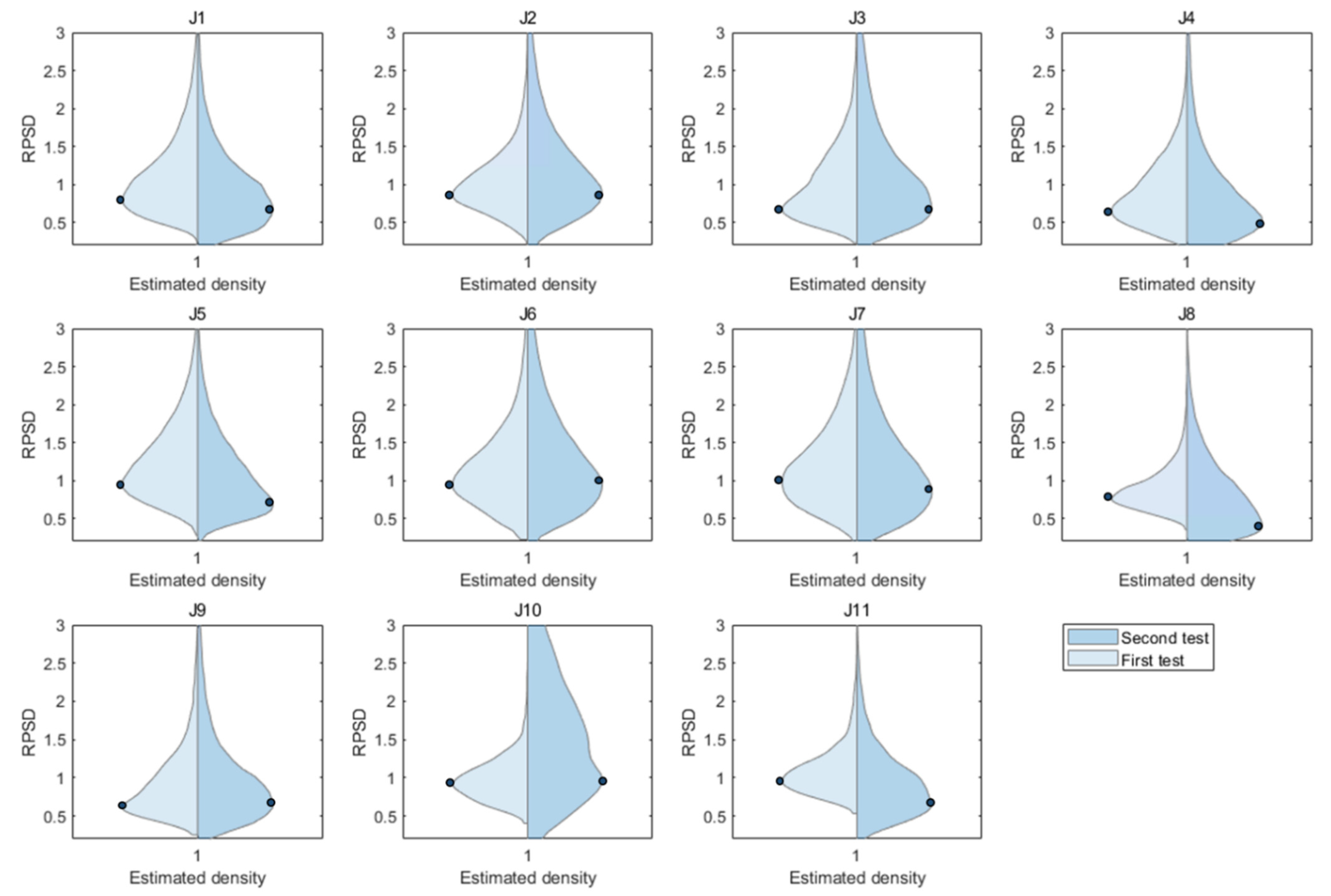
3.4. Results of the Ratio of Power Spectral Density (RPSD)
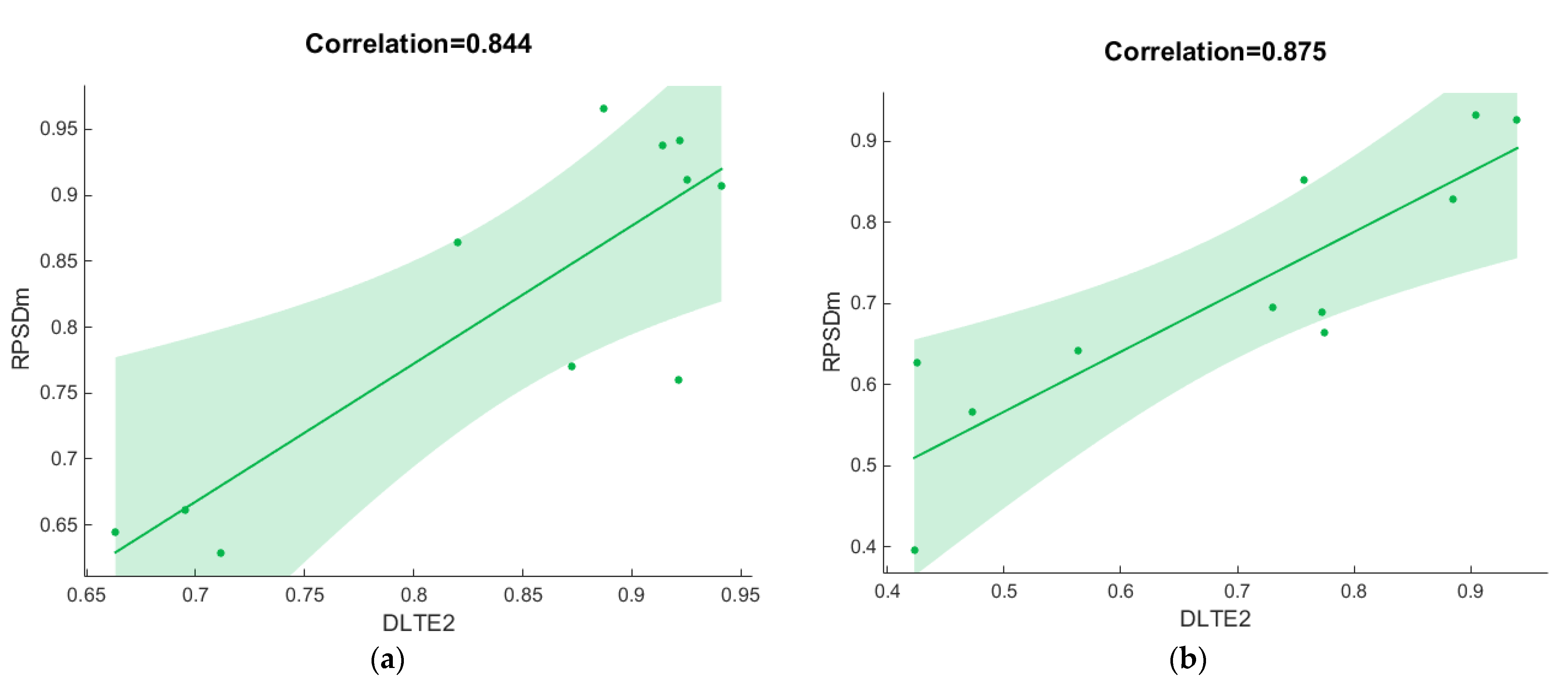
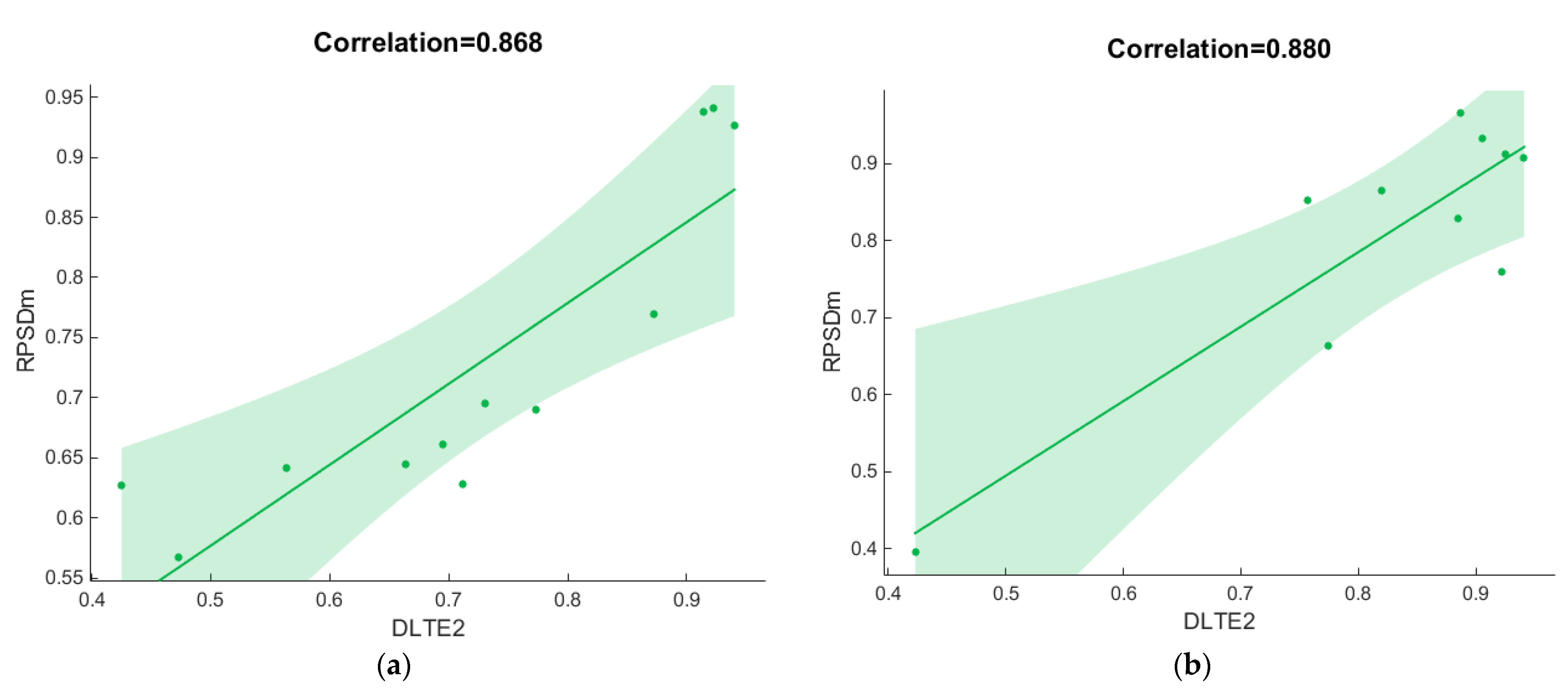
3.5. Discussion of the Correlation between DLTE and RPSD
4. Conclusions
- (1)
- Through theoretical analysis of vibration on the loaded and unloaded slab, the LTE of joints can be reflected by the ratio of power spectral density (RPSD) at natural frequencies. The field test results also indicate that LTE and RPSD have a strong correlation (0.871) and a slight difference (< ±0.03) overall, which proves the accuracy and effectiveness of the vibration-based method.
- (2)
- Distributed optical vibration sensor (DOVS) can measure the vibration around concrete pavement joints distributedly, which is beneficial for the precision of RPSD in practical measurement. According to the field test results, the correlation between LTE and RPSD is robust in different dates and types of joints (0.844~0.880), which proves the robustness of the vibration-based method in practical applications.
- (3)
- Future work will be made to apply this method under traffic loads. It is much more convenient to utilize traffic loads as excitation rather than impulse loads provided by a specific device. With traffic loads from passing by vehicles, LTE can be assessed and monitored continuously and in real time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- César, A.; Pradena, M. Sustainable engineering: Load transfer characterization for the structural design of thinner concrete pavements. Sustainability 2020, 12, 9153. [Google Scholar] [CrossRef]
- Khazanovich, L.; Gotlif, A. Evaluation of PCC joint stiffnesses using LTPP data. In Proceedings of the 8th International Conference on Concrete Pavements: Innovations for Concrete Pavement: Technology Transfer for the Next Generation, Colorado Springs, CO, USA, 18 August 2005; pp. 1120–1137. [Google Scholar]
- Lin, W.; Dong, Y.; Jung, Y.; Zheng, H.; Cho, Y.H. Performance evaluation of bedding sand and load transfer characteristic of concrete block pavements. Appl. Sci. 2021, 11, 10111. [Google Scholar] [CrossRef]
- Wadkar, A.; Mehta, Y.; Cleary, D.; Guo, E.; Musumeci, L.; Zapata, A.; Kettleson, W. Load-transfer efficiencies of rigid airfield pavement joints based on stresses and deflections. J. Mater. Civ. Eng. 2011, 23, 1171–1180. [Google Scholar] [CrossRef]
- Mackiewicz, P. Analysis of stresses in concrete pavement under a dowel according to its diameter and load transfer efficiency. Can. J. Civ. Eng. 2015, 42, 845–853. [Google Scholar] [CrossRef]
- Guo, H.; Petch, F.; Ricalde, L. Analysis of concrete pavement strain data and behaviour during joint formation. Int. J. Pavement Eng. 2010, 11, 173–187. [Google Scholar] [CrossRef]
- Khafajeh, R.; Shamsaei, M.; Tehrani, H.G.; Easa, S.M. Proposing load transfer efficiency as criterion for repairing longitudinal and transverse cracks of asphalt pavements. J. Transp. Eng. Part B Pavements 2021, 147, 06021002. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Gao, L.L. Effect of dowel bar position deviation on joint load-transfer ability of cement concrete pavement. Int. J. Pavement Res. Technol. 2016, 9, 30–36. [Google Scholar] [CrossRef][Green Version]
- Sok, T.; Hong, S.J.; Kim, Y.K.; Lee, S.W. Evaluation of load transfer characteristics in roller-compacted concrete pavement. Int. J. Pavement Eng. 2020, 21, 796–804. [Google Scholar] [CrossRef]
- Guo, E.H. Back-estimation of slab curling and joint stiffness. In Proceedings of the Seventh International Conference on Concrete Pavements: The Use of Concrete in Developing Long-Lasting Pavement Solutions for the 21st Century, Orlando, FL, USA, 13 September 2001. [Google Scholar]
- Cunliffe, C.; Joshi, A.; Mehta, Y.; Cleary, D. A study to determine the impact of cracking on load transfer efficiency of rigid airfield pavements. J. Test. Eval. 2014, 42, 375–389. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Zhang, Z. Rigid pavement load transfer ability of airport based on vibration characteristics. J. Beijing Univ. Aeronaut. Astronaut. 2018, 44, 1787–1796. [Google Scholar]
- Zhao, H.; Zeng, M.; Chen, H.; Ling, J.; Wu, D. Investigating the Effect of Prestress Force on Cross-Tensioned Concrete Pavement Vibration. Transp. Res. Rec. 2020, 2674, 875–886. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, M.; Zhao, H.; Wang, Y.; Du, Y. Detection and localization of debonding beneath concrete pavement using transmissibility function analysis. Mech. Syst. Signal Processing 2021, 159, 107802. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601. [Google Scholar] [CrossRef]
- Zeng, M.; Chen, H.; Ling, J.; Zhao, H.; Wu, D. Monitoring of prestressing forces in cross-tensioned concrete pavements during construction and maintenance based on distributed optical fiber sensing. Autom. Constr. 2022, 142, 104526. [Google Scholar] [CrossRef]
- Monsberger, C.M.; Lienhart, W. Distributed fiber optic shape sensing of concrete structures. Sensors 2021, 21, 6098. [Google Scholar] [CrossRef] [PubMed]
- Diouf, B.M.; Che, A.; Feng, S. Study of a Space-Time Monitoring of High-Speed Railway Underline Structure Using Distributed Optical Vibration Sensing Technology. Shock. Vib. 2019, 2019, 9263259. [Google Scholar] [CrossRef]
- Lienhart, W.; Wiesmeyr, C.; Wagner, R.; Klug, F.; Litzenberger, M.; Maicz, D. Condition monitoring of railway tracks and vehicles using fibre optic sensing techniques. In Proceedings of the Transforming the Future of Infrastructure through Smarter Information: Proceedings of the International Conference on Smart Infrastructure and Construction, Cambridge, UK, 27–29 June 2016; pp. 45–50. [Google Scholar]
- Klug, F.; Lackner, S.; Lienhart, W. Monitoring of railway deformations using distributed fiber optic sensors. In Proceedings of the Joint International Symposium on Deformation Monitoring, Wien, Austria, 30 March 2016. [Google Scholar]
- Buchmayer, F.; Monsberger, C.M.; Lienhart, W. Advantages of tunnel monitoring using distributed fibre optic sensing. J. Appl. Geod. 2021, 15, 1–12. [Google Scholar] [CrossRef]
- Monsberger, C.M.; Lienhart, W. Distributed fiber optic shape sensing along shotcrete tunnel linings: Methodology, field applications, and monitoring results. J. Civ. Struct. Health Monit. 2021, 11, 337–350. [Google Scholar] [CrossRef]
- Monsberger, C.M.; Lienhart, W.; Kluckner, A.; Schubert, W. In-Situ assessment of distributed strain and curvature characteristics in shotcrete tunnel linings based on fiber optic strain sensing. In Proceedings of the 14th International Congress on Rock Mechanics and Rock Engineering, Foz do Iguassu, Brazil, 13–18 September 2019; pp. 1324–1331. [Google Scholar]
- Wang, X.; Shi, B.; Wei, G.; Chen, S.E.; Zhu, H.; Wang, T. Monitoring the behavior of segment joints in a shield tunnel using distributed fiber optic sensors. Struct. Control Health Monit. 2018, 25, 2056. [Google Scholar] [CrossRef]
- Zhang, W.; Gao, J.; Shi, B.; Cui, H.; Zhu, H. Health monitoring of rehabilitated concrete bridges using distributed optical fiber sensing. Comput. Aided Civ. Infrastruct. Eng. 2006, 21, 411–424. [Google Scholar] [CrossRef]
- Abdel-Jaber, H.; Glisic, B. Monitoring of prestressing forces in prestressed concrete structures—An overview. Struct. Control. Health Monit. 2019, 26, 2374. [Google Scholar] [CrossRef]
- Xiang, P.; Wang, H. Optical fibre-based sensors for distributed strain monitoring of asphalt pavements. Int. J. Pavement Eng. 2018, 19, 842–850. [Google Scholar] [CrossRef]
- Hauswirth, D.; Fischli, F.; Rabaiotti, C.; Puzrin, A.M. Distributed fiber optic strain measurements in an airfield pavement. In Proceedings of the 9th International Conference on Maintenance and Rehabilitation of Pavements-Mairepav9, Zurich, Switzerland, 1–3 July 2020; pp. 825–834. [Google Scholar]
- Zhao, H.; Wu, D.; Zeng, M.; Tian, Y.; Ling, J. Assessment of concrete pavement support conditions using distributed optical vibration sensing fiber and a neural network. Constr. Build. Mater. 2019, 216, 214–226. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, D.; Zeng, M.; Zhong, S. A vibration-based vehicle classification system using distributed optical sensing technology. Transp. Res. Rec. 2018, 2672, 12–23. [Google Scholar] [CrossRef]
- Zeng, M.; Wu, D.; Zhao, H.; Chen, H.; Bian, Z. Novel assessment method for support conditions of concrete pavement under traffic loads using distributed optical sensing technology. Transp. Res. Rec. 2020, 2674, 42–56. [Google Scholar] [CrossRef]
- Zeng, M.; Zhao, H.; Wu, D.; Chen, H.; Cai, J. A vibration-based traffic monitoring system using distributed optical sensing technology. J. Test. Eval. 2019, 48, 1799–1813. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Bao, X. Wavelet denoising method for improving detection performance of distributed vibration sensor. IEEE Photonics Technol. Lett. 2012, 24, 542–544. [Google Scholar] [CrossRef]
- Du, Y.; Weng, Z.; Li, F.; Ablat, G.; Wu, D.; Liu, C. A novel approach for pavement texture characterisation using 2D-wavelet decomposition. Int. J. Pavement Eng. 2022, 23, 1851–1866. [Google Scholar] [CrossRef]






| Test Series | No. Joint | Measurements of Deflection-Based LTE | Average | Deviation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# July 2020 | J1 | 0.900 | 0.930 | 0.936 | 0.937 | 0.959 | 0.940 | 0.945 | 0.929 | 0.931 | 0.934 | 0.015 |
| J2 | 0.882 | 0.879 | 0.915 | 0.897 | 0.896 | 0.881 | 0.931 | 0.933 | 0.936 | 0.906 | 0.022 | |
| J3 | 0.828 | 0.838 | 0.823 | 0.838 | 0.834 | 0.814 | 0.852 | 0.840 | 0.838 | 0.834 | 0.010 | |
| J4 | 0.762 | 0.721 | 0.866 | 0.848 | 0.882 | 0.835 | 0.778 | 0.803 | 0.835 | 0.814 | 0.050 | |
| J5 | 0.987 | 0.965 | 0.985 | 0.915 | 0.954 | 0.990 | 0.954 | 0.963 | 1.018 | 0.970 | 0.028 | |
| J6 | 0.953 | 0.918 | 0.909 | 0.961 | 0.987 | 1.014 | 0.946 | 0.966 | 0.988 | 0.960 | 0.032 | |
| J7 | 0.945 | 0.929 | 0.925 | 0.936 | 0.960 | 0.933 | 0.951 | 0.949 | 0.950 | 0.942 | 0.011 | |
| J8 | 0.961 | 0.968 | 0.956 | 0.962 | 0.968 | 0.949 | 0.959 | 0.957 | 0.960 | 0.960 | 0.006 | |
| J9 | 0.856 | 0.852 | 0.833 | 0.866 | 0.817 | 0.844 | 0.819 | 0.844 | 0.863 | 0.844 | 0.017 | |
| J10 | 0.967 | 0.954 | 0.977 | 0.962 | 0.948 | 0.957 | 0.973 | 0.958 | 0.962 | 0.962 | 0.009 | |
| J11 | 0.927 | 0.903 | 0.916 | 1.000 | 0.989 | 0.963 | 0.964 | 0.972 | 0.973 | 0.956 | 0.031 | |
| 2# November 2020 | J1 | 0.879 | 0.880 | 0.880 | 0.878 | 0.877 | 0.878 | 0.881 | 0.880 | 0.880 | 0.879 | 0.001 |
| J2 | 0.869 | 0.870 | 0.872 | 0.872 | 0.874 | 0.871 | 0.865 | 0.868 | 0.871 | 0.870 | 0.003 | |
| J3 | 0.860 | 0.857 | 0.853 | 0.852 | 0.847 | 0.846 | 0.861 | 0.858 | 0.856 | 0.855 | 0.005 | |
| J4 | 0.671 | 0.672 | 0.667 | 0.695 | 0.694 | 0.690 | 0.705 | 0.698 | 0.697 | 0.688 | 0.013 | |
| J5 | 0.876 | 0.873 | 0.874 | 0.881 | 0.884 | 0.885 | 0.881 | 0.883 | 0.884 | 0.880 | 0.004 | |
| J6 | 0.978 | 0.977 | 0.976 | 0.964 | 0.962 | 0.962 | 0.969 | 0.969 | 0.970 | 0.970 | 0.006 | |
| J7 | 0.942 | 0.936 | 0.937 | 0.944 | 0.937 | 0.936 | 0.944 | 0.944 | 0.945 | 0.941 | 0.004 | |
| J8 | 0.625 | 0.618 | 0.611 | 0.649 | 0.653 | 0.651 | 0.681 | 0.685 | 0.679 | 0.650 | 0.026 | |
| J9 | 0.640 | 0.639 | 0.636 | 0.659 | 0.653 | 0.647 | 0.669 | 0.663 | 0.662 | 0.652 | 0.011 | |
| J10 | 0.951 | 0.952 | 0.956 | 0.954 | 0.949 | 0.948 | 0.951 | 0.949 | 0.953 | 0.951 | 0.002 | |
| J11 | 0.752 | 0.745 | 0.741 | 0.753 | 0.743 | 0.744 | 0.765 | 0.758 | 0.755 | 0.751 | 0.008 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, M.; Zhao, H.; Peng, K.; Bian, Z.; Wu, D. Load Transfer Efficiency Assessment of Concrete Pavement Joints Using Distributed Optical Vibration Sensor. Appl. Sci. 2022, 12, 9273. https://doi.org/10.3390/app12189273
Zeng M, Zhao H, Peng K, Bian Z, Wu D. Load Transfer Efficiency Assessment of Concrete Pavement Joints Using Distributed Optical Vibration Sensor. Applied Sciences. 2022; 12(18):9273. https://doi.org/10.3390/app12189273
Chicago/Turabian StyleZeng, Mengyuan, Hongduo Zhao, Kedi Peng, Zeying Bian, and Difei Wu. 2022. "Load Transfer Efficiency Assessment of Concrete Pavement Joints Using Distributed Optical Vibration Sensor" Applied Sciences 12, no. 18: 9273. https://doi.org/10.3390/app12189273
APA StyleZeng, M., Zhao, H., Peng, K., Bian, Z., & Wu, D. (2022). Load Transfer Efficiency Assessment of Concrete Pavement Joints Using Distributed Optical Vibration Sensor. Applied Sciences, 12(18), 9273. https://doi.org/10.3390/app12189273








