Design and Kinematic Analysis of Cable-Driven Target Spray Robot for Citrus Orchards
Abstract
:1. Introduction
2. Mechanical Design and Working Environment Analysis
2.1. Working Environment Analysis
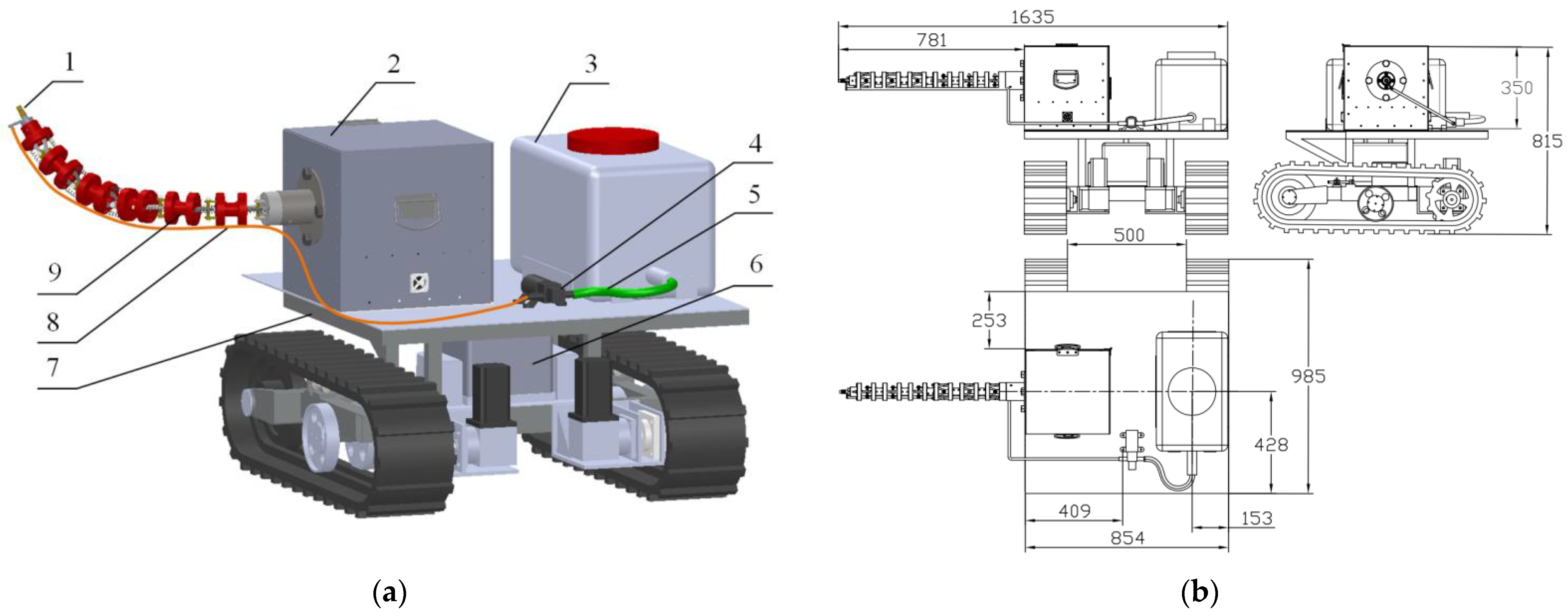
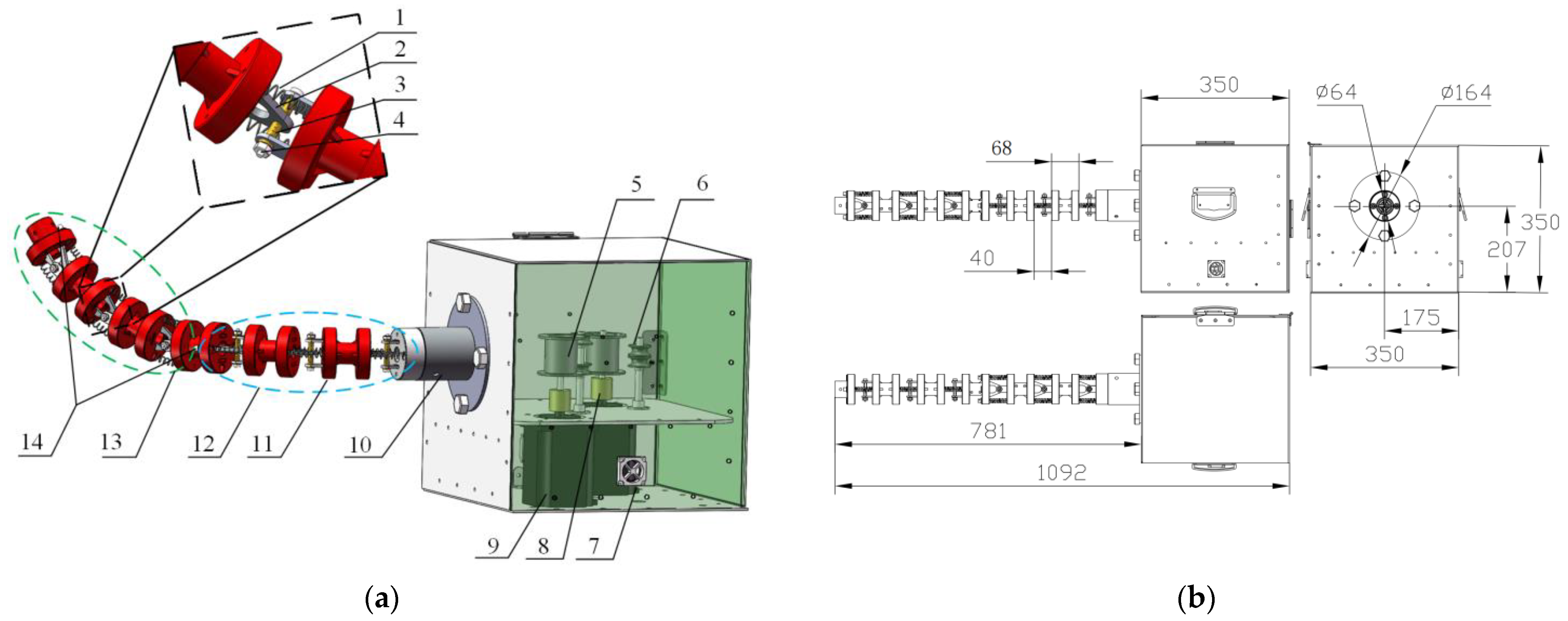
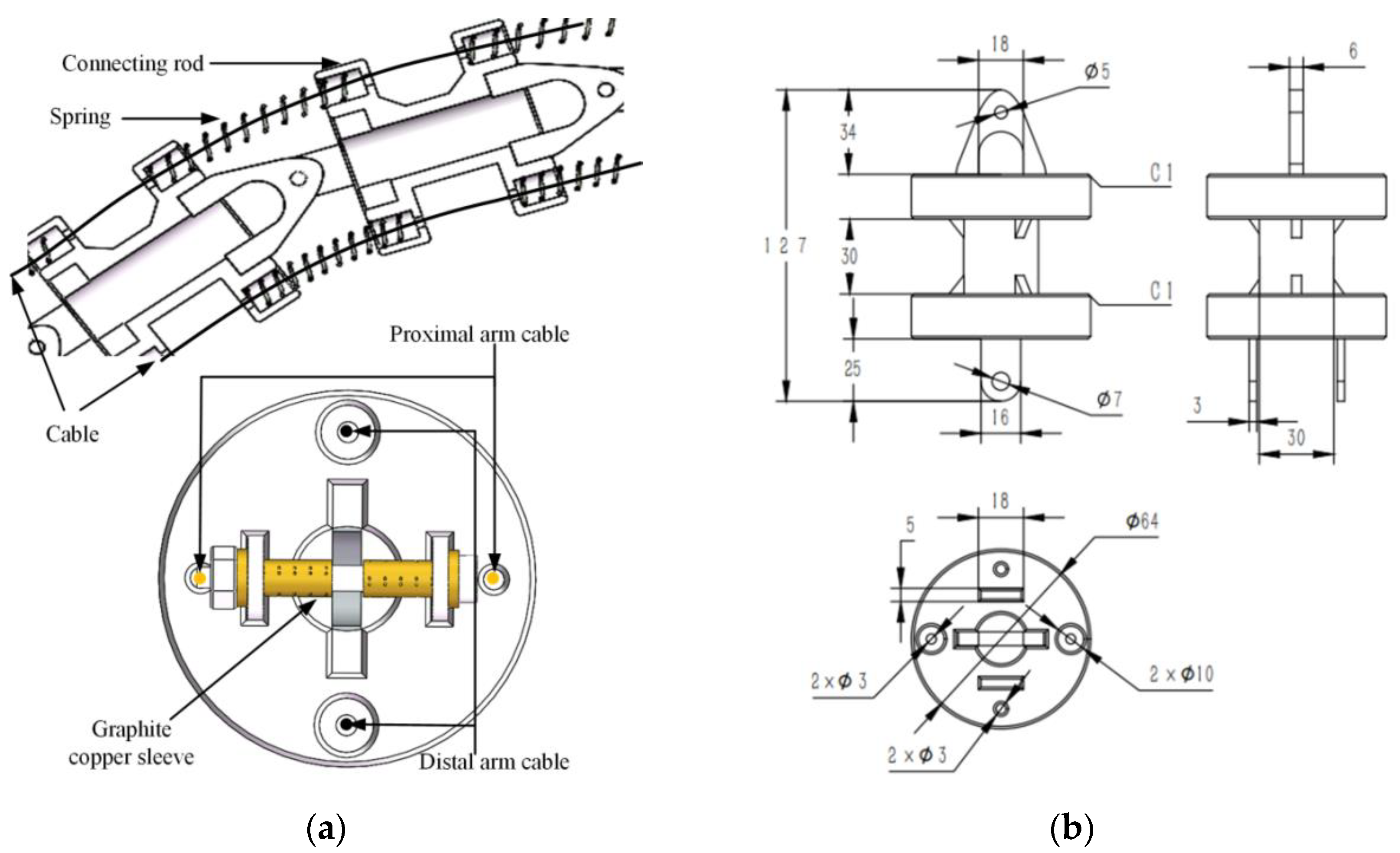
2.2. Mechanism Design of CDTSR
3. Kinematic Analysis of CDFM
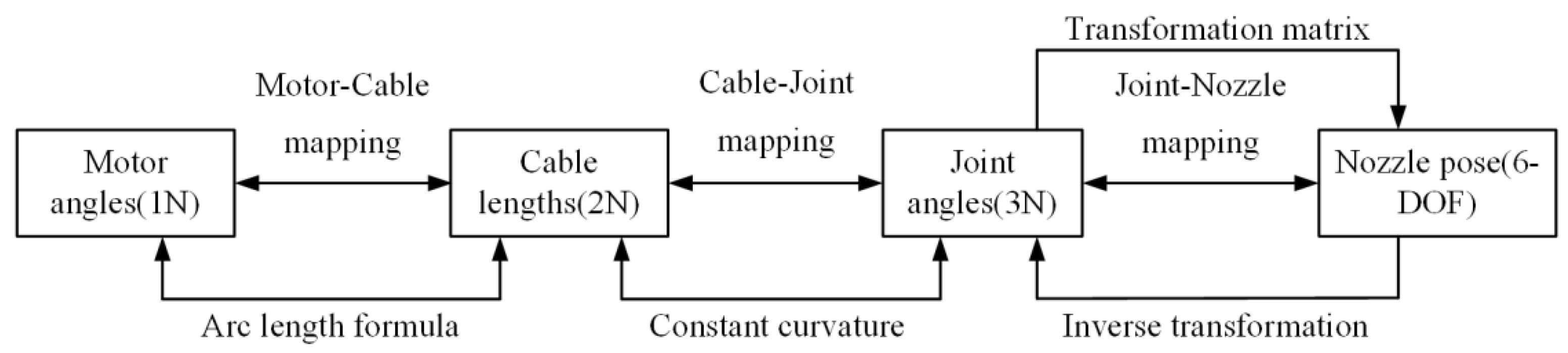
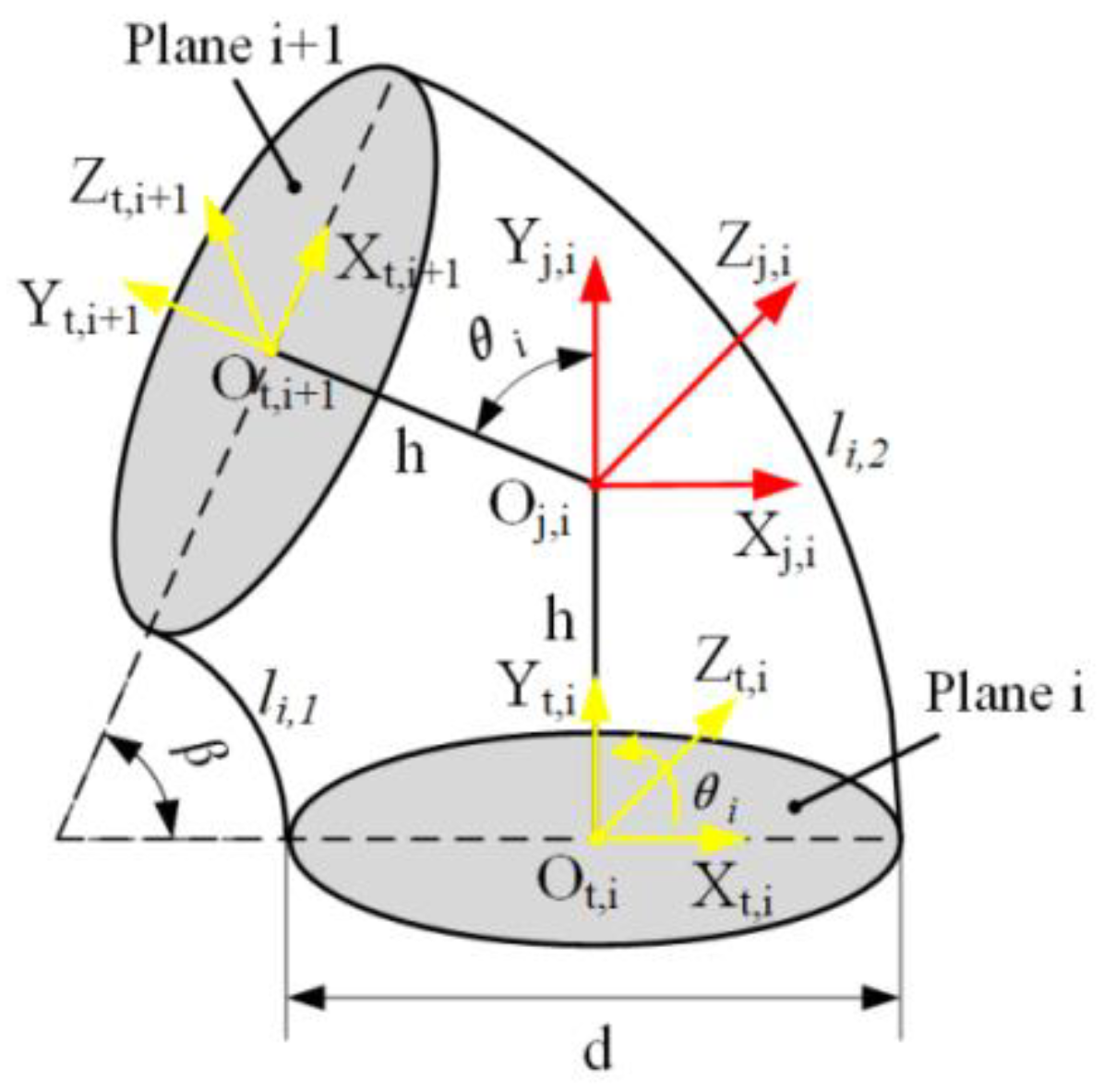
3.1. Multilevel Mapping Relationship of CDFM
3.2. Mapping between Motor and Cable
3.3. Mapping between Cable and Joint
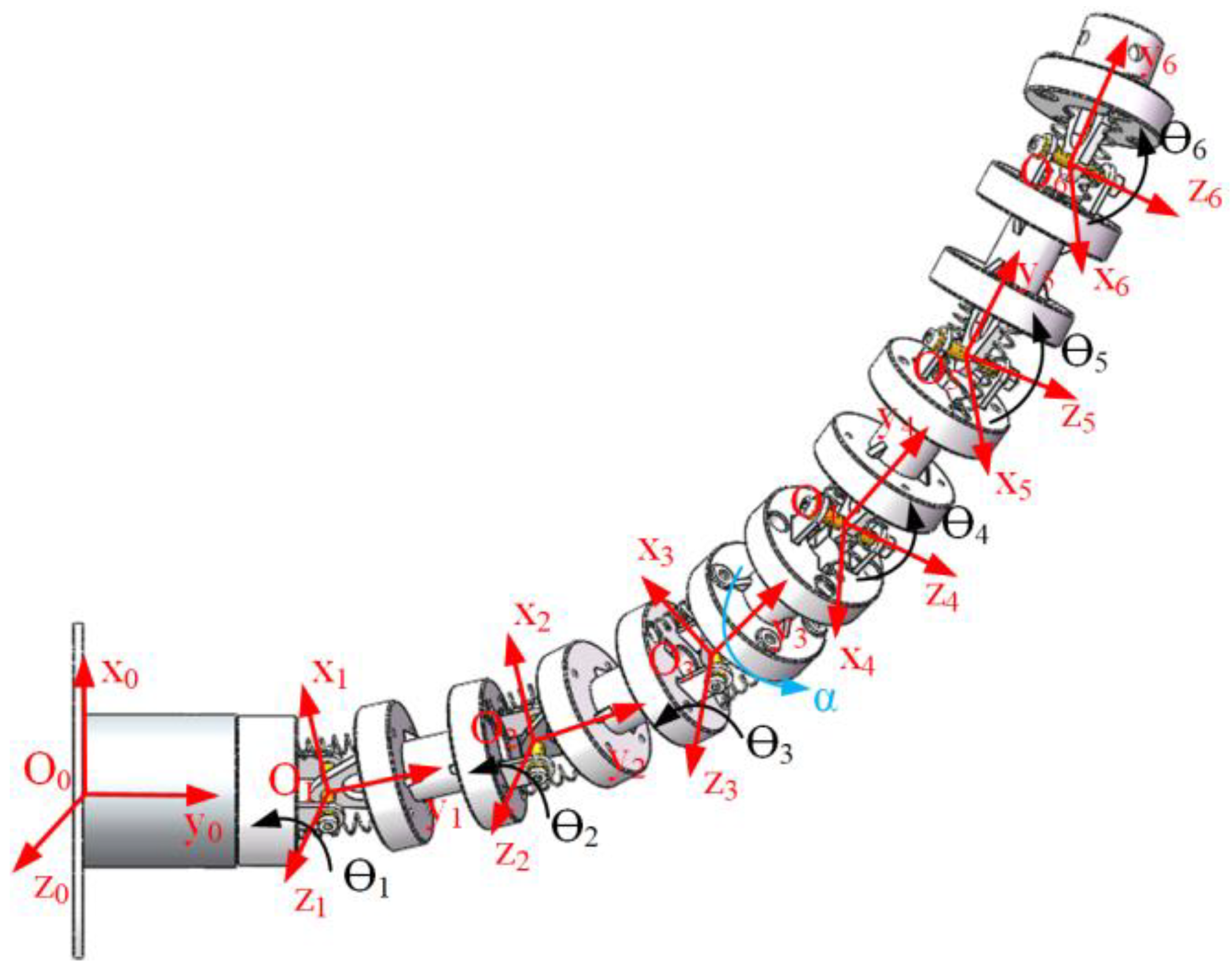
3.4. Kinematics between Joint and End
3.4.1. Forward Kinematics
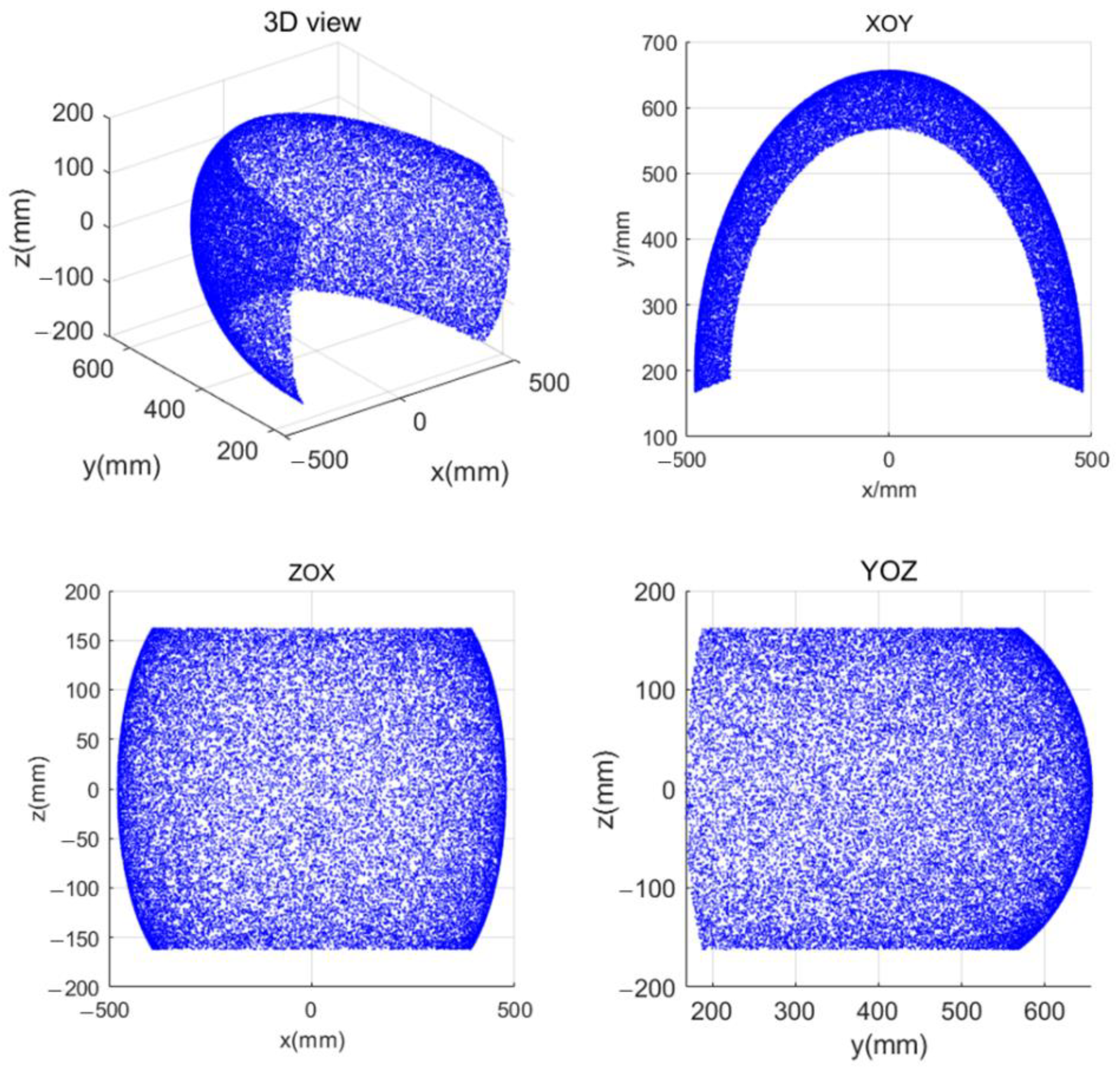
3.4.2. Inverse Kinematics
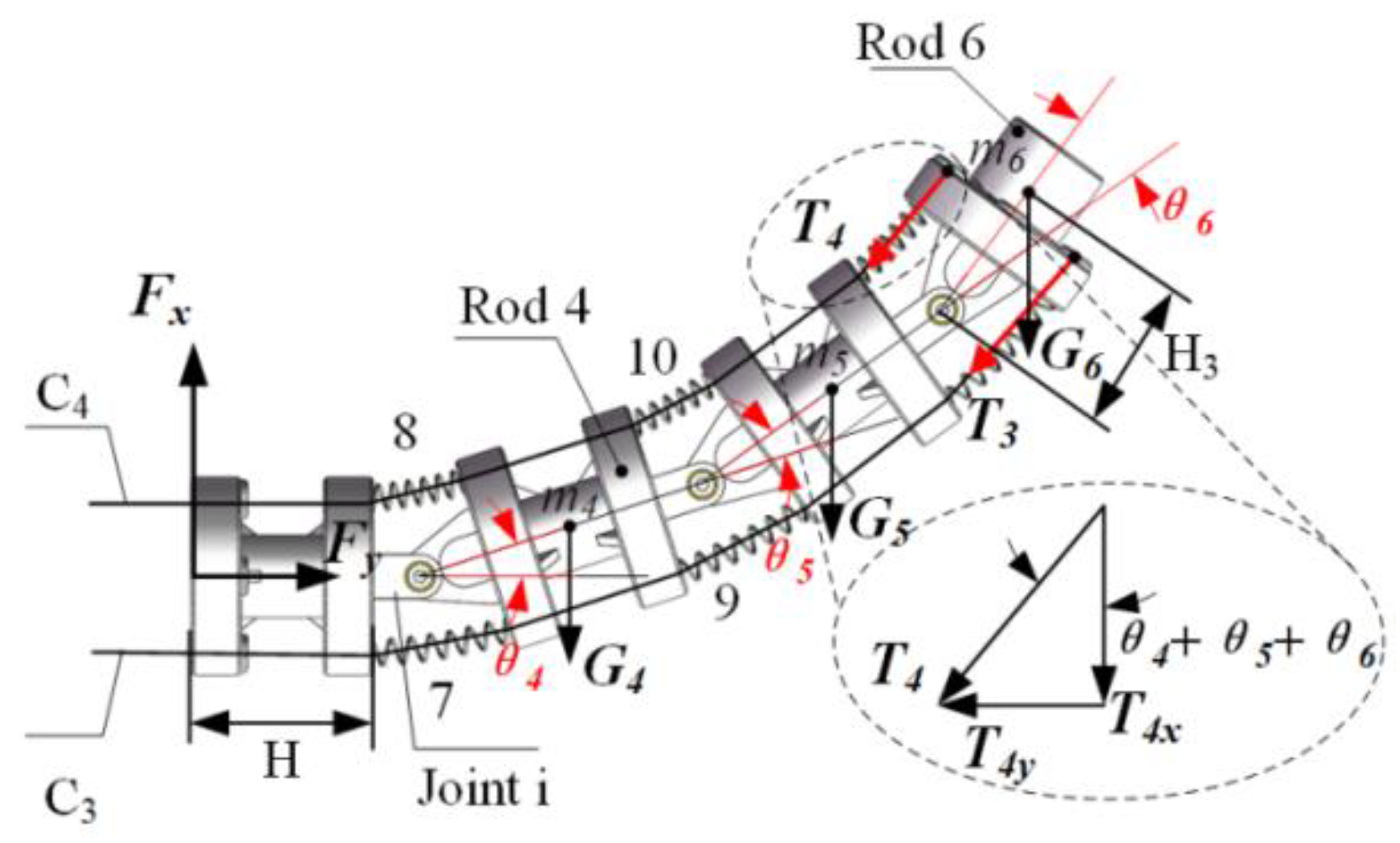
4. Dynamic Analysis of CDFM
5. Prototype and Experiments
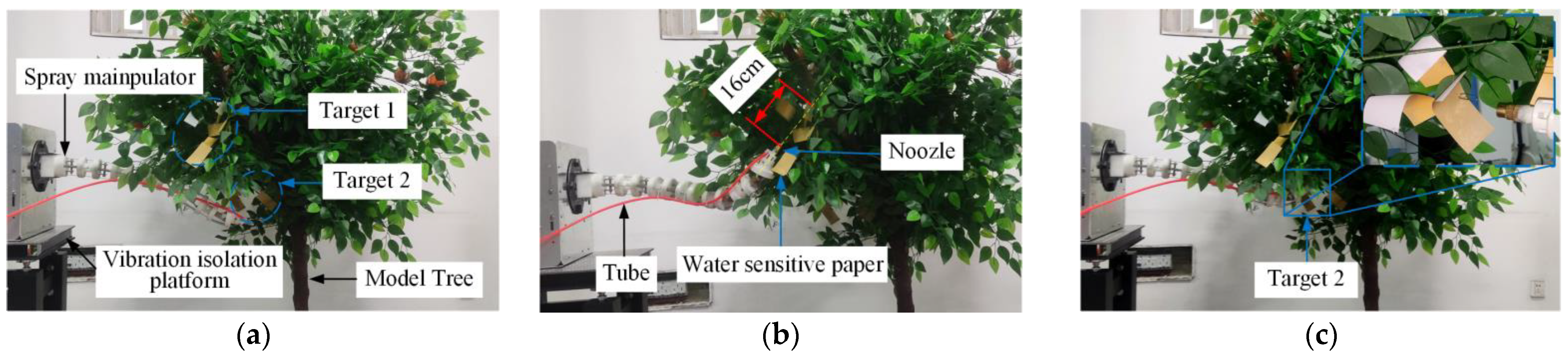
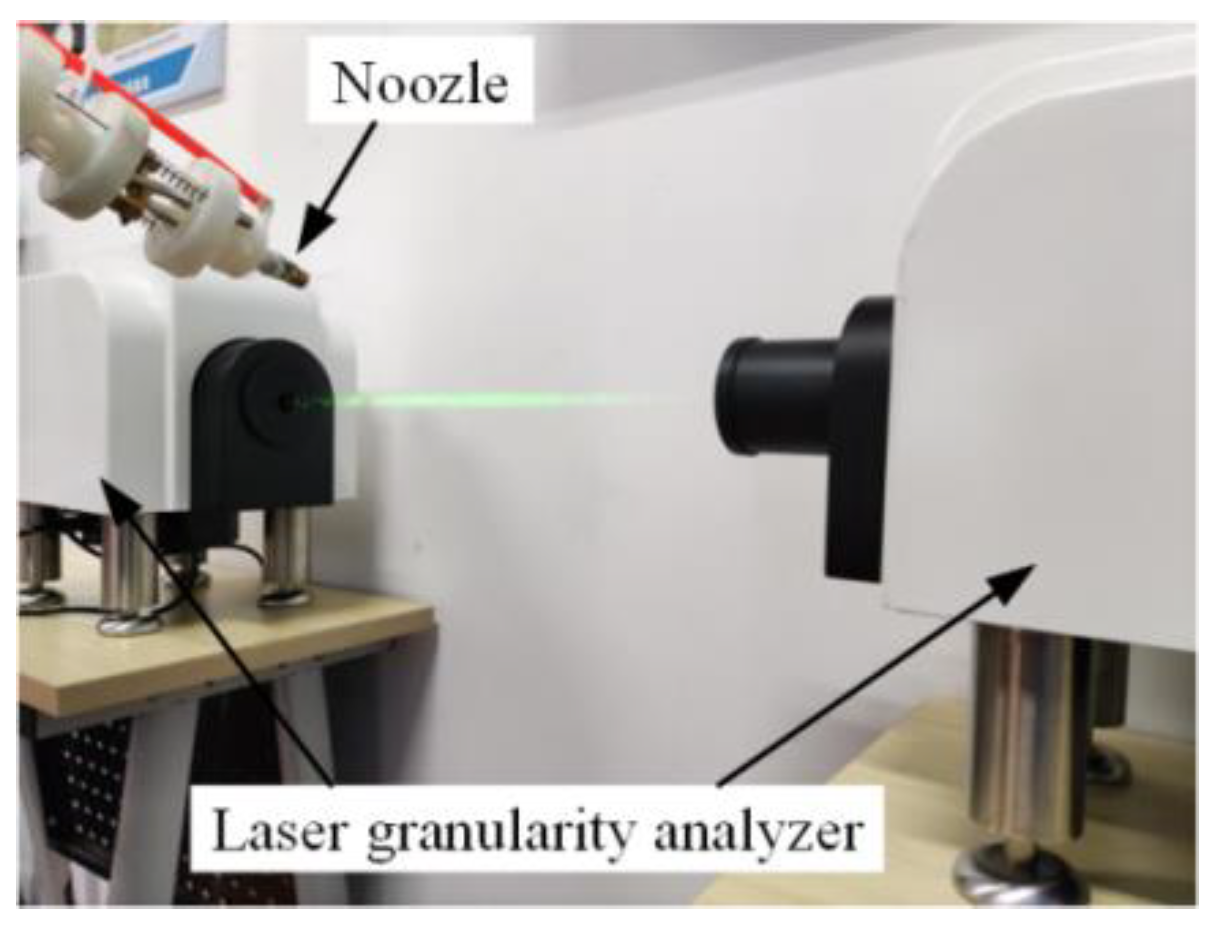
5.1. Prototype Building and Performance Testing
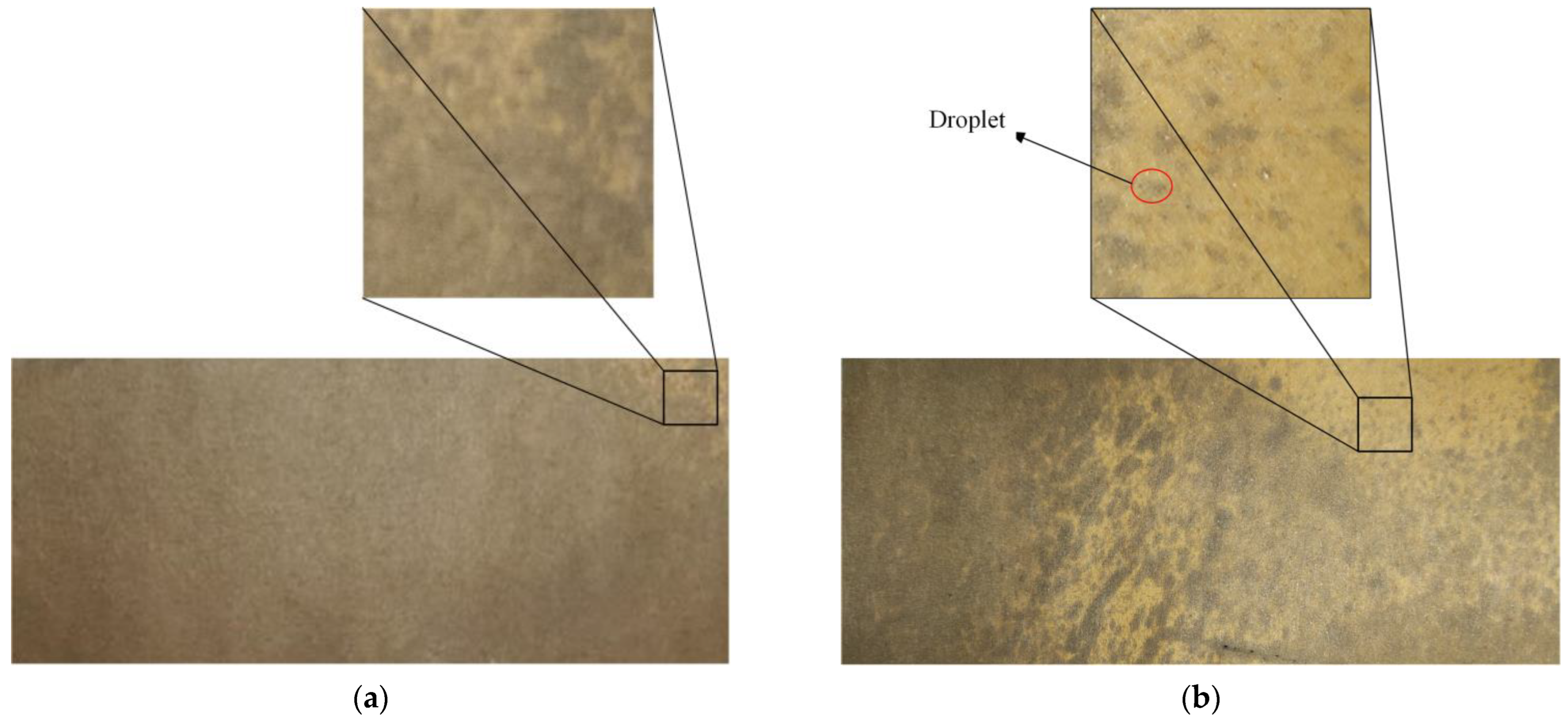
5.2. Spraying Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Xiao, H.; Mei, S.; Song, Z.; Ding, W.; Jing, Y.; Xia, X.; Yang, G. Current status and development strategies of orchard mechanization production in China. J. Chin. Agric. Univ. 2017, 22, 116–127. [Google Scholar]
- Hong, S.W.; Zhao, L.; Zhu, H. CFD simulation of airflow inside tree canopies discharged from air-assisted sprayers. Comput. Electron. Agric. 2018, 149, 121–132. [Google Scholar] [CrossRef]
- He, X. Research progress and developmental recommendations on precision spraying technology and equipment in China. Smart Agric. 2020, 2, 133–146. [Google Scholar]
- Song, S.; Sun, D.; Xue, X.; Dai, Q.; Li, Z.; Li, Z.; Hong, T. Design of pipeline constant pressure spraying equipment and facility in mountainous region orangery. In Proceedings of the 6th IFAC Conference on Bio-Robotics, Beijing, China, 13–15 July 2018. [Google Scholar]
- Zheng, Y.; Chen, B.; Lv, H.; Kang, F.; Jiang, S. Research progress of orchard plant protection mechanization technology and equipment in China. Trans. CSAE 2020, 36, 110–124. [Google Scholar]
- Sharda, A.; Karkee, M.; Hoheisel, G.; Zhang, Q.; Mangus, D. Design and Evaluation of Solid Set Canopy Delivery System for Spray Application in High-density Apple Orchards. Appl. Eng. Agric. 2019, 35, 751–757. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, H.; Reding, M.E.; Locke, J.C.; Leland, J.E.; Derksen, R.C.; Spongberg, A.L.; Krause, C.R. Delivery of chemical and microbial pesticides through drip irrigation systems. Appl. Eng. Agric. 2009, 25, 883–893. [Google Scholar] [CrossRef]
- Ranjan, R.; Sinha, R.; Khot, L.R.; Hoheisel, G.A.; Grieshop, M.; Ledebuhr, M. Spatial distribution of spray from a solid set canopy delivery system in a high-density apple orchard retrofitted with modified emitters. Appl. Sci. 2021, 11, 709. [Google Scholar] [CrossRef]
- Salcedo, R.; Zhu, H.; Zhang, Z.; Wei, Z.; Chen, L.; Ozkan, E.; Falchieri, D. Foliar deposition and coverage on young apple trees with PWM-controlled spray systems. Comput. Electron. Agric. 2020, 178, 105794. [Google Scholar] [CrossRef]
- Ma, C.; Li, G.; Peng, Q. Design and Test of a Jet Remote Control Spraying Machine for Orchards. AgriEngineering 2021, 3, 797–814. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, H.; Liu, H.; Chen, Y.; Ozkan, E. Development of a laser-guided, embedded-computer-controlled, air-assisted precision sprayer. Trans. ASABE 2017, 60, 1827–1838. [Google Scholar] [CrossRef]
- Fessler, L.; Fulcher, A.; Lockwood, D.; Wright, W.; Zhu, H. Advancing sustainability in tree crop pest management: Refining spray application rate with a laser-guided variable-rate sprayer in apple orchards. HortScience 2020, 55, 1522–1530. [Google Scholar] [CrossRef]
- Escolà, A.; Rosell-Polo, J.R.; Planas, S.; Gil, E.; Pomar, J.; Camp, F.; Llorens, J.; Solanelles, F. Variable rate sprayer. Part 1-Orchard prototype: Design, implementation and validation. Comput. Electron. Agric. 2013, 95, 122–135. [Google Scholar] [CrossRef]
- Manandhar, A.; Zhu, H.; Ozkan, E.; Shah, A. Techno-economic impacts of using a laser-guided variable-rate spraying system to retrofit conventional constant-rate sprayers. Precis. Agric. 2020, 21, 1156–1171. [Google Scholar] [CrossRef]
- Palleja, T.; Landers, A.J. Real time canopy density estimation using ultrasonic envelope signals in the orchard and vineyard. Comput. Electron. Agric. 2015, 115, 108–117. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, L.; Xue, X.; Ding, W.; Sun, Z.; Zhou, Q.; Cui, L. Design and experiment of 3WQ-400 double air-assisted electrostatic orchard sprayer. Trans. CSAE 2016, 32, 45–53. [Google Scholar]
- Qiu, W.; Sun, H.; Sun, Y.; Liao, Y.; Zhou, L.; Wen, Z. Design and test of circulating air-assisted sprayer for dwarfed orchard. Trans. CSAE 2021, 37, 18–25. [Google Scholar]
- Pergher, G.; Gubiani, R.; Cividino, S.R.; Dell’Antonia, D.; Lagazio, C. Assessment of spray deposition and recycling rate in the vineyard from a new type of air-assisted tunnel sprayer. Crop. Prot. 2013, 45, 6–14. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Zeng, A. Measuring method and experiment on spray drift of chemicals applied by UAV sprayer based on an artificial orchard test bench. Trans. CSAE 2020, 36, 56–66. [Google Scholar]
- Wen, S.; Zhang, Q.; Deng, J.; Lan, Y.; Yin, X.; Shan, J. Design and experiment of a variable spray system for unmanned aerial vehicles based on PID and PWM control. Appl. Sci. 2018, 8, 2482. [Google Scholar] [CrossRef]
- Guler, H.; Zhu, H.; Ozkan, H.E.; Derksen, R.C.; Yu, Y.; Krause, C.R. Spray characteristics and drift reduction potential with air induction and conventional flat fan nozzles. Trans. ASABE 2007, 50, 745–754. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, H.; Ozkan, E.; Derksen, R.C.; Krause, C.R. Spray drift and off-target loss reductions with a precision air-assisted sprayer. Trans ASABE 2013, 56, 1273–1281. [Google Scholar]
- Wang, C.; Song, J.; He, X.; Wang, Z.; Wang, S.; Meng, Y. Effect of flight parameters on distribution characteristics of pesticide spraying droplets deposition of plant-protection unmanned aerial vehicle. Trans. CSAE 2017, 33, 109–116. [Google Scholar]
- Qiu, W.; Sun, C.; Lv, X.; Ding, W.; Feng, X. Effect of air-assisted spray application rate on spray droplet deposition distribution on fruit tree canopies. Appl. Eng. Agric. 2016, 32, 739–749. [Google Scholar]
- Zhou, Q.; Tang, J.; Nie, Y.; Chen, Z.; Qin, L. Visual Tracking Control of Cable-Driven Hyper-Redundant Snake-Like Manipulator. Appl. Sci. 2021, 11, 6224. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Y.; Huang, F.; Li, J.; Chen, Z.; Song, W.; Zhu, S.; Gu, J. Design and kinematic control of the cable-driven hyper-redundant manipulator for potential underwater applications. Appl. Sci. 2019, 9, 1142. [Google Scholar] [CrossRef]
- Duan, J.; Wang, B.; Cui, K.; Dai, Z. Path Planning Based on NURBS for Hyper-Redundant Manipulator Used in Narrow Space. Appl. Sci. 2022, 12, 1314. [Google Scholar] [CrossRef]
- Xu, W.; Liu, T.; Li, Y. Kinematics, dynamics, and control of a cable-driven hyper-redundant manipulator. IEEE ASME Trans. Mechatron. 2018, 23, 1693–1704. [Google Scholar] [CrossRef]
- Liljebäck, P.; Pettersen, K.; Stavdahl, Ø.; Gravdahl, J.T. A review on modelling, implementation, and control of snake robots. Robot. Auton. Syst. 2012, 60, 29–40. [Google Scholar] [CrossRef]
- Ma, S.; Kobayashi, I. An obstacle avoidance control scheme for the Moray arm on the basis of posture space analysis. Robot. Auton. Syst. 2000, 32, 163–172. [Google Scholar] [CrossRef]
- Xu, W.; Mu, Z.; Liu, T.; Liang, B. A modified modal method for solving the mission-oriented inverse kinematics of hyper-redundant space manipulators for on-orbit servicing. Acta Astronaut. 2017, 139, 5–66. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Practical kinematics for real-time implementation of continuum robots. IEEE Trans. Robot. 2006, 22, 1087–1099. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Kinematics for multisection continuum robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Webster, R.J.; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Wang, H.; Gao, G.H.; Xia, Q.; Ren, H.; Li, L.; Zheng, Y. Accuracy estimation of a stretch-retractable single section continuum manipulator based on inverse kinematics. Ind. Robot. Int. J. Robot. Res. Appl. 2019, 46, 573–580. [Google Scholar] [CrossRef]
- Gao, G.; Liu, C.; Wang, H. Kinematic accuracy of picking robot constructed by wire-driven continuum structure. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 299–311. [Google Scholar] [CrossRef]
- Hannan, M.W.; Walker, I.D. Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef]




| Linkage (i) | ||||
|---|---|---|---|---|
| 1 | 108 | 0 | 0 | |
| 2 | 108 | 0 | 0 | |
| 3 | 108 | 0 | 0 | |
| 4 | 108 | 90 | 0 | |
| 5 | 108 | 0 | 0 | |
| 6 | 73 | 0 | 0 |
| Rod (i) | Mass of Rods (kg) | |||
|---|---|---|---|---|
| 1 | 0.191 | 0 | 61.056 | 0 |
| 2 | 0.191 | 0 | 169.056 | 0 |
| 3 | 0.187 | 0 | 276.826 | 0 |
| 4 | 0.191 | 0 | 385.056 | 0 |
| 5 | 0.191 | 0 | 493.056 | 0 |
| 6 | 0.092 | 0 | 575.818 | 0 |
| Components | Parameters | Values | Name | Model | Company (Country) |
|---|---|---|---|---|---|
| Cable-driven flexible manipulator | Distance between adjacent end plate | 40 mm | Stepper motors | 86BYG250D-14 | Wenzhou Pufeide Electric Co., LTD. (Wenzhou, China) |
| Radius of tubular unit | 32 mm | Microstep driver | MA860H | Wenzhou Pufeide Electric Co., LTD. (Wenzhou, China) | |
| Length of tubular unit | 68 mm | Lithium battery | DC-24V | Dongguan QiSuo Electronics Co., LTD. (Dongguan, China) | |
| Number of tubular units | 6 | Microcontroller | STM32 | STMicroelectronic (Geneva, Switzerland) | |
| Dimension of control box envelope | 350 × 350 × 350 mm | Cable | 1 × 7 | Jiangsu Langshan Wire Rope Co., LTD. (Nantong, China) | |
| Automatic spray-control system | Maximum pesticide load | 55 L | Lithium battery | DC-12V | Dongguan QiSuo Electronics Co., LTD. (Dongguan, China) |
| Diaphragm pump power | 60 W | Diaphragm pimp | FD-G4000Z | Taizhou Sprayer Plant Protection Machinery Co., LTD. (Taizhou, China) | |
| Tracked mobile platform | Boundary dimension | 860 × 850 × 500 mm | Brushless DC motor | 86BL 130S78-430 | Beijing Times Chaoqun Electric Technology Co., LTD. (Beijing, China) |
| Velocity | 0.5 m/s | Speed reducer | PXKW | Beijing Times Chaoqun Electric Technology Co., LTD. (Beijing, China) | |
| Maximum climbing angle | 35° | Battery | QS-48V | Dongguan QiSuo Electronics Co., LTD. (Dongguan, China) |
| Spray Flow Rate (mL/s) | Deposition Rate (%) | Coverage Rate of Spraying Center (%) | Coverage Rate of Spraying Margin (%) | Droplet Diameter (μm) |
|---|---|---|---|---|
| 4.0 | 88.0 | 98.4 | 64.3 | 97.671 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, X.; Niu, Y.; Li, Y.; Mao, J.; Li, S.; Ma, X.; Yin, Q.; Chen, B. Design and Kinematic Analysis of Cable-Driven Target Spray Robot for Citrus Orchards. Appl. Sci. 2022, 12, 9379. https://doi.org/10.3390/app12189379
Bao X, Niu Y, Li Y, Mao J, Li S, Ma X, Yin Q, Chen B. Design and Kinematic Analysis of Cable-Driven Target Spray Robot for Citrus Orchards. Applied Sciences. 2022; 12(18):9379. https://doi.org/10.3390/app12189379
Chicago/Turabian StyleBao, Xiulan, Yuxin Niu, Yishu Li, Jincheng Mao, Shanjun Li, Xiaojie Ma, Qilin Yin, and Biyu Chen. 2022. "Design and Kinematic Analysis of Cable-Driven Target Spray Robot for Citrus Orchards" Applied Sciences 12, no. 18: 9379. https://doi.org/10.3390/app12189379
APA StyleBao, X., Niu, Y., Li, Y., Mao, J., Li, S., Ma, X., Yin, Q., & Chen, B. (2022). Design and Kinematic Analysis of Cable-Driven Target Spray Robot for Citrus Orchards. Applied Sciences, 12(18), 9379. https://doi.org/10.3390/app12189379





