Delineation and Analysis of Regional Geochemical Anomaly Using the Object-Oriented Paradigm and Deep Graph Learning—A Case Study in Southeastern Inner Mongolia, North China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
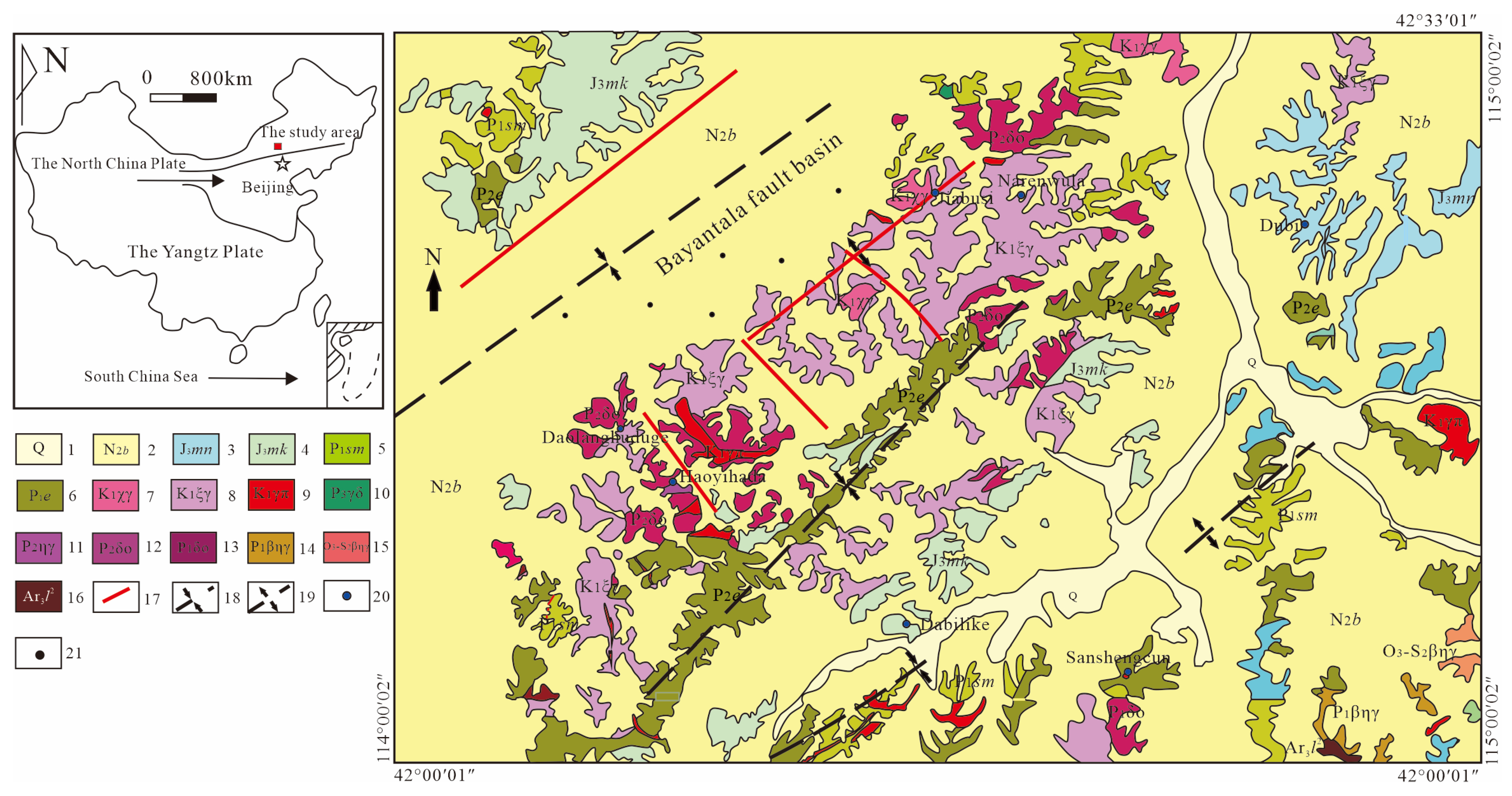
2.1.1. Geological Settings
2.1.2. Data Materials
2.2. Methodology
2.2.1. Data Pre-Processing
- (1)
- Pre-Processing of Original Geochemical Data
- (2)
- Multiresolution Segmentation
- (3)
- Find the Centroid of Each Object
2.2.2. Constructing the Geochemical Topology Graph
2.2.3. The Graph Network Architecture
- (1)
- The GAT-Dominated Encoder.
- (2)
- The GCN-Dominated Decoder.
- (3)
- The Loss Function.
2.2.4. Data Post-Processing
3. Results
3.1. Implementation Details
3.2. The Object-Based Anomaly Score Map
3.3. Elemental Within-Object Separability
- (1)
- The D2 values of the image objects containing the known ore spots vary in a wide range. For the I-series ore spots, the relevant dimension values fluctuate between 2 and 116 with a peak at 18 (The original D2 values were normalized to [0, 255]), and if we set D2 = 116 as the binarization threshold, the obtained anomalous area accounts for 98.63% of the total area. For the S-series ore spots, the relevant dimension values fluctuate between 1 and 32 with a peak at 14, and if we set D2 = 32 as the threshold, the obtained anomalous area will account for 78.93%.
- (2)
- As the histogram of the D2 map is usually right-skewed, so we empirically set the binarization threshold as the mode value + 1 × standard deviation (for a standard normal distribution, 68.3% of data falls within one standard deviation of the mean, so we suppose that most, if not all, of the ore-spots would fall within the objects with the D2 value ≤ mode + 1 × standard deviation). For I-series elements, the threshold is 36, and for S-series, it is 34. Our purpose of image binarization is not to delineate the anomalous regions like Figure 9, Figure 10 and Figure 11 do, but to delineate some highly confident non-anomalous objects. That is why in Figure 12, very few ore-spots fall in the colored patches. Naturally, by removing these non-anomalous objects from Figure 9 and Figure 10, we can obtain a moderately reduced prospecting-target-area as shown in Figure 13.
- (3)
- In Figure 13 (upper), the anomalous area of I-series elements decreases to 43.045% of the total area, and the buffered anomalous area decreases to 61.608%. Only 5 ore-spots fall outside the reduced anomalous target area, which are Au, Pb-Zn, and Ag-Zn mineral spots. In Figure 13 (lower), the anomalous area of S-series elements decreases to 43.172% of the total area, and the buffered area decreases to 61.534%. Only 2 ore-spots fall outside the target area, which are fluorite and Pb-Zn spots.
3.4. Comparison and Validation by Factor Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grunsky, E.C.; Drew, L.J.; Sutphin, D.M. Process recognition in multi-element soil and stream-sediment geochemical data. Appl. Geochem. 2009, 24, 1602–1616. [Google Scholar] [CrossRef]
- Cheng, Q.; Li, Q. A fractal concentration–area method for assigning a color palette for image representation. Comput. Geosci. 2002, 28, 567–575. [Google Scholar] [CrossRef]
- Zhao, B.; Gou, P.; Yang, F.; Tang, P. Improving object-oriented land use/cover classification from high resolution imagery by spectral similarity-based post-classification. Geocarto. Int. 2021, 37, 7065–7088. [Google Scholar] [CrossRef]
- Van den Bergh, M.; Boix, X.; Roig, G.; Van Gool, L. Seeds: Superpixels extracted via energy-driven sampling. Int. J. Comput. Vision. 2015, 111, 298–314. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Erdemir, M.Y.; Tonbul, H. Classification of semiurban landscapes from very high-resolution satellite images using a regionalized multiscale segmentation approach. J. Appl. Remote Sens. 2017, 11, 035016. [Google Scholar] [CrossRef]
- Li, X.; Shao, G. Object-based land-cover mapping with high resolution aerial photography at a county scale in midwestern USA. Remote Sens. 2014, 6, 11372–11390. [Google Scholar] [CrossRef] [Green Version]
- Chinese Academy of Geological Sciences. Application of Geophysical and Geochemical Analysis Methods Specific for Prospecting Typical Metallic Mineral Deposits in China; Geological Publishing House: Beijing, China, 2011; (In Chinese with English abstract). [Google Scholar]
- Liu, Y.; Cheng, Q.; Xia, Q.; Wang, X. Identification of REE mineralization-related geochemical anomalies using fractal/multifractal methods in the Nanling belt, South China. Environ. Earth Sci. 2014, 72, 5159–5169. [Google Scholar] [CrossRef]
- Daya, A.A.; Afzal, P. A comparative study of concentration-area (CA) and spectrum-area (SA) fractal models for separating geochemical anomalies in Shorabhaji region, NW Iran. Arab. J. Geosci. 2015, 8, 8263–8275. [Google Scholar] [CrossRef]
- Sridharan, H.; Qiu, F. Developing an object-based hyperspatial image classifier with a case study using Worldview-2 data. Photogramm. Eng. Rem. S. 2013, 79, 1027–1036. [Google Scholar]
- Geneletti, D.; Gorte, B.G.H. A method for object-oriented land cover classification combining Landsat TM data and aerial photographs. Int. J. Remote Sens. 2003, 24, 1273–1286. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hay, G.J.; Ghaffarian, S.; Hugenholtz, C.H. Geographic object-based image analysis: A primer and future directions. Remote Sens. 2020, 12, 2012. [Google Scholar] [CrossRef]
- Afzal, P.; Farhadi, S.; Shamseddin Meigooni, M.; Boveiri Konari, M.; Daneshvar Saein, L. Geochemical Anomaly Detection in the Irankuh District Using Hybrid Machine Learning Technique and Fractal Modeling. Geopersia. 2022, 12, 191–199. [Google Scholar]
- Farhadi, S.; Afzal, P.; Boveiri Konari, M.; Daneshvar Saein, L.; Sadeghi, B. Combination of Machine Learning Algorithms with Concentration-Area Fractal Method for Soil Geochemical Anomaly Detection in Sediment-Hosted Irankuh Pb-Zn Deposit, Central Iran. Minerals. 2022, 12, 689. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, J.J.; Yang, F.; Pilz, J.; Zhang, D.H. A novel approach for extraction of Gaoshanhe-Group outcrops using Landsat Operational Land Imager (OLI) data in the heavily loess-covered Baoji District, Western China. Ore Geol. Rev. 2019, 108, 88–100. [Google Scholar] [CrossRef]
- Zhao, B.; Luo, X.; Tang, P.; Liu, Y.; Wan, H.; Ouyang, N. STDecoder-CD: How to Decode the Hierarchical Transformer in Change Detection Tasks. Appl Sci-Basel. 2022, 12, 7903. [Google Scholar] [CrossRef]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Martins, V.S.; Kaleita, A.L.; Gelder, B.K.; da Silveira, H.L.; Abe, C.A. Exploring multiscale object-based convolutional neural network (multi-OCNN) for remote sensing image classification at high spatial resolution. ISPRS J. Photogramm. 2020, 168, 56–73. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S.; Emery, W.J. Object-based convolutional neural network for high-resolution imagery classification. IEEE J-STARS. 2017, 10, 3386–3396. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Zhang, S.; Ding, X.; Atkinson, P.M. Iterative Deep Learning (IDL) for agricultural landscape classification using fine spatial resolution remotely sensed imagery. Int. J. Appl. Earth Obs. 2021, 102, 102437. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, P.; Tapete, D.; Shangguan, B.; Wang, M.; Wu, Z. A multi-level context-guided classification method with object-based convolutional neural network for land cover classification using very high-resolution remote sensing images. Int. J. Appl. Earth Obs. 2020, 88, 102086. [Google Scholar] [CrossRef]
- Lv, X.; Shao, Z.; Ming, D.; Diao, C.; Zhou, K.; Tong, C. Improved object-based convolutional neural network (IOCNN) to classify very high-resolution remote sensing images. Int. J. Remote Sens. 2021, 42, 8318–8344. [Google Scholar] [CrossRef]
- Hobley, B.; Arosio, R.; French, G.; Bremner, J.; Dolphin, T.; Mackiewicz, M. Semi-supervised segmentation for coastal monitoring seagrass using RPA imagery. Remote Sens. 2021, 13, 1741. [Google Scholar] [CrossRef]
- Guan, Q.; Ren, S.; Chen, L.; Yao, Y.; Hu, Y.; Wang, R.; Feng, B.; Gu, L.; Chen, W. Recognizing Multivariate Geochemical Anomalies Related to Mineralization by Using Deep Unsupervised Graph Learning. Nat. Resour. Res. 2022, 31, 2225–2245. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Application of one-class support vector machine to quickly identify multivariate anomalies from geochemical exploration data. Geochem-Explor. Env. A 2017, 17, 231–238. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. Recognition of geochemical anomalies using a deep autoencoder network. Comput. Geosci. 2016, 86, 75–82. [Google Scholar] [CrossRef]
- Veli, V.C.; Kovi, C.P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Dibo Mining Co. LTD of Inner Mongolia Nonferrous Geology and Mining (Group). Overall Design of the Project of “Study of the Ore-Forming Regularity and Ore Prediction for Key Metallic Deposits in the Bayantala-Mingantu District, Inner Mongolia, China”; Dibo Mining Co., Ltd.: Hohhot, China, 2020; pp. 1–69. (In Chinese) [Google Scholar]
- Pirajno, F. Hydrothermal Processes and Mineral Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–527. [Google Scholar]
- Kigai, I.N. Redox problems in the “metallogenic specialization” of magmatic rocks and the genesis of hydrothermal ore mineralization. Petrology 2011, 19, 303–321. [Google Scholar] [CrossRef]
- Smith, M.; Goodchild, M.F.; Longley, P.A. Geospatial Analysis—A Comprehensive Guide to Principles, Techniques and Software Tools, 2. ed.; Troubador Publishing Ltd.: Market Harborough, UK, 2007; pp. 32–200. [Google Scholar]
- Zhang, Z.; Cui, P.; Zhu, W. Deep learning on graphs: A survey. IEEE T. Knowl. Data Eng. 2022, 34, 249–270. [Google Scholar] [CrossRef] [Green Version]
- Brody, S.; Alon, U.; Yahav, E. How attentive are graph attention networks. arXiv 2021, arXiv:2105.14491. [Google Scholar]
- Myint, S.W. Fractal approaches in texture analysis and classification of remotely sensed data: Comparisons with spatial autocorrelation techniques and simple descriptive statistics. Int. J. Remote Sens. 2003, 24, 1925–1947. [Google Scholar] [CrossRef]
- Zhao, B.; Han, L.; Pilz, J.; Wu, J.J.; Khan, F.; Zhang, D.H. Metallogenic efficiency from deposit to region–A case study in western Zhejiang Province, southeastern China. Ore Geol. Rev. 2017, 86, 957–970. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, F.; Zhang, R.; Shen, J.; Pilz, J.; Zhang, D.H. Application of unsupervised learning of finite mixture models in ASTER VNIR data-driven land use classification. J. Spatial Sci. 2019, 66, 89–112. [Google Scholar] [CrossRef]
- Chen, L.; Guan, Q.; Xiong, Y.; Liang, J.; Wang, Y.; Xu, Y. A spatially constrained multi-autoencoder approach for multivariate geochemical anomaly recognition. Comput. Geosci. 2019, 125, 43–54. [Google Scholar] [CrossRef]
- Drǎguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterization for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]


















| Element | Ag | As | Au | B | Be | Bi | Cu | F | Hg |
| Maximum | 4500 | 248.7 | 93.5 | 660 | 12 | 272.34 | 287.8 | 24,600 | 5511 |
| Minimum | 10 | 1.24 | 0.2 | 2.9 | 0.7 | 0.036 | 0.8 | 80 | 4.5 |
| Median | 60 | 8.60 | 0.8 | 38 | 2.1 | 0.24 | 13.3 | 340 | 16 |
| Average | 71.22 | 9.83 | 1.24 | 42.05 | 2.25 | 0.53 | 14.01 | 380.05 | 21.44 |
| CV | 1.87 | 0.97 | 2.43 | 0.92 | 0.36 | 14.36 | 0.88 | 1.89 | 7.08 |
| Element | Mo | Nb | Pb | Sb | Sn | U | W | Zn | Fe2O3 |
| Maximum | 5.64 | 4468 | 220.50 | 13.41 | 260 | 4.80 | 1299.20 | 841 | 7.91 |
| Minimum | 0.28 | 0.7 | 0.90 | 0.10 | 0.10 | 0.15 | 0.30 | 9.10 | 0.53 |
| Median | 0.8 | 10.1 | 14.6 | 0.56 | 2.5 | 1.5 | 1.36 | 43.6 | 3.18 |
| Average | 0.90 | 14.19 | 16.76 | 0.65 | 2.99 | 1.57 | 2.57 | 48.30 | 3.17 |
| CV | 0.47 | 8.64 | 0.70 | 0.95 | 2.44 | 0.32 | 13.90 | 0.78 | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, B.; Zhang, D.; Zhang, R.; Li, Z.; Tang, P.; Wan, H. Delineation and Analysis of Regional Geochemical Anomaly Using the Object-Oriented Paradigm and Deep Graph Learning—A Case Study in Southeastern Inner Mongolia, North China. Appl. Sci. 2022, 12, 10029. https://doi.org/10.3390/app121910029
Zhao B, Zhang D, Zhang R, Li Z, Tang P, Wan H. Delineation and Analysis of Regional Geochemical Anomaly Using the Object-Oriented Paradigm and Deep Graph Learning—A Case Study in Southeastern Inner Mongolia, North China. Applied Sciences. 2022; 12(19):10029. https://doi.org/10.3390/app121910029
Chicago/Turabian StyleZhao, Bo, Dehui Zhang, Rongzhen Zhang, Zhu Li, Panpan Tang, and Haoming Wan. 2022. "Delineation and Analysis of Regional Geochemical Anomaly Using the Object-Oriented Paradigm and Deep Graph Learning—A Case Study in Southeastern Inner Mongolia, North China" Applied Sciences 12, no. 19: 10029. https://doi.org/10.3390/app121910029
APA StyleZhao, B., Zhang, D., Zhang, R., Li, Z., Tang, P., & Wan, H. (2022). Delineation and Analysis of Regional Geochemical Anomaly Using the Object-Oriented Paradigm and Deep Graph Learning—A Case Study in Southeastern Inner Mongolia, North China. Applied Sciences, 12(19), 10029. https://doi.org/10.3390/app121910029







