Parametric Quasi-Static Study of the Effect of Misalignments on the Path of Contact, Transmission Error, and Contact Pressure of Crowned Spur and Helical Gear Teeth Using a Novel Rapidly Convergent Method

Abstract

Quasi-static modelling of non-conjugate contact of tooth-modified spur and helical gears has been studied at length, but existing models are hindered by convergence problems and require a brute-force numerical approach. Here, a novel, computationally efficient, and stable and unconditionally convergent model is developed for non-conjugate tooth contact in three dimensions and applied to crowned spur and helical gears to assess parametrically the sensitivity of various in- and out-of-plane misalignments on the path of contact, transmission error, and contact pressure. Performance metrics are defined, and comparisons are made between three different crowning modification functions.

1. Introduction

Computerized simulation of gear tooth contact is a significant part of gear design. It allows to assess all the processes of gearing at the design stage, which may include misalignment and transmission errors (TE), tooth damage, noise, and vibration. This field is well-studied by Litvin [1], who developed seminal methods for the so-called tooth contact analysis (TCA) and local synthesis, calculating contact between two teeth for machine tool settings. However, the key drawback of the model is the need for estimation of the position of the surface contact in order to achieve an accurate solution, which requires substantial computational power; otherwise, the numerical computations process suffers from convergence issues. Various researchers have proposed other computational methods of tooth contact analysis in order to resolve the stated and other problems associated with the method. Bracci [2] suggested a fast-geometric approach to calculate the contact pattern without the need to take into account the curvature of the surface. The study showed that the instantaneous contact area is estimated using the surface intersection procedure that mimics the removal of the marking compound during meshing. In addition, Lin and Fong [3] proposed that the use of normal vectors to evaluate the positions of the contact points according to the surface location can be avoided solely by using a numerical solution vector. Vijayakar [4] suggested a discrete optimization approach to define the minimum distance points between two surfaces to solve the contact problem. Later, a new type of fundamental two-dimensional tooth surface contact equations was suggested for the two-dimensional problem (i.e., spur parallel axis gearing) by Spitas et al. [5,6], which reduced Litvin’s model with five typically nonlinear equations with five unknowns and one independent parameter to a system with only two equations with two unknowns and one independent parameter.

Often, theoretical conjugate models of gears do not correspond to the practical application due to deliberate modifications of the tooth or to manufacturing errors [7]. Under these conditions, the use of the classical theory of gears can lead to erroneous results that do not agree with reality. The mesh analysis of these non-conjugate gears is necessary in order to account for the resulting non-uniformity in motion transmission in addition to the changed direction of contact. Therefore, over time, various models for non-conjugate action gears have been proposed. One of them was created by Zhang and Fang [8], who built a model for helical gears tooth meshing with deformed surfaces designed to minimize TE and account for production errors and complex load distribution. By applying this approach, the authors were able to enhance and adjust the quality of the meshing by accounting for load distribution.

During the power transmission of spur and helical gears, various errors such as machining errors, misalignment of the assembly, and other factors may cause noise and vibration during the operation. For a long time, gear alignment problems (or misalignments) have concerned engineers. Gear-pair misalignments can affect both the geometric and physical performances of the tooth flanks. Determining the loaded tooth contact performance with misalignments is crucial for improving strength and stabilizing the gear transmission system. In order to accomplish an assessment of the contact characteristics without edge contact and concentrated stresses, low vibration, and acceptable transmission error, research on loaded tooth contact analysis (LTCA) has been conducted [9,10,11]. The load distribution calculations proposed by V. Simon [9] showed that LTCA provides a more realistic contact pattern and contact pressure than the elliptical one. H. Ding et al. [10,11], by using LTCA, were able to obtain more accurate results of the tooth contact pattern by determining whole load distribution over the entire tooth surface.

To decrease the noise and vibration of a meshing helical and spur gear pair, Litvin et al. [12,13,14,15] suggested an equation system with a five degree of freedom to modify their geometry in order to lower TE and avoid contact at the edge of gear teeth. Later, they applied this approach to study the contact of the misaligned spur and the helical gear pairs by applying the double crowning of tooth surfaces with parabolic TE function. Moreover, Litvin et al. [16,17] used this novel topology of tooth surfaces to localize the bearing contact.

Misalignments of gears can be divided into two types: angular and linear, both of which have an adverse effect on the contact of gears and engagement. Researchers Hu and Mao [18] proposed a more detailed separation of gear misalignment, thus distinguishing them into four types: axial and radial misalignments (linear) and yaw and pitch misalignments (angular), where radial, axial, yaw (in-plane) misalignments, and pitch (out-of-plane) misalignment [19] influence the gear transmission and surface contact. The results of studies of spur gears have shown that the surface contact is more sensitive to angular misalignments than to linear ones and also that the contact area between two gears is significantly reduced in the case of angular misalignment compared to linear ones [20]. Ye and Tsai [21] discovered that high-contact-ratio gears under angular misalignment produce more significant stress compared to linear misalignment. Several solutions to gear misalignment have been suggested by various researchers. A representative example is the tooth modification proposed by Mao [22], who found that tooth modifications such as crowning can substantially reduce the stress concentration caused by misalignments. The gear tooth modifications, also called “corrections”, have been described in various guidelines [23,24,25,26]. The goal of such modifications is to remove the risk of edge contact and related failure during the tooth contact action. It must be mentioned that modifications are errors in themselves. In particular, unnecessary corrections lead to increased TE, overloads, and vibration [27]. The tooth modification focused on the crowning along the tooth flanks and the profile modification along the tooth height. The spur gear with modified tooth surface creates a relatively smooth distribution of pressure and prevents the edge contact effect, making it a capable solution for misalignment. Li, in his work [28], also discussed misalignment of the gears and recommended modification of the tooth flank as an appropriate solution. Furthermore, Li highlighted the significance of finding optimum criteria for crowning based on static loads and the amount of misalignment. The risk of micro-pitting in gears is lowered by optimum tooth surface adjustment. As has been mentioned earlier, excessive modification of the tooth creates vulnerability to micro-cracks and micro-pitting, which lowers the life of the gear and can potentially aggravate the dynamic response, whereas too little crowning creates issues with localization of contact [29]. Thus, modification of the gear tooth surface is an effective way to improve the meshing properties of gears in order to reduce the sensitivity of the alignment errors; however, there is a necessity to determine the proper amount of modification in order to obtain a smooth transmission of the gear system. Presently, in a pursuit to design higher transmission quality, many studies have focused on the selection of optimal tooth modifications designed to minimize TE by crowning with various types of profiles.

Longitudinal modification of gears is traditionally expressed as a parabolic curve. The idea of the predesigned parabolic function approach has been described by Litvin [30], who showed that double-crowned gears enable the reduction of vibration and noise of gear drives and provide a parabolic function of TE by absorbing the linear function of TE caused by gear misalignment. Lin et al. [31] investigated that parabolic relief is less sensitive to load changes and modification parameters compared to linear relief. Later, Gurumani and Shanmugam [32] proposed a circular arc crowing, which is simple and easy to produce. Litvin et al. [33] and Zhen et al. [34] described the benefits of double circular-arc helical gears, which decrease contact stress level and have the ability to increase the resistance to tooth bending. As a result, this type of gear is commonly used to shift greater torque. Furthermore, Bergesth and Bjorklund [35] suggested logarithmic crowning to shift the peak load from the edges to the middle of the tooth surface. The logarithmic modification was first designed for roller bearings to improve stress distribution, but there is not much work that would show that it could be used to modify the lead tooth surface of gears. The logarithmic crowning was created using Lundberg’s theory [36], and it was found to be superior to traditional modification. The findings revealed that as opposed to typical lead changes, the logarithmical curve has significantly lower contact pressures for minor misalignments. Later, Yangyang et al. [37] described the long-term development history of the logarithmic equation, in which many researchers made improvements and corrections to the theoretical logarithmic convex equation [38,39,40,41]. As stated by Harianto and Houser [42], lead modifications (longitudinal crowning) are used to compensate for misalignments and selected with respect to company-based requirements, manufacturing accuracy, or by a load distribution analysis with established peak misalignments.

This study presents a new surface engagement model for non-conjugate tooth contact analysis, which allows determining the contact of gear tooth surfaces at every instant in space without convergence issues that appear in Litvin’s model and with robust and fast numerical solutions. Building on our prior work on two-dimensional contact modelling [5,6], we propose an extended three-dimensional system of surface contact equations with two unknowns and one independent parameter rotating about two fixed axes in space, which, compared to Litvin’s method, gives more explicit and numerically stable results without convergence issues.

To demonstrate the developed model and method, the sensitivity to in-plane and out-of-plane misalignments on the contact paths, TE, and contact stresses is analyzed by means of parametric implementation of the effect of the longitudinal crown on a spur and helical gears. The three different types of longitudinal modification are expressed mathematically and compared based on appropriately introduced metrics. Loaded tooth contact analysis (LTCA) is also conducted, and contact ellipses are predicted. The presented method is shown to be suitable for accurate, numerically convergent, and unconditionally stable mapping of the parametric design space, allowing the determination of optimal designs.

2. Materials and Methods

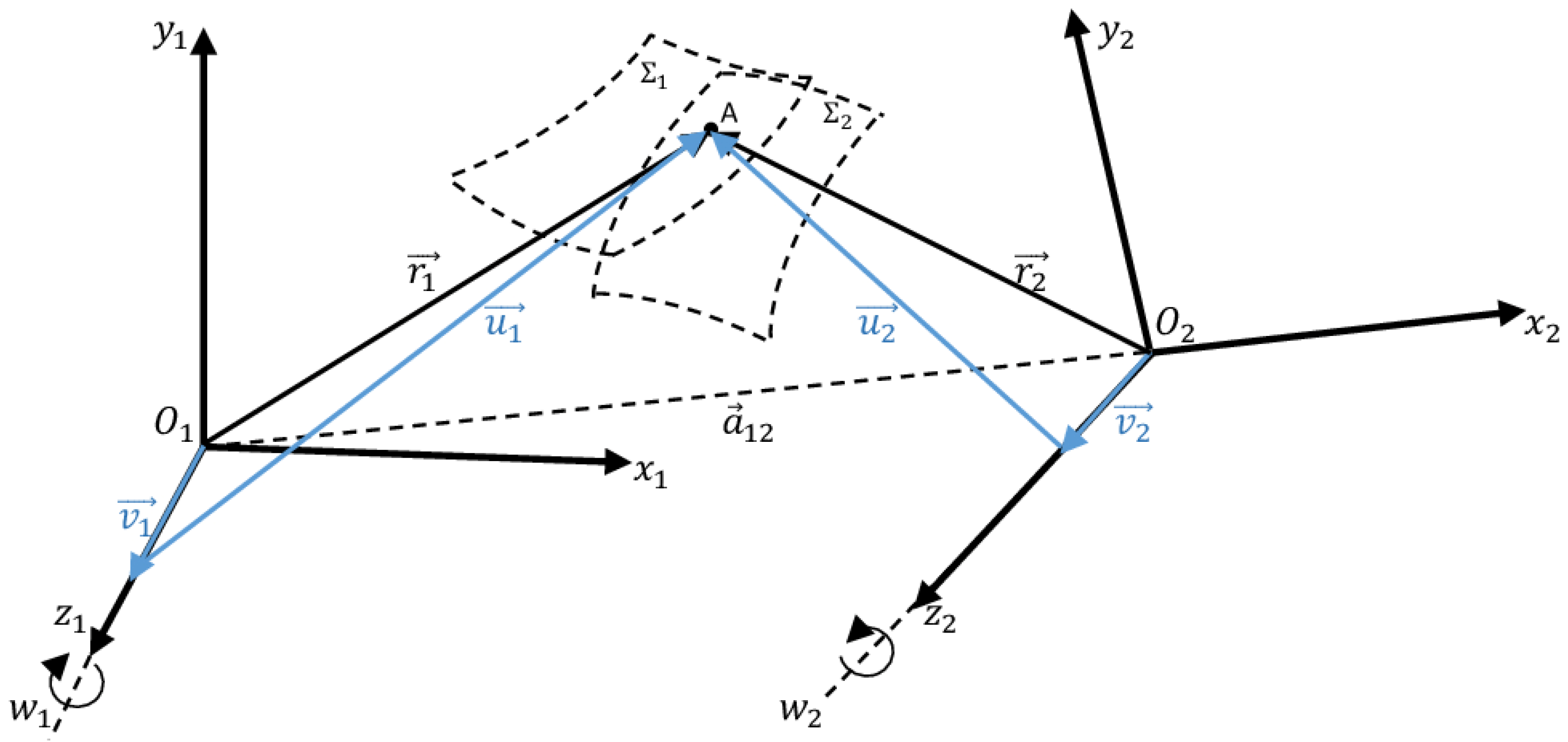
In this study, the gear tooth meshing problem was described with surface tangency conditions. The two meshing teeth surfaces ${\mathsf{\Sigma }}_1$ and ${\mathsf{\Sigma }}_2$ are assumed to be a continuous $C^1$ and rotating around a fixed axis ${\overrightarrow{w}}_i$:

$${\overrightarrow{n}}_i=\frac{\partial {\overrightarrow{r}}_i}{\partial {\overrightarrow{u}}_i}\times \frac{\partial {\overrightarrow{r}}_i}{\partial {\overrightarrow{v}}_i},i=1,2$$

(1)

where ${\overrightarrow{r}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)\in C^1, \left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)\in E_i$ (Figure 1).

The parameterization for ${\overrightarrow{u}}_i$ corresponds to the radial distance of a contact point from the surface axis of rotation, and ${\overrightarrow{v}}_i$ is the algebraic projection on the same axis, so:

$${\overrightarrow{u}}_i=\left|\left|{\overrightarrow{r}}_i-pro{j}_{{\overrightarrow{w}}_i}{\overrightarrow{r}}_i\right|\right|$$

(2)

$${\overrightarrow{v}}_i={\overrightarrow{w}}_i\cdot pro{j}_{{\overrightarrow{w}}_i}{\overrightarrow{r}}_i,$$

(3)

Thus, ${\overrightarrow{u}}_i$ and ${\overrightarrow{v}}_i$ form a right angle, where ${\overrightarrow{u}}_i$ is the length of the vertical leg, and ${\overrightarrow{v}}_i$ is the horizontal leg aligned along the axis of rotation ${\overrightarrow{w}}_i$, with the hypotenuse ${\overrightarrow{r}}_i$ is the position vector of any point on the surface ${\mathsf{\Sigma }}_i$. The surface equations $({\overrightarrow{f}}_i$) can be expressed in terms of the vectors mentioned above and by introducing a rotation matrix $R_i$(${\varphi }_i$), corresponding to the rotation around the axis ${\overrightarrow{w}}_i$ to the angle ${\varphi }_i$. Hence, vector ${\overrightarrow{r}}_i$ can be written as expressed as:

$${\overrightarrow{r}}_i=R_i\left({\varphi }_i\right){\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right), i=1,2$$

(4)

The surface tangency condition formulates the surface contact equations:

$${\overrightarrow{n}}_1\left(u_1,v_1\right)\times {\overrightarrow{n}}_2\left(u_2,v_2\right)=\overrightarrow{0},$$

(5)

When substituting Equation (1) to Equations (4) and (5) to express surface normal, the tangency condition yields:

$$R_1\left({\varphi }_1\right)\left(\frac{\partial {\overrightarrow{f}}_1\left(u_1,v_1\right)}{\partial u_1}\times \frac{\partial {\overrightarrow{f}}_1\left(u_1,v_1\right)}{\partial v_1}\right)\times R_2\left({\varphi }_2\right)\left(\frac{\partial {\overrightarrow{f}}_2\left(u_2,v_2\right)}{\partial u_2}\times \frac{\partial {\overrightarrow{f}}_2\left(u_2,v_2\right)}{\partial v_2}\right)=\overrightarrow{0},$$

(6)

Furthermore, a common point of contact can be expressed as a zero-vector sum:

$${\overrightarrow{r}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}-{\overrightarrow{r}}_2\left(u_2,v_2\right)=\overrightarrow{0},$$

(7)

The angle of rotation of the touching surface ${\varphi }_2$ can be determined by the function $u_2$ and $v_2$, which can be calculated directly in terms of $u_1$ and $v_1$ from specific geometric relationships:

$$\begin{gathered} {\overrightarrow{v}}_2=pro{j}_{{\overrightarrow{w}}_2}{\overrightarrow{r}}_2\left(u_2,v_2\right)=pro{j}_{{\overrightarrow{w}}_2}{\overrightarrow{f}}_2\left(u_2,v_2\right)={\overrightarrow{w}}_2\cdot \left({\overrightarrow{r}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)= \\ {\overrightarrow{w}}_2\cdot \left(R_1\left({\varphi }_1\right)f_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)={\mathcal{F}}_v\left({\varphi }_1,u_1,v_1\right), \end{gathered}$$

(8)

where ${\mathcal{F}}_{\theta }\left({\varphi }_1,u_1,v_1\right)$ is the function of ${\varphi }_1$, $u_1,$ and $v_1$. Then, Equations (2) and (3) can be combined by the Pythagoras’ theorem:

$${\overrightarrow{u}}_2{}^2+{\overrightarrow{v}}_2{}^2={\overrightarrow{r}}_2{(u_2,v_2)}^2,$$

(9)

thereby:

$$\begin{gathered} {\overrightarrow{u}}_2=\sqrt{{\overrightarrow{r}}_2{(u_2,v_2)}^2-{\overrightarrow{v}}_2{}^2}=\sqrt{{({\overrightarrow{r}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12})}^2-{\overrightarrow{v}}_2{}^2}= \\ \sqrt{{(R_1\left({\varphi }_1\right)f_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12})}^2-{\overrightarrow{v}}_2{}^2}={\mathcal{F}}_u\left({\varphi }_1,u_1,v_1\right), \end{gathered}$$

(10)

where ${\mathcal{F}}_u\left({\varphi }_1,u_1,v_1\right)$ is an explicit function of ${\varphi }_1$,$u_1,$ and $v_1$. In order to find the rotation angle ${\varphi }_2$ around the fixed axis ${\overrightarrow{w}}_2$ in terms of ${\varphi }_1$,$u_1$,$v_1$, we determine the projection of vectors $f_2\left(u_2,v_2\right)$ and $r_2\left(u_2,v_2\right)$ onto a plane perpendicular to the rotating axis ${\overrightarrow{w}}_2$, as shown in Figure 2. The vector function $f_2\left(u_2,v_2\right)$ and $r_2\left(u_2,v_2\right)$ can be described as follow:

$$\begin{gathered} p_2\left(u_2,v_2\right)=pro{j}_P{\overrightarrow{f}}_2\left(u_2,v_2\right) \\ ={\overrightarrow{f}}_2\left(u_2,v_2\right)-pro{j}_{{\overrightarrow{w}}_2}{\overrightarrow{f}}_2\left(u_2,v_2\right)={\overrightarrow{f}}_2\left(u_2,v_2\right)-\frac{{\overrightarrow{f}}_2\left(u_2,v_2\right)\cdot {\overrightarrow{w}}_2}{|\left|{\overrightarrow{w}}_2\right|{|}^2}{\overrightarrow{w}}_2, \end{gathered}$$

(11)

$$\begin{gathered} q_2\left(u_2,v_2\right)=pro{j}_P{\overrightarrow{r}}_2\left(u_2,v_2\right) \\ ={\overrightarrow{r}}_2\left(u_2,v_2\right)-pro{j}_{{\overrightarrow{w}}_2}{\overrightarrow{r}}_2\left(u_2,v_2\right)={\overrightarrow{r}}_2\left(u_2,v_2\right)-\frac{{\overrightarrow{r}}_2\left(u_2,v_2\right)\cdot {\overrightarrow{w}}_2}{|\left|{\overrightarrow{w}}_2\right|{|}^2}{\overrightarrow{w}}_2 \\ =\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)-\frac{\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)\cdot {\overrightarrow{w}}_2}{|\left|{\overrightarrow{w}}_2\right|{|}^2}{\overrightarrow{w}}_2, \end{gathered}$$

(12)

where $q_2\left(u_2,v_2\right)$ and $p_2\left(u_2,v_2\right)$ are the projection of vectors $f_2\left(u_2,v_2\right)$ and $r_2\left(u_2,v_2\right)$, respectively.

Then, by combining them with a dot product, we obtain:

$${\overrightarrow{p}}_2\left(u_2,v_2\right)\cdot {\overrightarrow{q}}_2\left(u_2,v_2\right)={\overrightarrow{q}}_2{}^2\cos {\varphi }_2,$$

(13)

or in terms of ${\varphi }_2$:

$${\varphi }_2=\pm {\cos }^{-1}\frac{{\overrightarrow{p}}_2\left(u_2,v_2\right)\cdot {\overrightarrow{q}}_2\left(u_2,v_2\right)}{{\overrightarrow{q}}_2{}^2}.$$

(14)

The direction of rotation for ${\varphi }_2$ in Equation (14) can be determined from the following relationship between vectors ${\overrightarrow{p}}_2$ and ${\overrightarrow{q}}_2$:

$$\frac{{\overrightarrow{p}}_2\left(u_2,v_2\right)\times {\overrightarrow{q}}_2\left(u_2,v_2\right)}{\left|\left|{\overrightarrow{p}}_2\left(u_2,v_2\right)\times {\overrightarrow{q}}_2\left(u_2,v_2\right)\right|\right|}\cdot {\overrightarrow{w}}_2=\pm 1$$

(15)

For an anticlockwise rotation, the right-hand side of Equation (15) will be negative, while for clockwise, it will be positive. By combining all the equations and expressing $v_2$ by function ${\mathcal{F}}_u$ and $u_2$ in terms of ${\mathcal{F}}_v$, the equation for ${\varphi }_2$ becomes:

$$\begin{gathered} {\varphi }_2=\frac{{\overrightarrow{p}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)\times \left(\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)-pro{j}_{{\overrightarrow{w}}_2}\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)\right)}{\left|\left|{\overrightarrow{p}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)\times \left(\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)-pro{j}_{{\overrightarrow{w}}_2}\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)\right)\right|\right|}\cdot {\overrightarrow{w}}_2 \\ {\cos }^{-1}\frac{{\overrightarrow{p}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)\cdot \left(\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)-pro{j}_{{\overrightarrow{w}}_2}\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)\right)}{{(\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right)-pro{j}_{{\overrightarrow{w}}_2}\left(R_1\left({\varphi }_1\right){\overrightarrow{f}}_1\left(u_1,v_1\right)-{\overrightarrow{a}}_{12}\right))}^2} \\ ={\mathcal{F}}_{\varphi }\left({\varphi }_1,u_1,v_1,{\mathcal{F}}_u,{\mathcal{F}}_v\right). \end{gathered}$$

(16)

Finally, from Equations (8), (10), and (16), unknowns such as ${\varphi }_2,u_2,v_2$ are expressed as functions of parameters ${\varphi }_1$, $u_1,$ and $v_1$. By replacing these unknowns with surface tangency condition Equation (6), the following equation is derived:

$$\begin{gathered} R_1\left({\varphi }_1\right)\left(\frac{\partial {\overrightarrow{r}}_1\left(u_1,v_1\right)}{\partial u_1}\times \frac{\partial {\overrightarrow{r}}_1\left(u_1,v_1\right)}{\partial v_1}\right)\times R_2\left({\mathcal{F}}_{\varphi }\right)\left(\frac{\partial {\overrightarrow{r}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)}{\partial u_1}\frac{\partial u_1}{\partial u_2}\times \frac{\partial {\overrightarrow{r}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)}{\partial v_1}\frac{\partial v_1}{\partial v_2}\right)=0, \\ {R}_1\left({\varphi }_1\right)\left(\frac{\partial {\overrightarrow{r}}_1\left(u_1,v_1\right)}{\partial u_1}\times \frac{\partial {\overrightarrow{r}}_1\left(u_1,v_1\right)}{\partial v_1}\right)\times \\ {R}_2\left({\mathcal{F}}_{\varphi }\right)\left(\frac{\partial {\overrightarrow{r}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)}{\partial u_1}\frac{\partial u_1}{\partial {\mathcal{F}}_u\left({\varphi }_1,u_1,v_1\right)}\times \frac{\partial {\overrightarrow{r}}_2\left({\mathcal{F}}_u,{\mathcal{F}}_v\right)}{\partial v_1}\frac{\partial v_1}{\partial {\mathcal{F}}_v\left({\varphi }_1,u_1,v_1\right)}\right)=0 \end{gathered}$$

(17)

Equation (17) gives only three scalar equations with two independent parameter $(u_1,v_1)$ and one applied parameter ${\varphi }_1$, which can be solved by a numerical method such as the Newton–Raphson method. The procedure for finding contact points and unknown parameters is illustrated in Figure 3. Compared to previous studies presented in the literature, the proposed numerical solution can be obtained with a few unknown parameters that are more efficient, reliable, and accurate.

3. Gear Misalignments

Spur gear meshing with instantaneous line contact of the gear tooth surfaces occurs, only theoretically, in the complete absence of tooth modifications and/or misalignment and manufacturing errors. In practice, the majority of spur gears tooth surfaces contain modifications (i.e., crowning), while it is impossible to completely avoid manufacturing errors during production or misalignment errors during assembly. In such circumstances instead of line contact, bearing contact occurs between the meshing gear tooth surfaces. It is well-established that gears are sensitive to angular misalignment errors [22,23,24,25,26,27,28], and such misalignment can be analytically expressed as an additional rotational geometric transformation:

$${\overrightarrow{r}}_i=\mathit{R}{\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)=R_x\left(\mathsf{\delta }\right)R_y\left(\mathsf{\gamma }\right)R_z\left({\varphi }_i\right){\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right),$$

(18)

where $\mathit{R}$ is the rotation matrix, which is composed of $\mathit{R}=R_x{R}_y{R}_z$; ${\varphi }_i$ is the rotation angle about the axis of revolution ${\overrightarrow{w}}_i$ of the driving gear around the z-axis. Figure 4a illustrates the in-plane angular misalignment of the gear or pinion that can be obtained by rotating the coordinate system about the $y$-axis by a misaligned angle $\mathsf{\gamma }$. Similarly, the out-of-plane angular misalignment can be achieved by rotating the coordinate system of gear or pinion about the x-axis through a misaligned angle $\mathsf{\delta }$ (Figure 4b).

4. Tooth Surface Modification

Modifications of a gear tooth, such as crowning, are used to reduce misalignment impacts during the assembly process. Crowning moves the peak load from the edges of the tooth flank and decreases the risk of edge contact pressures that could reduce the survivability of gears. Crowning is a longitudinally oriented modification that can localize the bearing contact. Such properly implemented modifications allow to transform discontinuous linear functions caused by misalignment to a continuous function of the TE of gear drives, decreasing vibration and noise [16,17,21,43,44]. The crowning of the tooth surface can typically be achieved by lightly altering the cutting tool path in relation to the gear frame of reference to remove more material at the edges of the tooth, according to a smooth, continuous function. Conventional choices for this function have been parabolic [30,31] and circular [32] functions, while logarithmic ones were proposed later in [35].

Figure 5 presents the lead crown chart of gear teeth, where it can be seen that the curves of circular and parabolic modifications decrease more from the center of the tooth flank compared to the logarithmical curve. Moreover, the logarithmic function deviates more than the circular and parabolic modifications at the edges of the tooth face. The black line corresponds to an unmodified tooth with a simple edge fillet, shown here only for reference. The function of the circular, parabolic, and logarithmic curves of the modified tooth demonstrated in Figure 5 is presented in Equations (19)–(21), respectively, as follows:.

$$y=R-\sqrt{R^2-x^2},\mathrm{where}R=\frac{4C_c^2+b^2}{8C_c },$$

(19)

$$y=c_1{x}^2+c_{2}x+c_{3,}$$

(20)

$$y=a_{1}Log\left(\frac{1}{1-a_2{\left(\frac{x}{b}\right)}^2}\right),$$

(21)

where, in this representation, the coordinate $y$ is the extent of modification and $x$-axis is the position at the face width. In addition, at the gear tooth center, $b$ is the half-face width length. To apply modifications to the meshing equation, Equations (19)–(21) must be rewritten in terms of the coordinate system of ${\overrightarrow{u}}_i$ and ${\overrightarrow{v}}_i$. The normal longitudinal relief of the parabolic modification ${\delta }_p$ with ${\overrightarrow{u}}_i$ and ${\overrightarrow{v}}_i$ parameters are defined as:

$${\delta }_p=c_1{\left(v-\frac{v_{max}-v_{min}}{2}\right)}^2+c_2\left(v-\frac{v_{max}-v_{min}}{2}\right)+c_3,$$

(22)

In the case when $c_2=c_3=0$, the longitudinal parabola modification curve will be symmetrical. More details of the generation of parabola modification can be found in Litvin’s work [1]. The amount of parabolic crowning, as well as circular crowning, primarily depends on the length of the face width. The magnitude of circular modification ${\delta }_c$ and radius of the curved circular crowning $R$ (with parameters $u_i$ and $v_i$) are determined as follows:

$${\delta }_c=R-\sqrt{R^2-{\left(v-\frac{v_{max}-v_{min}}{2}\right)}^2},\mathrm{where}R=\frac{4C_c^2+{\left(v_{max}-v_{min}\right)}^2}{8C_c^2}$$

(23)

where $C_c$ is the amount of crowning at the middle of the face width. The magnitude of longitudinal relief of the logarithmic modifications ${\delta }_l$ is defined as:

$${\delta }_l=a_{1}Log\left(\frac{1}{1-a_2{\left(\frac{2v-\left(v_{max}-v_{min}\right)}{v_{max}-v_{min}}\right)}^2}\right),$$

(24)

where coefficient $a_1$ represents the degree of crowning curvature and $a_2$ a surface factor that is a function of crown drop. To apply the modification to the surface, one of the crown functions ${\delta }_{c,p,l}$ are added to the vector function ${\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)$ of the parametric surface, and then, they are substituted into the rotation matrix. The change of the profile in the tooth height direction or tip and root relief is another widely used technique that optimizes the contact and transmission pattern of gears. It is mostly used to prevent transmission “contact shocks” that occur when a single-tooth contact converts to a double contact and vice versa. The tip relief function via surface parameterization $\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)$ is illustrated in Equation (25), where the Heaviside function is employed to alter only a portion of the profile.

$${\delta }_t=H\left(u-u_0\right)c_m{\left(\frac{u-u_0}{L}\right)}^2.$$

(25)

$L$ is the relief length, where $u_0$ indicates the beginning and $c_m$ the amount of modification. In the present work, the following constraints are made for the modification: (a) the tooth surface types are smooth and continuous; (b) the amount of relief selected for the lead surface results in a continuous transmission function with the path of contact concentrated around the center of the gear tooth.

5. Loaded Tooth Contact Analysis

Tooth modifications not only alter the kinematics of a gear pair but also the magnitude and the distribution of the contact stresses. Loaded tooth contact analysis is an important tool for contact stress assessment and the design of gears. Therefore, in this work, an analytical approach for stress analysis for misaligned gear drives with localized bearing contact is proposed. By implementing an analytical approach based on the Hertz theory, the area of contact and maximum contact stress is determined for spur and helical gear drives, wherein edge contact is avoided by crowning the tooth surfaces. During the engagement of the crowned gear teeth, the contact pressure is transmitted along a contact elliptical area. This will be affected by the contact geometry and therefore the different modifications. To determine the dimensions of the instantaneous contact ellipse, the principal curvatures of the surfaces of the gear teeth are used [45]. The solution to the elliptical point contact problem is based on the approach developed in [46].

5.1. Calculation of the Principal Curvatures

The principal curvatures measure the maximum and minimum of the normal curvature at a given point on a surface. To measure the maximum and minimum bending of a surface at each point, from Equation (1), the unit normal vector is determined:

$$\widehat{n}=\frac{\overrightarrow{n}}{\left|\overrightarrow{n}\right|},$$

(26)

By using surface parametric equation ${\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right),$ the first fundamental forms of the surface are defined:

$$E=\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial u}·\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial u} F=\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial u}·\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial v} G=\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial v}·\frac{\partial {\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial v}.$$

(27)

Then, through the unit normal vector, the second fundamental form of the surface is described as:

$$L=\widehat{n}·\frac{{\partial }^2{\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial u^2}N=\widehat{n}·\frac{{\partial }^2{\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial v^2}M=\widehat{n}·\frac{{\partial }^2{\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)}{\partial u\partial v}.$$

(28)

The Gaussian curvature of a surface ${\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)$ is an intrinsic property of curvature independent of the coordinate system and given by:

$$K=\frac{LN-M^2}{EG-F^2}.$$

(29)

Mean curvature of a surface ${\overrightarrow{f}}_i\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right)$ is an extrinsic property of curvature. It is the average of the two principal curvatures:

$$H=\frac{EN+GL-2FM}{2\left(EG-F^2\right)}.$$

(30)

At a given surface point $\left({\overrightarrow{u}}_i,{\overrightarrow{v}}_i\right),$ the maximum and minimum principal curvatures of the surface has a solution:

$${\kappa }_{max}=H+\sqrt{H^2-K} {\kappa }_{min}=H-\sqrt{H^2-K},$$

(31)

where the maximum and minimum radii of curvatures can be defined as:

$$R_{max}^{\left(i\right)}=\frac{1}{\left|{\kappa }_{max}\right|} R_{min}^{\left(i\right)}=\frac{1}{\left|{\kappa }_{min}\right|}.$$

(32)

5.2. Line Contact

Line contact occurs when the minimum radii of curvature of both bodies in contact are infinite, such as in the case of two parallel-axis cylindrical bodies in contact. This type of contact produces a rectangular contact area once the bodies are deformed. Line contact occurs during spur and helical gear meshing when the tooth is not crowned, and misalignment errors are not present in the transmission process. Given that the minimum principal curvature equals zero, the composite radii will be as follows:

$$A_o=\frac{1}{2R_x}=\frac{1}{2}\left(\frac{1}{R_{max}^{\left(1\right)}}+\frac{1}{R_{max}^{\left(2\right)}}\right) B_o=\frac{1}{2R_y}=0.$$

(33)

where $R_{max}^{\left(1\right)}$ and $R_{max}^{\left(2\right)}$ are the radii of curvature at the contact points of the two gears in mesh. The Hertzian contact patch $b_o$ under applied normal load $P$ is given by the following equation:

$$b_o=\sqrt{\frac{2C_{E}P }{\pi l{A}_o }}.$$

(34)

In Equation (34), $l$ is the length of the cylinders, $A_o$ is the composite radii, and $C_E$ is the composite modulus of elasticity of the materials:

$$C_E=\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}.$$

(35)

where $E_1$ and $E_2$ are the modulus of elasticity of the pinion, and gear ${\nu }_1$ and ${\nu }_2$ denote Poisson’s ratios of the pinion and gear, respectively. The maximum pressures are given by:

$$p_o=\frac{2P}{\pi b_{o}l}.$$

(36)

5.3. Point Contact

The contacting rigid convex surfaces such as crowned spur or helical gear tooth with involute profiles results in point contact. However, in practical applications, during the transmission process of gear system, as a consequence of elasticity of the gear materials, the mating point forms the contact area with an elliptical shape. To calculate the Hertzian contact pressure, the eccentricity of the contact area should be found. By setting the composite radii as:

$$\frac{1}{R_x}=2A=\frac{1}{R_{max}^{\left(1\right)}}+\frac{1}{R_{max}^{\left(2\right)}} \frac{1}{R_y}=2B=\frac{1}{R_{min}^{\left(1\right)}}+\frac{1}{R_{min}^{\left(2\right)}},$$

(37)

the eccentricity of the contact area is estimated through the expression below:

$$\frac{1}{\left[K\left(e\right)-E\left(e\right)\right]}\left[\frac{E\left[e\right]}{\left(1-e^2\right)}-K\left(e\right)\right]=\frac{B}{A},$$

(38)

where $K\left(e\right)$ and $E\left(e\right)$ are complete elliptic integrals of the first and second kind, respectively:

$$K\left(e\right)={{\displaystyle \int }}_0^{\pi /2}\frac{d\theta }{\sqrt{1-e^2{\sin }^2\theta }} E\left(e\right)={{\displaystyle \int }}_0^{\pi /2}\sqrt{1-e^2{\sin }^2\theta }d\theta .$$

(39)

Once eccentricity (e) is known, the major and minor axes a, b of the contact area can then be determined:

$$a={\left(\frac{3P{C}_E\left[K\left(e\right)-E\left(e\right)\right]}{2\pi e^{2}A}\right)}^{1/3} b=a\sqrt{1-e^2},$$

(40)

Once semi-axes a, b are known, and force P is specified, then the maximum contact pressure can be obtained as:

$$p=\frac{3P}{2\pi ab}.$$

(41)

5.4. Maximum Contact Pressure Ratio

During the stress analysis, values of maximum contact pressure were defined as the ratio between elliptical and cylindrical contact pressure to see how stresses of misaligned crowning teeth during the meshing change compared to unmodified aligned teeth contact. Thus, the maximum pressure ratio ($MPR$) is defined as:

$$MPR=\frac{p}{p_o}.$$

(42)

In the case when the $MPR$ is greater than one, the combined effect of modifications and misalignments increases the maximum pressure compared to the theoretical line contact of gears, as shown in Section 5.2. In contrast, in the case when the $MPR$ is less than one, the theoretical contact of the spur or helical gears produces a higher contact pressure value.

It is noted that instead of the maximum contact pressure, the maximum shear stress could be used to create the non-dimensional metric to assess the effect of modifications and misalignments on the gear tooth flanks. The maximum shear stress is considered mainly responsible for the surface fatigue failure of gear [47,48]. It develops at a point beneath the surface whose depth depends upon the eccentricity of the elliptical contact area, and it is proportional to the maximum contact pressure [49]. For example, in the case of two parallel cylindrical bodies, the maximum shear stress occurs at a depth of 0.78$b_0$, where $b_0$ is the Hertzian contact patch, and with a magnitude of 0.30$p_0$, where $p_0$ is the maximum contact pressure. Without any loss of generality, in the present work, the maximum contact pressure is used to assess the crowning of the tooth surface.

6. Simulation of Meshing

The tooth contact analysis (TCA) implemented in this work is based on the method presented in detail in Section 2 and is used to simulate the gear meshing and study the bearing contact between the crowned tooth surfaces by using the Wolfram Mathematica environment. TCA’s key objectives are to define the path of contact and the TE caused by misalignments of the gear shafts. During the simulation, the geometric parameters of the gear pair are given as well as the orientation and misalignment of the gear shafts. For all simulation cases, the pinion tooth surface was crowned in the longitudinal direction with one of the three types of modifications (parabolic, circular, or logarithmic) and meshed with an involute (not modified) gear tooth surface.

As stated in the introduction, the selection of the type and amount of crowning is critical for gear meshing. For instance, excessive crowning leads to an increase in TE, while insufficient crowning will cause the gear teeth to contact close to the flank edges. Therefore, the amount of crowning should be optimized to give a contact path close to the center of tooth surfaces or at a certain distance from the flank edges with a continuous TE function.

In this work, the three different types of crowning were designed to meet these requirements in case of various in- or out-of-plane misalignments. The parameters of each type of modification applied to the lead tooth flank (Figure 5) are selected so as to obtain a continuous TE function. This can prevent shock loads and rattling and diminish noise and vibrations. The function of TE is defined as the actual rotation angle of the output gear minus the theoretical rotation angle. The TE vary from zero due to surface mismatch or misalignment and can be calculated using the equation below:

$$∆\phi =\left({\phi }_2-{\phi }_{20}\right)-\frac{N_1}{N_2}\left({\phi }_1-{\phi }_{10}\right),$$

(43)

where ${\phi }_{10}$ and ${\phi }_{20}$ are the rotational angles of the pinion and the gear when tooth surfaces are in contact at an initial contact point. Here, ${\phi }_2$ is the gear rotational angle corresponding to the pinion rotational angle ${\phi }_1,$ which is an independent variable. The function $∆\phi$ is a periodic function with the period $T=2\pi /N_1$. $∆\phi$ has different shapes depending on conditions such as the angle of misalignment or applied crowning. Figure 6 displays the undesirable result $∆\phi$ caused by gear misalignment without applying any modification.

In the case where meshing gears without crowning are misaligned, their axes are crossed or intersected. In that case, the edge of the pinion tooth surface will be in tangency with the gear tooth surface, which will lead to the path of contact located at the edge of the tooth flank as in Figure 7, accompanied by the discontinuous function of TE. In this circumstance, gear transmission at the end of the meshing cycle is inevitably accompanied by a jump in the angular velocity, vibration, and noise.

6.1. Simulation of Spur Gears Meshing

The meshing simulation of a crowned involute spur gear pair is accomplished by solving the new type of fundamental three-dimensional tooth surface contact equations with two unknown parameters (${\overrightarrow{u}}_i$ and ${\overrightarrow{v}}_i$) presented in Section 2. Modelling was carried out for two types of angular misalignment—yaw (in-plane) and pitch (out-of-plane)—with different degrees of misalignment. The level of misalignment selected was based on the literature [1,50,51]. For each degree of misalignment, all three types of modification were applied in order to observe how each crowning would affect the TE function and the path of contact. Moreover, for every modification, a range of parameters that met the established criteria was determined, i.e., the continuous function of the TE and the contact path closest to the tooth surface center. To evaluate the results of each modification, the maximum amplitude $∆{\phi }_{max}$ and area $S_{c,p,l}$ of the TE functions were determined.

Table 1. Simulation parameters of spur gear pair.

Parameters	Pinion	Gears
Number of teeth	25	50
Module, mm	2.5
Pressure angle, degree	20
Face width, mm	25
Center distance, mm	60
Poisson’s ratio	0.3
Modulus of elasticity, GPa	206
Total load, N	150

shows the pinion and gear parameters that were used for the simulation. During the simulation, the rotating axes of the pinion and gear are parallel $({\overrightarrow{w}}_1||{\overrightarrow{w}}_2)$ and directed along the z-axis. In addition, it should be noted that during the simulation, crowning was applied only for the involute pinion, while the involute gear remained unmodified.

6.2. Spur Gear Pair with In-Plane Misalignment

In the case of in-plane misalignment, the deviation of the spur gear system is oriented along the y-axis (Figure 4a). As mentioned earlier, for each type of modification, the ranges of their main parameters, such as $C_c$, $c_1,$ and $a_1$, were defined, where $C_c$ is the amount of the circular crown in the middle of the face width, $c_1$ is the parabolic coefficient, and $a_1$ is the logarithmic coefficient. As shown in Equation (20), the parabolic function has other two coefficients, namely $c_2$ and $c_3$, but in the simulation, they were assumed to be zero since only the longitudinal parabolic modification that produces a symmetric curve was considered. Similarly, the logarithmic function Equation (21) has a second parameter, $a_2$, which is a surface factor that can have any value between zero and one ($0<a_2<1$), and it was chosen arbitrarily equal to 0.9.

For the analysis, different levels of crowning modification were applied to the gear to obtain the continuous TE function presented in Figure 8. It can be seen from the figure that an insufficient amount of crowning will lead to a discontinuous TE, and therefore, the amount of crowning should be optimized to give a contact path close to the center of tooth surfaces or at a certain distance from the flank edges to obtain a continuous TE function.

The results of the modification parameter values for all three types of crowing and different in-plane misalignment angles (0.01–0.4° or 0.17–7.0 mrad) that led to a continuous TE function is illustrated in

Table 2. Amount of modifications for different values of in-plane angular misalignment error during crowned spur gear meshing.

Angular Misalignment γ (deg)	Circular		Parabolic		Logarithmic
	${\mathit{C}}_{\mathit{c}}\left(\mathbf{mm}\right)$	$\mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{arcsec}\right)$	${\mathit{c}}_1$$\left(\mathbf{m}{\mathbf{m}}^{-1}\right)$	$$\begin{gathered} \mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$	${\mathit{a}}_1\left(\mathbf{mm}\right)$	$$\begin{gathered} \mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$
0.01°	1.00	−5.14156 10−6	0.0064	−5.13592 10−6	1.12	−5.12879 10−6
	1.03	−5.09568 10−6	0.0065	−5.11921 10−6	1.15	−5.05933 10−6
	1.07	−4.97422 10−6	0.0067	−5.02934 10−6	1.18	−4.97633 10−6
0.02°	1.00	−0.0000205679	0.0064	−0.0000205492	1.12	−0.000020519
	1.03	−0.0000204006	0.0065	−0.0000204674	1.15	−0.0000202502
	1.07	−0.0000199045	0.0067	−0.000020125	1.18	−0.0000199083
0.05°	1.00	−0.000128657	0.0064	−0.000128509	1.12	−0.000128355
	1.03	−0.000127628	0.0065	−0.000128061	1.15	−0.000126683
	1.07	−0.000124548	0.0067	−0.000125927	1.18	−0.000124563
0.1°	1.00	−0.000515344	0.0064	−0.000514651	1.12	−0.000514132
	1.03	−0.000511405	0.0065	−0.000513035	1.15	−0.000507639
	1.07	−0.000499124	0.0067	−0.000504661	1.18	−0.000499199
0.2°	1.00	−0.00206682	0.0064	−0.002064	1.12	−0.00206199
	1.03	−0.00205254	0.0065	−0.00205838	1.15	−0.00203845
	1.07	−0.00200505	0.0067	−0.00202598	1.18	−0.00200524
0.4°	1.00	−0.00830788	0.0064	−0.00830127	1.12	−0.00828852
	1.03	−0.00826259	0.0065	−0.00828041	1.15	−0.00821333
	1.07	−0.00808609	0.0067	−0.00815994	1.18	−0.00808494

. Moreover, the impact of the modification and misalignment on the maximum TE ($∆{\phi }_{max}$) is given. Based on the findings, for the misalignment angle between 0.01° and 0.4°, the modification parameter values that led to continuous TE function remained the same. In addition, the increase in the misalignment angle also increased the $∆{\phi }_{max}$, with the logarithmic modification having the least amount of TE. It is noted that although in practice, the magnitude of angular misalignment errors can rarely exceed a few hundreds of a degree (or equivalently a few tenths of a mrad), larger misalignment errors are also investigated in order to showcase the robustness and the effectiveness of the presented TCA model even in extreme cases of misalignment.

Since the difference between $∆{\phi }_{max}$ is very small for all misalignment angles and modification values, the difference is assessed through the integration of $∆\phi$ to find the area of each TE function as follows:

$$S_{c,p,l}={{\displaystyle \int }}_{{\phi }_{1i}}^{{\phi }_{1f}}∆\phi \partial {\phi }_1$$

(44)

where ${\phi }_{1i}$ and ${\phi }_{1f}$ are the angle of inclination of the pinion at the first and last point of engagement, and $S_{c,p,l}$ is the area of circular, parabolic, and logarithmic functions.

To showcase the different effects of each modification, the TE function ($∆\phi$) for a misalignment error of 0.4° (7.0 mrad) and for every modification is presented in Figure 9. In this way, the $S_{c,p,l}$ can be determined and is listed as follows:

$$S_c=-0.001595; S_p=-0.001611; S_l=-0.001575.$$

It can be seen that in this case, the integral of the logarithmic functions is smaller than the rest, and more specifically, less than the parabolic by 2.23% and about 1.25% smaller than the circular function.

Further, Figure 10 displays the comparison of the contact paths of all three modifications, which shows that for every type of modification, the point of contact is close to the center of the tooth surface. However, upon more precise examination, the contact path for a logarithmic function is located closer to the center of the tooth surfaces compared to others. For instance, along the tooth width, contact at the pitch point produced by the logarithmic function is closer to the center than the parabola by about 0.027 mm and to the circular function by approximately 0.015 mm. Simulations for other misalignment angles also show that different modifications almost equally affect the path of contact on the tooth surface, demonstrating similar results to each other but with marginally lower $∆\phi$ for the logarithmic function.

6.3. Simulation of Spur Gears Meshing with Out-of-Plane Misalignment

The misalignment angle and plane in the case of out-of-plane misalignment are shown in Figure 4b.

Table 3. Amount of modifications relative to out-of-plane angular misalignment for spur gears engagement.

$\mathbf{Angular}\mathbf{Misalignment}\mathit{\delta }$	Circular		Parabolic		Logarithmic
	${\mathit{C}}_{\mathit{c}}\left(\mathbf{mm}\right)$	$\mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{arcsec}\right)$	${\mathit{c}}_1$$\left(\mathbf{m}{\mathbf{m}}^{-1}\right)$	$$\begin{gathered} \mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$	${\mathit{a}}_1\left(\mathbf{mm}\right)$	$$\begin{gathered} \mathbf{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$
0.01°	1.00	−0.0000387913	0.0064	−0.0000392627	1.12	−0.0000404888
	1.03	−0.0000384708	0.0065	−0.0000416395	1.15	−0.0000378764
	1.07	−0.0000375354	0.0067	−0.000035942	1.18	−0.0000378489
0.02°	1.00	−0.000155166	0.0064	−0.000157006	1.12	−0.000161922
	1.03	−0.000153867	0.0065	−0.000166514	1.15	−0.000151557
	1.07	−0.000150135	0.0067	−0.000143725	1.18	−0.000151342
0.05°	1.00	−0.000969643	0.0064	−0.000980139	1.12	−0.00101093
	1.03	−0.000961633	0.0065	−0.00103955	1.15	−0.000948166
	1.07	−0.000938331	0.0067	−0.00089732	1.18	−0.000944981
0.1°	1.00	−0.00387772	0.0064	−0.00387332	1.12	−0.00386826
	1.03	−0.00384624	0.0065	−0.00385937	1.15	−0.00381755
	1.07	−0.00375321	0.0067	−0.00379493	1.18	−0.00375325
0.2°	1.00	−0.0155037	0.0064	−0.0154842	1.12	−0.015463
	1.03	−0.0153821	0.0065	−0.0154327	1.15	−0.0152617
	1.07	−0.0150117	0.0067	−0.0151784	1.18	−0.0150064
0.4°	1.00	−0.0619511	0.0064	−0.0618589	1.12	−0.061744
	1.03	−0.0615003	0.0065	−0.0616872	1.15	−0.0609428
	1.07	−0.0600497	0.0067	−0.0606985	1.18	−0.0599263

shows the values of the maximum amplitude of TE functions ($∆{\phi }_{max})$ and the modification parameters of the three crown types at an angular pitch misalignment of 0.01–0.4°. Similar to Section 6.2, in the case of out-of-plane misalignment, the range of the modification required for all three crowning types to obtain a continuous TE function remains the same for any level of misalignment between 0.01° and 0.4°. As for the results of the $∆{\phi }_{max}$, it can be observed that the logarithmic modification gives the smallest value of the $∆{\phi }_{max}$, followed by a circular and then a parabolic one. However, the difference in $∆{\phi }_{max}$ between all crowning is not significant.

In order to compare the different crowning functions, the area of the TE function for each crowing case for 0.4° misalignment was evaluated. Figure 11 displays the TE function of each crowning type for 0.4° out-of-plane misalignment. By calculating $S_{c,p,l}$ using Equation (44), the following results were obtained:

$$S_c=-0.01180; S_p=-0.01192; S_l=-0.01161$$

In this case, the area of the TE function with logarithmic modification is smaller than the parabolic by about 2.58% and than the circular by almost 1.59%, similar to in-plane misalignment.

In Figure 12, the same trend was observed as in the case of in-plane misalignment. The path of contact for the logarithmic function is slightly better than the others. Along the tooth width, the logarithmic function is closer to the center than the parabola by 0.0082 mm and the circular function by 0.048 mm.

The three-dimensional simulations of circular and logarithmic modifications are illustrated in Figure 13. All the surfaces in the middle have the same surface curvature; however, compared to other modifications, the curvature of the logarithmic crowning has a rapid change at the edges, which helps to avoid edge contact even for extreme misalignment errors.

Using the Hertz contact equations for the elliptical contact point described in Section 5, the MPR at various out-of-plane misalignment angles were calculated. Figure 14 presents the MPR for the three types of modification with varying misalignment of spur gears. At 0.01° (0.17 mrad) of out-of-plane misalignment, the parabolic crowning has the lowest MPR ($MPR=11.7864$), whereas the circular and logarithmic crowning has a slightly larger $MPR$, $11.8041$ and $11.8253$, respectively. The maximum pressure ratio remains relatively constant for small misalignments up to 0.1° (1.7 mrad), but then, the logarithmic modification $MPR$ start to increase, while the two traditional lead modifications decrease. At 0.4° (7.0 mrad) of misalignments, the $MPR$ for the parabolic crowning is $11.7779$, the circular one is $11.7959$, and for the logarithmic one is $11.8292$. These results indicate that with a larger angle of out-of-plane deviation, the contact area (or contact ellipse) becomes larger for the two conventional lead surfaces and smaller for the logarithmic modification. It is noted that despite the small differences, the values of MPR are very close for the different crowning functions. The selection of the range of the modification parameters for each crowning function aimed to accomplish that in order to be able to draw meaningful conclusions from the comparison of the different MPR values.

In Figure 15, the contact path and the contact ellipses for a spur gear with a circular crowning and an out-of-plane misalignment of 0.01° (0.17 mrad) are presented as a representative example. It can be seen that the $MPR$ in the lower part of the gear tooth is greater than in the upper part but reaches its peak around the center of the surface. Additionally, with each point of the contact path starting from the top, the MPR increases to a peak before it begins to decrease until the lowest point.

Figure 16 is similar to Figure 15, with the only difference being that, in the first one, we applied a profile modification by using Equation (25). It can be seen that the general path trace remains unchanged until it reaches the region of the tip relief, where contact shifts with a sharp increase in pressure. In this example, the relief length is $L=1\mathrm{mm}$ with $c_m=0.2\mathrm{mm}$ of modification amount.

6.4. Simulation of Helical Gears Meshing

The practice of design and the test of TE and bearing contact shows the necessity of modification of involute helical gears, particularly in presence of angular misalignment [13]. This is due to the involute gearing being sensitive to assembly errors, such as the change of the shaft angle. The traditional design of involute helical gear provides instantaneous contact of tooth surfaces along a line. However, due to angular misalignment, the contact line might transform to point contact at the edge of the tooth flank, which causes discontinuous linear functions of TE, noise, and vibration. The angular misalignment angles that are selected for the study are based on and consistent with the literature [1,52,53].

6.5. Helical Gear Pair with In-Plane Misalignment

As with the spur gear model, the TCA of misaligned helical gears was simulated by using a novel type of fundamental three-dimensional tooth surface contact equations presented in this work. To assess the effect of each type of crowning, the TE function, the path of contact, and the area $S_{c,p,l}$ of the TE functions were determined. A range of parameters was also set to meet certain criteria, just as was the case for the spur gears examined in the previous sections.

Table 4. Simulation parameters of helical gears.

Parameters	Gear	Pinion
Number of teeth	40	37
Module, mm	1
Pressure angle, degree	20
Helix angle, degree	14
Face width, mm	20
Center distance, mm	39.67
Poisson’s ratio	0.3
Modulus of elasticity, GPa	206
Total load, N	200

displays the simulation parameters of the helical gears. The axes of rotation of the pinion and gear were parallel during the simulation, and the modification was used only for the involute pinion, while the involute gear remained unchanged.

For the helical gear pair with parameters shown in Table 4, an evaluation on the level of crowning required to obtain a continuous TE function for all three crowning types is conducted and presented in Figure 17. Again, it can be observed that an insufficient amount of crowning will lead to a discontinuous TE function and hence should be optimized to obtain a contact path close to the center of tooth surfaces that results in a continuous TE function.

The findings that led to a continuous TE function for the modification parameter for all three types of crowning are listed in

Table 5. Amount of modifications for different in-plane angular misalignment errors for helical gears meshing.

Angular Misalignment γ (deg)	Circular		Parabolic		Logarithmic
	${\mathit{C}}_{\mathit{c}}\left(\mathbf{mm}\right)$	$\mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{arcsec}\right)$	${\mathit{c}}_1$$\left(\mathbf{m}{\mathbf{m}}^{-1}\right)$	$$\begin{gathered} \mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$	${\mathit{a}}_1\left(\mathbf{mm}\right)$	$$\begin{gathered} \mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$
−0.05°	2.398	−$0.15843$	0.0227	−0.158389	2.515	−0.158352
	2.400	−0.15384	0.0233	−0.159286	2.600	−0.158858
	2.565	−0.153797	0.0240	−0.154701	2.669	−0.153776
−0.1°	1.104	−0.31696	0.0110	−0.316706	1.201	−0.316326
	1.150	−0.316498	0.0113	−0.317616	1.236	−0.31794
	1.173	−0.316498	0.0115	−0.31153	1.275	−0.30746
−0.2°	0.507	−0.633315	0.0051	−0.635564	0.537	−0.628879
	0.520	−0.637441	0.0052	−0.636932	0.553	−0.632365
	0.535	−0.618792	0.0053	−0.625768	0.572	−0.611297

. It can be seen that the level of crowning required for continuous TE function decreases with an increased level of misalignment. Furthermore, for every modification, the maximum TE ($∆{\phi }_{max}$) is obtained. By comparing the values of the $∆{\phi }_{max}$ for every modification and misalignment angle, the logarithmic modification gives the smallest value, followed by the circular and then a parabolic one.

As with the model of the spur gear with the in-plane misalignment, the helical gear with in-plane misalignment shows small differences between the TE function of different modifications (Figure 18). To determine the exact difference, the area $S_{c,p,l}$ of the TE functions was calculated and resulted in the following:

$$S_c=-0.220082; S_p=-0.223297; S_l=-0.218083$$

From the calculations, it can be seen that the logarithmic modification gives better results than the others. The logarithmic modification TE function area is 2.33% and 0.9% smaller than the parabolic and circular modification, respectively.

The path of contact for different misalignment angles is shown in Figure 19. It is found that with the increase of misalignment angle, the contact path for all three modifications moves further away from the center. Additionally, a similar contact path is obtained for all three types of crowning. However, a detailed examination of the data showed that the circular crown at 0.1° (1.7 mrad) and 0.2° (3.5 mrad) of misalignment angle is closer to the center compared to the other two, whereas the logarithmic modification performs better for the smaller misalignment angle of 0.05° (0.87 mrad).

6.6. Helical Gear Pair with Out-of-Plane Misalignment

In this section, an examination of the deviation of the helical gear system in the case of out-of-plane misalignment oriented along the x-axis is conducted (Figure 4b).

Table 6. Amount of modifications relative to out-of-plane angular misalignment for helical gears engagement.

Angular Misalignment $\mathit{\delta }$	Circular		Parabolic		Logarithmic
	${\mathit{C}}_{\mathit{c}}\left(\mathbf{mm}\right)$	$\mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{arcsec}\right)$	${\mathit{c}}_1$$\left(\mathbf{m}{\mathbf{m}}^{-1}\right)$	$\mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}}\left(\mathbf{arcsec}\right)$	${\mathit{a}}_1\left(\mathbf{mm}\right)$	$$\begin{gathered} \mathit{∆}{\mathit{\phi }}_{\mathit{m}\mathit{a}\mathit{x}} \\ \left(\mathbf{arcsec}\right) \end{gathered}$$
0.05°	0.804	−$0.4225422$	0.00799	−0.42257	0.873	−0.42094
	0.830	−$0.424252$	0.00820	−0.424946	0.900	−0.423014
	0.853	−$0.410921$	0.00847	−0.410987	0.927	−0.409179
0.1°	0.360	−$0.845263$	0.00359	−0.845918	0.368	−0.831488
	0.370	−$0.850059$	0.00370	−0.849776	0.380	−0.836597
	0.381	−$0.823004$	0.00380	−0.825234	0.393	−0.809249
0.2°	0.143	−$1.69059$	0.00143	−1.69062	0.046	−1.4328
	0.146	−$1.70474$	0.00146	−1.7048	0.055	−1.49707
	0.150	−$1.66515$	0.00150	−1.66508	0.081	−1.48844

demonstrates the results required for each modification parameter ($C_c$, $c_1$, and $a_1$) of all three crown types for misalignment angles of 0.05–0.2° (0.87–3.5 mrad) to obtain continuous TE function. Moreover, $∆{\phi }_{max}$ was also obtained for every misalignment angle and crown type. It is observed that the amount of modification for all three crown types decreases with increasing misalignment. As for $∆{\phi }_{max}$, it is seen that the logarithmic modification gives the smallest value, followed by the circular and then the parabolic.

To obtain a better understanding of the difference between modifications, the area $S_{c,p,l}$ is obtained for all crown types for 0.2° (3.5 mrad) misalignment based on its TE function (Figure 20) and is calculated as:

$$S_c=-0.645048; S_p=-0.642903; S_l=-0.509613$$

It can be seen that the logarithmic function gives almost 21% less area compared to the circular and parabolic functions. This makes the logarithmic modification significantly better than the other two crowning types.

The contact path for every crown type and misalignment (0.05–0.2°) is illustrated in Figure 21. It is seen that with increasing out-of-plane misalignment angles, the point of contact moves further away from the center. The contact path obtained is similar for $0.05°$ and $0.1°$ misalignment. However, at $0.2°$ misalignment, the difference is more apparent since the contact path for the logarithmic crowning is furthest from the center compared to the other two crownings.

By comparing Figure 19 and Figure 21 with Figure 10 and Figure 12, it can be seen that the shift of the contact path from the center of the tooth surface is larger for the case of the helical gears. While for spur gears, there is a shift in the order of 0.3 mm and 1.0 mm for the in-plane and out-of-plane misalignment errors of 0.4°, respectively, for helical gears, the respective values are 1.3 mm for in-plane misalignment and 5.0–6.5 mm (depending on the crown type) for out-of-plane misalignment even though the misalignment angle is only 0.2°. Consequently, a significant finding from the comparison of the simulations of spur and helical gear meshing is that in the presence of misalignments, the shift of the contact path from the center of the tooth is significantly larger for helical gears in comparison with spur gears.

The three-dimensional mesh contact of helical gears in the case of circular and logarithmic modifications is presented in Figure 22. The parabolic crown is not illustrated as its surface is nearly identical to the circular crown. Looking at the figure, in the case of extreme misalignment between the two gear teeth, the surface with circular crowning will experience edge contact. In the logarithmic crowning case, for the same scenario, a much more extreme angle of misalignment is needed.

The maximum contact pressure ratio of two helical gear pairs at different angles of out-of-plane misalignment was determined using the Hertz contact equations for an elliptical contact point. Figure 23 shows the $MPR$ for all three types of modifications depending on the misalignment. Initially, at 0.01° (0.17 mrad) of out-of-plane misalignment, the logarithmic curve has the highest maximum contact pressure ($MPR=15.1803$), whereas the circular and parabolic curve has a lower pressure value (MPR of $15.0962$ and $15.1661$, respectively). Unlike the case of spur gears, where the lower MPR value was developed for the parabolic crowning at every misalignment angle, in the case of helical gears, the lower MPR value occurs for a different type of crowning for each case of misalignment. At 0.02° (0.35 mrad), the logarithmic crowning shows the lower MPR value (12.4127), while the circular crowning gives the highest MPR value (12.6628). Then, at 0.05° (0.87 mrad), the lowest value has the parabolic modification (MPR = 10.0767), while the highest value is found for the logarithmic modification (MPR = 10.1105). At 0.1° (1.7 mrad) of misalignment, the circular crown has the lowest value, and at 0.2° (3.5 mrad), the parabolic crown again has the lowest value. The values of MPR for different modifications at the misalignment angles among 0.01–0.1° were close to each other, but at 0.2° misalignment, the logarithmic crown was distinguished by a significantly higher MPR compared to the other two traditional crowns. All these differences are mainly related to the peculiarities of the curvature of the tooth, which is more noticeable in the helical gear.

Figure 24 shows an example of the contact path for the circular curve at an out-of-plane misalignment of 0.2° with contact ellipses. $MPR$ in the upper part of the gear tooth surface is greater than in the lower part, gradually decreasing along the path of contact. For other crowning, the pressure contact behavior is the same.

Figure 25 demonstrates the contact path in the case of out-of-plane misalignment with the minimum amount of longitudinal circular crowning and tip relief. It is clear that the overall path trace stays the same up until it reaches the tip relief, where contact switches with a significant rise in pressure and decrease in the contact ellipse. The relief length in this case is $L=0.2\mathrm{mm}$, and the modification amount is $c_m$= 0.2 mm.

7. Conclusions

In this study, a novel form of fundamental tooth contact equations for non-conjugate analysis is derived for a pair of gear teeth modelled as $C^1$ continuous rotating parametric surfaces. The proposed model reduces the contact model to two equations with two unknowns and one independent parameter, thus giving more explicit, stable, and precise numerical solutions without convergence issues compared to conventional Litvin’s model [1], which consists of five typically nonlinear equations with five unknowns and one independent parameter. The developed model was applied to crowned spur and helical gears to assess parametrically their sensitivity to different in- and out-of-plane angular misalignment angles in terms of the path of contact, TE, and maximum contact pressure. For this purpose, three types of modification functions were applied, including the conventional parabolic crown, the conventional circular crown, and the less-common logarithmic crown.

Modification functions were applied in the longitudinal direction and expressed mathematically in terms of the tooth surface planar coordinates (${\overrightarrow{u}}_{\mathrm{i}},{\overrightarrow{v}}_{\mathrm{i}}$) of spur and helical gears. Metrics were defined in terms of the TE function and the contact pressure to facilitate a comparison of the performance of each crown design. In terms of these metrics, optimal designs are identified. Key conclusions are summarized as follows:

(1)

The simulation showed the increase of TE and the deviation of the contact path from the tooth surface center is more pronounced in the out-of-plane misalignment compared to the in-plane.

(2)

In the case of spur gears, the logarithmic crowning modification produced a smaller negative effect on the TE function than the traditional types of crowning for both in-plane and out-of-plane misalignment although for the contact path, the improvement is not too substantial. In addition, the differences in results between the modifications are smaller in the in-plane misalignment, as demonstrated in Figure 9 and Figure 10 and Table 2. For the out-of-plane misalignment, the differences are slightly larger (Figure 11, Table 3).

(3)

The simulations of the helical gear system show that the circular crowning modification function produces a smaller shift of the path of contact in the case of in-plane misalignment, keeping it closer to the center in comparison with the other modifications (Figure 19), but the differences are not too weighty. In the case of out-of-plane misalignment, parabolic crowning shows better results for the contact path (Figure 21). This is especially noticeable for the large out-of-plane misalignment of $0.2°$ (3.5 mrad), where the contact path of the logarithmic function is shifted closer to the edge than for the case of the parabolic or circular one. Still, for small misalignment angles, the differences in the path of contact are not so significant. However, for the TE, the logarithmic crowning in all cases gives smaller values (Table 5 and Table 6). The integration of TE functions for the large misalignment angle of $0.2°$ (3.5 mrad) illustrates that the difference between the conventional modifications and the logarithmic ones is almost 21% (Figure 20).

(4)

The shift of the contact path from the center of the tooth during gear meshing in the presence of angular misalignments is almost an order of magnitude larger for the case of helical gears in comparison to spur gears.

(5)

The logarithmic modification is able to deal with extreme misalignments thanks to its increased curvature at the edges. In the case of circular and parabolic crowning, tooth surface contact under extreme misalignment will present a singularity at the tooth edge. However, around the middle of the tooth, longitudinally, all three crownings have similar surface curvatures and thus have similar effects for small values of misalignment. Moreover, logarithmic modification at a low misalignment angle gives lower pressures, but it starts to produce much higher pressure beyond a certain offset, around 0.1$°$ (0.17 mrad) in the cases considered, due to the rapidly increasing curvature.

(6)

The use of the tip relief in the current modelling process led to a change in the contact trajectory with a sharp increase in pressure and a decrease in the contact ellipse (Figure 16 and Figure 25).

(7)

Comparing the maximum contact pressure of the tooth with different crowning, it can be concluded that for spur gears, the logarithmic crown provides greater contact pressure, while it reduces with parabolic modification. For the helical gear, in most cases, logarithmic crowning shows higher pressure.

The optima reported by this study are obviously dependent on the metrics used, and it is not this work’s purpose to recommend one particular modification over another. Instead, it provides an easy-to-use and computationally robust method to allow gear designers to perform their own studies and explore the design space. Nevertheless, the study does evidence that even though the widely studied parabolic modification (e.g., as studied by Litvin et al. [12,13,14,15,16,17]) is, in many cases, the best type of crowning modification, other known types of modification can produce better results depending on the scenario and performance metrics, and yet, more possible modification functions may be explored. The method presented in this work serves as a framework for the further investigation of the effects of the different modifications on gear transmissions.