Investigation into the Modulation Characteristics of Motor Current Signals in a Belt Transmission System for Machining Monitoring
Abstract
:1. Introduction
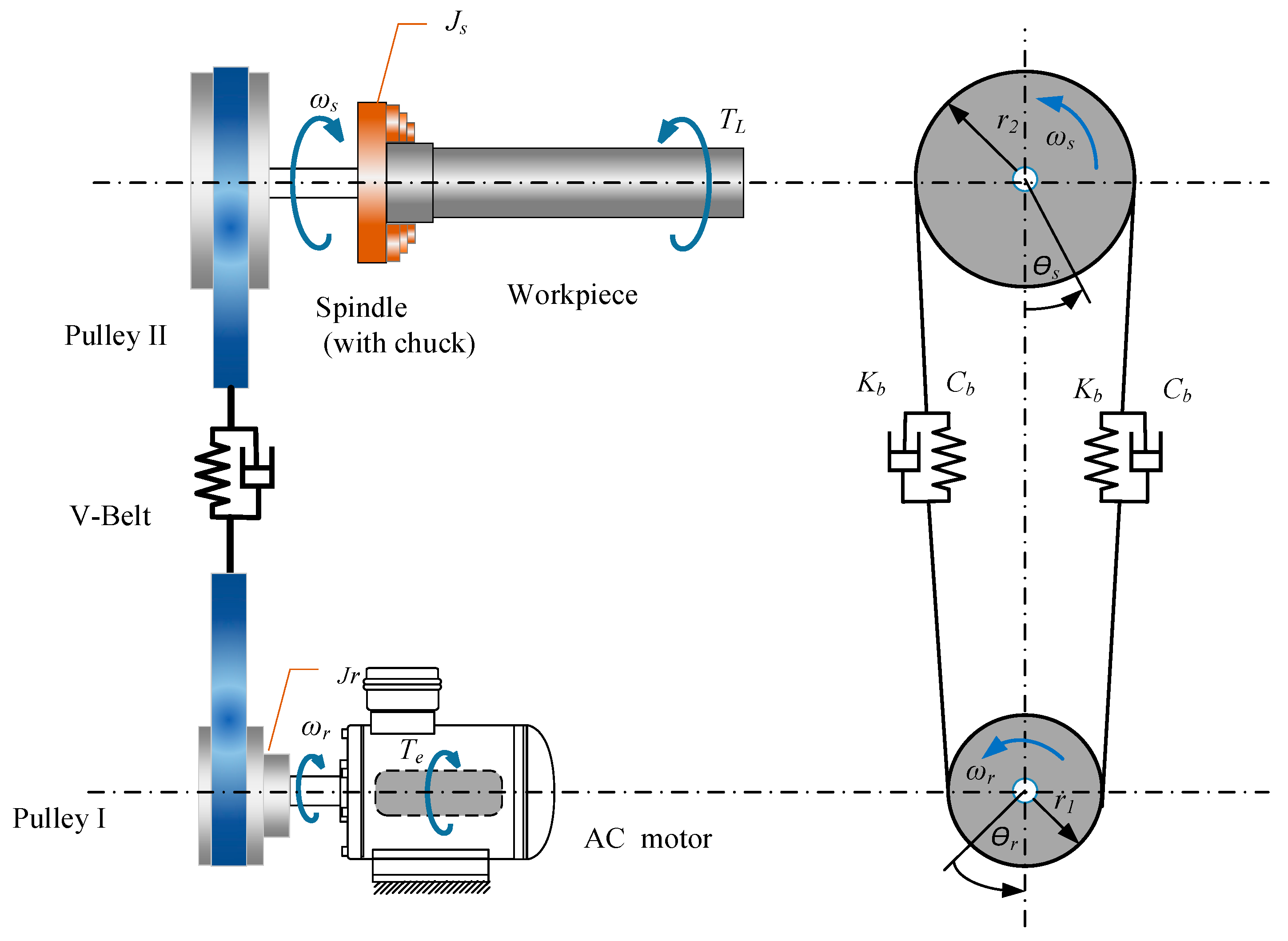
2. Dynamic Model of Belt-Driven Electromechanical Spindle System
2.1. System Modelling
2.2. Model of Belt Transmission
2.3. Galerkin Truncation Solutions
2.4. Numerical Solution Procedure
3. Numerical Analysis and Experimental Verification
3.1. Sideband Features
3.2. Modulation Due to Belt Defects
3.3. Influence of Belt Resonance
3.4. Modulation Due to Improper Tension
3.5. Experimental Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, W.T.; Derani, M.N.; Ratnam, M.M. Effect of Vibration on Surface Roughness in Finish Turning: Simulation Study. Int. J. Simul. Model. 2020, 19, 595–606. [Google Scholar] [CrossRef]
- Kishawy, H.A.; Hegab, H.; Umer, U.; Mohany, A. Application of Acoustic Emissions in Machining Processes: Analysis and Critical Review. Int. J. Adv. Manuf. Technol. 2018, 98, 1391–1407. [Google Scholar] [CrossRef]
- Hidayah, M.T.; Ghani, J.A.; Nuawi, M.Z.; Haron, C.H.C. A Review of Utilisation of Cutting Force Analysis in Cutting Tool Condition Monitoring. Int. J. Eng. Technol. 2015, 15, 150203–154848. [Google Scholar]
- Valtierra-Rodriguez, M.; Rivera-Guillen, J.R.; Basurto-Hurtado, J.A.; Jesus De-Santiago-Perez, J.; Granados-Lieberman, D.; Amezquita-Sanchez, J.P. Convolutional Neural Network and Motor Current Signature Analysis during the Transient State for Detection of Broken Rotor Bars in Induction Motors. Sensors 2020, 20, 3721. [Google Scholar] [CrossRef]
- Wong, S.Y.; Chuah, J.H.; Yap, H.J. Technical Data-Driven Tool Condition Monitoring Challenges for CNC Milling: A Review. Int. J. Adv. Manuf. Technol. 2020, 107, 4837–4857. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, B.; Zhu, L. Sequential Spindle Current-Based Tool Condition Monitoring with Support Vector Classifier for Milling Process. Int. J. Adv. Manuf. Technol. 2017, 92, 3319–3328. [Google Scholar] [CrossRef]
- Aghazadeh, F.; Tahan, A.; Thomas, M. Tool Condition Monitoring Using Spectral Subtraction and Convolutional Neural Networks in Milling Process. Int. J. Adv. Manuf. Technol. 2018, 98, 3217–3227. [Google Scholar] [CrossRef]
- Hopkins, C.; Hosseini, A. A Review of Developments in the Fields of the Design of Smart Cutting Tools, Wear Monitoring, and Sensor Innovation. IFAC-PapersOnLine 2019, 52, 352–357. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, L.; Yang, Z.; Bo, J.; Zhang, Y.; Khajavi, M.N.; Nasernia, E.; Rostaghi, M. Milling Tool Wear Diagnosis by Feed Motor Current Signal Using an Artificial Neural Network. J. Mech. Sci. Technol. 2016, 30, 2697–2709. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Sağlam, H. Investigation of Signal Behaviors for Sensor Fusion with Tool Condition Monitoring System in Turning. Meas. J. Int. Meas. Confed. 2021, 173, 108582. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Papacharalampopoulos, A.; Vasiliadis, E.; Chryssolouris, G. Tool Wear Predictability Estimation in Milling Based on Multi-Sensorial Data. Int. J. Adv. Manuf. Technol. 2016, 82, 509–521. [Google Scholar] [CrossRef]
- Zou, Z.; Huang, S.; Zou, X.; Lin, Y.; Gou, F.; Ball, A.D. Current Analysis Using a Modulation Signal Bispectrum for Machining Status Monitoring. In Mechanisms and Machine Science; Springer: Berlin/Heidelberg, Germany, 2021; Volume 105, pp. 254–264. [Google Scholar] [CrossRef]
- Hroncová, D.; Sivák, P.; Filas, J.; Kicko, M. Dynamic Analysis of Lathe Machine Tool. Am. J. Mech. Eng. 2016, 4, 280–288. [Google Scholar] [CrossRef]
- Bonci, A.; Longhi, S.; Nabissi, G. Fault Diagnosis in a Belt-Drive System under Non-Stationary Conditions. An Industrial Case Study. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; 2021; pp. 260–265. [Google Scholar] [CrossRef]
- Chowdhury, S.; Yedavalli, R.K. Dynamics of Belt-Pulley-Shaft Systems. Mech. Mach. Theory 2016, 98, 199–215. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, W.D.; Fan, W. Dynamic Modeling, Simulation and Experiment of Power Transmission Belt Drives: A Systematic Review. J. Sound Vib. 2021, 491, 115759. [Google Scholar] [CrossRef]
- Li, B.; Lu, R.; Yang, D. Analysis and Simulation of Transverse Vibration of Machine Tool Belt Drives. Coal Min. Mach. 2010, 31, 91–93. [Google Scholar] [CrossRef]
- Incerti, G. A Model for Analyzing the Startup Dynamics of a Belt Transmission Driven by a DC Motor. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2014, 8, 1537–1542. [Google Scholar]
- Kang, T.J.; Yang, C.; Park, Y.; Hyun, D.; Lee, S.B.; Teska, M. Electrical Monitoring of Mechanical Defects in Induction Motor-Driven V-Belt-Pulley Speed Reduction Couplings. In IEEE Transactions on Industry Applications; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; Volume 54, pp. 2255–2264. [Google Scholar] [CrossRef]
- Leamy, M. Dynamics Analysis of the Time-Varying Operation of Belt-Drives. In Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 5: 19th Biennial Conference on Mechanical Vibration and Noise, Parts A, B, and C, Chicago, IL, USA, 2–6 September 2003; pp. 399–408. [Google Scholar] [CrossRef]
- Frendo, F.; Bucchi, F. Enhanced Brush Model for the Mechanics of Power Transmission in Flat Belt Drives under Steady–State Conditions: Effect of Belt Elasticity. Mech. Mach. Theory 2020, 153, 103998. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Z.; Chen, L.Q. Vibration Reduction Effect of One-Way Clutch on Belt-Drive Systems. Eur. J. Mech. A/Solids 2018, 71, 378–385. [Google Scholar] [CrossRef]
- Vetyukov, Y.; Eliseev, V.; Krommer, M. Modeling the Dynamics of a Flexible Belt Drive Using the Equations of a Deformable String with Discontinuities. IFAC-PapersOnLine 2015, 28, 604–609. [Google Scholar] [CrossRef]
- Picot, A.; Fournier, E.; Régnier, J.; TientcheuYamdeu, M.; Andréjak, J.M.; Maussion, P. Statistic-Based Method to Monitor Belt Transmission Looseness Through Motor Phase Currents. IEEE Trans. Ind. Informatics 2017, 13, 1332–1340. [Google Scholar] [CrossRef] [Green Version]
- Fournier, E.; Picot, A.; Regnier, J.; Andrieux, C.; Saint-Michel, J.; Maussion, P. Effects of transmission belt looseness on electrical and mechanical measurements of an induction motor. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; 2015; pp. 259–265. [Google Scholar] [CrossRef] [Green Version]
- Zou, Z.; Lin, Y.; Li, B.; Wu, Q.; Gu, F.; Ball, A.D. In-Processing Monitoring of Turning Operations Based on Modulation Signal Bispectrum Analysis of Motor Current Signals. In Proceedings of the 2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020; 2020; pp. 345–350. [Google Scholar] [CrossRef]
- Zou, Z.; Lin, Y.; Lin, D.; Gu, F.; Ball, A.D. Online Tool Condition Monitoring of CNC Turnings based on Motor Current Signature Analysis. In Proceedings of the 2021 26th International Conference on Automation and Computing (ICAC), Portsmouth, UK, 2–4 September 2021; 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, H.; Zou, Z.; Sun, X.; Gu, F.; Ball, A.D. A numerical study of rotor eccentricity and dynamic load in induction machines for motor current analysis based diagnostics. Maint. Reliab. Cond. Monit. 2021, 1, 71–86. [Google Scholar] [CrossRef]
- Bagheri, A.; Ojaghi, M.; Bagheri, A. Air-Gap Eccentricity Fault Diagnosis and Estimation in Induction Motors Using Unscented Kalman Filter. Int. Trans. Electr. Energy Syst. 2020, 30, e12450. [Google Scholar] [CrossRef]
- Touhami, O.; Aibeche, A.; Abdelli, R.; Bouzida, A. Dynamic Eccentricity Fault Diagnosis in Induction Motors Using Finite Element Method and Experimental Tests. Int. J. Ind. Electron. Drives 2017, 3, 199–209. [Google Scholar] [CrossRef]
- Shangguan, W.B.; Feng, X.; Lin, H.; Yang, J. A Calculation Method for Natural Frequencies and Transverse Vibration of a Belt Span in Accessory Drive Systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 2268–2279. [Google Scholar] [CrossRef]
- Ding, H. Periodic Responses of a Pulley-Belt System with One-Way Clutch under Inertia Excitation. J. Sound Vib. 2015, 353, 308–326. [Google Scholar] [CrossRef]
- Ding, H. Steady-State Responses of a Belt-Drive Dynamical System under Dual Excitations. Acta Mech. Sin. Xuebao 2016, 32, 156–169. [Google Scholar] [CrossRef]















| Category | Item | Value |
|---|---|---|
| Motor | Supply power | 3.0 kW |
| Power supply voltage (V) | 220 V | |
| Power supply frequency (fe) | 50 Hz | |
| ) Mechanical inertia (J) | 19.1 N·m 0.009 | |
| ) | 1460 rpm | |
| Pole pairs (p) | 2 | |
| Phase | 3 | |
| Resistance | ||
| ) | ||
| Inductance | ) | 1.26 × 10−6 H/m |
| ) | 0.0075 H | |
| 0.0075 H | ||
| Others | Sampling frequency | 4000 Hz |
| Simulation time | 4.5 s |
| Item | Notation | Value |
|---|---|---|
| Radius of the driver pulley | 0.0577 m | |
| Radius of the driven pulley | 0.0796 m | |
| Belt stiffness | 4.47 × 105 N/m | |
| Torsion damping coefficient | 0.05 Nm s/rad | |
| Pulley and spindle inertia | 0.018 kg m2/rad | |
| Pulley and motor inertia | 0.009 kg m2 /rad | |
| Length of span | 0.447 m | |
| Young’s modulus | 2.0 × 109 N/m2 | |
| Area of the cross-section | m2 | |
| Static tension | 300 N | |
| Viscous damping | 2 × 104 N s /m | |
| Density | 1150 kg/m3 |
| Device | Parameters |
|---|---|
| CNC model | CAK3665 |
| Motor model | YVP112M-50-B5; 4 kW; 50 Hz; 2 Poles |
| Centre distance setting | D = 315 mm, 330 mm, 345 mm, 360 mm |
| Spindle speed | 850 rpm |
| Current clamp model | Fluke Is400; 40 A; 5-10 KHz |
| Data acquisition model | YMC9004 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Li, C.; Huang, B.; Shen, G.; Gu, F.; Ball, A.D. Investigation into the Modulation Characteristics of Motor Current Signals in a Belt Transmission System for Machining Monitoring. Appl. Sci. 2022, 12, 10088. https://doi.org/10.3390/app121910088
Zou Z, Li C, Huang B, Shen G, Gu F, Ball AD. Investigation into the Modulation Characteristics of Motor Current Signals in a Belt Transmission System for Machining Monitoring. Applied Sciences. 2022; 12(19):10088. https://doi.org/10.3390/app121910088
Chicago/Turabian StyleZou, Zhexiang, Chun Li, Baoshan Huang, Guoji Shen, Fengshou Gu, and Andrew D. Ball. 2022. "Investigation into the Modulation Characteristics of Motor Current Signals in a Belt Transmission System for Machining Monitoring" Applied Sciences 12, no. 19: 10088. https://doi.org/10.3390/app121910088








