Oxygen Isotope Phosphoric Acid Fractionation Factor and Uncertainty on the δ18O Measurements of Calcite
Abstract
:1. Introduction
2. Oxygen Phosphoric Acid Fractionation Factor for Low-Mg Calcite: Data and Discussion
2.1. Selection of Data at Different Temperatures
- (1)
- Only data sets that include values for more than two analytical temperatures were considered and compared.
- (2)
- We considered only data obtained with the individual-acid bath method (IAB).
2.2. Estimation of Oxygen Isotope Phosphoric Acid Fractionation Factor, , at 298.15 K
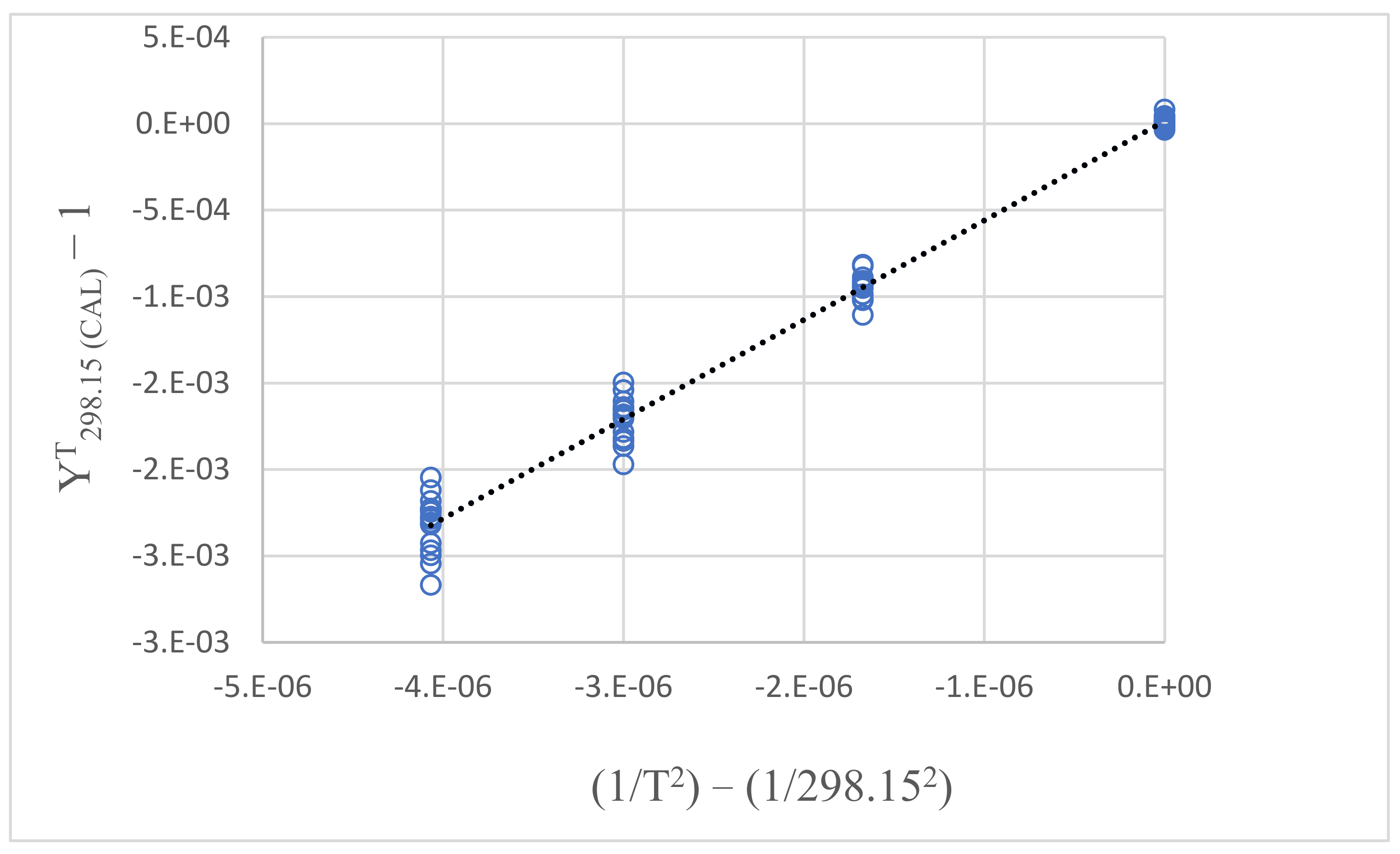
2.3. The Ratio vs. Temperature
2.4. Approximate Standard Uncertainty on
2.5. Calibration with the Low-Mg Calcite Standard NBS19 and Standard Uncertainty on New Analytical Data
3. Conclusions
- (a)
- The regressions on obtained for several low-Mg calcites do not have the same slope and elevation. This demonstrates that the mineral behavior during dissolution in H3PO4 is not always the same for different low-Mg calcites; this generated analytical uncertainty. The variable behavior is probably due to little variations in the chemical composition of low-Mg calcite.
- (b)
- To calculate the overall uncertainty of the estimated value obtained using the standard NBS19, the uncertainty at point (a) must be added to uncertainty due to the analytical calibration (prediction uncertainty): the overall value cannot be lower than 0.2‰. Uncertainties smaller than about 0.2 reported in the literature is unrealistic. These results must be considered when different data are compared.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grossman, E.L.; Joachimski, M.M. Oxygen isotope stratigraphy. In Geological Time Scale 2020; Grodstein, F.M., Ogg, J.G., Schmitz, M.D., Ogg, G.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 1, pp. 279–307. [Google Scholar]
- Bryant, J.D.; Koch, P.L.; Froelich, P.N.; Showers, W.J.; Genna, B.J. Oxygen isotope partitioning between phosphate and carbonate in mammalia apatite. Geochim. Cosmochim. Acta 1996, 60, 5145–5148. [Google Scholar] [CrossRef]
- Iacumin, P.; Bocherens, H.; Mariotti, A.; Longinelli, A. Oxygen isotope analysis of co-existing carbonate and phosphate in biogenic apatite: A way to monitor diagenetic alteration of bone phosphate? Earth Planet Sci. Lett. 1996, 142, 1–6. [Google Scholar] [CrossRef]
- Sharma, T.; Clayton, R.N. Measurements of O18/O16 ratios of total oxygen of carbonates. Geochim. Cosmochim. Acta 1965, 29, 1347–1353. [Google Scholar] [CrossRef]
- McCrea, J.M. On the isotopic chemistry of carbonates and a paleotemperature scale. J. Chem. Phys. 1950, 18, 849–853. [Google Scholar] [CrossRef]
- Crowley, S.F. Mineralogical and chemical composition of international carbon and oxygen isotope calibration material NBS 19, and reference materials NBS 18, IAEA-CO-1 and IAEA-CO-8. Geostand. Geoanalytical Res. 2010, 34, 193–206. [Google Scholar] [CrossRef]
- Rosembaum, J.; Sheppard, S.N.F. An isotopic study of siderites, dolomites and ankerites at high temperatures. Geochim. Cosmochim. Acta 1986, 50, 1147–1150. [Google Scholar] [CrossRef]
- Böttcher, M.E. 18O/16O and 13C/12C fractionation during reactions of carbonates with phosphoric acid: Effect of cationic substitution and reaction temperature. Isot. Environ. Health Stud. 1996, 32, 299–305. [Google Scholar] [CrossRef] [PubMed]
- Swart, P.K.; Burns, S.J.; Leder, J.J. Fractionation of the stable isotopes of oxygen and carbon in carbon-dioxide during reaction of calcite with phosphoric acid as a function of temperature and technique. Chem. Geol. 1991, 86, 89–96. [Google Scholar] [CrossRef]
- Kim, S.-T.; O’Neil, J.R. Equilibrium and non-equilibrium oxygen isotope effects in synthetic carbonates. Geochim. Cosmochim. Acta 1997, 61, 3461–3475. [Google Scholar] [CrossRef]
- Carothers, W.W.; Adami, L.H.; Rosenbauer, R.J. Experimental oxygen isotope fractionation between siderite-water and phosphoric acid liberated CO2-siderite. Geochim. Cosmochim. Acta 1988, 52, 2445–2450. [Google Scholar] [CrossRef]
- Das Sharma, S.; Patil, D.T.; Gopalan, K. Temperature dependence of oxygen isotope fractionation of CO2 from magnesite-phosphoric acid reaction. Geochim. Cosmochim. Acta 2002, 66, 589–593. [Google Scholar] [CrossRef]
- Gilg, H.A.; Struk, U.; Vennemann, T.; Boni, M. Phosphoric acid fractionation factors for smithsonite and cerussite between 25 and 72 °C. Geochim. Cosmochim. Acta 2003, 67, 4049–4055. [Google Scholar] [CrossRef]
- Ghosh, P.; Patecki, M.; Rothe, M.; Brand, W.A. Calcite-CO2 mixed into CO2-free air: A new CO2-in air stable isotope reference material for the VPDB scale. Rapid Comm. Mass Spectrom. 2005, 19, 1097–1119. [Google Scholar] [CrossRef]
- Kim, S.-T.; Mucci, A.; Taylor, B.E. Phosphoric acid fractionation factors for calcite and aragonite between 25 and 75 °C revisited. Chem. Geol. 2007, 246, 135–146. [Google Scholar] [CrossRef]
- Crowley, S.F. Effect of temperature on the oxygen isotope composition of carbon dioxide (δCO2 18O) prepared from carbonate minerals by reaction with polyphosphoric acid: An example for the rhombohedral CaCO3–MgCO3 group minerals. Geochim. Cosmochim. Acta 2010, 74, 6406–6421. [Google Scholar] [CrossRef]
- Kim, S.-T.; Coplen, T.B.; Horita, J. Normalization of stable isotope data for carbonate minerals: Implementation of IUPAC guidelines. Geochim. Cosmochim. Acta 2015, 158, 276–289. [Google Scholar] [CrossRef]
- Burke, S. Missing values, outliers, robust statistics and non-parametric methods. LC.GC Eur. Online Suppl.-Stat. Data Anal. 1998, 2, 19–24. [Google Scholar]
- Tukey, J.W. Exploring Data Analysis; Addison-Wesley: Menlo Park, CA, USA, 1977. [Google Scholar]
- Friedman, I.; O’Neil, J. Compilation of stable isotope fractionation factors of geochemical interest. In US Geological Survey Professional Paper, 6th ed.; Fleischer, M., Ed.; Data of Geochemistry; US Government Printing Office: Washington, DC, USA, 1977; Volume 440-KK, pp. 1–12. [Google Scholar]
- Land, L.S. The isotopic and trace element geochemistry of dolomite: The state of the art. In Concepts and Models of Dolomitization; Zenger, D.H., Dunham, J.B., Ethington, R.L., Eds.; Society for Sedimentary Geology, Special Publications: Tulsa, OK, USA, 1980; Volume 28, pp. 87–110. [Google Scholar]
- Verkouteren, R.; Klinedinst, D.B. Value Assignment and Uncertainty Estimation of Selected Light Stable Isotope Reference Materials: RMs 8543-8545, RMs 8562-8564, and RM 8566; NIST Special Publication: Gaithersburg, MD, USA, 2004; p. 260-149. [Google Scholar]
- Gonfiantini, R. Advisory Group Meeting on Stable Isotope Reference Samples for Geochemical and Hydrological Investigations; IAEA: Vienna, Austria, 1984. [Google Scholar]
- Hut, G. Consultant’s Meeting on Stable Isotope Reference Samples for Geochemical and Hydrological Investigations; IAEA: Vienna, Austria, 1987. [Google Scholar]
- Zar, J.H. Biostatistical Analysis; Pearson: Harlow, UK, 2010. [Google Scholar]
- Lavagnini, I.; Magno, F. A statistical overview on univariate calibration, inverse regression, and detection limit: Application to gas chromatography/mass spectrometry technique. Mass Spectrom Rev. 2007, 26, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods; Iowa State University Press: Ames, IA, USA, 1968. [Google Scholar]
| Regression | Calcite Sample | n | b | s(b) | a | s(a) | pa=0 | s(yx) |
|---|---|---|---|---|---|---|---|---|
| Crowley [16] | ||||||||
| 1 | NBS19 | 5 | 576 | 20 | 3.6 × 10−5 | 5.9 × 10−5 | 0.59 | 6.8 × 10−5 |
| 2 | NBS18 | 5 | 540 | 18 | −3.7 × 10−5 | 5.1 × 10−5 | 0.52 | 5.9 × 10−5 |
| 3 | IAEA-CO-1 | 5 | 514 | 16 | 4.4 × 10−5 | 4.7 × 10−5 | 0.41 | 5.3 × 10−5 |
| 4 | LIVM | 5 | 540 | 13 | 1.4 × 10−5 | 3.9 × 10−5 | 0.74 | 4.4 × 10−5 |
| 5 | LIVF | 5 | 541 | 30 | 8.1 × 10−5 | 8.7 × 10−5 | 0.42 | 9.9 × 10−5 |
| 6 | PCC | 5 | 566 | 8.1 | 1.5 × 10−5 | 2.3 × 10−5 | 0.56 | 2.7 × 10−5 |
| 7 | CM | 5 | 549 | 16 | 0.7 × 10−5 | 4.5 × 10−5 | 0.89 | 5.1 × 10−5 |
| 8 | IAEA-CO-8 | 5 | 652 | 24 | −1.6 × 10−5 | 6.8 × 10−5 | 0.83 | 7.8 × 10−5 |
| 9 | LIVC | 5 | 636 | 24 | 4.2 × 10−5 | 7.0 × 10−5 | 0.59 | 8.0 × 10−5 |
| 10 | BCS | 5 | 618 | 9.0 | 1.7 × 10−5 | 2.6 × 10−5 | 0.56 | 3.0 × 10−5 |
| 11 | CHALK | 5 | 601 | 21 | 1.8 × 10−5 | 6.2 × 10−5 | 0.79 | 7.1 × 10−5 |
| Kim et al. [15] | ||||||||
| 12 | Calcite H | 3 | 606 | 3.5 | −0.3 × 10−5 | 0.7 × 10−5 | 0.77 | 0.7 × 10−5 |
| Calcite H (1) | 20 | 604 | 17 | −0.2 × 10−5 | 3.0 × 10−5 | 0.95 | 9.8 × 10−5 | |
| Böttcher [8] | ||||||||
| 13 | Calcite MERK | 4 | 574 | 34 | 1.6 × 10−5 | 2.7 × 10−5 | 0.55 | 13 × 10−5 |
| Swart et al. [9] | ||||||||
| 14 | LMC | 5 | 552 | 12 | −2.8 × 10−5 | 2.7 × 10−5 | 0.37 | 3.7 × 10−5 |
| 15 | PSU-4 | 6 | 558 | 28 | 2.4 × 10−5 | 5.8 × 10−5 | 0.70 | 8.6 × 10−5 |
| T (K) | 298.15 | 323.15 | 348.15 | 373.15 |
|---|---|---|---|---|
| − | 0 | −1.6733 × 10−6 | −2.9992 × 10−6 | −4.0676 × 10−6 |
| 0.000081 | −0.00082 | −0.00150 | −0.00205 | |
| −0.000037 | −0.00111 | −0.00197 | −0.00267 | |
| 0.000033 | 0.000079 | 0.000127 | 0.000166 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iacumin, P.; Rossi, M.; Venturelli, G. Oxygen Isotope Phosphoric Acid Fractionation Factor and Uncertainty on the δ18O Measurements of Calcite. Appl. Sci. 2022, 12, 10094. https://doi.org/10.3390/app121910094
Iacumin P, Rossi M, Venturelli G. Oxygen Isotope Phosphoric Acid Fractionation Factor and Uncertainty on the δ18O Measurements of Calcite. Applied Sciences. 2022; 12(19):10094. https://doi.org/10.3390/app121910094
Chicago/Turabian StyleIacumin, Paola, Mattia Rossi, and Gianpiero Venturelli. 2022. "Oxygen Isotope Phosphoric Acid Fractionation Factor and Uncertainty on the δ18O Measurements of Calcite" Applied Sciences 12, no. 19: 10094. https://doi.org/10.3390/app121910094
APA StyleIacumin, P., Rossi, M., & Venturelli, G. (2022). Oxygen Isotope Phosphoric Acid Fractionation Factor and Uncertainty on the δ18O Measurements of Calcite. Applied Sciences, 12(19), 10094. https://doi.org/10.3390/app121910094







