XOR-Based (n, n) Visual Cryptography Schemes for Grayscale or Color Images with Meaningful Shares
Abstract
:1. Introduction
2. XOR-Based VCS
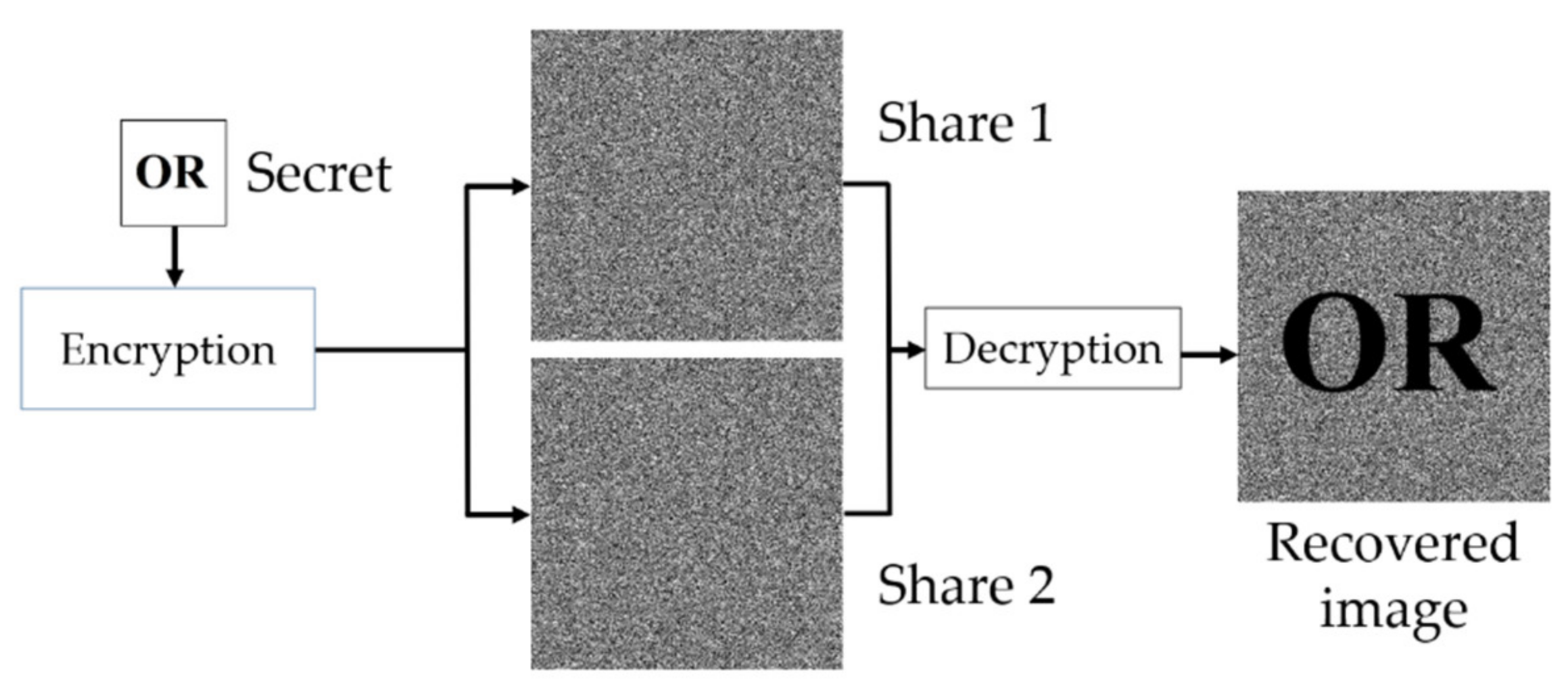
2.1. The Ou et al.’s XOR-Based VCS
| Algorithm 1. Generate a 2n × n matrix for (n, n) XOR-based VCS [16] |
| Input: A parameter n. Output: A 2n × n matrix Mn.
|
| Algorithm 2. The basic algorithm for XOR-based VCS with meaningful shares [16] |
| Input: A binary secret image S with H × W pixels, and a 2n × n matrix Mn. Output: n shares R1, …, Rn, each of which is H × W in size.
|
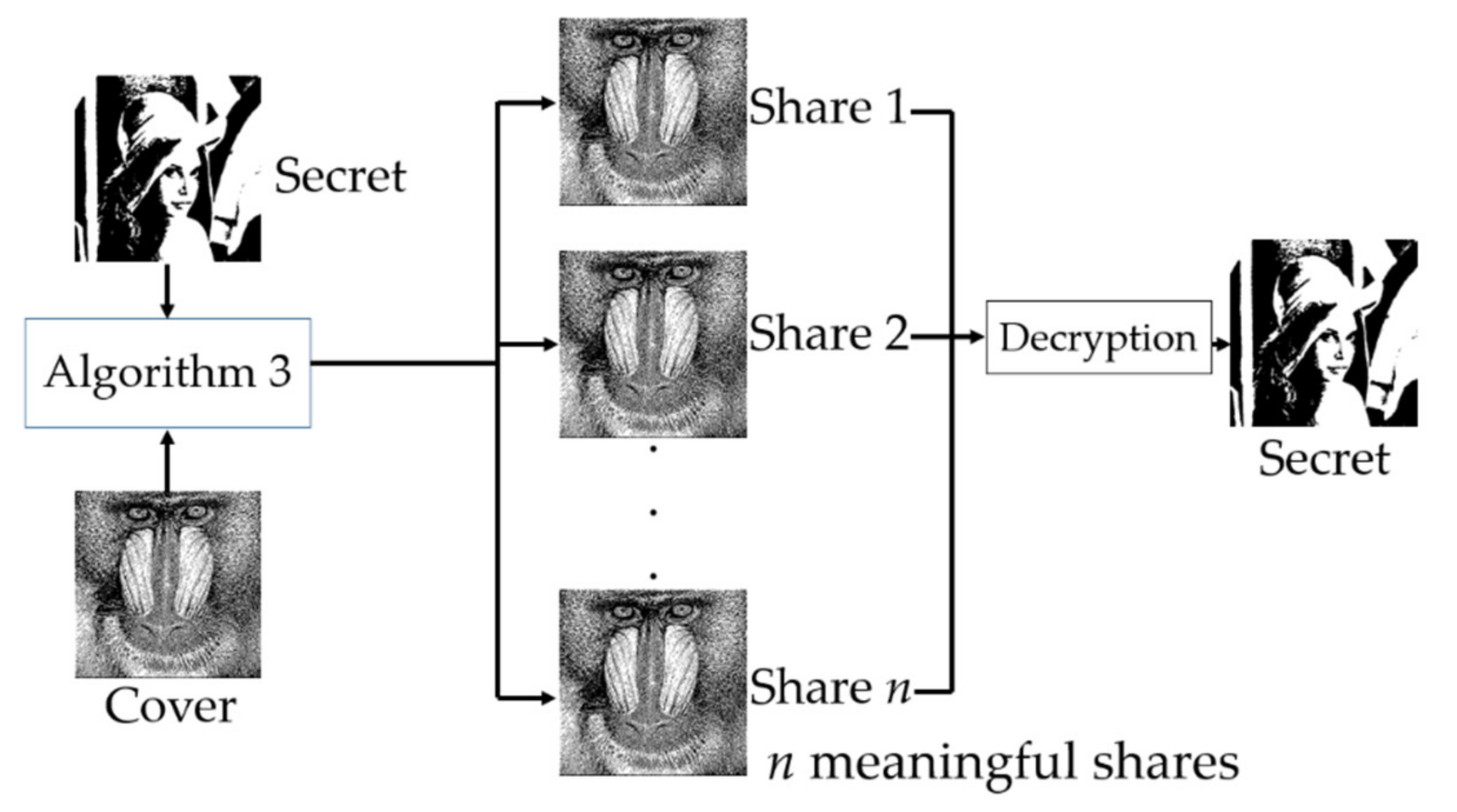
| Algorithm 3. (n, n) XOR-based VC scheme with meaningful shares [16] |
| Input: A binary secret image S and a cover image C, both with H × W pixels, and a parameter β. Output: n meaningful shares R1, …, Rn, each of which is H × W in size.
|
2.2. The Lo and Juan’s XOR-Based VCS
| Algorithm 4 [New method 2]. (n, n) XOR-based VC scheme with meaningful shares [17] |
| Input: A binary secret image S and n cover image C1, …, Cn , all of them with H × W pixels, and a parameter β. Output: n meaningful shares R1, …, Rn, each of which is H × W in size.
|
3. Main Results
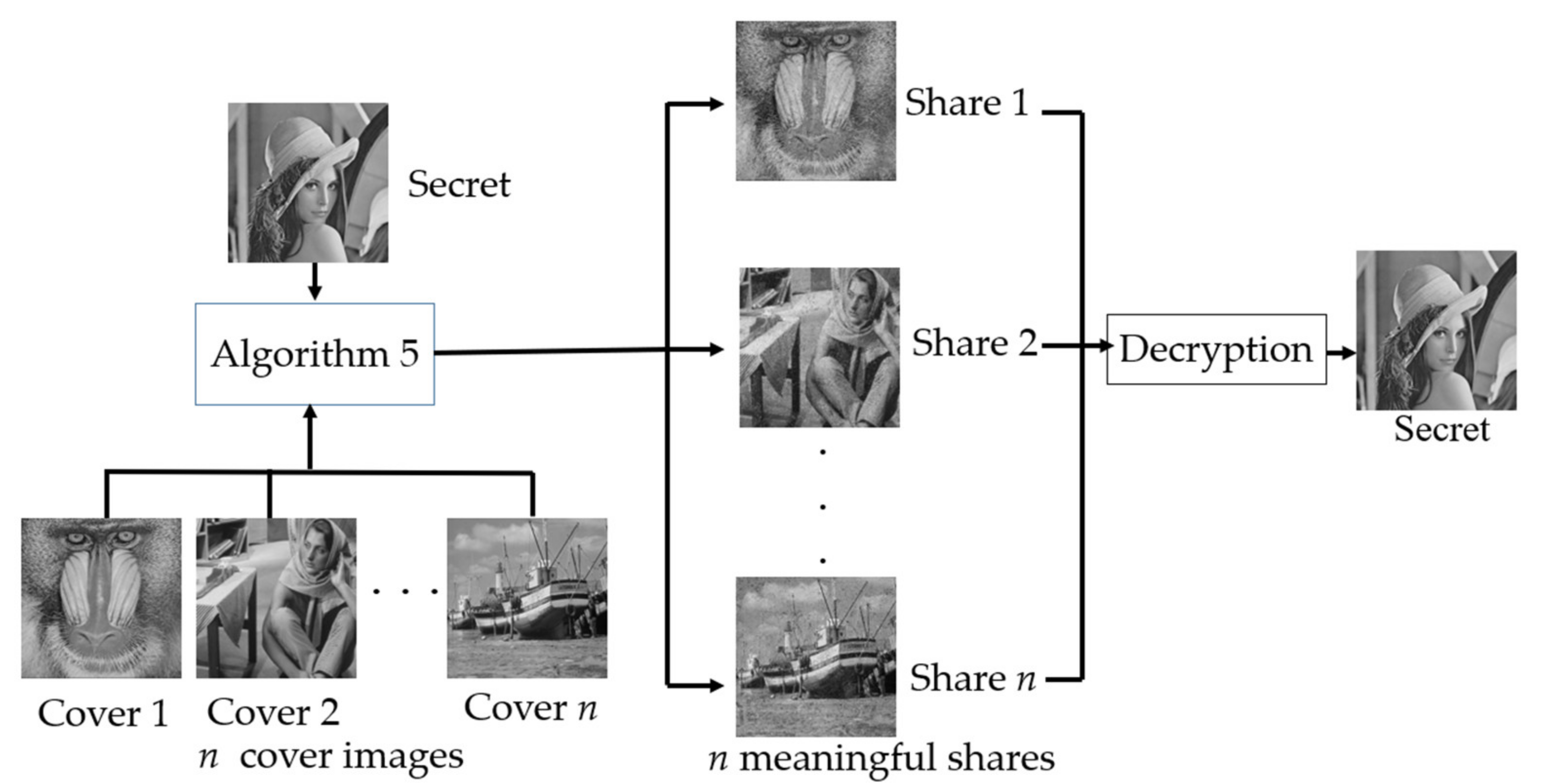
3.1. (n, n) XOR-Based VCS with Grayscale Secret and Covers
| Algorithm 5. (n, n) XOR-based VC scheme with grayscale meaningful shares. |
| Input: A secret grayscale image S and n cover grayscale image C1, …, Cn, all of them with H × W pixels. Output: n gray meaningful shares R1, …, Rn, each of which is H × W in size.
|
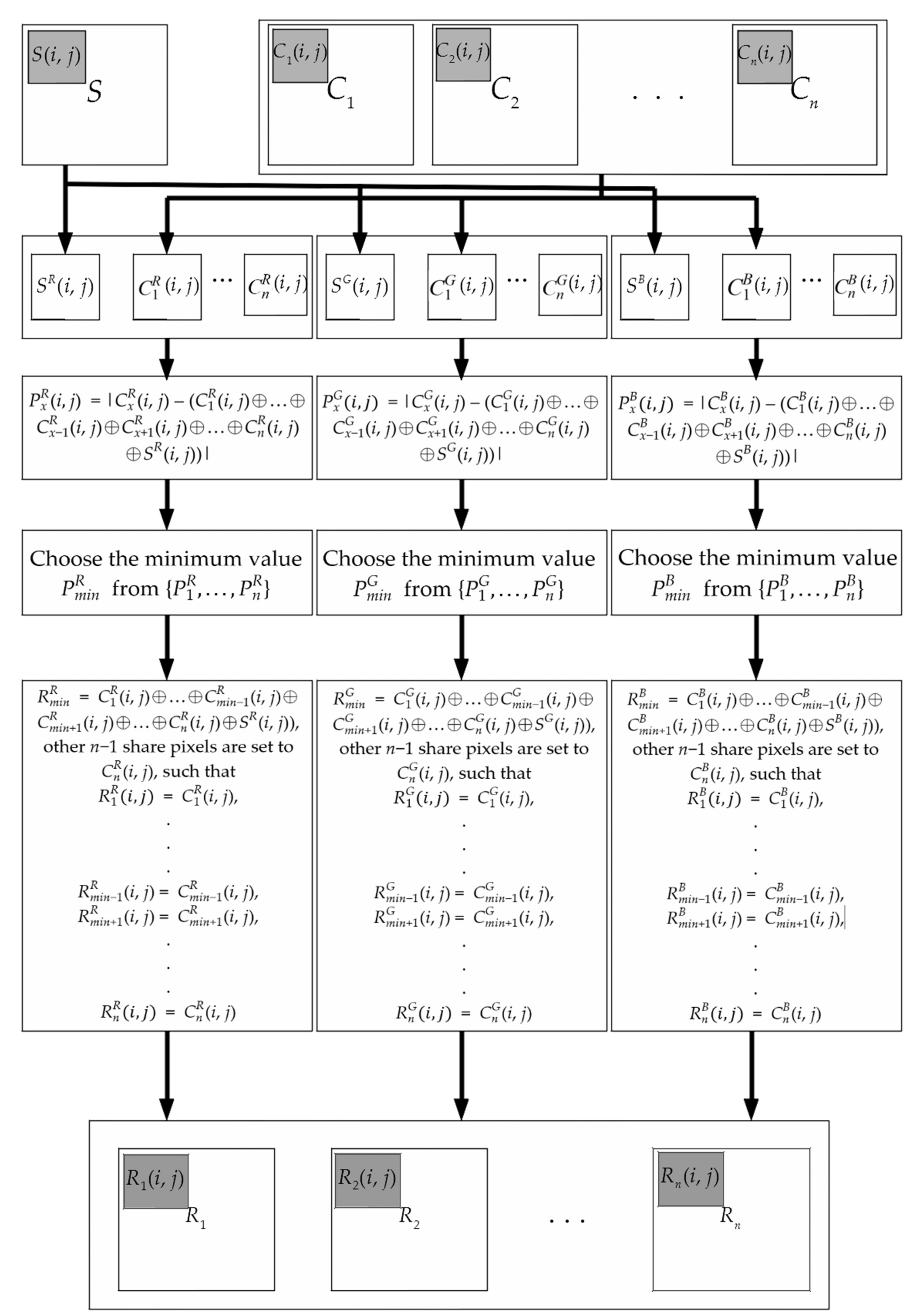
3.2. (n, n) XOR-Based VCS with Color Secret and Covers
| Algorithm 6. (n, n) XOR-based VC scheme with color meaningful shares |
| Input: A secret color image S and n cover color image C1,…, Cn , all of them with H × W pixels. Output: n color meaningful shares R1, …, Rn, each of which is H × W in size.
|
4. Experimental Results
4.1. Objective Evaluation Parameters
4.2. The Experimental Results of the Proposed VCS with Grayscale Images
4.3. The Experimental Results of the Proposed VCS with Color Images
5. Discussion
5.1. Correctness Analysis
5.2. Security Analysis
5.3. Theoretical and Experimental PSNR
5.4. Comparison with State-of-the-Art Approaches
- Type of images: In other schemes, the experimental images are all black-and-white or halftone images. There is only 1 bit used per pixel in each image. In our scheme, we use grayscale and color images, and the bits per pixel are 8 and 24, respectively.
- Pixel expansion: This refers to whether the scheme suffers from the pixel expansion problem. Pixel expansion increases the transmission time and decreases bandwidth utilization. There is no pixel expansion in our scheme.
- Number of cover image: This refers to how many covers can be imported. The higher the cover number, the more situations can be used.
- The number of share images: In our scheme, the amount of covers we import denotes how many shares we can generate. From Table 8, we can obviously see that our scheme is the same as the others.
- Meaningful share: This refers to whether the scheme can generate a meaningful share. Meaningful shares are more desirable than meaningless shares, because they look more natural and other people will not be attracted by them.
- Decryption operation: There are two operations for any VCS, OR, and XOR operation. The secret image can be completely reconstructed using the XOR operation, while at most one-half of the image can be reconstructed by the OR operation.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Naor, M.; Shamir, A. Visual cryptography. In Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1994; pp. 1–12. [Google Scholar]
- Kafri, O.; Keren, E. Encryption of pictures and shapes by random grids. Opt. Lett. 1987, 12, 377–379. [Google Scholar] [CrossRef]
- Shyu, S.J. Image encryption by random grids. Pattern Recognit. 2007, 40, 1014–1031. [Google Scholar] [CrossRef]
- Chen, T.; Tsao, K. Threshold visual secret sharing by random grids. J. Syst. Softw. 2011, 4, 1197–1208. [Google Scholar] [CrossRef]
- Juan, J.S.-T.; Chen, Y.-C.; Guo, S. Fault-Tolerant Visual Secret Sharing Schemes without Pixel Expansion. Appl. Sci. 2016, 6, 18. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.-Y.; Juan, J.S.-T. Flexible Meaningful Visual Multi-Secret Sharing Scheme by Random Grids. Multimed. Tools Appl. 2020, 79, 7705–7729. [Google Scholar] [CrossRef]
- Wang, L.; Yan, B.; Yang, H.M.; Pan, J.S. Flip extended visual cryptography for gray-scale and color cover images. Symmetry 2020, 13, 65. [Google Scholar] [CrossRef]
- Juan, J.S.-T.; Lin, J.Y.; Huang, B.Y.; Chung, Y.C. Advanced fault-tolerant visual multi-secret sharing scheme. J. Surveill. Secur. Saf. 2022, 3, 41–54. [Google Scholar] [CrossRef]
- Zhao, Y.; Fu, F.W. A cheating immune (k, n) visual cryptography scheme by using the rotation of shares. Multimed. Tools Appl. 2022, 81, 6235–6257. [Google Scholar] [CrossRef]
- Tuyls, P.; Kevenaar, T.; Schrijen, G.J.; Staring, A.A.M.; van Dijk, M. Visual crypto displays enabling secure communications. In Security in Pervasive Computing; Springer: Berlin/Heidelberg, Germany, 2003; pp. 271–284. [Google Scholar]
- Tuyls, P.; Hollmann, H.D.; van Lint, J.H.; Tolhuizen, L. XOR-based visual cryptography schemes. Des. Codes Cryptogr. 2005, 37, 169–186. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Jia, X.; Chu, Q.; Wang, D.A. Novel XOR-Based Threshold Visual Cryptography with Adjustable Pixel Expansion. Appl. Sci. 2020, 10, 1321. [Google Scholar] [CrossRef]
- Liu, S.M.; Yang, H.M.; Pan, J.S.; Liu, T.; Yan, B. A novel perfect contrast XOR-based visual cryptography scheme for multiple secrets. Multimed. Tools Appl. 2022, 2022, 1–19. [Google Scholar] [CrossRef]
- Wu, X.; An, N.; Xu, Z. Sharing multiple secrets in XOR-based visual cryptography by non-monotonic threshold property. In IEEE Transactions on Circuits and Systems for Video Technology; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Wu, X.; Sun, W. Generalized random grid and its applications in visual cryptography. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1541–1553. [Google Scholar] [CrossRef]
- Ou, D.; Sun, W.; Wu, X. Non-expansible XOR-based visual cryptography scheme with meaningful shares. Signal Process. 2015, 108, 604–621. [Google Scholar] [CrossRef]
- Lo, A.-H.; Juan, J.S.-T. (n, n) XOR-based visual cryptography schemes with different meaningful shares. In Proceedings of the 2021 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2021; pp. 15–17. [Google Scholar]
- Singh, P.; Raman, B.; Misra, M. A (n, n) threshold non-expansible XOR based visual cryptography with unique meaningful shares. Signal Process. 2018, 142, 301–319. [Google Scholar] [CrossRef]

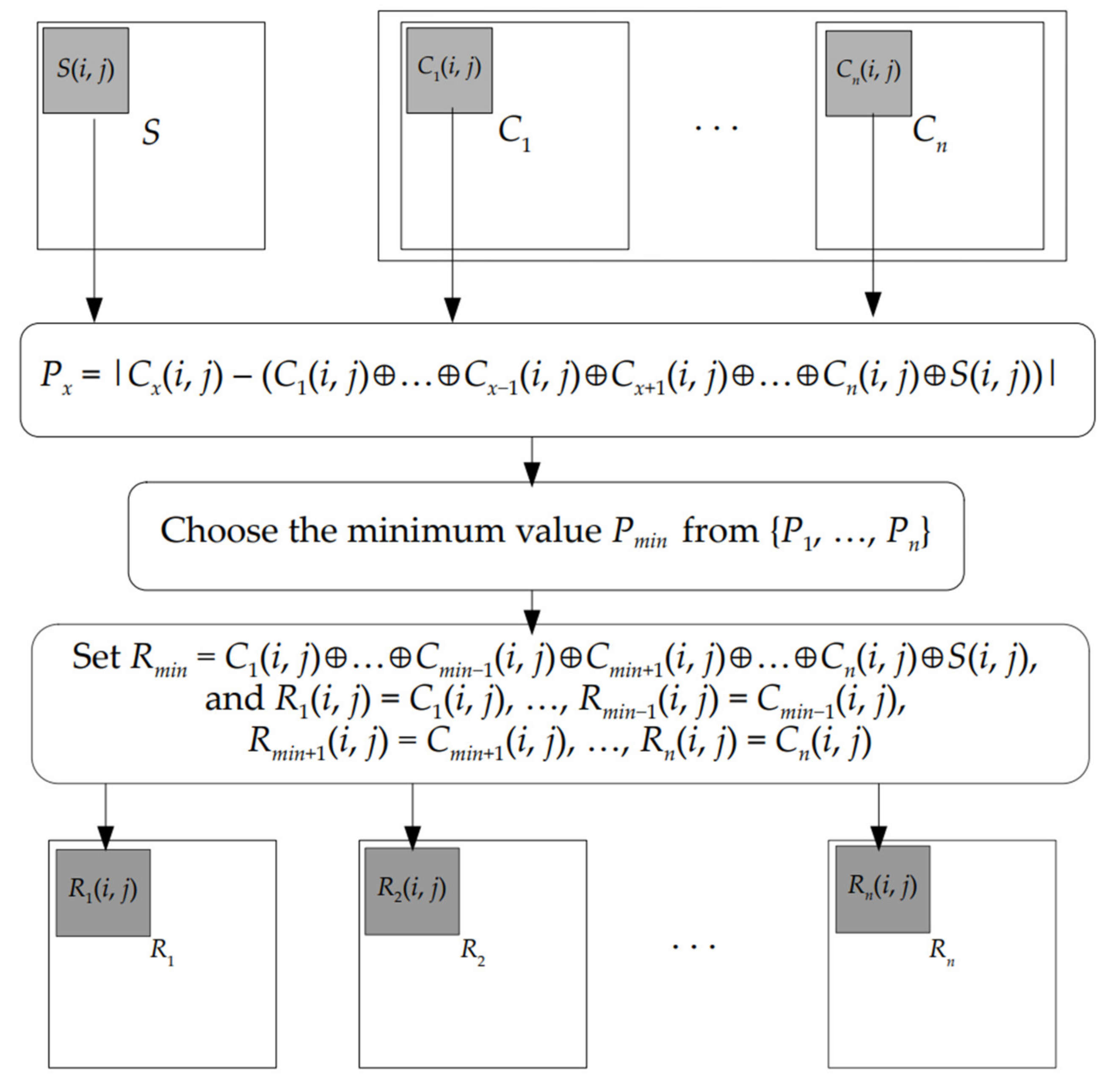





| Notations | Description |
|---|---|
| ⊕ | Boolean XOR operation |
| S | Secret image |
| C1, …, Cn | Cover images |
| R1, …, Rn | Shares generated by VCS |
| (i, j) | The position of i column and j row |
| S(i, j), Cx(i, j), Rx(i, j) | The value of S(i, j), Cx(i, j) and Rx(i, j) for any x ∈ {1, 2, …, n} (for black-and-white image, or grayscale image) |
| (i, j), (i, j), (i, j) | The value of red/green/blue channel of S(i, j), Cx(i, j) and Rx(i, j) for any x ∈ {1, 2, …, n} (for color image) |
| R{⊕, 1, …, n} | XOR-ed result by shares R1, …, Rn |
| Images | PSNR |
|---|---|
| R1 | 19.7081 |
| R2 | 19.4408 |
| R3 | 19.6550 |
| R4 | 19.5888 |
| R5 | 19.7651 |
| Cases (n, n) | C(15, n) | Average PSNR |
|---|---|---|
| (3, 3) | 455 | 16.4814 |
| (4, 4) | 1365 | 18.1383 |
| (5, 5) | 3003 | 19.4192 |
| (6, 6) | 5005 | 20.3865 |
| (7, 7) | 6435 | 21.1766 |
| Images | PSNR |
|---|---|
| R1 | 19.5757 |
| R2 | 19.1196 |
| R3 | 19.2015 |
| R4 | 19.4861 |
| R5 | 19.1398 |
| Cases (n, n) | C(15, n) | Average PSNR |
|---|---|---|
| (3, 3) | 455 | 16.2671 |
| (4, 4) | 1365 | 18.0392 |
| (5, 5) | 3003 | 19.2421 |
| (6, 6) | 5005 | 20.3442 |
| (7, 7) | 6435 | 21.4743 |
| Cases | Theoretical MSE | Theoretical PSNR | Experimental PSNR |
|---|---|---|---|
| (3, 3) | 2427.1851 | 14.2797 | 16.4814 |
| (4, 4) | 1820.3888 | 15.5291 | 18.1383 |
| (5, 5) | 1456.3110 | 16.4982 | 19.4192 |
| (6, 6) | 1213.5925 | 17.2900 | 20.3865 |
| (7, 7) | 1040.2221 | 17.7959 | 21.1766 |
| Cases | Theoretical MSE | Theoretical PSNR | Experimental PSNR |
|---|---|---|---|
| (3, 3) | 2427.1851 | 14.2797 | 16.2671 |
| (4, 4) | 1820.3888 | 15.5291 | 18.0392 |
| (5, 5) | 1456.3110 | 16.4982 | 19.2421 |
| (6, 6) | 1213.5925 | 17.2900 | 20.3442 |
| (7, 7) | 1040.2221 | 17.7959 | 21.4743 |
| Schemes | Type of Image | Pixel Expansion | Number of Cover Image | Number of Share Image | Meaningful Share | Decryption Operation | Contrast |
|---|---|---|---|---|---|---|---|
| [1] | Black and white | Yes | 0 | n | No | OR operation | 1/2 |
| [16] | Black and white | No | 1 | n | Yes | XOR operation | 1 |
| [18] | Black and white | No | n/2 | n | Yes | XOR operation | 1 |
| [17] | Black and white | No | n | n | Yes | XOR operation | 1 |
| Ours | Grayscale and color | No | n | n | Yes | XOR operation | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-H.; Juan, J.S.-T. XOR-Based (n, n) Visual Cryptography Schemes for Grayscale or Color Images with Meaningful Shares. Appl. Sci. 2022, 12, 10096. https://doi.org/10.3390/app121910096
Chen Y-H, Juan JS-T. XOR-Based (n, n) Visual Cryptography Schemes for Grayscale or Color Images with Meaningful Shares. Applied Sciences. 2022; 12(19):10096. https://doi.org/10.3390/app121910096
Chicago/Turabian StyleChen, Yu-Hong, and Justie Su-Tzu Juan. 2022. "XOR-Based (n, n) Visual Cryptography Schemes for Grayscale or Color Images with Meaningful Shares" Applied Sciences 12, no. 19: 10096. https://doi.org/10.3390/app121910096
APA StyleChen, Y. -H., & Juan, J. S. -T. (2022). XOR-Based (n, n) Visual Cryptography Schemes for Grayscale or Color Images with Meaningful Shares. Applied Sciences, 12(19), 10096. https://doi.org/10.3390/app121910096












