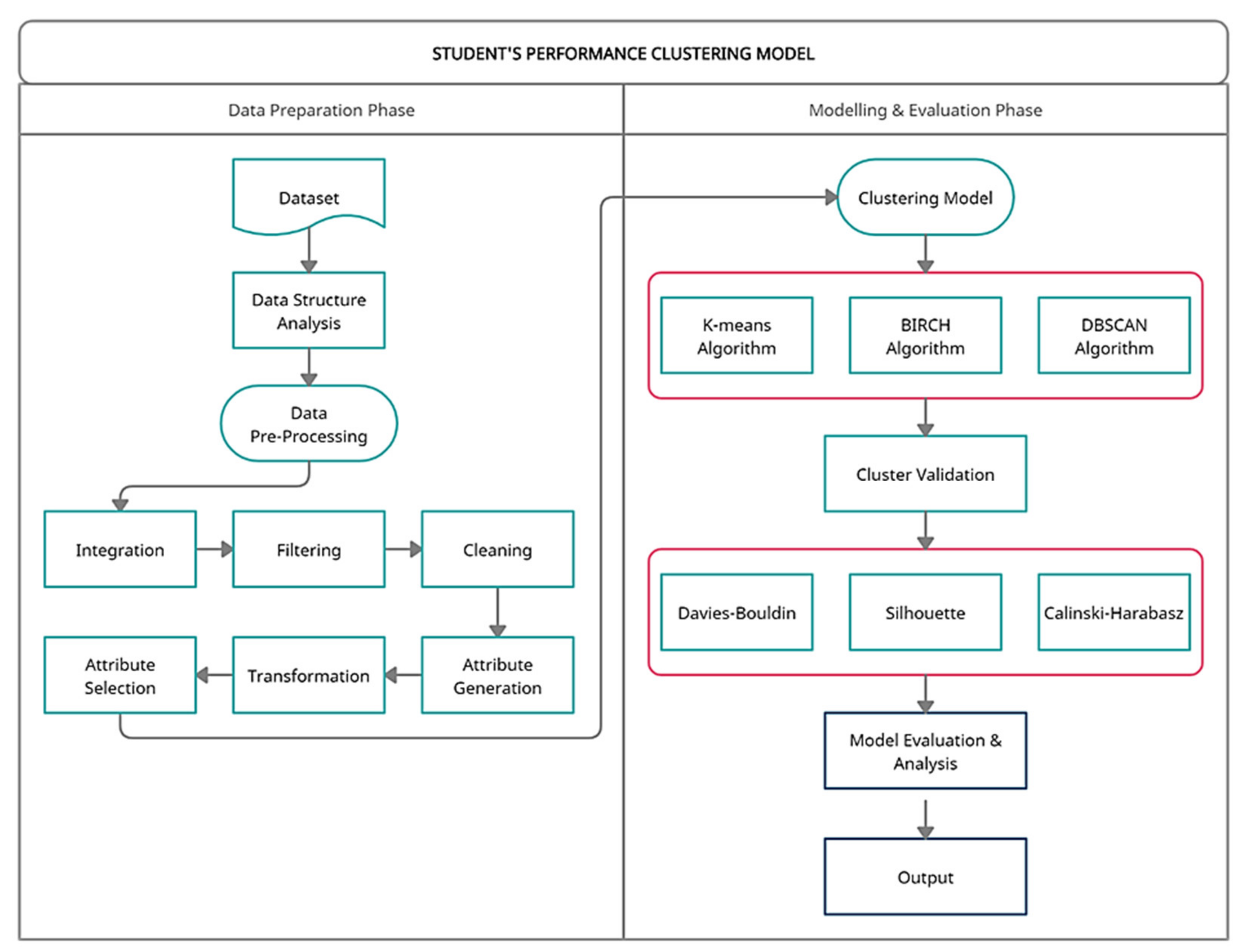
3.1. Data Preparation
Data Acquisition. The dataset used in this study was obtained from the Policy Planning and Research Division, Ministry of Higher Education (MOHE), consisting of 248,568 students’ records such as demographic, co-curricular activities, awards, industrial training, and employment data with 53 attributes. All of them were undergraduate students from 20 public universities who had dropped out or graduated from the intake year of 2015 to 2019.
Data Pre-processing. This method focusses on transforming the dataset to ensure it is suitable for the clustering algorithms and the data mining tool. As depicted in
Figure 1, six pre-processing techniques are involved: data integration, data filtering, data cleaning, attribute generation, data transformation, and attribute selection. Data integration was carried out at the start of the process, with six source files combined into a single dataset. The dataset was filtered where we only chose Malaysian citizens whose family income attribute ranges from RM 1 to RM 4000, which corresponded to the B40 group. We also consider full-time students for study mode attributes and undergraduate/first-degree students for the level of study attributes. Then, data cleaning was carried out to clear the attributes with too many missing values, such as postcode and parliamentary attributes with more than 30,000 missing values. The attributes that contain some missing values are replaced manually with specified values. Repeated and redundant attributes also have been removed from the dataset. Besides that, two attributes have been generated: registration age based on the date of birth and date of registration, and the number of activities based on the count of student activities. From a total of 53 attributes, only 16 attributes are left, and
Table 2 shows the list of the attributes with its description.
Most machine learning algorithms generally require numeric input and output variables [
32,
33,
34,
35,
36,
37]. This restriction must be addressed for implementing and developing machine learning models. This implies that all characteristics, including categories or nominal variables, must be transformed into numeric variables before being fed into the clustering and classification model. All these have been dealt with in the data transformation process.
Machine learning models learn how to map input variables to output variables. As a result, the scale and distribution of the domain data may differ for each variable. Input variables may have distinct units, which means they may have different scales. Differences in scaling among input variables may increase the difficulty of the modelled problem. Large input values (for example, a spread of hundreds or thousands of units) can result in a model that learns large weight values. A model with large weight values is frequently unstable, so it may perform poorly during learning and be sensitive to input values, resulting in a larger generalisation error. On top of that, normalization was performed using the StandardScaler or z-transformation and MinMaxScaler methods to form datasets for three different models. The first method, StandardScaler, allows each attribute’s values to be in the same range so that a comparison can be made. Z-transformation normalisation refers to normalising every value in a dataset such that the mean of all values is 0 and the standard deviation is 1 [
38]. The equation to perform the z-transformation normalisation on every value in a dataset is as Equation (1), where
xj is the input value of the sample
j,
is the sample mean, and
σ is the standard deviation of the sample data.
In the second method, MinMaxScaler converts all attributes into a range [0,1], which means the minimum value of the attribute is zero, and the maximum value of the attribute is one [
38]. The mathematical formula for MinMaxScaler is defined as Equation (2), where the minimum
xmin, and maximum
xmax values correspond to the normalised value x.
Descriptive Analysis.Table 3 shows the descriptive analysis of the student’s dataset after it has been transformed into numerical data. A variable containing categories that lack a natural order or ranking is referred to as a nominal scale. Calculations like a mean, median, or standard deviation would be pointless for nominal variables because they are arbitrary. Hence,
Table 3 does not generate the mean, median, or standard deviation for the nominal variables. Descriptive analysis of student’s dataset. Attributes with the highest standard deviations are CGPA and number of activities (0.922 and 1.684, respectively). Besides these two, a huge gap between the other attributes can be observed.
Feature Selection. Too many attributes in educational datasets can cause a curse of dimensionality and difficulties when processing and analysing the data. Moreover, calculation of distance by clustering algorithms may not be effective for high-dimensional data. To solve this problem, feature selection methods are applied to find the best attributes for this study. The feature selection methods can be divided into supervised and unsupervised. The features in supervised feature selection methods are chosen based on their relationship to the class label. It chooses qualities that are most relevant to the class label. On the other hand, unsupervised feature selection approaches assess feature relevance by exploring data using an unsupervised learning method [
38].
The attributes in the dataset will go through the supervised feature selection process using random forest, extra tree, info gain, and chi-square techniques. After the execution, the attributes have been allocated weights based on their relative importance and are sorted in order. For this experiment, drop-out status has been selected as the class label. The selected attributes which were found to be significant are the place of birth, income groups, secondary school, number of activities, CGPA, employment status, registration age, entry qualification, sponsorship, university, the field of study, and drop-out status.
Then, Kendall’s W statistic is used to assess agreements between all the raters by showing the statistical value between 0 and 1. If the value is “zero”, there is no agreement between the raters, while the value “one” indicates complete agreement. Kendall’s W assessment produced a score of 0.8862 and showed good and strong agreement among all raters used.
For unsupervised feature selection, a variance threshold will be used on the dataset. Variance is a metric that measures how dispersed the data distribution is within a dataset. Selecting attributes with considerable variance is necessary to avoid developing a biased clustering model and skewed toward certain attributes. Before developing an unsupervised machine learning model, choosing attributes based on their variance is essential. A high variance indicates that the attribute’s value is unique or has a high cardinality. Attributes with low variation have relatively comparable values, but attributes with zero variance have similar values. Furthermore, low-variance attributes are close to the mean value, providing minimal clustering information [
8]. Because it solely evaluates the input attribute (
x) without considering data from the dependant attribute, the variance thresholding technique is appropriate for unsupervised modelling (
y). The variance of all student attributes is shown in
Figure 2. As suggested by [
39], in this study, the variance threshold value for attribute selection was set to 0.3 to eliminate redundant features with low variance. Based on observations from the figure, there are ten attributes with variance values exceeding 0.3, which indicates that its behavioural patterns are high. The features that have high variance are the place of birth, income groups, secondary school, university, registration age, entry qualification, the field of study, sponsorship, CGPA, number of activities, and employment status. On the other hand, there are four attributes with a variance value of less than 0.3, namely gender, marital status, residence, and industrial training. The attributes of the state of birth, field of study, and the number of activities show the highest variance value and can be used to show student performance patterns.
Additionally, gender, marital status, residence, and industrial training attributes are low-variance features. As all three attributes’ marital status has the lowest variance, the other two are close to the threshold, as seen in
Figure 2. Furthermore, only 12 attributes with high variance (i.e., place of birth, income groups, secondary school, university, registration age, entry qualification, field of study, sponsorship, CGPA, number of activities, and employment status) are chosen at the end of the unsupervised feature selection, including the drop-out status attribute, and will be used in the next phase.
Final Dataset.Table 4,
Table 5 and
Table 6 show a list of selected sets of attributes after the attribute selection paired with StandardScaler and MinMaxScaler normalization methods. These sets of attributes are named Model A, Model B, and Model C, which will then be the inputs to the clustering models. Model A is a dataset that is normalized with StandardScaler and has 10 attributes after the supervised feature selection. Model B is a dataset that is normalized with MinMaxScaler and has 10 attributes after the supervised feature selection. Lastly, Model C is a dataset that is normalized with MinMaxScaler and has 12 attributes after the unsupervised feature selection.
3.2. Proposed Clustering Methodology
In recent years, the effectiveness of the use of clustering techniques in student performance prediction studies has attracted the interest of many researchers. The clustering technique refers to one method of grouping several similar objects into one cluster while different objects into another. The clustering technique will be very useful if the labelled information from students in the dataset is unknown. In addition, the division of large data sets into small, logical clusters will make it easier for researchers to examine and explain the meaning of the data.
K-means Algorithm. The researchers’ main choice is the k-means algorithm, a popular clustering technique. This technique is popular because the way it is implemented is very simple, and the results are also easy to understand. The k-means algorithm is a method for grouping nearby objects into the k number of the centroid. The elbow method is a popular way to figure out the best number of clusters. When given several clusters, k, this approach calculates the total of the within-cluster variance, also known as inertia, and then shows the variance curve concerning k. The best number of clusters could be the k value at the curve’s initial turning point.
The alternative technique is to use silhouette plot analysis by calculating the coefficients for each data point to measure its similarity with its cluster as compared to other clusters. The value of the silhouette coefficient is in the range [1,−1] where a high value indicates that the object is well matched to its cluster.
BIRCH Algorithm. The BIRCH algorithm is an agglomerate hierarchical clustering technique that excels at huge datasets with high dimensionality. By aggregating the cluster’s zero, first, and second moments, BIRCH generates a height-balanced clustering feature tree of nodes that summarises data. The clustering feature (CF) produced is utilised to determine the centroids and quantify the cluster’s compactness and distance. This storage of statistical information in the CF, such as the number of data points, the linear sum of N points, and the sum of squares of N points, reduces the number of recalculations and allows for incremental sub-cluster merging.
DBSCAN Algorithm. One of the most popular algorithms in the density clustering category is DBSCAN, which was introduced by Martin Ester, Hans-Peter Kriegel, Jorg Sander, and Xiaowei Xu in 1996. This algorithm separates the data points into three parts. The first part is the main point which is the points that are in the cluster. The second part is the boundary points which are the points that fall into the neighbourhood of the main point. The last part is the noise, which is the points not included in the main and boundary points. DBSCAN is very sensitive to the setting of epsilon parameters where a small value will cause the resulting clusters to be categorized as noise. At the same time, the change to a larger value will cause the clusters to be merged and become denser. DBSCAN does not require setting the number of clusters at the start-up phase of the algorithm.
3.4. Clustering Model Evaluation
In the clustering analysis phase, the accuracy or quality of clustering results will be determined and confirmed. It is an important measurement in determining which algorithm achieved the best performance by using input data for the study. Clustering evaluation is a stand-alone process and is not included during the clustering process. It is always carried out after the final output of the clustering is produced [
38]. There are two methods practiced in measuring the quality of clustering results: internal validation and external validation.
Internal validation is the process of evaluating clustering that is compared to the results of the clustering itself, namely the relationship between the structures of clusters that have been formed. This is more realistic and efficient in solving problems involving educational datasets with increasing daily sizes and dimensions.
This study used three types of internal validation methods that are often used in recent clustering studies: (1) the Davies-Bouldin index (DB), (2) the silhouette coefficient index, and (3) the Calinski-Harabasz index (CH). Important notations to be used in mathematical formulas for grouping assessment measurements are as follows: D is the input data set, n is the number of data points in D, g is the midpoint for the entire D data set, P is the dimension number of D, NC is the number of the group, C
i is the
i-th group, n
i is the number of data points in
Ci,
Ci is the midpoint for the C
i group, and
d(x,y) is the distance between points x and y [
40].
Davies-Bouldin. The Davies-Bouldin (DB) metric is a method that has long been introduced but is still widely used in internal validation measurements. DB uses intra-group variance and inter-group midpoint distance to determine the worst group pairs. Thus, the reduction in DB index value provides the optimum group number. The mathematical formula for DB is defined as Equation (3) [
40].
Silhouette Coefficient Index. The silhouette coefficient index is used to evaluate the quality and strength of a group. The high silhouette coefficient value indicates a model with a better batch and signals that an object is well matched to its batch and does not match the adjacent batches. The equation for calculating the value of the silhouette coefficient of a single sample is as Equation (4):
where
and
.
S does not consider
ci or
g and uses pairwise distances between all objects in the clusters to calculate the density
a(x). At the same time,
b(x) measures separation, the average distance of objects to alternative groups or the nearest second group. Of Equation (2), the silhouette coefficient values range can be between −1 and 1. The greater the positive value of the coefficient, the higher the probability of it being grouped in the right cluster. In contrast, elements with negative coefficient values are more likely to be grouped in the wrong cluster [
41,
42].
Calinski-Harabasz Index. The Calinski-Harabasz (CH) index measures two criteria simultaneously using the average power-added result between two groups and the average yield of two plus forces in the group. The numerator in the formula describes the degree of separation, the extent to which the midpoint of the group is scattered. The denominator also describes the density that is as close as the objects in the group gather around the midpoint. The mathematical formula for CH is defined as Equation (5):