Influence of Masonry Infill Wall Position and Openings in the Seismic Response of Reinforced Concrete Frames
Abstract
:1. Introduction
2. Modelling of Infills Masonry
3. Case Study
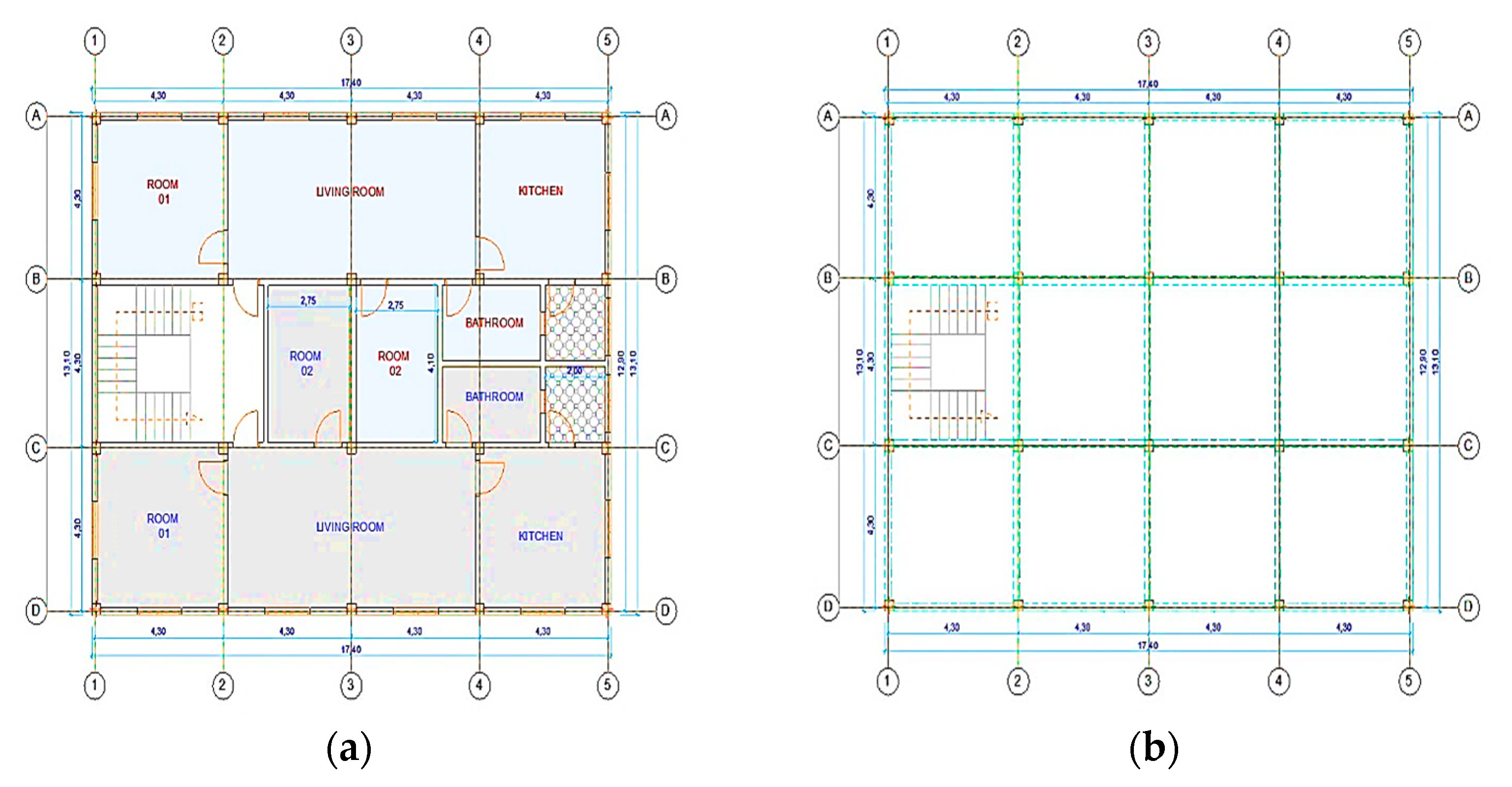
3.1. Description of the Building Structure
3.2. RC Element Modelling
3.3. Infill Walls
4. Methodology
4.1. Methodology
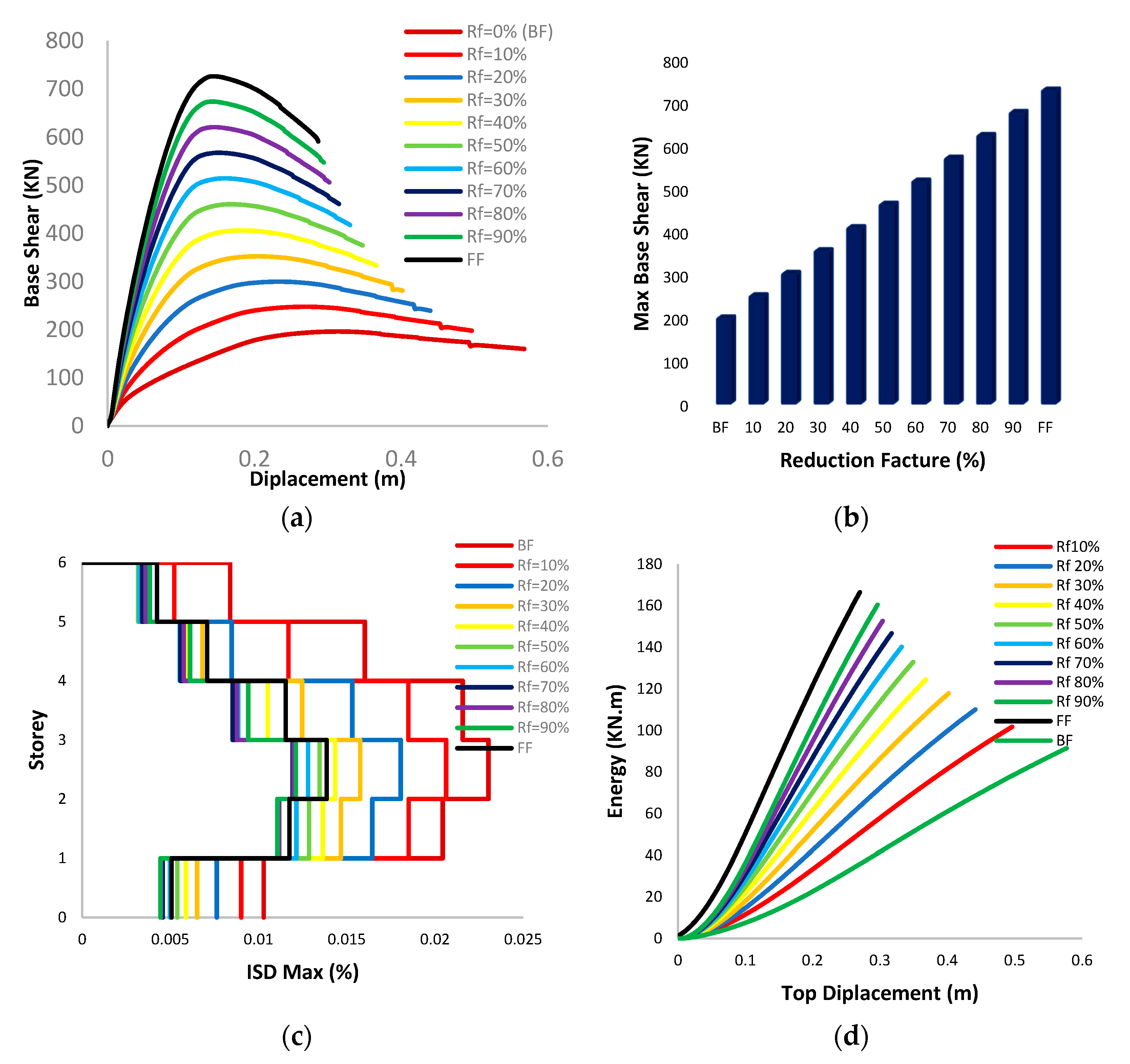
4.2. Effect of Infill Openings on the Global Response
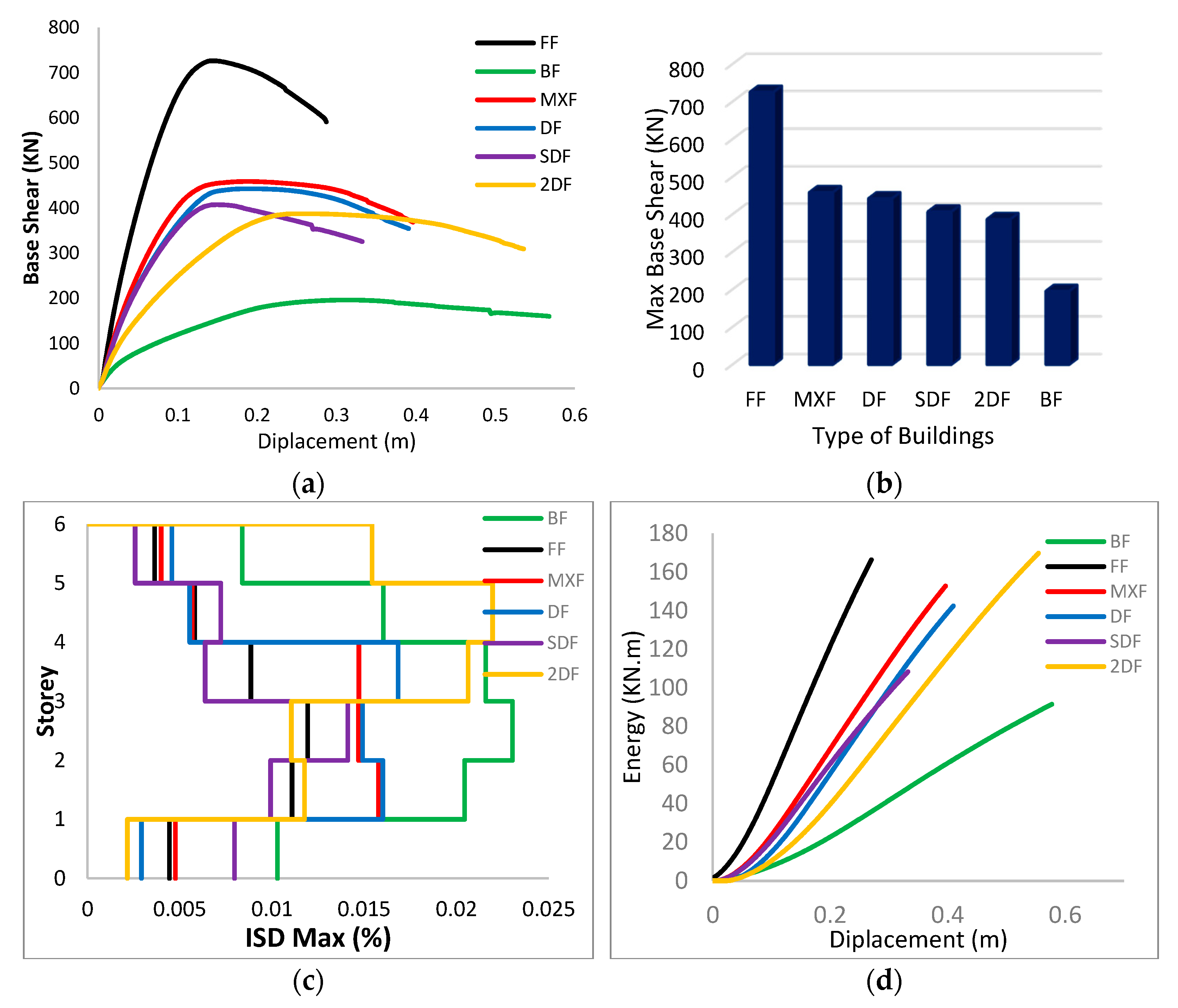
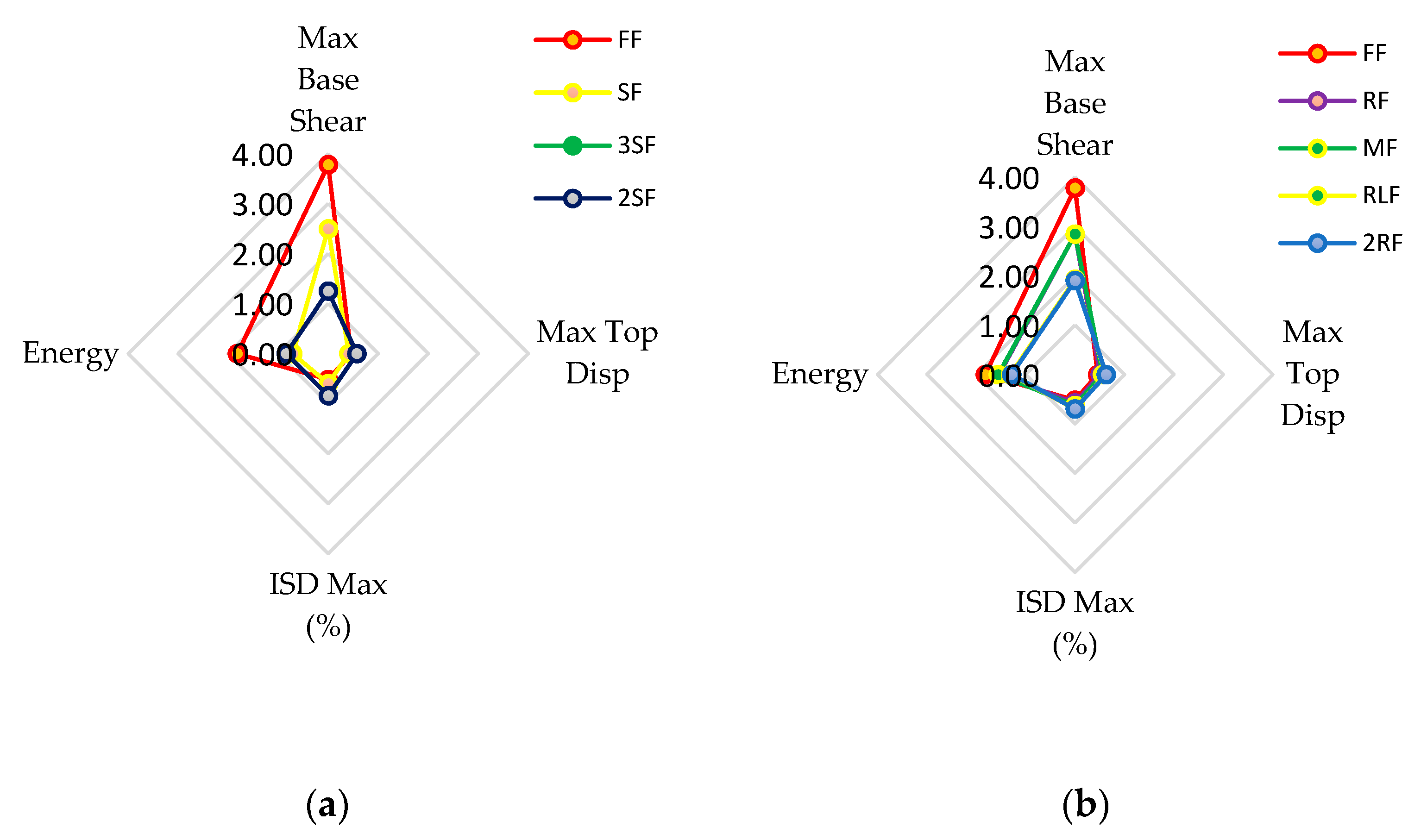
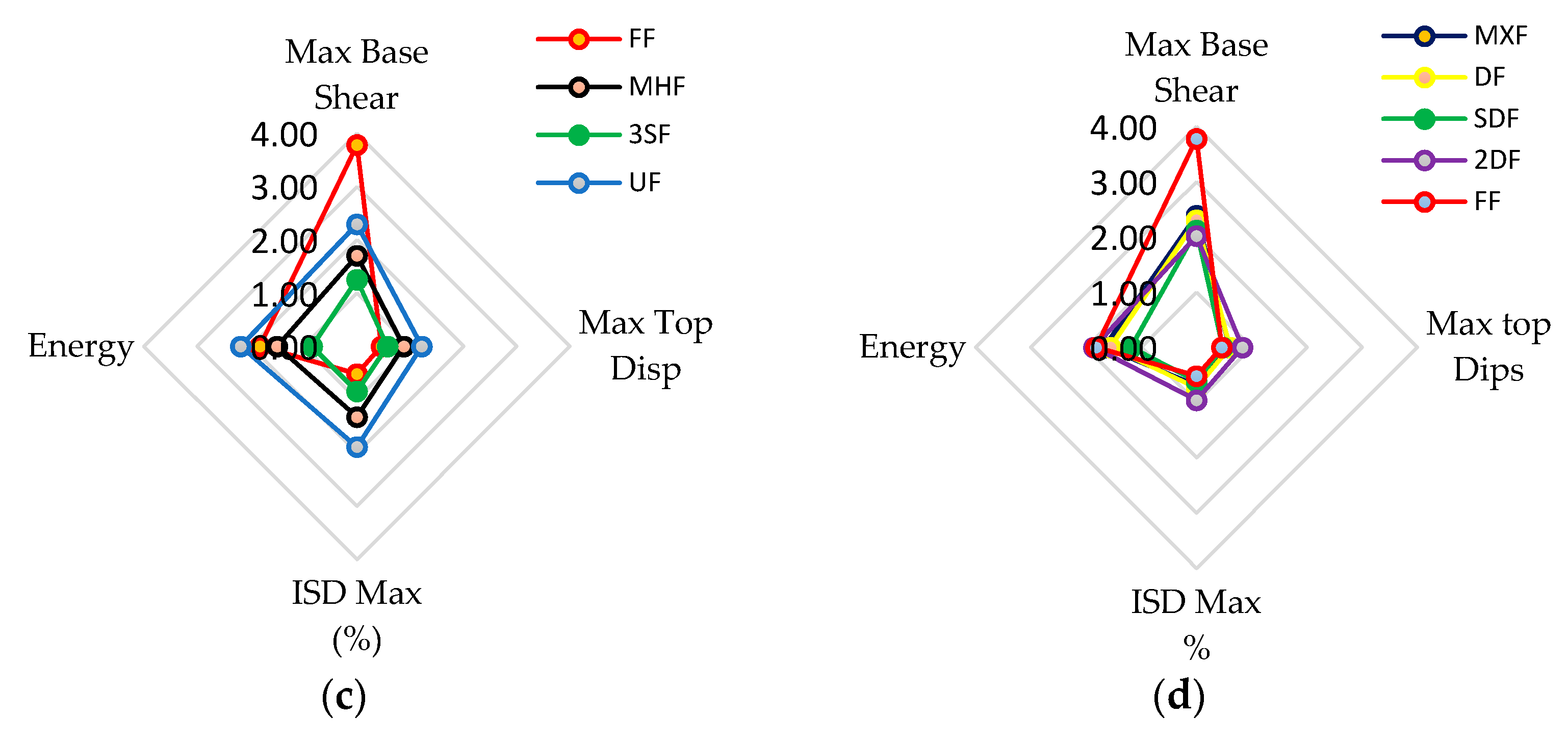
4.3. Influence of the Presence of Infill in the Global Response
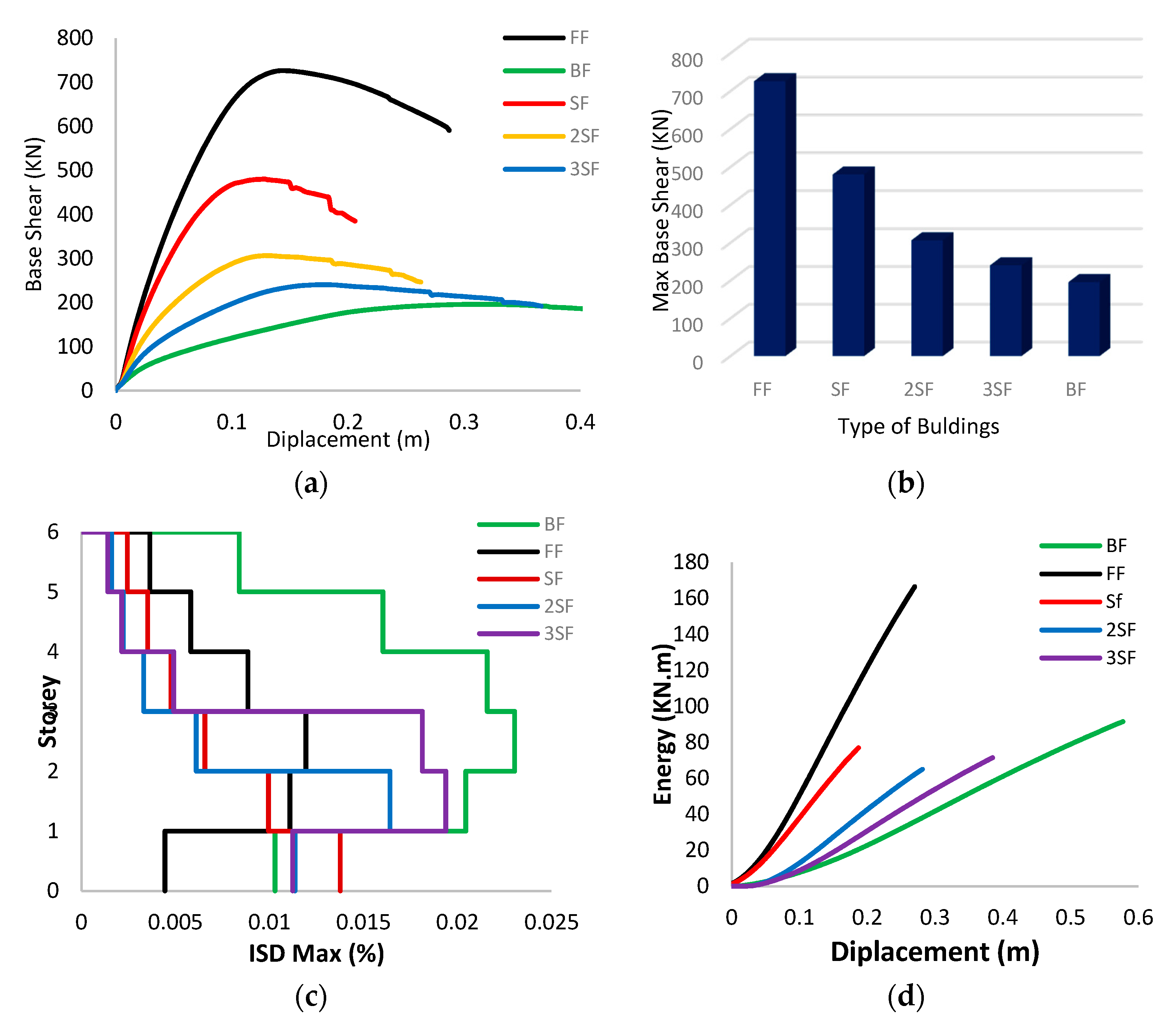
4.3.1. Case N°:1
4.3.2. Case N°:2
4.3.3. Case N°:3
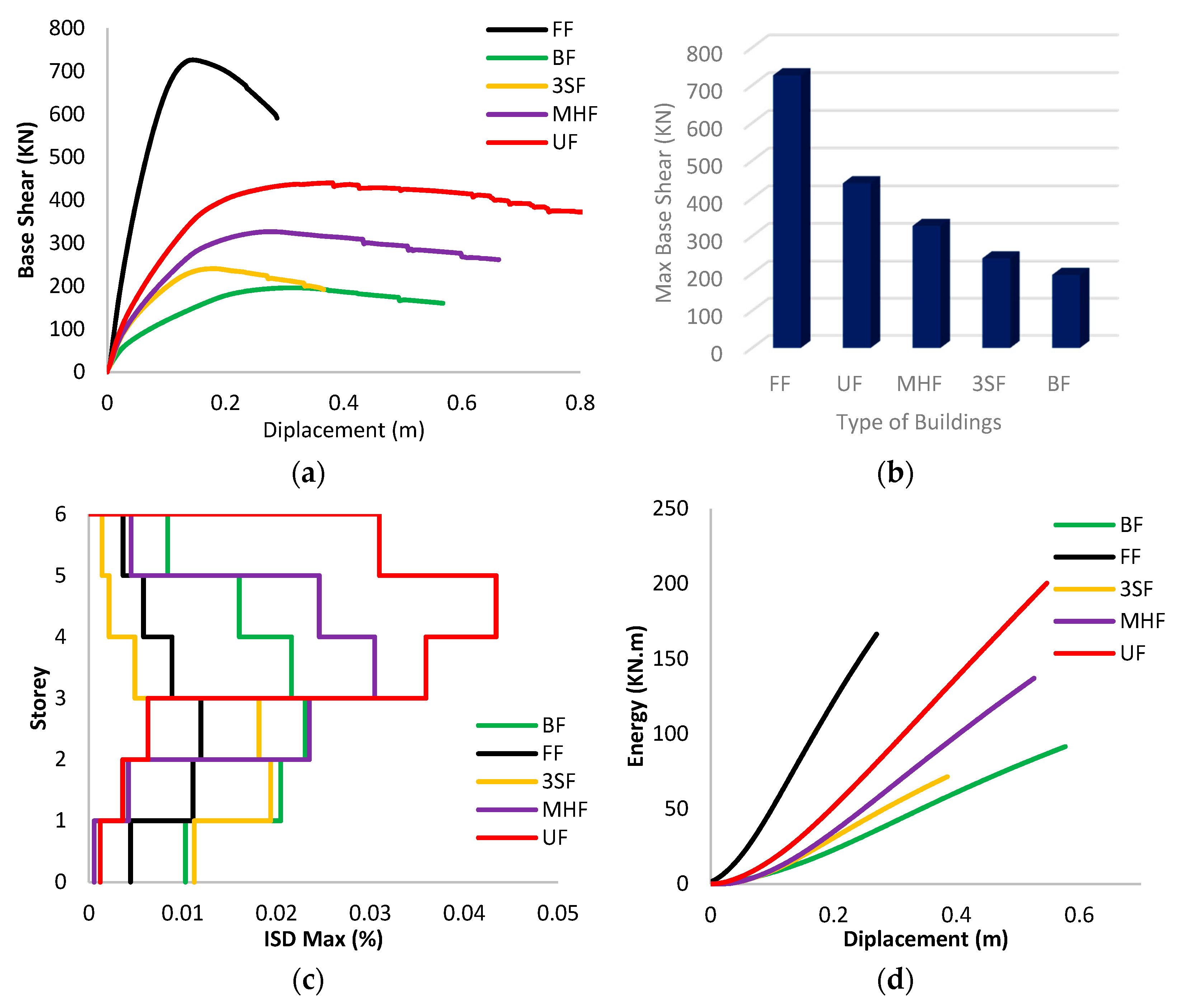
4.3.4. Case N°:4
5. Final Remarks
- The results of the pushover analysis show an increase in the initial stiffness and resistance capacity for the full infill frame compared to the bare frame, despite the brittle failure modes of the masonry wall. The presence of masonry walls has a significant effect on the observed collapse mechanism.
- The size of the openings in the infill walls has a significant influence on the stiffness. Generally, it decreases as the size of the opening increases, indicating that the decrease in stiffness is more important than the decrease in mass.
- The infill panels increase the lateral stiffness of the frames, the presence of openings reduces the lateral stiffness of the frame, and with the increase in the size of the openings, the deformation capacity increases; in general, the bare frame shows better ductility than the infill walls frame; this can be attributed to the brittle behavior of masonry infill panels.
- It appears on the one hand that the masonry increases the lateral load-bearing capacity and reduces the deformation demand, which can reduce the damage in the structures; on the other hand, an irregular distribution of the masonry can result in the relatively fragile behavior of the structure. The failure modes of the bare frames are distributed over the height of the structures; in the case of the infilled frames, the failure modes are concentrated in the lower levels.
- The infill walls distributed homogeneously over the entire height of the building, such as FF, or the alternating distribution over the entire height of the building leads (as an example: RF, MF), to an increase in the stiffness of the structural system, and thus, a decrease in the desired ductility in the disposal of the structure before reaching the collapse.
- The ratio of the contribution of the infill walls affects the energy damping, as changing the distribution of the infill walls over the entire height of the building would increase the amount of energy absorbed by the buildings, by controlling the collapse mechanism associated with the shape of this distribution (how plastic hinges are formed).
- The change in the distribution of infill walls, while maintaining their number in the building, has a major role in changing the percentage of building walls’ contribution to bearing the base shear.
- The change in the number of masonry infill walls in the building plays a major role in changing the values of the contribution ratio, as the percentage of the building walls’ contribution to bearing the base shear increases with the increase in the number of masonry walls in the building.
- The percentage of building walls’ contribution to the bearing of the base shear is mainly related to the number and distribution of the filling walls.
Author Contributions
Funding
Conflicts of Interest
References
- Uva, G.; Porco, F.; Fiore, A. Appraisal of masonry infill walls effect in the seismic response of RC framed buildings: A case study. Eng. Struct. 2012, 34, 514–526. [Google Scholar] [CrossRef]
- Uva, G.; Raffaele, D.; Porco, F.; Fiore, A. On the role of equivalent strut models in the seismic assessment of infilled RC buildings. Eng. Struct. 2012, 42, 83–94. [Google Scholar] [CrossRef]
- Gong, M.; Zuo, Z.; Wang, X.; Lu, X.; Xie, L. Comparing seismic performances of pilotis and bare RC frame structures by shaking table tests. Eng. Struct. 2019, 199, 109442. [Google Scholar] [CrossRef]
- Romão, X.; Costa, A.; Paupério, E.; Rodrigues, H.; Vicente, R.; Varum, H. Field observations and interpretation of the structural performance of constructions after the 11 May 2011 Lorca earthquake. Eng. Fail. Anal. 2013, 34, 670–692. [Google Scholar] [CrossRef]
- Mohamed, H.; Xavier, R. Robust calibration of macro-models for the in-plane behav-ior of masonry infilled RC frames. J. Earthq. Eng. 2021, 25, 407–433. [Google Scholar] [CrossRef]
- Mazza, F.; Mazza, M. A Numerical Model for the Nonlinear Seismic Analysis of Three-Dimensional RC Frames. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Mazza, F. Base-isolation of a hospital pavilion against in-plane-out-of-plane seismic collapse of masonry infills. Eng. Struct. 2020, 228, 111504. [Google Scholar] [CrossRef]
- Rayegani, A.; Nouri, G. Application of Smart Dampers for Prevention of Seismic Pounding in Isolated Structures Subjected to Near-fault Earthquakes. J. Earthq. Eng. 2020, 26, 4069–4084. [Google Scholar] [CrossRef]
- Memari, A.M.; Aliaari, M. Seismic Isolation of Masonry Infill Walls. In Proceedings of the Structures Congress 2004, Nashville, TN, USA, 22–26 May 2004. [Google Scholar] [CrossRef]
- Tsantilis, A.V.; Triantafillou, T.C. Innovative seismic isolation of masonry infills using cellular materials at the interface with the surrounding RC frames. Eng. Struct. 2018, 155, 279–297. [Google Scholar] [CrossRef]
- Jin, W.; Zhai, C.; Kong, J.; Liu, W.; Zhang, M. In-plane and out-of-plane quasi-static tests on RC frames with a new type of frame-isolated infills. Eng. Struct. 2021, 246, 113079. [Google Scholar] [CrossRef]
- Lyu, H.; Deng, M.; Han, Y.; Ma, F.; Zhang, Y. In-plane cyclic testing of full-scale reinforced concrete frames with innovative isolated infill walls strengthened by highly ductile concrete. J. Build. Eng. 2022, 57, 104934. [Google Scholar] [CrossRef]
- Centre de National Recherche Appliquee En Genie Parasismique. Regles Parasismiques Algeriennes RPA 99/Version 2003; Edition CGS; Centre de National Recherche Appliquee En Genie Parasismique: Alger, Algeria, 2003. [Google Scholar]
- Centre Scientifique et Technique du Batiment. Règles Techniques de Conception et de Calcul des Ouvrages et Constructions en Béton armé, Suivant la Méthode des états Limites: Règles BAEL 91, Révisées 99; Centre Scientifique et Technique du Batiment, Eyrolles: Paris, France, 2001; ISBN 978-2-212-10013-6. [Google Scholar]
- Dias-Oliveira, J.; Rodrigues, H.; Asteris, P.G.; Varum, H. On the Seismic Behavior of Masonry Infilled Frame Structures. Buildings 2022, 12, 1146. [Google Scholar] [CrossRef]
- Mallick, D.V.; Severn, R.T. The Behaviour of Infilled Frames under Static Loading. Proc. Inst. Civ. Eng. 1967, 38, 639–656. [Google Scholar] [CrossRef]
- Mallick, D.; Garg, R. Effect of Openings on the Lateral Stiffness of Infilled Frames. Proc. Inst. Civ. Eng. 1971, 49, 193–209. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Shing, P.B. Performance of masonry- infilled RC frames under in-plane lateral loads: Analytical modeling. In Proceedings of the NCEER Workshop on Seismic Response of Masonry, San Francisco, CA, USA, 4–5 February 1994. [Google Scholar]
- Lourenco, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Oliveira, D.; Lourenço, P. Implementation and validation of a constitutive model for the cyclic behaviour of interface elements. Comput. Struct. 2004, 82, 1451–1461. [Google Scholar] [CrossRef]
- Koutromanos, I.; Stavridis, A.; Shing, P.B.; Willam, K. Numerical modeling of masonry-infilled RC frames subjected to seismic loads. Comput. Struct. 2011, 89, 1026–1037. [Google Scholar] [CrossRef]
- Polyakov, S.V. On the interaction between masonry filler walls and enclosing frame when loaded in the plane of the wall. Transl. Earthq. Eng. 1960, 2, 36–42. [Google Scholar]
- Holmes, M. Steel Frames with Brickwork and Concrete Infilling. Proc. Inst. Civ. Eng. 1961, 19, 473–478. [Google Scholar] [CrossRef]
- Smith, B.S. Lateral Stiffness of Infilled Frames. J. Struct. Div. 1962, 88, 183–199. [Google Scholar] [CrossRef]
- Smith, B.S.; Carter, C.; Mallick, D. Discussion. A Method of Analysis for Infilled Frames. Proc. Inst. Civ. Eng. 1970, 46, 229–231. [Google Scholar] [CrossRef] [Green Version]
- Mainstone, R.J. Summary of Paper 7360. On The Stiffness and Strengths of Infilled Frames. Proc. Inst. Civ. Eng. 1971, 49, 230. [Google Scholar] [CrossRef]
- Mainstone, R.J.; Weeks, G.A. The Influence of a Bounding Frame on the Racking Stiffnesses and Strengths of Brick Walls. In Proceedings of the 2nd International Brick Masonry Conference, Building Research Establishment, Watford, UK, 12–15 April 1970; pp. 165–171. [Google Scholar]
- Saneinejad, A.; Hobbs, B. Inelastic Design of Infilled Frames. J. Struct. Eng. 1995, 121, 634–650. [Google Scholar] [CrossRef]
- Žarnić, R.; Gostič, S. Masomy infilled frames as an effective structural sub-assemblage. In Seismic Design Methodologies for the Next Generation of Codes; Routledge: New York, NY, USA, 2019; pp. 335–346. [Google Scholar]
- Dolšek, M.; Fajfar, P. The effect of masonry infills on the seismic response of a four-storey reinforced concrete frame—A deterministic assessment. Eng. Struct. 2008, 30, 1991–2001. [Google Scholar] [CrossRef]
- El-Dakhakhni, W.; Elgaaly, M.; Hamid, A.A. Three-Strut Model for Concrete Masonry-Infilled Steel Frames. J. Struct. Eng. 2003, 129, 177–185. [Google Scholar] [CrossRef]
- Crisafulli, F.J.; Carr, A.J. Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 2007, 40, 69–77. [Google Scholar] [CrossRef]
- Rodrigues, H.; Varum, H.; Costa, A. Simplified Macro-Model for Infill Masonry Panels. J. Earthq. Eng. 2010, 14, 390–416. [Google Scholar] [CrossRef]
- McKenna, F. OpenSees: A Framework for Earthquake Engineering Simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]
- O’Reilly, G.J.; Sullivan, T.J. Modeling Techniques for the Seismic Assessment of the Existing Italian RC Frame Structures. J. Earthq. Eng. 2017, 23, 1262–1296. [Google Scholar] [CrossRef]
- Scott, M.H.; Ryan, K.L. Moment-Rotation Behavior of Force-Based Plastic Hinge Elements. Earthq. Spectra 2013, 29, 597–607. [Google Scholar] [CrossRef]
- Scott, M.H.; Fenves, G.L. Plastic Hinge Integration Methods for Force-Based Beam–Column Elements. J. Struct. Eng. 2006, 132, 244–252. [Google Scholar] [CrossRef]
- Paulay, T.; Priestly, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1992; p. 744. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. IABSE reports. Available online: https://www.e-periodica.ch/digbib/view?pid=bse-re-001:1973:13::9#90 (accessed on 29 April 2022).
- Mondal, G.; Jain, S.K. Lateral Stiffness of Masonry Infilled Reinforced Concrete (RC) Frames with Central Opening. Earthq. Spectra 2008, 24, 701–723. [Google Scholar] [CrossRef]
- Hendry, A. Structural Masonry; Macmillan: Houndmills, UK, 1990; ISBN 978-1-349-14829-5. [Google Scholar] [CrossRef]
- Mohamed, H.; Romão, X. Analysis of the performance of strut models to simulate the seismic behaviour of masonry infills in partially infilled RC frames. Eng. Struct. 2020, 222, 111124. [Google Scholar] [CrossRef]
- Decanini, L.D.; Liberatore, L.; Mollaioli, F. Strength and stiffness reduction factors for infilled frames with openings. Earthq. Eng. Eng. Vib. 2014, 13, 437–454. [Google Scholar] [CrossRef]
- Asteris, P.G.; Cotsovos, D.M.; Chrysostomou, C.Z.; Mohebkhah, A.; Al-Chaar, G.K. Mathematical mi-cromodeling of infilled frames: State of the art. Eng. Struct. 2013, 56, 1905–1921. [Google Scholar] [CrossRef]
- Hamburger, R.O.; Chakradeo, A.S. Methodology for seismic capacity evaluation of steel-frame buildings with infill unreinforced masonry. In Mitigation and Damage to the Built Environment; U.S. Central United States Earthquake Consortium (CUSEC): Memphis, TN, USA, 1993; pp. 173–182. [Google Scholar]
- Thiruvengadam, V. On the natural frequencies of infilled frames. Earthq. Eng. Struct. Dyn. 1985, 13, 401–419. [Google Scholar] [CrossRef]
- Tripathy, D.; Singhal, V. Estimation of in-plane shear capacity of confined masonry walls with and without openings using strut-and-tie analysis. Eng. Struct. 2019, 188, 290–304. [Google Scholar] [CrossRef]
- Anil, Ö.; Altin, S. An experimental study on reinforced concrete partially infilled frames. Eng. Struct. 2007, 29, 449–460. [Google Scholar] [CrossRef]
- Mughal, U.A.; Qazi, A.U.; Ahmed, A.; Abbass, W.; Abbas, S.; Salmi, A.; Sayed, M.M. Impact of Openings on the In-Plane Strength of Confined and Unconfined Masonry Walls: A Sustainable Numerical Study. Sustainability 2022, 14, 7467. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. Capacity-Demand-Diagram Methods for Estimating Seismic Deformation of Inelastic Structures: SDF Systems, Report No. PEER-1999/02; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1999.
- Niewiarowski, R.W.; Rojahn, C. Seismic Evaluation and Retrofit of Concrete Buildings SEISMIC SAFE-TY COMMISSION State of California Products 1.2 and 1.3 of the Proposition 122 Seismic Retrofit Practices Improvement Program; 1996. Available online: https://www.atcouncil.org/pdfs/atc40toc.pdf (accessed on 29 April 2022).
- CEN. EN 1998-3: Eurocode 8: Design of Structures for Earthquake Resistance–Part 3: Assessment and Retrofitting of Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- FEMA 356. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]


| Concrete Fc (MPa) | Steel | Infill Panel Material | ||
|---|---|---|---|---|
| Yield Stress (MPa) | Elastic Modulus E (GPa) | Brick Unit Compressive Strength fbrick (MPa) | Mortar Compressive Strength fmortat (MPa) | |
| 25.0 | 522.0 | 190.0 | 2.7 | 10.0 |
| Columns Beams | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Axis | Section (cm2) | Steel | Section (cm2) | Reinforcement | |||||
| Start | Middle | End | |||||||
| Upper | Lower | Upper | Lower | Upper | Lower | ||||
| A | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
| B | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
| C | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
| D | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
| E | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
| F | 30 × 30 | 8 ∅15 | 25 × 40 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 | 4 ∅12 |
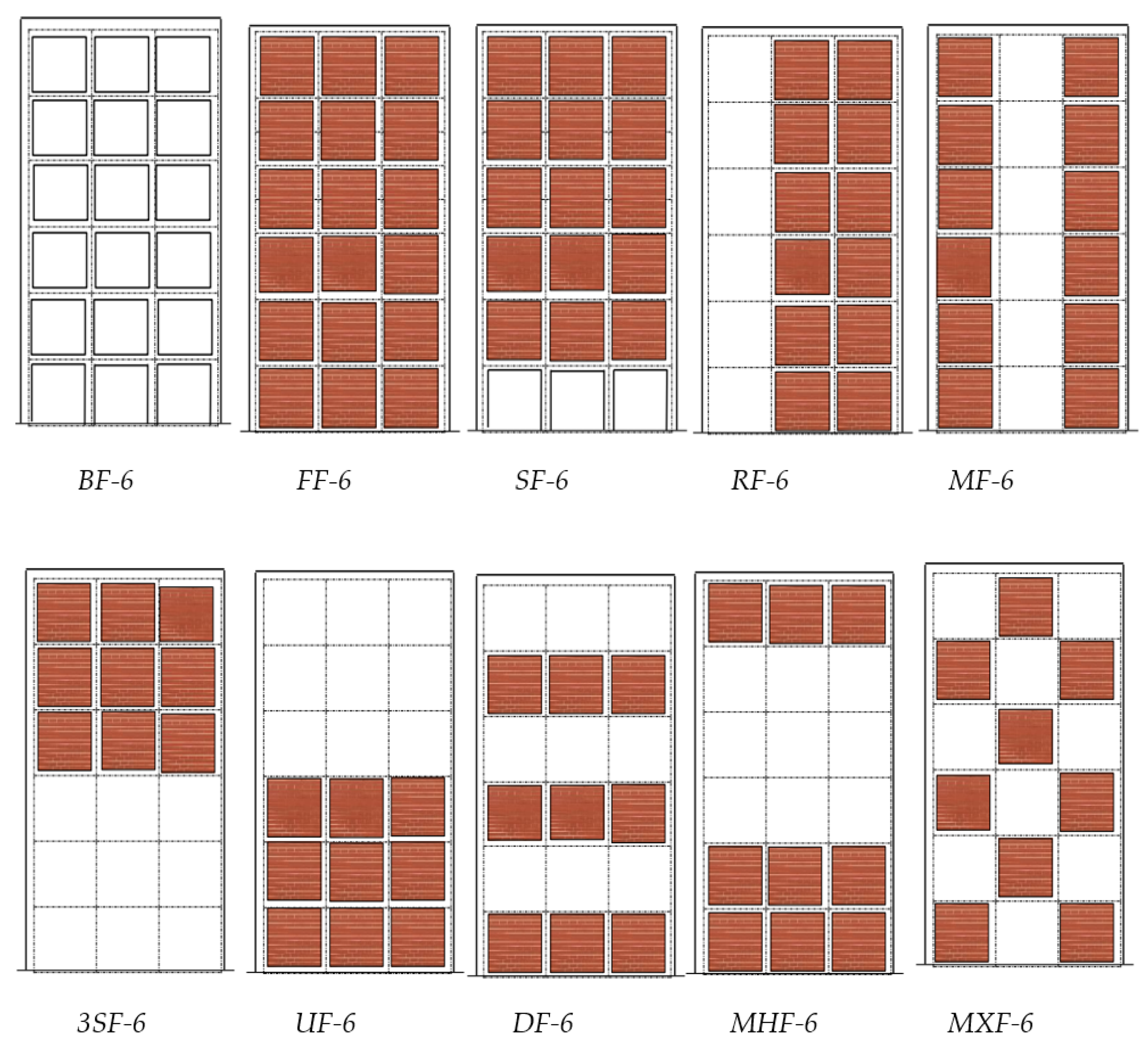
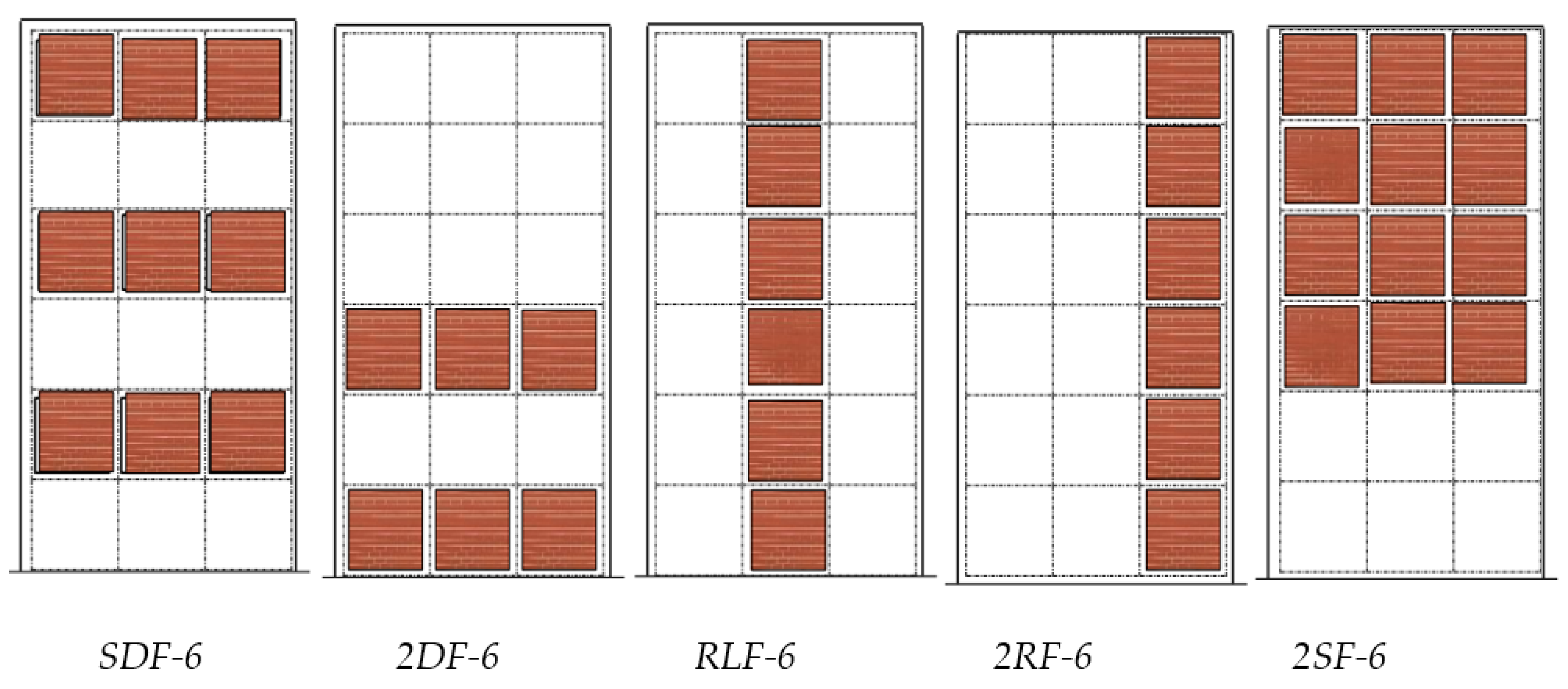
| No. | Acronym | Masonry Type | Fm (MPa) | Thickness (cm) | Full Frame | Partial Frame | Variation Presence of Infill |
|---|---|---|---|---|---|---|---|
| 1 | BF | / | / | / | / | / | / |
| 2 | FF | HB15 | 2.7 | 15 |  | ||
| 3 | FW10 | HB15 | 2.7 | 15 |  | ||
| 4 | FW20 | HB15 | 2.7 | 15 |  | ||
| 5 | FW30 | HB15 | 2.7 | 15 |  | ||
| 6 | FW40 | HB15 | 2.7 | 15 |  | ||
| 7 | F5W50 | HB15 | 2.7 | 15 |  | ||
| 8 | FW60 | HB15 | 2.7 | 15 |  | ||
| 9 | FW70 | HB15 | 2.7 | 15 |  | ||
| 10 | FW80 | HB15 | 2.7 | 15 |  | ||
| 11 | FW90 | HB15 | 2.7 | 15 |  | ||
| 12 | SF | HB15 | 2.7 | 15 | |||
| 13 | 2SF | HB15 | 2.7 | 15 | |||
| 14 | 3SF | HB15 | 2.7 | 15 | |||
| 15 | RF | HB15 | 2.7 | 15 |  | ||
| 16 | MF | HB15 | 2.7 | 15 |  | ||
| 17 | UF | HB15 | 2.7 | 15 |  | ||
| 18 | DF | HB15 | 2.7 | 15 |  | ||
| 19 | MHF | HB15 | 2.7 | 15 |  | ||
| 20 | MXF | HB15 | 2.7 | 15 |  | ||
| 21 | RLF | HB15 | 2.7 | 15 |  | ||
| 22 | 2RF | HB15 | 2.7 | 15 |  | ||
| 23 | 2DF | HB15 | 2.7 | 15 |  | ||
| 24 | SDF | HB15 | 2.7 | 15 |  |
 —type of infill distribution.
—type of infill distribution.| Models | Base Shear (KN) | Ration (%) | Max Top Displacement (m) | Ratio (%) | ISD Max (%) | Ratio (%) | Energy (KN.m) | Ratio (%) |
|---|---|---|---|---|---|---|---|---|
| BF | 196.21 | / | 0.313 | / | 0.023 | / | 91.45 | / |
| Rf = 10% | 247.7 | 26.24% | 0.2699 | −13.77% | 0.02098 | −8.78% | 101.72 | 11.23% |
| Rf = 20% | 299.72 | 52.75% | 0.234 | −25.24% | 0.0188 | −18.26% | 110.01 | 20.30% |
| R f= 30% | 352.45 | 79.63% | 0.205 | −34.50% | 0.0172 | −25.22% | 117.8 | 28.81% |
| Rf = 40% | 406.17 | 107.01% | 0.183 | −41.53% | 0.0155 | −32.61% | 124.44 | 36.07% |
| Rf = 50% | 460.63 | 134.76% | 0.168 | −46.33% | 0.0141 | −38.70% | 132.89 | 45.31% |
| Rf = 60% | 514.44 | 162.19% | 0.16 | −48.88% | 0.0136 | −40.87% | 140.17 | 53.28% |
| Rf = 70% | 567.75 | 189.36% | 0.151 | −51.76% | 0.0129 | −43.91% | 146.565 | 60.27% |
| Rf = 80% | 620.75 | 216.37% | 0.145 | −53.67% | 0.0124 | −46.09% | 152.63 | 66.90% |
| Rf = 90% | 673.99 | 243.50% | 0.143 | −54.31% | 0.0121 | −47.39% | 160.43 | 75.43% |
| FF | 726.34 | 270.19% | 0.143 | −54.31% | 0.0119 | −48.26% | 166.45 | 82.01% |
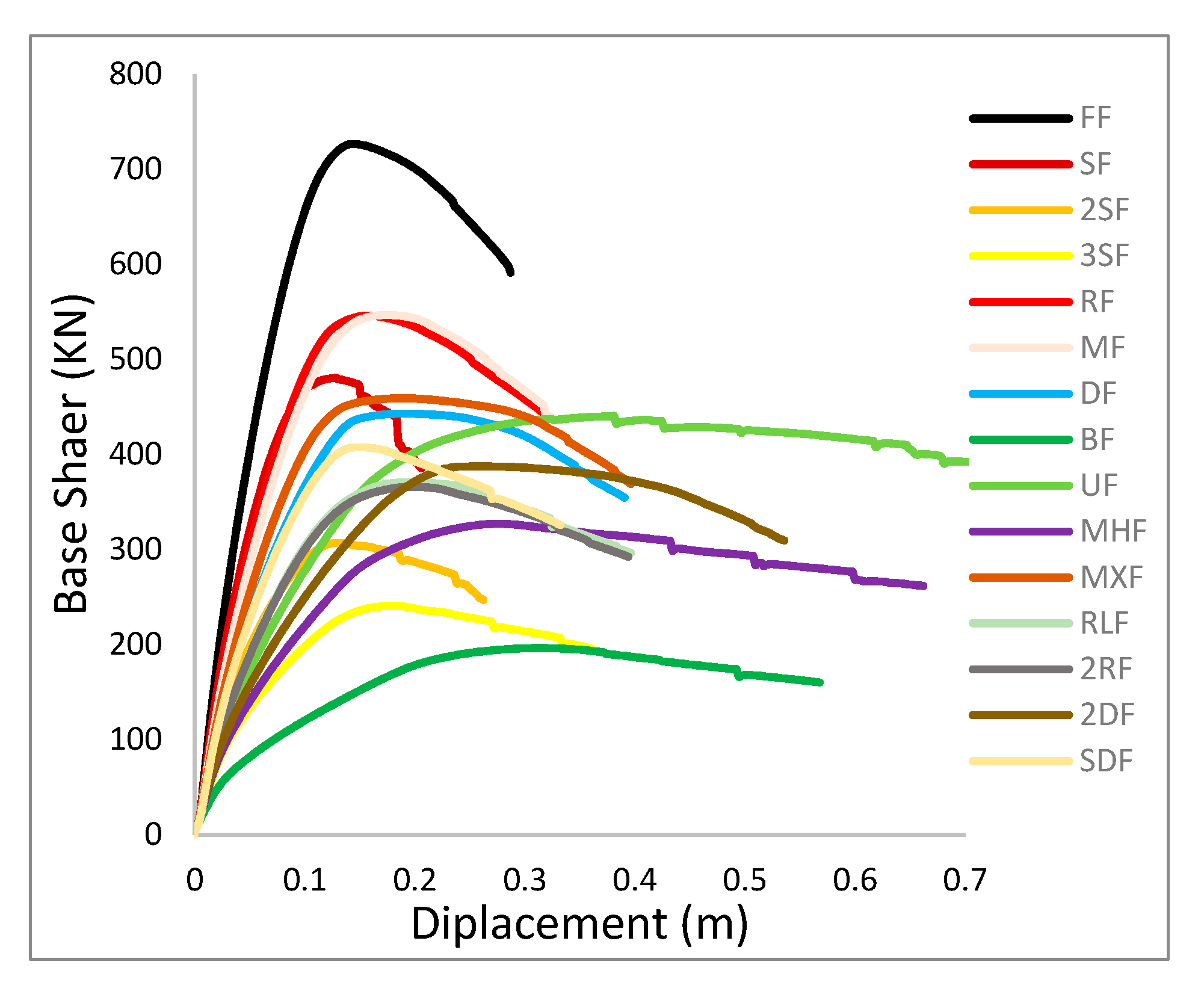
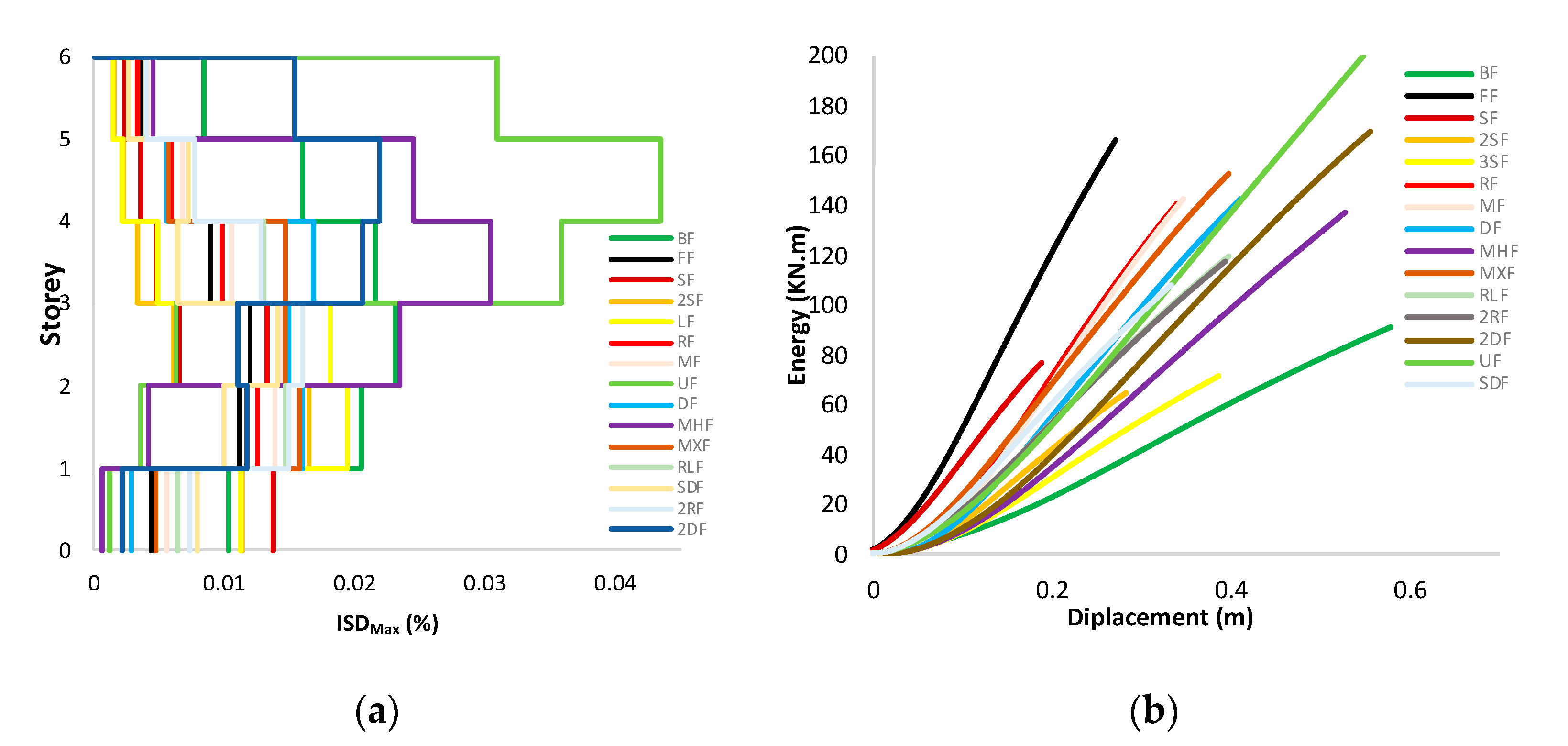
| Models | Base Shear (KN) | Max Top Displacement (m) | ISD Max (%) | Energy (KN.m) |
|---|---|---|---|---|
| BF | 192.21 | 0.313 | 0.0230 | 91.45 |
| FF | 726.34 | 0.143 | 0.0119 | 166.45 |
| SF | 480.36 | 0.128 | 0.0138 | 64.92 |
| 2SF | 306.85 | 0.128 | 0.0164 | 71.39 |
| 3SF | 240.74 | 0.179 | 0.0194 | 76.89 |
| RF | 545.83 | 0.158 | 0.0132 | 140.57 |
| MF | 546.47 | 0.173 | 0.0144 | 142.45 |
| UF | 440.13 | 0.381 | 0.0434 | 199.52 |
| DF | 442.9 | 0.19 | 0.0168 | 142.47 |
| MHF | 326.95 | 0.275 | 0.0305 | 137.02 |
| MXF | 459.04 | 0.187 | 0.0158 | 152.76 |
| RLF | 370.61 | 0.194 | 0.016 | 119.5 |
| 2RF | 365.88 | 0.197 | 0.016 | 117.34 |
| 2DF | 387.45 | 0.26 | 0.022 | 169.79 |
| SDF | 407.45 | 0.149 | 0.0141 | 108.31 |
| Models | Base Shear (KN) | Max Top Displacement (m) | ISD Max (%) | Energy (KN.m) |
|---|---|---|---|---|
| FF | 3.78 | 0.46 | 0.52 | 1.82 |
| SF | 2.50 | 0.41 | 0.60 | 0.71 |
| 2SF | 1.60 | 0.41 | 0.71 | 0.78 |
| 3SF | 1.25 | 0.57 | 0.84 | 0.84 |
| RF | 2.84 | 0.50 | 0.57 | 1.54 |
| MF | 2.84 | 0.55 | 0.63 | 1.56 |
| UF | 2.29 | 1.22 | 1.89 | 2.18 |
| DF | 2.30 | 0.61 | 0.73 | 1.56 |
| MHF | 1.70 | 0.88 | 1.33 | 1.50 |
| MXF | 2.39 | 0.60 | 0.69 | 1.67 |
| RLF | 1.93 | 0.62 | 0.70 | 1.31 |
| 2RF | 1.90 | 0.63 | 0.70 | 1.28 |
| 2DF | 2.02 | 0.83 | 0.96 | 1.86 |
| SDF | 2.12 | 0.48 | 0.61 | 1.18 |
| Study Case No°:1 | Study Case No°:2 | Study Case No°:3 | Study Case No°:4 |
|---|---|---|---|
 BF |  BF |  BF |  BF |
 FF |  FF |  FF |  FF |
 SF |  RF |  3SF |  MXF |
 2SF |  MF |  UF |  DF |
 3SF |  RLFF |  MHF |  SDF |
 2RF |  2DF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Messaoudi, A.; Chebili, R.; Mohamed, H.; Rodrigues, H. Influence of Masonry Infill Wall Position and Openings in the Seismic Response of Reinforced Concrete Frames. Appl. Sci. 2022, 12, 9477. https://doi.org/10.3390/app12199477
Messaoudi A, Chebili R, Mohamed H, Rodrigues H. Influence of Masonry Infill Wall Position and Openings in the Seismic Response of Reinforced Concrete Frames. Applied Sciences. 2022; 12(19):9477. https://doi.org/10.3390/app12199477
Chicago/Turabian StyleMessaoudi, Abdelghaffar, Rachid Chebili, Hossameldeen Mohamed, and Hugo Rodrigues. 2022. "Influence of Masonry Infill Wall Position and Openings in the Seismic Response of Reinforced Concrete Frames" Applied Sciences 12, no. 19: 9477. https://doi.org/10.3390/app12199477
APA StyleMessaoudi, A., Chebili, R., Mohamed, H., & Rodrigues, H. (2022). Influence of Masonry Infill Wall Position and Openings in the Seismic Response of Reinforced Concrete Frames. Applied Sciences, 12(19), 9477. https://doi.org/10.3390/app12199477








