Aerodynamic Modeling and Performance Analysis of Variable-Speed Coaxial Helicopter
Abstract
:1. Introduction
2. Establishment of an Aerodynamic Model
2.1. Rotor Aerodynamic Model
2.1.1. Definition of the Coordinate System
2.1.2. Rotor Aerodynamic Force
2.2. Induced Velocity Model
2.3. Dynamic Model of Blade Swing
3. Model Solution and Experimental Verification
3.1. Verification Machine D-07
- (1)
- A new type of coaxial helicopter control mechanism is proposed, which adopts the control strategy of fixed pitch and variable speed, which greatly reduces the weight of the control system.
- (2)
- A coaxial helicopter transmission system is proposed, which adopts new materials and optimizes the processing mode to make its empty weight meet the requirements.
- (3)
3.2. Model Solution
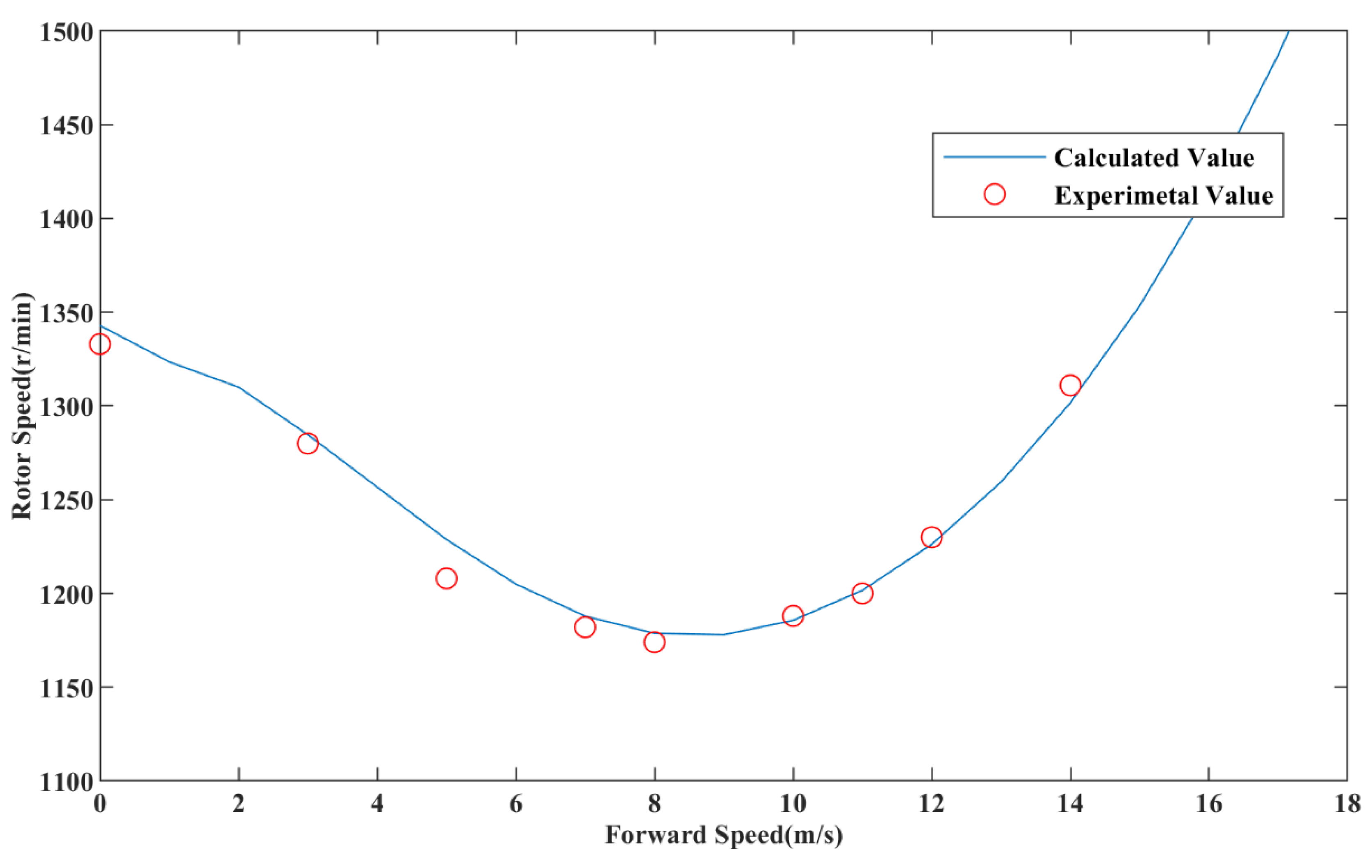
3.3. Calculation Results and Experimental Verification
4. Comparison of Required Power of Variable Speed and Variable Total Distance
5. Conclusions
- (1)
- When the forward speed is less than the corresponding hovering rotor speed, the variable-speed coaxial helicopter has lower rotor power. This speed range applies to coaxial helicopters with strict flight time requirements, which have wide application.
- (2)
- When the forward speed is higher than the corresponding hovering rotor speed, the variable-pitch coaxial helicopter has lower rotor power. This speed range is applicable to coaxial helicopters that are required to perform high-speed flight missions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, Q.; Xu, J. Load modelling and experimental verification of variable speed coaxial rotor. Exp. Mech. 2012, 27, 433–439. [Google Scholar]
- Cheney, M.C.J. The ABC helicopter. J. Am. Helicopter Soc. 1969, 14, 10–19. [Google Scholar] [CrossRef]
- Coleman, P. A Survey of Theoretical and Experimental Coaxial Rotor; NASA Technical Paper 3675; NASA: Washington, DC, USA, March 1997.
- Leishman, J.G.; Ananthan, S. An optimum coaxial rotor system for axial flight. J. Am. Helicopter Soc. 2008, 53, 366–381. [Google Scholar] [CrossRef]
- Leishman, J.G.; Bhagwat, M.J.; Bagai, A. Free-vortex filament methods for the analysis of helicopter rotor wake. J. Aircr. 2002, 39, 759–775. [Google Scholar] [CrossRef]
- Griffiths, D.; Ananthan, S.; Leishman, J. Predictions of Rotor Performance in Ground Effect Using a Free-Vortex Wake Model. J. Am. Helicopter Soc. 2005, 50, 302–314. [Google Scholar] [CrossRef]
- Nagashima, T.; Nakanishi, K. Optimum performance and wake geometry of the co-axial rotor in hover. In Proceedings of the 7th European Rotorcraft and Powered Life Forum, Garmisch-Partenkirchen, Germany, 8–11 September 1981. [Google Scholar]
- Brown, R.E.; Kim, H.W. Coaxial Rotor Performance and Wake Dynamics in Steady and Manoeuvring Flight. In Proceedings of the American Helicopter Society 62nd Annual Forum, Phoenix, AZ, USA, 9–11 May 2006. [Google Scholar]
- Qi, H.; Xu, G.; Lu, C.; Shi, Y. A study of coaxial rotor aerodynamic interaction mechanism in hover with the high-efficient trim model. Aerosp. Sci. Technol. 2019, 84, 1116–1130. [Google Scholar] [CrossRef]
- Ramasamy, M. Measurements comparing hover performance of single, Coaxial, Tandem, and tilt-rotor configurations. Annu. Forum Proc.—AHS Int. 2013, 4, 2439–2461. [Google Scholar]
- Passe, B.; Sridharan, A.; Baeder, J. Computational investigation of coaxial rotor interactional aerodynamics in steady forward flight. In Proceedings of the 33rd 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Gessow, A. Effect of Rotor-Blade Twist and Plan-Form Taper on a Helicopter Hovering Performance; NASA: Washington, DC, USA, 1948.
- Zhao, Q.; Liu, Y. Controllability Analysis of multi-rotor aircraft. J. Aeronaut. 2017, 38 (Suppl. S1), 163–170. [Google Scholar]
- Song, Y.; Wang, H.; Lin, Z. Performance analysis and test of variable pitch and variable speed multi-axis rotor aircraft. J. Aeronaut. Dyn. 2018, 33, 1033–1040. [Google Scholar]
- López-Martínez, M.; Ortega, M.G.; Vivas, C.; Rubio, F.R. Nonlinear L 2 control of a laboratory helicopter with variable speed rotors. Automatica 2007, 43, 655–661. [Google Scholar] [CrossRef]
- Belmonte, L.M.; Morales, R.; Fernandez-Caballero, A.; Somolinos, J.A. A Tandem Active Disturbance Rejection Control for a Laboratory Helicopter with Variable-Speed Rotors. IEEE Trans. Ind. Electron. 2016, 63, 6395–6406. [Google Scholar] [CrossRef]
- Zhou, G.; Hu, J.; Cao, Y.; Wang, J. Study on flight dynamics simulation mathematical model of coaxial helicopter. J. Aeronaut. 2003, 24, 293–295. [Google Scholar]
- Zhou, G.; Hu, J.; Cao, Y.; Wang, J. Study on load calculation model of twin rotors of coaxial helicopter. J. Aeronaut. Dyn. 2003, 18, 343–347. [Google Scholar]
- McAlister, K.W.; Tung, C. Experimental study of a hovering coaxial rotor with highly twisted blades. In Proceedings of the American Helicopter Society International Annual Forum, Montreal, QC, USA, 29 April–1 May 2008; Volume 3, pp. 1765–1781. [Google Scholar]
- Chen, R. A survey of nonuniform inflow models for rotorcraft flight. Flight Dyn. Control Appl. 1990, 14, 147–184. [Google Scholar]
- Johnson, W. Helicopter Theory; Dover Publications: New York, NY, USA, 1980; pp. 121–139. [Google Scholar]
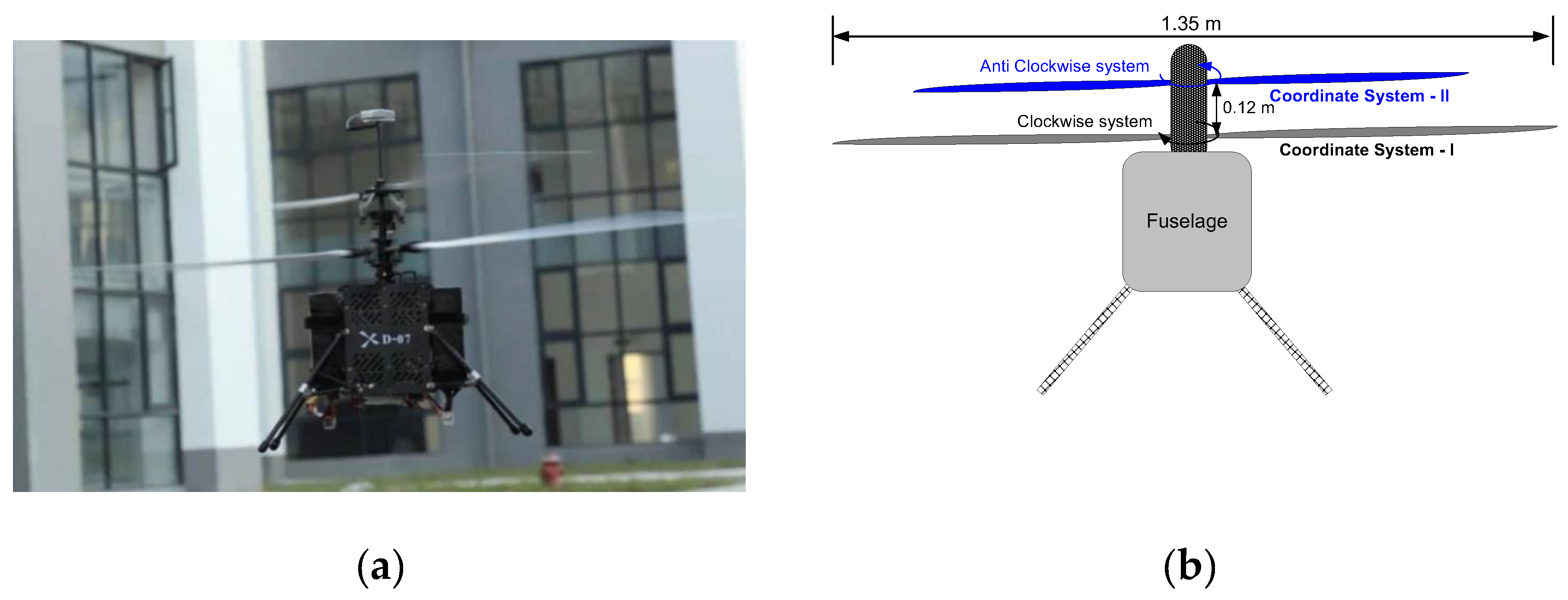


| Parameter | Numerical Value |
|---|---|
| Rotor diameter | 1.35 m |
| Number of rotors | 2 |
| Rotor mounting angle | 12° |
| Maximum takeoff weight | 7 kg |
| Battery capacity | 16 Ah |
| Swing hinge offset | 0.011 m |
| Distance between upper and lower rotors | 0.12 m |
| Flapping rubber stiffness coefficient | 288 N·m/rad |
| Blade weight | 150 g |
| Lower rotor coordinates (under fuselage coordinate system) | (0, 0, 0.13) |
| Rotor coordinates (under fuselage coordinate system) | (0, 0, 0.25) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, A.; Wang, F.; Chen, M.; Li, L. Aerodynamic Modeling and Performance Analysis of Variable-Speed Coaxial Helicopter. Appl. Sci. 2022, 12, 9534. https://doi.org/10.3390/app12199534
Xu A, Wang F, Chen M, Li L. Aerodynamic Modeling and Performance Analysis of Variable-Speed Coaxial Helicopter. Applied Sciences. 2022; 12(19):9534. https://doi.org/10.3390/app12199534
Chicago/Turabian StyleXu, Anan, Fang Wang, Ming Chen, and Liang Li. 2022. "Aerodynamic Modeling and Performance Analysis of Variable-Speed Coaxial Helicopter" Applied Sciences 12, no. 19: 9534. https://doi.org/10.3390/app12199534
APA StyleXu, A., Wang, F., Chen, M., & Li, L. (2022). Aerodynamic Modeling and Performance Analysis of Variable-Speed Coaxial Helicopter. Applied Sciences, 12(19), 9534. https://doi.org/10.3390/app12199534









