Development and Comparison of Ten Differential-Evolution and Particle Swarm-Optimization Based Algorithms for Discount-Guaranteed Ridesharing Systems
Abstract
1. Introduction
- First, we propose a decision problem that offers a minimal cost savings discount for drivers and passengers. The ability to offer a minimal cost savings discount to users is essential for incentivizing participants to accept a ridesharing model. However, the existing literature and our previous paper only focused on the maximization of the overall savings or benefits. The issue of guaranteeing a minimal cost savings discount in ridesharing systems has not been addressed in the literature. Hence, the problem addressed and the decision model proposed in this paper are different from those discussed in our previous studies and the existing literature, in that we focus on the discount-guaranteed ridesharing problem.
- Second, ten solution algorithms are proposed in this study to provide decision support tools for finding a set of users for whom the minimal cost savings discount can be guaranteed and the total cost savings achieved can be optimized.
- Third, we compare the proposed algorithms by analyzing the results of several test cases to provide a guideline for selecting an appropriate solution algorithm.
2. Literature Review
3. Discount-Guaranteed Ridesharing Problem
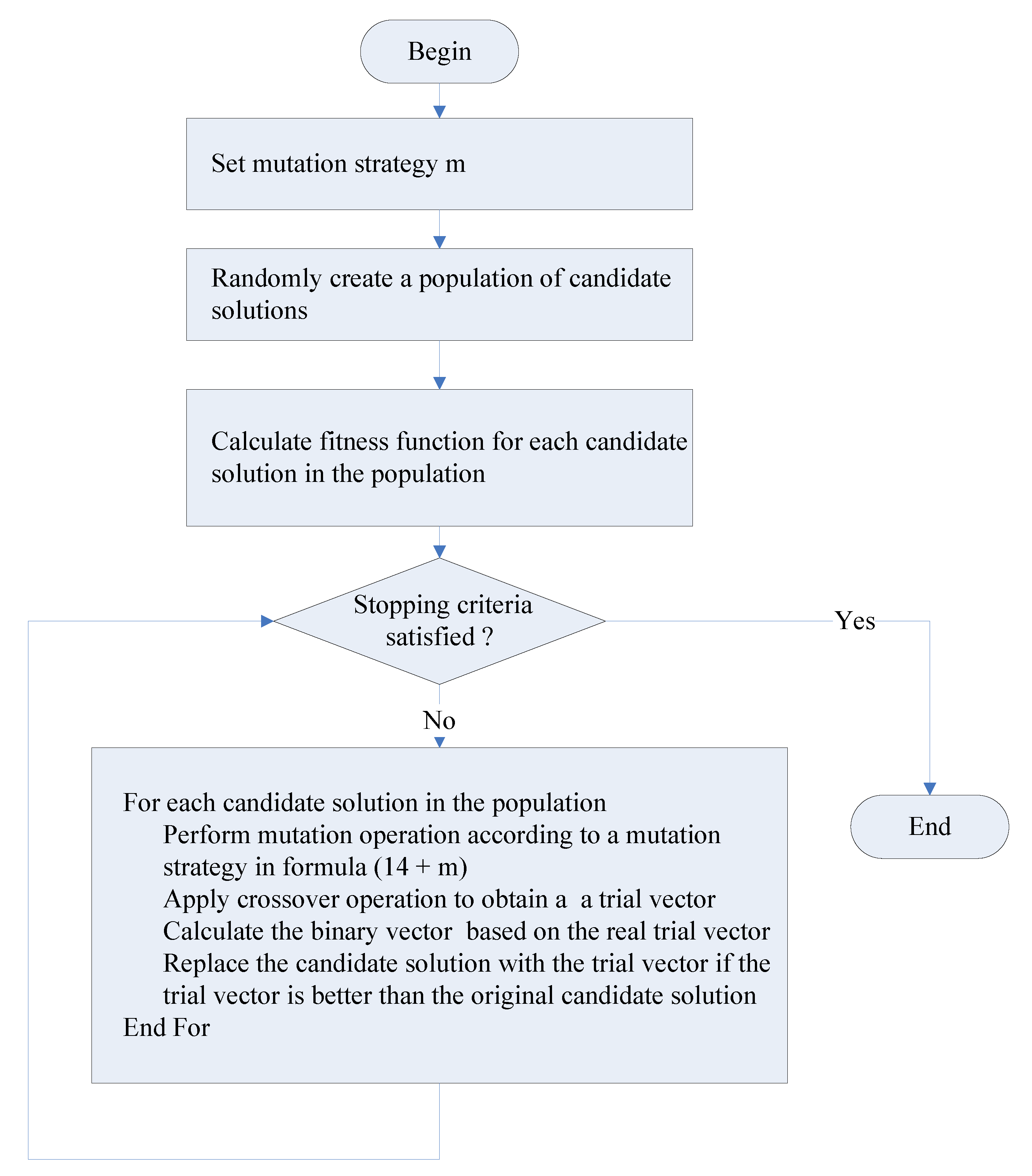
4. Solution Approach
| Algorithm1. Discrete Differential Evolution (DE) Algorithm with Mutation Strategy m |
| Step 0: Set parameters |
| Step 0-1: Set mutation strategy m |
| Step 0-2: Set parameters |
| Set G |
| Set NP |
| CR = 0.5 |
| Set Fi for |
| Step 1: Initialization |
| Step 1-1: |
| Generate a population {zi, } randomly |
| Step 1-2: |
| Compute H1(zi) |
| Step 1-3: |
| Step 2: Main Loop |
| While (t < G) |
| For i = 1 to NP |
| Step 2.1: Perform mutation operations |
| If (m = 1) |
| Perform mutation operation to compute mutant vector vi according to formula (15) |
| Else If (m = 2) |
| Perform mutation operation to compute mutant vector vi according to formula (16) |
| Else If (m = 3) |
| Perform mutation operation to compute mutant vector vi according to formula (17) |
| Else If (m = 4) |
| Perform mutation operation to compute mutant vector vi according to formula (18) |
| Else If (m = 5) |
| Perform mutation operation to compute mutant vector vi according to formula (19) |
| Else If (m = 6) |
| Perform mutation operation to compute mutant vector vi according to formula (20) |
| Else If (m = 7) |
| Generate Fi = Ni(0.5,0.5) |
| Perform mutation operation to compute mutant vector vi according to formula (21) |
| Step 2.2: Apply crossover operation to compute trial vector ui according to formula (22) |
| Step 2.3: Compute the binary vector associated with ui |
| Step 2.4:RealToBinary for |
| Step 2.5: Update candidate i |
| If |
| zi = ui |
| End If |
| End For |
| End While |
| Algorithm 2. Discrete Particle Swarm Optimization Algorithm with Velocity Updating Strategy |
| Step 0: Set parameters |
| Step 0-1: Set velocity updating strategy v |
| Step 0-2: Set parameters |
| Set G |
| Set NP |
| Step 1: Initialization |
| Step 1-1: |
| Generate a population {zi, } of particles randomly |
| Step 1-2: |
| Compute H1(zi) |
| Step 1-3: |
| Step 2: Main Loop |
| While (t < G) |
| For each |
| For each |
| Update the velocity of particle zi according to velocity updating strategy v |
| If (v = 1) |
| Generate a random variable r1 with uniform distribution U(0,1) |
| Generate a random variable r2 with uniform distribution U(0,1) |
| Update the velocity of particle zi according to formula (23) |
| Else If (v = 2) |
| Generate a random variable r1 with uniform distribution U(0,1) |
| Generate a random variable r2 with uniform distribution U(0,1) |
| Generate a random variable r3 with uniform distribution U(0,1) |
| Update the velocity of particle zi according to Formula (24) and |
| Formula (25) |
| Else |
| Generate a random variable rp with uniform distribution U(0,1) |
| If rp > pc |
| Generate a random variable r1 with uniform distribution U(0,1) |
| Generate a random variable r2 with uniform distribution U(0,1) |
| Update the velocity of particle zi according to Formula (26) |
| Else |
| Generate a random variable r1 with uniform distribution U(0,1) |
| Update the velocity of particle zi according to formula (27) |
| End If |
| End If |
| End For |
| Step 2.3: Compute the binary vector associated with |
| RealToBinary for |
| Step 2.5:Update personal best and global best |
| If |
| = |
| End If |
| If |
| = |
| End If |
| End For |
| End While |
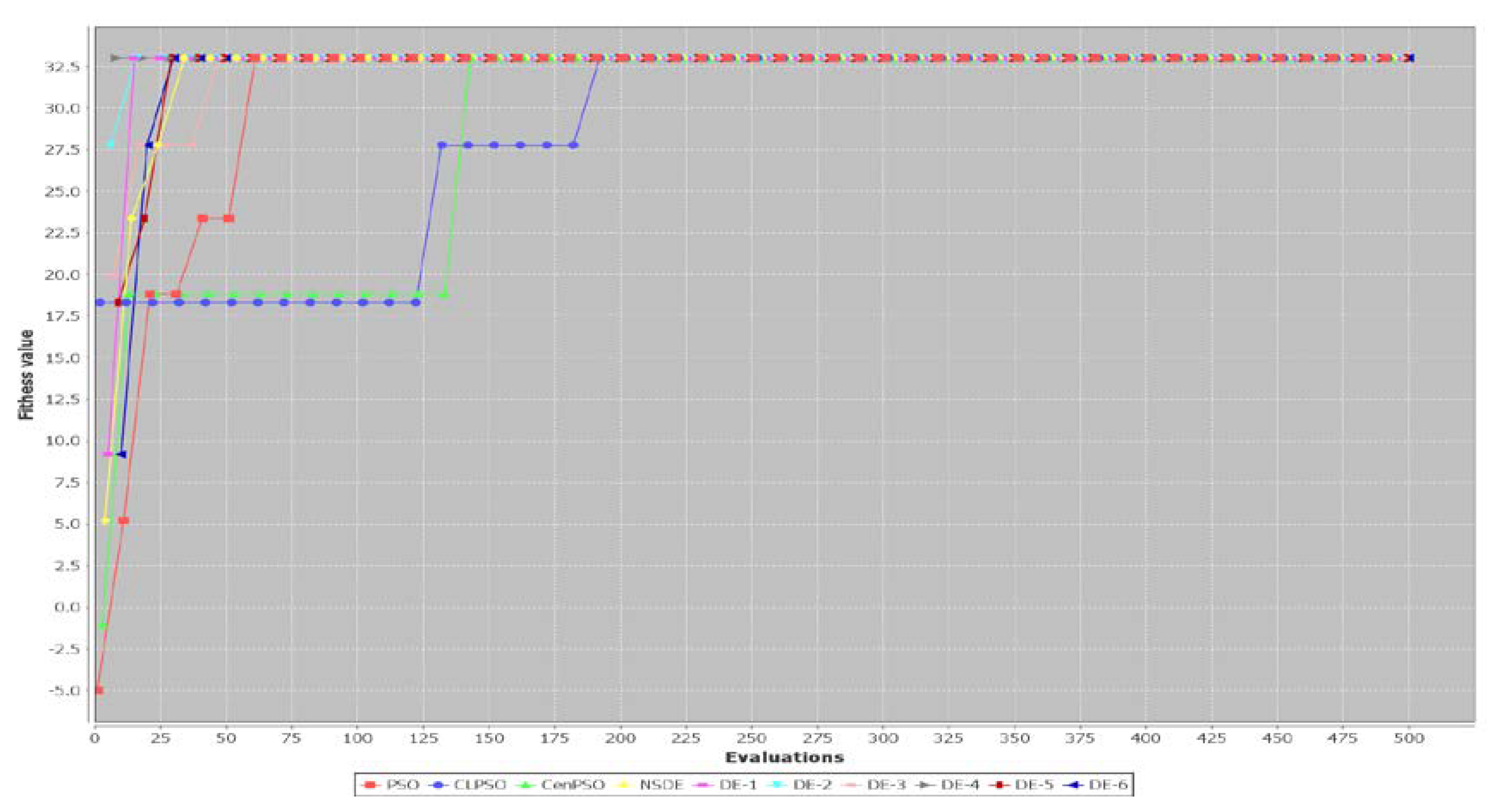
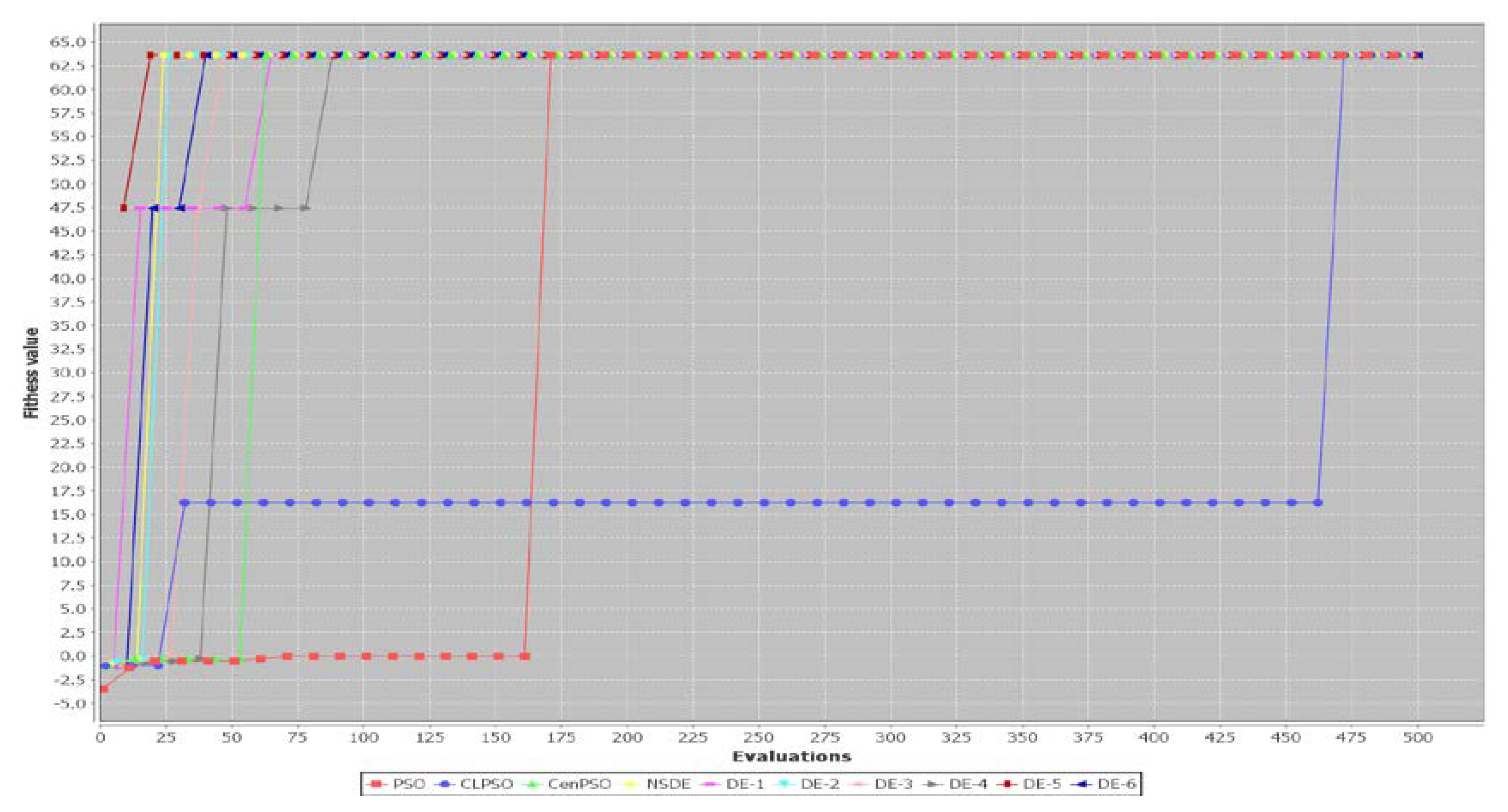
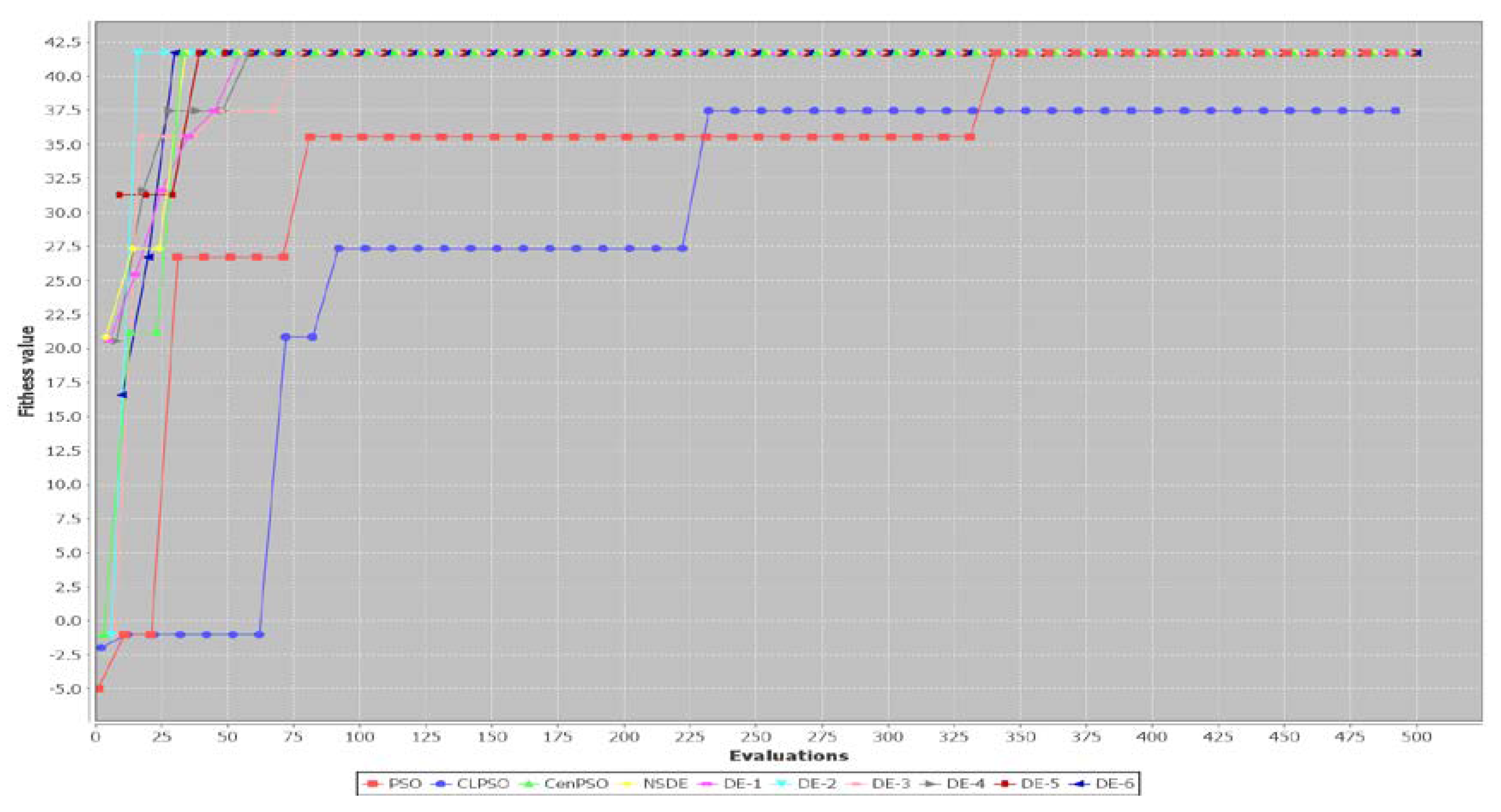
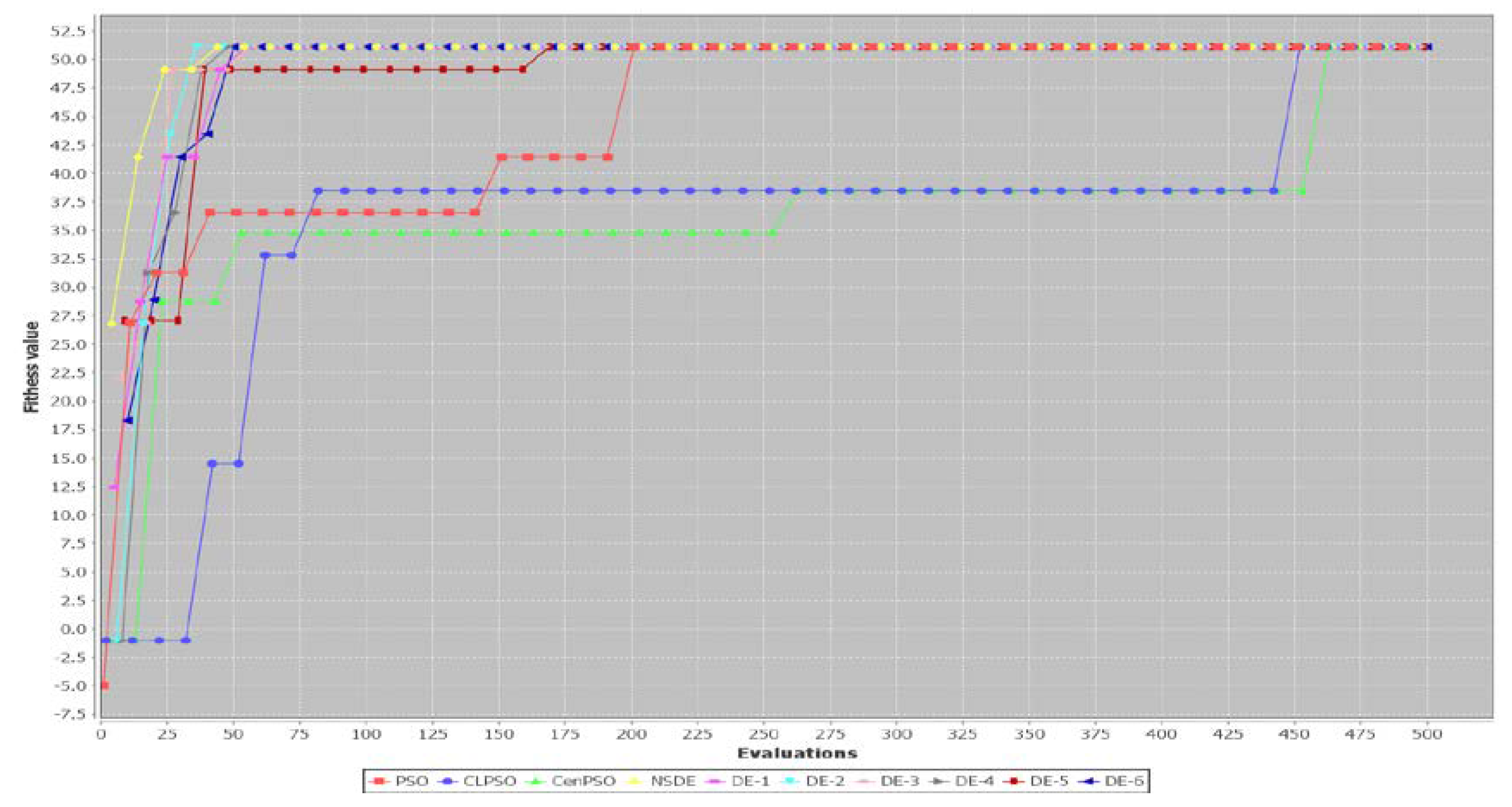
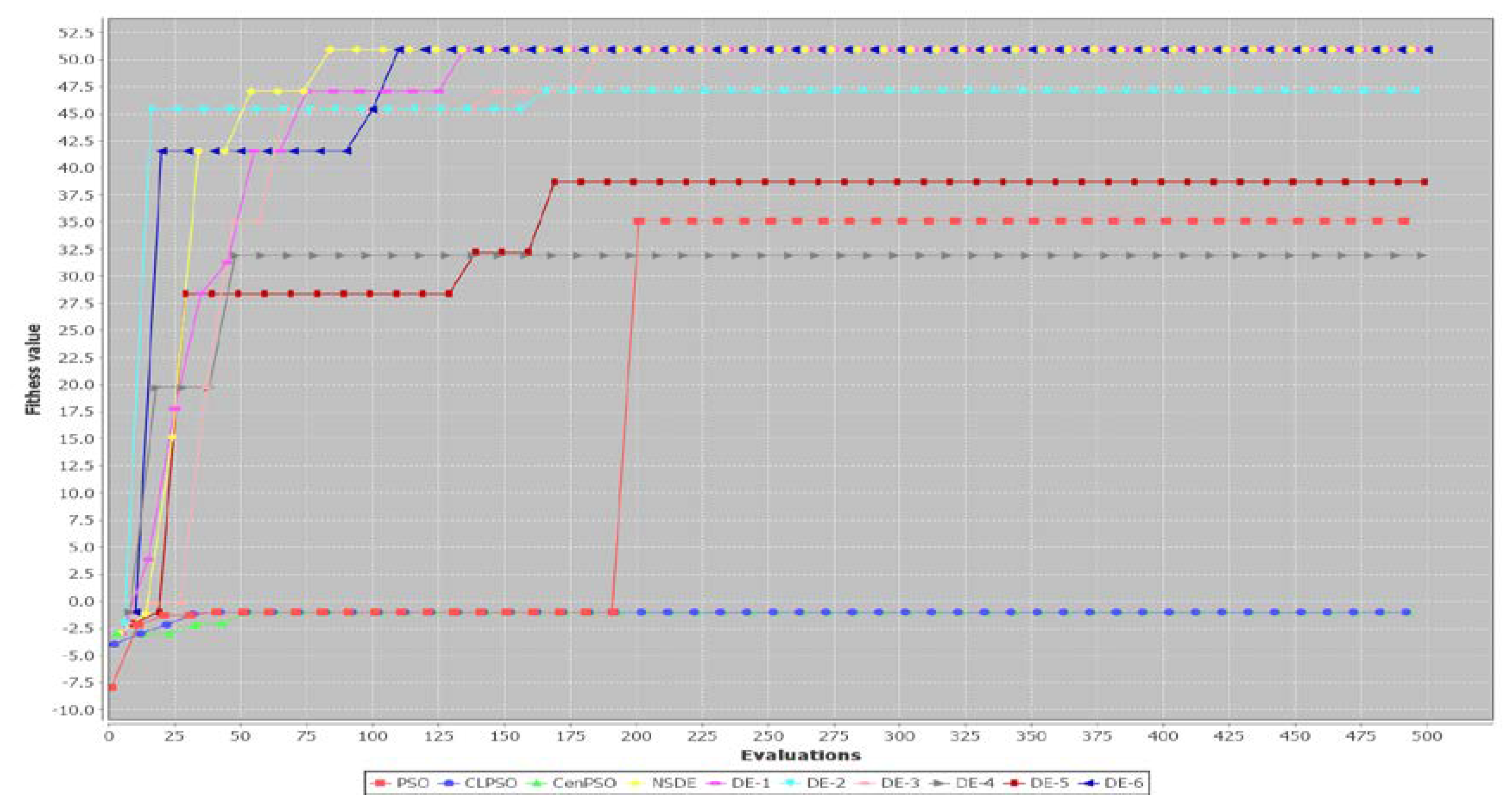
5. Results
5.1. A Small Example
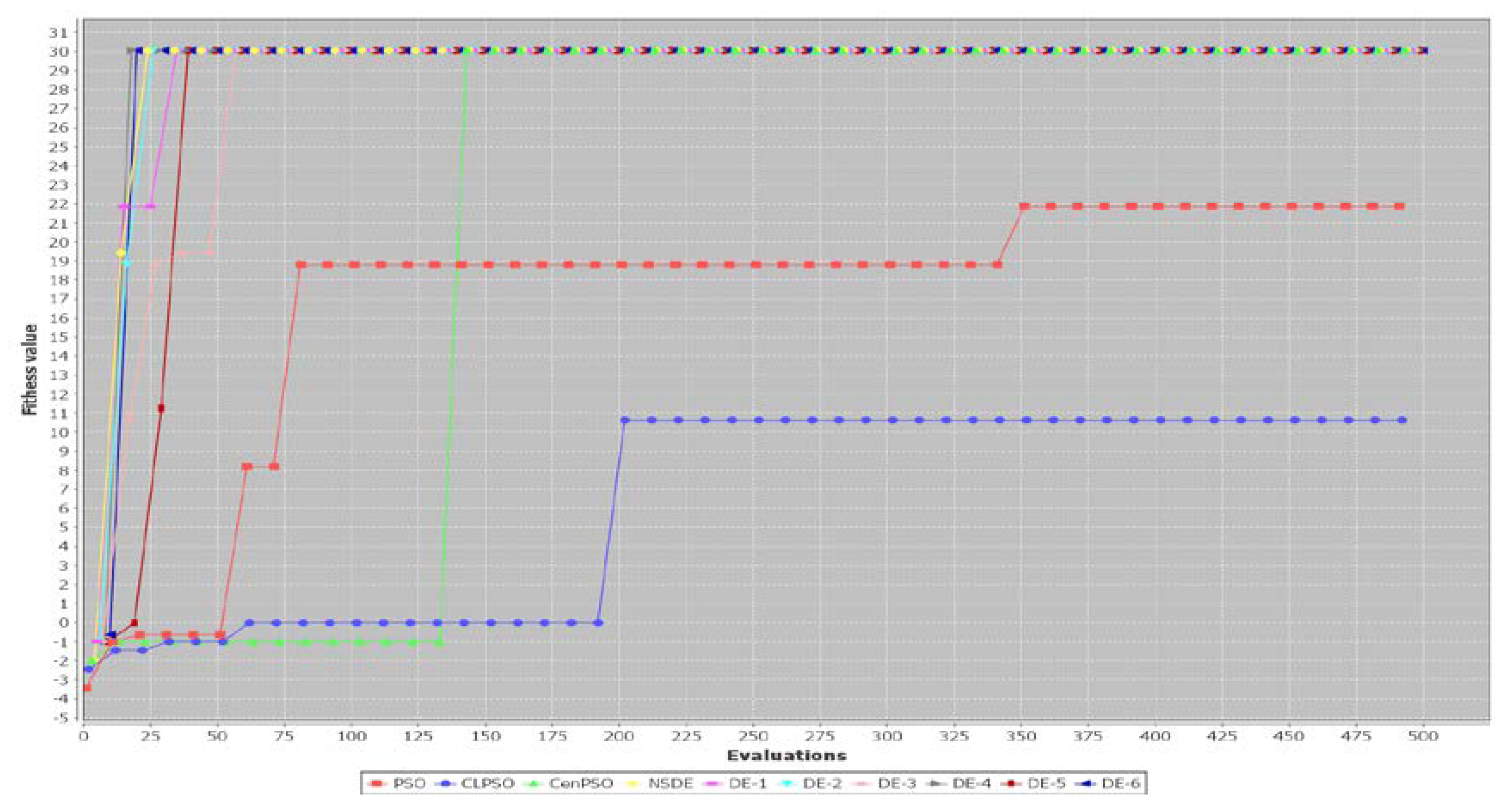
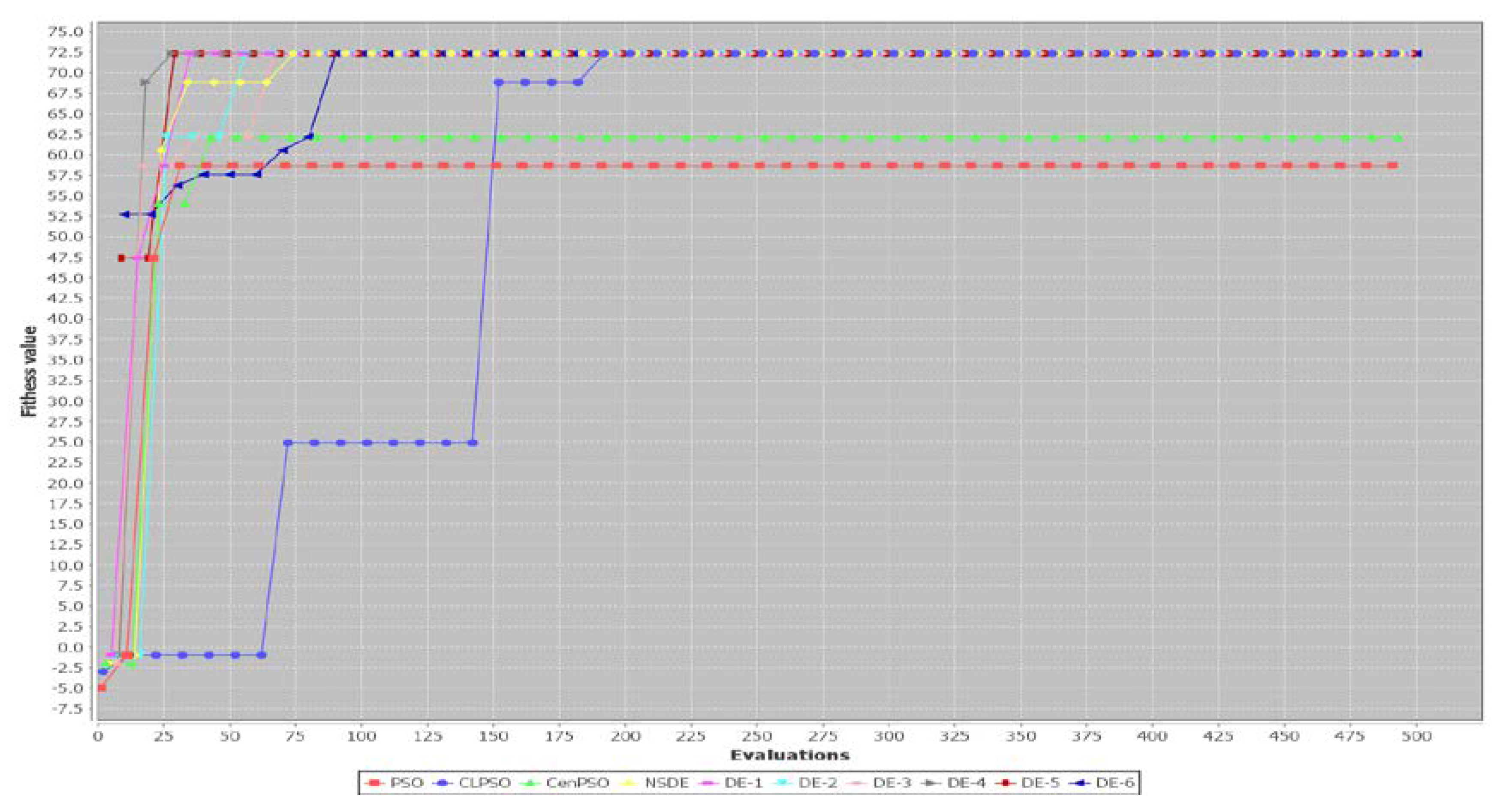
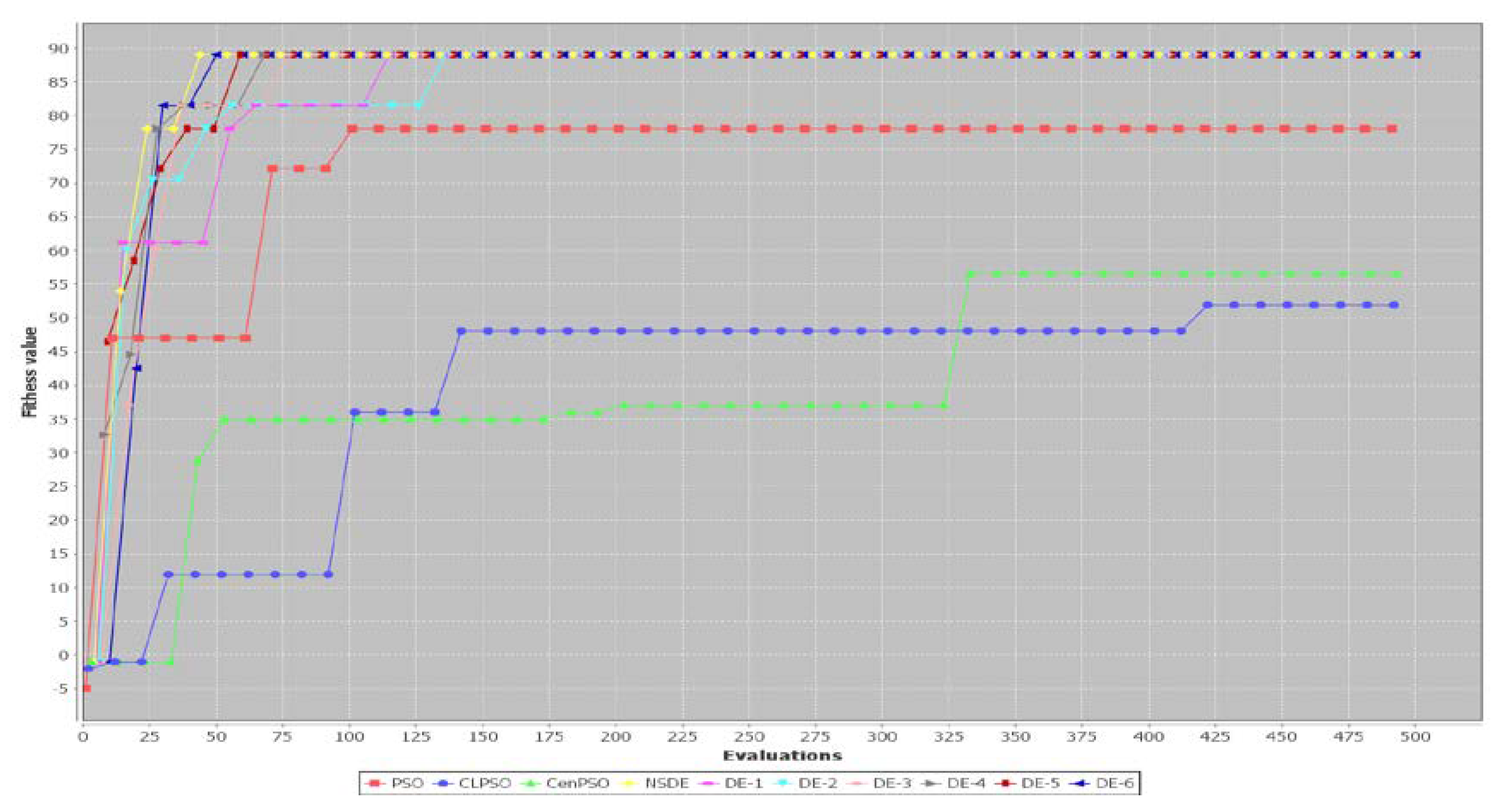
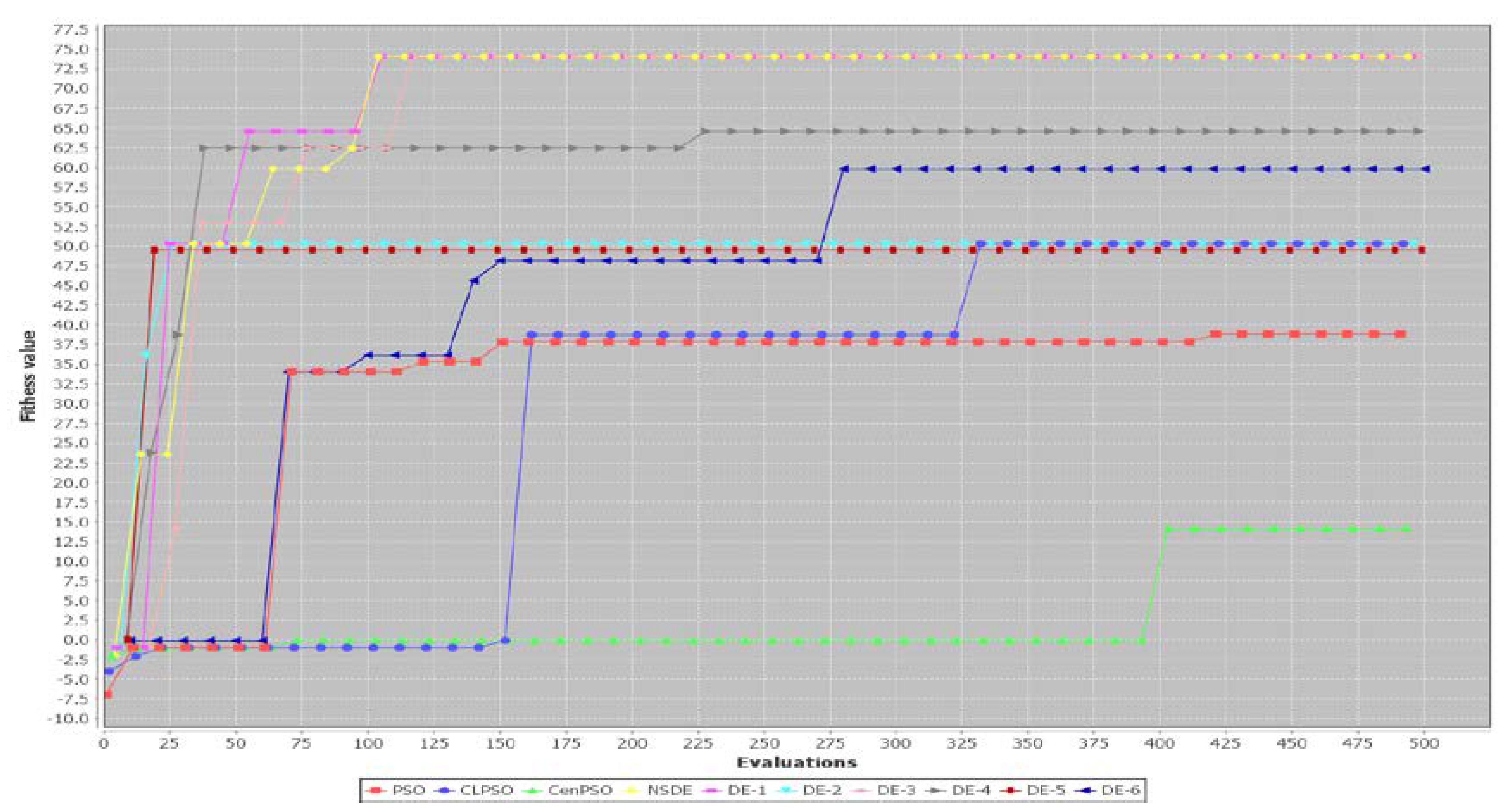
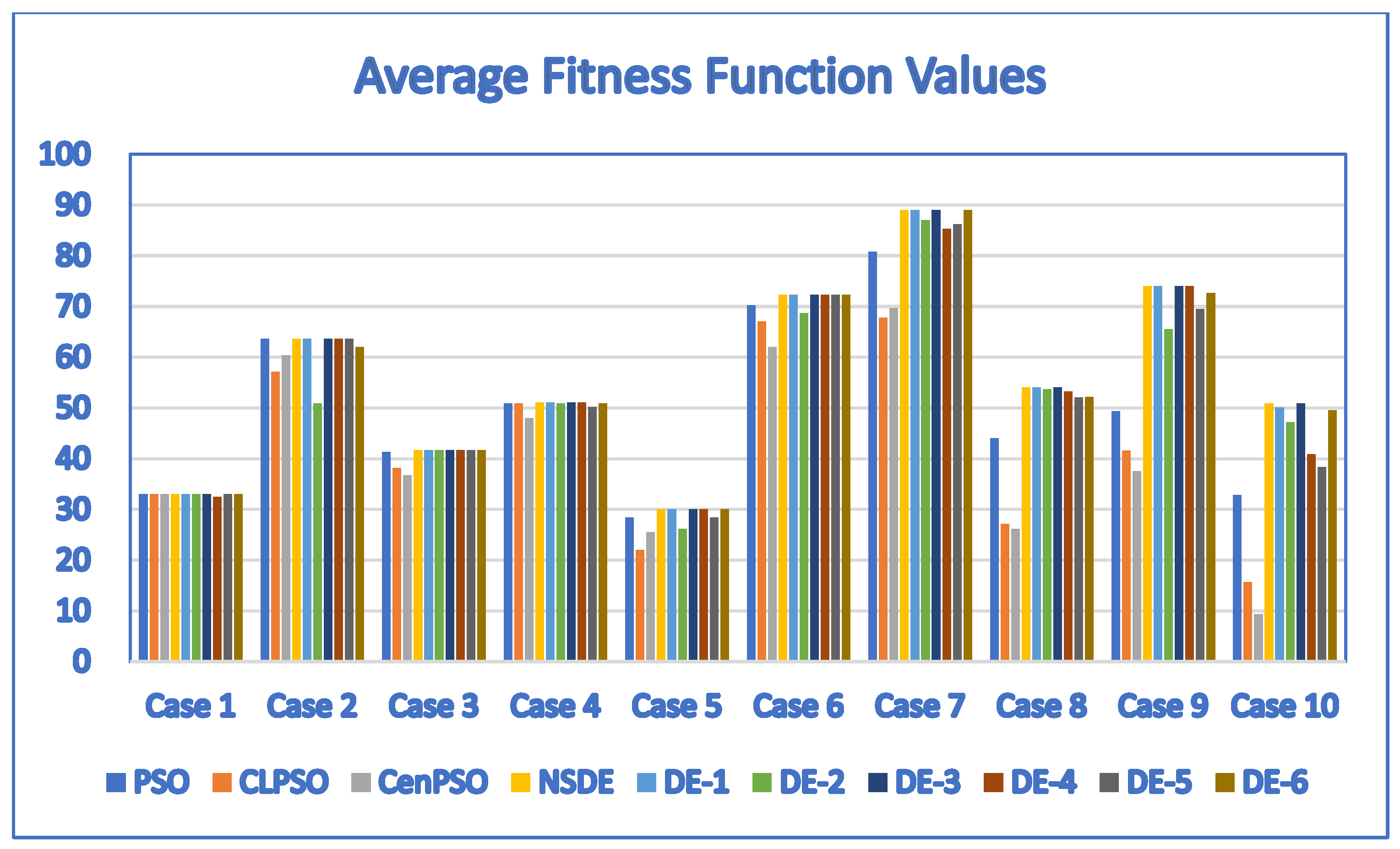
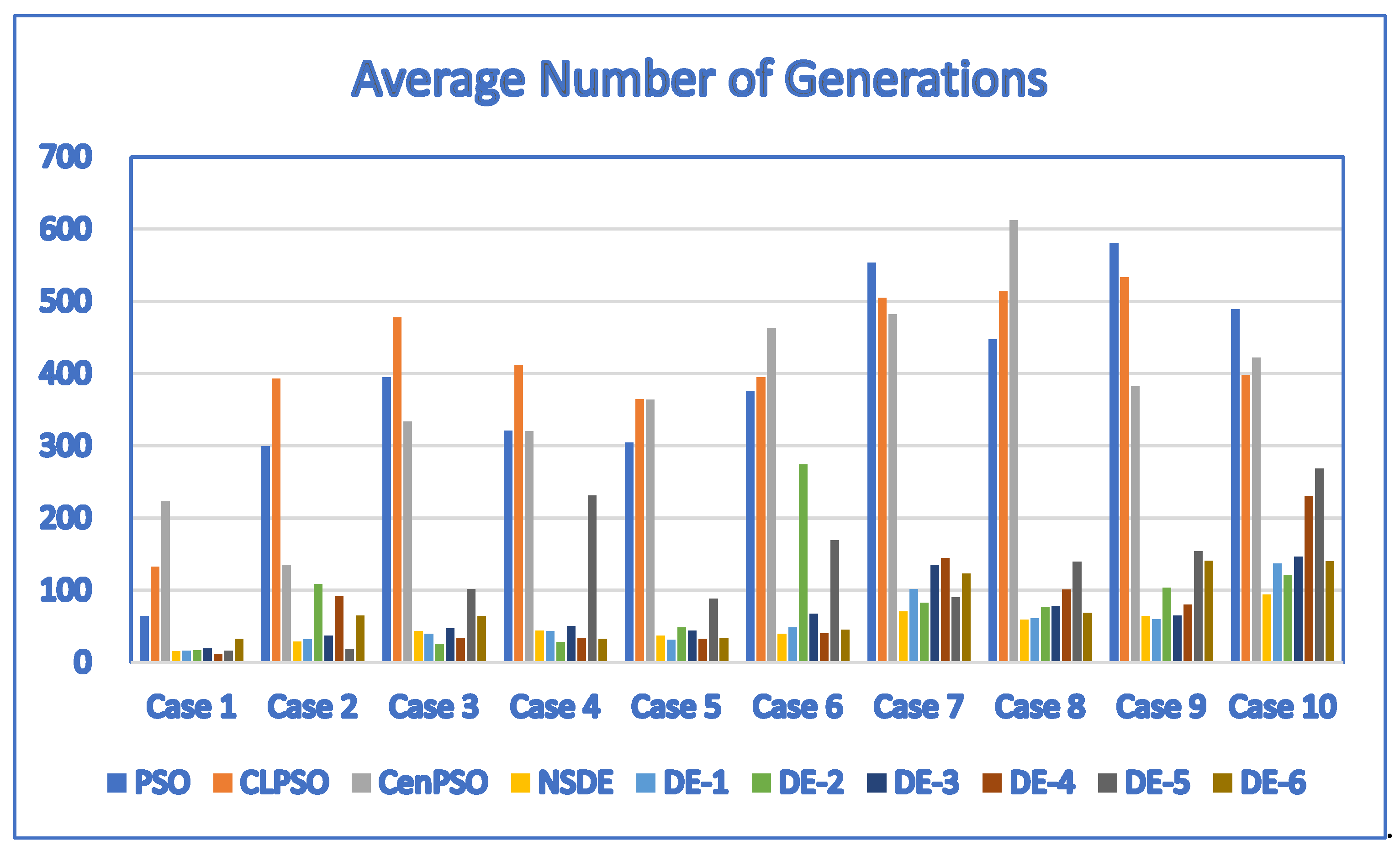
5.2. Performance of Three PSO-Based Algorithms and Seven DE-Based Algorithms
6. Discussion
7. Conclusions
- The issue of guaranteeing a minimal cost savings discount in ridesharing systems has not been addressed in the literature. Hence, the problem addressed and the decision model proposed in this study differentiate it from our previous studies and other studies in the literature. We proposed a decision model that offers a minimal cost savings discount for drivers and passengers.
- We proposed ten solution algorithms to provide decision support tools for finding a set of users for whom the minimal cost savings discount can be guaranteed and the total cost savings achieved can be optimized.
- We provided guidelines for selecting an appropriate solution algorithm by analyzing the results of several test cases and comparing the proposed algorithms.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- If
- Else If and
- Else
- End If
- If
- Else
- End If
- Return c
Appendix B

References
- Hyland, M.; Mahmassani, H.S. Operational benefits and challenges of shared-ride automated mobility-on-demand services. Transp. Res. Part A Policy Pract. 2020, 134, 251–270. [Google Scholar] [CrossRef]
- Delhomme, P.; Gheorghiu, A. Comparing French carpoolers and non-carpoolers: Which factors contribute the most to carpooling? Transp. Res. Part D Transp. Environ. 2016, 42, 1–15. [Google Scholar] [CrossRef]
- Julagasigorn, P.; Banomyong, R.; Grant, D.B.; Varadejsatitwong, P. What encourages people to carpool? A conceptual framework of carpooling psychological factors and research propositions. Transp. Res. Interdiscip. Perspect. 2021, 12, 100493. [Google Scholar] [CrossRef]
- Tsai, Y.T.; Yu, C.H.; Boonprakob, R. Assessing carpooling drivers and barriers: Evidence from Bangkok, Thailand. Transp. Res. Part F Traffic Psychol. Behav. 2021, 82, 84–95. [Google Scholar] [CrossRef]
- Mitropoulos, L.; Kortsari, A.; Ayfantopoulou, G. A systematic literature review of ride-sharing platforms, user factors and barriers. Eur. Transp. Res. Rev. 2021, 13, 61. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. Eur. J. Oper. Res. 2012, 223, 295–303. [Google Scholar] [CrossRef]
- Furuhata, M.; Dessouky, M.; Ordóñez, F.; Brunet, M.; Wang, X.; Koenig, S. Ridesharing: The state-of-the-art and future direc-tions. Transp. Res. Part B Methodol. 2013, 57, 28–46. [Google Scholar] [CrossRef]
- Ferber, J. Multi-Agent Systems, an Introduction to Distributed Artificial Intelligence; Addison Wesley: Reading, MA, USA, 1999. [Google Scholar]
- Nilsson, N.J. Artificial Intelligence: A New Synthesis; Morgan Kaufmann: San Francisco, CA, USA, 1998. [Google Scholar]
- De Vries, S.; Vohra, R.V. Combinatorial Auctions:A Survey. INFORMS J. Comput. 2003, 15, 284–309. [Google Scholar] [CrossRef]
- Satunin, S.; Babkin, E. A multi-agent approach to Intelligent Transportation Systems modeling with combinatorial auctions. Expert Syst. Appl. 2014, 41, 6622–6633. [Google Scholar] [CrossRef]
- Hsieh, F.S.; Zhan, F.; Guo, Y. A solution methodology for carpooling systems based on double auctions and cooperative coevolutionary particle swarms. Appl. Intell. 2019, 49, 741–763. [Google Scholar] [CrossRef]
- Rothkopf, M.; Pekeč, A.; Harstad, R. Computationally manageable combinational auctions. Manag. Sci. 1998, 44, 1131–1147. [Google Scholar] [CrossRef]
- Xia, M.; Stallaert, J.; Whinston, A.B. Solving the combinatorial double auction problem. Eur. J. Oper. Res. 2005, 164, 239–251. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Rahmi BA, K.I.; Birgoren, B.; Aktepe, A. Identifying factors affecting intention to use in distance learning systems. Turk. Online J. Distance Educ. 2021, 22, 58–80. [Google Scholar]
- Gerte, R.; Konduri, K.C.; Eluru, N. Is There a Limit to Adoption of Dynamic Ridesharing Systems? Evidence from Analysis of Uber Demand Data from New York City. Transp. Res. Rec. 2018, 2672, 127–136. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Y.; Zhou, H.; Jiao, J.; Overstreet, R.E. Travel behaviours, user characteristics, and social-economic impacts of shared transportation: A comprehensive review. Int. J. Logist. Res. Appl. 2021, 24, 51–78. [Google Scholar] [CrossRef]
- Abrahamse, W.; Keall, M. Effectiveness of a web-based intervention to encourage carpooling to work: A case study of Wellington. New Zealand. Transp. Policy 2012, 21, 45–51. [Google Scholar] [CrossRef]
- Hwang, K.; Giuliano, G. The Determinants of Ridesharing: Literature Review; Working Paper UCTC No. 38; The University of California Transportation Center: Berkeley, CA, USA, 1990; Available online: https://escholarship.org/uc/item/3r91r3r4 (accessed on 10 August 2022).
- Liu, K.; Liu, J. Optimization Approach to Improve the Ridesharing Success Rate in the Bus Ridesharing Service. IEEE Access 2020, 8, 208296–208310. [Google Scholar] [CrossRef]
- Chen, L.; Zhong, Q.; Xiao, X.; Gao, Y.; Jin, P.; Jensen, C.S. Price-and-Time-Aware Dynamic Ridesharing. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering (ICDE), Paris, France, 16–19 April 2018; pp. 1061–1072. [Google Scholar]
- Hsieh, F.-S. A Hybrid Firefly-DE algorithm for Ridesharing Systems with Cost Savings Allocation Schemes. In Proceedings of the 2022 IEEE World AI IoT Congress (AIIoT), Seattle, WA, USA, 6–9 June 2022; pp. 649–653. [Google Scholar]
- Hsieh, F.-S. A Comparison of Three Ridesharing Cost Savings Allocation Schemes Based on the Number of Acceptable Shared Rides. Energies 2021, 14, 6931. [Google Scholar] [CrossRef]
- Fu, X. Social-Aware Ridesharing. In Proceedings of the 2019 20th IEEE International Conference on Mobile Data Management (MDM); 2019; pp. 367–368. [Google Scholar]
- Guidotti, R.; Sassi, A.; Berlingerio, M.; Pascale, A.; Ghaddar, B. Social or Green? A Data-Driven Approach for More Enjoyable Carpooling. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 842–847. [Google Scholar]
- Hsieh, F.S. Trust-Based Recommendation for Shared Mobility Systems Based on a Discrete Self-Adaptive Neighborhood Search Differential Evolution Algorithm. Electronics 2022, 11, 776. [Google Scholar] [CrossRef]
- Braverman, A.; Dai, J.G.; Liu, X.; Ying, L. Empty-Car Routing in Ridesharing Systems. Oper. Res. 2019, 67, 1437–1452. [Google Scholar] [CrossRef]
- Fielbaum, A.; Alonso-Mora, J. Unreliability in ridesharing systems: Measuring changes in users’ times due to new requests. Transp. Res. Part C Emerg. Technol. 2020, 121, 102831. [Google Scholar] [CrossRef]
- Naoum-Sawaya, J.; Cogill, R.; Ghaddar, B.; Sajja, S.; Shorten, R.; Taheri, N.; Tommasi, P.; Verago, R.; Wirth, F. Stochastic optimization approach for the car placement problem in ridesharing systems. Transp. Res. Part B Methodol. 2015, 80, 173–184. [Google Scholar] [CrossRef]
- Thaithatkul, P.; Seo, T.; Kusakabe, T.; Asakura, Y. A passengers matching problem in ridesharing systems by considering user preference. J. East. Asia Soc. Transp. Stud. 2015, 11, 1416–1432. [Google Scholar]
- Mourad, A.; Puchinger, J.; Chu, C. A survey of models and algorithms for optimizing shared mobility. Transp. Res. Part B Methodol. 2019, 123, 323–346. [Google Scholar] [CrossRef]
- Martins, L.C.; Torre, R.; Corlu, C.G.; Juan, A.A.; Masmoudi, M.A. Optimizing ride-sharing operations in smart sustainable cities: Challenges and the need for agile algorithms. Comput. Ind. Eng. 2021, 153, 107080. [Google Scholar] [CrossRef]
- Agatz, N.A.H.; Erera, A.L.; Savelsbergh, M.W.P.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Transp. Res. Part B Methodol. 2011, 45, 1450–1464. [Google Scholar] [CrossRef]
- Wang, X.; Agatz, N.; Erera, A. Stable Matching for Dynamic Ride-Sharing Systems. Transp. Sci. 2018, 52, 850–867. [Google Scholar] [CrossRef]
- Nourinejad, M.; Roorda, M.J. Agent based model for dynamic ridesharing. Transp. Res. Part C Emerg. Technol. 2016, 64, 117–132. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Z.-L.; Zhang, L. Nonprofit peer-to-peer ridesharing optimization. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102053. [Google Scholar] [CrossRef]
- Tafreshian, A.; Masoud, N. Trip-based graph partitioning in dynamic ridesharing. Transp. Res. Part C Emerg. Technol. 2020, 114, 532–553. [Google Scholar] [CrossRef]
- Hsieh, F.S. A Comparative Study of Several Metaheuristic Algorithms to Optimize Monetary Incentive in Ridesharing Systems. ISPRS Int. J. Geo-Inf. 2020, 9, 590. [Google Scholar] [CrossRef]
- Lu, M.; Chen, Z.; Shen, S. Optimizing the Profitability and Quality of Service in Carshare Systems Under Demand Uncertainty. Manuf. Serv. Oper. Manag. 2017, 20, 162–180. [Google Scholar] [CrossRef]
- Shaheen, S.; Cohen, A. Innovative Mobility: Carsharing Outlook Carsharing Market Overview, Analysis, and Trends; Transportation Sustainability Research Center: Berkeley, CA, USA, 2020; Available online: https://escholarship.org/uc/item/9jh432pm (accessed on 10 August 2022).
- Ghallab, M.; Nau, D.S.; Traverso, P. Automated Planning: Theory and Practice, Morgan Kaufmann; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 1-55860-856-7. [Google Scholar]
- Smith, R.G. The Contract net protocol: High-level communication and control in a distributed problem solver. IEEE Trans. Comput. 1980, 29, 1104–1113. [Google Scholar] [CrossRef]
- Durfee, E.H.; Lesser, V.R. Partial global planning:a coordination framework for distributed hypothesis formation. IEEE Trans. Syst. Man Cybern. 1991, 21, 1167–1183. [Google Scholar] [CrossRef]
- Wooldridge, M.; Jennings, N.R. The cooperative problem solving process. J. Log. Comput. 1999, 9, 563–592. [Google Scholar] [CrossRef]
- Guajardoa, M.; Ronnqvist, M. A review on cost allocation methods in collaborative transportation. Int. Trans. Oper. Res. 2016, 23, 371–392. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games. A Value N-Pers. Games 1952, 28, 307–317. [Google Scholar] [CrossRef]
- Schmeidler, D. The Nucleolus of a Characteristic Function Game. SIAM J. Appl. Math. 1969, 17, 1163–1170. [Google Scholar] [CrossRef]
- Kalai, E. Proportional solutions to bargaining situations: Intertemporal utility comparisons. Econometrica 1977, 45, 1623–1630. [Google Scholar] [CrossRef]
- Fatima, S.S.; Wooldridge, M.; Jennings, N.R. A linear approximation method for the Shapley value. Artif. Intell. 2008, 172, 1673–1699. [Google Scholar] [CrossRef]
- Perea, F.; Puerto, J. A heuristic procedure for computing the nucleolus. Comput. Oper. Res. 2019, 112, 104764. [Google Scholar] [CrossRef]
- Baki, R. An integrated, multi-criteria approach based on environmental, economic, social, and competency criteria for supplier selection. RAIRO-Oper. Res. 2021, 55, 1487–1500. [Google Scholar] [CrossRef]
- Majumder, S.; Saha, B.; Anand, P.; Kar, S.; Pal, T. Uncertainty based genetic algorithm with varying population for random fuzzy maximum flow problem. Expert Syst. 2018, 35, e12264. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive Learning Particle Swarm Optimization Algorithm With Local Search for Multimodal Functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Rahnamayan, S. CenPSO: A Novel Center-based Particle Swarm Optimization Algorithm for Large-scale Optimization. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 2066–2071. [Google Scholar]
- Yang, Z.; He, J.; Yao, X. Making a difference to differential evolution. In Advances in Metaheuristics for Hard Optimization; Michalewicz, Z., Siarry, P., Eds.; Springer: Berlin, Germany, 2007; pp. 415–432. [Google Scholar]
- Ravindran, A.; Ragsdell, K.M.; Reklaitis, G.V. Enginering Optimization: Methods and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; Prentice-Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Data of Test Cases. Available online: https://drive.google.com/drive/folders/19Zj69lRsQP8z0uuiJOqfkHBegCvZE2Pe?usp=sharing (accessed on 11 August 2022).
- Triguero, S.; González, J.M.; Moyano, S.; García, J.; Alcalá-Fdez, J.; Luengo, A.; Fernández, M.J.; del Jesus, L.; Sánchez, L.; Herrera, F. KEEL 3.0: An Open Source Software for Multi-Stage Analysis in Data Mining. Int. J. Comput. Intell. Syst. 2017, 10, 1238–1249. [Google Scholar] [CrossRef]



| Variable | Meaning |
|---|---|
| P | Total no. of passengers. |
| D | Total no. of drivers. |
| p | . |
| d | . |
| k | . |
| Jd | . |
| j | . |
| DBdj | DBdj = (qdj1, qdj2, qdj3, …, qdjP, odj, cdj): the j-th bid of driver agent d, where qdjp is the available seats to serve passenger p, odj is the original cost when the driver travels alone, and cdj is the travel cost of the bid. |
| . | |
| . | |
| PBp | PBp = (Sp1, Sp2, Sp3, …, SpK, fp): the bid of passenger agent p, where Spk is the number of seats requested by passenger p for location k and fp is the cost of passenger p without ridesharing. |
| . | |
| . | |
| xdj | A decision variable: xdj = 1 if the j-th bid of driver d is a winning bid and xdj = 0 otherwise. |
| yp | A binary decision variable: yp = 1 if the bid of passenger p is a winning bid and yp = 0 otherwise. |
| rD | Minimal expected cost savings discount for drivers. |
| rP | Minimal expected cost savings discount for passengers. |
| H(x,y) | The total cost savings objective function, . |
| The set of passengers on the ride corresponding to the j-th bid submitted by driver d. | |
| Hdj(x,y) | The cost savings of the j-th bid submitted by driver d . |
| cfpdj | . |
| Variable | Meaning |
|---|---|
| N | . |
| m | A mutation strategy. |
| NP | Population size. |
| G | Number of generations. |
| t | The generation index. |
| zi | The i–th candidate solution in the population. |
| Fi | Scale factor of individual i. |
| CR | Crossover rate of individual i. |
| vi | A mutant vector. |
| ui | A trial vector. |
| The transformed binary trial vector corresponding to ui. | |
| zb | The best candidate solution in the current population. |
| zr | A candidate solution randomly selected from the population, where r is a random integer between 1 and NP. |
| r1, r2, r3, r4, r5 | Random integers between 1 and NP. |
| . |
| Variable | Meaning |
|---|---|
| N | . |
| m | A mutation strategy. |
| NP | Population size. |
| S | The number of particles randomly selected from the population. |
| G | Number of generations. |
| t | The generation index. |
| zi | The i-th candidate solution in the population. |
| . | |
| GZ | . |
| vi | The velocity of particle i; vin denotes the n-th element of the vector vi. |
| c1, c2, c3 | Non-negative real parameters less than 1. |
| r1, r2, r3 | Random variables with uniform distribution U(0,1). |
| Driver | Start Location (Latitude/Longitude) | Destination Location (Latitude/Longitude) |
|---|---|---|
| Driver 1 | 24.23785/120.66993 | 24.11308/120.65914 |
| Driver 2 | 24.1692536/120.6848233 | 24.20195/120.56815 |
| Driver 3 | 24.13425/120.5539 | 24.14289/120.70549 |
| Driver | Start Location (Latitude/Longitude) | Destination Location (Latitude/Longitude) |
|---|---|---|
| Passenger 1 | 24.21872/120.6469 | 24.12877/120.66223 |
| Passenger 2 | 24.1790507/120.6657476 | 24.17369/120.61354 |
| Passenger 3 | 24.0611/120.64342 | 24.1465287/120.6532456 |
| Passenger 4 | 24.07962/120.69454 | 24.12438/120.66244 |
| Passenger 5 | 24.19422/120.69538 | 24.15288/120.69704 |
| Passenger 6 | 24.16048/120.69173 | 24.16359/120.65138 |
| Passenger 7 | 24.0611/120.64342 | 24.11009/120.64146 |
| Passenger 8 | 24.19422/120.69538 | 24.13046/120.7047 |
| Passenger 9 | 24.13623/120.60693 | 24.13527/120.6571 |
| Passenger 10 | 24.16429/120.68522 | 24.15345/120.65495 |
| Driver ID (d) | j | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | { 5 } |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | { 10 } |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | { 9 } |
| Driver ID (d) | j | odj | cdj |
|---|---|---|---|
| 1 | 1 | 50.4025 | 51.4975 |
| 2 | 1 | 36.745 | 41.1575 |
| 3 | 1 | 57.485 | 57.485 |
| Passenger ID (p) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37.0475 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18.3475 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28.12 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 19.07 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 14.1675 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 12.25 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 17.1175 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 33.11 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 14.6925 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9.645 |
| Driver Decision Variable | x11 | x21 | x31 |
|---|---|---|---|
| Value | 1 | 1 | 1 |
| Passenger Decision Variable | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| Algorithm | Algorithm-Specific Parameters | Common Parameter Setting 1 | Common Parameter Setting 2 |
|---|---|---|---|
| PSO | , , | POP = 30, Gen = 1000 | POP = 50, Gen = 1000 |
| CLPSO | , , , | POP = 30, Gen = 1000 | POP = 50, Gen = 1000 |
| CenPSO | , , , | POP = 30, Gen = 1000 | POP = 50, Gen = 1000 |
| DE-m ) | CR = 0.5 Fi: a value arbitrarily selected from uniform (0, 2) | POP = 30, Gen = 1000 | POP = 50, Gen = 1000 |
| DE-7 (NSDE) | CR = 0.5; Fi = 0.5r1 + 0.5, where r1 is a random value with Gaussian distribution N(0,1). | POP = 30, Gen = 1000 | POP =50, Gen =1000 |
| Case | D | P | PSO | CLPSO | CenPSO | DE-7 (NSDE) |
|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 32.998 | 32.998 | 32.998 | 32.998 |
| 2 | 5 | 11 | 63.615 | 57.1262 | 60.3706 | 63.615 |
| 3 | 5 | 12 | 41.2892 | 38.1928 | 36.6922 | 41.715 |
| 4 | 6 | 12 | 50.9085 | 50.9085 | 47.9958 | 51.11 |
| 5 | 7 | 13 | 28.4254 | 21.9635 | 25.482 | 30.063 |
| 6 | 8 | 14 | 70.2629 | 67.0561 | 62.0001 | 72.328 |
| 7 | 9 | 15 | 80.8106 | 67.7562 | 69.6551 | 89.03 |
| 8 | 10 | 16 | 44.0023 | 27.1189 | 26.1877 | 54.02 |
| 9 | 11 | 17 | 49.356 | 41.6211 | 37.5057 | 74.05 |
| 10 | 12 | 18 | 32.8349 | 15.6644 | 9.361 | 50.9 |
| Case | D | P | DE-1 | DE-2 | DE-3 | DE-4 | DE-5 | DE-6 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 32.998 | 32.998 | 32.998 | 32.4747 | 32.998 | 32.998 |
| 2 | 5 | 11 | 63.615 | 50.8922 | 63.615 | 63.615 | 63.615 | 61.9928 |
| 3 | 5 | 12 | 41.715 | 41.715 | 41.715 | 41.715 | 41.715 | 41.715 |
| 4 | 6 | 12 | 51.11 | 50.9085 | 51.11 | 51.11 | 50.141 | 50.9085 |
| 5 | 7 | 13 | 30.063 | 26.1379 | 30.063 | 30.063 | 28.4254 | 30.063 |
| 6 | 8 | 14 | 72.328 | 68.6614 | 72.328 | 72.328 | 72.328 | 72.328 |
| 7 | 9 | 15 | 89.03 | 86.9898 | 89.03 | 85.323 | 86.213 | 89.03 |
| 8 | 10 | 16 | 54.02 | 53.7046 | 54.02 | 53.2235 | 52.0531 | 52.1271 |
| 9 | 11 | 17 | 74.05 | 65.5666 | 74.05 | 74.05 | 69.4864 | 72.6228 |
| 10 | 12 | 18 | 50.0623 | 47.1623 | 50.9 | 40.9119 | 38.3571 | 49.5823 |
| Algorithm | Ranking |
|---|---|
| PSO | 6.85 |
| CLPSO | 8.55 |
| CenPSO | 9.1 |
| NSDE | 3 |
| DE-1 | 3.15 |
| DE-2 | 6.25 |
| DE-3 | 3 |
| DE-4 | 4.7 |
| DE-5 | 5.75 |
| DE-6 | 4.65 |
| Case | D | P | PSO | CLPSO | CenPSO | DE-7 (NSDE) |
|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 64.6 | 132.5 | 222.7 | 15.6 |
| 2 | 5 | 11 | 299.6 | 392.6 | 134.9 | 29.1 |
| 3 | 5 | 12 | 394.5 | 477.9 | 333.4 | 43.3 |
| 4 | 6 | 12 | 320.9 | 411.9 | 320 | 44.1 |
| 5 | 7 | 13 | 304.1 | 364.4 | 363.7 | 37.3 |
| 6 | 8 | 14 | 375.6 | 394.9 | 462.5 | 39.6 |
| 7 | 9 | 15 | 553.6 | 505.1 | 482 | 70.7 |
| 8 | 10 | 16 | 447.5 | 513.6 | 612.6 | 59.5 |
| 9 | 11 | 17 | 580.7 | 533.3 | 382.3 | 64.2 |
| 10 | 12 | 18 | 489.3 | 397.8 | 421.9 | 94.3 |
| Case | D | P | DE-1 | DE-2 | DE-3 | DE-4 | DE-5 | DE-6 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 16.6 | 16.7 | 19.8 | 11.9 | 16.4 | 32.9 |
| 2 | 5 | 11 | 32.2 | 108.5 | 36.9 | 91.3 | 18.6 | 65.3 |
| 3 | 5 | 12 | 39.7 | 26 | 47.6 | 33.9 | 101.9 | 64.6 |
| 4 | 6 | 12 | 43.8 | 28.3 | 50.3 | 34.3 | 231.2 | 32.6 |
| 5 | 7 | 13 | 31.8 | 48.5 | 44.1 | 32.7 | 88.7 | 33.7 |
| 6 | 8 | 14 | 48.3 | 274 | 67.8 | 40.3 | 169.1 | 45.5 |
| 7 | 9 | 15 | 101.4 | 82.9 | 135 | 144.8 | 90.3 | 122.9 |
| 8 | 10 | 16 | 61.3 | 77.2 | 78.6 | 101.1 | 139.7 | 69 |
| 9 | 11 | 17 | 59.7 | 103.3 | 65 | 80.1 | 154.3 | 140.8 |
| 10 | 12 | 18 | 136.8 | 121.1 | 146.3 | 229.7 | 268.6 | 140.2 |
| Case | D | P | PSO | CLPSO | CenPSO | DE-7 (NSDE) |
|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 32.998 | 32.998 | 32.998 | 32.998 |
| 2 | 5 | 11 | 63.615 | 63.615 | 58.7484 | 63.615 |
| 3 | 5 | 12 | 41.2892 | 40.2464 | 40.0118 | 41.715 |
| 4 | 6 | 12 | 51.11 | 49.2425 | 50.707 | 51.11 |
| 5 | 7 | 13 | 30.063 | 27.3001 | 26.7878 | 30.063 |
| 6 | 8 | 14 | 69.9483 | 65.5762 | 68.2854 | 72.328 |
| 7 | 9 | 15 | 80.5986 | 76.1522 | 75.207 | 89.03 |
| 8 | 10 | 16 | 46.8013 | 34.9718 | 34.544 | 54.02 |
| 9 | 11 | 17 | 55.9356 | 40.201 | 51.2736 | 74.05 |
| 10 | 12 | 18 | 31.1131 | 19.7403 | 20.5417 | 50.9 |
| Case | D | P | DE-1 | DE-2 | DE-3 | DE-4 | DE-5 | DE-6 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 32.998 | 32.998 | 32.998 | 32.998 | 32.998 | 32.998 |
| 2 | 5 | 11 | 63.615 | 58.8758 | 63.615 | 63.615 | 63.615 | 61.9928 |
| 3 | 5 | 12 | 41.715 | 40.2785 | 41.715 | 41.715 | 41.2892 | 41.715 |
| 4 | 6 | 12 | 51.11 | 51.11 | 51.11 | 48.3931 | 51.11 | 51.11 |
| 5 | 7 | 13 | 30.063 | 30.063 | 30.063 | 30.063 | 30.063 | 30.063 |
| 6 | 8 | 14 | 72.328 | 68.4738 | 72.328 | 72.328 | 72.328 | 72.328 |
| 7 | 9 | 15 | 89.03 | 84.7331 | 89.03 | 89.03 | 88.2778 | 88.091 |
| 8 | 10 | 16 | 54.02 | 52.2693 | 54.02 | 53.8623 | 53.8623 | 52.4425 |
| 9 | 11 | 17 | 74.05 | 68.1678 | 74.05 | 73.1033 | 68.2863 | 71.9426 |
| 10 | 12 | 18 | 50.9 | 50.3477 | 50.9 | 44.9773 | 49.3177 | 37.2349 |
| Algorithm | Ranking |
|---|---|
| PSO | 6.65 |
| CLPSO | 8.75 |
| CenPSO | 9.05 |
| NSDE | 3.2 |
| DE-1 | 3.2 |
| DE-2 | 6.4 |
| DE-3 | 3.2 |
| DE-4 | 4.65 |
| DE-5 | 5.15 |
| DE-6 | 4.75 |
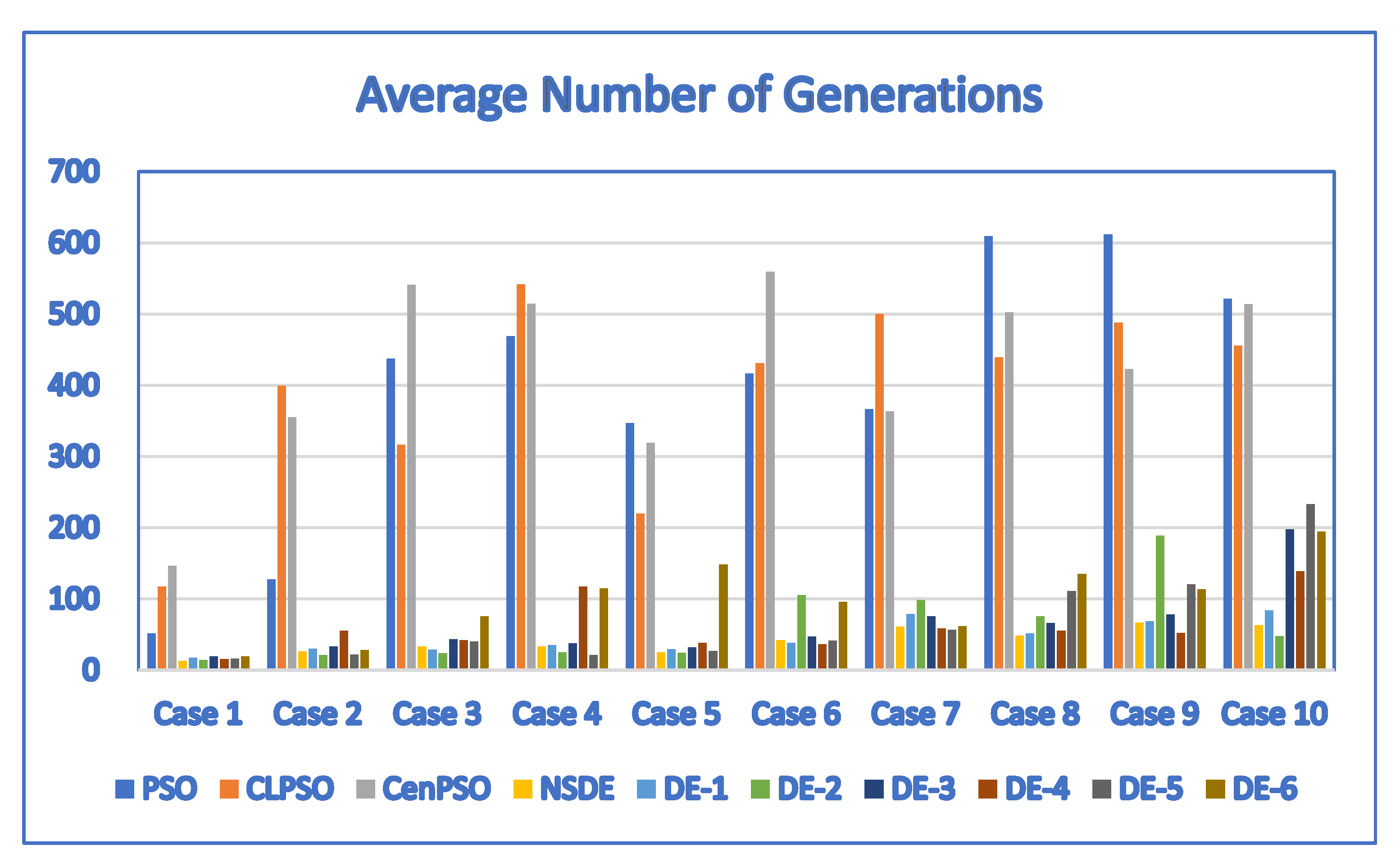
| Case | D | P | PSO | CLPSO | CenPSO | DE-7 (NSDE) |
|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 51.5 | 117.3 | 146.6 | 12.9 |
| 2 | 5 | 11 | 127.3 | 399.3 | 355 | 26.4 |
| 3 | 5 | 12 | 437.2 | 316.6 | 540.7 | 32.9 |
| 4 | 6 | 12 | 468.6 | 541.4 | 514.6 | 33.2 |
| 5 | 7 | 13 | 347.1 | 219.9 | 319.3 | 24.8 |
| 6 | 8 | 14 | 416.4 | 431.1 | 559.3 | 41.9 |
| 7 | 9 | 15 | 366.4 | 499.8 | 363.6 | 61.3 |
| 8 | 10 | 16 | 609.5 | 438.9 | 502.1 | 48.6 |
| 9 | 11 | 17 | 611.5 | 487.6 | 422.8 | 67 |
| 10 | 12 | 18 | 521.5 | 455.6 | 513.6 | 63.1 |
| Case | D | P | DE-1 | DE-2 | DE-3 | DE-4 | DE-5 | DE-6 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 17.6 | 14 | 19.2 | 15.5 | 16.2 | 19.2 |
| 2 | 5 | 11 | 30.2 | 21.2 | 33 | 55.3 | 22.1 | 28 |
| 3 | 5 | 12 | 28.7 | 23.7 | 43.3 | 41.9 | 40.1 | 75.7 |
| 4 | 6 | 12 | 35.4 | 25.2 | 37.4 | 117.3 | 21.4 | 114.7 |
| 5 | 7 | 13 | 29.3 | 24.3 | 32.2 | 38.1 | 26.7 | 148.6 |
| 6 | 8 | 14 | 38 | 105.2 | 47.1 | 36.6 | 41.7 | 96 |
| 7 | 9 | 15 | 78.9 | 98.2 | 75.4 | 58.7 | 56.7 | 61.9 |
| 8 | 10 | 16 | 51.5 | 75.7 | 66.3 | 55.6 | 110.7 | 135.3 |
| 9 | 11 | 17 | 68.7 | 188.5 | 78.4 | 51.9 | 120.2 | 113.6 |
| 10 | 12 | 18 | 83.6 | 47.9 | 197.9 | 138.7 | 233.2 | 194.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, F.-S. Development and Comparison of Ten Differential-Evolution and Particle Swarm-Optimization Based Algorithms for Discount-Guaranteed Ridesharing Systems. Appl. Sci. 2022, 12, 9544. https://doi.org/10.3390/app12199544
Hsieh F-S. Development and Comparison of Ten Differential-Evolution and Particle Swarm-Optimization Based Algorithms for Discount-Guaranteed Ridesharing Systems. Applied Sciences. 2022; 12(19):9544. https://doi.org/10.3390/app12199544
Chicago/Turabian StyleHsieh, Fu-Shiung. 2022. "Development and Comparison of Ten Differential-Evolution and Particle Swarm-Optimization Based Algorithms for Discount-Guaranteed Ridesharing Systems" Applied Sciences 12, no. 19: 9544. https://doi.org/10.3390/app12199544
APA StyleHsieh, F.-S. (2022). Development and Comparison of Ten Differential-Evolution and Particle Swarm-Optimization Based Algorithms for Discount-Guaranteed Ridesharing Systems. Applied Sciences, 12(19), 9544. https://doi.org/10.3390/app12199544






