Design of Optical Tweezers Manipulation Control System Based on Novel Self-Organizing Fuzzy Cerebellar Model Neural Network
Abstract
:1. Introduction
2. Model of NSOFCMNN
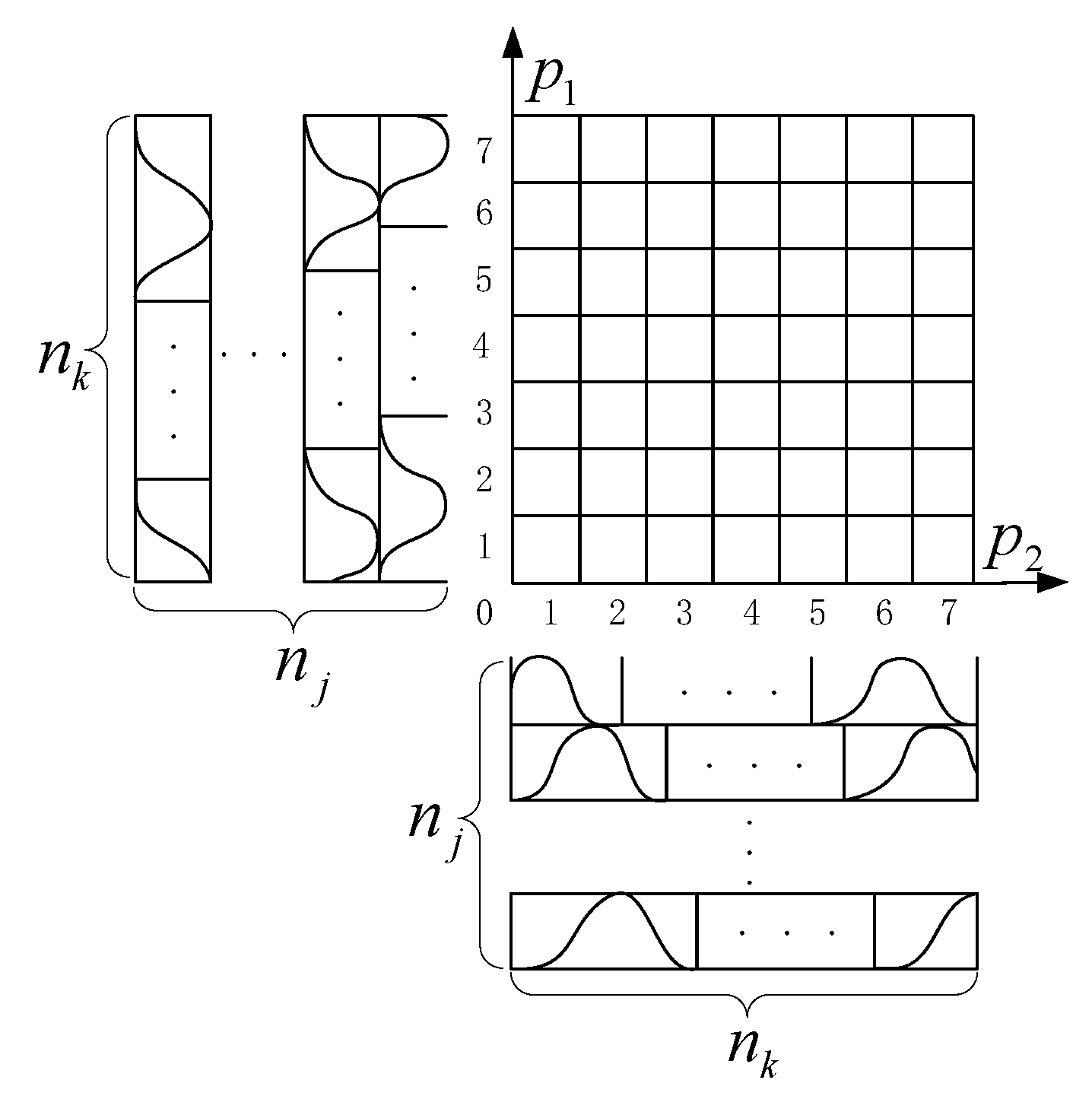
2.1. Fuzzy Rules of the NSOFCMNN
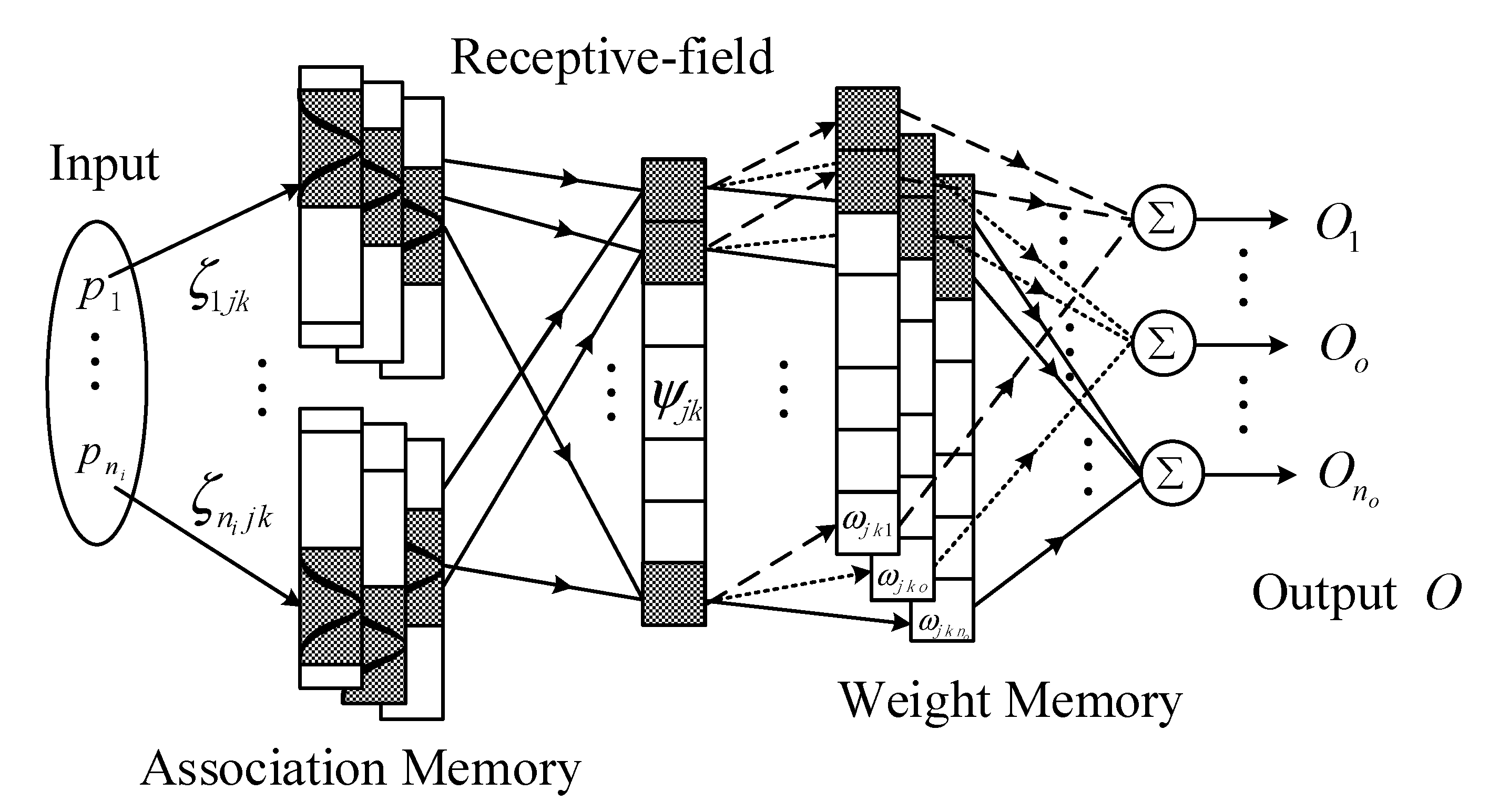
2.2. Structure of the NSOFCMNN
2.3. Updating Law
2.4. Novel Self-Organizing Adjustment Mechanism
3. Cell Manipulation Control
3.1. Holographic Optical Tweezers System
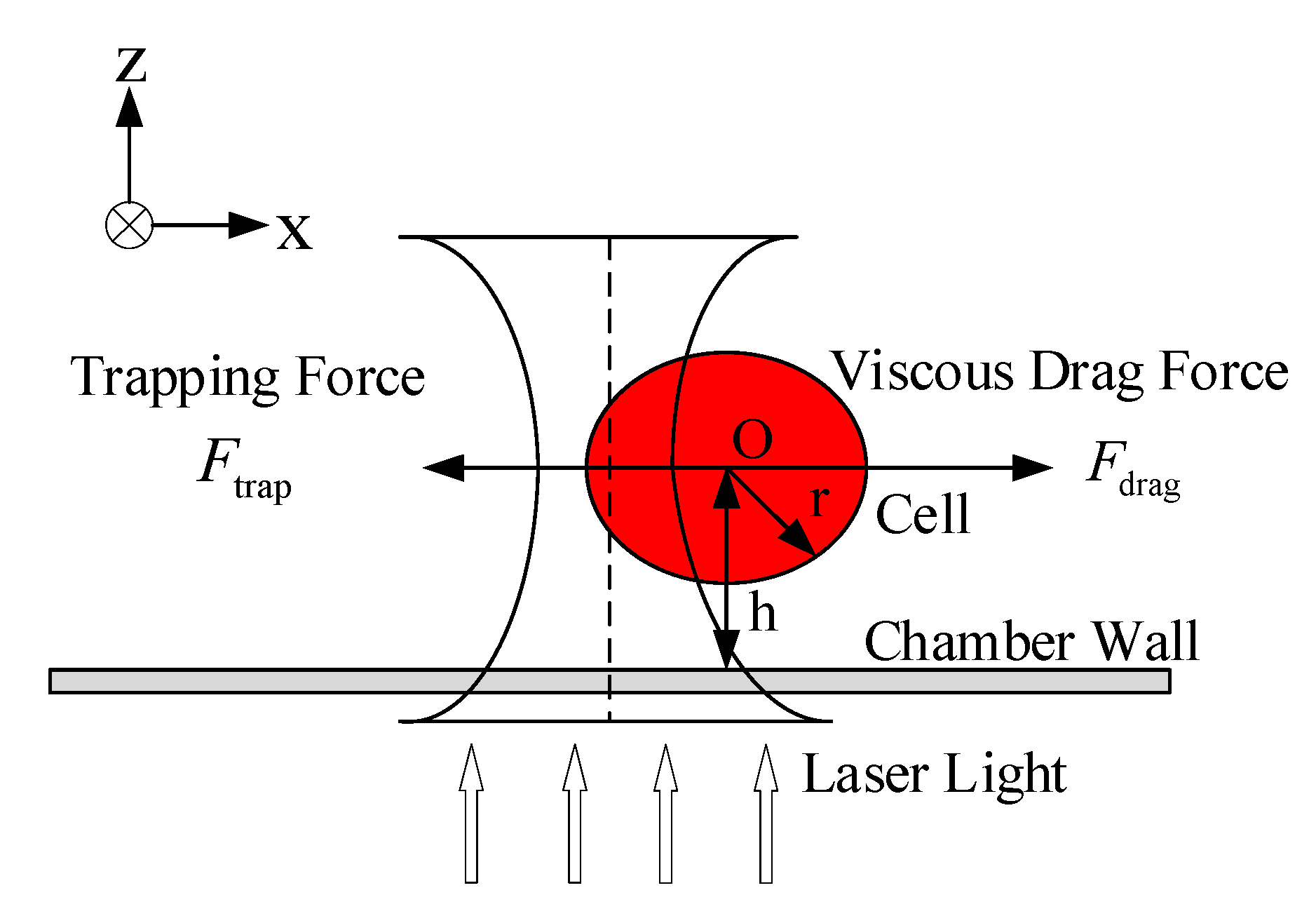
3.2. Cell Dynamics Model
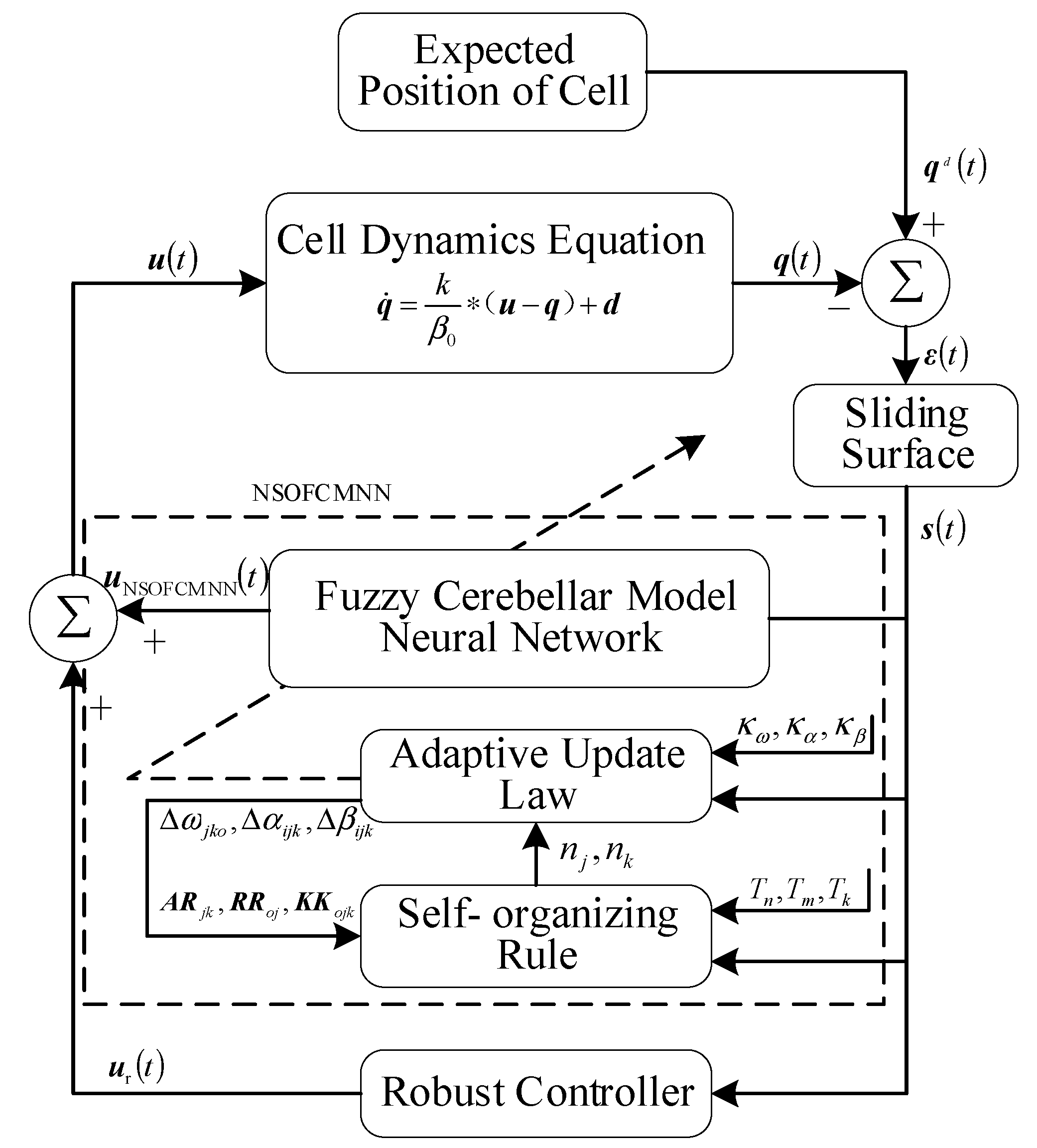
3.3. Cell Manipulation Control System
3.4. Lyapunov Convergence Analysis
4. Simulation Results
4.1. Case (1): Holographic Optical Tweezers Manipulate Control for Single Cells
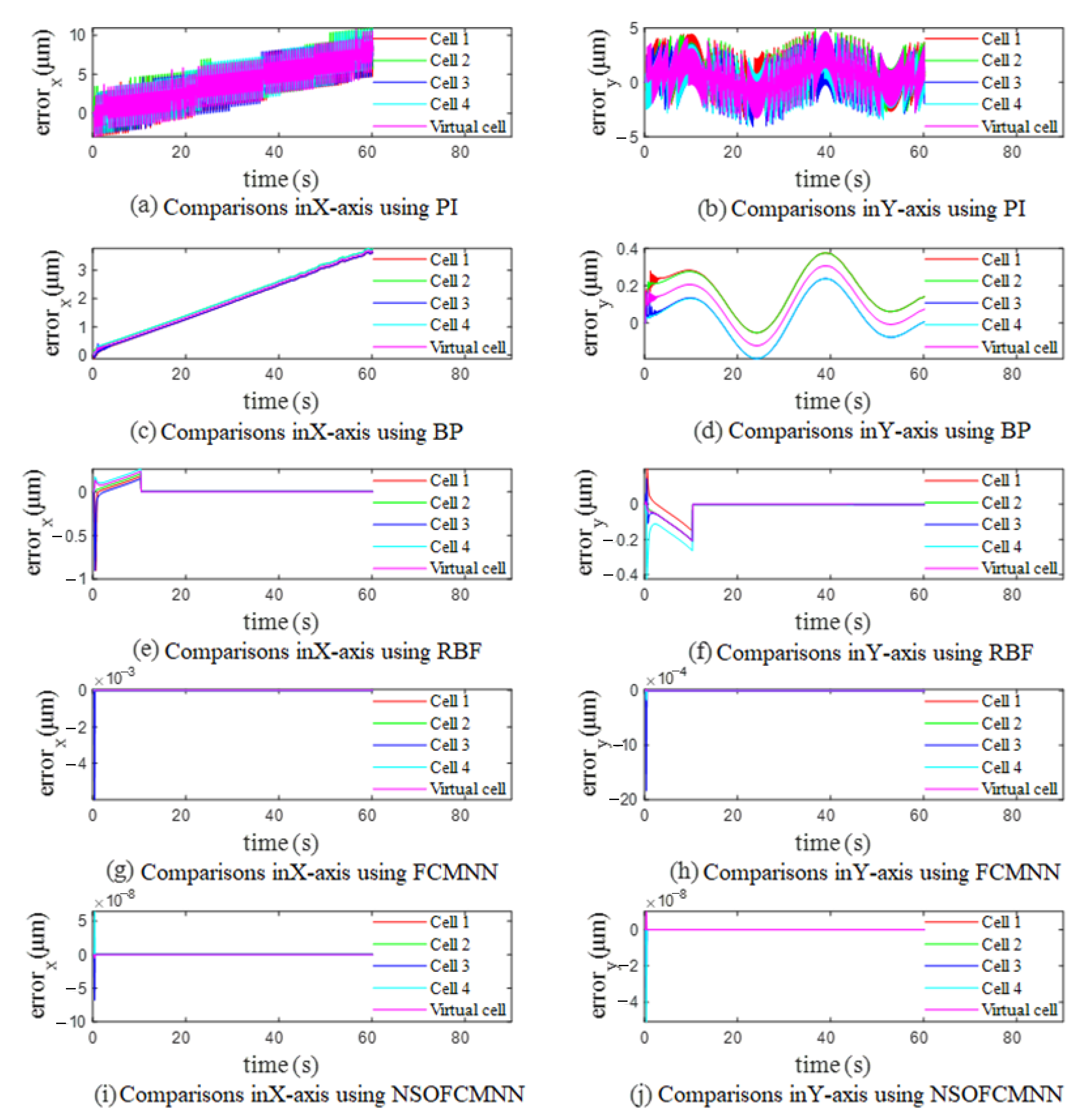
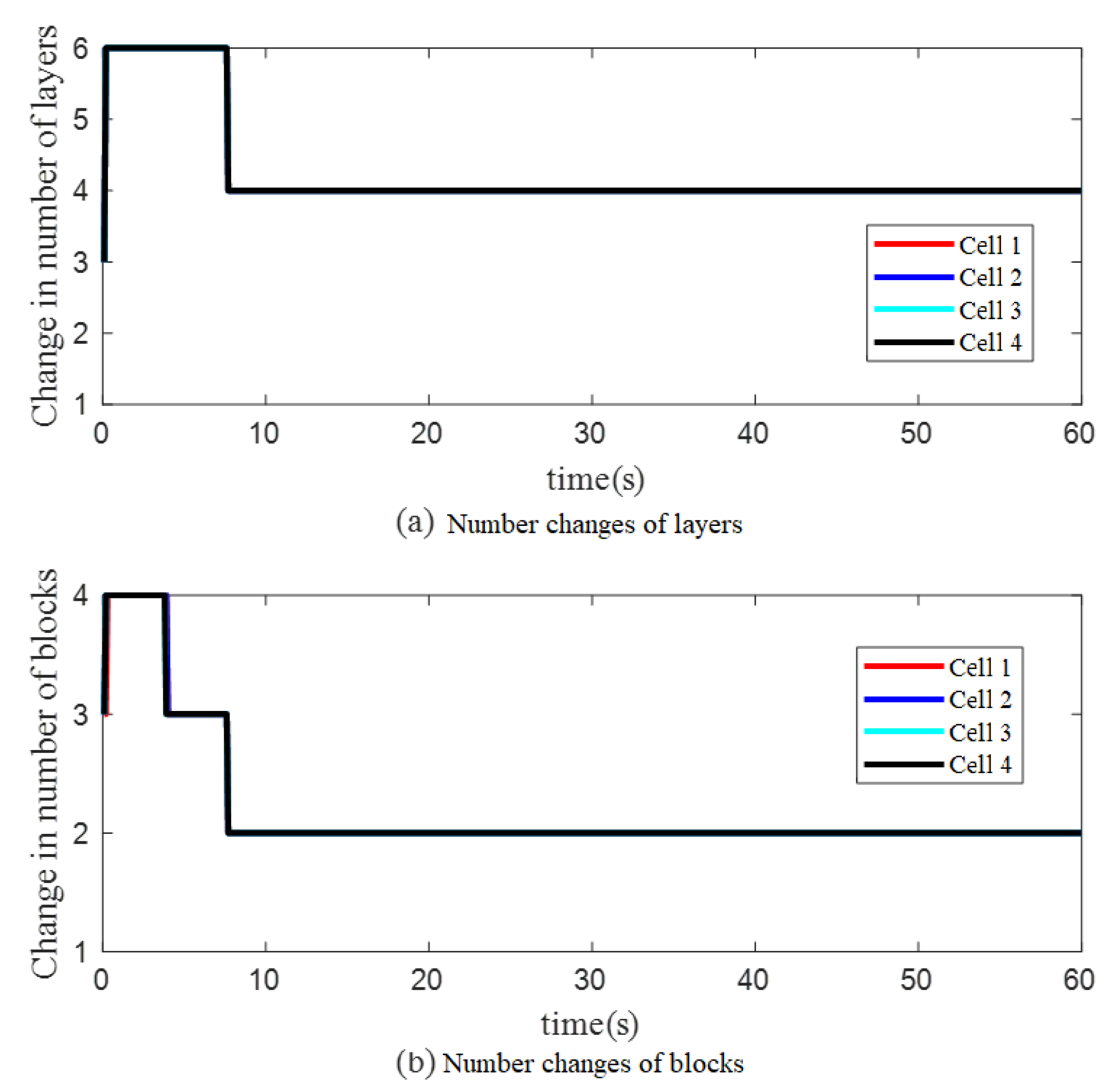
4.2. Case (2): Holographic Optical Tweezers Manipulate Control for Multiple Cells
5. Conclusions and Outlook
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Junno, T.; Deppert, K.; Montelius, L.; Samuelson, L. Controlled manipulation of nanoparticles with an atomic force microscope. Appl. Phys. Lett. 1995, 66, 3627–3629. [Google Scholar] [CrossRef]
- Lee, G.Y.; Lim, C.T. Biomechanics approaches to studying human diseases. Trends Biotechnol. 2007, 25, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Sun, D.; Huang, W. A mechanical model of biological cells in microinjection. IEEE Trans. NanoBioscience 2008, 7, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Diller, E.; Giltinan, J.; Sitti, M. Independent control of multiple magnetic microrobots in three dimensions. Int. J. Robot. Res. 2013, 32, 614–631. [Google Scholar] [CrossRef]
- Wang, X.; Chen, S.; Kong, M.; Wang, Z.; Costa, K.D.; Li, R.A.; Sun, D. Enhanced cell sorting and manipulation with combined optical tweezer and microfluidic chip technologies. Lab A Chip 2011, 11, 3656–3662. [Google Scholar] [CrossRef]
- Zhong, M.-C.; Wei, X.-B.; Zhou, J.-H.; Wang, Z.-Q.; Li, Y.-M. Trapping red blood cells in living animals using optical tweezers. Nat. Commun. 2013, 4, 1768. [Google Scholar] [CrossRef]
- Ge, Q.; Guo, Y.; Ye, K.; Chang, W.; Zhao, X.; Cui, Y. Research progress of single-cell optical manipulation techniques. Sci. Sin. Vitae 2020, 50, 575–588. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, Y.; Hu, C.; Liu, Z.; Yang, X.; Zhang, J.; Yang, J.; Yuan, L. HACF-based optical tweezers available for living cells manipulating and sterile transporting. Opt. Commun. 2018, 427, 563–566. [Google Scholar] [CrossRef]
- Xie, M.; Shakoor, A.; Wu, C. Manipulation of biological cells using a robot-aided optical tweezers system. Micromachines 2018, 9, 245. [Google Scholar] [CrossRef]
- Gou, X.; Yang, H.; Fahmy, T.M.; Wang, Y.; Sun, D. Direct measurement of cell protrusion force utilizing a robot-aided cell manipulation system with optical tweezers for cell migration control. Int. J. Robot. Res. 2014, 33, 1782–1792. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, D.; Huang, W.; Xi, N. Dynamics analysis and motion planning for automated cell transportation with optical tweezers. IEEE ASME Trans. Mechatron. 2013, 18, 706–713. [Google Scholar] [CrossRef]
- Banerjee, A.G.; Pomerance, A.; Losert, W.; Gupta, S.K. Developing a Stochastic Dynamic Programming Framework for Optical Tweezer-Based Automated Particle Transport Operations. IEEE Trans. Autom. Sci. Eng. 2009, 7, 218–227. [Google Scholar]
- Li, X.; Cheah, C.C. Robotic Cell Manipulation Using Optical Tweezers with Unknown Trapping Stiffness and Limited FOV. IEEE ASME Trans. Mechatron. 2015, 20, 1624–1632. [Google Scholar] [CrossRef]
- Keloth, A.; Anderson, O.; Risbridger, D.; Paterson, L. Single Cell Isolation Using Optical Tweezers. Micromachines 2018, 9, 434. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, H.-W.; Yu, P.-P.; Zhang, S.-H.; Zhou, J.-H.; Li, Y.-M.; Gong, L. Trapping and Manipulation of Single Cells in Crowded Environments. Front. Bioeng. Biotechnol. 2020, 8, 422. [Google Scholar] [CrossRef]
- Cheah, C.C.; Li, X.; Yan, X.; Sun, D. Simple PD Control Scheme for Robotic Manipulation of Biological Cell. IEEE Trans. Autom. Control 2015, 60, 1427–1432. [Google Scholar] [CrossRef]
- Xie, M.; Li, X.; Wang, Y.; Liu, Y.; Sun, D. Saturated PID Control for the Optical Manipulation of Biological Cells. IEEE Trans. Control Syst. Technol. 2018, 26, 1909–1916. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Truong, H.T. Novel semiactive suspension using a magnetorheological elastomer (MRE)-based absorber and adaptive neural network controller for systems with input constraints. Mech. Sci. 2020, 11, 465–479. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Sun, X.; Zheng, W.; Yin, L. Improved bilateral neural network adaptive controller using neural network and adaptive method. Basic Clin. Pharmacol. Toxicol. 2020, 127, 50–51. [Google Scholar]
- Ma, Z.; Huang, P. Adaptive Neural-Network Controller for an Uncertain Rigid Manipulator with Input Saturation and Full-Order State Constraint. IEEE Trans. Cybern. 2022, 52, 2907–2915. [Google Scholar] [CrossRef]
- Ebrahimnejad, A. An effective computational attempt for solving fully fuzzy linear programming using MOLP problem. J. Ind. Prod. Eng. 2019, 36, 59–69. [Google Scholar] [CrossRef]
- Nasseri, S.H.; Attari, H.; Ebrahimnejad, A. Revised simplex method and its application for solving fuzzy linear programming problems. Eur. J. Ind. Eng. 2012, 6, 259–280. [Google Scholar] [CrossRef]
- Sori, A.A.; Ebrahimnejad, A.; Motameni, H. The fuzzy inference approach to solve multi-objective constrained shortest path problem. J. Intell. Fuzzy Syst. 2020, 38, 4711–4720. [Google Scholar] [CrossRef]
- Ebrahimnejad, A.; Nasseri, S.H.; Lotfi, F.H. Bounded linear programs with trapezoidal fuzzy numbers. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2010, 18, 269–286. [Google Scholar] [CrossRef]
- Ebrahimnejad, A.; Nasseri, S. Linear programmes with trapezoidal fuzzy numbers: A duality approach. Int. J. Oper. Res. 2012, 13, 67–89. [Google Scholar] [CrossRef]
- Ebrahimnejad, A.; Karimnejad, Z.; Alrezaamiri, H. Particle swarm optimisation algorithm for solving shortest path problems with mixed fuzzy arc weights. Int. J. Appl. Decis. Sci. 2015, 8, 203–222. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, L.-Y.; Lin, C.-M. A General Fuzzy Cerebellar Model Neural Network Multidimensional Classifier Using Intuitionistic Fuzzy Sets for Medical Identification. Comput. Intell. Neurosci. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Chung, C.-C.; Chen, T.-S.; Lin, L.-H.; Lin, Y.-C.; Lin, C.-M. Bankruptcy Prediction Using Cerebellar Model Neural Networks. Int. J. Fuzzy Syst. 2016, 18, 160–167. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, C.-M. An Interval-Valued Fuzzy Cerebellar Model Neural Network Based on Intuitionistic Fuzzy Sets. Int. J. Fuzzy Syst. 2017, 19, 881–894. [Google Scholar] [CrossRef]
- Chao, F.; Zhou, D.; Lin, C.-M.; Zhou, C.; Shi, M.; Lin, D. Fuzzy cerebellar model articulation controller network optimization via self-adaptive global best harmony search algorithm. Soft Comput. 2018, 22, 3141–3153. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, C.-M. Wavelet-TSK-Type Fuzzy Cerebellar Model Neural Network for Uncertain Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 549–558. [Google Scholar] [CrossRef]
- Lin, C.-M.; Hou, Y.-L.; Chen, T.-Y.; Chen, K.-H. Breast Nodules Computer-Aided Diagnostic System Design Using Fuzzy Cerebellar Model Neural Networks. IEEE Trans. Fuzzy Syst. 2014, 22, 693–699. [Google Scholar] [CrossRef]
- Hu, J.; Pratt, G. Self-Organizing CMAC neural networks and adaptive dynamic control. In Proceedings of the 1999 IEEE International Symposium on Intelligent Control Intelligent Systems and Semiotics, Cambridge, MA, USA, 17 September 1999. [Google Scholar] [CrossRef]
- Lee, H.-M.; Chen, C.-M.; Lu, Y.-F. A self-organizing HCMAC neural-network classifier. IEEE Trans. Neural Netw. 2003, 14, 15–27. [Google Scholar] [PubMed]
- Le, T.-L.; Huynh, T.-T.; Hong, S.-K. Self-Organizing Interval Type-2 Fuzzy Asymmetric CMAC Design to Synchronize Chaotic Satellite Systems Using a Modified Grey Wolf Optimizer. IEEE Access 2020, 8, 53697–53709. [Google Scholar] [CrossRef]
- Xie, M.; Wang, Y.; Feng, G.; Sun, D. Automated pairing manipulation of biological cells with a robot-tweezers manipulation system. IEEE ASME Trans. Mechatron. 2015, 20, 2242–2251. [Google Scholar] [CrossRef]
- Li, X.; Cheah, C.C. Tracking Control for Optical Manipulation with Adaptation of Trapping Stiffness. IEEE Trans. Control Syst. Technol. 2016, 24, 1432–1440. [Google Scholar] [CrossRef]
- Hu, S.; Chen, S.; Chen, S.; Xu, G.; Sun, D. Automated transportation of multiple cell types using a robot-aided cell manipulation system with holographic optical tweezers. IEEE ASME Trans. Mechatron. 2017, 22, 804–814. [Google Scholar] [CrossRef]
- Oertel, H. Prandtl’s Essentials of Fluid Mechanics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hu, S.; Sun, D. Automatic transportation of biological cells with a robot-tweezer manipulation system. Int. J. Robot. Res. 2011, 30, 1681–1694. [Google Scholar] [CrossRef]
- Li, H.; Hong, C.; Pan, J.; Zhu, L.; Liu, Y.; Yang, K. Development and application of portable neutrophil chemotaxis research system. Sci. Technol. Eng. 2021, 21, 6695–6703. [Google Scholar]
- Banerjee, A.G.; Chowdhury, S.; Losert, W.; Gupta, S.K. Real-Time Path Planning for Coordinated Transport of Multiple Particles Using Optical Tweezers. IEEE Trans. Autom. Sci. Eng. 2012, 9, 669–678. [Google Scholar] [CrossRef] [Green Version]
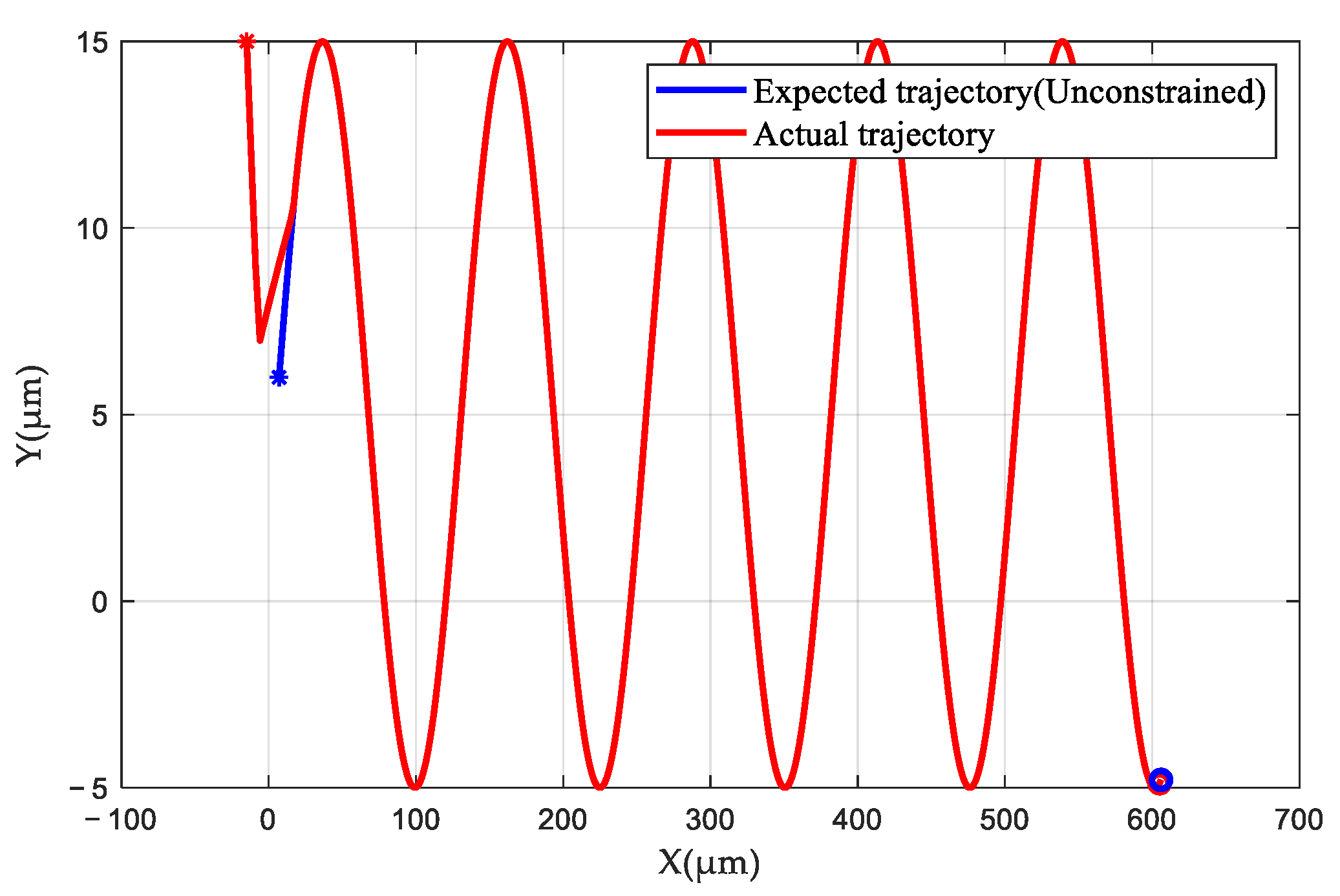
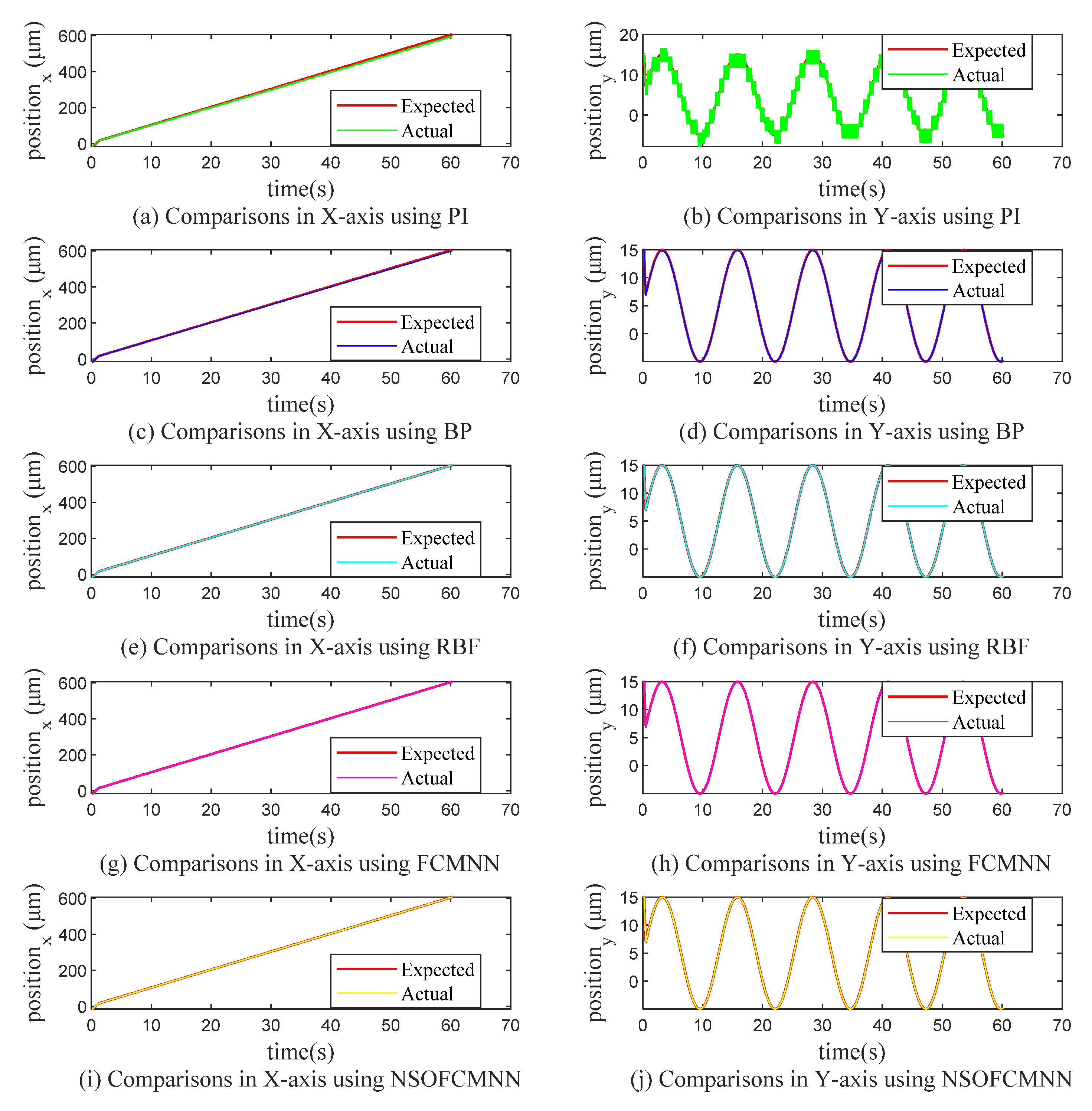
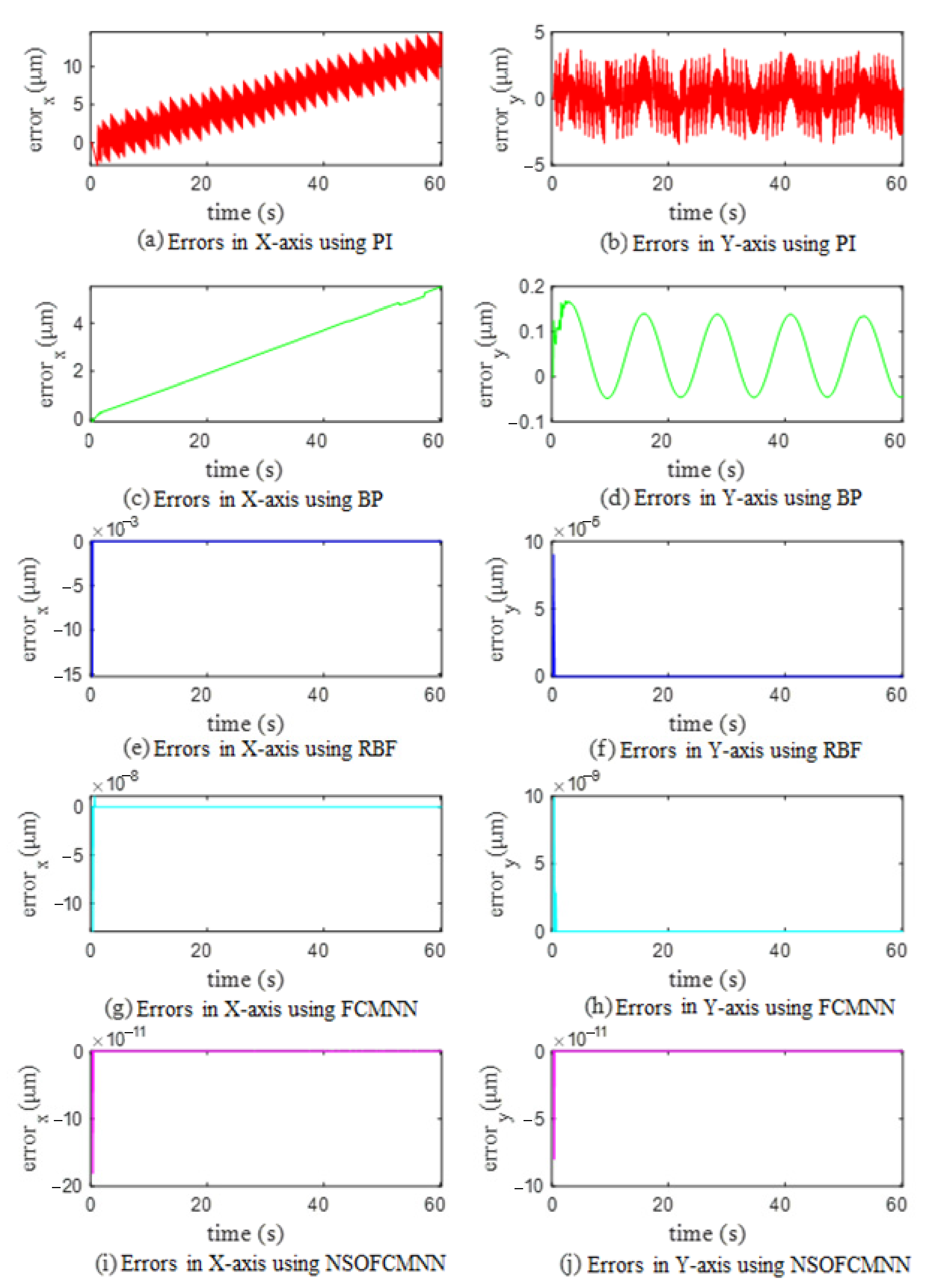
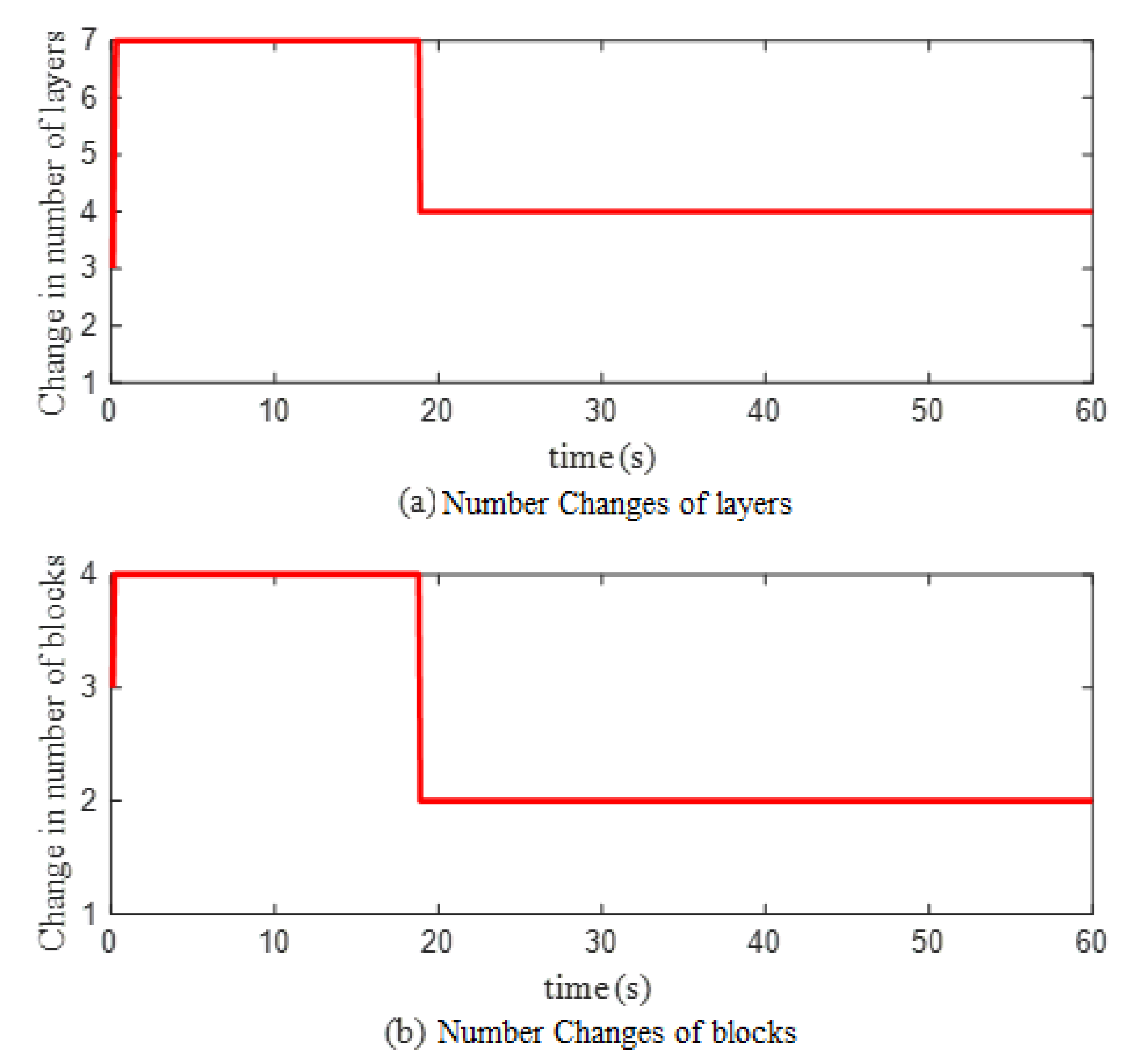
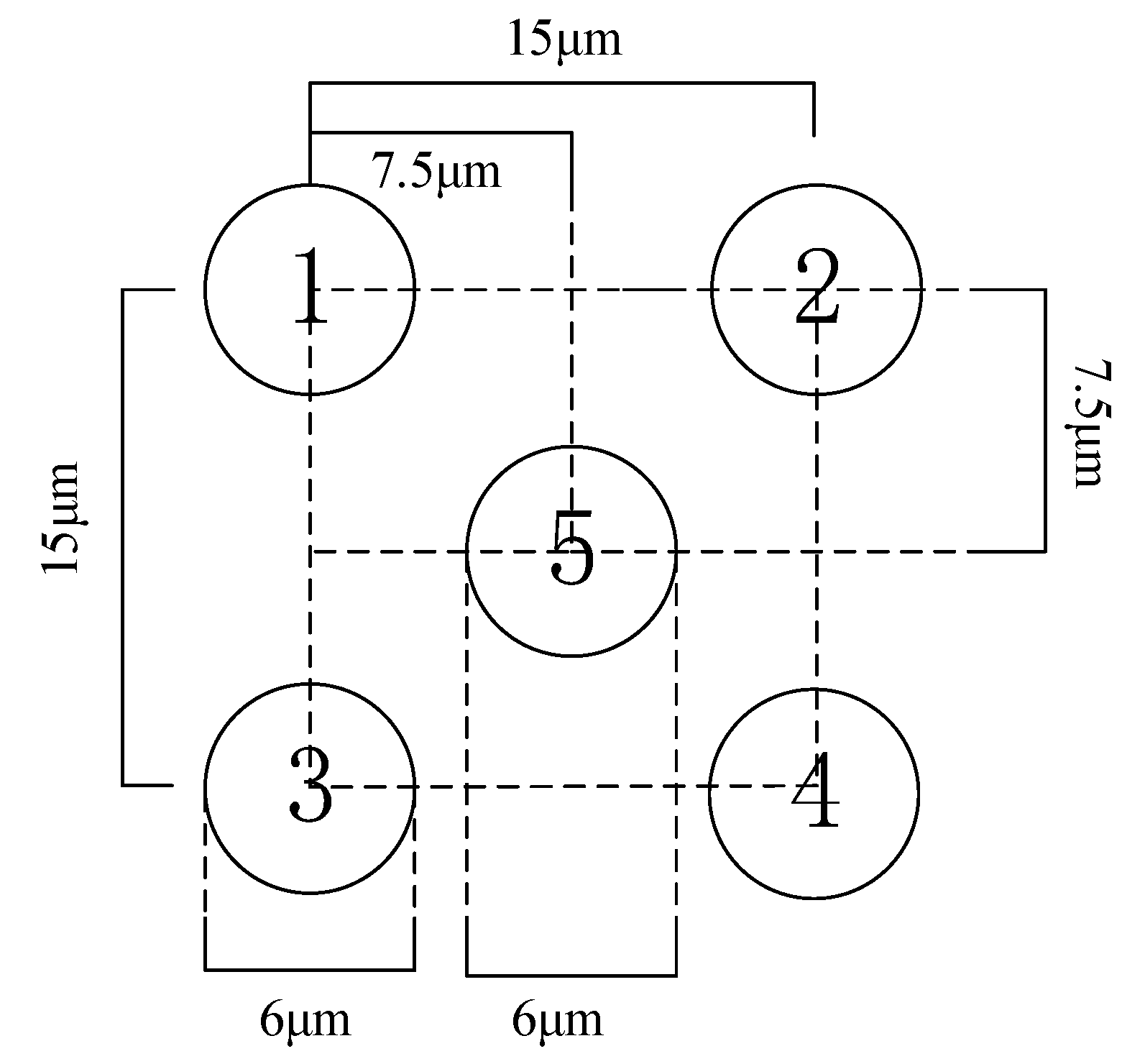
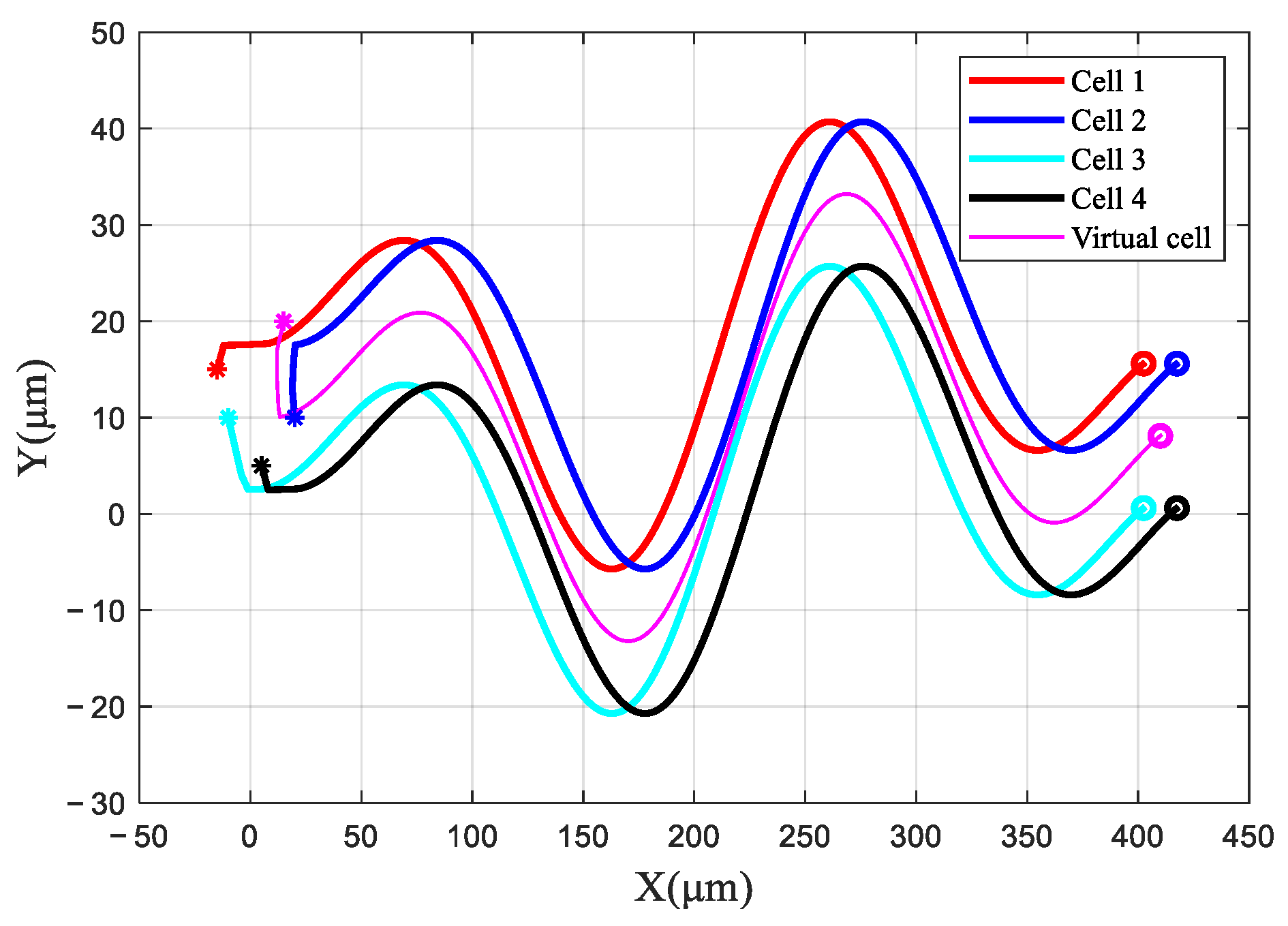
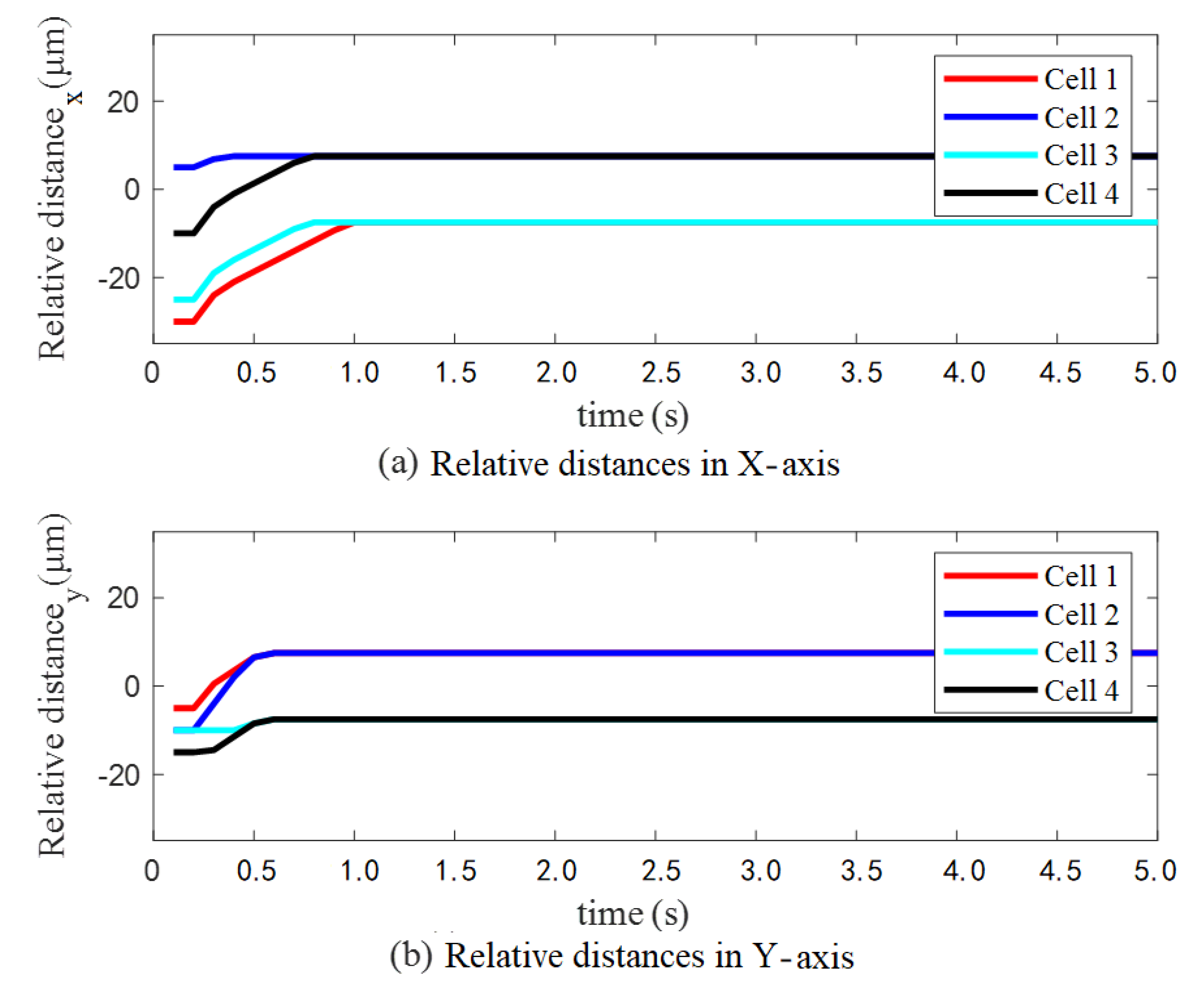
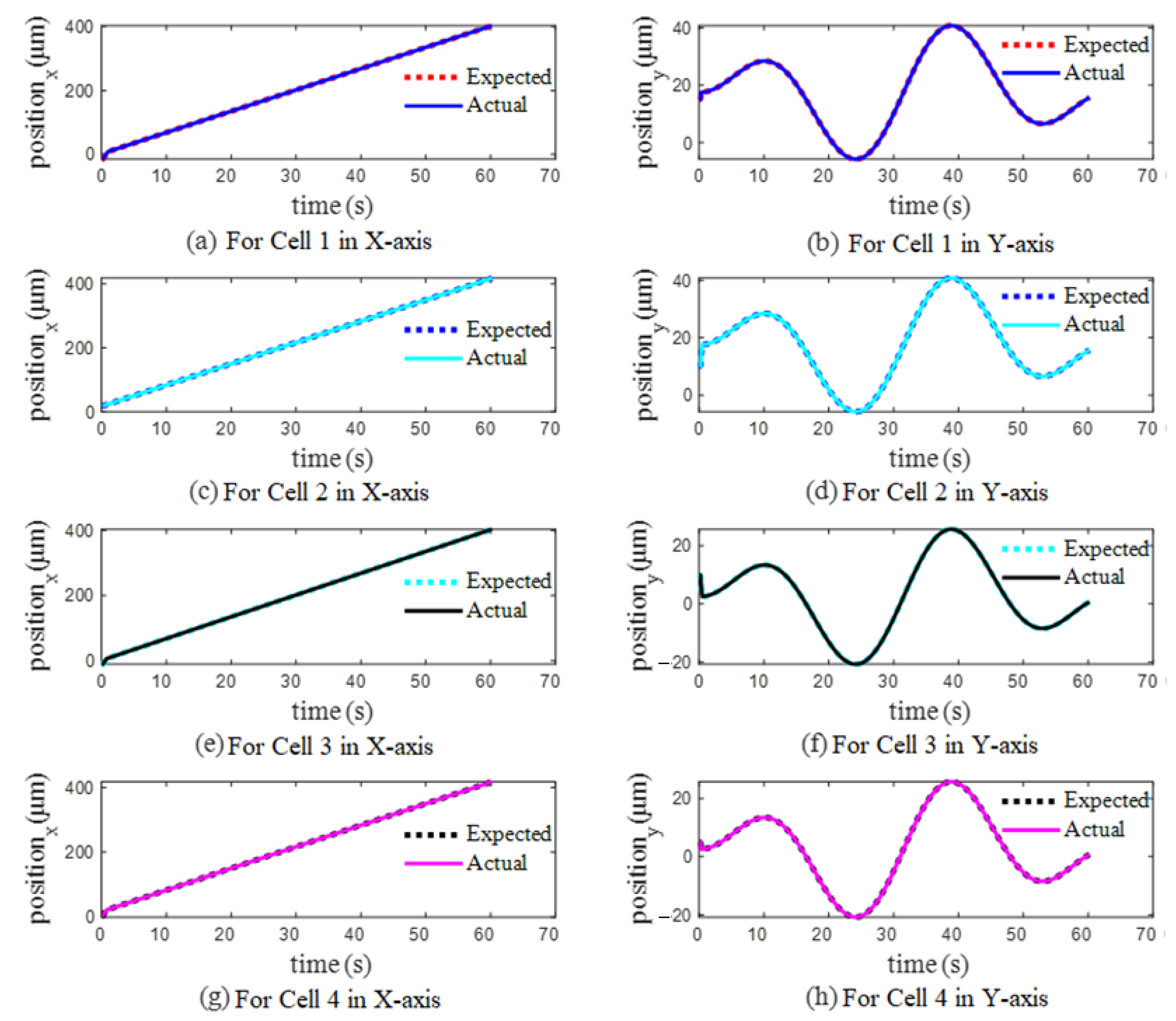
| Cell Velocity (μm/s) | ±5 | ±7.5 | ±10 |
|---|---|---|---|
| 0.09 | 0.1 | 0.09 |
| Data Type | Main Controller | X-Axis | Y-Axis |
|---|---|---|---|
| RMSE of single-cell manipulation | PI | 7.0 × 10−6 | 1.8 × 10−6 |
| BP | 3.2 × 10−6 | 8.4 × 10−8 | |
| RBF | 6.2 × 10−10 | 4.0 × 10−12 | |
| FCMNN | 5.3 × 10−15 | 4.2 × 10−16 | |
| This work | 7.4 × 10−18 | 3.3 × 10−18 | |
| MAE of single-cell manipulation | PI | 5.5 × 10−5 | 3.7 × 10−6 |
| BP | 1.3 × 10−5 | 5.8 × 10−8 | |
| RBF | 2.5 × 10−11 | 2.1 × 10−13 | |
| FCMNN | 2.0 × 10−16 | 2.1 × 10−17 | |
| This work | 3.0 × 10−19 | 1.3 × 10−19 |
| Cell 1 | Cell 2 | Cell 3 | Cell 4 | Virtual Cell | |
|---|---|---|---|---|---|
| initial position (μm) | [−15, 15] | [20, 10] | [−10, 10] | [5, 5] | [15, 20] |
| Data Type | Main Controller | Cell 1 | Cell 2 | Cell 3 | Cell 4 |
|---|---|---|---|---|---|
| RMSE of each cell in the X-axis direction | PI | 4.7 × 10−6 | 5.1 × 10−6 | 4.7 × 10−6 | 5.0 × 10−6 |
| BP | 2.2 × 10−6 | 2.7 × 10−6 | 2.2 × 10−6 | 2.7 × 10−6 | |
| RBF | 7.0 × 10−8 | 5.0 × 10−8 | 6.4 × 10−10 | 7.0 × 10−8 | |
| FCMNN | 8.4 × 10−15 | 1.4 × 10−19 | 2.4 × 10−10 | 2.1 × 10−12 | |
| This work | 2.1 × 10−20 | 1.8 × 10−20 | 2.8 × 10−15 | 2.1 × 10−15 | |
| RMSE of each cell in the Y-axis direction | PI | 2.2 × 10−6 | 2.1 × 10−6 | 1.9 × 10−6 | 2.0 × 10−6 |
| BP | 2.1 × 10−7 | 2.1 × 10−7 | 1.2 × 10−7 | 1.2 × 10−7 | |
| RBF | 3.3 × 10−8 | 5.0 × 10−8 | 5.1 × 10−8 | 7.7 × 10−8 | |
| FCMNN | 2.7 × 10−15 | 1.9 × 10−19 | 7.5 × 10−11 | 7.1 × 10−12 | |
| This work | 3.1 × 10−20 | 9.0 × 10−21 | 1.6 × 10−15 | 2.1 × 10−15 |
| Data Type | Main Controller | Cell 1 | Cell 2 | Cell 3 | Cell 4 |
|---|---|---|---|---|---|
| MAE of each cell in the X-axis direction | PI | 2.6 × 10−5 | 3.1 × 10−5 | 2.5 × 10−5 | 2.9 × 10−5 |
| BP | 6.5 × 10−6 | 7.2 × 10−6 | 6.5 × 10−6 | 7.2 × 10−6 | |
| RBF | 1.5 × 10−8 | 2.1 × 10−8 | 8.9 × 10−9 | 2.8 × 10−8 | |
| FCMNN | 3.4 × 10−16 | 3.8 × 10−20 | 9.9 × 10−12 | 4.8 × 10−14 | |
| This work | 5.4 × 10−21 | 4.6 × 10−21 | 1.1 × 10−16 | 8.5 × 10−18 | |
| MAE of each cell in the Y-axis direction | PI | 5.7 × 10−6 | 5.2 × 10−6 | 4.0 × 10−6 | 4.0 × 10−6 |
| BP | 2.1 × 10−7 | 2.1 × 10−7 | 4.1 × 10−8 | 4.0 × 10−8 | |
| RBF | 7.9 × 10−9 | 1.7 × 10−8 | 1.7 × 10−8 | 2.5 × 10−8 | |
| FCMNN | 1.1 × 10−16 | 7.6 × 10−21 | 3.0 × 10−12 | 2.9 × 10−13 | |
| This work | 5.6 × 10−23 | 3.0 × 10−23 | 6.4 × 10−17 | 8.4 × 10−17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Hou, H.; Huang, Q.-Y.; Zhong, X.-G.; Zheng, P.-S. Design of Optical Tweezers Manipulation Control System Based on Novel Self-Organizing Fuzzy Cerebellar Model Neural Network. Appl. Sci. 2022, 12, 9655. https://doi.org/10.3390/app12199655
Zhao J, Hou H, Huang Q-Y, Zhong X-G, Zheng P-S. Design of Optical Tweezers Manipulation Control System Based on Novel Self-Organizing Fuzzy Cerebellar Model Neural Network. Applied Sciences. 2022; 12(19):9655. https://doi.org/10.3390/app12199655
Chicago/Turabian StyleZhao, Jing, Hui Hou, Qi-Yu Huang, Xun-Gao Zhong, and Peng-Sheng Zheng. 2022. "Design of Optical Tweezers Manipulation Control System Based on Novel Self-Organizing Fuzzy Cerebellar Model Neural Network" Applied Sciences 12, no. 19: 9655. https://doi.org/10.3390/app12199655
APA StyleZhao, J., Hou, H., Huang, Q.-Y., Zhong, X.-G., & Zheng, P.-S. (2022). Design of Optical Tweezers Manipulation Control System Based on Novel Self-Organizing Fuzzy Cerebellar Model Neural Network. Applied Sciences, 12(19), 9655. https://doi.org/10.3390/app12199655





