A Novel Radial Artery P-S Curve Model Based on Radial Vibration of Vascular Wall
Abstract
:1. Introduction
2. Models and Methods
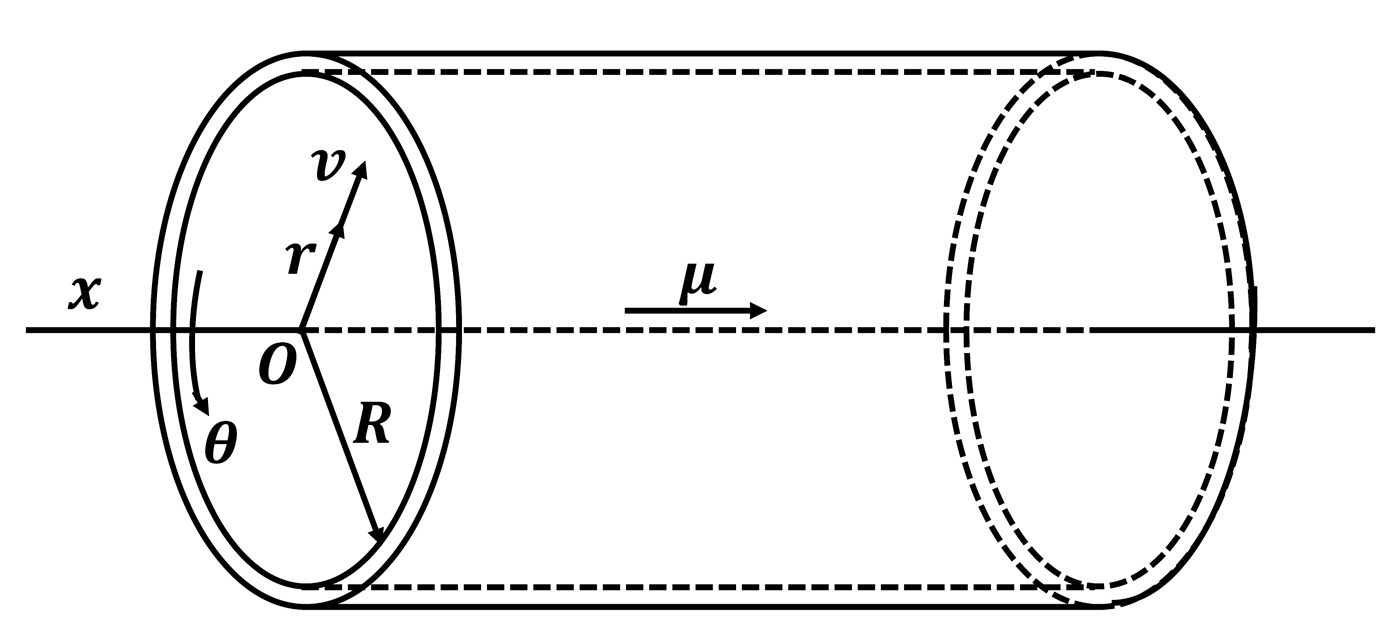
2.1. Model of Blood Movement
2.2. Model of Vascular Wall Movement
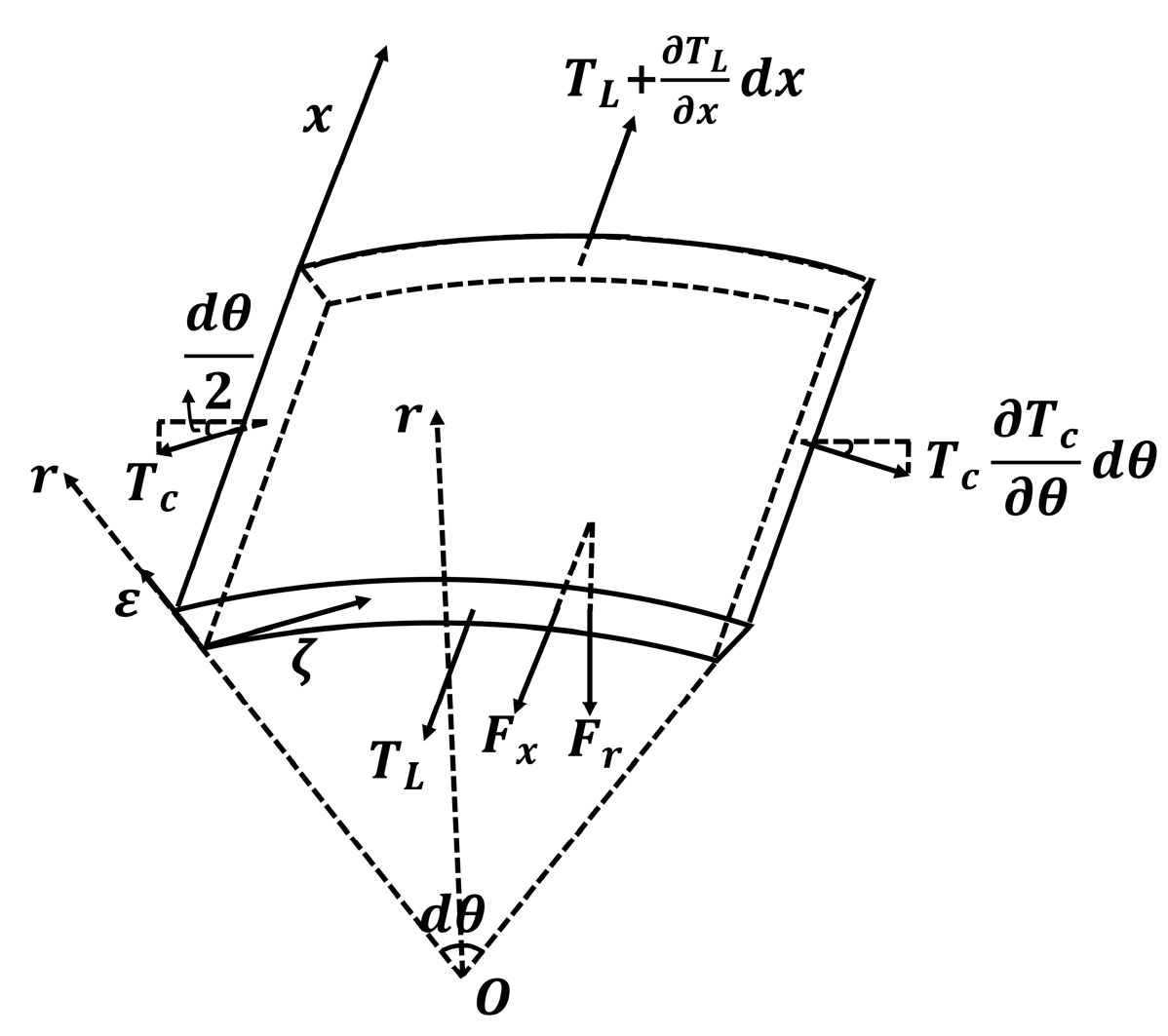
2.3. Model of Elastic Deformation of the Vascular Wall
3. Model Validation Experiments and Results
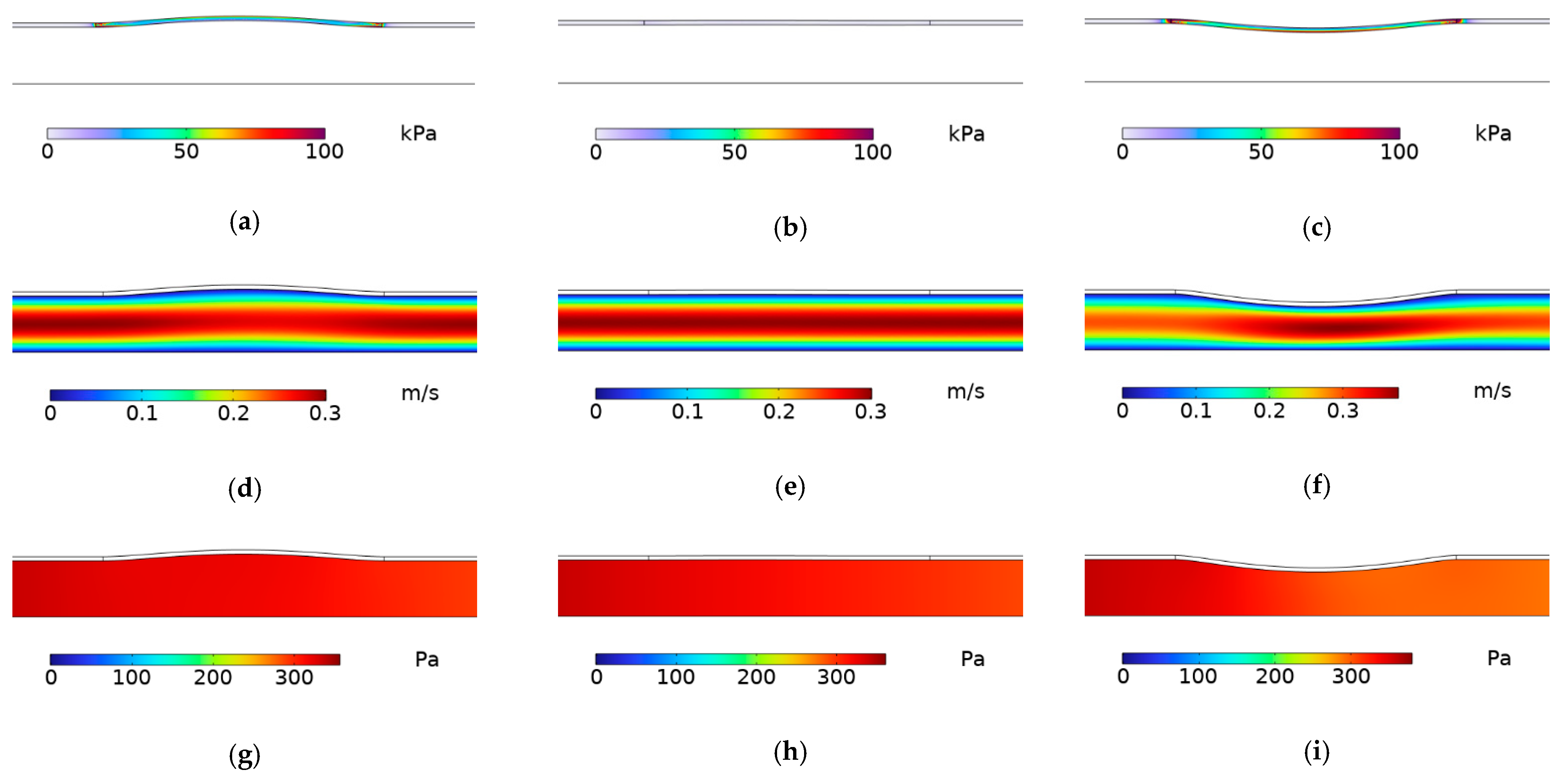
3.1. Simulation Experiment
3.2. Human Validation Experiments
3.2.1. Data Sources
- Good physical condition and no cold symptoms;
- No chronic diseases or genetic diseases;
- No malformation or injury of the radial artery;
- No heart bypass.
3.2.2. P-S Curve Acquisition
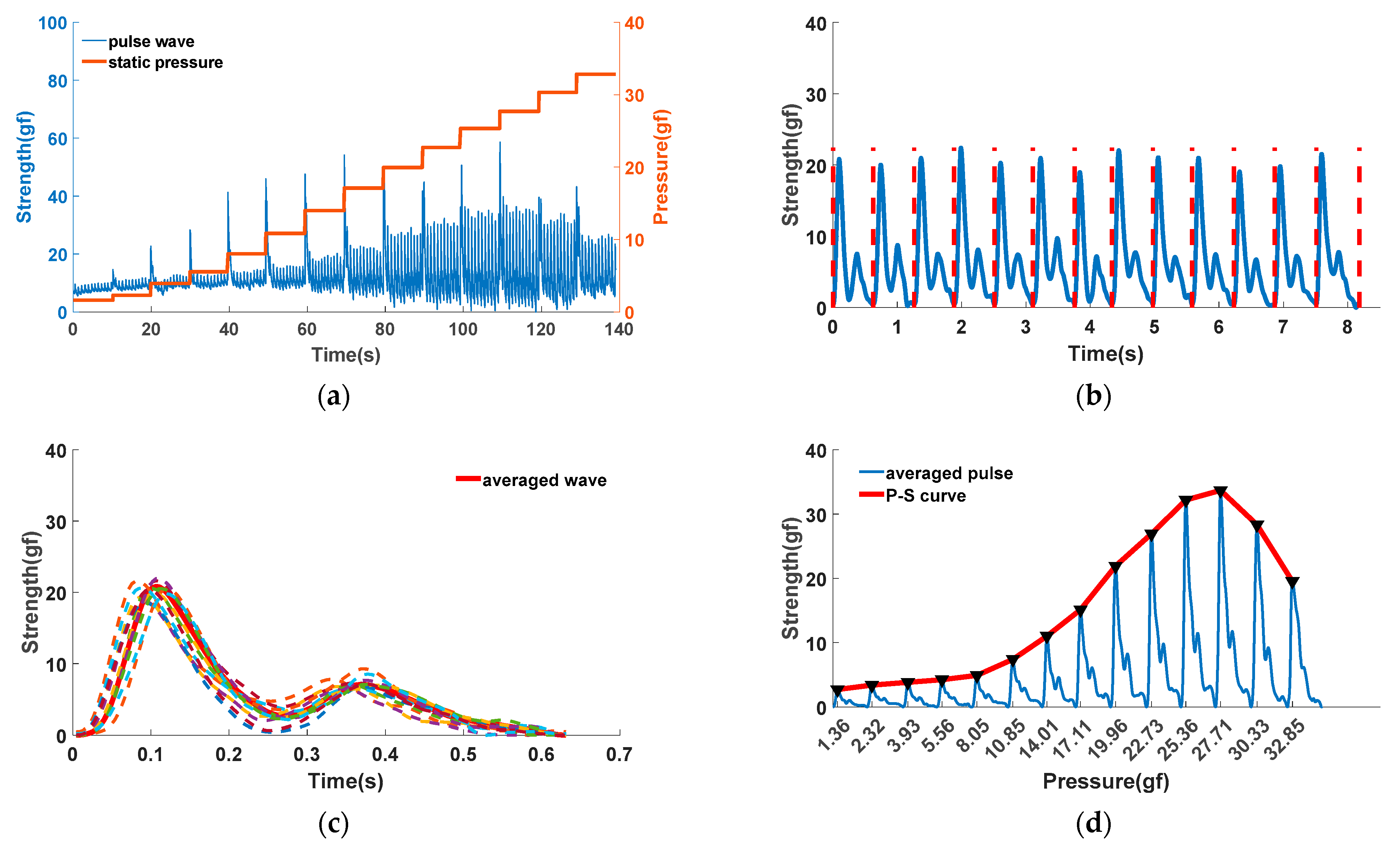
- Based on the wavelet filtering algorithm and bandpass filtering algorithm, the noise interference caused by motion, environment and power frequency is eliminated, As shown in Figure 6a;
- Based on the principle of cardiac cycle similarity, the pulse signal under each pressure segment is divided into a single cycle, and a set of single-cycle pulse wave signals is obtained, as shown in Figure 6b;
- Based on the cubic spline interpolation method, the pulse wave under the same pressure is partitioned by their cycles. Then, pulse waves are interpolated into a group of waveforms with the same cycle, and averaged these reorganized waveforms in the time domain. In this way, we obtained a representative waveform of a single cycle, as shown in Figure 6c;
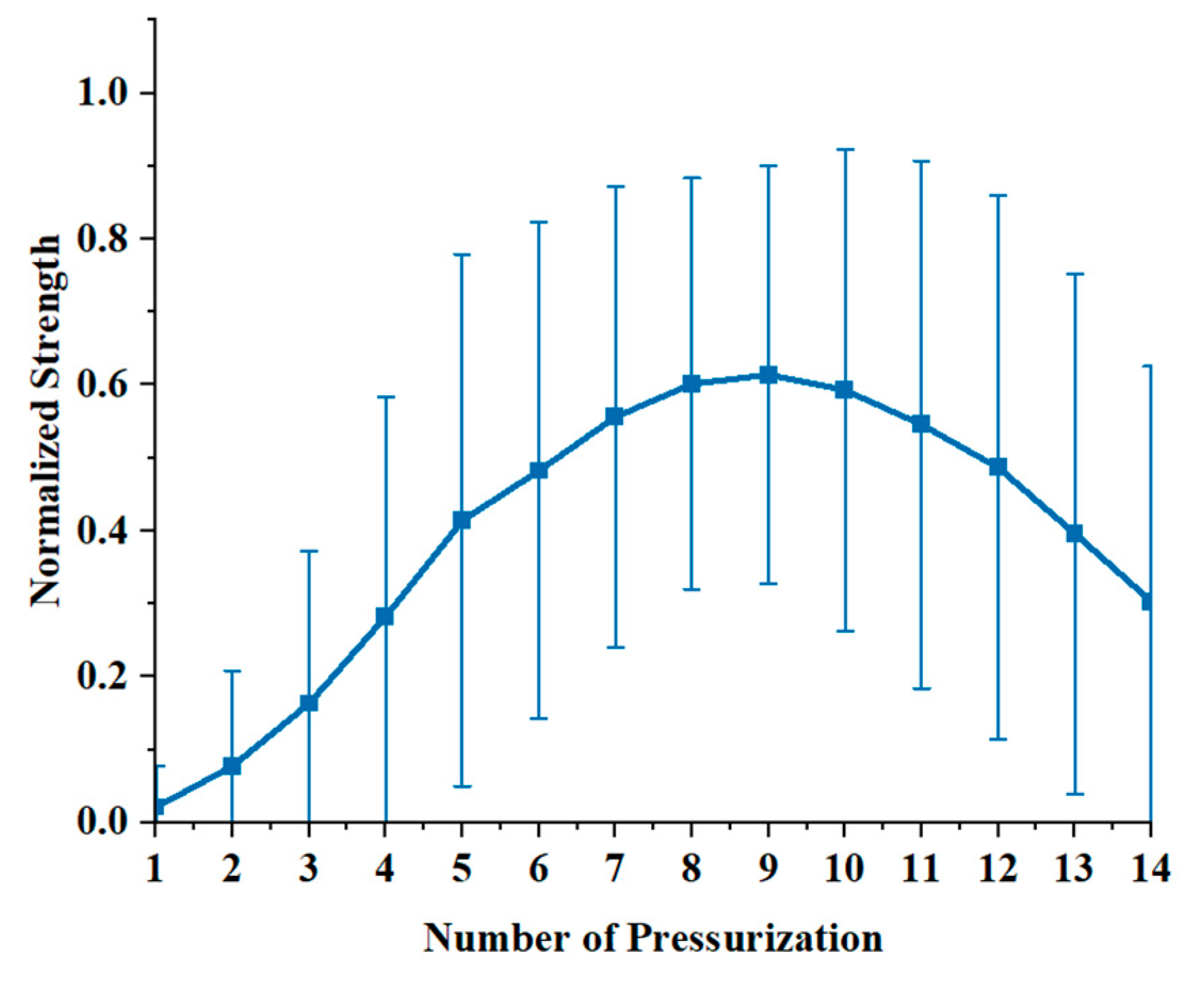
- Based on the stepped pressurization method, the pulse strength envelope under the continuous pressure sequence is extracted, that is, the pulse P-S curve, as shown in Figure 6d.
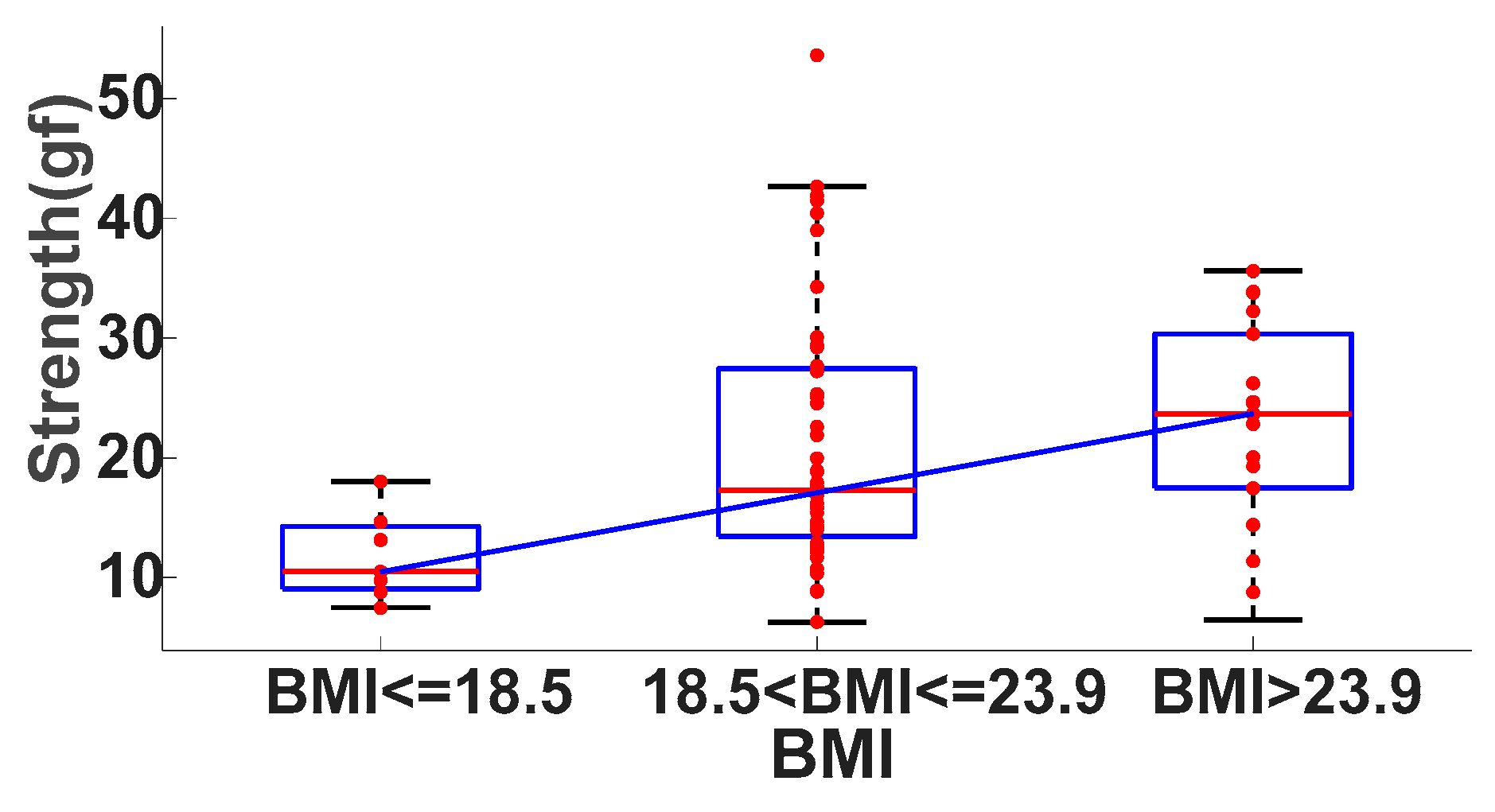
3.2.3. P-S Curve Analysis
- Lean weight, BMI < = 18.5;
- Moderate weight, 18.5 < BMI < = 23.9;
- Overweight, BMI > 23.9.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guyton, A.C.; Hall, J.E. Textbook of Medical Physiology, 11th ed.; xxxv; Elsevier Saunders: Philadelphia, PA, USA, 2006; 1116p. [Google Scholar]
- Hall, J.E. Guyton and Hall Textbook of Medical Physiology, 13th ed.; xix; Elsevier: Philadelphia, PA, USA, 2016; 1145p. [Google Scholar]
- Zhao, Y.C.; Vatankhah, P.; Goh, T.; Michelis, R.; Kyanian, K.; Zhang, Y.; Li, Z.; Ju, L.A. Hemodynamic analysis for stenosis microfluidic model of thrombosis with refined computational fluid dynamics simulation. Sci. Rep. 2021, 11, 6875. [Google Scholar] [CrossRef] [PubMed]
- Nichols, W.W. Clinical measurement of arterial stiffness obtained from noninvasive pressure waveforms. Am. J. Hypertens. 2005, 18, 3S–10S. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.D.; Lopes, A.J. Pulse waveform analysis as a bridge between pulse examination in Chinese medicine and cardiology. Chin. J. Integr. Med. 2013, 19, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Bae, J.H.; Ku, B.; Yim, M.H.; Ang, L.; Kim, H.; Jeon, Y.J. A comparative study of the radial pulse between primary dysmenorrhea patients and healthy subjects during the menstrual phase. Sci. Rep. 2019, 9, 9716. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.M.; Chang, C.W.; Wang, S.H.; Chang, Y.T.; Chen, Y.C.; Wang, G.C. The first harmonic of radial pulse wave predicts major adverse cardiovascular and microvascular events in patients with type 2 diabetes. J. Diabetes Complicat. 2019, 33, 107420. [Google Scholar] [CrossRef]
- Xu, K.; Butlin, M.; Avolio, A.P. Effects of pressure-dependent segmental arterial compliance and postural changes on pulse wave transmission in an arterial model of the human upper limb. In Proceedings of the 011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6450–6453. [Google Scholar]
- Ribeiro de Moura, N.G.; Cordovil, I.; de Sá Ferreira, A. Traditional Chinese medicine wrist pulse-taking is associated with pulse waveform analysis and hemodynamics in hypertension. J. Integr. Med. 2016, 14, 100–113. [Google Scholar] [CrossRef]
- O’Rourke, M.F. Time domain analysis of the arterial pulse in clinical medicine. Med. Biol. Eng. Comput. 2009, 47, 119–129. [Google Scholar] [CrossRef]
- Wang, J.J.; Parker, K.H. Wave propagation in a model of the arterial circulation. J. Biomech. 2004, 37, 457–470. [Google Scholar] [CrossRef]
- Stergiopulos, N.; Westerhof, B.E.; Westerhof, N. Total arterial inertance as the fourth element of the windkessel model. Am. J. Physiol.-Heart C 1999, 276, H81–H88. [Google Scholar] [CrossRef]
- Yoon, Y.Z.; Lee, M.H.; Soh, K.S. Pulse type classification by varying contact pressure. IEEE Eng. Med. Biol. Mag. 2000, 19, 106–110. [Google Scholar]
- Wei, C.C. An innovative method to measure the peripheral arterial elasticity: Spring constant modeling based on the arterial pressure wave with radial vibration. Ann. Biomed. Eng. 2011, 39, 2695–2705. [Google Scholar] [CrossRef] [PubMed]
- Lin Wang, Y.-Y.; Chiu, W.-B.; Jan, M.-Y.; Bau, J.-G.; Li, S.-P.; Wang, W.-K. Analysis of transverse wave as a propagation mode for the pressure pulse in large arteries. J. Appl. Phys. 2007, 102, 064702. [Google Scholar] [CrossRef]
- Alastruey, J. On the mechanics underlying the reservoir-excess separation in systemic arteries and their implications for pulse wave analysis. Cardiovasc. Eng. 2010, 10, 176–189. [Google Scholar] [CrossRef] [PubMed]
- Yoo, S.K.; Shin, K.Y.; Lee, T.B.; Jin, S.O. New pulse wave measurement method using different hold-down wrist pressures according to individual patient characteristics. Springerplus 2013, 2, 406. [Google Scholar] [CrossRef] [PubMed]
- Geng, X.; Liu, S.; Zhang, Y.; Zhang, S.; Hou, J.; Zhang, J.; Asif, M.; Zhang, H.-Y. Adjacent Channel Interference Modeling of Single Vibration Point on Multichannel Dynamic Pressure Sensors. J. Sens. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Geng, X.; Liu, S.; Zhang, Y.; Hou, J.; Zhang, S.; Zhang, J.; Zhang, H. A Noncontact Method for Locating Radial Artery above Radial Styloid Process in Thermal Image. Evid. Based Complement. Altern. Med. 2020, 2020, 4057154. [Google Scholar] [CrossRef]
- Chen, C.; Li, Z.; Zhang, Y.; Zhang, S.; Hou, J.; Zhang, H. A 3D Wrist Pulse Signal Acquisition System for Width Information of Pulse Wave. Sensors 2019, 20, 11. [Google Scholar] [CrossRef]
- Coccarelli, A.; Carson, J.M.; Aggarwal, A.; Pant, S. A framework for incorporating 3D hyperelastic vascular wall models in 1D blood flow simulations. Biomech. Model. Mechanobiol. 2021, 20, 1231–1249. [Google Scholar] [CrossRef]
- Kim, H.J.; Vignon-Clementel, I.E.; Coogan, J.S.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Patient-specific modeling of blood flow and pressure in human coronary arteries. Ann. Biomed. Eng. 2010, 38, 3195–3209. [Google Scholar] [CrossRef]
- Razavi, A.; Shirani, E.; Sadeghi, M.R. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. J. Biomech. 2011, 44, 2021–2030. [Google Scholar] [CrossRef]
- Secomb, T.W. Hemodynamics. Compr. Physiol. 2016, 6, 975–1003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sriram, K.; Intaglietta, M.; Tartakovsky, D.M. Non-Newtonian flow of blood in arterioles: Consequences for wall shear stress measurements. Microcirculation 2014, 21, 628–639. [Google Scholar] [CrossRef] [PubMed]
- Rosenson, R.S.; McCormick, A.; Uretz, E.F. Distribution of blood viscosity values and biochemical correlates in healthy adults. Clin. Chem. 1996, 42, 1189–1195. [Google Scholar] [CrossRef]
- Sandeep, S.; Shine, S.R. Effect of stenosis and dilatation on the hemodynamic parameters associated with left coronary artery. Comput. Methods Programs Biomed. 2021, 204, 106052. [Google Scholar] [CrossRef]
- Rosito, G.A.; D’Agostino, R.B.; Massaro, J.; Lipinska, L.; Mittleman, M.A.; Sutherland, P.; Wilson, P.W.F.; Levy, D.; Muller, J.E.; Tofler, G.H. Association between obesity and a prothrombotic state: The Framingham Offspring Study. Thromb. Haemost. 2004, 91, 683–689. [Google Scholar] [CrossRef] [PubMed]
- Seki, K.; Sumino, H.; Nara, M.; Ishiyama, N.; Nishino, M.; Murakami, M. Relationships between blood rheology and age, body mass index, blood cell count, fibrinogen, and lipids in healthy subjects. Clin. Hemorheol. Microcirc. 2006, 34, 401–410. [Google Scholar]
- Ercan, M.; Konukoglu, D. Role of plasma viscosity and plasma homocysteine level on hyperinsulinemic obese female subjects. Clin. Hemorheol. Microcirc. 2008, 38, 227–234. [Google Scholar] [PubMed]
- Korpas, D.; Halek, J.; Dolezal, L. Parameters describing the pulse wave. Physiol. Res. 2009, 58, 473–479. [Google Scholar] [CrossRef]
- Parittotokkaporn, S.; de Castro, D.; Lowe, A.; Pylypchuk, R. Carotid Pulse Wave Analysis: Future Direction of Hemodynamic and Cardiovascular Risk Assessment. JMA J. 2021, 4, 119–128. [Google Scholar] [CrossRef]


| Parameter (Unit) | Value |
|---|---|
| (m) | |
| (m) | |
| (Pa) | |
| (Pa) | |
| () | |
| (Pa) | 0 |
| () | |
| (m) | |
| L2 (m) | |
| L3 (m) |
| Pressure Relationship | Stress (kPa) | Intravascular Pressure (Pa) | |
|---|---|---|---|
| 32.57 | 0.28 | 319 | |
| 0.47 | 0.30 | 316 | |
| 45.84 | 0.37 | 302 |
| Pressure Relationship | Viscosity Coefficient (Pa∙s) | Intravascular Pressure (Pa) |
|---|---|---|
| 157 | ||
| 316 | ||
| 474 |
| Characteristic (Unit) | Number or Mean ± SD |
|---|---|
| Number (n) | 69 |
| Age (year) | 27.54.9 |
| Weight (kg) | 66.2 |
| BMI (kg/m2) | 23.6.2 |
| BP–diastolic (mmHg) | 69.4 |
| BP–systolic (mmHg) | |
| T-body (°C) | 36.80.3 |
| T-ambient (°C) | 23.61.2 |
| SaO2 | 97.80.8 |
| HR (times/minute) | 71.610.3 |
| Group | BMI | Number (n) | Strength (gf) |
|---|---|---|---|
| Lean weight | 17.6 ± 0.6 | 7 | 11.7 ± 3.7 |
| Moderate weight | 21.4 ± 1.5 | 44 | 21.3 ± 11.0 |
| Overweight | 26.2 ± 3.8 | 18 | 22.7 ± 8.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Geng, X.; Kang, X.; Zhang, Y.; Zhang, J.; Zhang, H. A Novel Radial Artery P-S Curve Model Based on Radial Vibration of Vascular Wall. Appl. Sci. 2022, 12, 9706. https://doi.org/10.3390/app12199706
Wang G, Geng X, Kang X, Zhang Y, Zhang J, Zhang H. A Novel Radial Artery P-S Curve Model Based on Radial Vibration of Vascular Wall. Applied Sciences. 2022; 12(19):9706. https://doi.org/10.3390/app12199706
Chicago/Turabian StyleWang, Guotai, Xingguang Geng, Xiaoxiao Kang, Yitao Zhang, Jun Zhang, and Haiying Zhang. 2022. "A Novel Radial Artery P-S Curve Model Based on Radial Vibration of Vascular Wall" Applied Sciences 12, no. 19: 9706. https://doi.org/10.3390/app12199706
APA StyleWang, G., Geng, X., Kang, X., Zhang, Y., Zhang, J., & Zhang, H. (2022). A Novel Radial Artery P-S Curve Model Based on Radial Vibration of Vascular Wall. Applied Sciences, 12(19), 9706. https://doi.org/10.3390/app12199706






