AHA-AO: Artificial Hummingbird Algorithm with Aquila Optimization for Efficient Feature Selection in Medical Image Classification
Abstract
:1. Introduction
- Proposal of a novel FS method based on improving the behavior of the Artificial Hummingbird Algorithm using Aquila Optimization. This model aims to choose the most important features from each image representation to make the classification process more efficient (using a reduced set of features).
- Presentation of a comprehensive experimental study of the proposed system with a comparison of the proposed method with various state-of-the-art methods by utilizing four real-world datasets.
2. Related Work
3. Background
3.1. Efficient Neural Networks
3.2. Aquila Optimizer (AO)
3.3. Artificial Hummingbird Algorithm
3.3.1. Guided Foraging
3.3.2. Territorial Foraging
3.3.3. Migration Foraging
4. Proposed Method
4.1. Deep Learning for Feature Extraction
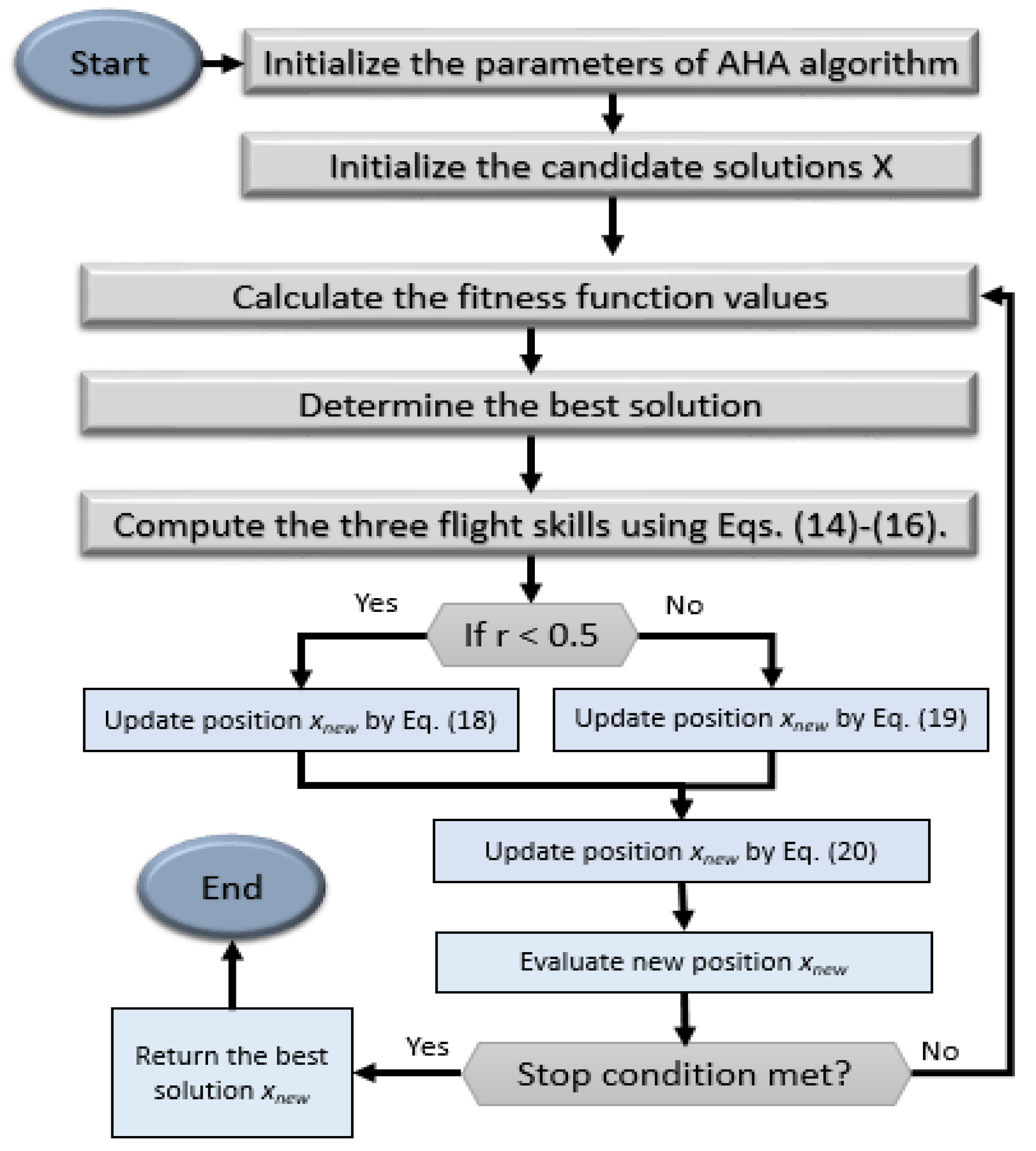
4.2. Feature-Selection-Based AHA-AO
5. Experimental Results
5.1. Performance Measures
5.2. Experiment 1: Results without the Feature Selection Optimization
5.3. Experiment 2: Results Based on the ISIC-2016 Dataset
5.4. Experiment 3: Results Based on the PH2 Dataset
5.5. Experiment 4: Results Based on the Chest-XRay Dataset
5.6. Experiment 5: Results Based on the Blood-Cell Dataset
5.7. Comparison with Studies in the Literature
6. Limitations of the Study and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Wang, H.; Huang, Y.; Yan, B.; Chang, Z.; Liu, Z.; Zhao, M.; Cui, L.; Song, J.; Li, F. Trends in the application of deep learning networks in medical image analysis: Evolution between 2012 and 2020. Eur. J. Radiol. 2022, 146, 110069. [Google Scholar] [CrossRef] [PubMed]
- Kisilev, P.; Walach, E.; Barkan, E.; Ophir, B.; Alpert, S.; Hashoul, S.Y. From medical image to automatic medical report generation. IBM J. Res. Dev. 2015, 59, 2:1–2:7. [Google Scholar] [CrossRef]
- Liu, F.; Tian, Y.; Chen, Y.; Liu, Y.; Belagiannis, V.; Carneiro, G. ACPL: Anti-Curriculum Pseudo-Labelling for Semi-Supervised Medical Image Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–20 June 2022; pp. 20697–20706. [Google Scholar]
- Cheng, J.; Tian, S.; Yu, L.; Gao, C.; Kang, X.; Ma, X.; Wu, W.; Liu, S.; Lu, H. ResGANet: Residual group attention network for medical image classification and segmentation. Med. Image Anal. 2022, 76, 102313. [Google Scholar] [CrossRef] [PubMed]
- Mahapatra, D. Unsupervised Domain Adaptation Using Feature Disentanglement And GCNs For Medical Image Classification. arXiv 2022, arXiv:2206.13123. [Google Scholar]
- Gao, Y.; Liu, H.; Wang, X.; Zhang, K. On an artificial neural network for inverse scattering problems. J. Comput. Phys. 2022, 448, 110771. [Google Scholar] [CrossRef]
- Yin, W.; Yang, W.; Liu, H. A neural network scheme for recovering scattering obstacles with limited phaseless far-field data. J. Comput. Phys. 2020, 417, 109594. [Google Scholar] [CrossRef]
- Ding, M.H.; Liu, H.; Zheng, G.H. Shape reconstructions by using plasmon resonances. ESAIM Math. Model. Numer. Anal. 2022, 56, 705–726. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, H.; Zheng, G.H. Mathematical analysis of plasmon resonances for curved nanorods. J. Math. Pures Appl. 2021, 153, 248–280. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, H.; Zheng, G.H. Plasmon resonances of nanorods in transverse electromagnetic scattering. J. Differ. Equations 2022, 318, 502–536. [Google Scholar] [CrossRef]
- Singhal, A.; Phogat, M.; Kumar, D.; Kumar, A.; Dahiya, M.; Shrivastava, V.K. Study of deep learning techniques for medical image analysis: A review. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Salahuddin, Z.; Woodruff, H.C.; Chatterjee, A.; Lambin, P. Transparency of deep neural networks for medical image analysis: A review of interpretability methods. Comput. Biol. Med. 2022, 140, 105111. [Google Scholar] [CrossRef] [PubMed]
- Karimi, D.; Warfield, S.K.; Gholipour, A. Transfer learning in medical image segmentation: New insights from analysis of the dynamics of model parameters and learned representations. Artif. Intell. Med. 2021, 116, 102078. [Google Scholar] [CrossRef] [PubMed]
- Niu, S.; Liu, M.; Liu, Y.; Wang, J.; Song, H. Distant domain transfer learning for medical imaging. IEEE J. Biomed. Health Inform. 2021, 25, 3784–3793. [Google Scholar] [CrossRef]
- Adel, H.; Dahou, A.; Mabrouk, A.; Abd Elaziz, M.; Kayed, M.; El-Henawy, I.M.; Alshathri, S.; Amin Ali, A. Improving Crisis Events Detection Using DistilBERT with Hunger Games Search Algorithm. Mathematics 2022, 10, 447. [Google Scholar] [CrossRef]
- Rehman, A.; Khan, M.A.; Saba, T.; Mehmood, Z.; Tariq, U.; Ayesha, N. Microscopic brain tumor detection and classification using 3D CNN and feature selection architecture. Microsc. Res. Tech. 2021, 84, 133–149. [Google Scholar] [CrossRef] [PubMed]
- Öztürk, Ş. Class-driven content-based medical image retrieval using hash codes of deep features. Biomed. Signal Process. Control 2021, 68, 102601. [Google Scholar] [CrossRef]
- Anwar, S.M.; Majid, M.; Qayyum, A.; Awais, M.; Alnowami, M.; Khan, M.K. Medical image analysis using convolutional neural networks: A review. J. Med. Syst. 2018, 42, 1–13. [Google Scholar] [CrossRef]
- Samala, R.K.; Chan, H.P.; Hadjiiski, L.M.; Helvie, M.A.; Richter, C.; Cha, K. Evolutionary pruning of transfer learned deep convolutional neural network for breast cancer diagnosis in digital breast tomosynthesis. Phys. Med. Biol. 2018, 63, 095005. [Google Scholar] [CrossRef]
- Vijh, S.; Sharma, S.; Gaurav, P. Brain tumor segmentation using OTSU embedded adaptive particle swarm optimization method and convolutional neural network. In Data Visualization and Knowledge Engineering; Springer: Berlin/Heidelberg, Germany, 2020; pp. 171–194. [Google Scholar]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Ramadan, A.; Ebeed, M.; Kamel, S.; Ahmed, E.M.; Tostado-Véliz, M. Optimal allocation of renewable DGs using artificial hummingbird algorithm under uncertainty conditions. Ain Shams Eng. J. 2022, 101872. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Mirjalili, S.; Wang, L.; Khodadadi, N.; Mirjalili, S.M. An effective multi-objective artificial hummingbird algorithm with dynamic elimination-based crowding distance for solving engineering design problems. Comput. Methods Appl. Mech. Eng. 2022, 398, 115223. [Google Scholar] [CrossRef]
- Sadoun, A.M.; Najjar, I.R.; Alsoruji, G.S.; Abd-Elwahed, M.; Elaziz, M.A.; Fathy, A. Utilization of improved machine learning method based on artificial hummingbird algorithm to predict the tribological behavior of Cu-Al2O3 nanocomposites synthesized by in situ method. Mathematics 2022, 10, 1266. [Google Scholar] [CrossRef]
- Abid, M.S.; Apon, H.J.; Morshed, K.A.; Ahmed, A. Optimal Planning of Multiple Renewable Energy-Integrated Distribution System With Uncertainties Using Artificial Hummingbird Algorithm. IEEE Access 2022, 10, 40716–40730. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Subba Reddy, T.; Harikiran, J.; Enduri, M.K.; Hajarathaiah, K.; Almakdi, S.; Alshehri, M.; Naveed, Q.N.; Rahman, M.H. Hyperspectral Image Classification with Optimized Compressed Synergic Deep Convolution Neural Network with Aquila Optimization. Comput. Intell. Neurosci. 2022, 2022, 6781740. [Google Scholar] [CrossRef]
- Ewees, A.A.; Algamal, Z.Y.; Abualigah, L.; Al-qaness, M.A.; Yousri, D.; Ghoniem, R.M.; Abd Elaziz, M. A Cox Proportional-Hazards Model Based on an Improved Aquila Optimizer with Whale Optimization Algorithm Operators. Mathematics 2022, 10, 1273. [Google Scholar] [CrossRef]
- Rajinikanth, V.; Aslam, S.M.; Kadry, S.; Thinnukool, O. Semi/Fully-Automated Segmentation of Gastric-Polyp Using Aquila-Optimization-Algorithm Enhanced Images. CMC-Comput. Mater. Contin. 2022, 70, 4087–4105. [Google Scholar] [CrossRef]
- Ayan, E.; Ünver, H.M. Diagnosis of pneumonia from chest X-ray images using deep learning. In Proceedings of the 2019 Scientific Meeting on Electrical-Electronics & Biomedical Engineering and Computer Science (EBBT), Istanbul, Turkey, 24–26 April 2019; pp. 1–5. [Google Scholar]
- Chouhan, V.; Singh, S.K.; Khamparia, A.; Gupta, D.; Tiwari, P.; Moreira, C.; Damaševičius, R.; De Albuquerque, V.H.C. A novel transfer learning based approach for pneumonia detection in chest X-ray images. Appl. Sci. 2020, 10, 559. [Google Scholar] [CrossRef]
- Ge, Z.; Demyanov, S.; Bozorgtabar, B.; Abedini, M.; Chakravorty, R.; Bowling, A.; Garnavi, R. Exploiting local and generic features for accurate skin lesions classification using clinical and dermoscopy imaging. In Proceedings of the 2017 IEEE 14th international symposium on biomedical imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 986–990. [Google Scholar]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Chen, H.; Dou, Q.; Qin, J.; Heng, P.A. Automated melanoma recognition in dermoscopy images via very deep residual networks. IEEE Trans. Med. Imaging 2016, 36, 994–1004. [Google Scholar] [CrossRef]
- Guo, Y.; Ashour, A.S.; Si, L.; Mandalaywala, D.P. Multiple convolutional neural network for skin dermoscopic image classification. In Proceedings of the 2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Louisville, KY, USA, 6–8 December 2018; pp. 365–369. [Google Scholar]
- Kawahara, J.; BenTaieb, A.; Hamarneh, G. Deep features to classify skin lesions. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 1397–1400. [Google Scholar]
- Lopez, A.R.; Giro-i Nieto, X.; Burdick, J.; Marques, O. Skin lesion classification from dermoscopic images using deep learning techniques. In Proceedings of the 2017 13th IASTED International Conference on Biomedical Engineering (BioMed), Innsbruck, Austria, 20–21 February 2017; pp. 49–54. [Google Scholar]
- Ayan, E.; Ünver, H.M. Data augmentation importance for classification of skin lesions via deep learning. In Proceedings of the 2018 Electric Electronics, Computer Science, Biomedical Engineerings’ Meeting (EBBT), Istanbul, Turkey, 18–19 April 2018; pp. 1–4. [Google Scholar]
- Yu, Z.; Jiang, X.; Zhou, F.; Qin, J.; Ni, D.; Chen, S.; Lei, B.; Wang, T. Melanoma recognition in dermoscopy images via aggregated deep convolutional features. IEEE Trans. Biomed. Eng. 2018, 66, 1006–1016. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Xie, Y.; Wu, Q.; Xia, Y. Medical image classification using synergic deep learning. Med. Image Anal. 2019, 54, 10–19. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, F.; Zhou, F.; He, X.; Ni, D.; Chen, S.; Wang, T.; Lei, B. Convolutional descriptors aggregation via cross-net for skin lesion recognition. Appl. Soft Comput. 2020, 92, 106281. [Google Scholar] [CrossRef]
- Wei, L.; Ding, K.; Hu, H. Automatic skin cancer detection in dermoscopy images based on ensemble lightweight deep learning network. IEEE Access 2020, 8, 99633–99647. [Google Scholar] [CrossRef]
- Shankar, K.; Lakshmanaprabu, S.; Khanna, A.; Tanwar, S.; Rodrigues, J.J.; Roy, N.R. Alzheimer detection using Group Grey Wolf Optimization based features with convolutional classifier. Comput. Electr. Eng. 2019, 77, 230–243. [Google Scholar]
- Goel, T.; Murugan, R.; Mirjalili, S.; Chakrabartty, D.K. OptCoNet: An optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2021, 51, 1351–1366. [Google Scholar] [CrossRef]
- Elhoseny, M.; Shankar, K. Optimal bilateral filter and convolutional neural network based denoising method of medical image measurements. Measurement 2019, 143, 125–135. [Google Scholar] [CrossRef]
- Zhang, N.; Cai, Y.X.; Wang, Y.Y.; Tian, Y.T.; Wang, X.L.; Badami, B. Skin cancer diagnosis based on optimized convolutional neural network. Artif. Intell. Med. 2020, 102, 101756. [Google Scholar] [CrossRef]
- El-Shafeiy, E.; Sallam, K.M.; Chakrabortty, R.K.; Abohany, A.A. A clustering based Swarm Intelligence optimization technique for the Internet of Medical Things. Expert Syst. Appl. 2021, 173, 114648. [Google Scholar] [CrossRef]
- Liu, J.; Inkawhich, N.; Nina, O.; Timofte, R. NTIRE 2021 multi-modal aerial view object classification challenge. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 588–595. [Google Scholar]
- Ignatov, A.; Romero, A.; Kim, H.; Timofte, R. Real-time video super-resolution on smartphones with deep learning, mobile ai 2021 challenge: Report. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 2535–2544. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 6105–6114. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. Mnasnet: Platform-aware neural architecture search for mobile. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 10–15 June 2019; pp. 2820–2828. [Google Scholar]
- Abd Elaziz, M.; Dahou, A.; Alsaleh, N.A.; Elsheikh, A.H.; Saba, A.I.; Ahmadein, M. Boosting COVID-19 Image Classification Using MobileNetV3 and Aquila Optimizer Algorithm. Entropy 2021, 23, 1383. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. J. Med. Imaging Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Elfwing, S.; Uchibe, E.; Doya, K. Sigmoid-weighted linear units for neural network function approximation in reinforcement learning. Neural Netw. 2018, 107, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Pathan, S.; Prabhu, K.G.; Siddalingaswamy, P. Automated detection of melanocytes related pigmented skin lesions: A clinical framework. Biomed. Signal Process. Control 2019, 51, 59–72. [Google Scholar] [CrossRef]
- Ozkan, I.A.; Koklu, M. Skin lesion classification using machine learning algorithms. Int. J. Intell. Syst. Appl. Eng. 2017, 5, 285–289. [Google Scholar] [CrossRef]
- Moradi, N.; Mahdavi-Amiri, N. Kernel sparse representation based model for skin lesions segmentation and classification. Comput. Methods Programs Biomed. 2019, 182, 105038. [Google Scholar] [CrossRef]
- Al Nazi, Z.; Abir, T.A. Automatic skin lesion segmentation and melanoma detection: Transfer learning approach with u-net and dcnn-svm. In Proceedings of the International Joint Conference on Computational Intelligence, Budapest, Hungary, 2–4 November 2020; pp. 371–381. [Google Scholar]
- Rodrigues, D.D.A.; Ivo, R.F.; Satapathy, S.C.; Wang, S.; Hemanth, J.; Reboucas Filho, P.P. A new approach for classification skin lesion based on transfer learning, deep learning, and IoT system. Pattern Recognit. Lett. 2020, 136, 8–15. [Google Scholar] [CrossRef]
- Afza, F.; Sharif, M.; Mittal, M.; Khan, M.A.; Hemanth, D.J. A hierarchical three-step superpixels and deep learning framework for skin lesion classification. Methods 2021, 202, 88–102. [Google Scholar] [CrossRef]
- Madani, A.; Moradi, M.; Karargyris, A.; Syeda-Mahmood, T. Chest X-ray generation and data augmentation for cardiovascular abnormality classification. In Proceedings of the Medical Imaging 2018: Image Processing, Houston, TX, USA, 11–13 February 2018; Volume 10574, p. 105741M. [Google Scholar]
- Salehi, M.; Mohammadi, R.; Ghaffari, H.; Sadighi, N.; Reiazi, R. Automated detection of pneumonia cases using deep transfer learning with paediatric chest X-ray images. Br. J. Radiol. 2021, 94, 20201263. [Google Scholar] [CrossRef]
- Habibzadeh, M.; Krzyżak, A.; Fevens, T. White blood cell differential counts using convolutional neural networks for low resolution images. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 9–13 June 2013; pp. 263–274. [Google Scholar]
- Zhao, J.; Zhang, M.; Zhou, Z.; Chu, J.; Cao, F. Automatic detection and classification of leukocytes using convolutional neural networks. Med. Biol. Eng. Comput. 2017, 55, 1287–1301. [Google Scholar] [CrossRef]
- Sharma, M.; Bhave, A.; Janghel, R.R. White blood cell classification using convolutional neural network. In Soft Computing and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 135–143. [Google Scholar]







| Algorithm | Parameter Settings |
|---|---|
| PSO | VMax = 6, WMax = 0.9, WMin = 0.2 |
| MFO | |
| WOA | = −1 to −2 |
| AO | , , |
| AHA | |
| AHA-AO | , , , |
| Dataset Name | Class | Training Data | Test Data | Total Images |
|---|---|---|---|---|
| ISIC-2016 | Malignant | 173 | 75 | 248 |
| Benign | 727 | 304 | 1031 | |
| Common Nevus | 68 | 12 | 80 | |
| Atypical Nevus | 68 | 12 | 80 | |
| Melanoma | 34 | 6 | 40 | |
| Chest-XRay | Normal | 1349 | 234 | 1583 |
| Pneumonia | 3883 | 390 | 4273 | |
| Blood-Cell | Neutrophil | 2499 | 624 | 3123 |
| Monocyte | 2478 | 620 | 3098 | |
| Lymphocyte | 2483 | 620 | 3103 | |
| Eosinophil | 2497 | 623 | 3120 |
| Dataset | Classifier | Accuracy | Recall | Precision | F1-Score |
|---|---|---|---|---|---|
| ISIC-2016 | DT | 0.8259 | 0.8258 | 0.8192 | 0.8221 |
| LDA | 0.8602 | 0.8601 | 0.8518 | 0.8541 | |
| SVM | 0.8602 | 0.8601 | 0.8546 | 0.8567 | |
| PH2 | DT | 0.9179 | 0.9178 | 0.9206 | 0.9177 |
| LDA | 0.9536 | 0.9535 | 0.955 | 0.9535 | |
| SVM | 0.9571 | 0.9571 | 0.9574 | 0.9572 | |
| Chest-XRay | DT | 0.8253 | 0.8253 | 0.8384 | 0.8156 |
| LDA | 0.8478 | 0.8477 | 0.8739 | 0.8373 | |
| SVM | 0.8718 | 0.8717 | 0.8906 | 0.8651 | |
| Blood-Cell | DT | 0.8786 | 0.8785 | 0.9001 | 0.8809 |
| LDA | 0.8834 | 0.8833 | 0.9041 | 0.8853 | |
| SVM | 0.8846 | 0.8845 | 0.905 | 0.8865 |
| Alg. | Model | Accuracy | BA | F1-Score | Recall | Precision | Time | No. of Features |
|---|---|---|---|---|---|---|---|---|
| PSO | DT | 0.8153 | 0.6991 | 0.8134 | 0.8153 | 0.8117 | 0.0449 | 86 |
| LDA | 0.8549 | 0.7438 | 0.8504 | 0.8549 | 0.8479 | 0.0463 | ||
| SVM | 0.8628 | 0.7488 | 0.8573 | 0.8628 | 0.8551 | 0.155 | ||
| MFO | DT | 0.7995 | 0.6641 | 0.7951 | 0.7995 | 0.7916 | 0.044 | 58 |
| LDA | 0.8575 | 0.7455 | 0.8527 | 0.8575 | 0.8503 | 0.0511 | ||
| SVM | 0.8628 | 0.7437 | 0.8564 | 0.8628 | 0.8544 | 0.1232 | ||
| WOA | DT | 0.8074 | 0.6791 | 0.8038 | 0.8074 | 0.8008 | 0.0395 | 56 |
| LDA | 0.8602 | 0.7571 | 0.8567 | 0.8602 | 0.8546 | 0.0379 | ||
| SVM | 0.8549 | 0.7438 | 0.8504 | 0.8549 | 0.8479 | 0.148 | ||
| AO | DT | 0.7942 | 0.6859 | 0.7962 | 0.7942 | 0.7984 | 0.039 | 53 |
| LDA | 0.8628 | 0.7387 | 0.8554 | 0.8628 | 0.8538 | 0.0373 | ||
| SVM | 0.8575 | 0.7304 | 0.8499 | 0.8575 | 0.8478 | 0.1196 | ||
| AHA | DT | 0.8285 | 0.7274 | 0.8281 | 0.8285 | 0.8276 | 0.0492 | 60 |
| LDA | 0.8681 | 0.747 | 0.861 | 0.8681 | 0.8598 | 0.038 | ||
| SVM | 0.8628 | 0.7337 | 0.8544 | 0.8628 | 0.8533 | 0.1225 | ||
| AHA-AO | DT | 0.8179 | 0.7208 | 0.8193 | 0.8179 | 0.8207 | 0.0398 | 52 |
| LDA | 0.8628 | 0.7588 | 0.859 | 0.8628 | 0.8569 | 0.0349 | ||
| SVM | 0.8734 | 0.7654 | 0.8683 | 0.8734 | 0.8667 | 0.1132 |
| Alg. | Model | Accuracy | BA | F1-Score | Recall | Precision | Time | No. of Features |
|---|---|---|---|---|---|---|---|---|
| PSO | DT | 0.8893 | 0.9048 | 0.89 | 0.8893 | 0.9037 | 0.1484 | 326 |
| LDA | 0.9643 | 0.9702 | 0.9643 | 0.9643 | 0.9648 | 0.2309 | ||
| SVM | 0.9643 | 0.9702 | 0.9643 | 0.9643 | 0.9644 | 0.1442 | ||
| MFO | DT | 0.9179 | 0.9167 | 0.9185 | 0.9179 | 0.9245 | 0.0813 | 222 |
| LDA | 0.9607 | 0.9673 | 0.9607 | 0.9607 | 0.9614 | 0.1393 | ||
| SVM | 0.9643 | 0.9702 | 0.9643 | 0.9643 | 0.9644 | 0.0947 | ||
| WOA | DT | 0.8786 | 0.869 | 0.8794 | 0.8786 | 0.8991 | 0.0927 | 221 |
| LDA | 0.9679 | 0.9732 | 0.9679 | 0.9679 | 0.9681 | 0.1445 | ||
| SVM | 0.9679 | 0.9732 | 0.9679 | 0.9679 | 0.9679 | 0.0961 | ||
| AO | DT | 0.9179 | 0.9226 | 0.9179 | 0.9179 | 0.9261 | 0.0708 | 159 |
| LDA | 0.9607 | 0.9673 | 0.9607 | 0.9607 | 0.961 | 0.1135 | ||
| SVM | 0.9643 | 0.9702 | 0.9643 | 0.9643 | 0.9643 | 0.0764 | ||
| AHA | DT | 0.925 | 0.9256 | 0.9251 | 0.925 | 0.9293 | 0.0602 | 141 |
| LDA | 0.9643 | 0.9702 | 0.9643 | 0.9643 | 0.9643 | 0.1095 | ||
| SVM | 0.9607 | 0.9673 | 0.9607 | 0.9607 | 0.961 | 0.0773 | ||
| AHA-AO | DT | 0.9107 | 0.9048 | 0.9115 | 0.9107 | 0.9192 | 0.0482 | 107 |
| LDA | 0.9571 | 0.9643 | 0.9571 | 0.9571 | 0.9573 | 0.0937 | ||
| SVM | 0.975 | 0.9792 | 0.975 | 0.975 | 0.975 | 0.0523 |
| Alg. | Model | Accuracy | BA | F1-Score | Recall | Precision | Time | No. of Features |
|---|---|---|---|---|---|---|---|---|
| PSO | DT | 0.8013 | 0.7487 | 0.7875 | 0.8013 | 0.8177 | 0.3909 | 79 |
| LDA | 0.8446 | 0.7953 | 0.8339 | 0.8446 | 0.87 | 0.1306 | ||
| SVM | 0.8478 | 0.8004 | 0.838 | 0.8478 | 0.8706 | 0.7182 | ||
| MFO | DT | 0.8141 | 0.7641 | 0.802 | 0.8141 | 0.8307 | 0.4391 | 91 |
| LDA | 0.8462 | 0.7983 | 0.8361 | 0.8462 | 0.8694 | 0.1405 | ||
| SVM | 0.8574 | 0.8132 | 0.8492 | 0.8574 | 0.8774 | 0.7427 | ||
| WOA | DT | 0.8237 | 0.7778 | 0.8137 | 0.8237 | 0.8371 | 0.4166 | 98 |
| LDA | 0.8397 | 0.788 | 0.8278 | 0.8397 | 0.8685 | 0.1709 | ||
| SVM | 0.8558 | 0.8103 | 0.847 | 0.8558 | 0.8778 | 0.6557 | ||
| AO | DT | 0.8189 | 0.7722 | 0.8085 | 0.8189 | 0.8321 | 0.419 | 91 |
| LDA | 0.8446 | 0.7944 | 0.8336 | 0.8446 | 0.8718 | 0.1464 | ||
| SVM | 0.8558 | 0.8111 | 0.8473 | 0.8558 | 0.8763 | 0.6305 | ||
| AHA | DT | 0.8061 | 0.756 | 0.7937 | 0.8061 | 0.8204 | 0.5743 | 99 |
| LDA | 0.851 | 0.8038 | 0.8414 | 0.851 | 0.8744 | 0.1867 | ||
| SVM | 0.8542 | 0.8081 | 0.8451 | 0.8542 | 0.8767 | 0.6737 | ||
| AHA-AO | DT | 0.8269 | 0.7812 | 0.8171 | 0.8269 | 0.8409 | 0.5981 | 96 |
| LDA | 0.8494 | 0.8017 | 0.8396 | 0.8494 | 0.8733 | 0.1783 | ||
| SVM | 0.8686 | 0.8274 | 0.8617 | 0.8686 | 0.8869 | 0.6623 |
| Alg. | Model | Accuracy | BA | F1-Score | Recall | Precision | Time | No. of Features |
|---|---|---|---|---|---|---|---|---|
| PSO | DT | 0.8733 | 0.8733 | 0.8764 | 0.8733 | 0.8978 | 2.0821 | 347 |
| LDA | 0.8838 | 0.8837 | 0.8859 | 0.8838 | 0.9053 | 1.2637 | ||
| SVM | 0.8858 | 0.8858 | 0.8877 | 0.8858 | 0.906 | 0.8885 | ||
| MFO | DT | 0.881 | 0.8809 | 0.8824 | 0.881 | 0.8976 | 1.5234 | 225 |
| LDA | 0.8814 | 0.8813 | 0.8834 | 0.8814 | 0.9031 | 0.738 | ||
| SVM | 0.8838 | 0.8838 | 0.8859 | 0.8838 | 0.9055 | 0.7944 | ||
| WOA | DT | 0.8778 | 0.8777 | 0.88 | 0.8778 | 0.9005 | 1.4109 | 226 |
| LDA | 0.8806 | 0.8805 | 0.8828 | 0.8806 | 0.9027 | 0.7313 | ||
| SVM | 0.8838 | 0.8838 | 0.8856 | 0.8838 | 0.9041 | 0.7249 | ||
| AO | DT | 0.8806 | 0.8805 | 0.8822 | 0.8806 | 0.898 | 0.8553 | 125 |
| LDA | 0.879 | 0.8789 | 0.8811 | 0.879 | 0.9014 | 0.5041 | ||
| SVM | 0.8838 | 0.8838 | 0.886 | 0.8838 | 0.9058 | 0.6661 | ||
| AHA | DT | 0.8721 | 0.8721 | 0.8753 | 0.8721 | 0.8977 | 0.8567 | 132 |
| LDA | 0.8818 | 0.8817 | 0.884 | 0.8818 | 0.9037 | 0.4571 | ||
| SVM | 0.8846 | 0.8846 | 0.8863 | 0.8846 | 0.9035 | 0.53 | ||
| AHA-AO | DT | 0.8749 | 0.8749 | 0.877 | 0.8749 | 0.8956 | 0.4053 | 65 |
| LDA | 0.8826 | 0.8825 | 0.8844 | 0.8826 | 0.903 | 0.1887 | ||
| SVM | 0.8862 | 0.8862 | 0.8878 | 0.8862 | 0.9053 | 0.2579 |
| Dataset | Model | Accuracy (%) | Year | Ref. |
|---|---|---|---|---|
| ISIC-2016 | CUMED | 85.50 | 2016 | [34] |
| BL-CNN | 85.00 | 2017 | [32] | |
| DCNN-FV | 86.81 | 2018 | [39] | |
| MC-CNN | 86.30 | 2019 | [40] | |
| MFA | 86.81 | 2020 | [41] | |
| AHA-AO | 87.30 | present | Our | |
| PH2 | ANN | 92.50 | 2017 | [60] |
| Kernel Sparse | 93.50 | 2019 | [61] | |
| DenseNet201 + SVM | 92.00 | 2020 | [62] | |
| DenseNet201 + KNN | 93.16 | 2020 | [63] | |
| ResNet50 + NB | 95.40 | 2021 | [64] | |
| AHA-AO | 97.50 | present | Our | |
| Chest-XRay | DCGAN | 84.19 | 2018 | [65] |
| DenseNet121 | 86.80 | 2021 | [66] | |
| AHA-AO | 86.90 | present | Our | |
| Blood-Cell | CNN + SVM | 85.00 | 2013 | [67] |
| CNN | 87.08 | 2017 | [68] | |
| CNN + Augmentation | 87.00 | 2019 | [69] | |
| AHA-AO | 88.60 | present | Our |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elaziz, M.A.; Dahou, A.; El-Sappagh, S.; Mabrouk, A.; Gaber, M.M. AHA-AO: Artificial Hummingbird Algorithm with Aquila Optimization for Efficient Feature Selection in Medical Image Classification. Appl. Sci. 2022, 12, 9710. https://doi.org/10.3390/app12199710
Elaziz MA, Dahou A, El-Sappagh S, Mabrouk A, Gaber MM. AHA-AO: Artificial Hummingbird Algorithm with Aquila Optimization for Efficient Feature Selection in Medical Image Classification. Applied Sciences. 2022; 12(19):9710. https://doi.org/10.3390/app12199710
Chicago/Turabian StyleElaziz, Mohamed Abd, Abdelghani Dahou, Shaker El-Sappagh, Alhassan Mabrouk, and Mohamed Medhat Gaber. 2022. "AHA-AO: Artificial Hummingbird Algorithm with Aquila Optimization for Efficient Feature Selection in Medical Image Classification" Applied Sciences 12, no. 19: 9710. https://doi.org/10.3390/app12199710
APA StyleElaziz, M. A., Dahou, A., El-Sappagh, S., Mabrouk, A., & Gaber, M. M. (2022). AHA-AO: Artificial Hummingbird Algorithm with Aquila Optimization for Efficient Feature Selection in Medical Image Classification. Applied Sciences, 12(19), 9710. https://doi.org/10.3390/app12199710









