Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System
Abstract
:1. Introduction
2. Principles and Methods Analysis
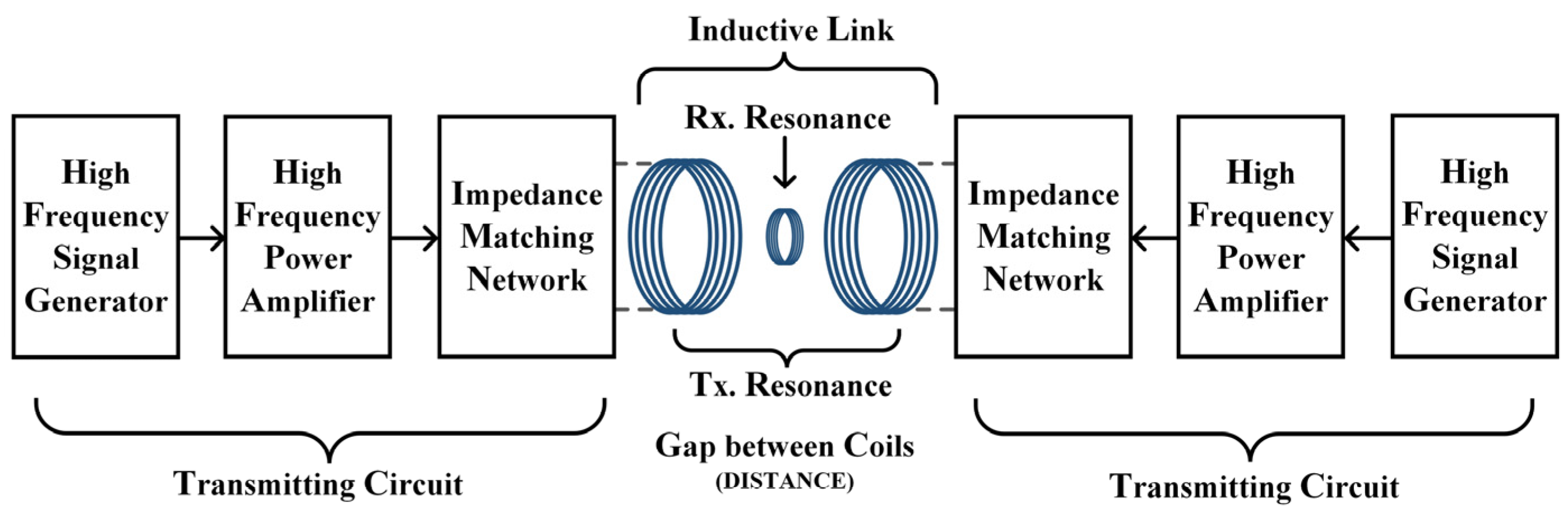
2.1. Magnetically Coupled Resonant Wireless Power Transfer System
2.2. Wireless Power Transfer System Based on Helmholtz Coils
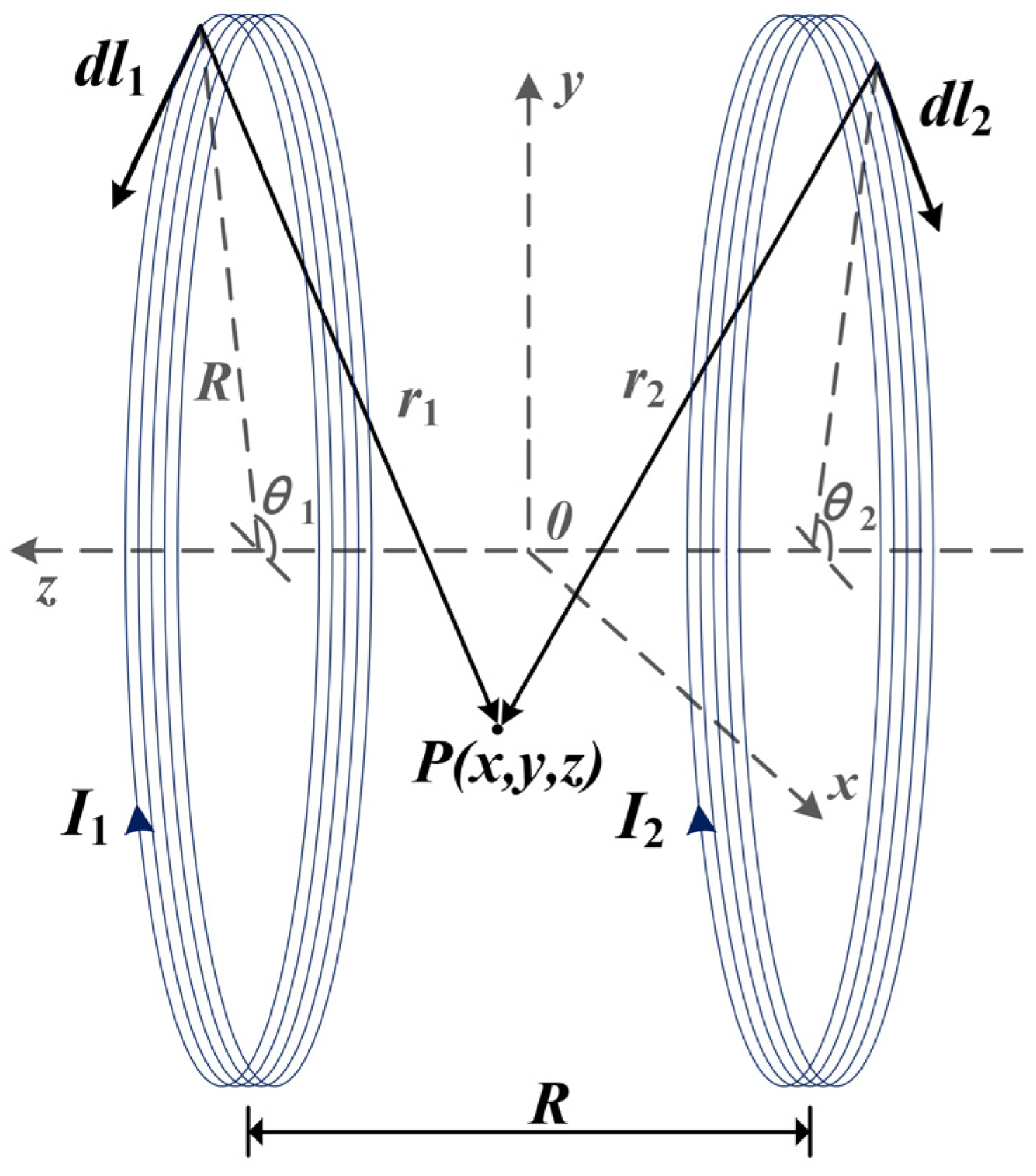
2.2.1. Magnetic Fields Generated by Helmholtz Coils
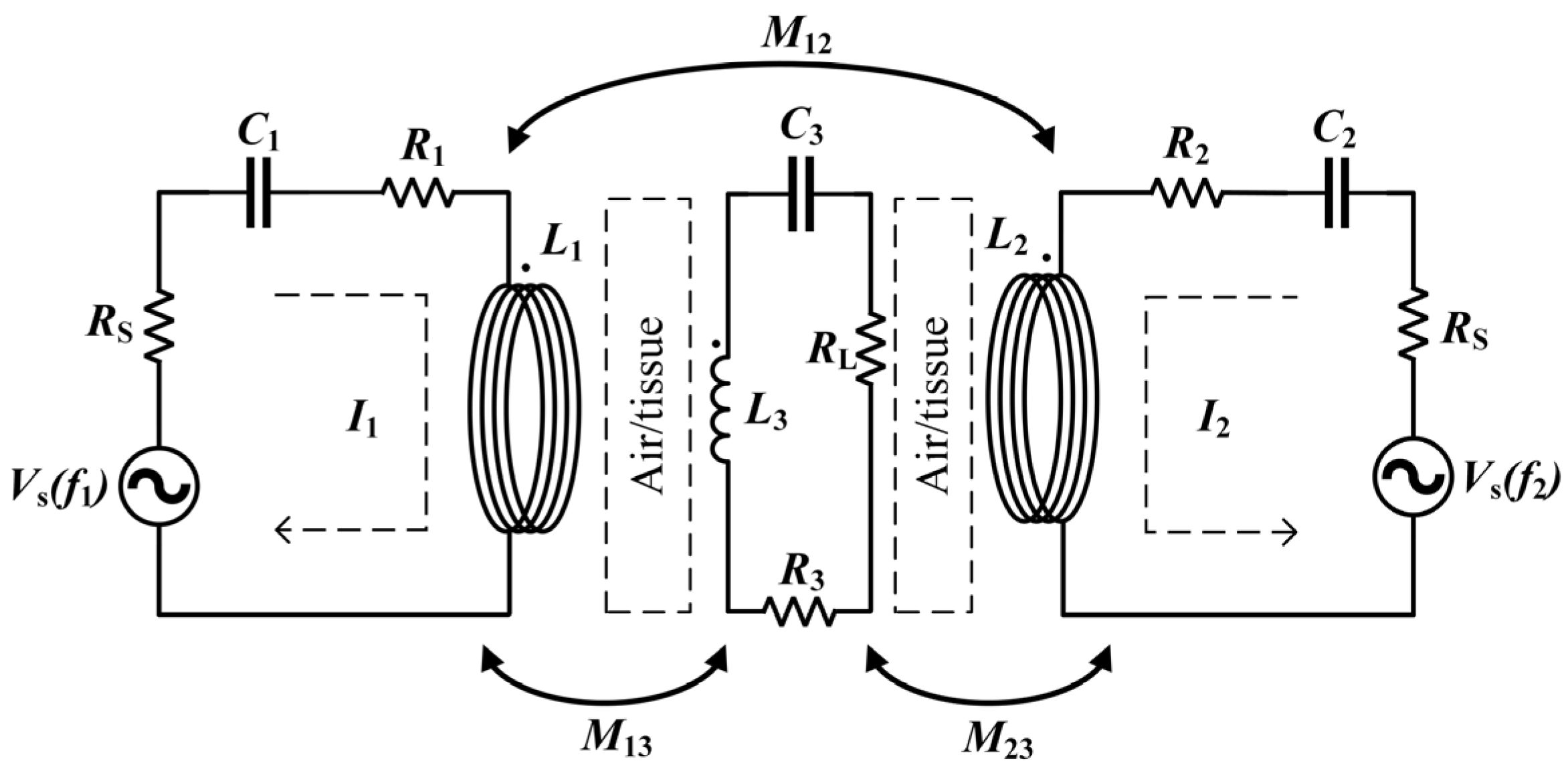
2.2.2. Circuit Analysis of a WPT System with Helmholtz Coils
2.3. Differential Frequency Electrical Stimulation System Based on Temporal Interference
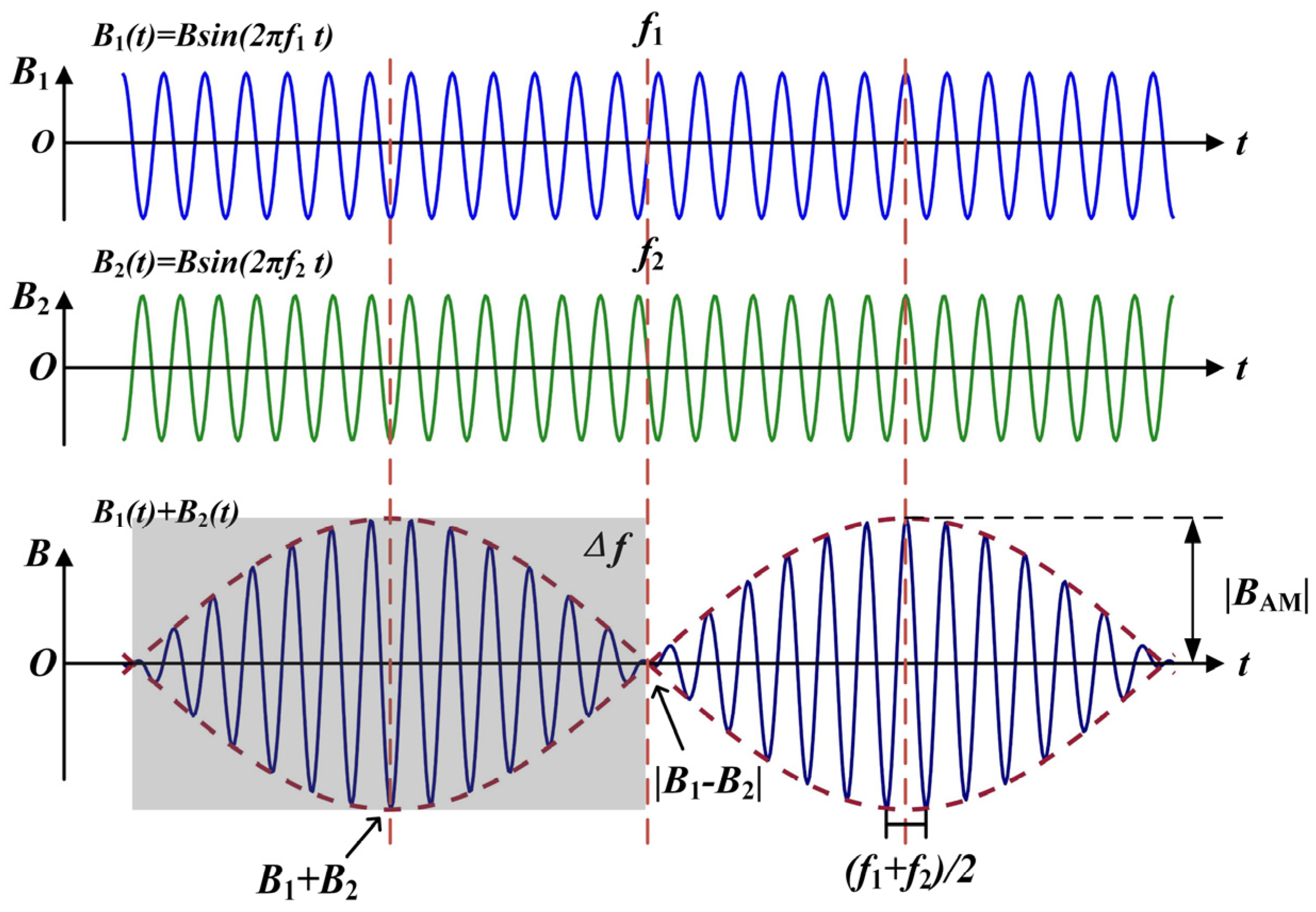
2.3.1. Temporal Interference Generates Low-Frequency Envelope Modulated Magnetic Fields
2.3.2. Non-Physical Type Dynamic Adjustment of the Stimulation Location
3. Analysis of Calculation and Experimental Results
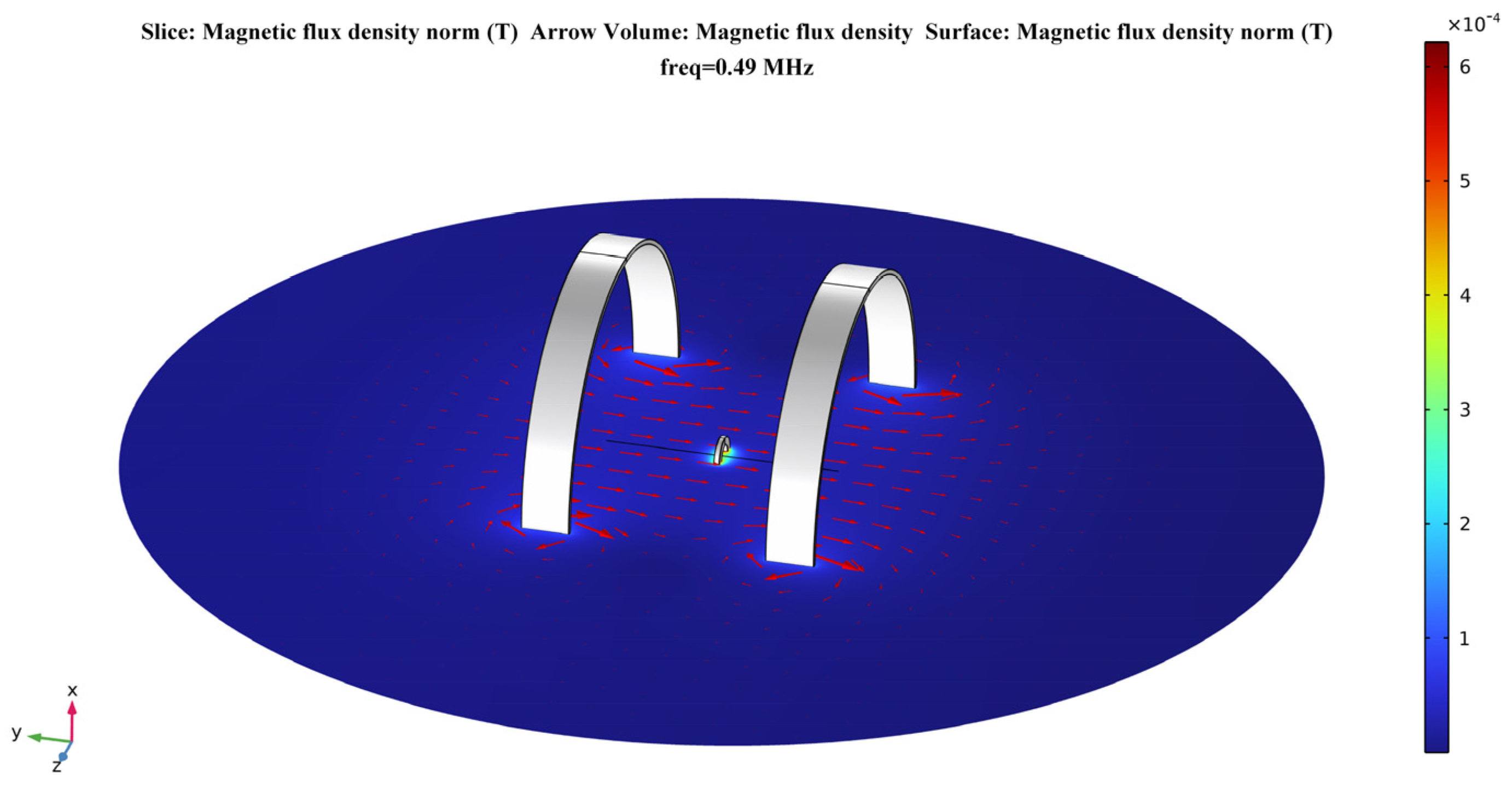
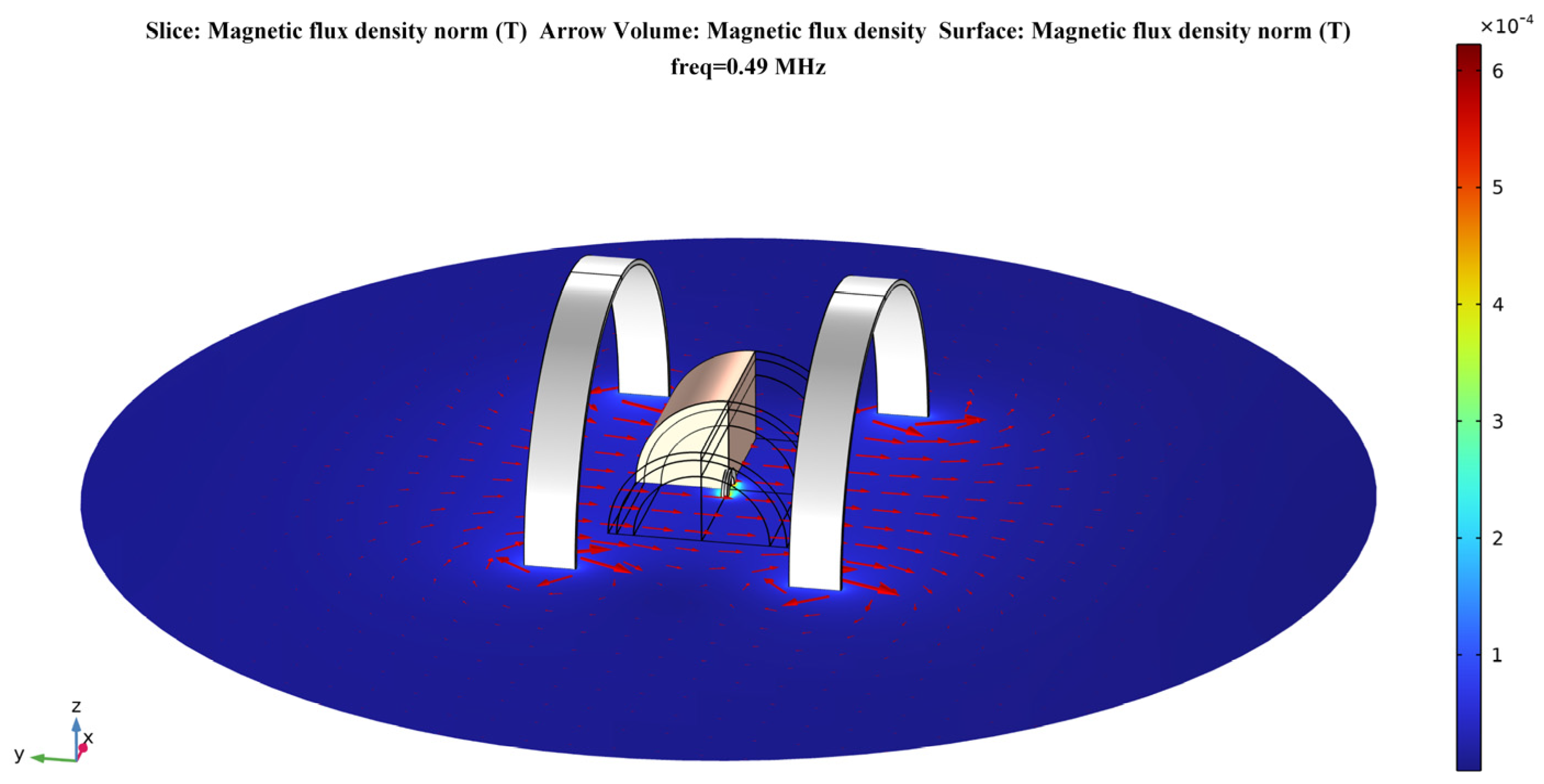
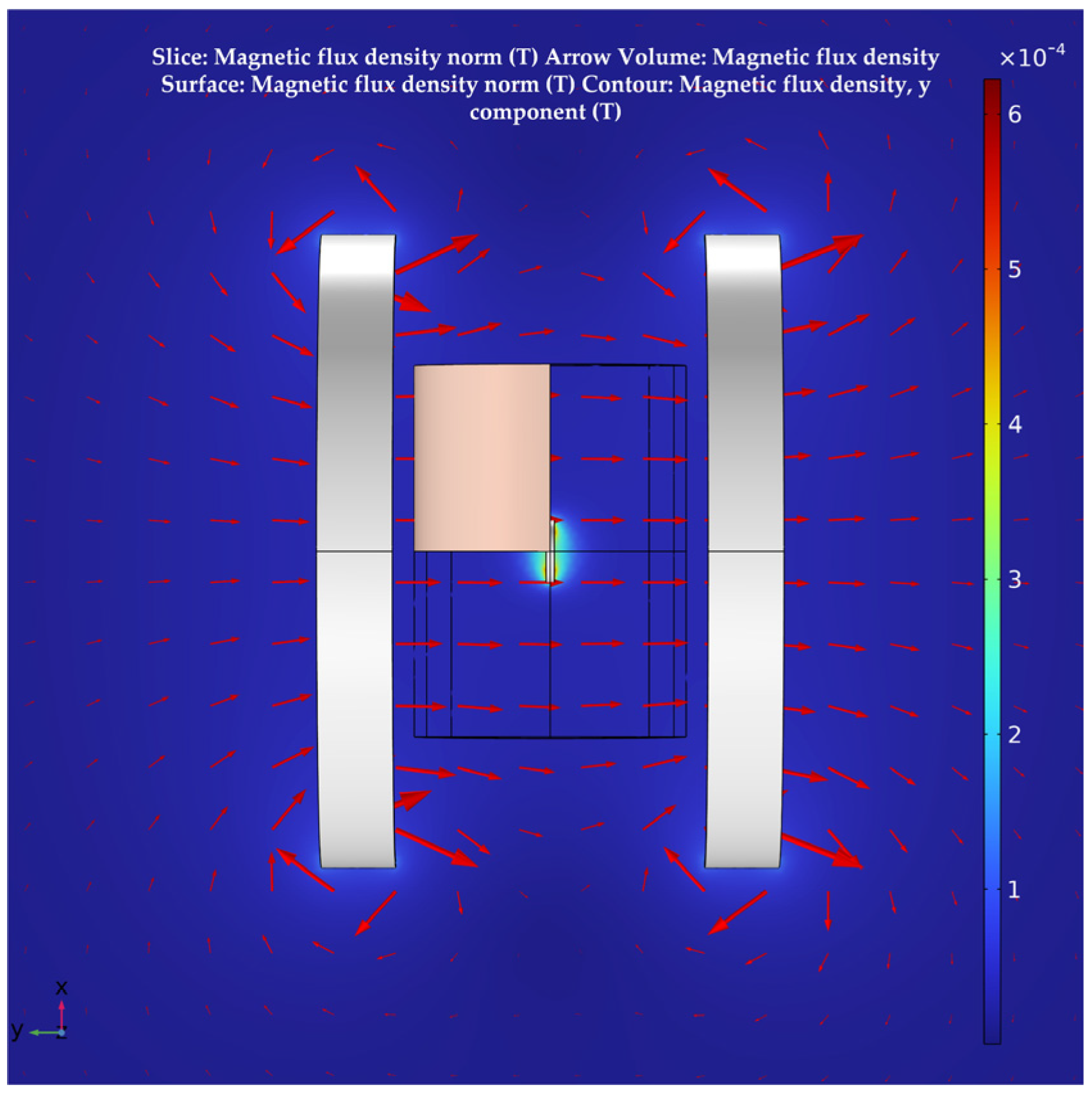
3.1. Calculation in Free Space
3.2. Calculation of a Simplified Multi–Layer Human Tissue Model
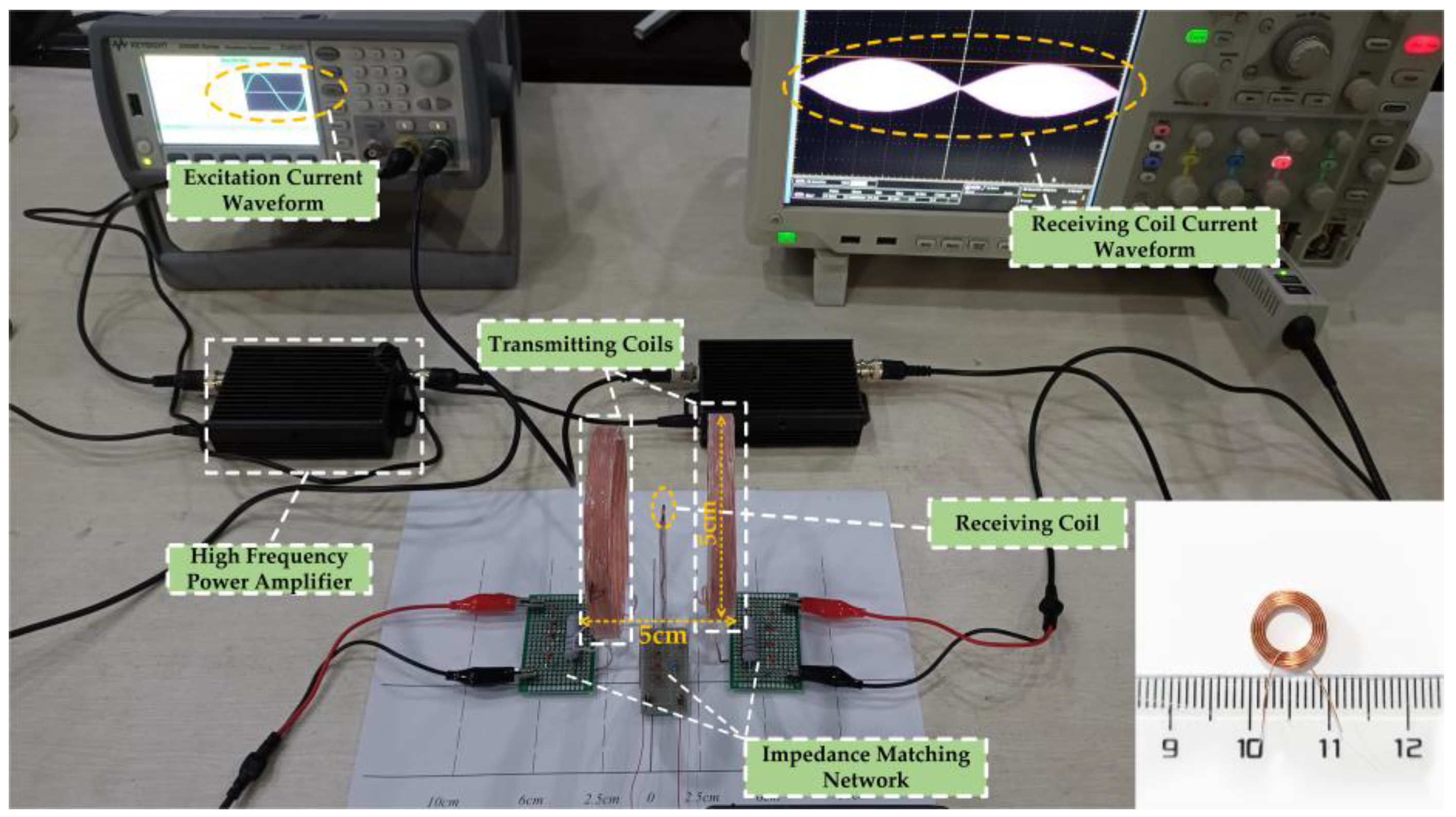
3.3. Experimental Study of the Current at the Receiving Coil
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lawson, E.F.; Castellanos, J.P. Complex Regional Pain Syndrome; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Marinus, J.; Moseley, G.L.; Birklein, F.; Baron, R.; Maihöfner, C.; Kingery, W.S.; van Hilten, J.J. Clinical features and pathophysiology of complex regional pain syndrome. Lancet Neurol. 2011, 10, 637–648. [Google Scholar] [CrossRef]
- Eldufani, J.; Elahmer, N.; Blaise, G. A medical mystery of complex regional pain syndrome. Heliyon 2020, 6, e03329. [Google Scholar] [CrossRef] [PubMed]
- Buwembo, J.; Munson, R.; Rizvi, S.A.; Ijaz, A.; Gupta, S. Direct sciatic nerve electrical stimulation for complex regional pain syndrome Type 1. Neuromodulation Technol. Neural Interface 2021, 24, 1075–1082. [Google Scholar] [CrossRef] [PubMed]
- Mond, H.G.; Freitag, G. The cardiac implantable electronic device power source: Evolution and revolution. Pacing Clin. Electrophysiol. 2014, 37, 1728–1745. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Ye, H.; Jain, G.; Schmidt, C. Remaining useful life assessment of lithium-ion batteries in implantable medical devices. J. Power Sources 2018, 375, 118–130. [Google Scholar] [CrossRef]
- Zhang, Y.; Mickle, A.D.; Gutruf, P.; McIlvried, L.A.; Guo, H.; Wu, Y.; Golden, J.P.; Xue, Y.; Grajales-Reyes, J.G.; Wang, X. Battery-free, fully implantable optofluidic cuff system for wireless optogenetic and pharmacological neuromodulation of peripheral nerves. Sci. Adv. 2019, 5, eaaw5296. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Yi, Z.; Ma, Y.; Xie, F.; Huang, Y.; Tian, Y.; Dong, X.; Liu, Y.; Shao, X.; Li, Y. Direct powering a real cardiac pacemaker by natural energy of a heartbeat. ACS Nano 2019, 13, 2822–2830. [Google Scholar] [CrossRef]
- Xu, G.; Yang, X.; Yang, Q.; Zhao, J.; Li, Y. Design on magnetic coupling resonance wireless energy transmission and monitoring system for implanted devices. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, J.; Xu, G.; Li, X.; Li, W.; Li, Y. The Experimental Research on a Small Size Magnetic Coupling Resonance Wireless Energy Transmission System. Trans. China Electrotech. Soc. 2016, 31, 13–17. [Google Scholar]
- Wright, J.P.; Mughrabi, I.T.; Wong, J.; Mathew, J.; Jayaprakash, N.; Crosfield, C.; Chang, E.H.; Chavan, S.S.; Tracey, K.J.; Pavlov, V.A. A fully implantable wireless bidirectional neuromodulation system for mice. Biosens. Bioelectron. 2022, 200, 113886. [Google Scholar] [CrossRef]
- Yoo, S.; Lee, J.; Joo, H.; Sunwoo, S.H.; Kim, S.; Kim, D.H. Wireless power transfer and telemetry for implantable bioelectronics. Adv. Healthc. Mater. 2021, 10, 2100614. [Google Scholar] [CrossRef] [PubMed]
- Haerinia, M.; Shadid, R. Wireless power transfer approaches for medical implants: A Review. Signals 2020, 1, 209–229. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Y. A 13.56 MHz wireless power transfer system with bidirectional data link and closed-loop power control for implantable neuromuscular stimulator. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), New Delhi, India, 10–13 December 2019; pp. 1002–1004. [Google Scholar]
- Zhang, X.; Meng, H.; Wei, B.; Wang, S.; Yang, Q. An improved three-coil wireless power link to increase spacing distance and power for magnetic resonant coupling system. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Qiao, T.; Yang, X.; Lai, X.; Tang, H. Modeling and analysis of multi-coil magnetic resonance wireless power transfer systems. In Proceedings of the 2018 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (Wow), Montréal, QC, Canada, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef]
- McIntyre, C.C.; Grill, W.M. Extracellular stimulation of central neurons: Influence of stimulus waveform and frequency on neuronal output. J. Neurophysiol. 2002, 88, 1592–1604. [Google Scholar] [CrossRef]
- Mortimer, J.T.; Bhadra, N. Fundamentals of electrical stimulation. In Neuromodulation; Elsevier: Amsterdam, The Netherlands, 2018; pp. 71–82. [Google Scholar]
- Luan, S.; Williams, I.; Nikolic, K.; Constandinou, T.G. Neuromodulation: Present and emerging methods. Front. Neuroeng. 2014, 7, 27. [Google Scholar] [CrossRef]
- Chapman, K.B.; Yousef, T.A.; Foster, A.; Stanton-Hicks, M.D.; van Helmond, N. Mechanisms for the clinical utility of low-frequency stimulation in neuromodulation of the dorsal root ganglion. Neuromodulation Technol. Neural Interface 2021, 24, 738–745. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271. [Google Scholar] [CrossRef]
- Barnes, F.S.; Greenebaum, B. Handbook of Biological Effects of Electromagnetic Fields-Two Volume Set; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Vinko, D.; Biondić, I.; Bilandžija, D. Impact of receiver power and coupling coefficient on resonant frequency in wireless power transfer system. In Proceedings of the 2019 International Symposium ELMAR, Zadar, Croatia, 23–25 September 2019; pp. 207–210. [Google Scholar]
- Zhang, P.; Saeedifard, M.; Onar, O.C.; Yang, Q.; Cai, C. A field enhancement integration design featuring misalignment tolerance for wireless EV charging using LCL topology. IEEE Trans. Power Electron. 2020, 36, 3852–3867. [Google Scholar] [CrossRef]
- Restrepo, A.F.; Franco, E.; Cadavid, H.; Pinedo, C.R. A comparative study of the magnetic field homogeneity for circular, square and equilateral triangular helmholtz coils. In Proceedings of the 2017 International Conference on Electrical, Electronics, Communication, Computer, and Optimization Techniques (ICEECCOT), Kunming, China, 8–10 December 2017; pp. 13–20. [Google Scholar]
- Bronaugh, E.L. Helmholtz coils for calibration of probes and sensors: Limits of magnetic field accuracy and uniformity. In Proceedings of the International Symposium on Electromagnetic Compatibility, Atlanta, GA, USA, 14–18 August 1995; pp. 72–76. [Google Scholar]
- García-Farieta, J.E.; Márquez, A.H. Exploring the magnetic field of Helmholtz and Maxwell coils: A computer-based approach exploiting the superposition principle. Rev. Bras. Ensino Fis. 2020, 42, 226434271. [Google Scholar] [CrossRef]
- Zhang, K.; Ren, X.; Liu, Y.; Hui, S.; Song, B. Analytical Solution and Experimental Validation of the Electromagnetic Field in an IPT System. Appl. Sci. 2019, 9, 1323. [Google Scholar] [CrossRef]
- Ma, Y.; Mao, Z.; Zhang, K. Optimization Design of Planar Circle Coil for Limited-Size Wireless Power Transfer System. Appl. Sci. 2022, 12, 2286. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Zhang, F.; Liu, X.; Zhang, P.; Zhou, Y.-G. A multichannel wireless UAV charging system with compact receivers for improving transmission stability and capacity. IEEE Syst. J. 2021, 16, 997–1008. [Google Scholar] [CrossRef]
- Cai, C.; Saeedifard, M.; Wang, J.; Zhang, P.; Zhao, J.; Hong, Y. A cost-effective segmented dynamic wireless charging system with stable efficiency and output power. IEEE Trans. Power Electron. 2022, 37, 8682–8700. [Google Scholar] [CrossRef]
- Yu, Z.; Shi-you, Y. Frequency tracking and controlling of wireless power transfer system. Electr. Mach. Control 2020, 24. [Google Scholar]
- Gao, X.; Deng, M.; Masaki, K. Tracking operator-based optimal load control for loosely coupled wireless power transfer systems. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 2188–2193. [Google Scholar]
- Li, Y.; Jiang, S.; Liu, X.-L.; Li, Q.; Dong, W.-H.; Liu, J.-M.; Ni, X. Influences of coil radius on effective transfer distance in WPT system. IEEE Access 2019, 7, 125960–125968. [Google Scholar] [CrossRef]
- Li, K.; Zhao, H.; Lv, L.; Sun, Z.; Shi, Y.; Hua, Y.; Liu, Q. Influence of Coil Radius, Distance and Working Frequency on Efficiency in Two-Coil Magnetically Coupled Resonant Wireless Power Transmission System. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 2121–2125. [Google Scholar]
- Qingdong, C.; Junping, W. Simulation and Analysis of Magnetostatic Field based on COMSOL Software. Phys. Exp. Coll. 2018, 31, 88–91. [Google Scholar]
- Grossman, N.; Bono, D.; Dedic, N.; Kodandaramaiah, S.B.; Rudenko, A.; Suk, H.-J.; Cassara, A.M.; Neufeld, E.; Kuster, N.; Tsai, L.-H. Noninvasive deep brain stimulation via temporally interfering electric fields. Cell 2017, 169, 1029–1041.e16. [Google Scholar] [CrossRef]
- Grossman, N. Modulation without surgical intervention. Science 2018, 361, 461–462. [Google Scholar] [CrossRef]
- Sorkhabi, M.M.; Wendt, K.; Denison, T. Temporally interfering TMS: Focal and dynamic stimulation location. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montréal, QC, Canada, 20–24 July 2020; pp. 3537–3543. [Google Scholar]
- Kim, J.; Jeong, J. Range-adaptive wireless power transfer using multiloop and tunable matching techniques. IEEE Trans. Ind. Electron. 2015, 62, 6233–6241. [Google Scholar] [CrossRef]
- Truong, B.D.; Andersen, E.; Casados, C.; Roundy, S. Magnetoelectric wireless power transfer for biomedical implants: Effects of non-uniform magnetic field, alignment and orientation. Sens. Actuators A 2020, 316, 112269. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Huang, S. Literature analysis of electroacupuncture stimulation index on the treatment of sciatica. Zhongguo Zhenjiu 2009, 29, 1026–1028. [Google Scholar]
- “Technical and Operating Parameters and Spectrum Use for Short-Range Radiocommunication Devices” in International Telecommunication Union. Available online: www.itu.int/pub/R-REP-SM.2153-2-2011 (accessed on 16 May 2022).
- ETSI EN 302 536 V2.2.1 European Telecommunications Standards Institute. 2017. Available online: https://www.etsi.org/deliver/etsi_en/302500_302599/302536/02.01.01_60/en_302536v020101p.pdf (accessed on 17 May 2022).
- Donas, K.P.; Schulte, S.; Ktenidis, K.; Horsch, S. The role of epidural spinal cord stimulation in the treatment of Buerger’s disease. J. Vasc. Surg. 2005, 41, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Bendersky, D.; Yampolsky, C. Is spinal cord stimulation safe? A review of its complications. World Neurosurg. 2014, 82, 1359–1368. [Google Scholar] [CrossRef] [PubMed]
- Grill, W.M. Temporal pattern of electrical stimulation is a new dimension of therapeutic innovation. Curr. Opin. Biomed. Eng. 2018, 8, 1–6. [Google Scholar] [CrossRef]


| Continuity of Power Supply | Battery Units | Signal Processing Modules | Coupling Type | |
|---|---|---|---|---|
| Battery Powered | Consumed | Yes | Yes | None |
| Conventional Resonant WPT | Sustainability | Yes | Yes | Magnetically coupled |
| Temporal Interference WPT | Sustainability | None | None | Magnetically coupled |
| Coils | Parameters | Symbol | Value |
|---|---|---|---|
| Transmitting Coils | Number of turns | 10 | |
| Radius | 5 cm | ||
| Inductance | 18.12 μH | ||
| Capacitances | 5823 pF | ||
| Distance between coils | 5 cm | ||
| Receiving Coil | Wire diameter | 0.2 mm | |
| Outer diameter | 10 mm | ||
| Inner diameter | 6 mm | ||
| Inductance | 19.93 μH | ||
| Capacitances | 5393 pF |
| Skin | Fat | Muscle | |
|---|---|---|---|
| Electrical Conductivity (S/m) | 0.13 | 0.045 | 0.5 |
| Thickness (mm) | 2 | 4 | 16 |
| Experimental Equipment | Parameters | Value |
|---|---|---|
| Transmitting Coil 1 | Current Frequency | 490 kHz |
| Current Amplitude | 0.2 A | |
| Resistances | 10 Ω | |
| Inductance | 19 μH | |
| Capacitances | 5553 pF | |
| Transmitting Coil 2 | Current Frequency | 490 kHz + 10 Hz |
| Current Amplitude | 0.2 A | |
| Resistances | 10 Ω | |
| Inductance | 18.94 μH | |
| Capacitances | 5570 pF | |
| Receiving Coil | Resistances | 1.09 Ω |
| Current Frequency | 10 Hz | |
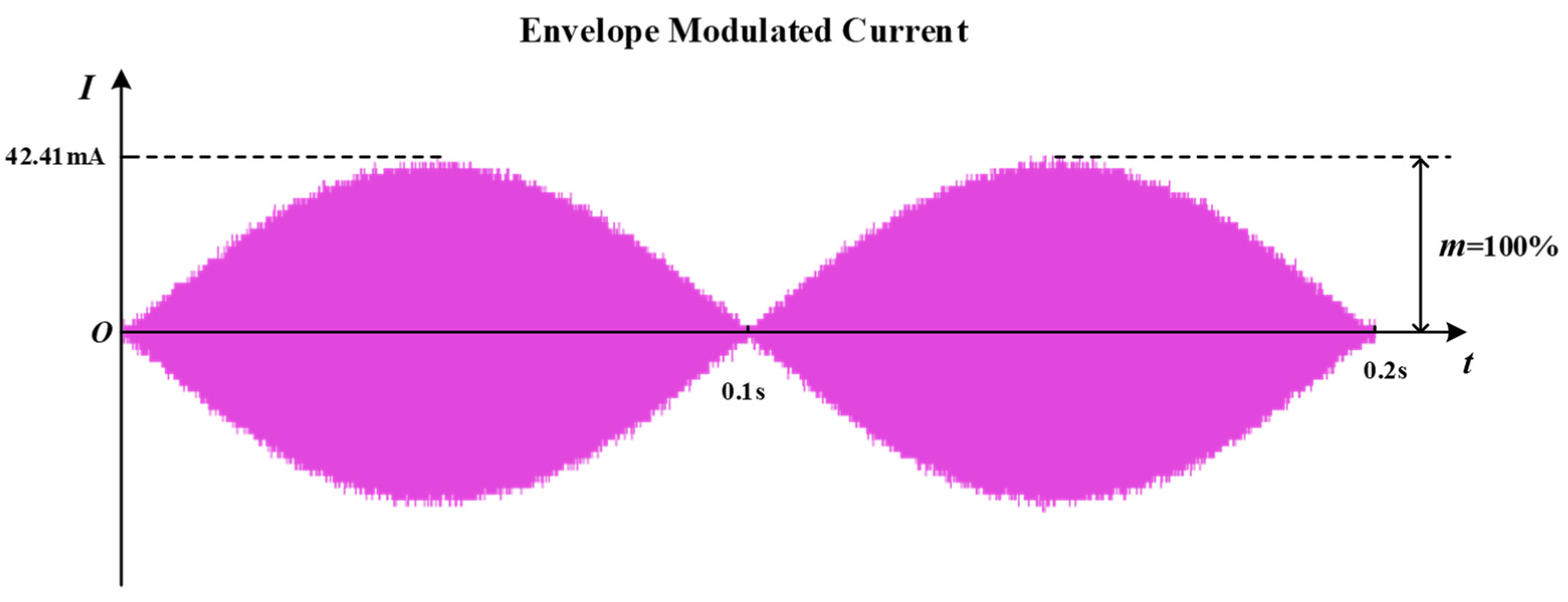
| Current Amplitude | 42.4 mA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Gao, P.; Yang, X.; Ji, D.; Sun, J.; Yang, Z. Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System. Appl. Sci. 2022, 12, 9832. https://doi.org/10.3390/app12199832
Jiang C, Gao P, Yang X, Ji D, Sun J, Yang Z. Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System. Applied Sciences. 2022; 12(19):9832. https://doi.org/10.3390/app12199832
Chicago/Turabian StyleJiang, Chenyu, Panlong Gao, Xinsheng Yang, Dezheng Ji, Jialun Sun, and Zhenghao Yang. 2022. "Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System" Applied Sciences 12, no. 19: 9832. https://doi.org/10.3390/app12199832
APA StyleJiang, C., Gao, P., Yang, X., Ji, D., Sun, J., & Yang, Z. (2022). Helmholtz Coils Based WPT Coupling Analysis of Temporal Interference Electrical Stimulation System. Applied Sciences, 12(19), 9832. https://doi.org/10.3390/app12199832







