Design and Development of a Mathematical Model for an Industrial Process, in a System Dynamics Environment
Abstract
1. Introduction
2. Materials and Methods
Methodology
3. Results
3.1. Proposed Approach to the Knitting Operation
3.1.1. Manufacturing Process Mapping
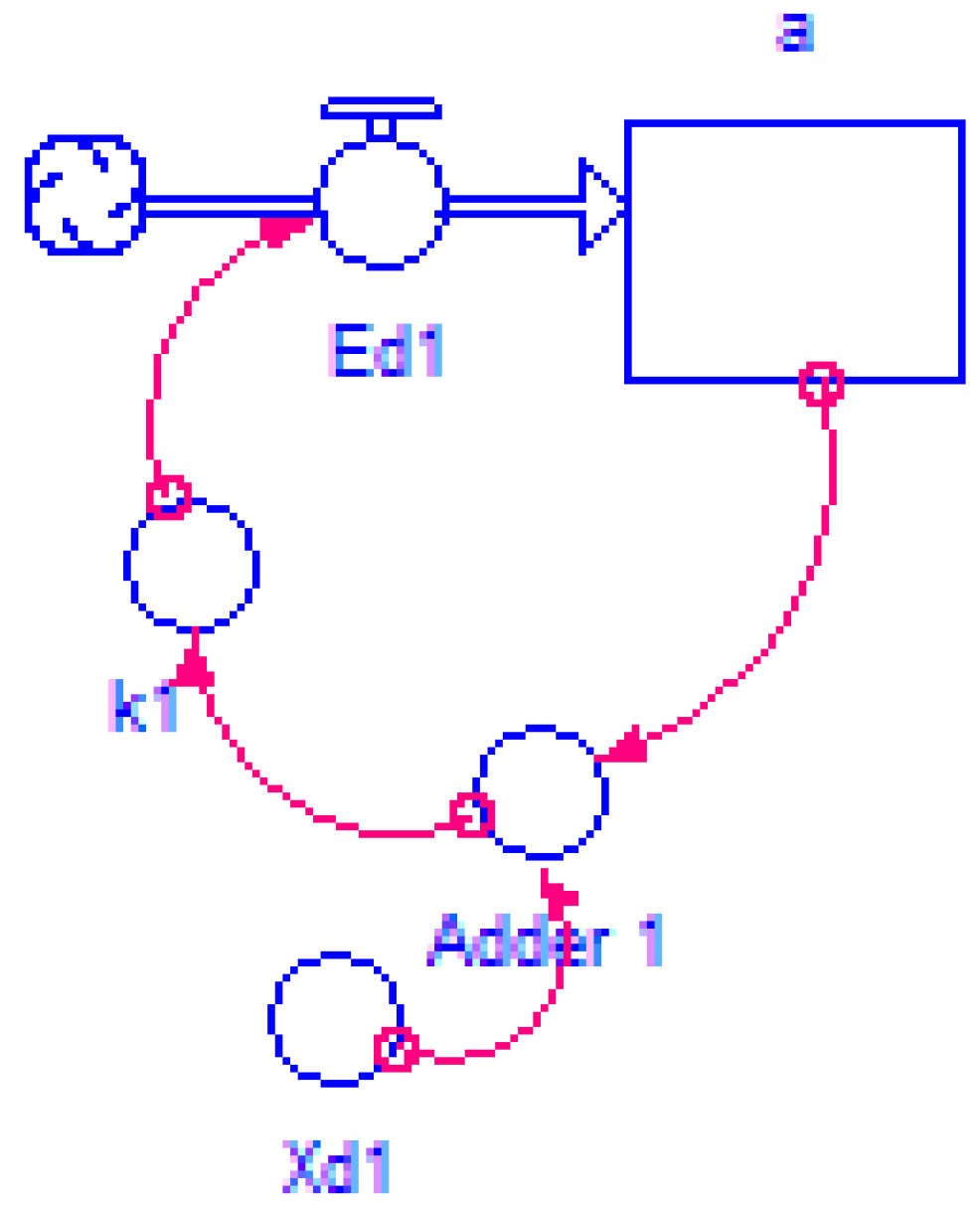
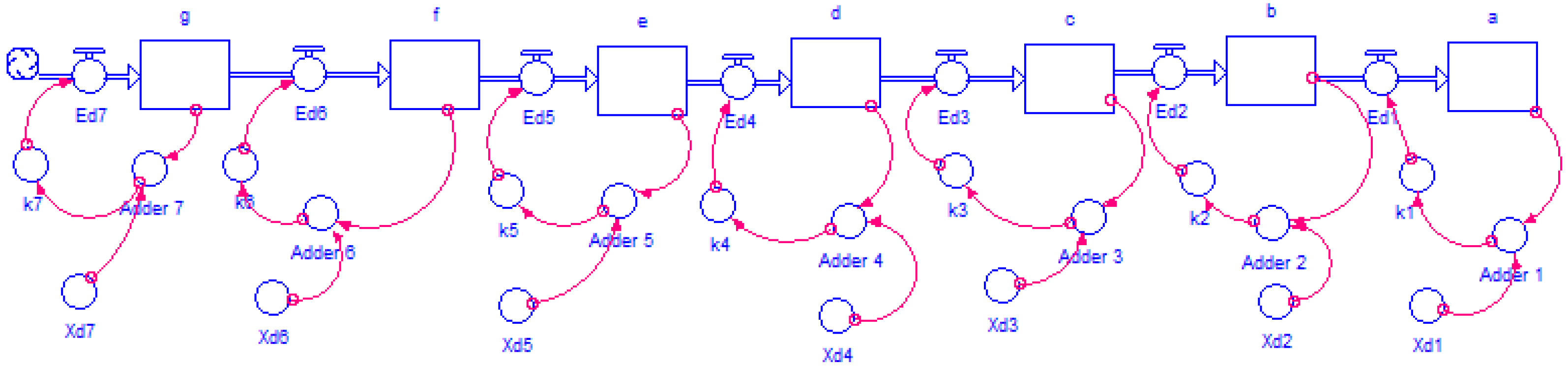
3.1.2. Forrester Diagram and Identification of the Differential Equation
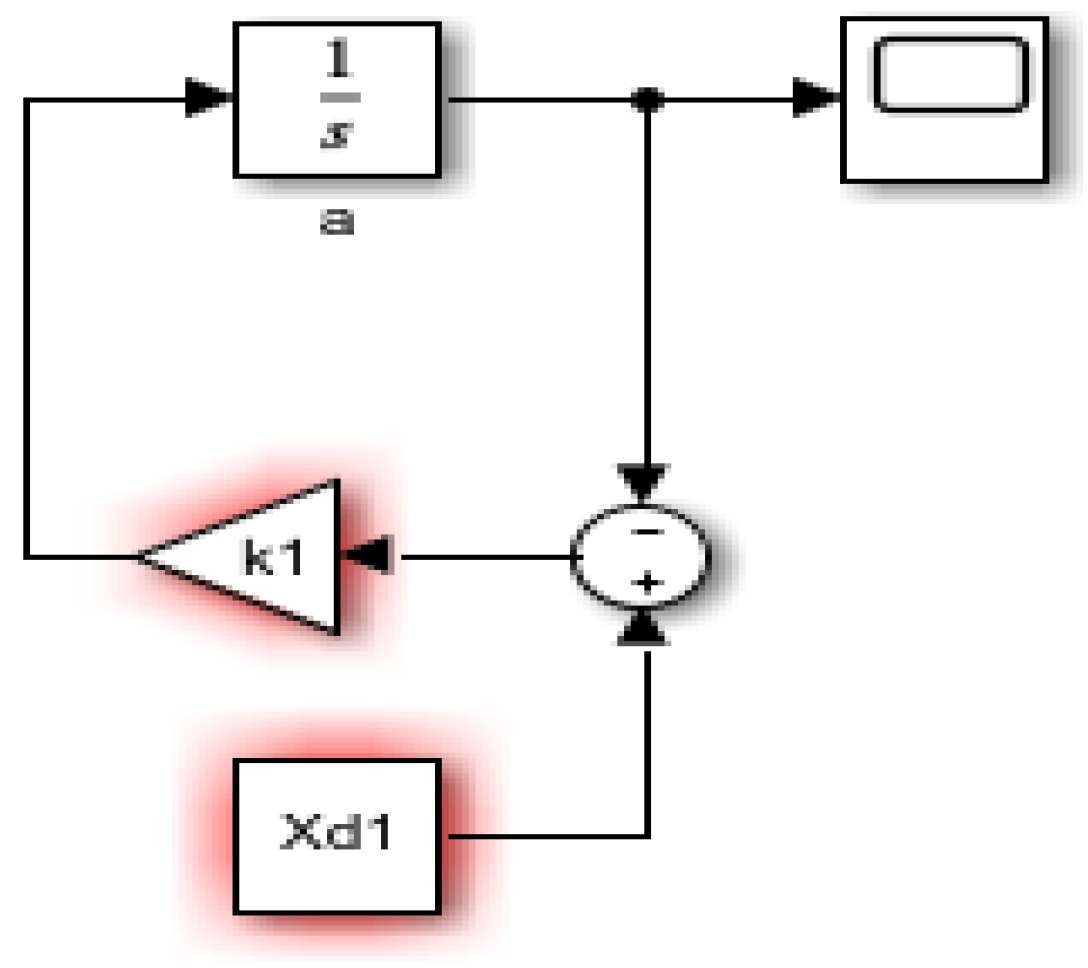
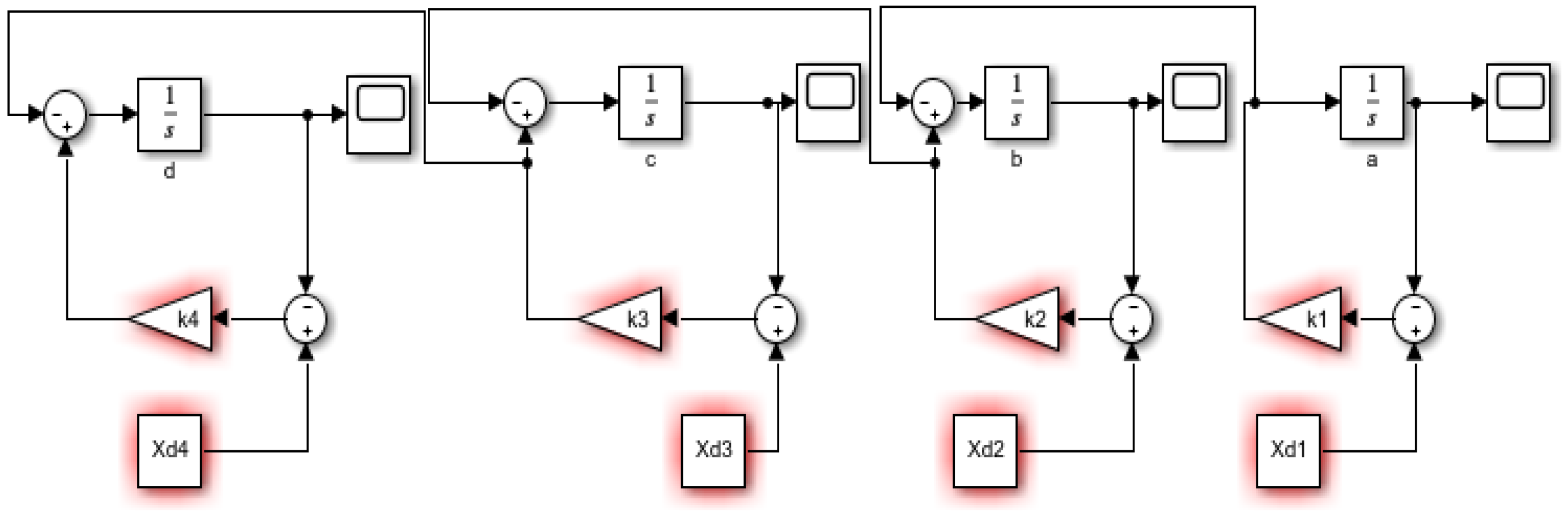
3.1.3. Knitting Process Block Diagram
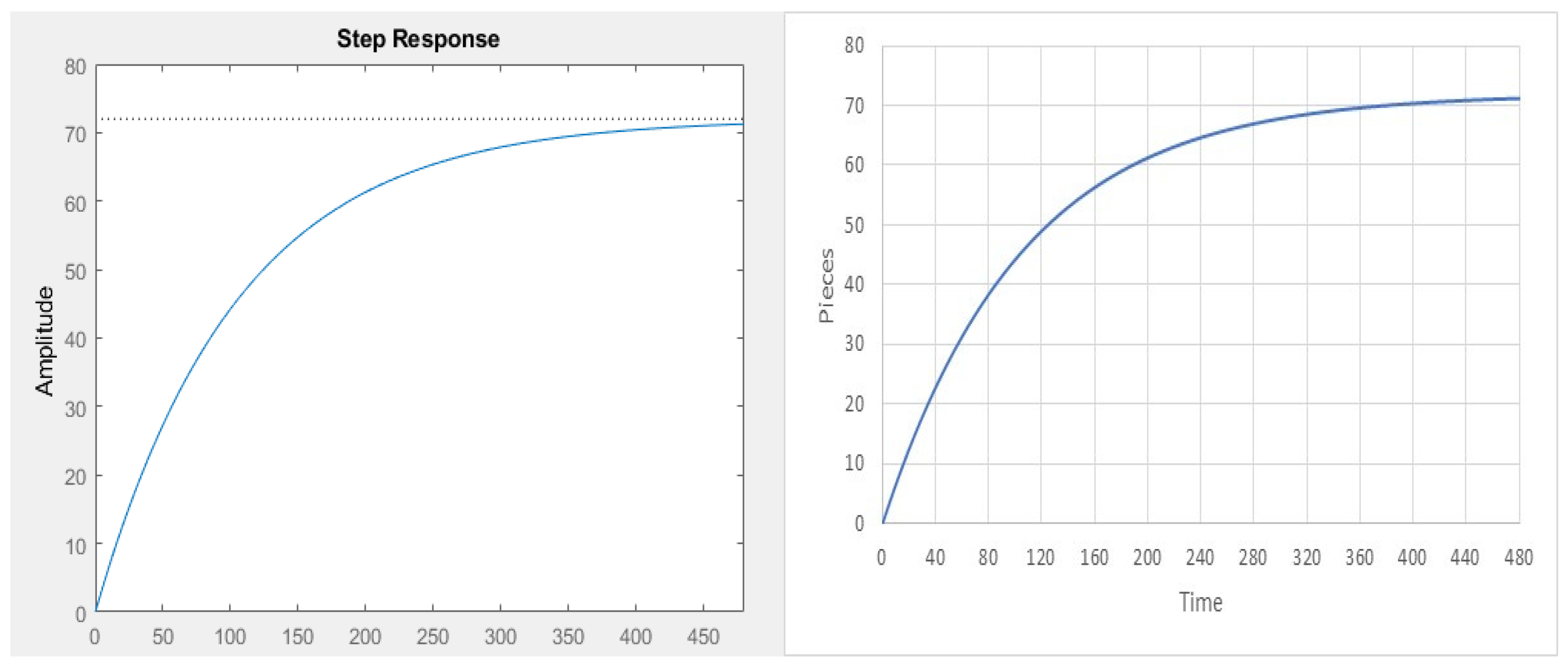
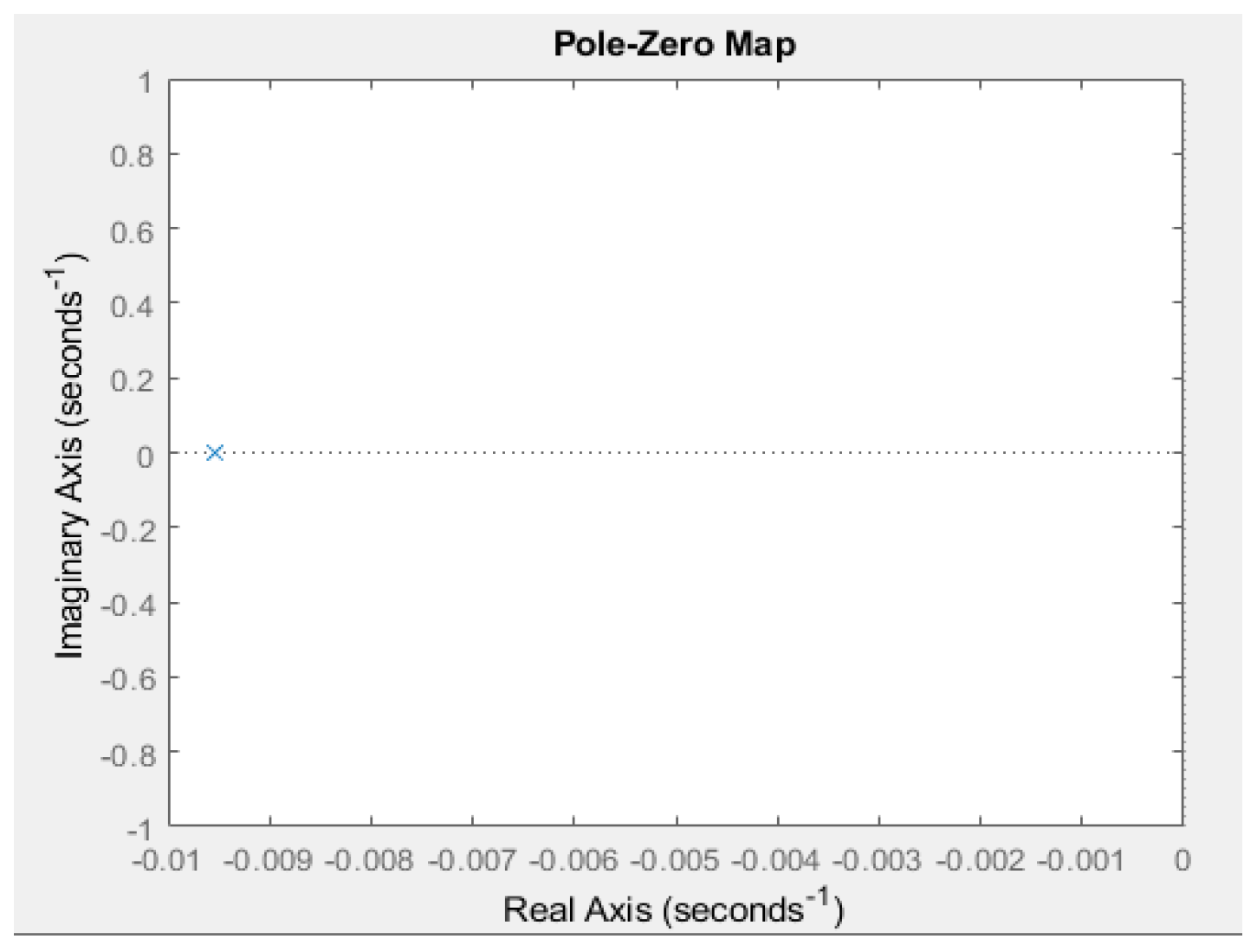
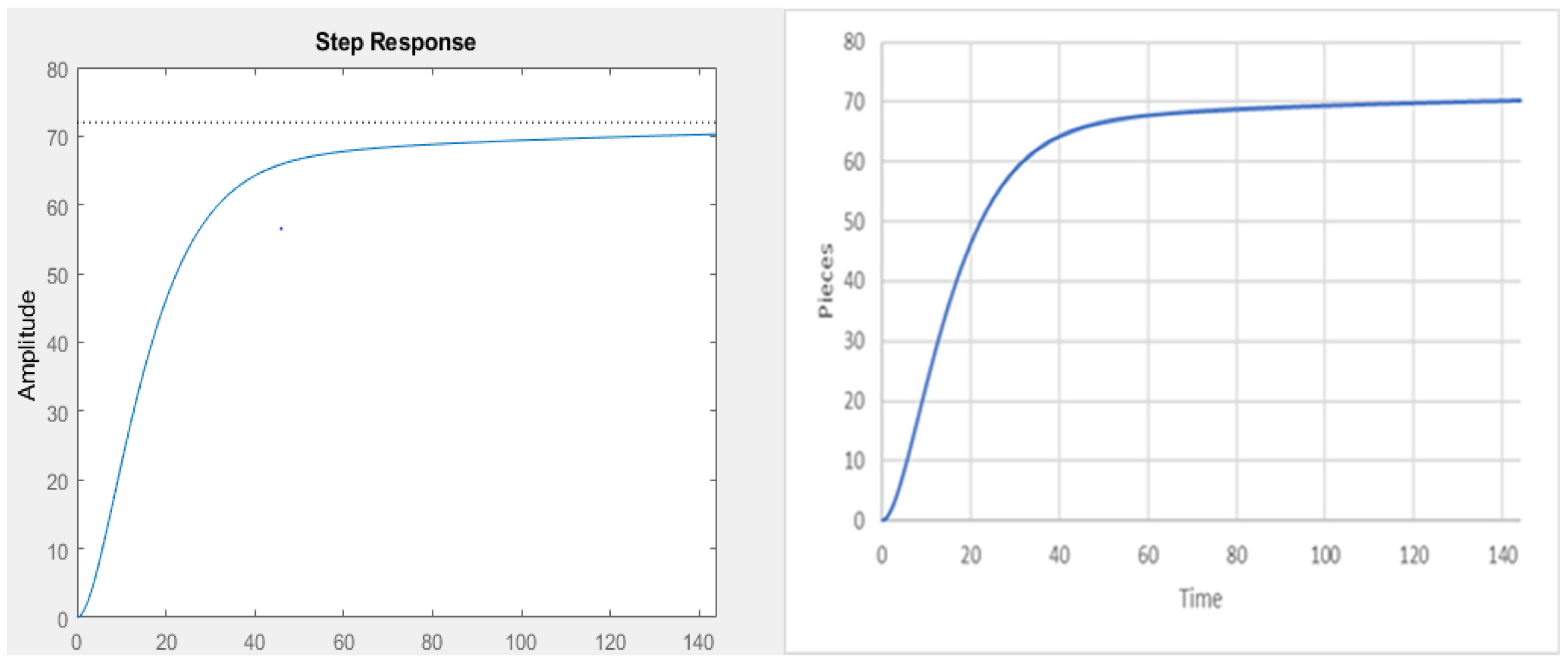
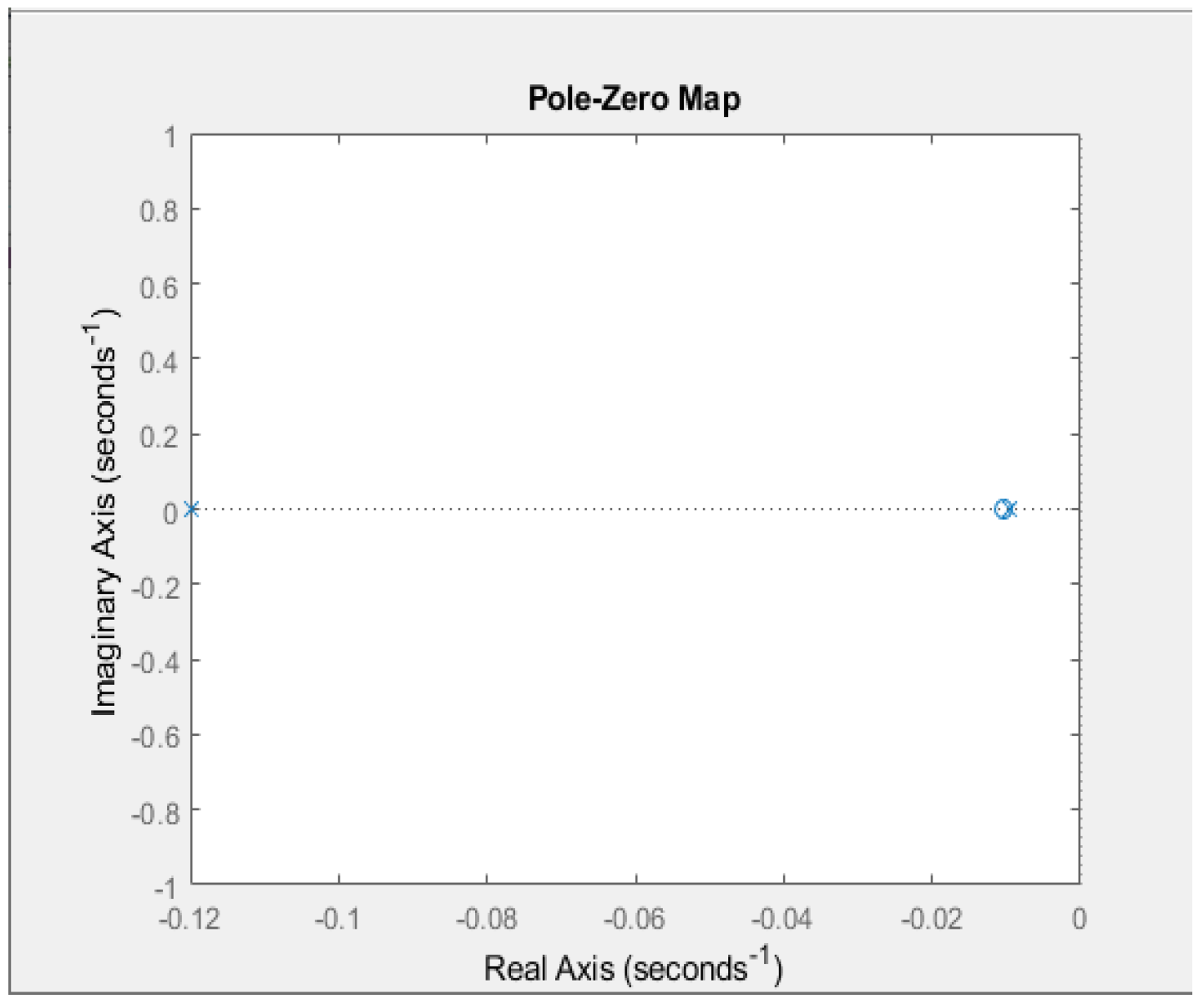
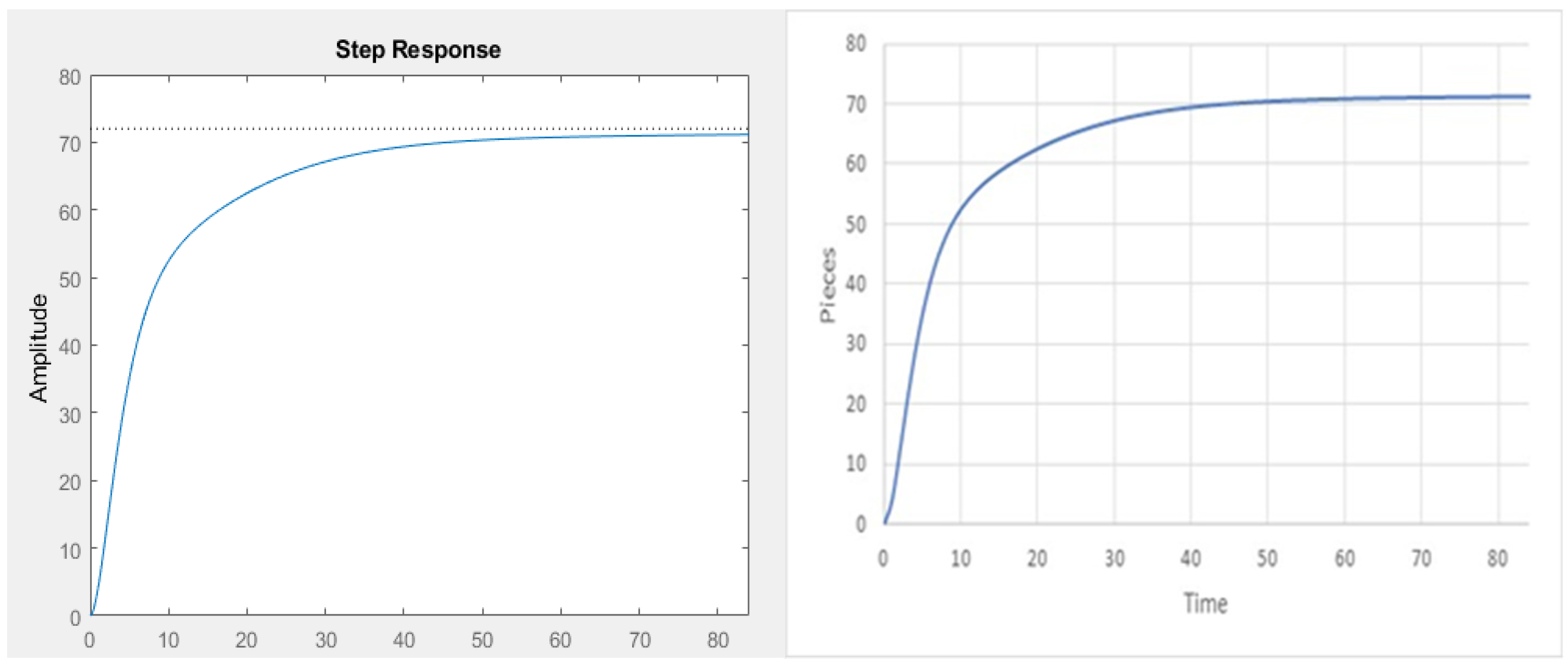
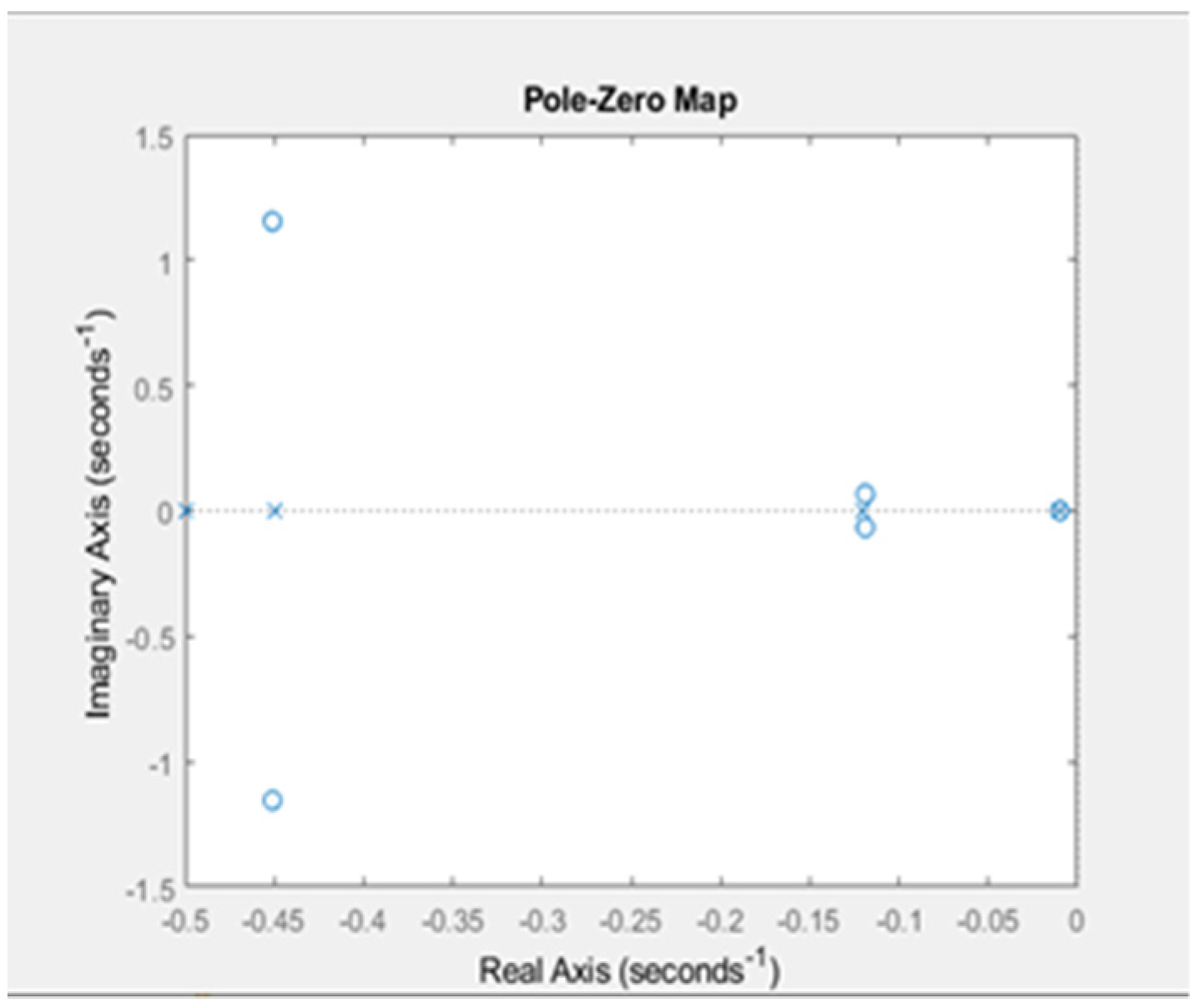
3.1.4. Stability of the Knitting Process System
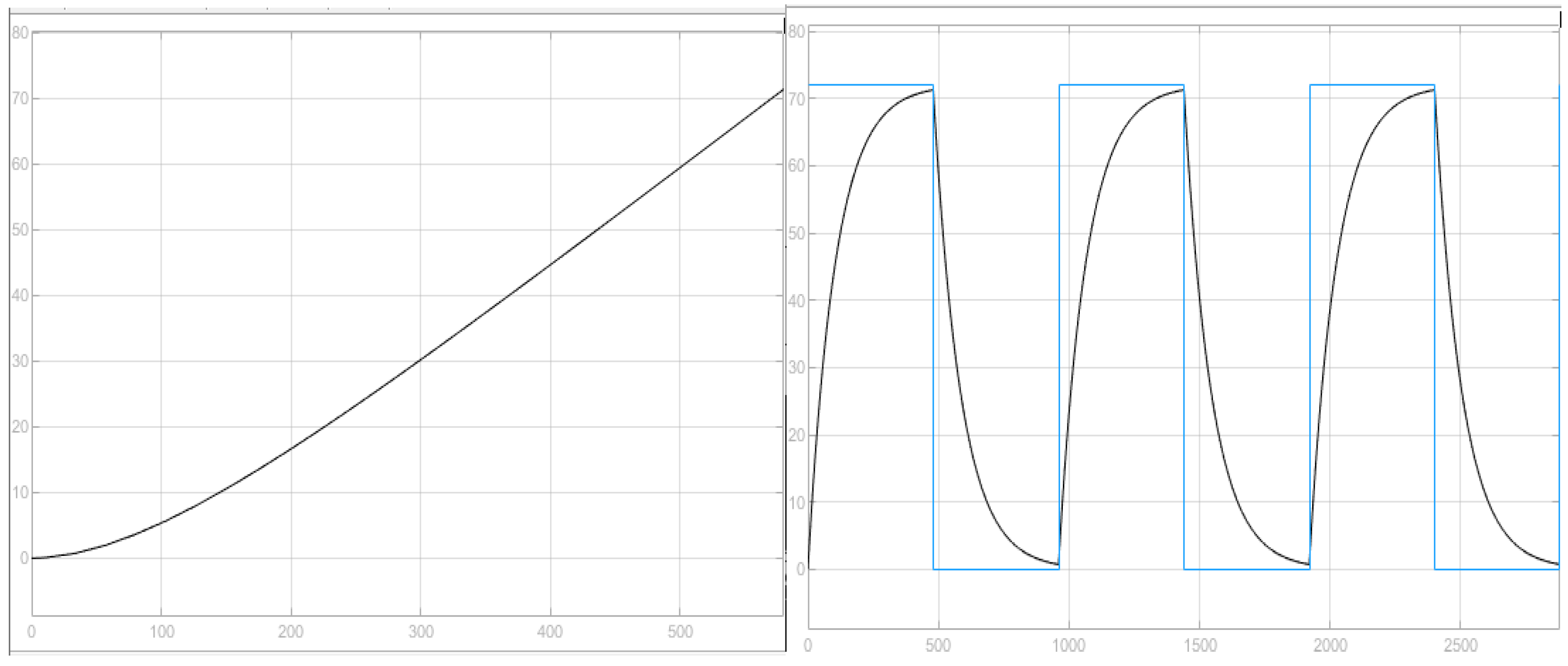
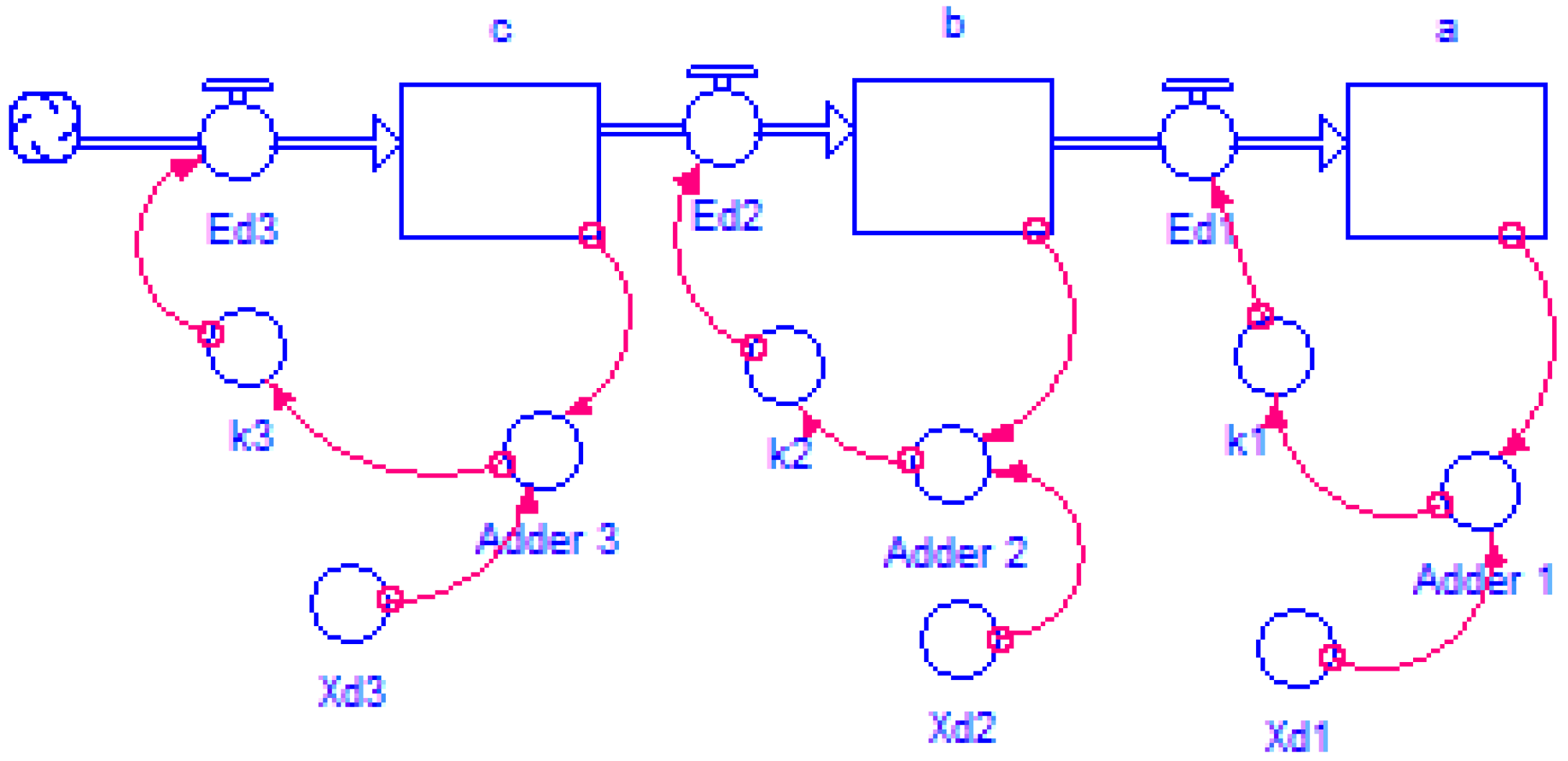
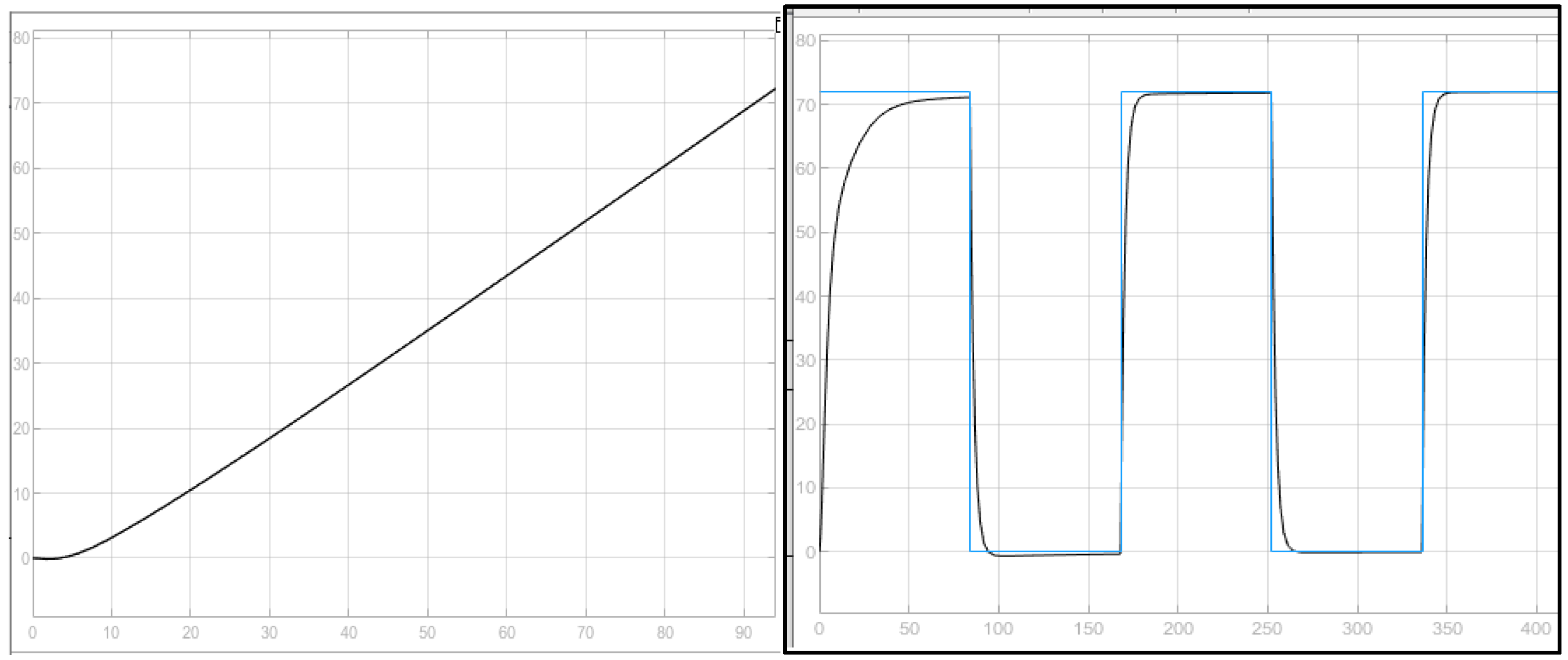
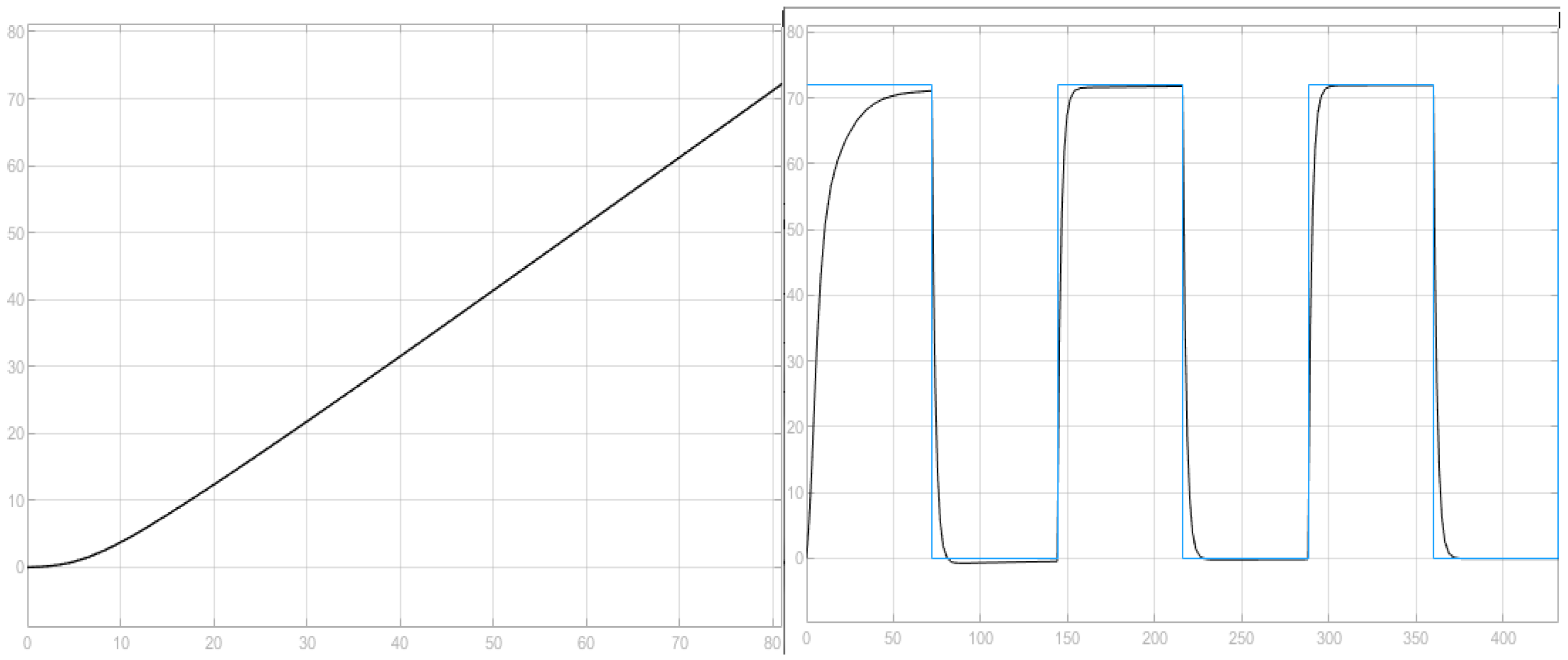
3.1.5. Multiple Inputs-Knitting Process
3.2. Proposed Approach to the Basting Operation
3.2.1. Forrester Diagram-Basting Process
3.2.2. Diagram of Blocks-Basting Process
3.2.3. Stability of the Basting-System-Process
3.2.4. Multiple Inputs-Basting Process

3.3. Proposed Approach to the Ironing Operation
3.3.1. Forrester Diagram-Ironing Process
3.3.2. Block Diagram-Ironing Process
3.3.3. System Stability-Ironing Process
3.3.4. Multiple Inputs-Ironing Process
3.4. Proposed Approach to the Cutting Operation
3.4.1. Forrester Diagram-Cutting Process
3.4.2. Block Diagram-Cutting Process
3.4.3. Stability of the System-Ironing Process
3.4.4. Multiple Inputs-Cutting Process
3.5. Proposed Approach to the Making Operation
3.5.1. Forrester’s Diagram-Making Operation Process
3.5.2. Block Diagram-Making Operation Process
3.5.3. Stability of the System-Making Operation Process
3.5.4. Multiple Inputs-Making Operation Process
3.6. Proposed Approach to the Finishing Operation
3.6.1. Forrester Diagram-Finishing Operation Process
3.6.2. Block Diagram-Finishing Operation Process
3.6.3. System Stability-Finishing Process
3.6.4. Multiple Inputs-Finishing Process
3.7. Proposed Approach to the Packing Operation
3.7.1. Forrester Diagram-Packing Operation Process
3.7.2. Block Diagram-Packing Process
3.7.3. Stability of the System-Packing Process
3.7.4. Multiple Inputs-Packing Process
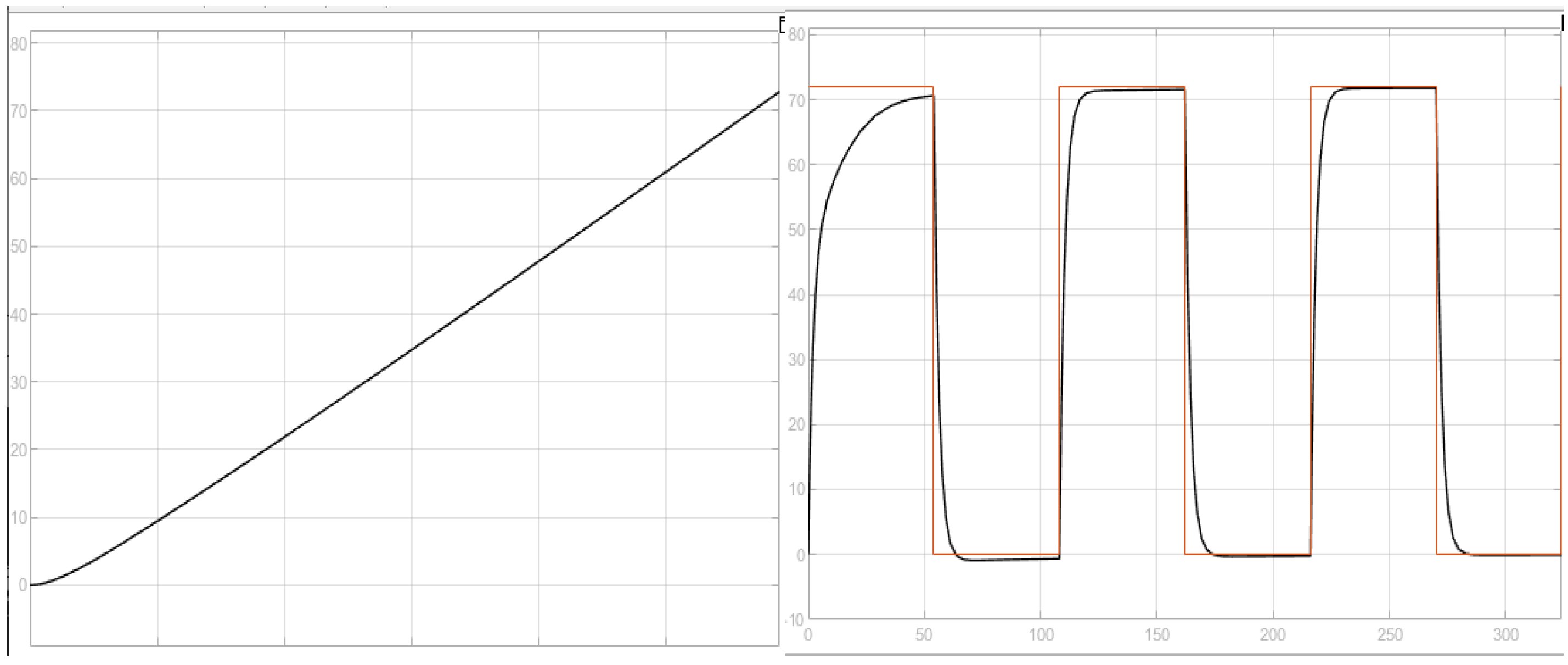
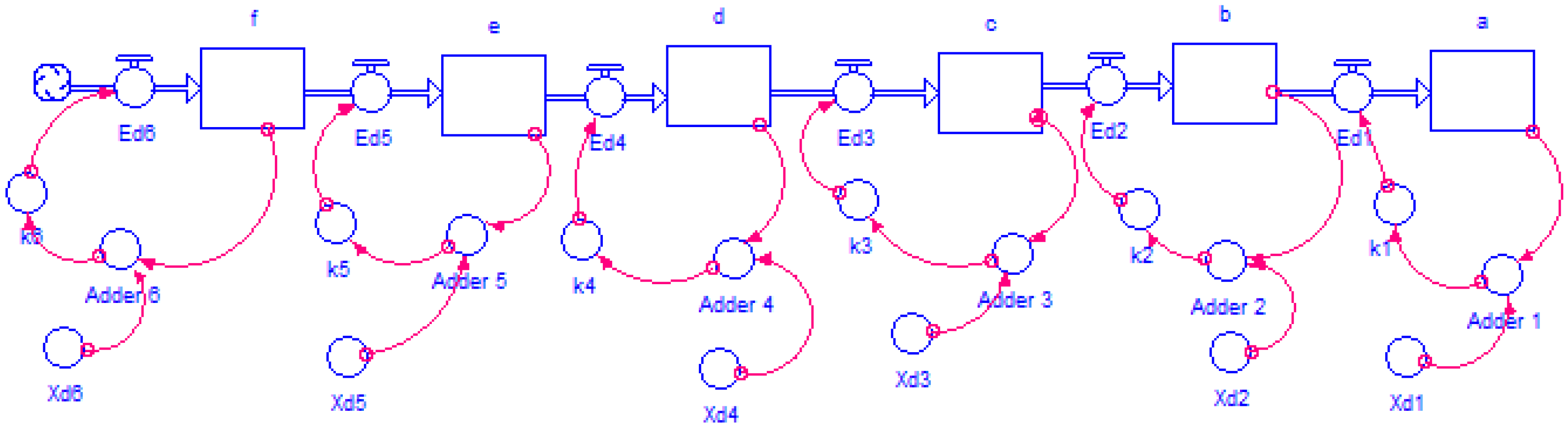
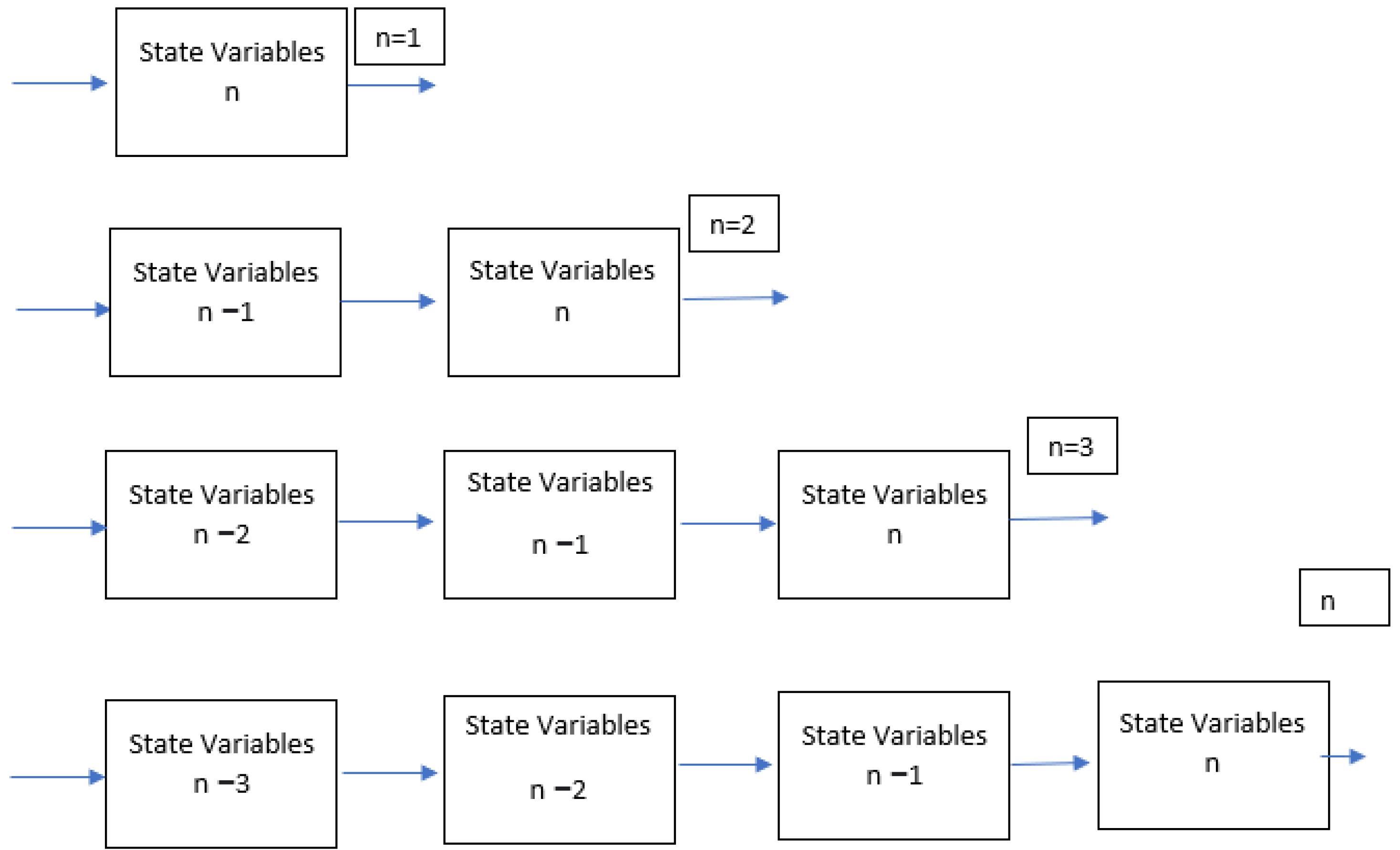
3.8. General Approach Proposed
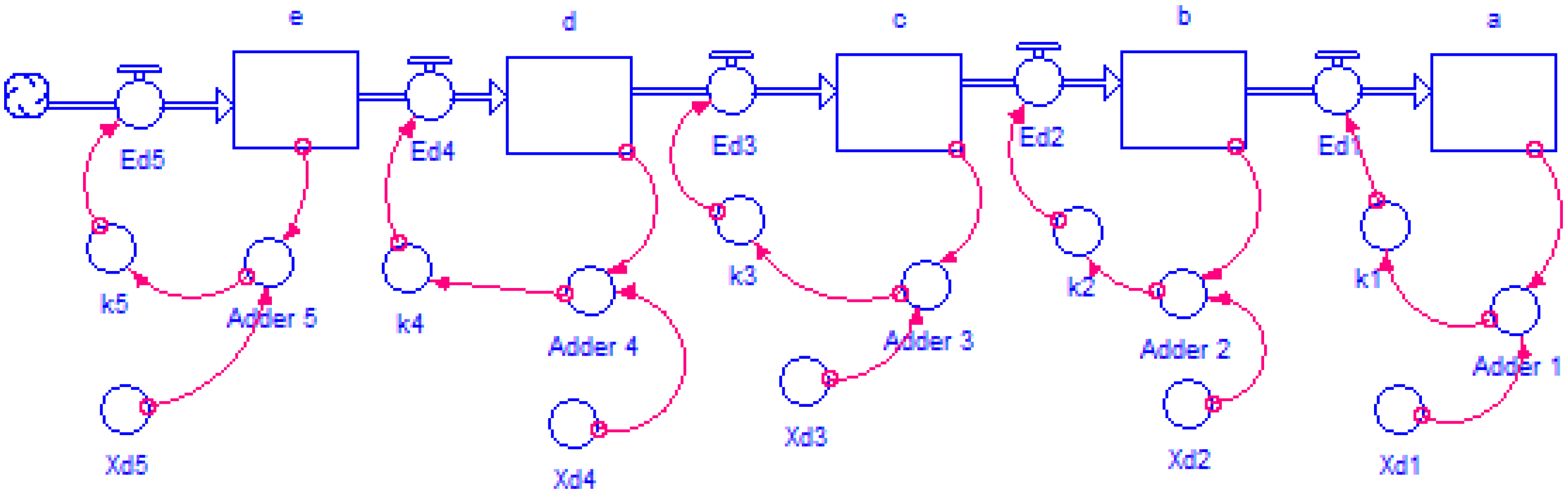
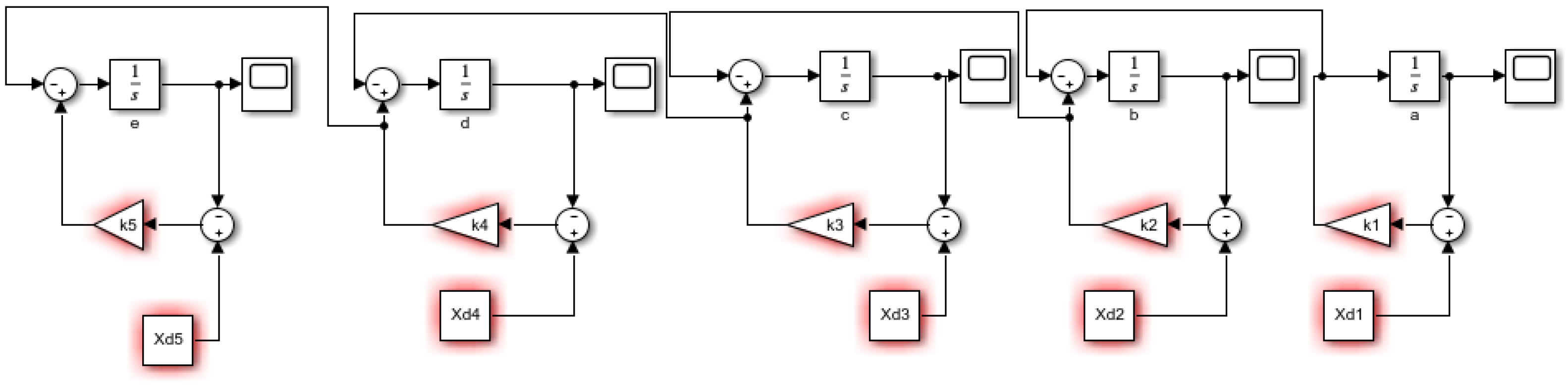
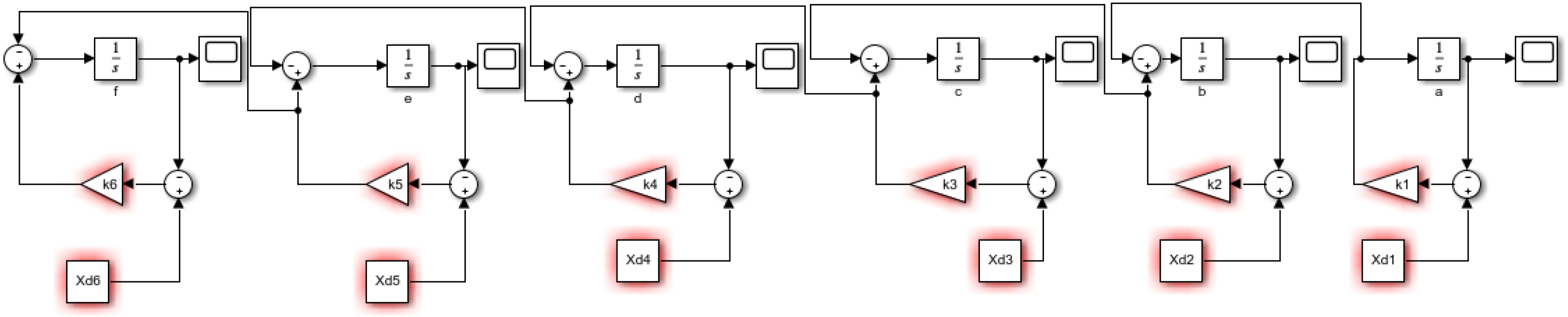
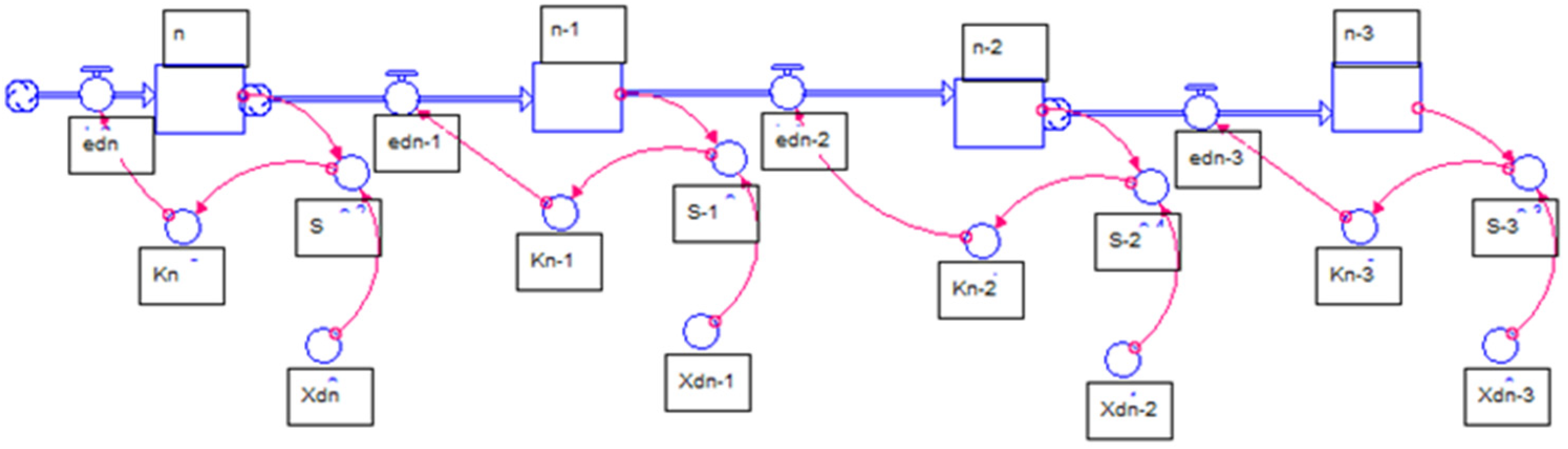
3.8.1. Forrester Diagram-(n)-State Variables
3.8.2. Block-n-Process Diagram
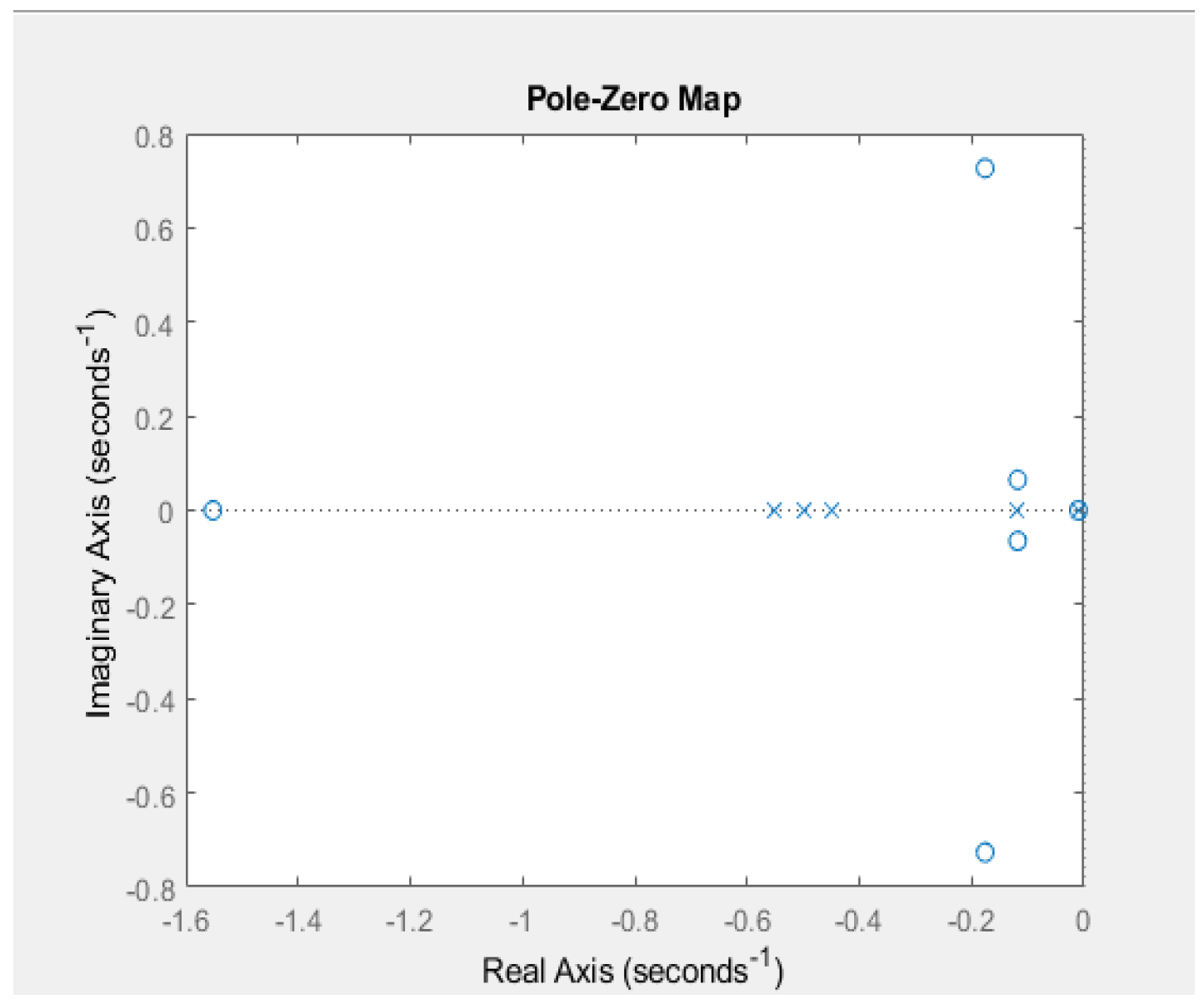
3.8.3. Stability of the System-n-State Variables
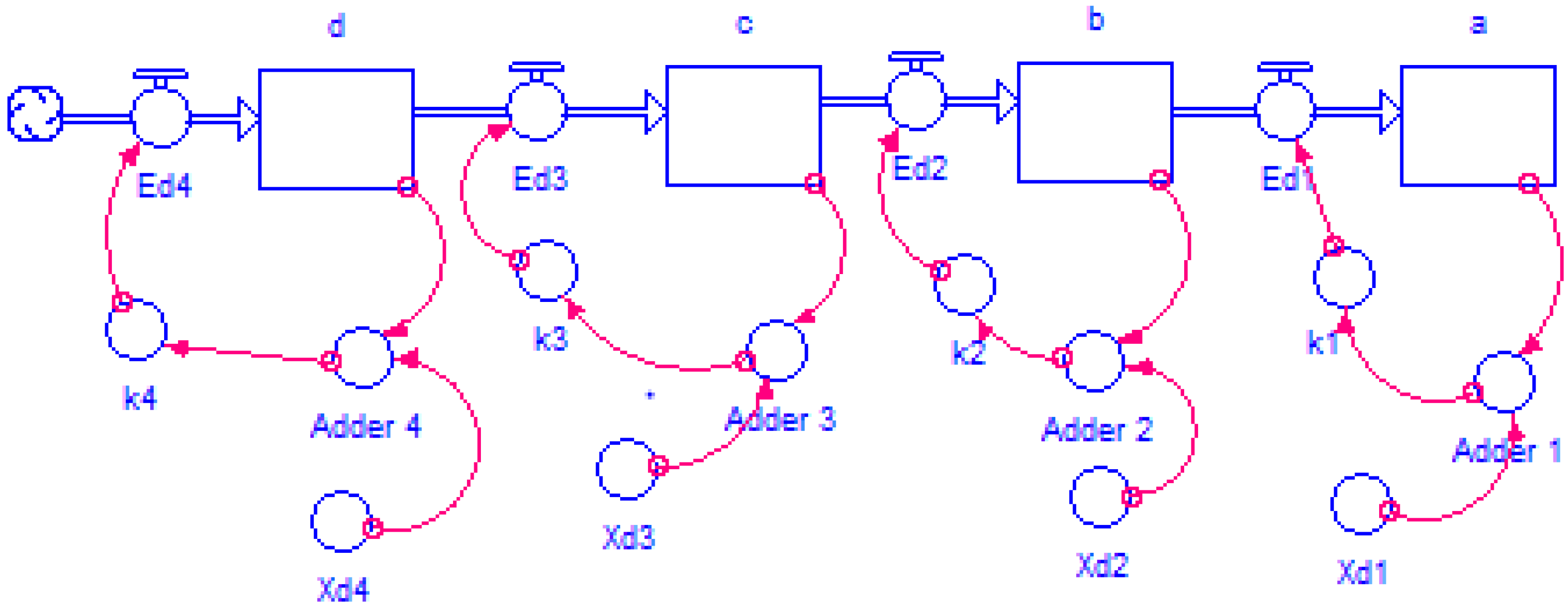
3.8.4. Multiple Inputs-n State Variables
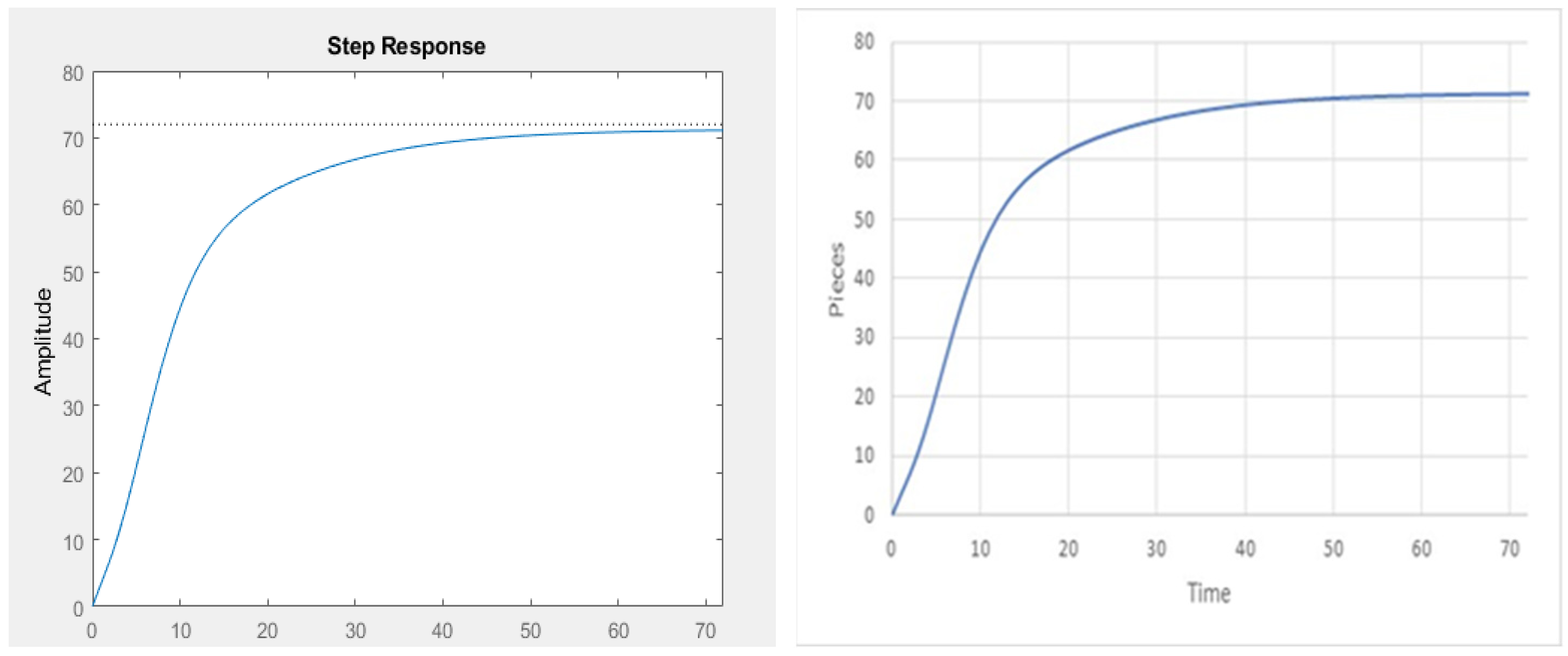
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aracil, J. Introducción a la Dinámica de Sistemas; Alianza Editorial: Madrid, Spain, 1986. [Google Scholar]
- Sterman, J. Business Dynamics; McGraw-Hill, Inc.: New York, NY, USA, 2000. [Google Scholar]
- García, J.M. Teoría y Ejercicios Prácticos de Dinámica de Sistemas: Dinámica de Sistemas (Cuarta Edición); Spain. 2018. Available online: https://www.amazon.com.mx/Teor%C3%ADa-Ejercicios-Prácticos-Dinámica-Sistemas/dp/1718137931#customerReviews (accessed on 2 March 2022).
- Lagarda-Leyva, E.A.; Ruiz, A. A Systems Thinking Model to Support Long-Term Bearability of the Healthcare System: The Case of the Province of Quebec. Sustainability 2019, 11, 7028. [Google Scholar] [CrossRef]
- Cuartas Orozco, A.K. Estudio del efecto del clima sobre la producción de un hato bovino lechero desde la dinámica de sistemas. 2021. Available online: http://repositorio.unal.edu.co/handle/unal/80261 (accessed on 3 March 2022).
- De Leo, E.; Aranda, D.; Addati, G.A. Introducción a la Dinámica de Sistemas (No. 739). Serie Documentos de Trabajo. 2020. Available online: https://www.econstor.eu/bitstream/10419/238364/1/739.pdf (accessed on 1 February 2022).
- Lagarda-Leyva, E.A. System dynamics and lean approach: Development of a technological solution in a regional product packaging company. Appl. Sci. 2021, 11, 7938. [Google Scholar] [CrossRef]
- Assumma, V.; Bottero, M.; Datola, G.; De Angelis, E.; Monaco, R. Dynamic models for exploring the resilience in territorial scenarios. Sustainability 2019, 12, 3. [Google Scholar] [CrossRef]
- Di Nardo, M.; Clericuzio, M.; Murino, T.; Sepe, C. An economic order quantity stochastic dynamic optimization model in a logistic 4.0 environment. Sustainability 2020, 12, 4075. [Google Scholar] [CrossRef]
- Facchini, F.; Oleśków-Szłapka, J.; Ranieri, L.; Urbinati, A. A maturity model for logistics 4.0: An empirical analysis and a roadmap for future research. Sustainability 2019, 12, 86. [Google Scholar] [CrossRef]
- Nagy, J.; Oláh, J.; Erdei, E.; Máté, D.; Popp, J. The role and impact of Industry 4.0 and the internet of things on the business strategy of the value chain—The case of Hungary. Sustainability 2018, 10, 3491. [Google Scholar] [CrossRef]
- Montoya, R.A.G.; Arenas, J.A.C.; Bernal, E.M. Método costeo ABC con simulación de Monte Carlo en la logística en la cadena de suministro en la industria 4.0. Cuad. De Contab. 2020, 21, 20. [Google Scholar]
- Golshanimanesh, M.; Abbasianjahromi, H.; Ehsanifar, M.; Mirhosseini, S.M. Providing a System Dynamic Model to Predict Construction Status in Iran Using Sustainable Development Indicators. J. Ind. Eng. Int. 2021, 17, 1–19. [Google Scholar]
- Gu, C.; Ye, X.; Cao, Q.; Guan, W.; Peng, C.; Wu, Y.; Zhai, W. System dynamics modelling of urbanization under energy constraints in China. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Laimon, M.; Mai, T.; Goh, S.; Yusaf, T. Energy sector development: System dynamics analysis. Appl. Sci. 2019, 10, 134. [Google Scholar] [CrossRef]
- Zuo, Y.; Shi, Y.L.; Zhang, Y.Z. Research on the sustainable development of an economic-energy-environment (3E) system based on system dynamics (SD): A case study of the Beijing-Tianjin-Hebei Region in China. Sustainability 2017, 9, 1727. [Google Scholar] [CrossRef]
- Parra, P.Y.; Hare, B.; Hutfilter, U.F.; Roming, N. Evaluating the Significance of Australia’s Global Fossil Fuel Carbon Footprint; Climate Analytics: Berlin, Germany, 2019. [Google Scholar]
- Laimon, M.O. Sustainable Energy Sector Development Using Systems Thinking and System Dynamics Analysis. Ph.D. Thesis, University of Southern Queensland, Toowoomba, QLD, Australia, 2019. [Google Scholar]
- Grida, M.; Zeid, M. A system dynamics-based model to implement the Theory of Constraints in a healthcare system. Simulation 2019, 95, 593–605. [Google Scholar] [CrossRef]
- Davahli, M.R.; Karwowski, W.; Taiar, R. A system dynamics simulation applied to healthcare: A systematic review. Int. J. Environ. Res. Public Health 2020, 17, 5741. [Google Scholar] [CrossRef] [PubMed]
- Shoaib, M.; Ramamohan, V. Simulation modeling and analysis of primary health center operations. Simulation 2020, 98, 183–208. [Google Scholar] [CrossRef]
- Hasan, I.; Bahalkeh, E.; Yih, Y. Evaluating intensive care unit admission and discharge policies using a discrete event simulation model. Simulation 2020, 96, 501–518. [Google Scholar] [CrossRef]
- Kampmann, C.E.; Oliva, R. Analytical methods for structural dominance analysis in system dynamics: An assessment of the current state of affairs. In Proceedings of the 25th International Conference of the System Dynamics Society, Boston, MA, USA, 29 July–2 August 2007. [Google Scholar]
- Gooyert, V.; Goncalves, P.; Herrera, H.; Kampmann, C.; Kapmeier, F.; Kopainsky, B.; Zimmermann, N. System dynamics and sustainability: A research agenda for the coming decade(s). In Proceedings of the International System Dynamics Conference, Chicago, IL, USA, 26–31 July 2021. [Google Scholar]
- Saleh, M.; Davidsen, P. Extending eigenvalue analysis to nonlinear models via incorporating higher order terms of Taylor series expansion. In Proceedings of the 25th International Systems Dynamics Conference, Boston, MA, USA, 29 July–2 August 2007. [Google Scholar]
- Oliva, R. Model structure analysis through graph theory: Partition heuristics and feedback structure decomposition. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2004, 20, 313–336. [Google Scholar] [CrossRef]
- Kampmann, C.E.; Oliva, R. Loop eigenvalue elasticity analysis: Three case studies. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2006, 22, 141–162. [Google Scholar] [CrossRef]
- Saleh, M.; Oliva, R.; Davidsen, P.; Kampmann, C.E. Eigenvalue analysis of system dynamics models: Another perspective. In Proceedings of the International System Dynamics Conference, Neijmegen, The Netherlands, 23–27 July 2006. [Google Scholar]
- González Ponzón, E.R. Herramienta computacional para un análisis formal de modelos de dinámica de sistemas bajo el método Loop Eigenvalue elasticity analysis (Leea) con soporte a modelos de gran escala. 2015. Available online: http://manglar.uninorte.edu.co/handle/10584/8983#page=1 (accessed on 5 April 2022).
- Oliva, R. Structural dominance analysis of large and stochastic models. Syst. Dyn. Rev. 2016, 32, 26–51. [Google Scholar] [CrossRef]
- Oliva, R. Linking structure to behavior using eigenvalue elasticity analysis. In Analytical Methods for Dynamic Modelers; MIT Press: Boston, MA, USA, 2015; pp. 207–239. [Google Scholar]
- Kampmann, C.E.; Oliva, R. Analytical methods for structural dominance analysis in system dynamics. In System Dynamics: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 153–176. [Google Scholar]
- Oliva, R. On structural dominance analysis. Syst. Dyn. Rev. 2020, 36, 8–28. [Google Scholar] [CrossRef]
- Gonçalves, P. Behavior modes, pathways and overall trajectories: Eigenvector and eigenvalue analysis of dynamic systems. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2009, 25, 35–62. [Google Scholar] [CrossRef]


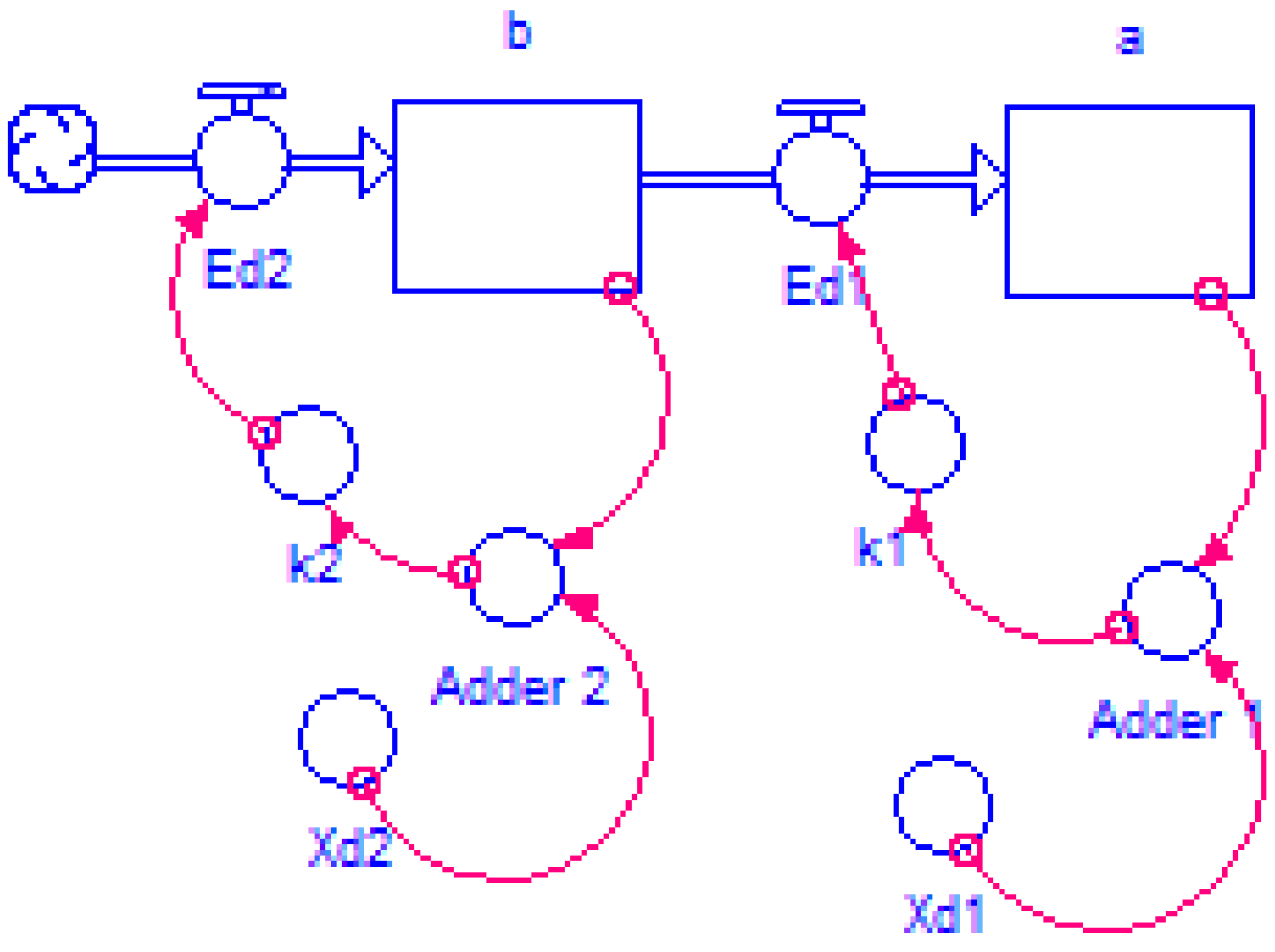
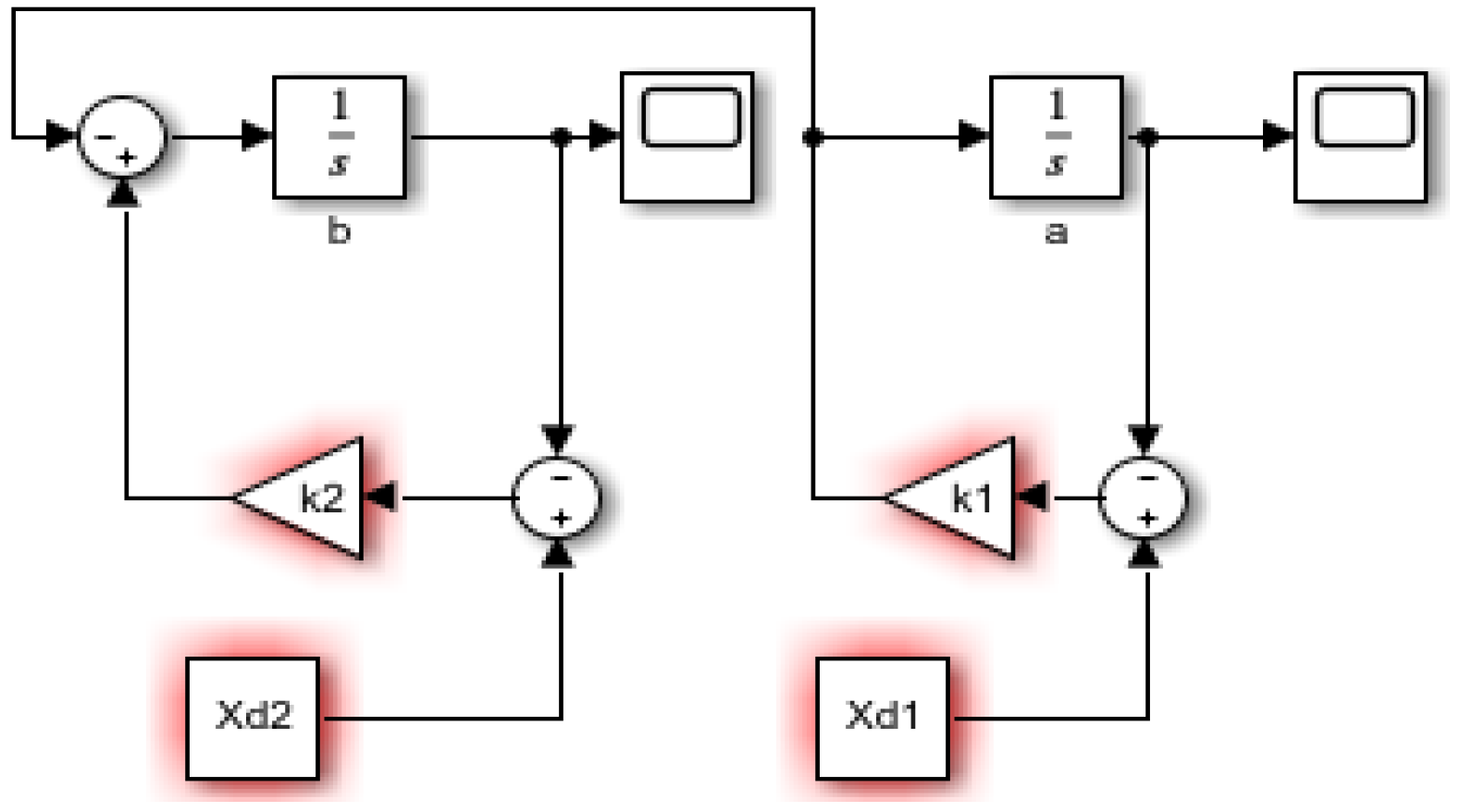
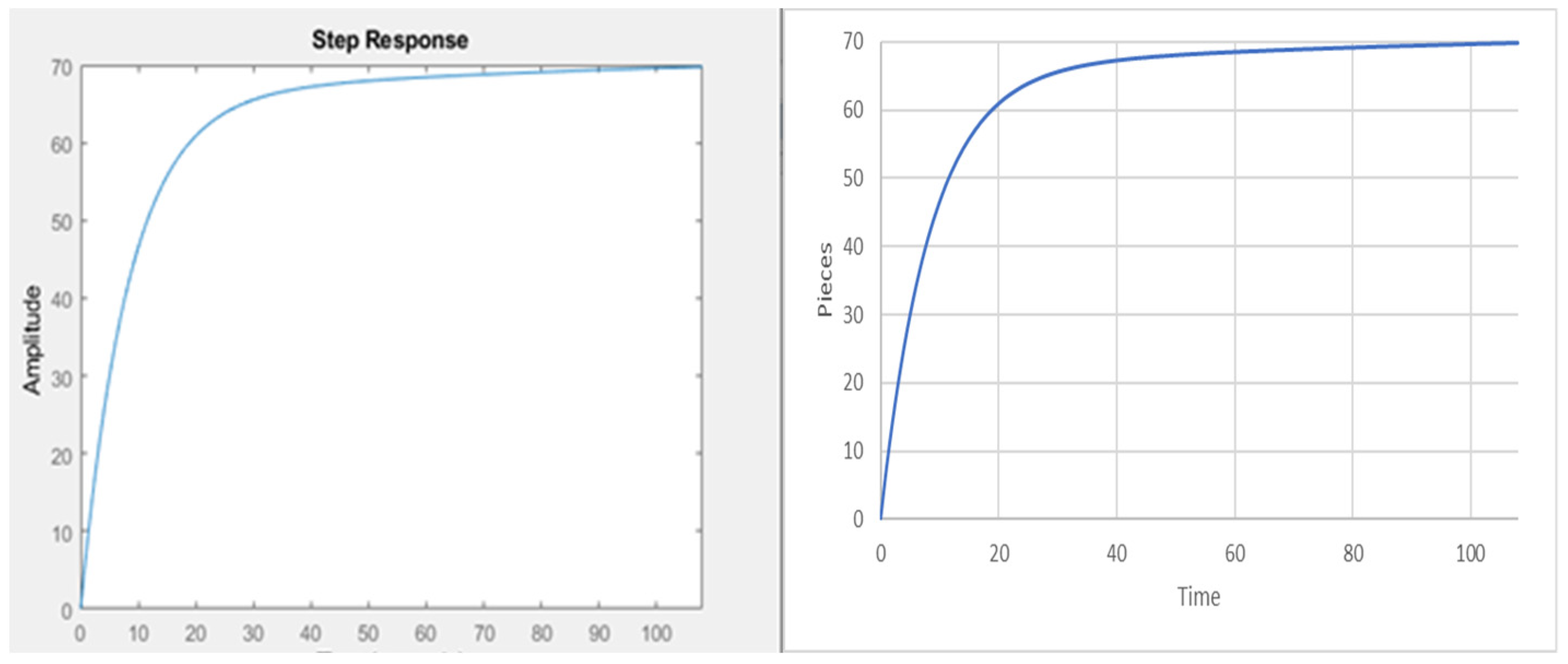
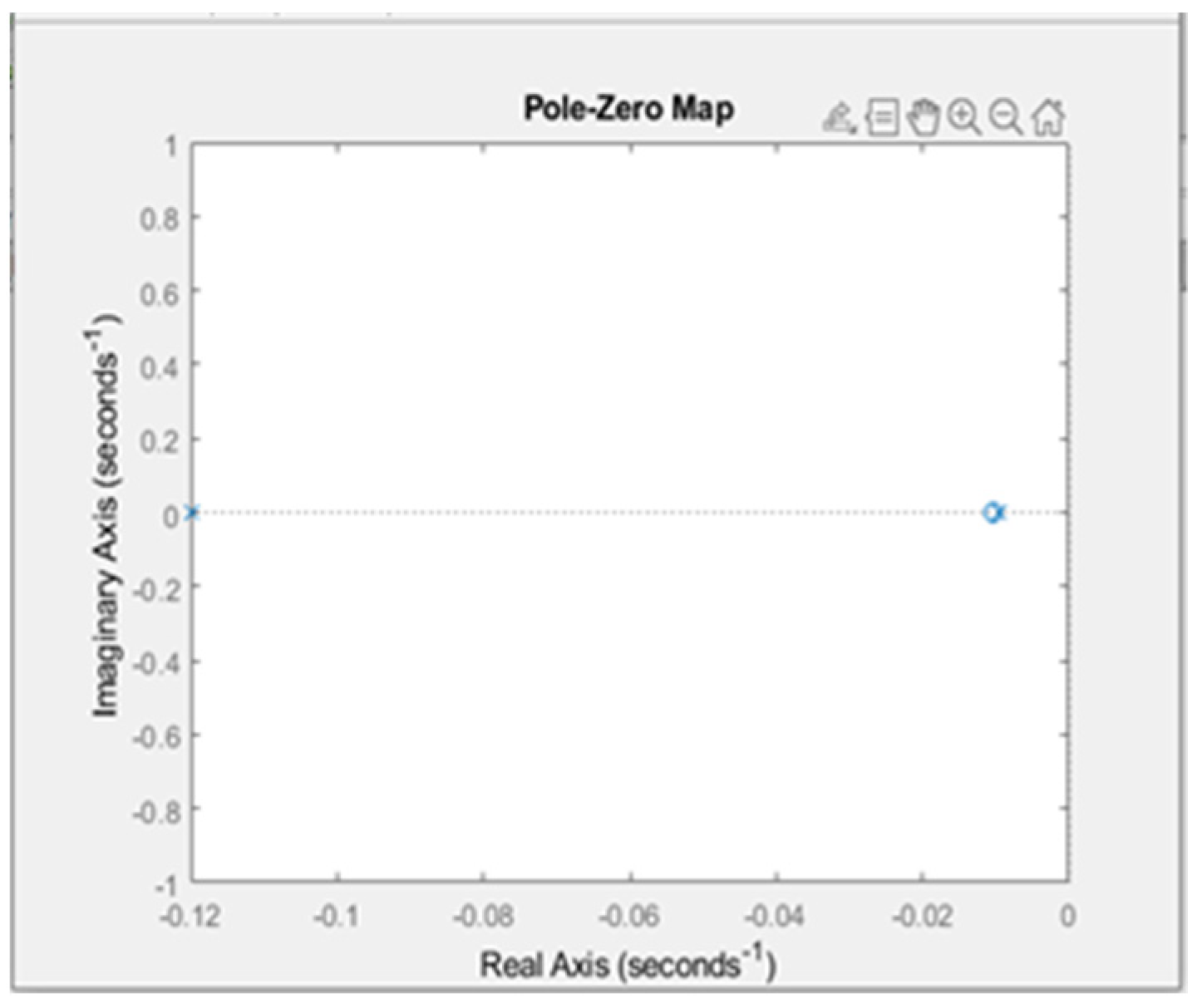


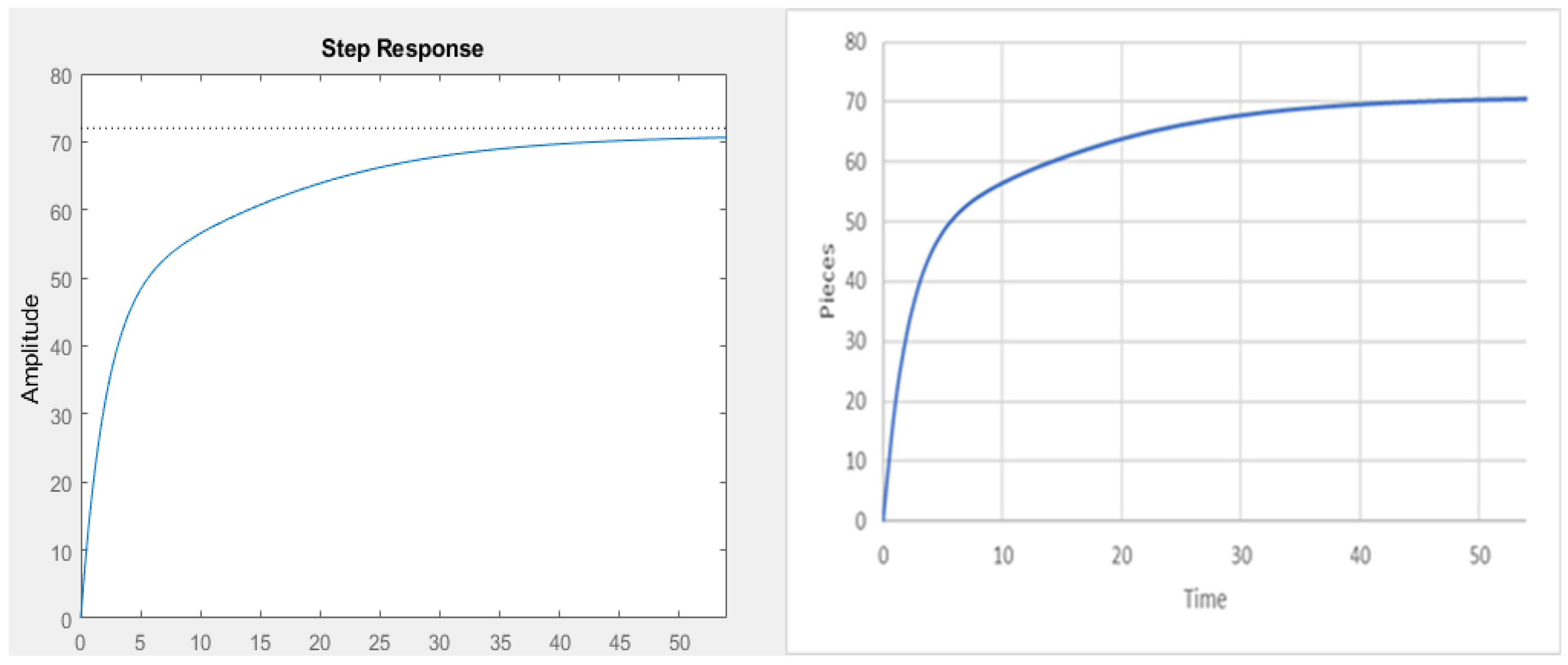
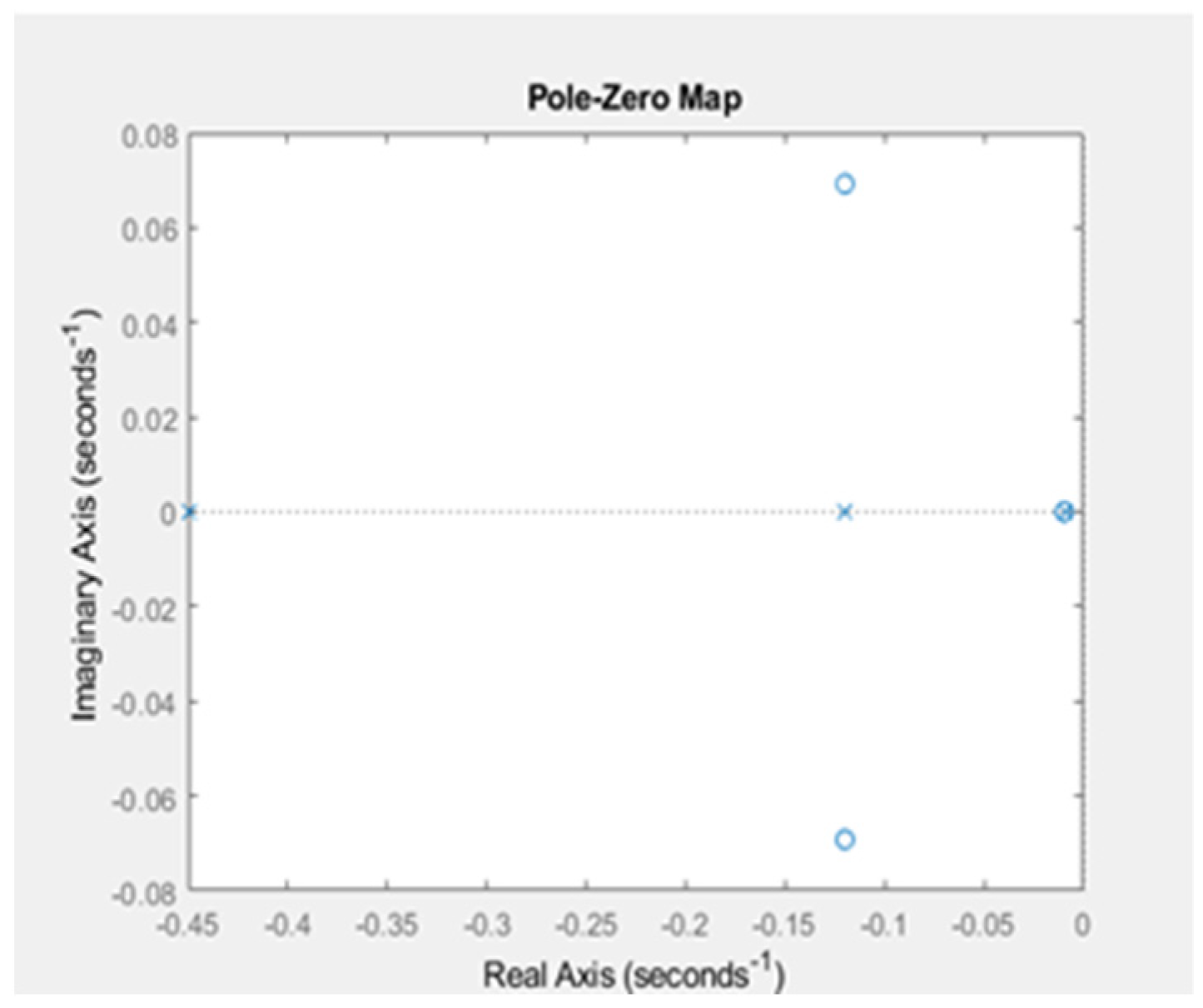





| State Variable | Cycle Time (minutes) | Number of Machines | Establishment Time for 72 Sweaters |
|---|---|---|---|
| Knitting | 40 | 6 | 480 |
| Basting | 3 | 2 | 108 |
| Ironing | 4 | 2 | 144 |
| Cutting | 3 | 4 | 54 |
| Making | 7 | 6 | 84 |
| Finishing | 2 | 2 | 72 |
| Packing | 2 | 2 | 72 |
| State Variable (m) | k | Notation of the Variable | Differential Equations |
|---|---|---|---|
| Knitting | 0.009541 | a | da/dt = k1(Xd1 − a) |
| Basting | 0.12 | b | k1(Xd1 − a) |
| Ironing | 0.12 | c | k2(Xd2 − b) |
| Cutting | 0.45 | d | k3(Xd3 − c) |
| Making | 0.45 | e | de/dt = k5(Xd5 − k4(Xd4 − d) |
| Finishing | 0.5 | f | df/dt = k6(Xd6 − k5(Xd5 − e) |
| Packing | 0.55 | g | k6(Xd6 − f) |
| State Variables. | Transfer Function |
|---|---|
| a | |
| b | |
| c | |
| d | |
| e | |
| f | |
| g |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrios Sánchez, J.M.; Baeza Serrato, R.; Bianchetti, M. Design and Development of a Mathematical Model for an Industrial Process, in a System Dynamics Environment. Appl. Sci. 2022, 12, 9855. https://doi.org/10.3390/app12199855
Barrios Sánchez JM, Baeza Serrato R, Bianchetti M. Design and Development of a Mathematical Model for an Industrial Process, in a System Dynamics Environment. Applied Sciences. 2022; 12(19):9855. https://doi.org/10.3390/app12199855
Chicago/Turabian StyleBarrios Sánchez, Jorge Manuel, Roberto Baeza Serrato, and Marco Bianchetti. 2022. "Design and Development of a Mathematical Model for an Industrial Process, in a System Dynamics Environment" Applied Sciences 12, no. 19: 9855. https://doi.org/10.3390/app12199855
APA StyleBarrios Sánchez, J. M., Baeza Serrato, R., & Bianchetti, M. (2022). Design and Development of a Mathematical Model for an Industrial Process, in a System Dynamics Environment. Applied Sciences, 12(19), 9855. https://doi.org/10.3390/app12199855





