Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet
Abstract
:1. Introduction
2. Materials and Methods
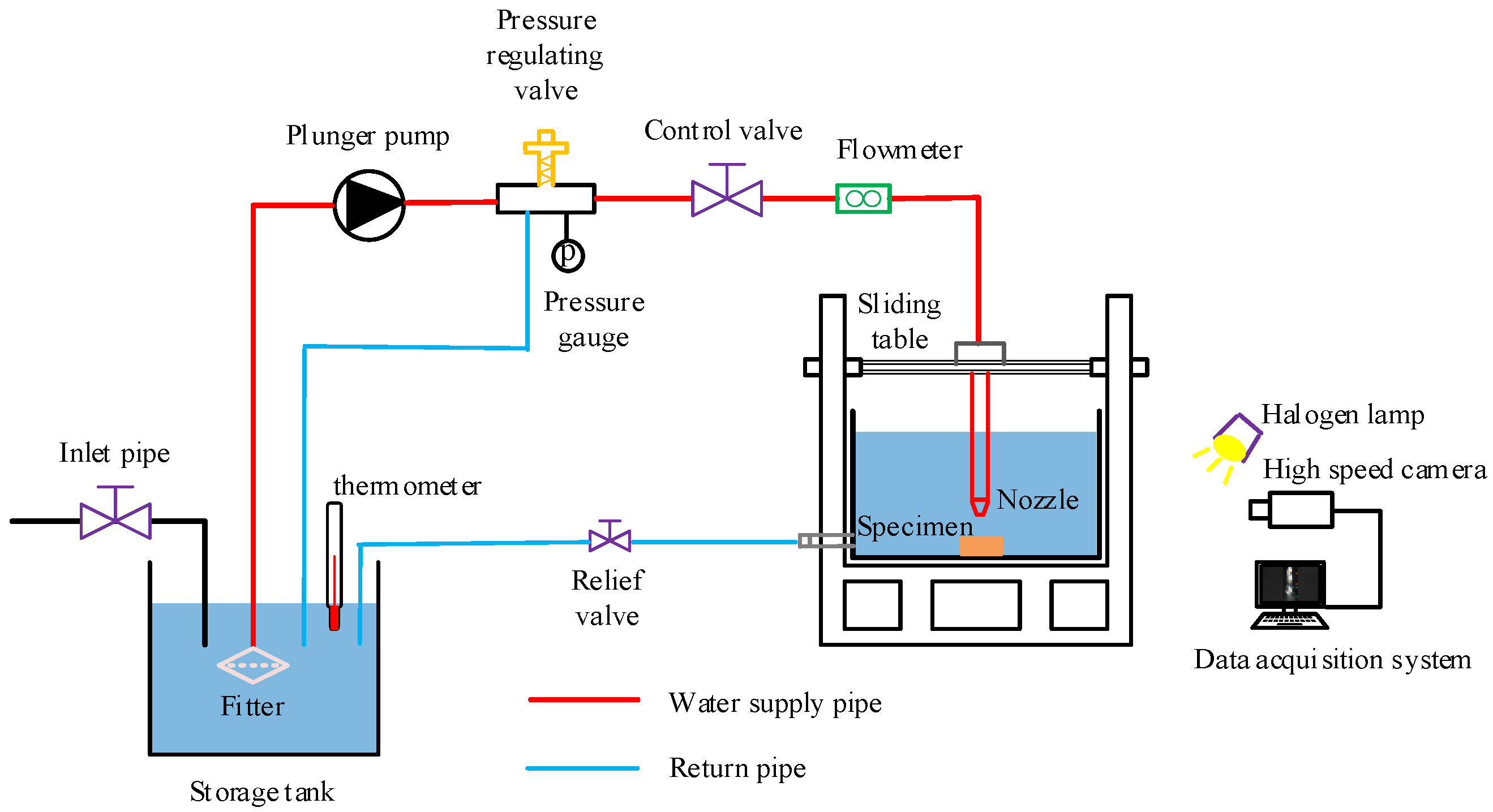
2.1. Experimental Setup
2.2. Image Analysis
2.3. Cavitation Intensity Evaluation
3. Results and Discussion
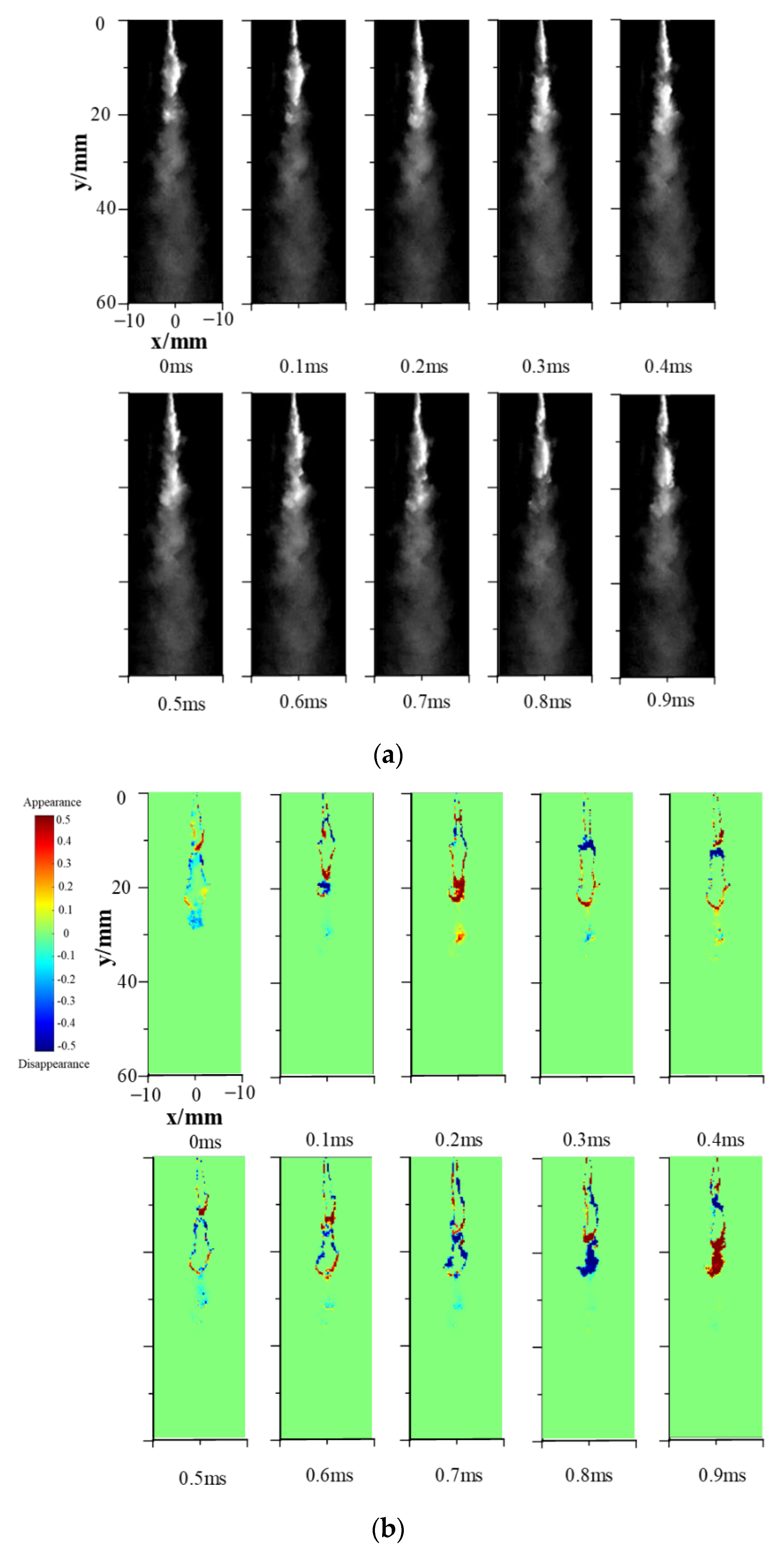
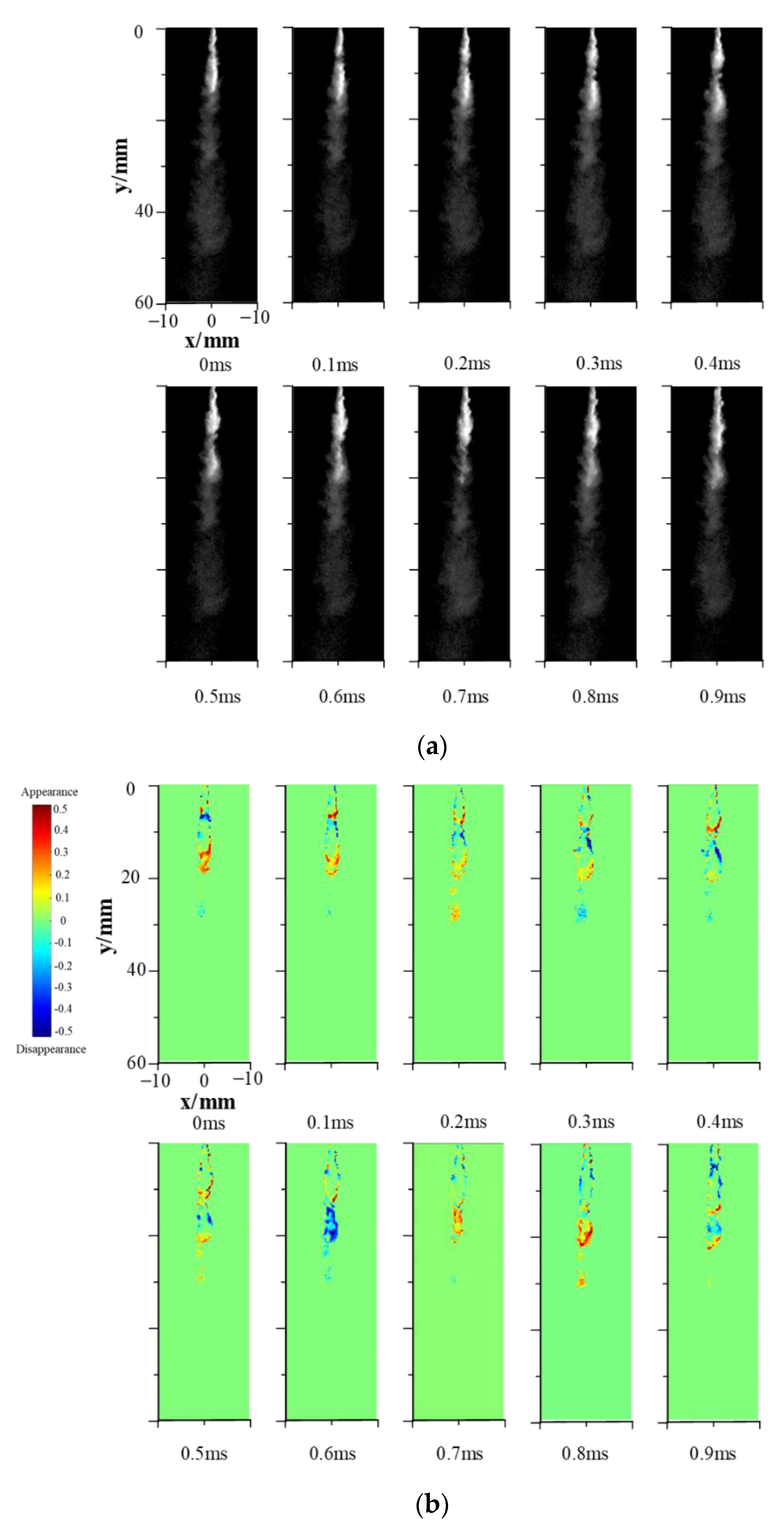
3.1. Dynamic Change in the Cavitation Cloud in a Single Period
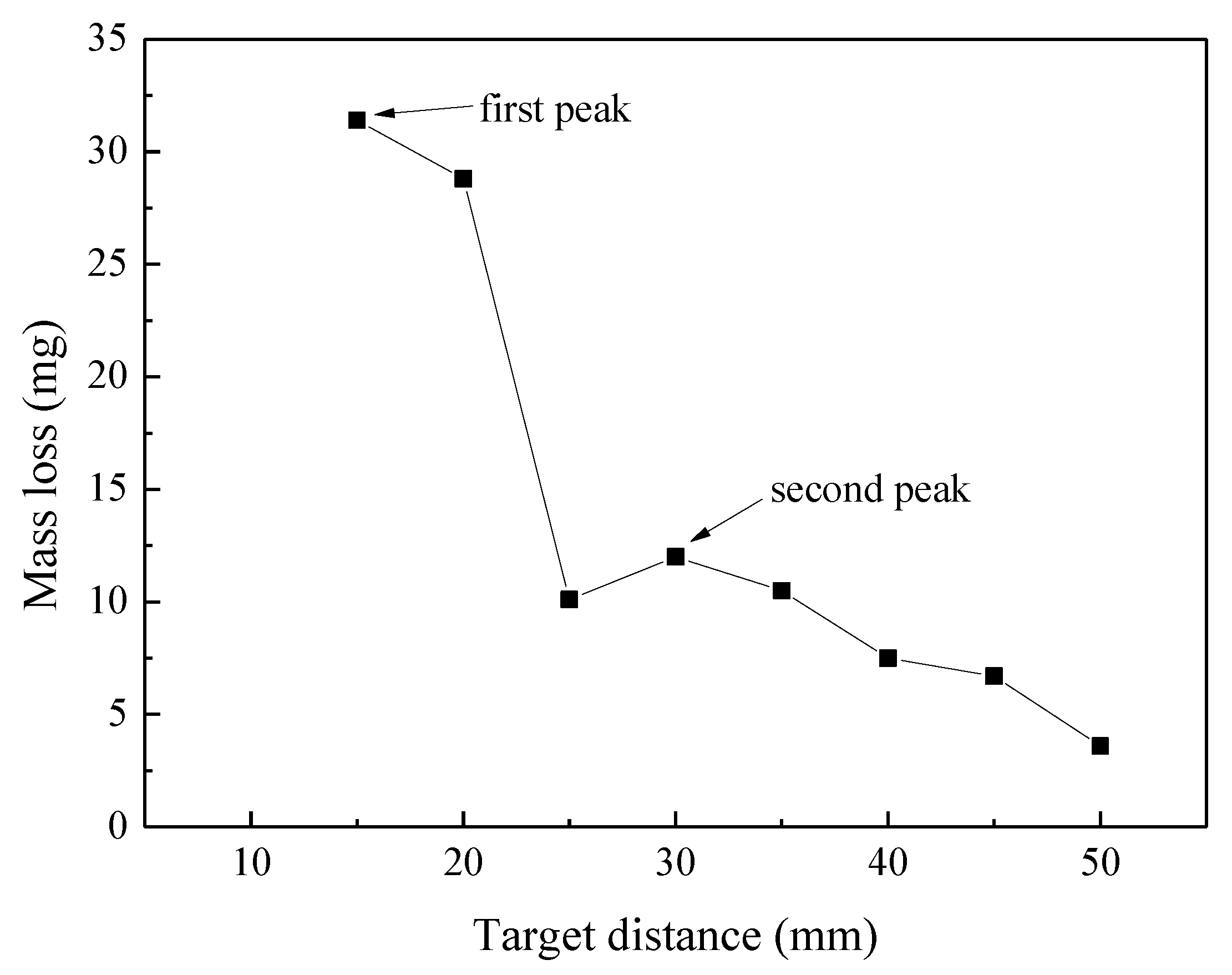
3.2. Macroscopic Evaluation of Cavitation Characteristics
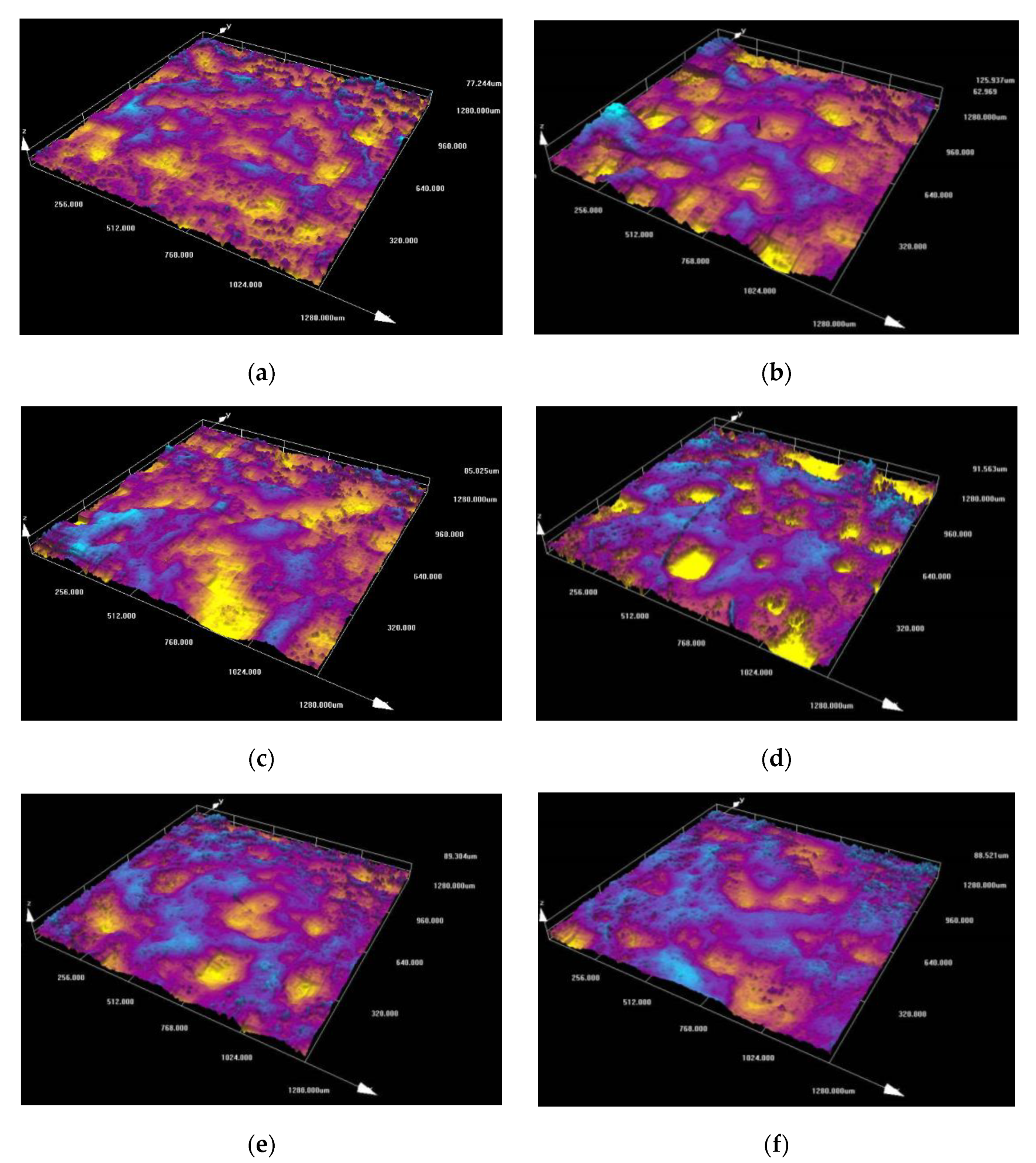
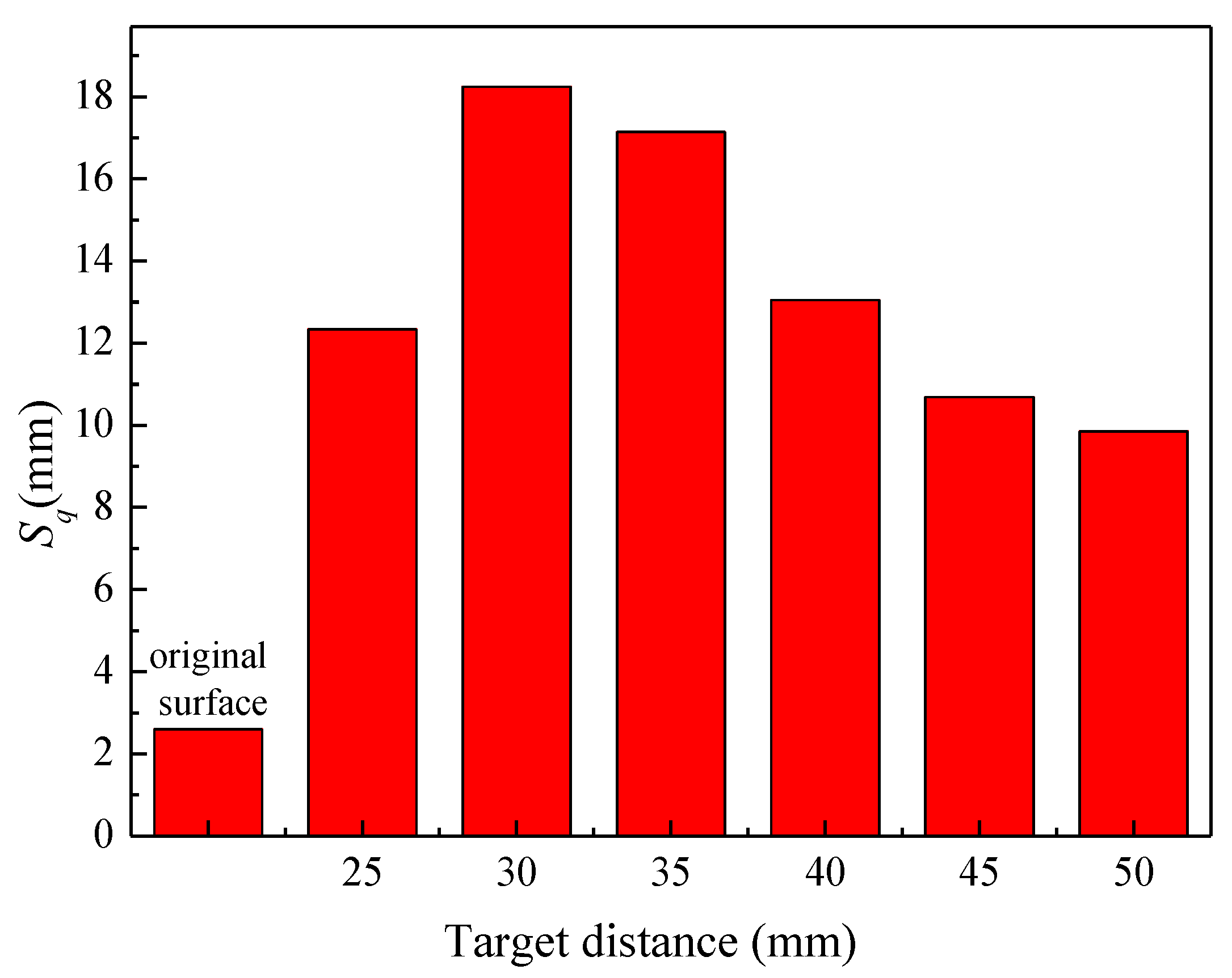
3.3. Microscopic Evaluation of Cavitation Characteristics
4. Conclusions
- (1)
- The two-throat nozzle submerged jet cavitation cloud has obvious periodicity. With the increase in inlet pressure, the length, width, and area of the cavitation cloud increased, and the period of the cavitation cloud was slightly prolonged.
- (2)
- With the increase in target distance, the cavitation intensity was enhanced and then weakened, and the effect of the high-speed water jet continued to decrease. In addition, the cavitation cloud fully developed and collapsed near the sample surface to achieve the maximum cavitation effect when the target distance was 30 mm.
- (3)
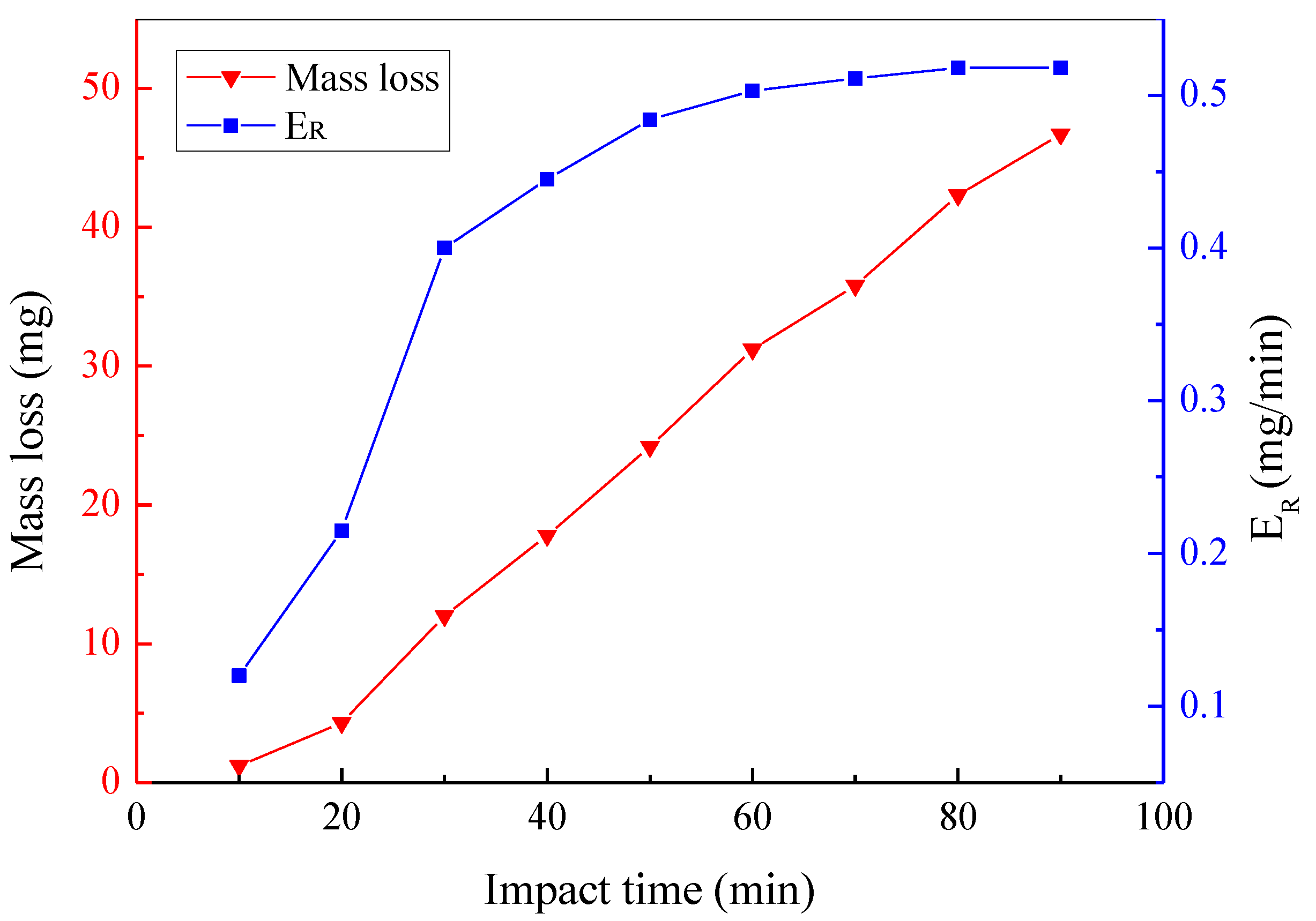
- As the impact time increased, the mass loss of the sample gradually increased. The mass loss rate first increased, then decreased, and finally stabilized.
- (4)
- From a microscopic point of view, the large cavitation pits were highly overlapping regions of cavitation collapse. The magnitude of the absolute values of the RMS surface roughness and surface skewness increased with the increase in cavitation intensity.
Author Contributions
Funding
Conflicts of Interest
References
- Hua, J.; Chiu, Y.S.; Tsai, C.Y. En-route operated hydroblasting system for counteracting biofouling on ship hull. Ocean Eng. 2018, 152, 249–256. [Google Scholar] [CrossRef]
- Bax, N.; Williamson, A.; Aguero, M.; Gonzalez, E.; Geeves, W. Marine invasive alien species: A threat to global biodiversity. Mar. Policy 2003, 27, 313–323. [Google Scholar] [CrossRef]
- Godwin, L.S. Hull Fouling of Maritime Vessels as a Pathway for Marine Species Invasions to the Hawaiian Islands. Biofouling 2003, 19, 123–131. [Google Scholar] [CrossRef]
- Choi, J.K.; Chahine, G.L. Relationship between material pitting and cavitation field impulsive pressures. Wear 2016, 352, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Liu, G.; Yan, Z. Study on cleaning effect of different water flows on the pulsed cavitating jet nozzle. Shock Vib. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Yamauchi, Y.; Soyama, H.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R. Suitable region of high-speed submerged water jets for cutting and peening. JSME Int. J. 1995, 38, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Soyama, H. Comparison between the improvements made to the fatigue strength of stainless steel by cavitation peening, water jet peening, shot peening and laser peening. J. Mater. Process. Technol. 2018, 269, 65–78. [Google Scholar] [CrossRef]
- Peng, K.; Tian, S.; Li, G.; Huang, Z.; Zhang, Z. Cavitation in water jet under high ambient pressure conditions. Exp. Therm. Fluid Sci. 2017, 89, 9–18. [Google Scholar] [CrossRef]
- Liu, W.; Kang, Y.; Zhang, M.; Wang, X.; Li, D.; Xie, L. Experimental and theoretical analysis on chamber pressure of a self-resonating cavitation waterjet. Ocean Eng. 2018, 151, 33–45. [Google Scholar] [CrossRef]
- Pan, Y.; Ma, F.; Liu, B.; Cai, T. Cavitation intensity and erosion pattern of a self-excited cavitating jet. J. Mater. Process. Technol. 2020, 282, 116668. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, H.; Wei, K. Resistance of curved surfaces to the cavitation erosion produced through high-pressure submerged waterjet. Wear 2019, 440, 203091. [Google Scholar] [CrossRef]
- Liu, H.; Kang, C.; Soyama, H. Experimental study of the influence of test chamber dimensions on aggressive intensity of the cavitating jet. J. Test. Eval. 2019, 48, 3588–3601. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.S.; Bonyar, A.; Legrady, D. Experimental study on the influence of geometrical parameters on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2017, 80, 281–292. [Google Scholar] [CrossRef] [Green Version]
- Soyama, H. High-Speed Observation of a Cavitating Jet in Air. J. Fluids Eng. 2005, 127, 1095–1101. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.S. Frequency in shedding/discharging cavitation clouds determined by visualization of a submerged cavitating jet. J. Fluids Eng. 2008, 130, 021304. [Google Scholar] [CrossRef]
- Petkovsek, M.; Dular, M. Simultaneous observation of cavitation structures and cavitation erosion. Wear 2013, 300, 55–64. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.; Li, G. Joint experiments of cavitation jet: High-speed visualization and erosion test. Ocean Eng. 2018, 149, 1–13. [Google Scholar] [CrossRef]
- Watanabe, R.; Yanagisawa, K.; Yamagata, T.; Fujisawa, N. Simultaneous shadowgraph imaging and acceleration pulse measurement of cavitating jet. Wear 2016, 358–359, 72–79. [Google Scholar] [CrossRef]
- Fujisawa, N.; Fujita, Y.; Yanagisawa, K.; Fujisawa, K. Simultaneous observation of cavitation collapse and shock wave formation in cavitating jet. Exp. Therm. Fluid Sci. 2018, 94, 159–167. [Google Scholar] [CrossRef]
- Fujisawa, N.; Kikuchi, K.; Fujisawa, K.; Yamagata, T. Time-resolved observations of pit formation and cloud behavior in cavitating jet. Wear 2017, 386-387, 99–105. [Google Scholar] [CrossRef]
- Cai, T.; Pan, Y.; Ma, F. Effects of nozzle lip geometry on the cavitation erosion characteristics of self-excited cavitating waterjet. Exp. Therm. Fluid Sci. 2020, 117, 110137. [Google Scholar] [CrossRef]
- Soyama, H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet. Wear 2013, 297, 895–902. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Yuan, M.; Fan, Q.; Wang, X. Effects of nozzle exit angle on the pressure characteristics of SRWJs used for deep-hole drilling. Appl. Sci. 2019, 9, 155. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.; Pan, Y.; Ma, F.; Xu, P. Effects of organ-pipe chamber geometry on the frequency and erosion characteristics of the self-excited cavitating waterjet. Energies 2020, 13, 978. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Hu, Y.; Chen, S.; Zhou, L.; Xu, W.; Lien, F. Investigation of self excited oscillation chamber cavitation effect with special emphasis on wall shape. Trans. Can. Soc. Mech. Eng. 2019, 44, 244–255. [Google Scholar] [CrossRef]
- Fang, Z.; Kang, Y.; Yang, X.; Yuan, B.; Li, D. The influence of collapse wall on self-excited oscillation pulsed jet nozzle performance. IOP Conf. Ser. Earth Environ. Sci. 2013, 15, 052022. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.; Liu, W. Experimental study on the effects of feeding pipe diameter on the cavitation erosion performance of self-resonating cavitating waterjet. Exp. Therm. Fluid Sci. 2017, 82, 314–325. [Google Scholar] [CrossRef]
- Yuan, M.; Li, D.; Kang, Y.; Shi, H. The characteristics of self-resonating jet issuing from the helmholtz nozzle combined with a venturi tube structure. Appl. Fluid Mech. 2020, 13, 779–791. [Google Scholar] [CrossRef]
- Chi, B. World’s first eject cycle for denso’s transport refrigerator. Refrig. Technol. 2008, 28, 19–26. [Google Scholar]
- Huang, K.; Guo, X.; Zhang, P. Influence of Structural Parameters of Two-throat Nozzle Ejector on Performance of Two-phase Flow Ejector Refrigeration System. Energy Procedia 2017, 105, 5091–5097. [Google Scholar] [CrossRef]
- Sato, K.; Sugimoto, Y.; Ohjimi, S. Pressure-wave formation and collapses of cavitation clouds impinging on solid wall in a submerged water jet. In Proceedings of the 7th International Symposium on Cavitation, Ann Arbor, MI, USA, 17–22 August 2009. [Google Scholar]
- Momma, T.; Lichtarowicz, A. A study of pressures and erosion produced by collapsing cavitation. Wear 1995, 186, 425–436. [Google Scholar] [CrossRef]
- Soyama, H.; Yamauchi, Y.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R. High-Speed observations of the cavitation cloud around a high-speed submerged water jet. JSME INT J B-FLUID T 2008, 22, 1919–1924. [Google Scholar]
- Soyama, H. Surface mechanics design of metallic materials on mechanical surface treatments. Mech. Eng. Rev. 2015, 2, 14-00192. [Google Scholar] [CrossRef] [Green Version]
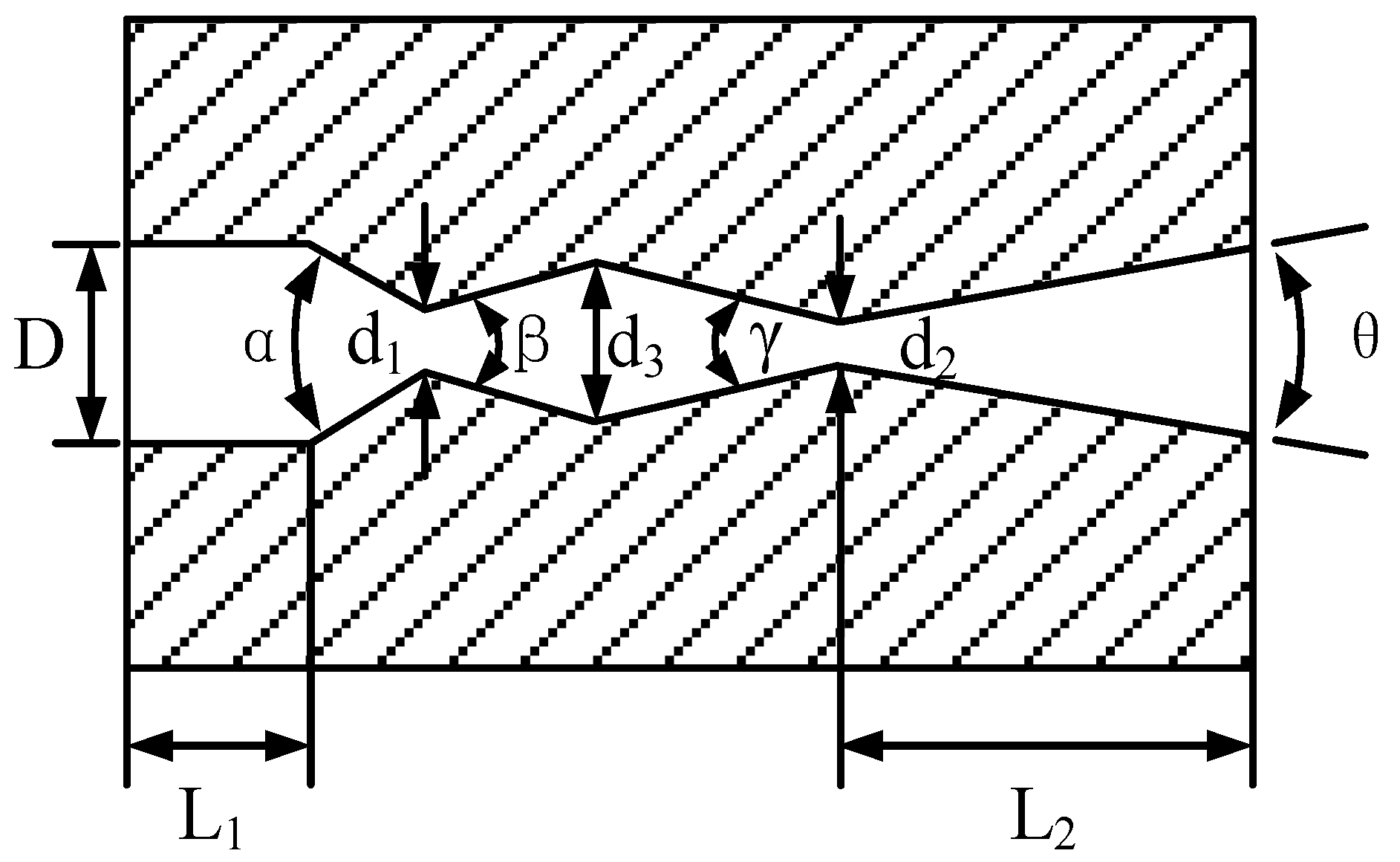





| Parameter Description | Symbol | Value | Units |
|---|---|---|---|
| First throat diameter | d1 | 1.5 | mm |
| Second throat diameter | d2 | 1.0 | mm |
| Connection diameter | d3 | 4 | mm |
| Inlet diameter | D | 5 | mm |
| Entrance length | L1 | 5 | mm |
| Length of outlet diffusion angle | L2 | 11 | mm |
| First throat inlet constriction angle | α | 60 | ° |
| First throat outlet diffusion angle | ß | 30 | ° |
| Second throat inlet constriction angle | γ | 27 | ° |
| Second throat outlet diffusion angle | θ | 20 | ° |
| Al | Si | Cu | Mg | Zn | Mn | Ti | Fe |
|---|---|---|---|---|---|---|---|
| 99.6 | ≤0.25 | ≤0.05 | ≤0.03 | ≤0.05 | ≤0.03 | ≤0.03 | ≤0.35 |
| Density/kg·m−3 | Elasticity Modulus/GPa | Tensile Strength/MPa | Offset Yield Stength/MPa | Surface Roughness/μm | Vickers Hardness HV0.2 |
|---|---|---|---|---|---|
| 2710 | 71 | 80 | 35 | 1.5 | 31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Li, S.; Meng, R.; Zhong, X.; Pan, X. Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet. Appl. Sci. 2022, 12, 536. https://doi.org/10.3390/app12020536
Dong J, Li S, Meng R, Zhong X, Pan X. Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet. Applied Sciences. 2022; 12(2):536. https://doi.org/10.3390/app12020536
Chicago/Turabian StyleDong, Jingming, Shuai Li, Rongxuan Meng, Xiao Zhong, and Xinxiang Pan. 2022. "Research on Cavitation Characteristics of Two-Throat Nozzle Submerged Jet" Applied Sciences 12, no. 2: 536. https://doi.org/10.3390/app12020536






