Identification of Track Stability Model Parameters Based on Numerical Experiments

Abstract

In the article, an identification method of railway track stability model parameters based on energy equilibrium is presented by the authors. A study of two parameters directly influencing the continuous welded track (CWR) stability is described by the authors, i.e., the rail-sleeper structure stiffness B_z is considered one beam, and the ballast lateral resistance r₀. These parameters were estimated with the use of a numerical model for various railway track types. The adopted concept is based on the assumption that it is possible to determine substitute values for both parameters. Therefore, using one value of both of these parameters, we label them substitute parameters. The assumed numerical model forced lateral displacements of a track section, and, based on the obtained track section displacement results, energy equilibrium was determined. The equilibrium takes into account the work of external load and the bending work of rail-sleeper structure with the substitute stiffness B_z and the ballast deformation work, also with the substitute value of lateral resistance r₀ with lateral displacement. The aim is to identify these substitute values to be used for analysing track stability with the semi-analytical model. These analyses are part of the studies related to the development of a method of assessing various methods of increasing track stability.

1. Introduction

The issue of continuous welded rail (CWR) track stability, both straight and curved, has been the subject of many scientific and technical studies.

Track stability loss can take place on two planes—vertical and horizontal. Rail bending stiffness value along the x axis is much bigger, and dead weight of the rail-sleeper structure is also important. Therefore, track deformations most frequently take place laterally to the axis [1]. The buckling wave usually is from 0.3 to 0.5 m, and it appears in a section of 8–20 m, although there have been cases recorded of it reaching even 1 m. Before buckling, smaller track deformations may also appear, the length of which is much smaller [2,3]. By formulating the criteria of track stability taking into consideration the required level of safety factors, it is possible to perform a pre- and post-buckling analysis of the track. The analysis of railway track stability was presented, i.a., in articles [4,5]. The issue of CWR track stability generally is related to the horizontal plane. The analysis of track stability on the vertical plane is discussed in articles [6,7], and the analysis of the impact of vertical loads on the stability is presented in articles [8,9,10].

Experimental studies are related to the determination of ballast resistances—lateral and longitudinal in relation to track axis, less often to artificial track buckling. The experiments are also related to the studies aimed at assessing the effectiveness of applying various methods of structural strengthening to increase track stability. However, theoretical analyses, including the improvement of calculation models, are necessary for assessing the degree of stability of a used CWR track. This is related specifically to the assessment of various methods of decreasing the risk of losing stability [11].

Railway track is a complex mechanical system. If a vehicle–railway track system, in which the vehicle is moving with constant speed, is included in the deliberations, a mechanical system with multiple degrees of freedom can be obtained [12]. In such a system, due to dynamic stability, there are many critical configurations and speeds.

When analysing a CWR track as a rail beam on an elastic foundation loaded with a concentrated force system (these forces reflect the pressure from the wheels of a train), the interaction of railway track structure with the foundation during train passage is taken into consideration. Directly under the wheels, the lateral resistance is increased as a result of applying vertical force. It is different in the mid-section between the wheels, in which the track is elevated and lateral resistances are decreased. As a result, the track in the area with the train is more vulnerable to deformations. This may cause the loss of stability of the railway track’s structure, and buckling. This means that vertical load from vehicles has a significant influence on the analysis of track stability in the lateral dimension [4].

A semi-analytical approach for the analysis of track stability in the horizontal plane is based on two concepts:

(1)

Analysis of a substitute beam, where rail-sleeper structure bending stiffness is described by EI_z (E—Young’s modulus of rail steel) and the substitute moment of inertia I_z is determined by experiments (physical or numerical, e.g., [5] presented paper);

(2)

Analysis of a substitute beam, where rail-sleeper structure stiffness is equal 2EI_st (I_st—moment of inertia of one rail on the horizontal plane) and unit stiffness of rotation in fasteners s* decrease thermal force in rails (e.g., [7,13]).

In the second case, the differential equation has the form:

$$\left(2·\mathrm{E}·{\mathrm{I}}_{\mathrm{st}}\right)·\frac{{\mathrm{d}}^4\mathrm{y}}{{\mathrm{dx}}^4}+\left(\mathrm{N}·{\mathrm{s}}^{*}\right)·\frac{{\mathrm{d}}^2\mathrm{y}}{{\mathrm{dx}}^{2 }}+\mathrm{F}\left(\mathrm{y}\right)=0$$

(1)

where

F—describes ballast resistance as a function of lateral displacements;

s*—stiffness of rotation in fasteners;

E—Young’s modulus of rail steel;

I_st—moment of inertia of one rail on the horizontal plane;

N—thermal force in rails.

In European conditions, as shown in many experiments (comp. [14,15]), the function F, besides the initial part of characteristics, may be treated as constant ballast resistance. This assumption is reasonable in the analysis of large lateral displacements, which occur for buckled track.

In both concepts, linear resistance is assumed in the longitudinal direction. These are also known in the papers in which constant ballast resistance is assumed (comp. e.g., [7]).

The calculations made by the authors have shown that the equilibrium paths (stable and unstable track positions) obtained by using unit stiffness s* and substitute moment of inertia I_z (for the same values of other track parameters) are similar. It is clear that by introducing a steel slab in the central zone of track, an increase in horizontal bending stiffness is obtained by a different mechanism than with the increase in the torsional resistance of fasteners. Therefore, the concept of substitute bending stiffness is justified in estimating this effect for this reinforcement.

In the numerical model analysed in this paper, experimental characteristics of fasteners (longitudinal and torsional resistances), as well as experimental characteristics of ballast were applied. Therefore, the substitute parameters (rail-sleeper structure bending stiffness and ballast resistance) were identified by comparing the energy of deformation of the numerical model (real fasteners and ballast characteristics) with the energy of deformation of a simple beam with substitute bending stiffness and energy of deformation of beam foundation with substitute constant resistance, which should be considered a good estimation of basic parameters of the proposed simplified semi-analytical model. This model will be used for the assessment of the effect to introduce various methods of track reinforcement to increase its stability during service.

There are many articles, e.g., [16,17], describing studies of railway track stability, and most of the presented studies are limited to vertical or horizontal planes, i.e., to a 2D model with the application of simple beams; however, some references present solutions with 3D models.

The results of a 3D model of a CWR track, which assesses the influence of various structural elements, such as rails, sleepers, fastening system elements, and ballast layer on track stability, is described in [16]. Studies prove that some parameters, such as the type of sleepers used in the track, fastening system torsional stiffness, as well as ballast stiffness, do not have a big influence on CWR track buckling. However, the type of the used rail and ballast resistance influence the buckling temperature, and therefore they should be considered in detail at the design stage, mostly of newly constructed tracks with lesser ballast resistance and small radius curves.

Another model for the non-linear track analysis is the model described in [17], which describes a three-dimensional model of a CWR track. The numerical model presented in [17] can be applied both for the analysis of straight sections and the curves of a CWR track, which are subjected to thermal load. This solution is general enough to be applied for all conditions on the track.

In this paper, the method of identification of two basic parameters influencing the stability of a CWR track on the horizontal plane, i.e., the lateral resistance of ballast r₀ and the stiffness of rail-sleeper structure B_z, is presented. The rail-sleeper structure (sleepers, fastening systems, and rails) is treated as a beam; therefore, it is possible to use the notion of substitute stiffness in the context of the whole system. The essence of the concept is based on the assumption that it is possible to determine substitute values for both of these parameters. This applies to both the stable and unstable conditions of track equilibrium, i.e., the whole equilibrium path. Lateral resistance of ballast r₀ depends on lateral displacement. However, to estimate the effect of the selected methods of track reinforcement on track stability, a constant r₀ value (independent from lateral displacement) is introduced into the track model. It was also assumed that both of these basic parameters are constant throughout the track. Therefore, using one value of both of these parameters, they were labelled as substitute parameters. In a numerical model, the experimental characteristics of the fastening system (longitudinal resistance and rail torsional resistance), as well as the experimental characteristics of ballast (lateral resistance and longitudinal resistance), were taken into consideration. In reference to rail and sleepers, geometrical characteristics—simplified in relation to the real ones—and real material parameters were assumed. By forcing a lateral displacement of a track section, energy equilibrium was determined, taking into account the work of external load and the bending work of a rail-sleeper structure with substitute stiffness B_z and the work of ballast deformation, also with the substitute value of lateral resistance r₀ with lateral displacement. The aim was to identify these substitute values, which could be used for the analysis of track stability with the application of the analytical model. The energy equilibrium skips the work related to longitudinal resistances of the fastening system and the ballast, and the torsional resistance of a fastened rail—the resistances of the fastening system (specifically the torsional resistance) are taken into consideration in the substitute stiffness of the rail-sleeper structure bending on the horizontal plane. The longitudinal displacement of the ballast and the fastening system in the energy equilibrium were skipped due to their significantly lower value in relation to lateral displacements.

The substitute stiffness of the rail-sleeper structure is determined as a product of the substitute moment of inertia Iz (m⁴) and Young’s modulus of rail steel E (kN/m²). The substitute moment of inertia was determined based on numerical data and physical experiments. It is estimated that in the case of a rail-sleeper structure with beam sleepers without reinforcement in the horizontal direction, the substitute moment of inertia is two to four times greater than the total of moments of inertia of two rails [5].

$$\left({\mathrm{I}}_{\mathrm{z}}=\left(2÷4\right)·2·{\mathrm{I}}_{\mathrm{st}}\right)$$

(2)

where

I_z—substitute moment of inertia of the rail-sleeper structure;

I_st—moment of inertia of one rail on the horizontal plane.

However, the values of lateral resistances of the ballast depend on a great number of factors, i.a., the stage of track operation and the processes of repairing it, the vertical load, or the type of the sleeper used. In light of the above, it is difficult to unambiguously determine the value of this resistance. The values of lateral resistances of the ballast assumed in analytical calculations correspond to their different conditions, and they were selected in a way allowing for the comparison of the influence of the degree of ballast stabilisation on track stability, and for the comparison of various types of tracks in similar technical conditions (with similar level of stabilisation) [15].

The goal of this paper is to present the method of identification of two basic parameters influencing the stability of a CWR track on the horizontal plane; i.e., the lateral resistance of ballast r₀ and the stiffness of rail-sleeper structure B_z.

2. Description of the Assumed Semi-Analytical Model

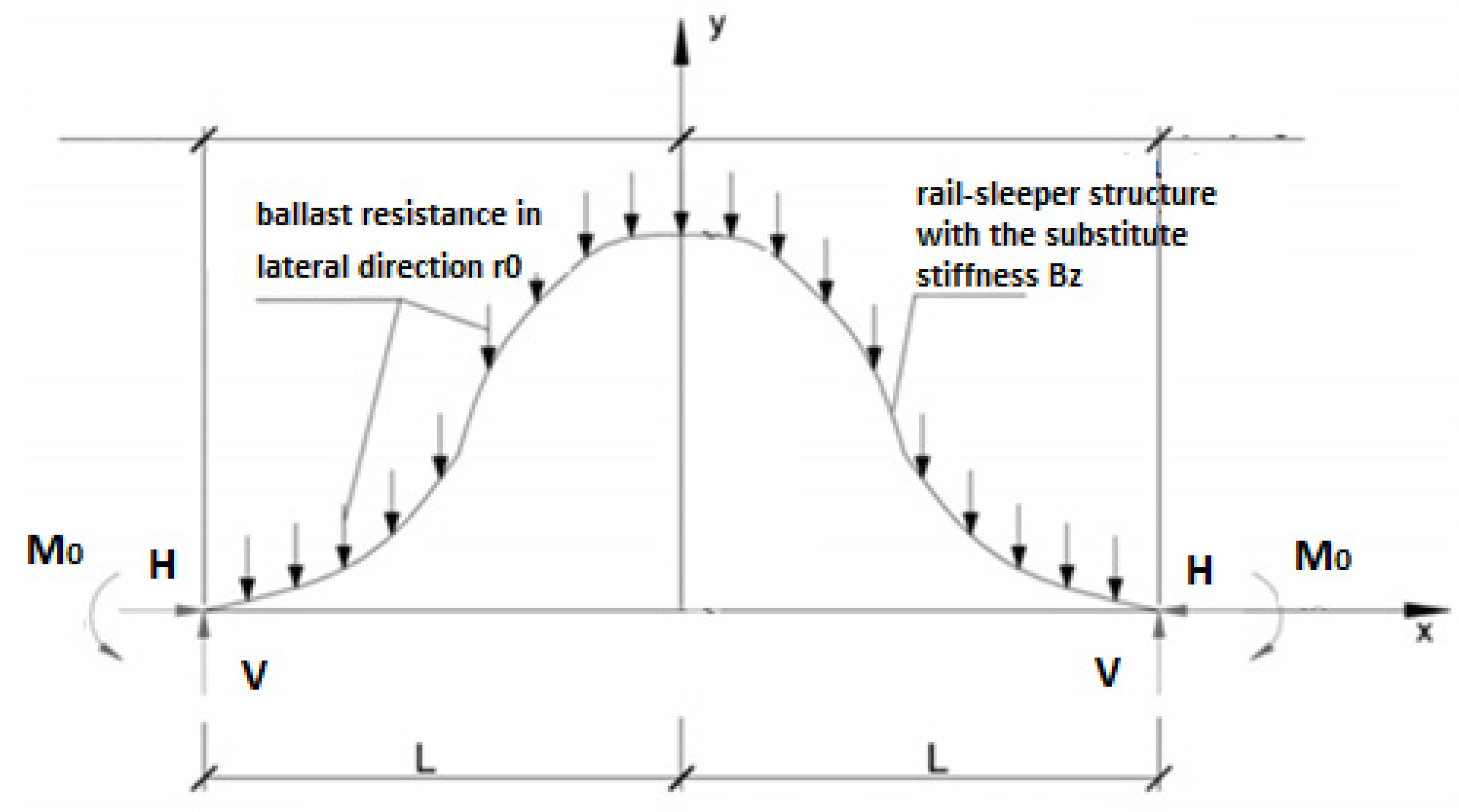
The applied model is an expansion of Huber’s work [6]. Huber’s work was related to vertical planes, and this method was adapted to the horizontal plane [5]. In the presented calculation model, a coordinate system (x,y) was assumed, which determines symmetry according to the y axis. The length of the deformation wave is 2 L, and the maximum displacement δ will take place in the middle part of the system. At the ends of a buckled section, there are reactions: from lateral forces V, horizontal forces H, which are different from the values of longitudinal forces in beam N, and bending moment M₀ [5]. The assumed model is presented in Figure 1.

• In the analyses, the following assumption was introduced: ballast resistance in lateral direction r₀ (kN/m) has constant value, independent from x and the lateral displacement y;
• Longitudinal resistance of beam has elastic character, described with the constant $\mathrm{k}$ (kN/m²), in the beam deformation zone this resistance was skipped—it is present only in sections adjacent to the deformation zone;
• Rails create a substitute beam with bending stiffness B (kN/m²);
• Area of cross-section of substitute beam A (m²) is equal to the sum of the areas of cross-sections of two rails;
• Thermal force and force other than thermal N (kN) are applied along the beam;
• Equilibrium for unstable and pre-buckling equilibrium path of CWR track is a symmetrical system in relation to point x = 0 of the assumed coordinate system.

Basic equation of the equilibrium for system has a well-known simplified form:

$$\mathrm{B}· \mathrm{y}″=-\mathrm{M}\left(\mathrm{x}\right)$$

(3)

where the bending moment describes the formula (comp. Figure 1):

$$\mathrm{M}\left(\mathrm{x}\right)={\mathrm{M}}_0+0.5·{\mathrm{r}}_0·{\left(\mathrm{L}-\mathrm{x}\right)}^2-{\mathrm{r}}_0·\mathrm{L}·\left(\mathrm{L}-\mathrm{x}\right)+\mathrm{H}·\mathrm{y}$$

(4)

After simple transformations, one can obtain:

$$\mathrm{M}\left(\mathrm{x}\right)={\mathrm{M}}_0+0.5·{\mathrm{r}}_0·{\mathrm{x}}^2-0.5·{\mathrm{r}}_0·{\mathrm{L}}^2+\mathrm{H}·\mathrm{y}$$

(5)

Substituting formula (5) to Equation (3), after rearrangement and knowing that M₀ = 0 (comp. [6]), differential equation of the system has the form:

$$\mathrm{y}″+{\mathsf{\omega }}^2·\mathrm{y}=\mathsf{\Psi }\left(\mathrm{x}\right)$$

(6)

where

$${\mathsf{\omega }}^2=\frac{\mathrm{H}}{\mathrm{B}}$$

(7)

$$\mathsf{\Psi }\left(\mathrm{x}\right)=\frac{1}{\mathrm{B}}·\left[-0.5·{\mathrm{r}}_0·{\mathrm{x}}^2+0.5·{\mathrm{r}}_0·{\mathrm{L}}^2\right]$$

(8)

H—horizontal reaction on the ends of the buckling zone ($\mathrm{H}\ne \mathrm{N}$).

M₀—bending moment at the end of the deformed section,

L—half of the length of the deformed section,

r₀—lateral resistance

In considerations based on the general integral of homogeneous equation

$$\mathrm{y}={\mathrm{C}}_1·\cos \left(\mathsf{\omega }·\mathrm{x}\right)+{\mathrm{C}}_2\sin \left(\mathsf{\omega }·\mathrm{x}\right)$$

(9)

Its interpretation, transformation into a particular integral of nonhomogeneous equation in the form of quadratic function, and reaching the solution are significant [5]:

$$\mathrm{y}={\mathrm{C}}_1·\cos \left(\mathsf{\omega }·\mathrm{x}\right)+{\mathrm{C}}_2\sin \left(\mathsf{\omega }·\mathrm{x}\right)-\frac{{\mathrm{r}}_0}{2\mathrm{H}}·{\mathrm{x}}^2+\frac{1}{\mathrm{H}}\left(\frac{{\mathrm{r}}_0·{\mathrm{L}}^2}{2}+\frac{{\mathrm{r}}_0·\mathrm{B}}{\mathrm{H}}\right)$$

(10)

To solve the above equation and obtain the aforementioned system symmetry, the following boundary conditions are assumed:

$$\begin{gathered} \frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{x}=0\right)=0 \\ \mathrm{y}\left(\mathrm{x}=\mathrm{L}\right)=0 \end{gathered}$$

(11)

As in Equation (6), there are two parameters the values of which we do not know, i.e., force at the end of the buckled section H, and the length of the buckled section L, we need to assume an additional boundary condition. This condition is derivative zeroing at the end of the buckled section, i.e.,

$$\frac{\mathrm{dy}}{\mathrm{dx}}\left(\mathrm{x}=\mathrm{L}\right)=0$$

(12)

In order to determine the value of the reaction to the horizontal force at the end of the buckled section, the concept of longitudinal displacement compatibility was used. The original concept was described in [5] as an expansion of the works of Polish researchers, mostly of M.T. Huber [6]. According to this concept, the decrease in longitudinal force N in the sections adjacent to the buckling zone brings both cross-sections closer, limiting the deformation wave 2u₀. This means a decrease in the longitudinal force from the value equal to force N to the value equal to force H at the ends of the deformed section. Therefore, to determine the buckling length L, the following equation was used:

$${\mathrm{u}}_0={\mathrm{u}}_1-{\mathrm{u}}_2$$

(13)

where

u₁—displacement resulting from curving a part of track (without changes in length);

u₂—displacement resulting from decreasing the compression forces in the deformed section of the track.

The value of displacement u₀ can be determined with the equation for longitudinal displacement of the track:

$${\mathrm{u}}_0=\frac{\mathrm{N}-\mathrm{H}}{\sqrt{\mathrm{k}·\mathrm{EA}}}$$

(14)

The value of displacement u₁ can be determined from approximation between the length of the curve and its chord:

$${\mathrm{u}}_1=\frac{1}{2}·{\int }_0^{\mathrm{L}}{(\frac{\mathrm{dy}}{\mathrm{dx}})}^2\mathrm{dx}$$

(15)

The displacement resulting from decreasing the compression forces in the deformed section of the track is expressed by the formula:

$${\mathrm{u}}_2=\frac{\mathrm{NL}}{\mathrm{EA}}-\frac{\mathrm{HL}}{\mathrm{EA}}$$

(16)

By substituting the statements (14), (15), and (16) in the equation of longitudinal displacement compatibility (13), knowing that $\mathrm{N}=\mathsf{\alpha }·\mathrm{EA}·\mathsf{\Delta }\mathrm{T}$ and $\mathsf{\beta }=\sqrt{\frac{\mathrm{k}}{\mathrm{EA}}}$, the following equation is obtained:

$$\mathsf{\alpha }·\mathsf{\Delta }\mathrm{T}=\frac{1}{\left(\frac{1}{\mathsf{\beta }}+\mathrm{L}\right)}·\left[{\mathrm{u}}_1+\mathrm{H}·\left(\frac{\mathrm{L}}{\mathrm{EA}}+\frac{1}{\sqrt{\mathrm{k}·\mathrm{EA}}}\right)\right]$$

(17)

In the assumed procedure, the numerical calculations were skipped, force H was assumed—which enabled the determination of the character of the equilibrium path in different technical conditions.

In calculation analyses, the semi-analytical model developed in the Chair of Roads, Railways and Traffic Engineering, Faculty of Civil Engineering, Cracow University of Technology. The analyses were performed in Mathcad calculation software and—as an auxiliary—in Excel software. Figure 2 presents an example of determined equilibrium path with the lateral resistance of the ballast determined to be r₀ = 7 kN/m and different type rail-sleeper structure bending stiffness.

The presented chart shows the influence of the substitute moment of inertia on the growth of equivalent temperature. The chart shows that the lower the substitute moment of inertia of the rail-sleeper structure, the lower the minimum temperature in which track buckling may occur.

In the developed calculation model, track parameters were assumed according to literature, laboratory test results and field test results.

3. Description of the Assumed Numerical Model

In order to identify the data assumed in the analytical model, a numerical model was used—developed at the Chair of Roads, Railways and Traffic Engineering, Faculty of Civil Engineering, Cracow University of Technology. The analyses were performed in Autodesk Simulation Multiphysics 2013 calculation software and—as an auxiliary—in Excel software. The following type of analysis was performed: MES (Mechanical Event Simulation) with Nonlinear Material Models, using elements of the model—type 2-D (2D strain state).

To develop numerical models of track with a given structure, the following types of materials were used:

(1)

Elastic (isotropic) materials: rails, sleepers, selected parts of fastening system

• Density—ρ (kg/m³);
• Modulus of elasticity—E (N/mm²);
• Poisson’s Ratio—ν (−);
• Shear modulus of elasticity—G (N/mm²).

Table 1. Assumed data of the numerical model for elastic materials.

UIC 60 Rails	Sleepers	Fastening System–Rail Pad
steel	concrete	steel
ρ—7872 kg/m3	ρ—2351 kg/m3	ρ—7872 kg/m3
E—200,000 N/mm2	E—31,026,408 N/mm2	E—200,000 N/mm2
ν—0.29	ν—0.15	ν—0.29
G—80,000 N/mm2	G—13,489 N/mm2	G—80,000 N/mm2

presents the assumed data of the numerical model for elastic materials.

(2)

Elastic-plastic materials with reinforcement (two-line material) (von Mises with Isotropic Hardening): ballast and fastening system elements.

• Mass density—ρ kg/m³;
• Modulus of elasticity—E (N/mm²);
• Poisson’s Ratio—ν (−);
• Yield strength—σ_Y (N/mm²);
• Strain hardening modulus—E_T (N/mm²).

Table 2. Assumed data of the numerical model for elastic–plastic materials.

Loose Ballast	Medium-Stabilised Ballast	Fastening System
Substitute element	Substitute element	Substitute element
ρ—2351 kg/m3	ρ—2351 kg/m3	ρ—7872 kg/m3
E—1900 N/mm2	E—1900 N/mm2	E—2000 N/mm2
ν—0.25	ν—0.25	ν—0.25
σY—1.9 N/mm2	σY—2.7 N/mm2	σY—5.4 N/mm2
ET—1.8 N/mm2	ET—1.8 N/mm2	ET—10 N/mm2

presents the assumed data of the numerical model for elastic–plastic materials. Resistances of the ballast and of the fastening system both in the lateral and longitudinal directions are elastic in a very small range. The values of the parameters describing a given material in the model have been assumed in such a way that even with forcing small displacement, the results correspond to the shapes of the charts of experiments. The critical value in which material characteristics change is variable and depends on numerous factors. The range of the elastic zone of ballast response in lateral and longitudinal directions typically is 5 ÷ 7 mm. For the fastening system, the critical value of elastic response for longitudinal resistance is approximately 0.4 ÷ 0.6 mm.

The selection of the above material parameters was based on the charts of longitudinal resistance, lateral resistance, and torsional resistance of the fastening system, and the ballast resistance.

Rails were modelled as beams, determining the cross-section, moments of inertia, and Young’s modulus.

Fastening system parameters were selected in such a way that the characteristics of the longitudinal resistances and rotation moment of the model corresponded to the charts of elastic–plastic characteristics obtained as a result of experimental studies selected in literature review. The assumed longitudinal resistance and rotation characteristic of fastening system (Figure 3) of the fastening system were described with the use of a chart assumed on the basis of [5].

In order to obtain more accurate results, contact surfaces between the rails and the fastening system (e.g., anchor and steel plate) were used in the model Figure 4 presents the model and the details of the contact surface between the rail and the fastening system element.

Sleepers, as elements with variable cross-sections in their lengths, were modelled as beams consisting of two elements with different cross-sections and moments of inertia. Figure 5 presents the sleeper model.

Ballast parameters were selected in such a way that their behaviour corresponded to the lateral and longitudinal resistance curves obtained as a result of experimental studies selected in the literature review. The ballast was modelled as a 2D, non-linear substitute element. In the analysis, two experimental lateral ballast resistance characteristics were chosen for numerical analysis. Figure 6 presents these lateral ballast resistances curves.

Figure 7 presents the layout of the whole rail-sleeper ballast structure with external force assumed for calculations in the numerical model.

4. Energy Equilibrium as Identification Criterion

A series of experiments allowing for the identification of the two basic parameters (B_z and r₀) were performed with the application of the described numerical model.

Based on energy equilibrium equations, the work of force P (kN) resulting from the maximum displacement was determined, calculating energy of the system as a sum of the bending energy of the substitute beam and the work of ballast deformation in the lateral direction. On this basis, the substitute stiffness of the rail-sleeper structure with a given material solution (B_z) and the ballast resistance (r₀) were determined. In the equilibrium, the longitudinal track resistance parameters were neglected and only three elements were taken into account. The energy equation takes the following form:

$${\mathrm{W}}_{\mathrm{p}}={\mathrm{E}}_{\mathrm{zg}}+{\mathrm{E}}_{\mathrm{sp}}$$

(18)

where

$${ \mathrm{E}}_{\mathrm{zg}}=\frac{1}{2}·{\mathrm{B}}_{\mathrm{z}}{\int }_{-\infty }^{+\infty } \mathrm{y}″ \mathrm{dx}$$

(19)

$${\mathrm{E}}_{\mathrm{sp}}={\mathrm{r}}_0{\int }_{-\infty }^{+\infty }\mathrm{ydx}$$

(20)

$${ \mathrm{W}}_{\mathrm{p}}=\frac{\mathrm{P}·{\mathrm{y}}_{\max }}{2}$$

(21)

${\mathrm{E}}_{\mathrm{zg}}$—bending energy (N*m);

${\mathrm{E}}_{\mathrm{sp}}$—ballast deformation work in lateral direction (N*m);

${\mathrm{B}}_{\mathrm{z}}$—substitute stiffness of rail-sleeper structure (N*m²);

${\mathrm{r}}_0$—substitute lateral resistance of ballast (N/m);

${\mathrm{W}}_{\mathrm{p}}$—work of the external force P with the lateral displacement y (N*m);

$\mathrm{P}$—force (kN);

${\mathrm{y}}_{\max }$—maximum lateral displacement (mm).

For the assumed interval of admissible ranges of parameters B_z and r₀, the values of the left and right sides of the Equation (18) are comparable, and the differences are minimised. The energy equilibrium is formulated for a few (three to four) external forces. The lateral displacement function (20) and the second derivative (19) were calculated with the use of numerical data.

The analyses were performed for two types of tracks and two levels of ballast stabilisation. First, the basic rail-sleeper structure was analysed, i.e., rail, concrete sleepers, and the elastic fastening system. Afterwards, the reinforced rail-sleeper structure was analysed. The reinforcement was the introduction of steel slabs welded to flat bars and fastened to the sleepers with screws anchored in the sleepers, used in the type of sleepers for fastening guard rails on bridges (PS-94/M and PS-93/M sleepers). Flat bars approximately 12 mm thick and 400 mm width were welded to concrete sleepers in their lowered parts. Afterwards, after careful placement of the sleepers and track adjustment in the vertical and horizontal planes, slabs approximately 12 mm thick and 0.25 m wide were welded to the flat bars [18]. Figure 8 presents the reinforced rail-sleeper structure.

Additionally, both the loose ballast and the stable ballast were taken into consideration in the analyses [9].

For calculations the following Bz and r₀ parameter intervals were assumed:

(1)

For loose ballast:

(a)

Track without reinforcement:

• Lateral resistance of ballast r₀ ∈ (6.5 ÷ 8 kN/m);
• Substitute stiffness of rail-sleeper structure B_Z ∈ (7000 ÷ 9000 kNm²);

(b)

Track with reinforcement:

• Lateral resistance of ballast r₀ ∈ (6.5 ÷ 8 kN/m);
• Substitute stiffness of rail-sleeper structure B_Z ∈ (10,000 ÷ 30,000 kNm²);

(2)

For medium-stabilised and stable ballast:

(a)

Track without reinforcement

• Lateral resistance of ballast r₀ ∈ (11 ÷ 15 kN/m);
• Substitute stiffness of rail-sleeper structure B_Z ∈ (7000 ÷ 9000 kNm²);

(b)

Track with reinforcement

• Lateral resistance of ballast r₀ ∈ (11 ÷ 15 kN/m);
• Substitute stiffness of rail-sleeper structure B_Z ∈ (10,000 ÷ 30,000 kNm²).

For the energy equilibrium, the results of track lateral displacements depending on the applied force and obtained in numerical calculations were used. Figure 9a,b and Figure 10a,b present the results of these calculations both for the track without reinforcement and with reinforcement.

As a result of the identification process the following parameters are obtained:

(1)

For loose ballast:

(a)

Track without reinforcement:

• Lateral resistance of ballast r₀ = 6.68 kN/m;
• Substitute stiffness of rail-sleeper structure B_Z = 8618.4 kNm²;

(b)

Track with reinforcement:

• Lateral resistance of ballast r₀ = 7.06 kN/m;
• Substitute stiffness of rail-sleeper structure B_Z = 23,928.69 kNm²;

(2)

For medium-stabilised and stable ballast:

(a)

Track without reinforcement

• Lateral resistance of ballast r₀ = 11.74 kN/m;
• Substitute stiffness of rail-sleeper structure B_Z = 8453.52 kNm²;

(b)

Track with reinforcement

• Lateral resistance of ballast r₀ = 12.15 kN/m;
• Substitute stiffness of rail-sleeper structure B_Z = 23,998.76 kNm².

The obtained values of substitute stiffness of the rail-sleeper structure B_z and lateral resistance of the ballast r₀ are in the admissible range assumed interval described below. The introduction of the steel slab in the central zone of the track as its reinforcement influences a significant increase in the substitute stiffness of the rail-sleeper structure (about 3 times), and the growth of maximum lateral displacement is more than 4 times higher. Maximum lateral displacements are 30–40% smaller in the cases with the medium stabilised ballast compared to the loose ballast.

The identified parameters of ballast lateral resistance for track with and without reinforcement are similar. For the loose ballast and in the case of medium stabilised and stable ballast, the reinforcement of the track causes the change in r₀ value from 6.68 kN/m to 7.06 kN/m (about 6%) and from 11.74 kN/m to 12.15 kN/m (about 3%), respectively. The conducted analyses show that a double increase in force P causes an increase in the deformation wave by over 30%. Reinforcement of the standard track (without reinforcement) changes the shape of track deformation, e.g., eliminates deflections in the direction opposite to the applied force, and diminishes a wave character of the response for the majority of parameters.

5. Summary

The conducted analyses prove that the energy equilibrium calculation results obtained by using the identified parameters r₀ and B_z or, alternatively, by considering various cases within a wide range of lateral displacements and lengths of deformation wave, are similar. These calculations show that the chosen substitute values of rail-sleeper structure stiffness B_z and lateral resistance of ballast r₀ describe the behaviour of track structure well enough. Therefore, it is possible to apply the semi-analytical model with these substitute parameters to assess the effectiveness of various methods of increasing track stability. Further investigations should be directed to the experimental validation of the range of the lateral track displacement and length of deformation, similar to the one considered in the numerical model.