Analytical Method for the Bending Resistance of Slim Floor Beams with Asymmetric Double-T Steel Section under ISO Fire

Featured Application

The simplified method can be used by practitioner engineers as a tool for computing the fire resistance of slim floor beams with double-T steel section.

Abstract

The slim floor beams, characterized by the steel profile embedded in the concrete slab, may be found in different configurations, based on the shape of the steel profile cross-section, which can vary from a rectangular to double-T section. While the most common shape used nowadays is the double-T cross-section, the Eurocodes do not provide a simplified method for the fire resistance assessment. The literature offers a simplified method for computation of bending resistance under elevated temperature, based on existing research on thermal models, and was validated for a particular type of slim floor beams (SFB). The current study extends the scope of application of this method, for different types of slim floor beam, which include an asymmetric double-T steel cross-section. The objective was reached through a numerical procedure, by analyzing 162 configurations subjected to four different fire requirements (R30, R60, R90, R120), resulting in a total of 648 analyses, performed with a validated numerical model in SAFIR software. The results in terms of bending resistance showed that the simplified method represents a strong tool for the fire design of slim floor beams.

1. Introduction

In slim floor (or shallow floor) systems, the beams are integrated in the thickness of the slab, thus reducing the height of the floor. The first slim floor system appeared in England during the last decade of the nineteenth century, as the Jack arch floor system [1], made of double-T section steel beams with flat masonry arches in-between. Although this flooring system was very popular [2], improvement has been made by replacing the masonry with the concrete material, which provides better behavior under horizontal dynamic loads [3].

Nowadays, there are different types of slim floor beam made of steel and concrete [4]. While in all existing configurations, the steel profile is embedded in the concrete slab, the shape of the steel profile cross-section can vary from rectangular [5,6,7] to double-T shapes [7,8,9,10,11]. However, the steel double-T cross-section remains the most widely used.

A common and economical slim floor beam configuration was developed by ArcelorMittal in the 1990s, consisting of a double-T profile with a welded plate underneath (SFB, slim floor beam) or of an asymmetric double-T profile with the bottom flange wider than the upper flange (IFB, integrated floor beam), as shown in Figure 1 [7]. The composite behavior is ensured by a concrete dowel, placed perpendicular to the steel profile web and embedded in the concrete poured in situ (Figure 2).

Other asymmetrical double-T steel beams can be realized by direct manufacturing (ASB type, Figure 3a) [12], by welded plates (Figure 3b), or by reducing the width of the top flange of a European H-profile (SB type, Figure 3d).

Slim floor systems present a series of advantages, among which are their inherent fire resistance, as the bottom flange is the unique part directly exposed to fire. Extensive experimental research has been conducted in the last decades [13,14,15], which demonstrated an enhanced fire resistance compared to the classical composite beams, without additional fire protection. The fire resistance of slim floor beams can be determined by numerical simulations or by experimental tests. Despite their popularity, the standards do not yet comprise a regulated method for the fire design of such elements. The Eurocodes offer the possibility to compute a mean value of temperature on the entire cross section of an element, based on its section factor. This method cannot be applied in case of slim floor beams, as the steel profile is embedded in concrete, thus resulting in temperature variation along the height.

Zaharia and Franssen [15] proposed a simplified method for calculating the temperature in the steel profile (on lower flange and along the web height) and in the rebars above the bottom flange. This method was developed based on numerical simulations of an IFB system, subjected to an ISO fire. Hanus et al. [16] proposed an improved equation to calculate the temperature in the reinforcement bars placed longitudinally. The set of equations was obtained from isotherms of the EN 1992-1-2 [17], used there for the computation of temperature on concrete element cross-sections. A correct evaluation of the rebars temperature is very important, especially for high fire resistance requirements. The temperature evolution on the lower plate and lower flange of an SFB type was analyzed by Cajot et al. [18] and Romero [19]. They noticed a positive influence of thermal resistance at the interface between the lower flange and the plate welded beneath [20].

Recently, Zanon et al. [21] presented a simplified method for the fire design of slim floor beams, based on the models existing in the literature, i.e., Zaharia and Franssen [15], Hanus et al. [16], Cajot [18] and Romero et al. [19]. The authors [21] integrated the previously developed equations, and proposed a unitary concept with some adaptations to ensure consistency of results within the given field of application.

Zanon et al. [21] validated the method with a comprehensive analysis of tests and a broad numerical parametric study, but only for one type of slim floor beams(SFB type, which consists in a double-T profile with a supplementary wider plate welded below the bottom flange). The current study aims to extend the scope of application of Zanon et al.’s [21] method for different configurations of slim floor beams, made of asymmetric double-T steel cross-sections, in which no supplementary plate is welded on the bottom of the profile. The objective was reached through a numerical procedure, by analysing 162 configurations subjected to four different fire requirements (R30, R60, R90, R120) resulting in a total of 648 numerical analyses. Simulations were carried out with the SAFIR software, using a validated numerical model, and existing experimental data from the literature [13]. The study covers the configurations presented in Figure 3.

2. Validation of the Numerical Model

The numerical simulations were performed with the SAFIR software [22]. The numerical model was validated against two previous experimental tests existing in the literature [23,24].

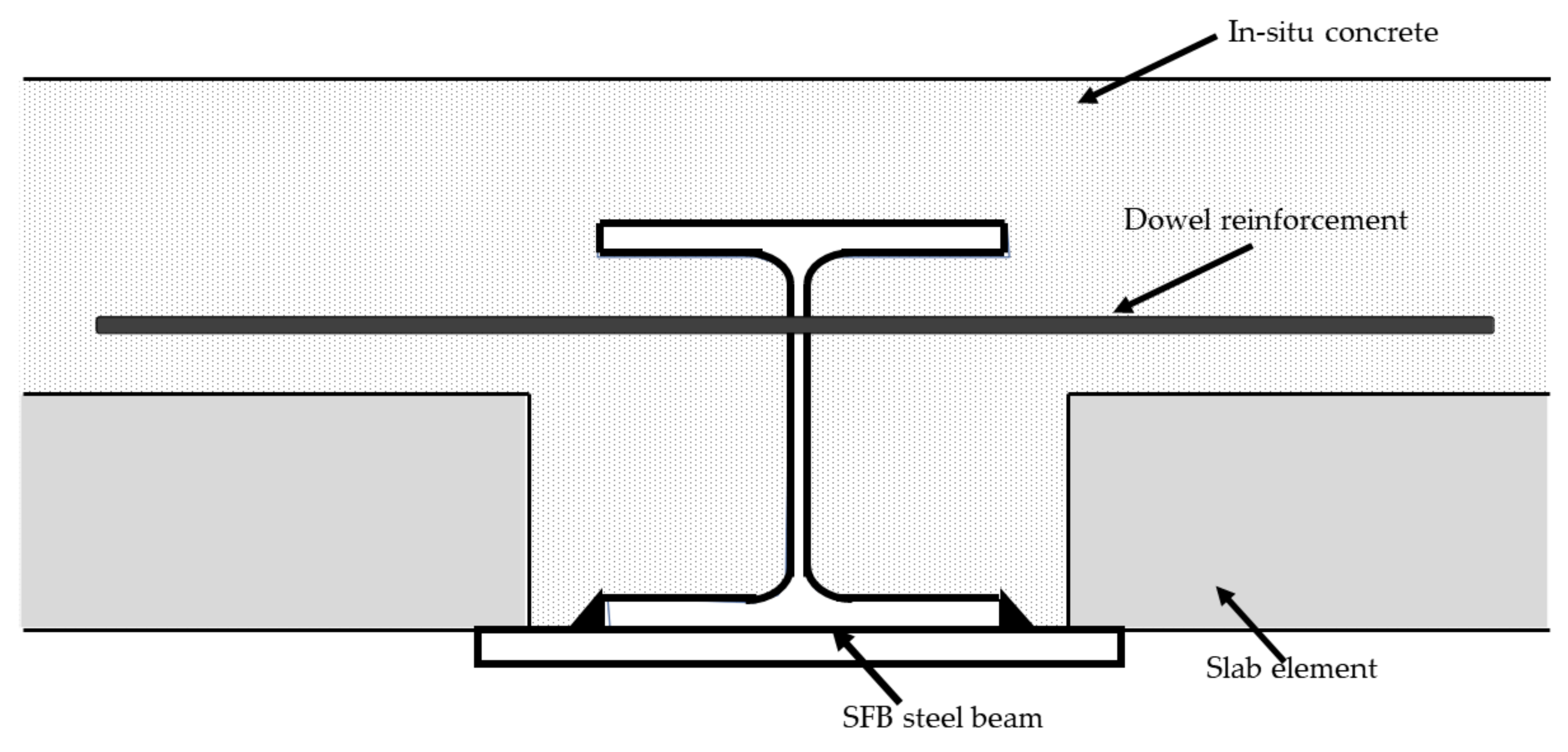
2.1. Experimental Tests

A series of experimental tests were carried out in the 1990s, in 21 configurations of different types of slim floor beams, and a final compendium was written in 2008 [13]. Among these configurations, two were considered herein for the validation of the numerical model: WFRC 44174 [23] and WFRC 66162 [24]. The steel beams in the experimental tests were double-T profiles (Figure 4), similar to the slim floor beam types assessed in this study (only the steel profile, no supplementary plate welded under the bottom flange).

The selected experimental tests, conducted in 1989 [23] and 1996 [24], respectively, at the Warrington Fire Research Center, consisted of a simply supported beam with a 4.5 m distance between the supports. The test assemblies were placed on top of the oven, with the beam supports outside of the oven, in such a way that only a 4 m span was heated under ISO fire. They were loaded through four hydraulic rams, along the longitudinal axis of the steel profile, in four points at 1/8, 3/8, 5/8, and 7/8 of the supported span. The load applied through each ram was 76.59 kN for the WFRC 44174 test and 84.6 kN for the WFRC 66162 test, respectively.

Figure 4a shows the cross-section of the WFRC 44174 composite behavior test, with a 254 × 254 mm, S275 steel profile, and the upper part embedded in a Grade 30 light weight concrete slab. The bottom part of the steel profile was covered with Grade 30 normal weight concrete, and the lower flange remained exposed. The tensile test made on a material sample taken from the tested steel profile showed a value of 267 N/mm² for the yield strength.

Figure 4b shows the cross-section of WRFC 66162 non-composite behavior test, realized of an asymmetric 280 mm deep 280/180 mm wide hot rolled profile, steel grade S355. On the lower flange, a 210 mm deep metal decking was placed to support the Grade 30 normal weight concrete cast in place. The tensile test made on a material sample taken from the steel profile showed a value of 402 N/mm² for yield strength.

The failure criterion was considered when reaching a vertical displacement of l/20 of span, in both configurations. The WFRC 44174 test was stopped when the vertical displacement at mid-span reached 226 mm after 52 min, while the WFRC 66162 test was stopped at 225 mm after 107.5 min.

2.2. Validated Model

The material properties used in the numerical models are according to the fire design Eurocodes [17,25,26,27]. For the thermal analysis, the emissivity used was 0.7 for both steel and concrete, on heated surfaces as well as on unheated surfaces, whereas the coefficient of convection was 25 W/m²K on heated surfaces and 4 W/m²K on unheated surfaces, for both materials. The upper limit of the thermal conductivity was considered for concrete. For experiment No. 66162, the value of concrete density was considered 2300 kg/m³. For experiment No. 44174, the measured concrete density was 2200 kg/m³ for normal weight concrete and 1850 kg/m³ for light weight concrete. The moisture content of the concrete was taken in accordance to the technical notes of the experimental tests [23,24]. For experiment No. 44174, the measured moisture content was 39 kg/m³ for normal weight concrete and 47 kg/m³ for light weight concrete. For experiment No. 66162, the moisture content was 42 kg/m³. Safir software takes into account the energy dissipated by the evaporation of free water, in concrete. This energy is resealed at a constant rate from 100 °C to 115 °C, and then the energy release rate is linearly decreasing from 115 °C to 200 °C [22].

The cross-sections of the beam were exposed to the ISO fire only from below, the temperature in the air on the top of the floor being considered 20 °C.

To describe the geometry of the cross section and the temperature distribution, linear isoparametric finite elements were used [22]. A 2D thermal analysis was realized on the cross-sections with triangle shape elements to describe the meshing. For the mechanical model, 2D beam finite elements were used, with constant cross-section along the longitudinal axis. The thermal analysis and the mechanical analysis were realized separately and subsequently, which means that the temperature distribution would obviously influence the mechanical response, but the opposite was not true [22]. In the cases with non-composite behaviour, the concrete material was considered only with thermal properties, but no mechanical properties. Thus, the presence of the concrete influenced the thermal analysis, but not the mechanical one.

The boundary conditions and the loads were considered as in the fire resistance tests. The mechanical models, for both tests, consisted of 4.5 m simply supported beams, heated over 4 m, loaded with four concentrated loads, as described in Section 2.1. The materials were isotropic, not submitted to movements, not compressible and had no mechanical dissipation. No heat flux was considered along the longitudinal axis of the beam finite element [22].

Figure 5 shows the meshed cross-section for the WFRC 44174 test, while Figure 6 shows the meshed cross-sections for the WFRC 66162 test. Due to the deep-decking metal sheet, the cross-section of the WFRC 66162 beam varies along the length of the beam. Therefore, three cross-sections were modelled: a cross-section with a thinner depth of the concrete slab (Figure 6a), a cross-section with a concrete slab standing on the lower flange of the I section (Figure 6c), and an intermediate cross-section (Figure 6b) which makes the transition between the other two.

The temperature variation on the cross-section was analyzed in the same points where the thermocouples were placed during the experimental test. The article presents the comparison in the points where the temperature was reaching important values i.e., above 400 °C. Figure 5 and Figure 6 present the points where the temperatures obtained through the numerical simulation were compared with the values recorded during the experimental model. The points were chosen in the lower part of the steel profile as follows: point 1 was considered at a quarter of the bottom flange length, point 2 at 10 mm on the web height, and points 3, 4 at 30 mm and 50 mm above the bottom flange, respectively.

The temperature comparisons are presented in Figure 7, for both tests, and demonstrate a good fit between the temperatures computed with SAFIR and those measured during the experiments.

The displacement-time evolutions are presented in Figure 8, for both tests. Even if the numerical models do not present a perfect fit with the experiments, in both cases, the results are on the safe side. The larger displacements lead to a failure time of 94 min, compared to 107 min obtained in the WFRC 66162 test, while for the WFRC 44174 test the failure time was 52 min, in comparison with the 43 min obtained numerically. This phenomenon was also noticed by Zanon et al. [21] during their study for SFB type slim floors, using tests from the same experimental campaign.

A possible explanation for the conservative results may be related to the support conditions within the experimental set-up, as the supports were outside the oven, and the assembly was part of its roof. This means that the oven walls might have interfered with the specimen during the test. Therefore, a second numerical analysis was made, in which the support conditions were simulated by considering a reduced span length of 4.25 m. A very good fit was obtained, in terms of both displacement and failure time, as shown in Figure 8. The assumption of the reduced span does not influence the validation of the numerical model, which was proved to be suitable by providing similar time-displacement evolutions and conservative failure times, considering the initial span of 4.5 m mentioned in the experimental report [23,24].

3. Validation of the Simplified Design Method

3.1. Presentation of the Simplified Design Method

The simplified method presented by Zanon et al. [21] was validated against SFB configurations, and was valid within the limits given in

Table 1. Application range—general scope [21].

Criteria	Range
Maximum span	12 m
Cross-section class	1 and 2
Slab type	Composite slab with steel sheeting Solid concrete slab Prefabricated slab with in-situ concrete
Steel grade	S235 to S460
Concrete class	C20/25 to C50/60
Reinforcement bars	Diameter 6 to 32 mm B500B/C

and

Table 2. Application range—geometric limits for SFB type [21].

Steel Profile	Concrete Slab	Reinforcement
10 ≤ ep ≤ 40	30 ≤ cz ≤ 150	ur ≥ 30
8 ≤ ef ≤ 40	hc.1 ≥ 20	uc ≥ 40
0.7 ≤ ep/ef ≤ 2	la ≥ 40	uw ≥ 40
6 ≤ ew ≤ 30	bf + 60 ≤ bw	hs ≤ hw−2 × ur
160 ≤ h ≤ 450		As ≤ 0.5 bp × ep
160 ≤ bf ≤ 450		As ≤ 5% × bw × (h + cz)
160 ≤ bp-bf ≤ 250		As ≤ 2 × beff × cz × (fck/fsk)

All values are expressed in [mm].

. The current study extends its scope of application to the asymmetric double-T cross-sections, as specified in

Table 3. Application range—Geometric limits for asymmetric double-T type.

Steel Profile	Concrete Slab	Reinforcement
12 ≤ efb ≤ 40	30 ≤ cz ≤ 150	ur ≥ 25
10 ≤ eft ≤ 40	hc.1 ≥ 20	uc ≥ 30
0.7 ≤ efb/ef ≤ 2.4	la ≥ 40	uw ≥ 30
6 ≤ ew ≤ 30	bf + 60 ≤ bw	hs ≤ hw−2 × ur
135 ≤ h ≤ 450		As ≤ 0.5 bfb × efb
160 ≤ bfb ≤ 500		As ≤ 5% × bw × (h + cz)
110 ≤ bfb-bft ≤ 250		As ≤ 2 × beff × cz × (fck/fsk)

All values are expressed in [mm].

. All the symbols from Table 2 and Table 3 are represented in Figure 9. In the following, the simplified method by Zanon et al. [21] is presented:

The method uses the following equation to compute the design moment resistance M_fi,t,Rd:

$${\mathrm{M}}_{\mathrm{fi},\mathrm{t},\mathrm{Rd}}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}}\cdot {\mathrm{z}}_{\mathrm{i}}\cdot {\mathrm{k}}_{\mathrm{y},\mathsf{\theta },\mathrm{i}}\cdot \left(\frac{{\mathrm{f}}_{\mathrm{y},\mathrm{i}}}{{\mathsf{\gamma }}_{\mathrm{M},\mathrm{fi},\mathrm{a}}}\right)+{\mathsf{\alpha }}_{\mathrm{slab}}\cdot {\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{A}}_{\mathrm{j}}\cdot {\mathrm{z}}_{\mathrm{j}}\cdot {\mathrm{k}}_{\mathrm{c},\mathsf{\theta },\mathrm{j}}\cdot \left(\frac{{\mathrm{f}}_{\mathrm{c},\mathrm{j}}}{{\mathsf{\gamma }}_{\mathrm{M},\mathrm{fi},\mathrm{c}}}\right)$$

(1)

• z_i, z_j is the distance from the plastic neutral axis to the centroid of the area A_i or A_j
• f_y,i is the nominal yield strength;
• f_y, for the steel area A_i, (structural steel or reinforcement) taken as positive on the compression side of the plastic neutral axis and negative on the tension side—the reinforcement can be considered only in tension;
• f_c,j is the design strength of the concrete area A_j at 20 °C;
• k_y,θ,i and k_{c, θ,j} are defined in Tables 3.2 and 3.3 of EN 1994-1-2 [27];
• α_slab is the coefficient considering the assumption of the rectangular stress block when designing slabs and shallow composite floor beams—α_slab = 0.85.

The possible contribution of the concrete below the upper flange of the steel section should be neglected in the calculation, and thus only the concrete above the upper flange is considered. The design value of the concrete compression force can be calculated using the following equation:

$${\mathrm{N}}_{\mathrm{fi},\mathrm{c},\mathrm{Rd}}=\frac{{\mathrm{f}}_{\mathrm{c}}}{{\mathsf{\gamma }}_{\mathrm{M},\mathrm{fi},\mathrm{c}}}\cdot {\mathrm{b}}_{\mathrm{eff}}\cdot {\mathrm{c}}_{\mathrm{z}}\cdot {\mathrm{k}}_{\mathrm{h}}\le {\mathrm{N}}_{\mathrm{fi},\mathrm{t},\mathrm{Rd}}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}}\cdot {\mathrm{k}}_{\mathrm{y},\mathsf{\theta },\mathrm{i}}\cdot \left(\frac{{\mathrm{f}}_{\mathrm{y},\mathrm{i}}}{{\mathsf{\gamma }}_{\mathrm{M},\mathrm{fi},\mathrm{a}}}\right)$$

(2)

where:

• k_h = 0.85 for c_z/h > 0.4
• k_h = 1.0 for all other cases

The width of the bottom flange is reduced to a value b_fb,eff,fi using Equation (3), as follows:

$${\mathrm{b}}_{\mathrm{fb}.\mathrm{eff}.\mathrm{fi}}=\max \left({\mathrm{b}}_{\mathrm{ft}} ;{\mathrm{b}}_{\mathrm{fb}}-2\cdot \left({\mathrm{l}}_{\mathrm{a}}+{\mathrm{e}}_{\mathrm{fb}}\right)\cdot {\mathrm{k}}_{\mathrm{c}}\right)$$

(3)

where:

• k_c = 0.5 for a solid slab that covers 100% of the upper surface of the welded plate
• k_c = 1.0 for all other cases

Based on Zaharia and Franssen [15], the temperature θ_fb of the bottom flange can be assumed constant and is calculated using Equation (4):

$${\mathsf{\Theta }}_{\mathrm{fb}}={\mathrm{A}}_{\mathrm{i}}\cdot {{\mathrm{e}}_{\mathrm{fb}}}^2+{\mathrm{B}}_{\mathrm{i}}\cdot {\mathrm{e}}_{\mathrm{fb}}+{\mathrm{C}}_{\mathrm{i}}$$

(4)

where:

• A_i, B_i, C_i are given in

  Table 4. Coefficients for the simplified analytical method [15,16].

  Coefficient	R30	R60	R90	R120
  Ai	0.113	0.130	0	0
  Bi	−12.80	−11.80	−2.60	−1.25
  Ci	760	980	990	1025
  Aw	−140.70	−103.80	−108.60	−70.44
  Bw	832.42	968.60	1146.70	1124.40
  Cw	0.0317	0.0232	0.0198	0.0158
  Dw	−0.230	−0.182	−0.154	−0.134
  Ar	0	0.0954	0.0548	0.0381
  Br	0	−19.254	−15.130	−12.797
  Cr	300	1105.4	1135.9	1138.1

  [15].

The temperature of the profile web θ_w is assumed constant and is calculated using Equation (5), based on Zaharia and Franssen [15]:

$${\mathsf{\Theta }}_{\mathrm{w}}=\left({\mathrm{A}}_{\mathrm{w}}\cdot \ln e_{\mathrm{fb}}+{\mathrm{B}}_{\mathrm{w}}\right)\cdot {\mathrm{e}}^{\left({\mathrm{C}}_{\mathrm{w}}\cdot \ln {\mathrm{e}}_{\mathrm{fb}}+{\mathrm{D}}_{\mathrm{w}}\right)\cdot \frac{{\mathrm{h}}_{\mathrm{w}}}{40}}$$

(5)

where:

• A_w, B_w, C_w, D_w are given in Table 4 [15].

In this equation, e_fb and h_w are expressed in [mm].

Within the field of application of slim floor beams, the upper flange can be assumed as non-affected by the fire exposure.

For the longitudinal reinforcement placed within the zone determined by h_s and u_c, u_w, u_r according to Figure 9, the temperature θ_r can be calculated using the equation, based on Hanus et al. [16]:

$${\mathsf{\Theta }}_{\mathrm{r}}={\mathrm{A}}_{\mathrm{r}}\cdot {{\mathrm{u}}_{\mathrm{eq}}}^2+{\mathrm{B}}_{\mathrm{r}}\cdot {\mathrm{u}}_{\mathrm{eq}}+{\mathrm{C}}_{\mathrm{r}}$$

(6)

where:

• A_r, Br, and C_r are given in Table 4 [16];
• e_fb and h_w shall be expressed in [mm];
• u_eq is the equivalent distance, and is calculated with Equation (7):

  $${\mathrm{u}}_{\mathrm{eq}}=\min (45\mathrm{mm},25\mathrm{mm}+\frac{{\mathrm{e}}_{\mathrm{fb}}}{2})+\frac{5\mathrm{mm}}{{\mathrm{k}}_{\mathrm{c}}}$$

  (7)

3.2. Parametric Study on Asymmetric Double-T Cross-Section

We considered 81 geometrical configurations of asymmetric slim beam cross-sections (

Table 5. The evaluated geometrical configurations.

Steel Profile Type	Slab Type 1	h [mm]	bfb [mm]	bft [mm]	efb [mm]	eft [mm]	ew [mm]	cz [mm]	L [m]	l [m]	Steel	Concrete	Reinforcement
													No of Bars	Φ [mm]	uw [mm]	ur [mm]
ASB	2	258	285	175	14	14	10	60	9	1.5	S355	C50/60	4	25	37.5	32.5
ASB	2	258	285	175	14	14	10	90	9	1.5	S460	C30/37	4	25	37.5	42.5
ASB	2	258	285	175	14	14	10	60	9	1.5	S235	C25/30	0	-	-	-
ASB	2	258	285	175	14	14	10	120	9	1.5	S355	C50/60	4	16	42	32
ASB	2	258	285	175	14	14	10	60	9	1.5	S235	C50/60	2	20	50	30
ASB	1	258	285	175	14	14	10	90	9	1.5	S460	C30/37	4	25	37.5	42.5
ASB	1	258	285	175	14	14	10	60	9	1.5	S355	C50/60	2	25	47.5	32.5
ASB	1	258	285	175	14	14	10	60	9	1.5	S460	C40/50	0	-	-	-
ASB	2	266	300	190	22	22	25	40	8	2	S275	C30/37	0	-	-	-
ASB	2	266	300	190	22	22	25	120	8	2	S235	C50/60	0	-	-	-
ASB	2	266	300	190	22	22	25	60	8	2	S355	C30/37	2	25	37.5	32.5
ASB	2	266	300	190	22	22	25	120	8	2	S460	C25/30	0	-	-	-
ASB	2	266	300	190	22	22	25	40	8	2	S275	C50/60	2	20	40	30
ASB	1	266	300	190	22	22	25	120	8	2	S235	C50/60	0	-	-	-
ASB	1	266	300	190	22	22	25	120	8	2	S275	C30/37	2	25	37.5	37.5
ASB	1	266	300	190	22	22	25	120	8	2	S460	C35/45	0	-	-	-
ASB	1	266	300	190	22	22	25	90	8	2	S235	C25/30	2	25	22.5	37.5
ASB	1	302	293	183	40	40	20	40	9	2	S355	C30/37	2	25	47.5	27.5
ASB	1	302	293	183	40	40	20	60	9	2	S235	C50/60	2	25	47.5	27.5
ASB	1	302	293	183	40	40	20	40	9	2	S235	C30/37	4	32	29	34
ASB	1	302	293	183	40	40	20	40	9	1.5	S460	C30/37	0	-	-	-
ASB	2	302	293	183	40	40	20	40	9	2	S355	C50/60	4	25	32.5	32.5
ASB	2	302	293	183	40	40	20	40	9	2	S235	C25/30	2	16	52	32
ASB	2	302	293	183	40	40	20	40	9	2	S460	C40/50	2	25	47.5	32.5
ASB	2	302	293	183	40	40	20	120	9	2	S235	C30/37	2	25	47.5	42.5
Welded	1	220	500	280	20	20	10	80	10	2.25	S235	C25/30	4	20	35	30
Welded	1	220	500	280	20	20	10	80	10	2.25	S460	C30/37	4	25	32.5	27.5
Welded	1	220	500	280	20	20	10	40	10	2.25	S355	C40/50	4	20	35	30
Welded	1	220	500	280	20	20	10	120	10	2.25	S275	C25/30	4	20	35	30
Welded	1	220	500	280	20	20	10	40	10	2.25	S235	C25/30	0	-	-	-
Welded	2	220	500	280	16	16	10	80	10	2.25	S355	C25/30	4	20	35	30
Welded	2	220	500	280	20	20	10	80	10	2.25	S235	C40/50	4	20	35	40
Welded	2	220	500	280	20	20	10	80	10	2.25	S460	C35/45	4	25	32.5	27.5
Welded	2	220	500	280	20	20	10	80	10	2.25	S275	C30/37	4	20	35	35
Welded	2	220	500	280	20	20	20	80	10	2.25	S235	C35/45	4	25	32.5	27.5
IFB	2	135	270	135	10.2	15	6.6	125	6	1.5	S355	C30/37	4	20	30	25
IFB	2	135	270	135	10.2	20	6.6	125	6	1.5	S235	C30/37	2	20	30	25
IFB	2	135	270	135	10.2	12	6.6	125	6	1.5	S460	C50/60	4	20	30	25
IFB	2	135	270	135	10.2	15	6.6	40	6	1.5	S355	C30/37	4	20	30	25
IFB	2	135	270	135	10.2	20	6.6	40	6	1.5	S355	C50/60	4	20	30	25
IFB	2	135	270	135	10.2	12	6.6	40	6	1.5	S235	C30/37	2	20	30	25
IFB	2	135	270	135	10.2	20	6.6	40	6	1.5	S460	C25/30	4	20	30	25
IFB	1	225	400	190	14.6	25	9.4	60	11	2.5	S460	C35/45	4	25	37.5	32.5
IFB	1	225	400	190	14.6	15	9.4	60	11	2.5	S460	C50/60	2	25	37.5	42.5
IFB	1	225	400	190	14.6	25	9.4	60	11	2.5	S355	C25/30	4	25	37.5	32.5
IFB	1	225	400	190	14.6	35	9.4	120	11	2.5	S275	C35/45	4	16	42	52
IFB	1	225	400	190	14.6	25	9.4	120	11	2.5	S235	C35/45	4	32	34	29
IFB	1	225	400	190	14.6	25	9.4	100	11	2.5	S460	C25/30	2	25	37.5	32.5
IFB	1	225	400	190	14.6	15	9.4	40	11	2.5	S355	C50/60	4	20	40	35
IFB	2	225	400	190	14.6	35	9.4	60	11	2.5	S235	C35/45	2	25	37.5	32.5
IFB	2	225	400	190	14.6	15	9.4	60	11	2.5	S355	C25/30	4	16	42	47
IFB	2	225	400	190	14.6	25	9.4	100	11	2.5	S235	C50/60	4	32	34	39
IFB	2	225	400	190	14.6	25	9.4	40	11	2.5	S355	C35/45	4	25	37.5	32.5
IFB	2	180	320	170	12.7	20	8	40	8	2	S275	C50/60	2	25	37.5	37.5
IFB	2	180	320	170	12.7	20	8	120	8	2	S235	C30/37	2	25	37.5	42.5
IFB	2	180	400	170	12.7	15	8	60	8	2	S355	C25/3	4	25	37.5	37.5
IFB	2	180	320	170	12.7	20	8	120	8	2	S460	C50/60	4	20	40	45
IFB	2	180	320	170	12.7	25	8	40	8	2	S275	C50/60	2	32	34	34
IFB	1	180	400	170	12.7	20	8	120	8	2	S235	C30/37	4	16	42	32
IFB	1	180	320	170	12.7	30	8	120	8	2	S275	C50/60	2	25	37.5	37.5
IFB	1	180	320	170	12.7	20	8	120	8	2	S460	C40/50	2	25	37.5	37.5
IFB	1	180	400	170	12.7	20	8	90	8	2	S460	C50/60	4	20	40	40
IFB	1	180	400	170	12.7	20	8	90	8	2	S235	C50/60	4	14	42	37
SB	2	376	300	180	24	24	13.5	40	12	3	S460	C40/50	4	25	37.5	47.5
SB	2	376	300	180	24	24	13.5	40	12	3	S355	C25/30	0	-	-	-
SB	2	376	300	180	24	24	13.5	80	12	3	S460	C50/60	4	32	34	44
SB	2	376	300	180	24	24	13.5	120	12	3	S275	C30/37	4	25	37.5	47.5
SB	2	376	300	180	24	24	13.5	40	12	3	S355	C40/50	4	20	40	40
SB	1	376	300	180	24	24	13.5	80	12	3	S460	C25/30	2	32	34	44
SB	1	376	300	180	24	24	13.5	40	12	3	S235	C50/60	2	25	37.5	47.5
SB	1	376	300	180	24	24	13.5	150	12	3	S355	C30/37	2	20	40	50
SB	2	301	310	200	39	39	21	40	8	1.5	S355	C50/60	4	25	37.5	37.5
SB	2	301	310	200	39	39	21	40	8	1.5	S275	C25/30	2	25	37.5	37.5
SB	2	301	310	200	39	39	21	40	8	1.5	S235	C50/60	4	32	34	39
SB	2	301	310	200	39	39	21	60	8	1.5	S355	C30/37	2	16	42	42
SB	2	301	310	200	39	39	21	40	8	1.5	S355	C40/50	4	25	37.5	32.5
SB	2	301	310	200	39	39	21	80	8	1.5	S460	C50/60	4	25	37.5	37.5
SB	1	301	310	200	39	39	21	70	8	1.5	S235	C50/60	2	32	34	34
SB	1	301	310	200	39	39	21	100	8	1.5	S460	C40/50	4	20	40	40
SB	1	301	310	200	39	39	21	40	8	1.5	S355	C25/30	2	25	37.5	37.5

¹ Type No. 1 represents a prefabricated slab with in-situ concrete; Type No. 2 represents solid concrete slab.

), using the numerical model validated in Section 2. Four types of asymmetric double-T steel profile were assessed, as shown in Figure 3 (ASB type, welded steel cross-section, IFB type, and SB type). Each geometrical configuration was considered twice, with composite and non-composite behavior. For all cases, the model was evaluated for four different fire resistances (R30, R60, R90, R120) resulting in a total of 648 analyses. The varying parameters are explained in Table 5, using the notations from Figure 9b. The ranges proposed by Zanon et al. [21], presented in Table 2, were respected and even extended as shown in Table 3.

The bending resistance was determined numerically, considering a simply supported beam with a uniform load. The value of the applied load was determined in order to obtain the requested fire resistance demand of 30, 60, 90, or 120 min.

The simplified method has been applied in all 648 cases. The results obtained analytically were compared against the numerical results, in terms of bending resistance, for composite (Figure 10 and Figure 11) and non-composite behavior (Figure 12 and Figure 13). Figure 10 shows the comparison of composite behavior configurations, for R30 (a), R60 (b), R90 (c), and R120 (d), respectively. Figure 12 shows the comparison of non-composite behavior configurations, for R30 (a), R60 (b), R90 (c), and R120 (d), respectively.

As Figure 10 and Figure 12 suggest, the considered configurations cover a large interval of bending resistance values. The simplified method offers good results in comparison with the numerical values. The results obtained for R30 are underestimated by the simplified method up to 15%, due to the concrete thickness simplification, i.e., only the concrete thickness above the top flange is taken into consideration, while the plastic neutral axis is still in the steel profile height. The results obtained for R60 provide the closest results (up to 10%), as the PNA is close to the interface between the top steel flange and the concrete topping. The values for R90 and R120 demonstrate higher differences compared to the numerically results (up to about 30%, 40%, respectively), due to the simplification made to the temperature on the steel profile web which, in the simplified method, is considered to be uniform throughout the height. In the original equation of Zaharia and Franssen [15], the temperature in the web was calculated considering the distance along the height of the web measured from the top of the bottom flange. In Zanon et al.’s [21] method, a simplification was considered in the original equation, i.e., the temperature was determined only for the distance equal to a quarter of the web height and it was applied to the whole web. For R30 and R60, at this location, in many cases, the temperature does not exceed 400 °C. According to EN 1993-1-2 [25], at this level of temperature the streel strength remains unaffected. The situation is different in the cases of R90 and R120, as the temperature along the web is substantially increased, in particular in the lower part of the web. This is the reason why the simplified method leads to conservative values for longer fire exposures, up to a difference of about 40%.

The ratio between the bending resistance computed with the simplified method and the values obtained with SAFIR is analyzed in Figure 11, for composite behavior and in Figure 13, for non-composite behavior, respectively, while Figure 14 shows the results of all situations. Figure 11a, show the Gaussian curve of the studied data, and Figure 11b, Figure 13b and Figure 14b show a boxplot assessment. It can be noted from Figure 14b that the median value of the data is 0.933, for composite behavior cases and 0.853, for non-composite behavior. The first quartile is 0.86 (25% of the values are below 0.86), for composite behavior and 0.722 for non-composite behavior cases. The third quartile is 0.97 (75% of the values are below 0.97), for composite behavior, and 0.905 for non-composite behavior. For 95% of cases (613 configurations) the simplified method offered a ratio less or equal to 1. For the remaining 5% of cases (35 configurations), the computed bending moment was higher than that obtained with SAFIR, with a maximum ratio of 1.05.

4. Conclusions

A simplified approach for the design of slim floor systems under fire conditions was recently proposed by Zanon et al. [21], based on models existing in the literature. The method was validated through a comprehensive analysis of tests and a broad parametric study, but only for SFB type slim floor beams.

The scope of application of this method was extended in this paper, for other types of asymmetric double-T steel sections (without a welded plate below), as well as for extended geometric limits. This was done by means of a parametrical study, comprising 162 configurations, assessed for fire resistances R30, R60, R90 and R120, resulting in 648 analyses carried out with SAFIR software. The numerical model was validated considering composite and non-composite behavior against two corresponding experimental tests available in the literature.

The design moment resistance of the studied configurations was determined both numerically and analytically, using the simplified method, and showed good agreement. The best similitude between the results in terms of moment resistance was obtained for R60, the difference being below 10%.

The study demonstrated that the simplified method can cover a larger range of configurations, for both SFB and asymmetric double-T types, and may represent a strong tool for the fire design of slim floor beams.