Influence of Dry Friction on the Dynamics of Cantilevered Pipes Conveying Fluid
Abstract
:1. Introduction
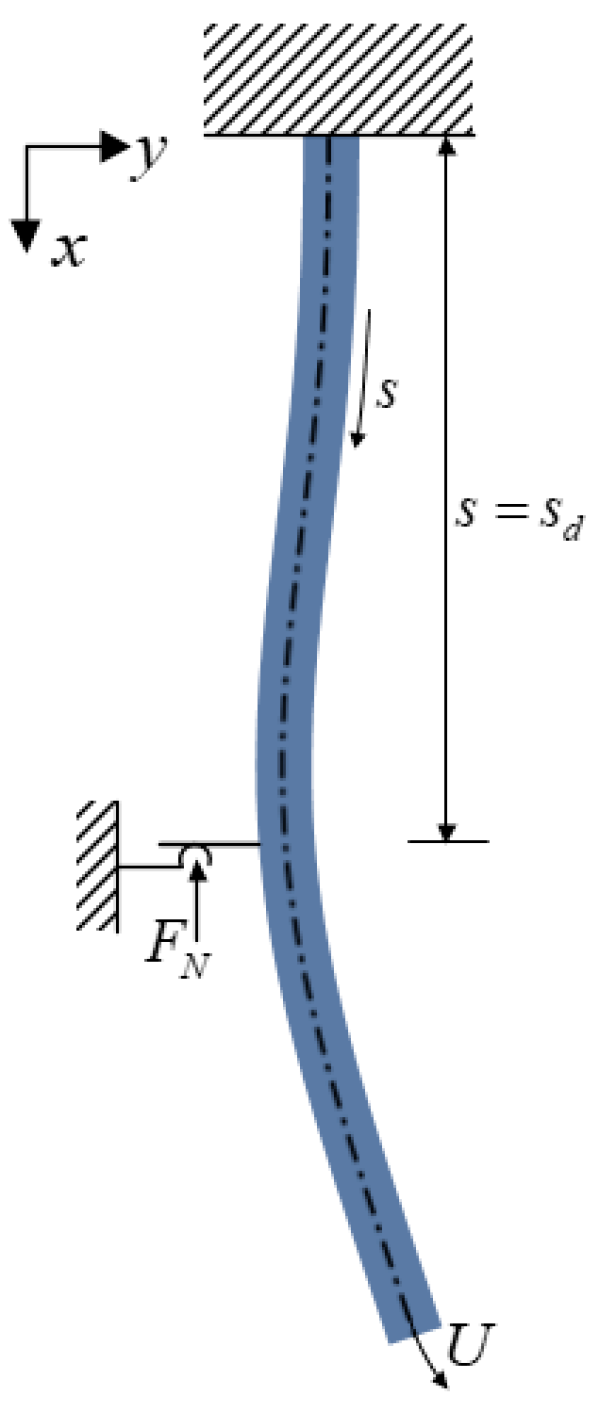
2. Theoretical Model
3. Numerical Solution
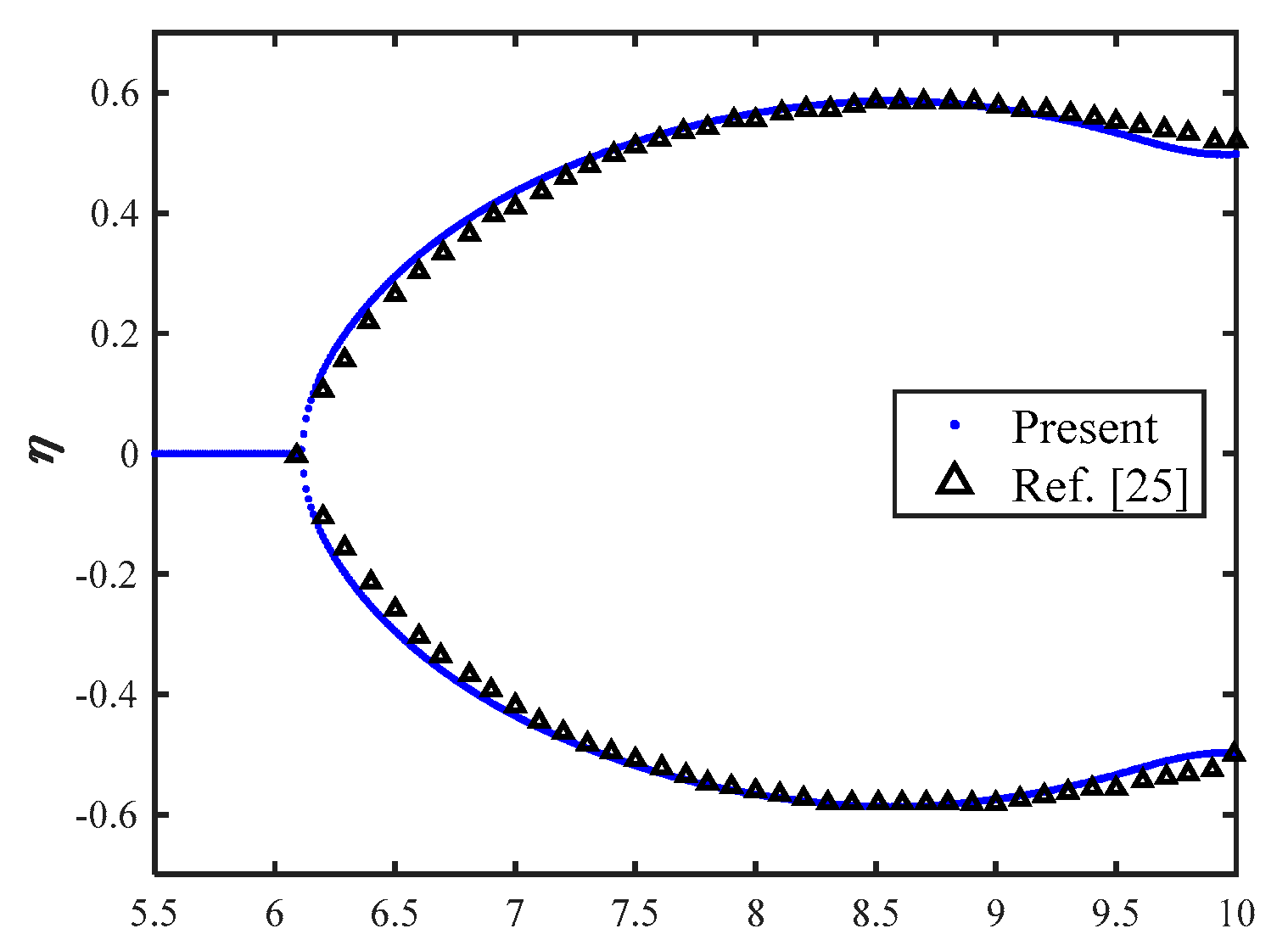
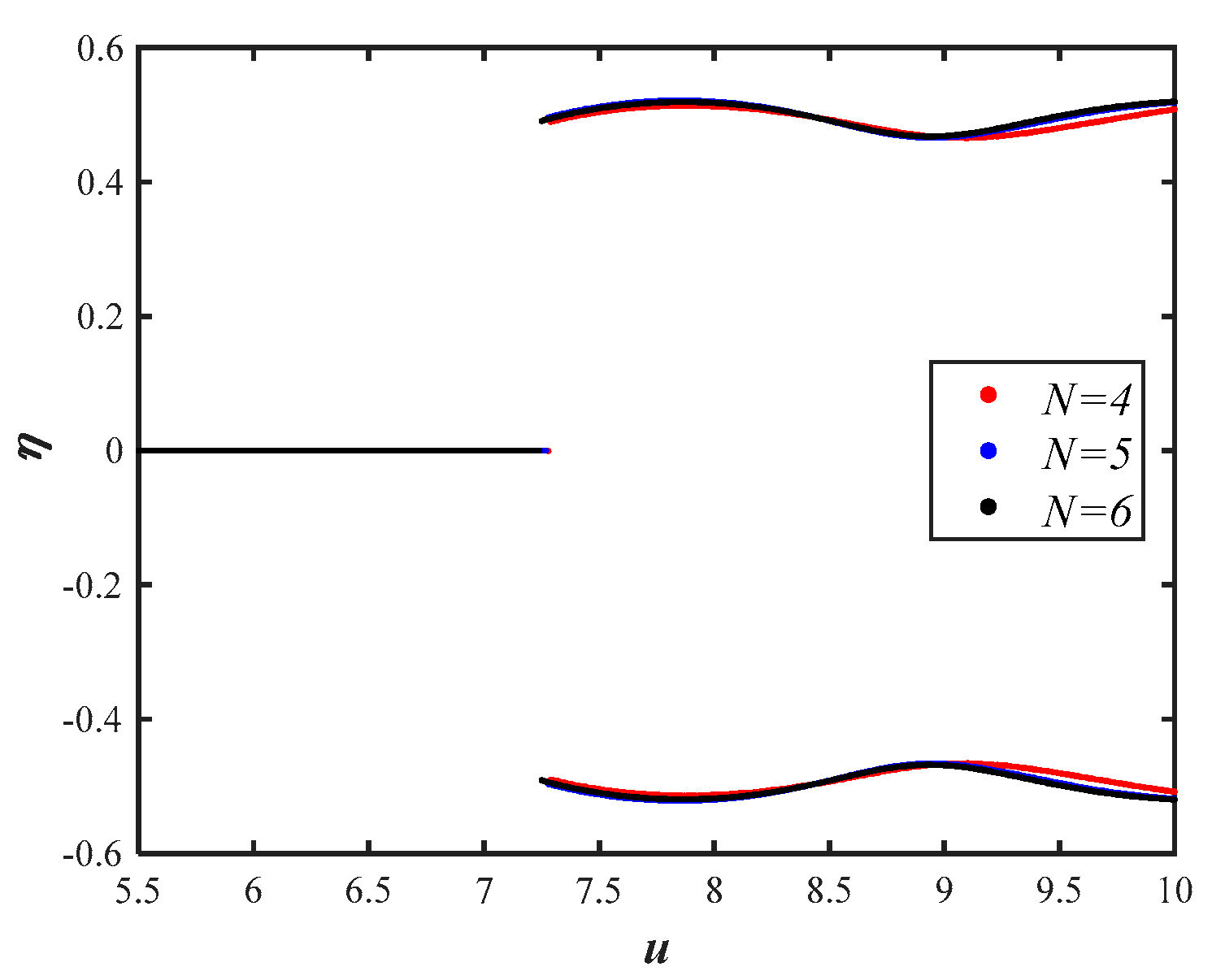
4. Algorithm Validation and Convergence Analysis
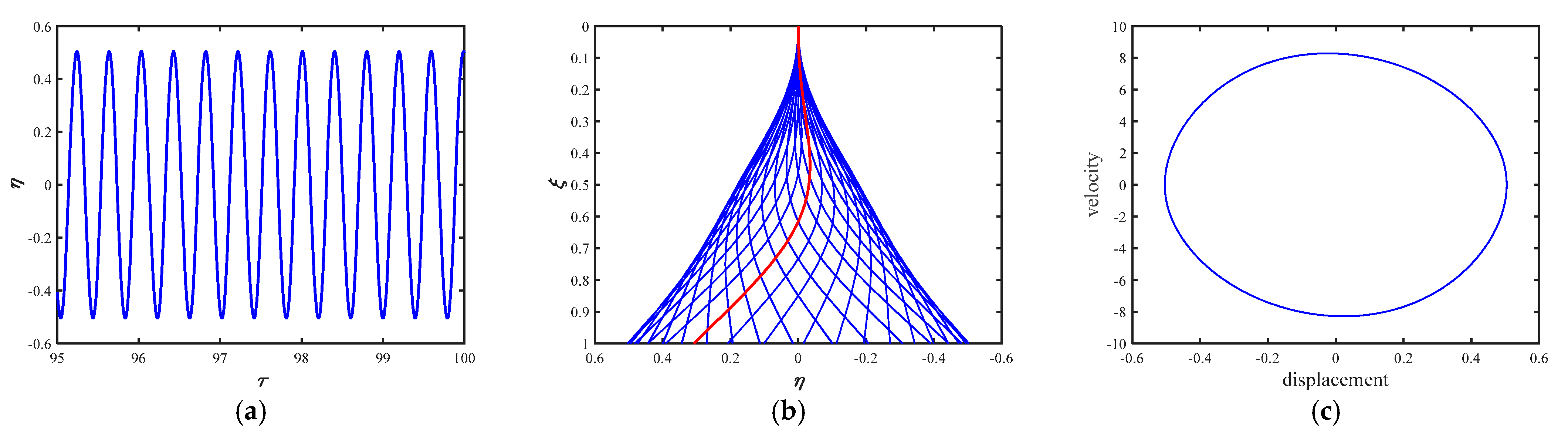
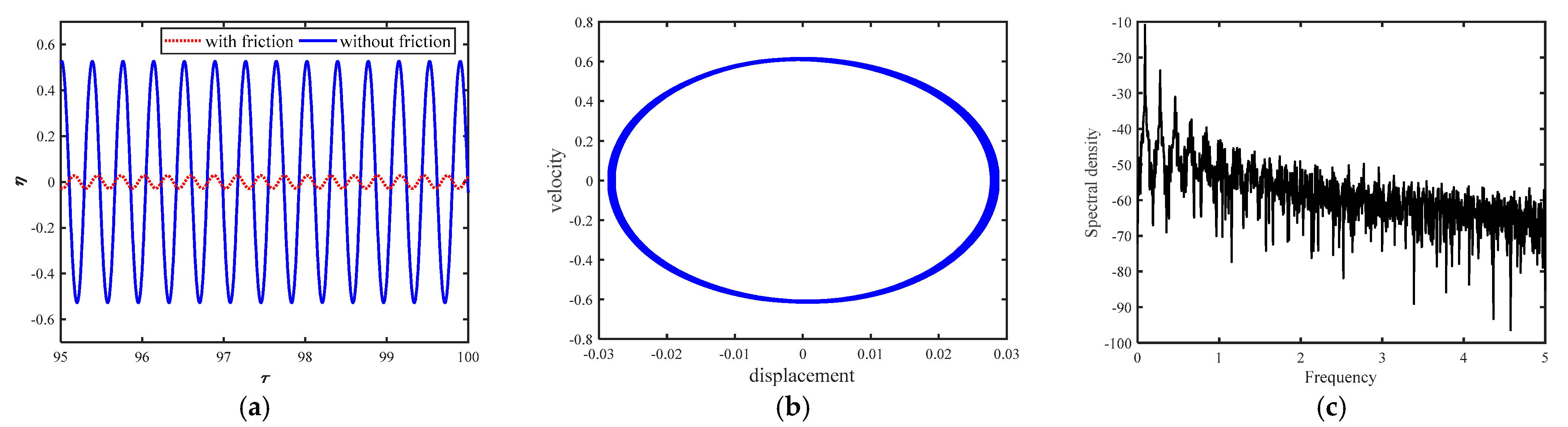
5. Results
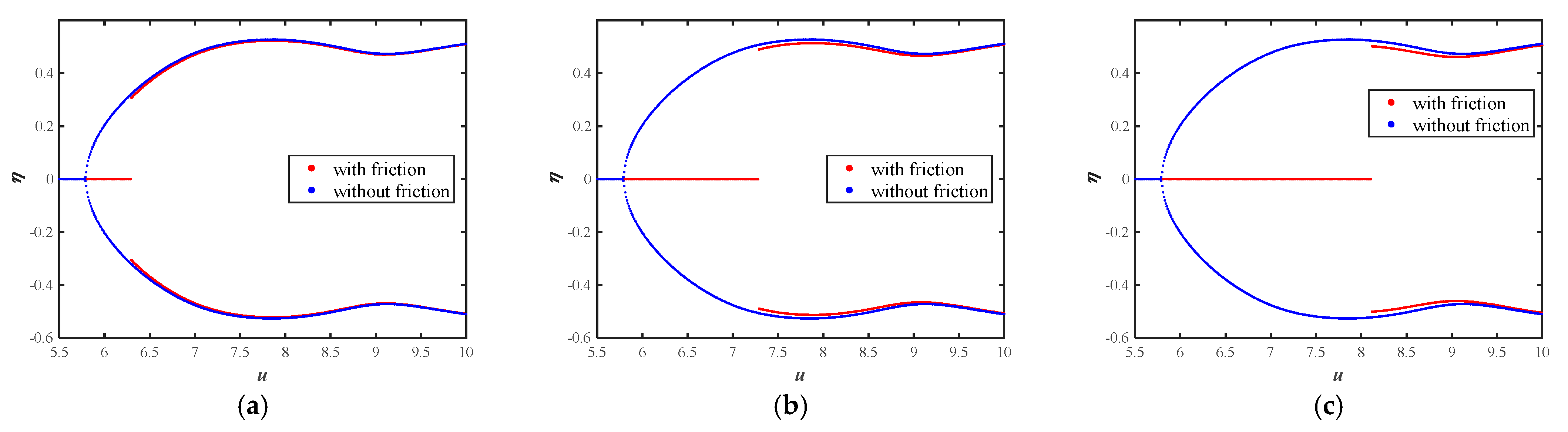
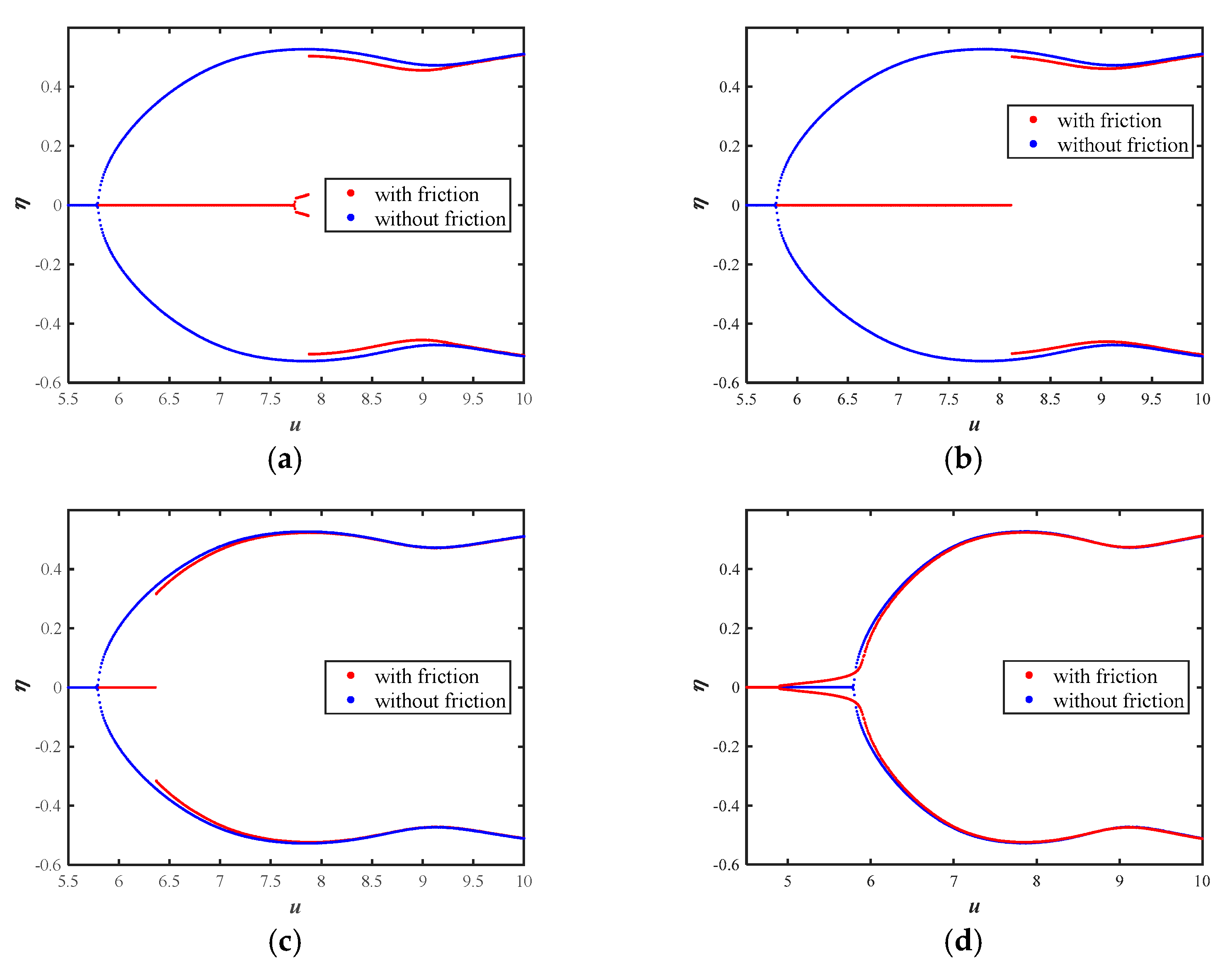
5.1. Effect of Friction Force fn
5.2. Effect of Installation Position ξd
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Guo, X.Q.; Wang, G.R.; Liu, Q.Y.; Fang, D.; Huang, L.; Mao, L.J. Bi-nonlinear vibration model of tubing string in oil & gas well and its experimental verification. Appl. Math. Model. 2020, 81, 50–69. [Google Scholar] [CrossRef]
- Wan, M.; Yin, Y.X.; Liu, J.; Guo, X.Q. Active boundary control of vibrating marine riser with constrained input in three-dimensional space. Nonlinear Dyn. 2021, 106, 2329–2345. [Google Scholar] [CrossRef]
- Tang, D.M.; Dowell, E.H. Chaotic oscillations of a cantilevered pipe conveying fluid. J. Fluids Struct. 1988, 2, 263–283. [Google Scholar] [CrossRef]
- Szmidt, T.; Przybylowicz, P. Critical flow velocity in a pipe with electromagnetic actuators. J. Theor. Appl. Mech.-Pol. 2013, 51, 487–496. [Google Scholar]
- Dai, H.L.; Wang, L. Dynamics and stability of magnetically actuated pipes conveying fluid. Int. J. Struct. Stab. Dyn. 2016, 16, 1550026. [Google Scholar] [CrossRef]
- Khajehpour, S.; Azadi, V. Vibration suppression of a rotating flexible cantilever pipe conveying fluid using piezoelectric layers. Lat. Am. J. Solids Struct. 2015, 12, 1042–1060. [Google Scholar] [CrossRef] [Green Version]
- Lyu, X.; Chen, F.; Ren, Q.; Tang, Y.; Ding, Q.; Yang, T. Ultra-thin Piezoelectric Lattice for Vibration Suppression in Pipe Conveying Fluid. Acta Mech. Solida Sin. 2020, 33, 770–780. [Google Scholar] [CrossRef]
- Paidoussis, M.P.; Li, G.X. Pipes Conveying Fluid: A Model Dynamical Problem. J. Fluids Struct. 1993, 7, 137–204. [Google Scholar] [CrossRef]
- Semler, C.; Li, G.X.; Paidoussis, M.P. The non-linear equations of motion of pipes conveying fluid. J. Sound Vib. 1994, 169, 577–599. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow, 2nd ed.; Elsevier Academic Press: San Diego, CA, USA, 2014; Volume 1. [Google Scholar]
- Wang, Y.K.; Wang, L.; Ni, Q.; Dai, H.; Yan, H.L.; Luo, Y. Non-planar responses of cantilevered pipes conveying fluid with intermediate motion constraints. Nonlinear Dyn. 2018, 93, 505–524. [Google Scholar] [CrossRef]
- Liu, L.; Li, B.; Zhang, J.S.; Li, P.F.; Xiao, X.X.; Xing, Y.; Tan, U.X. Dynamic simulation for beam to beam frictionless contact using a novel region detection algorithm. Comput. Methods Appl. Mech. Eng. 2021, 385, 114025. [Google Scholar] [CrossRef]
- Zakirnichnaya, M.M.; Rubtsov, A.V.; Kulakov, P.A.; Galiullina, N.J. The assessment of stressed-deformed state of tube bundle of the heat-exchange apparatus with the fixed pipe grids. J. Phys. Conf. Ser. 2020, 1679, 042050. [Google Scholar] [CrossRef]
- Lee, S.I.; Chung, J. New non-linear modelling for vibration analysis of a straight pipe conveying fluid. J. Sound Vib. 2002, 254, 313–325. [Google Scholar] [CrossRef]
- Tan, X.; Mao, X.Y.; Ding, H.; Chen, L.Q. Vibration around non-trivial equilibrium of a supercritical Timoshenko pipe conveying fluid. J. Sound Vib. 2018, 428, 104–118. [Google Scholar] [CrossRef]
- Sazesh, S.; Shams, S. Vibration analysis of cantilever pipe conveying fluid under distributed random excitation. J. Fluids Struct. 2019, 87, 84–101. [Google Scholar] [CrossRef]
- Olsson, H.; Strm, K.J.; Wit, C.; Gfvert, M.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 5517–5522. [Google Scholar] [CrossRef] [Green Version]
- Berger, E. Friction modeling for dynamic system simulation. Appl. Mech. Rev. 2002, 55, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Wit, C.C.D.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Automat. Control 1995, 40, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Kinkaid, N.M.; O’Reilly, O.M.; Papadopoulos, P. Automotive disc brake squeal. J. Sound Vib. 2003, 267, 105–166. [Google Scholar] [CrossRef]
- Miyasato, H.H.; Segala Simionatto, V.G.; Junior, M.D. On the interaction between rigid discs and rotating damped contact elements. Mech. Res. Commun. 2021, 111, 103644. [Google Scholar] [CrossRef]
- Ren, Y.S.; Qin, H.Z.; Zhao, Z.L. Nonlinear vibration analysis of a beam with dry friction at the supports. Mech. Res. Commun. 1999, 26, 83–90. [Google Scholar] [CrossRef]
- Go, Y.J.; Kim, Y.H.; Chang, H.G. An analysis of the behavior of a simply supported beam with a dry friction damper attached. Appl. Acoust. 1998, 55, 31–41. [Google Scholar] [CrossRef]
- Guida, D.; Nilvetti, F.; Pappalardo, C.M. Instability induced by dry friction. Int. J. Mech. 2009, 3, 44–51. [Google Scholar]
- Zhou, K.; Xiong, F.R.; Jiang, N.B.; Dai, H.L.; Yan, H.; Wang, L.; Ni, Q. Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink. Nonlinear Dyn. 2018, 95, 1435–1456. [Google Scholar] [CrossRef]
- Miguélez, M.H.; Rubio, L.; Loya, J.A.; Fernández-Sáez, J. Improvement of chatter stability in boring operations with passive vibration absorbers. Int. J. Mech. Sci. 2010, 52, 1376–1384. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Ding, H.; Du, R.; Chen, L. A suspension system with quasi-zero stiffness characteristics and inerter nonlinear energy sink. J. Vib. Control 2022, 28, 143–158. [Google Scholar] [CrossRef]
- Wong, W.O.; Tang, S.L.; Cheung, Y.L.; Cheng, L. Design of a dynamic vibration absorber for vibration isolation of beams under point or distributed loading. J. Sound Vib. 2007, 301, 898–908. [Google Scholar] [CrossRef]
- Li, Q.; Liu, W.; Lu, K.; Yue, Z. Nonlinear Parametric Vibration of a Fluid-Conveying Pipe Flexibly Restrained at the Ends. Acta Mech. Solida Sin. 2019, 33, 327–346. [Google Scholar] [CrossRef]
- Paidoussis, M.P.; Semler, C. Non-linear dynamics of a fluid-conveying cantilevered pipe with a small mass attached at the free end. Int. J. NonLinear Mech. 1998, 33, 15–32. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Ni, Q.; Wang, L.; Zhou, K.; Meng, X. Influence of Dry Friction on the Dynamics of Cantilevered Pipes Conveying Fluid. Appl. Sci. 2022, 12, 724. https://doi.org/10.3390/app12020724
Guo Z, Ni Q, Wang L, Zhou K, Meng X. Influence of Dry Friction on the Dynamics of Cantilevered Pipes Conveying Fluid. Applied Sciences. 2022; 12(2):724. https://doi.org/10.3390/app12020724
Chicago/Turabian StyleGuo, Zilong, Qiao Ni, Lin Wang, Kun Zhou, and Xiangkai Meng. 2022. "Influence of Dry Friction on the Dynamics of Cantilevered Pipes Conveying Fluid" Applied Sciences 12, no. 2: 724. https://doi.org/10.3390/app12020724
APA StyleGuo, Z., Ni, Q., Wang, L., Zhou, K., & Meng, X. (2022). Influence of Dry Friction on the Dynamics of Cantilevered Pipes Conveying Fluid. Applied Sciences, 12(2), 724. https://doi.org/10.3390/app12020724




