Computational Investigation of a Novel Box-Wing Aircraft Concept
Abstract
:1. Introduction
2. Computational Approach
3. Aero-Structural Characterization of CRM Aircraft
3.1. Main Characteristics of CRM Aircraft
3.2. Computational Set-Up
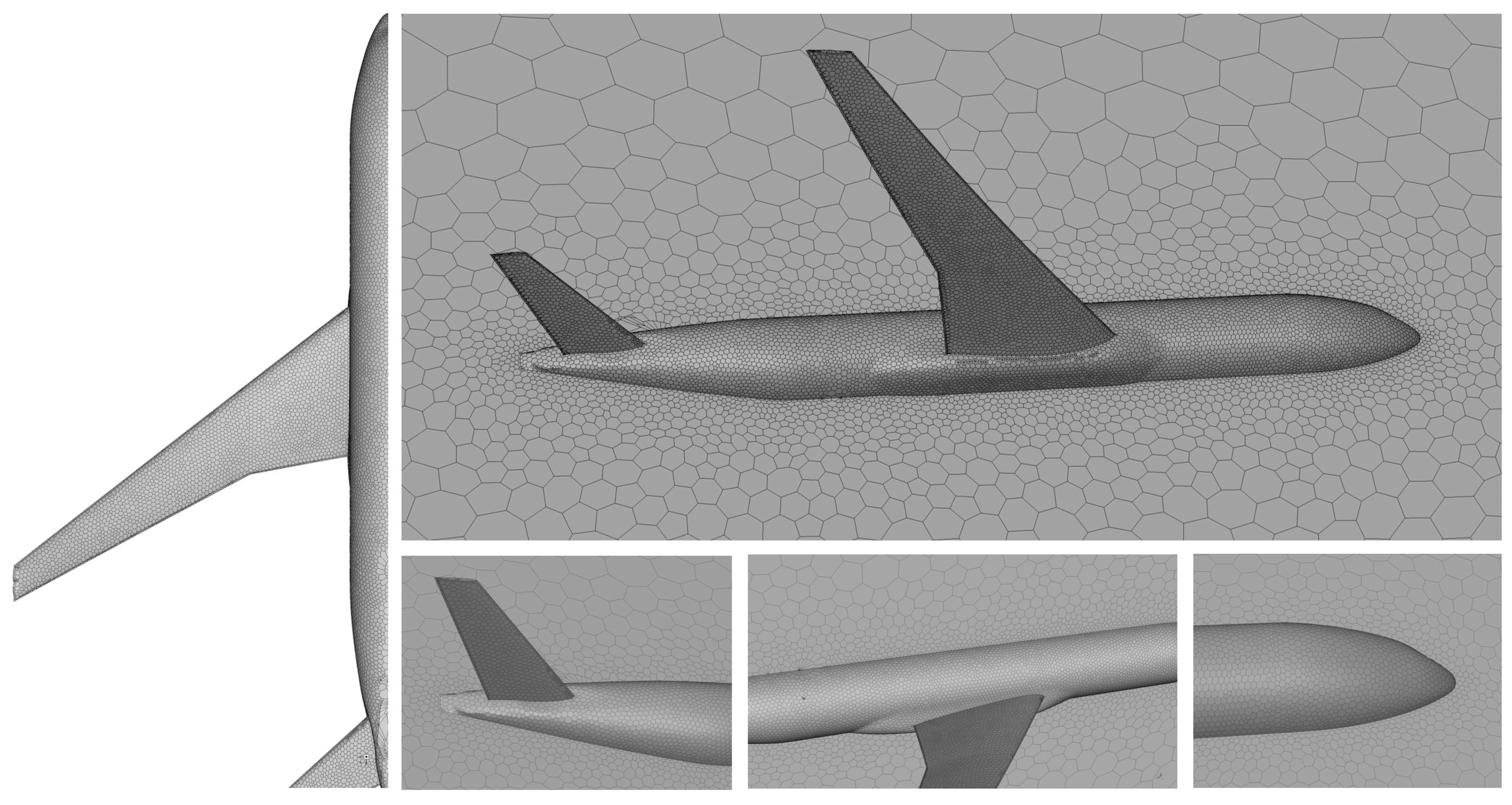
3.2.1. CFD Computational Set-Up
3.2.2. FSI Computational Set-Up
3.2.3. Computational Matrix
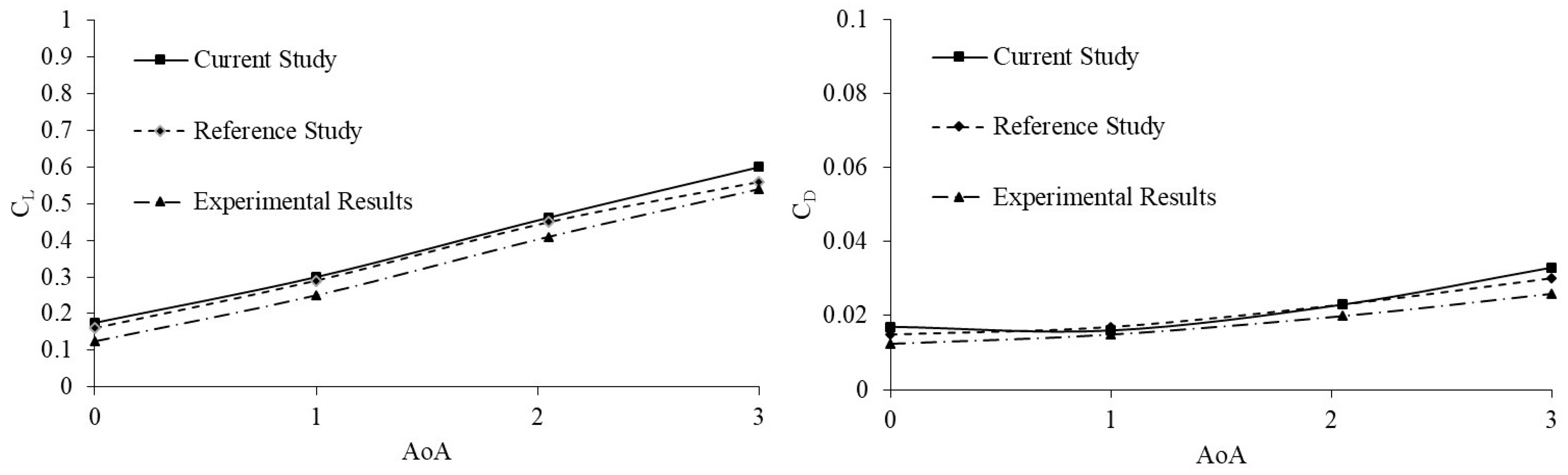
3.3. Computational Results and Analysis (Incl. Validation)
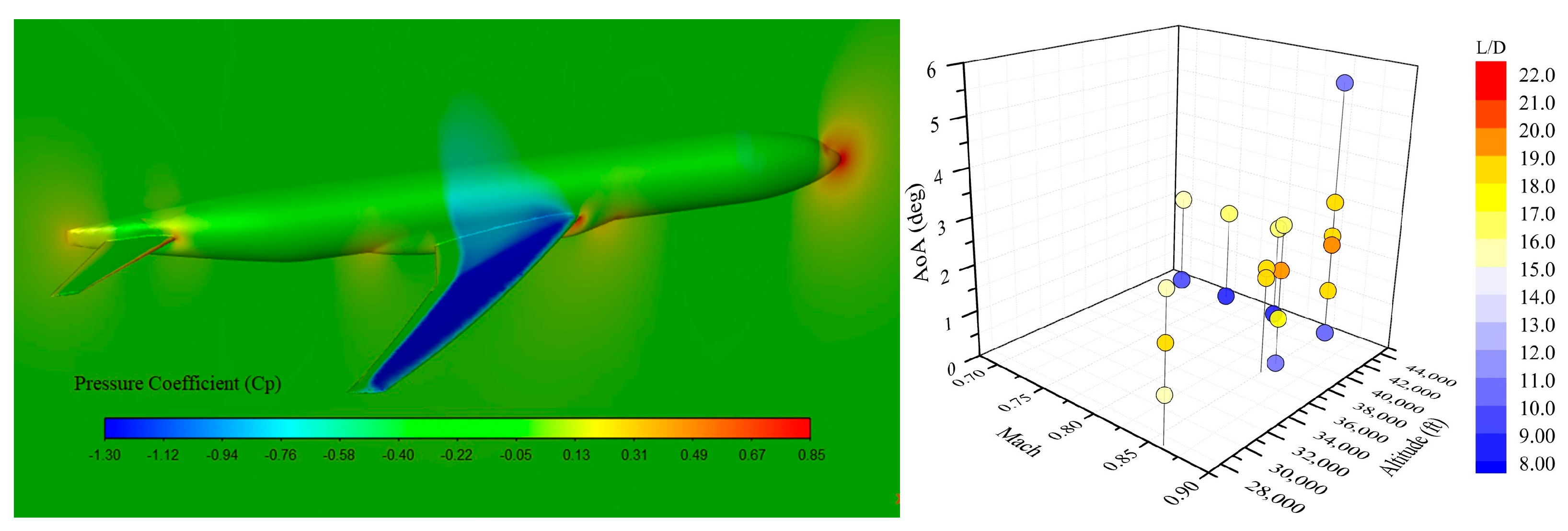
3.3.1. Aerodynamic (CFD) Results
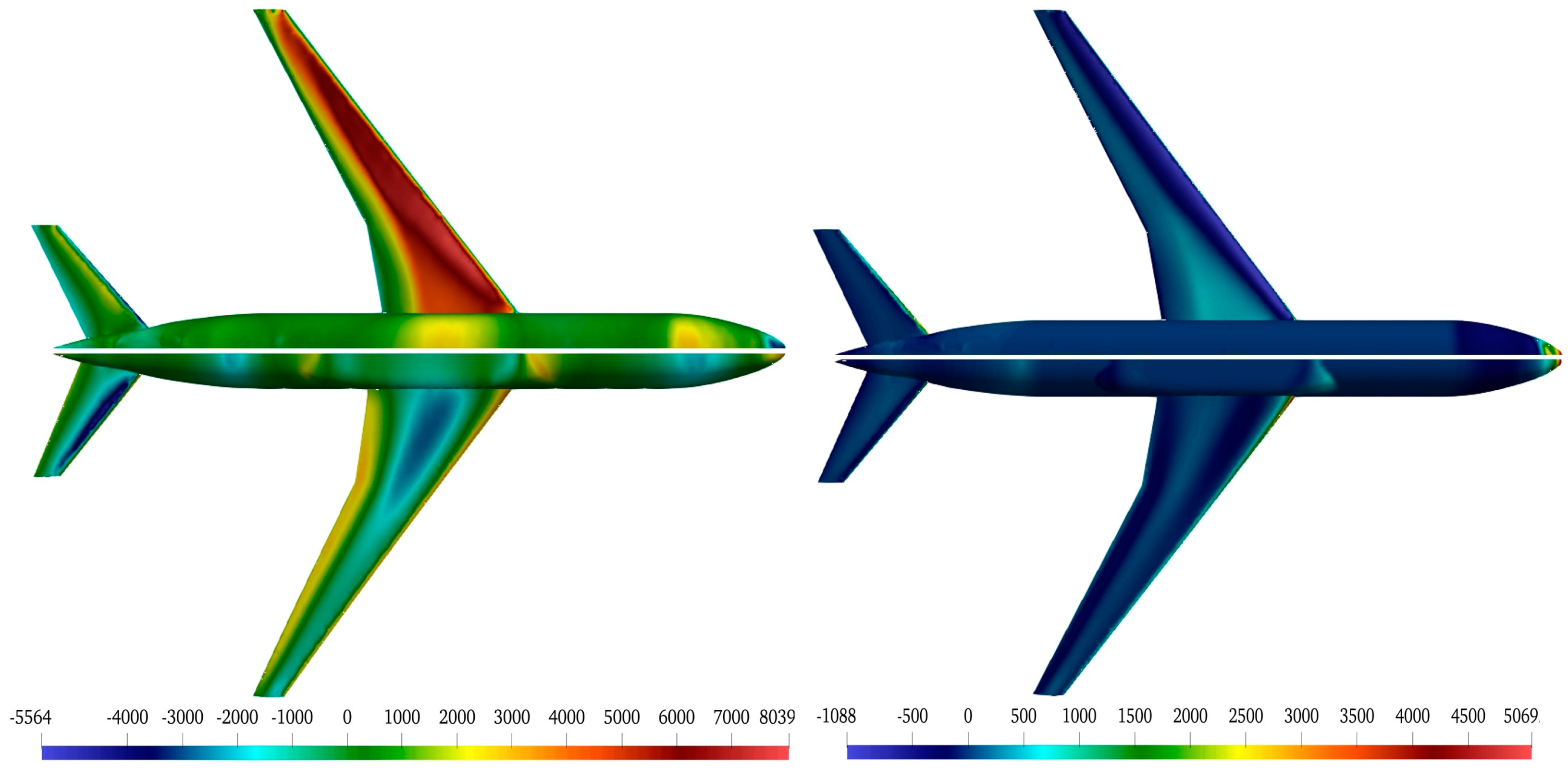
3.3.2. Structural (FSI) Results
4. Aero-Structural Characterization of BWA/SL Aircraft
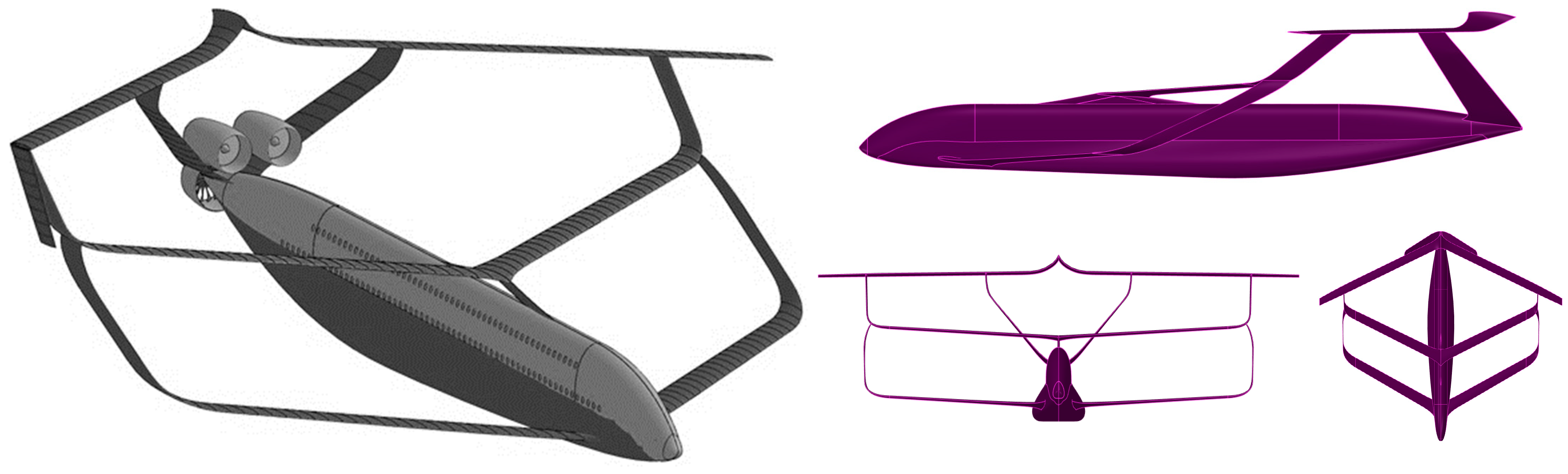
4.1. Main Characteristics of BWA/SL Aircraft
4.2. Computational Set-Up
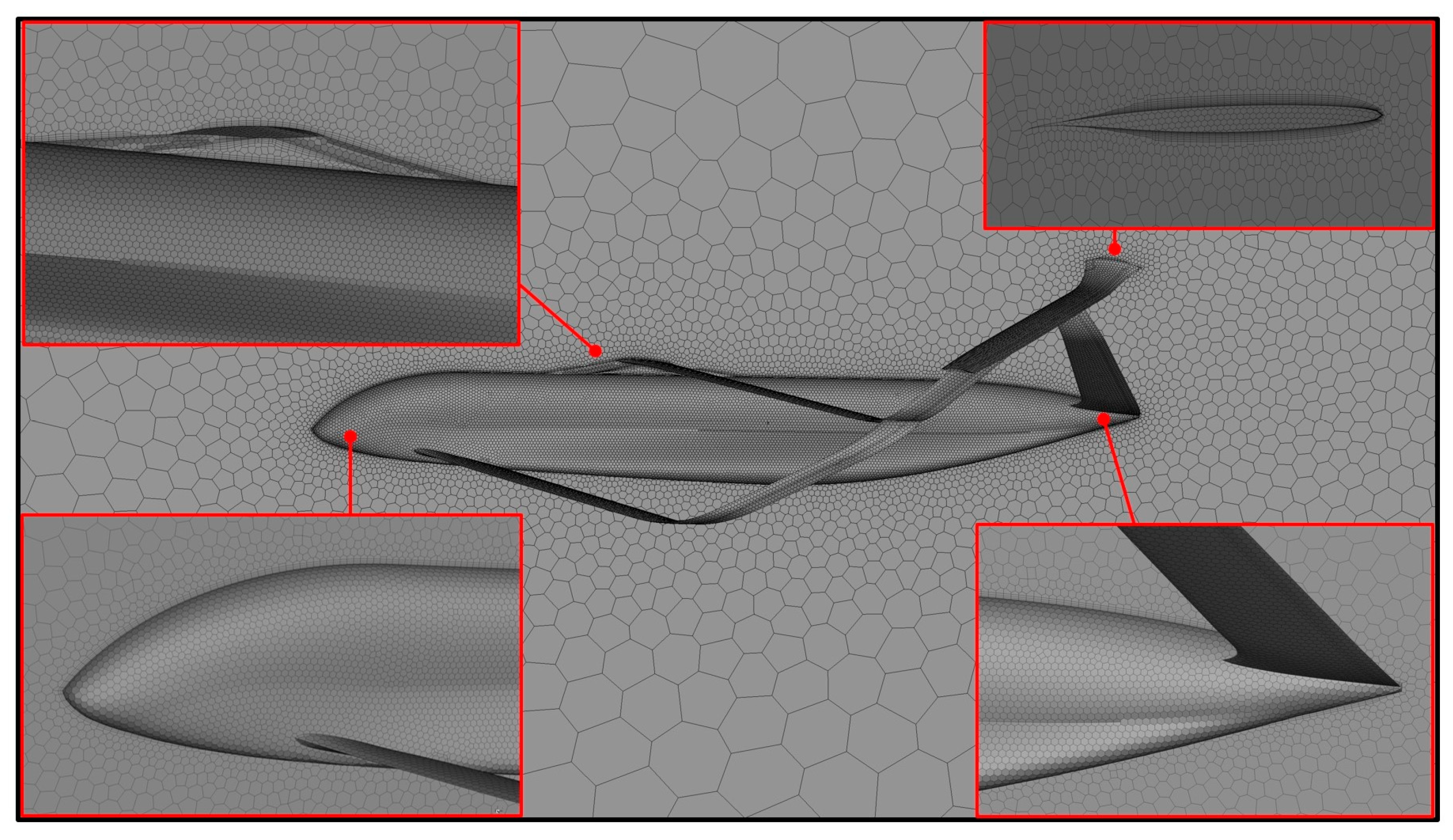
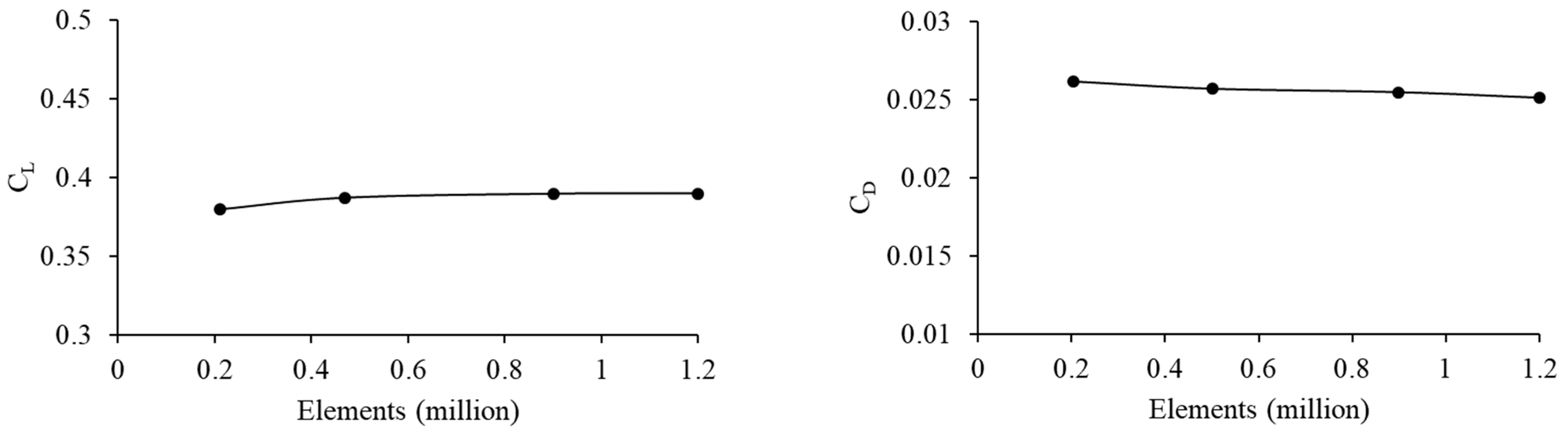
4.2.1. CFD Computational Set-Up
4.2.2. FSI Computational Set-Up
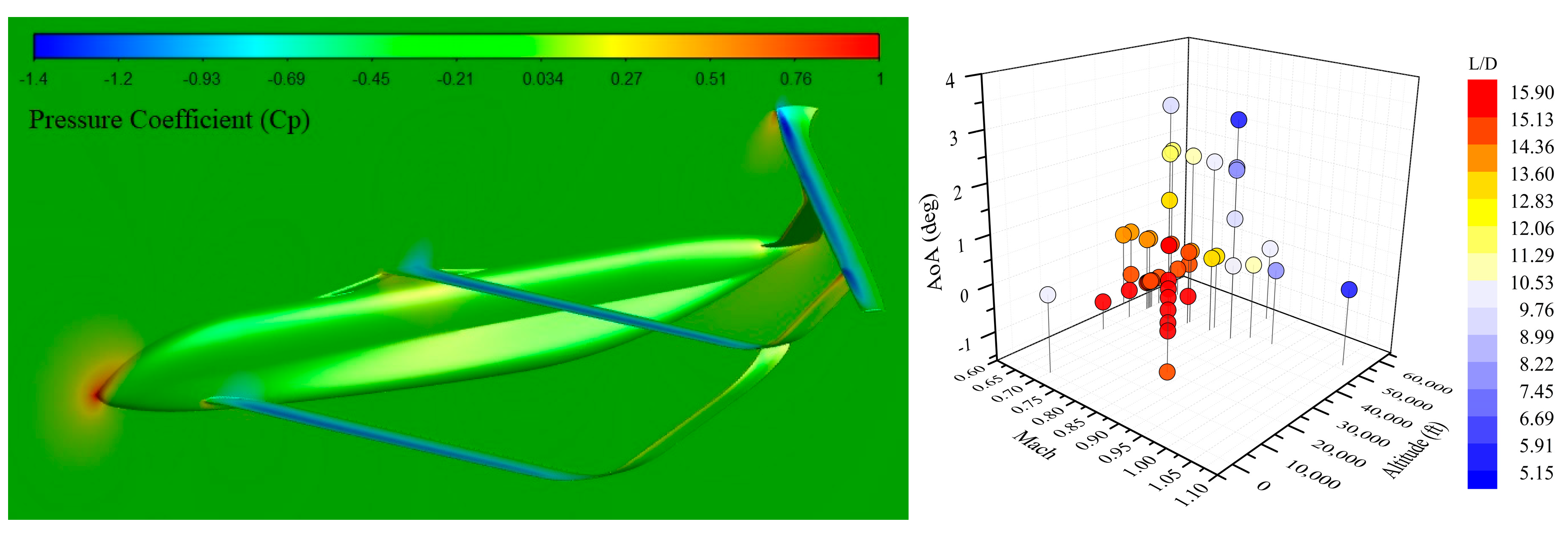
4.2.3. Computational Matrix
4.3. Computational Results and Analysis (Incl. Validation)
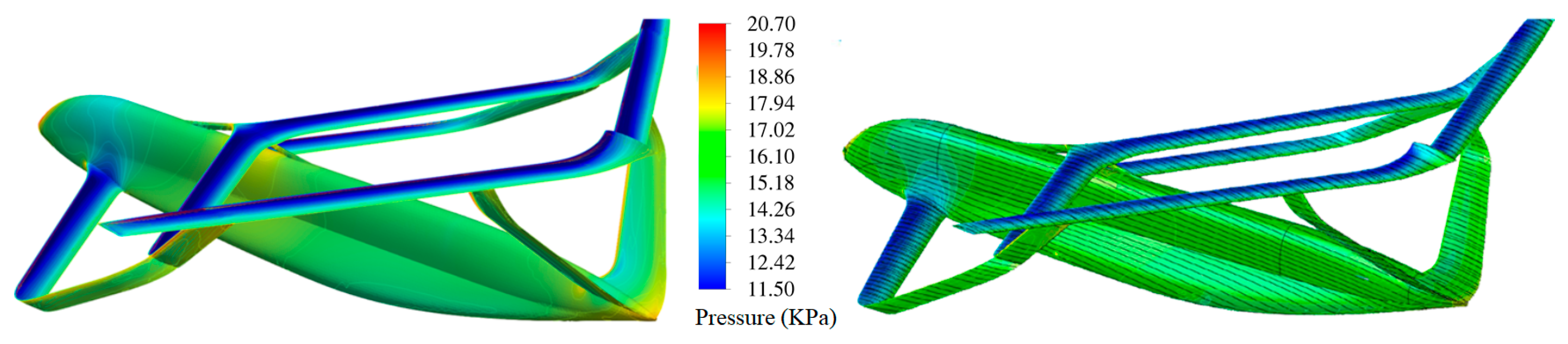
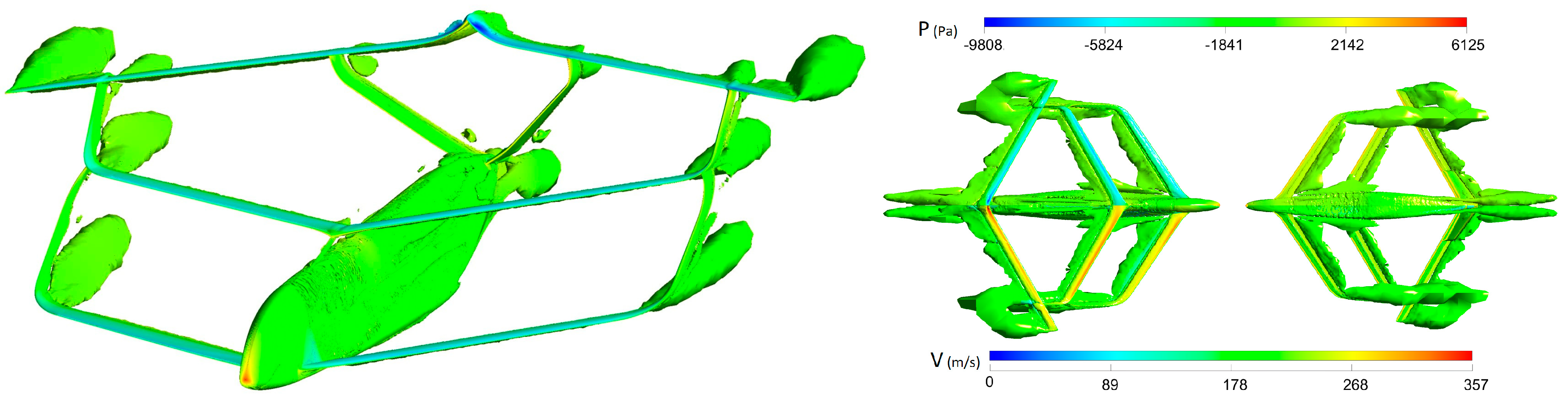
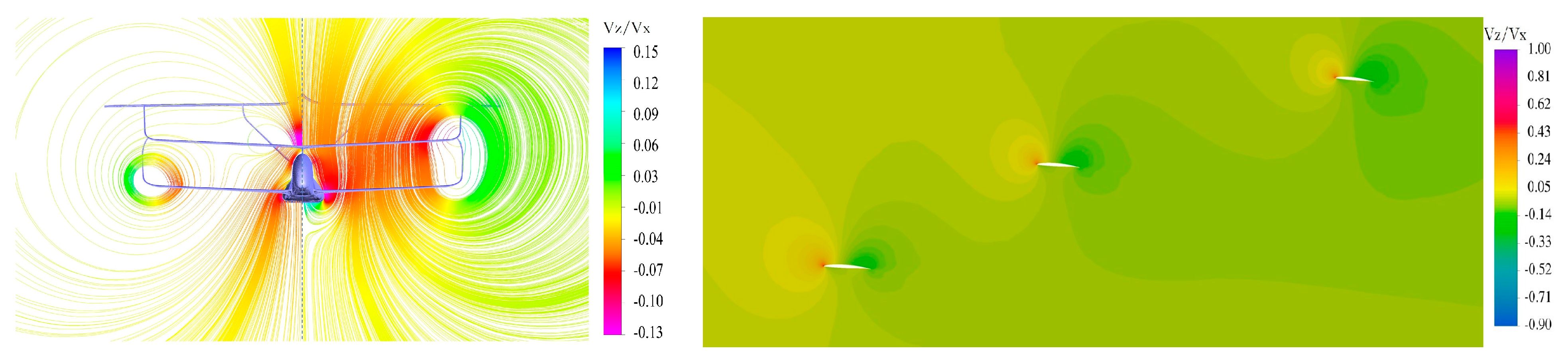
4.3.1. Aerodynamic (CFD) Results
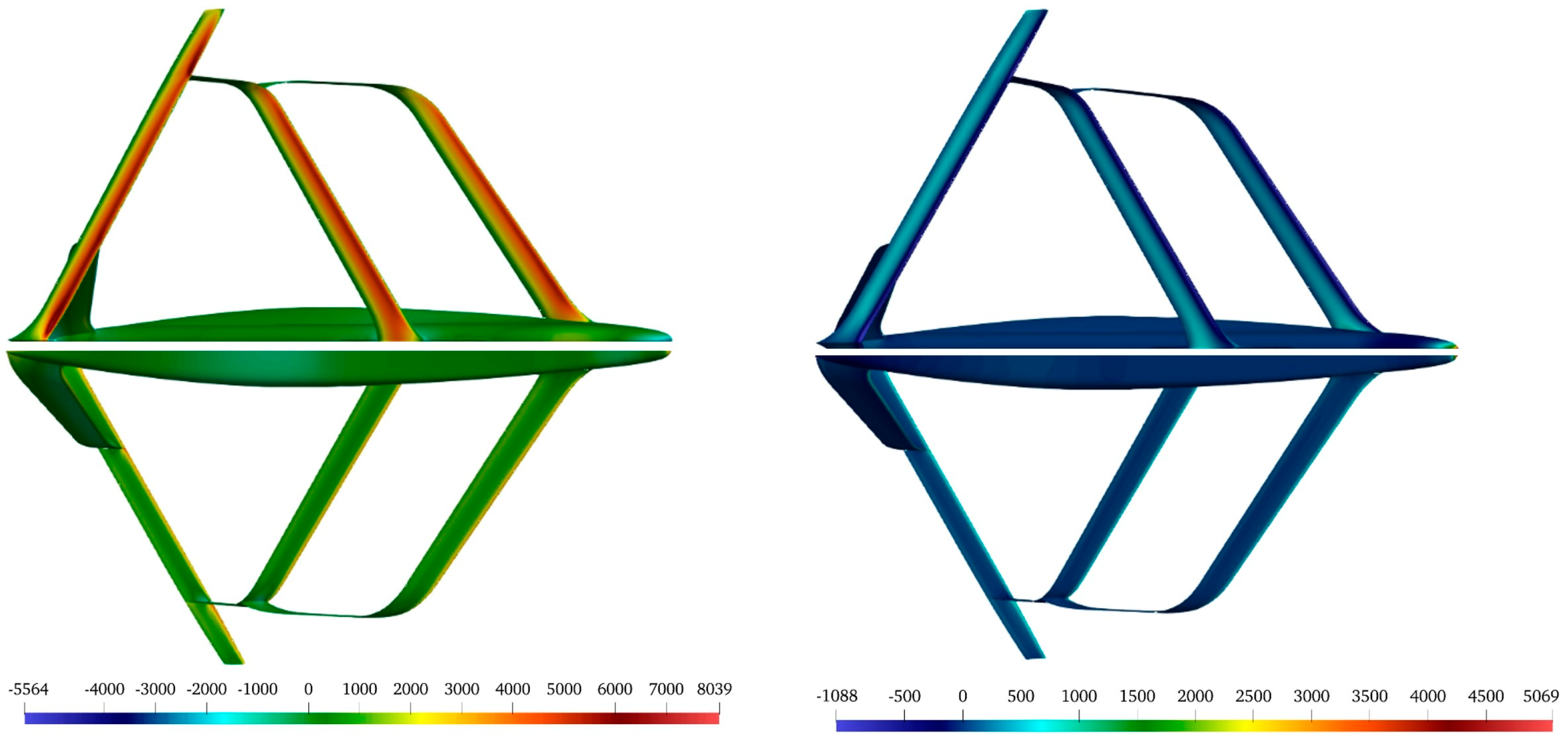
4.3.2. Structural (FSI) Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Okonkwo, P.; Smith, H. Review of evolving trends in blended wing body aircraft design. Prog. Aerosp. Sci. 2016, 82, 1–23. [Google Scholar] [CrossRef]
- Secco, N.R.; Martins, J.R. RANS-Based Aerodynamic Shape Optimization of a Strut-Braced Wing with Overset Meshes. J. Aircr. 2019, 56, 217–227. [Google Scholar] [CrossRef]
- Wolkovitch, J. The joined wing—An overview. J. Aircr. 1986, 23, 161–178. [Google Scholar] [CrossRef]
- Lewis, P. British Aircraft 1809–1914; Putnam: London, UK, 1962. [Google Scholar]
- Elliot, B.A. Bleriot: Herald of an Age; Arcadia Publishing: Mount Pleasant, CA, USA, 2000. [Google Scholar]
- Prandtl, L. Induced Drag of Multiplanes. In Technical Note from the National Advisory Committee for Aeronautics; NACA: Washington, DC, USA, 1924. [Google Scholar]
- Munk, M.M. General biplane theory. In Technical Report from the National Advisory Committee for Aeronautics; NACA: Washington, DC, USA, 1923. [Google Scholar]
- Suder, K.L. Overview of the NASA Environmentally Responsible Aviation Project’s Propulsion Technology Portfolio. In AIAA Paper No. 2012-4038; AIAA: Reston, VA, USA, 2012. [Google Scholar]
- Abu Salem, K.; Binante, V.; Cipolla, V.; Maganzi, M. PARSIFAL Project: A Breakthrough Innovation in Air Transport. Aerotec. Missili Spaz. 2018, 97, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Frediani, A.; Cipolla, V.; Abu Salem, K.; Binante, V.; Scardaoni, M.P. Conceptual design of PrandtlPlane civil transport aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1675–1687. [Google Scholar] [CrossRef] [Green Version]
- Frediani, A.; Cipolla, V.; Salem, K.A.; Binante, V.; Scardaoni, M.P. On the preliminary design of PrandtlPlane civil transport aircraft. In Proceedings of the 7th EUCASS Conference (paper #546), Milano, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Oliviero, F.; Frediani, A.; Rizzo, E. Design of an airfreight system based on an innovative PrandtlPlane aircraft. In AIAA Paper No. 2015-1186; AIAA: Reston, VA, USA, 2015. [Google Scholar]
- Cipolla, V.; Salem, K.A.; Scardaoni, M.P.; Binante, V. Preliminary design and performance analysis of a box-wing transport aircraft. In AIAA Paper No. 2020-0267; AIAA: Reston, VA, USA, 2020. [Google Scholar]
- Cipolla, V.; Abu Salem, K.; Bachi, F. Preliminary stability analysis methods for PrandtlPlane aircraft in subsonic conditions. Aircr. Eng. Aerosp. Technol. 2019, 91, 525–537. [Google Scholar] [CrossRef] [Green Version]
- Carini, M.; Meheut, M.; Kanellopoulos, S.; Cipolla, V.; Salem, K.A. Aerodynamic analysis and optimization of a box-wing architecture for commercial airplanes. In AIAA Paper No. 2020-1285; AIAA: Reston, VA, USA, 2020. [Google Scholar]
- Frediani, A.; Cipolla, V.; Salem, K.A.; Binante, V.; Scardaoni, M.P. Preliminary transonic CFD analyses of a PrandtlPlane transport aircraft. Transp. Res. Procedia 2018, 29, 82–91. [Google Scholar]
- Scardaoni, M.P.; Montemurro, M.; Panettieri, E. PrandtlPlane wing-box least-weight design: A multi-scale optimisation approach. Aerosp. Sci. Technol. 2020, 106, 106156. [Google Scholar] [CrossRef]
- Cipolla, V.; Frediani, A.; Oliviero, F.; Pinucci, M.; Rizzo, E.; Rossi, R. Ultralight amphibious PrandtlPlane: The final design. In Proceedings of the Italian Association of Aeronautics and Astronautics XXII Conference, Naples, Italy, 9–12 September 2013. [Google Scholar]
- Frediani, A.; Cipolla, V.; Oliviero, F. IDINTOS: The first prototype of an amphibious PrandtlPlane-shaped aircraft, Aerotecnica Missili & Spazio. J. Aerosp. Sci. Technol. Syst. 2015, 94, 195–209. [Google Scholar]
- Zohlandt, C.N. Conceptual Design of High Subsonic PrandtlPlanes. Master’s Thesis, Delft University, Delft, The Netherlands, 2016. [Google Scholar]
- Schiktanz, D.; Scholz, D. Box wing fundamentals—An aircraft design perspective. In Proceedings of the German Aerospace Conference, Bremen, Germany, 27–29 September 2011; ISBN 978-3-932182-74-X. [Google Scholar]
- Andrews, S.; Perez, R. Multidisciplinary Analysis of a Box-Wing Aircraft Designed for a Regional-Jet Mission. In AIAA Paper No. 2015-2793; AIAA: Reston, VA, USA, 2015. [Google Scholar]
- Syamsudin, H. Development of an Approach and Tool to Improve the Conceptual-Design Process of Wing Box Structure of Low-Subsonic Transport Aircraft. Master’s Thesis, Cranfield University, Bedford, UK, 2009. [Google Scholar]
- Jemitola, P.; Fielding, J. Box Wing Aircraft Conceptual Design. In Proceedings of the 28th International Congress of the Aeronautical Sciences (ICAS), Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Jemitola, P. Conceptual Design and Optimization Methodology for Box Wing Aircraft. Ph.D. Thesis, Canfield University, Bedford, UK, 2012. [Google Scholar]
- Salam, I.R.; Bil, C. Multi-disciplinary analysis and optimisation methodology for conceptual design of a box-wing aircraft. Aeronaut. J. 2016, 120, 1315–1333. [Google Scholar] [CrossRef]
- Ribeiro, F.C.; de Paula, A.; Scholz, D.; Gil, R.; da Silva, A. Wing geometric parameter studies of a box wing aircraft configuration for subsonic flight. In Proceedings of the 7th EUCASS Conference (paper #447), Milano, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Khalid, A.; Kumar, P. Aerodynamic Optimization of Box Wing–A Case Study. Int. J. Aviat. Aeronaut. Aerospace 2014, 1, 6. [Google Scholar]
- Kumar, P.; Khalid, A. Analysis of aspect ratio and winglet height of a box wing design. In AIAA Paper No. 2014-3002; AIAA: Reston, VA, USA, 2014. [Google Scholar]
- Chau, T.; Zingg, D. Aerodynamic Shape Optimization of a Box-Wing Regional Aircraft Based on the Reynolds-Averaged Navier-Stokes Equations. In AIAA Paper No. 2017-3258; AIAA: Reston, VA, USA, 2017. [Google Scholar]
- Lee, J.Y.; Tan, K.J.; Wang, P.C. Parametric Investigation of Box Wing Configuration in Viscous Flow Regime. In AIAA Paper No. 2018-3814; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Russo, L.; Tognaccini, R.; Demasi, L. Box-Wing and Induced Drag: Compressibility Effects in Subsonic and Transonic Regimes. In AIAA Paper No. 2020-0447; AIAA: Reston, VA, USA, 2020. [Google Scholar]
- Gagnon, H.; Zingg, D.W. Aerodynamic Optimization Trade Study of a Box-Wing Aircraft Configuration. J. Aircr. 2016, 53, 971–981. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Álvarez, J.; Cuerno-Rejado, C.; Meseguer, J. Aerodynamic parametric analysis of an unconventional joined-wing aircraft configuration. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 1917–1933. [Google Scholar] [CrossRef] [Green Version]
- Jemitola, P.; Okonkwo, P. Review of Structural Issues in the Design of a Box Wing Aircraft. J. Aerosp. Eng. Mech. 2019, 3, 161–166. [Google Scholar]
- Jemitola, P.O.; Monterzino, G.; Fielding, J. Wing mass estimation algorithm for medium range box wing aircraft. Aeronaut. J. 2016, 117, 329–340. [Google Scholar] [CrossRef]
- Schiktanz, D.; Scholz, D. The Conflict of Aerodynamic Efficiency and Static Longitudinal Stability of Box Wing Aircraft. In Proceedings of the 3rd CEAS AirSpace Conference, Venice, Italy, 24–28 October 2011. [Google Scholar]
- Andrews, S.; Perez, R. Stability and Control Effects on the Design Optimization of a Box-Wing Aircraft. In AIAA Paper No. 2014-2592; AIAA: Reston, VA, USA, 2014. [Google Scholar]
- Caja-Calleja, R.; Scholz, D. Box Wing Flight Dynamics in the Stage of Conceptual Aircraft Design. In Proceedings of the German Aerospace Conference, Oberpfaffenhofen, Germany, 24–26 October 2012. [Google Scholar]
- Sousa, A.; de Paula, A.; Ribeiro, F.C.; Cardoso-Ribeiro, F. Box wing longitudinal flight quality evaluation. In AIAA Paper No. 2019-3490; AIAA: Reston, VA, USA, 2019. [Google Scholar]
- Frediani, A. The Prandtl Wing, from Innovative Configurations and Advanced Concepts for Future Civil transport Aircraft. In VKI Lecture Series; VKI: Sint-Genesius-Rode, Belgium, 2005. [Google Scholar]
- Frediani, A.; Montanari, G. Best wing system: An exact solution of the Prandtl’s problem. In Variational Analysis and Aerospace Engineering; Springer: New York, NY, USA, 2009; Volume 33. [Google Scholar]
- Bulat, M.P.; Bulat, P.V. Comparison of turbulence models in the calculation of supersonic separated flows. World Appl. Sci. J. 2013, 27, 1263–1266. [Google Scholar]
- Vassberg, J.C.; DeHaan, M.A.; Rivers, S.M.; Wahls, R.A. Development of a Common Research Model for Applied CFD Validation Studies. In AIAA Paper No. 2008-6919; AIAA: Reston, VA, USA, 2008. [Google Scholar]
- Lacy, D.; Sclafani, A. Development of the High-Lift Common Research Model (HL-CRM): A Representative High Lift Configuration for Transonic Transports. In AIAA Paper No. 2016-0308; AIAA: Reston, VA, USA, 2016. [Google Scholar]
- Brooks, T.; Kenway, G.; Martins, J. Benchmark Aero-structural Models for the Study of Transonic Aircraft Wings. AIAA J. 2018, 58, 2840–2855. [Google Scholar] [CrossRef]
- Rivers, M.B.; Dittberner, A. Experimental Investigation of the NASA Common Research Model. In AIAA Paper No. 2010-4218; AIAA: Reston, VA, USA, 2010. [Google Scholar]
- Keye, S.; Rudnik, R. Validation of Wing Deformation Simulations for the NASA CRM Model using Fluid-Structure Interaction Computations. In AIAA Paper No. 2015-0619; AIAA: Reston, VA, USA, 2015. [Google Scholar]
- Martínez-Val, R.; Pérez, E.; Palacín, J.F. Historical evolution of air transport productivity and efficiency. In AIAA Paper No. 2005-121; AIAA: Reston, VA, USA, 2005. [Google Scholar]
- Redonnet, S.; Desquesnes, G.; Manoha, E.; Parzani, C. Numerical Study of Acoustic Installation Effects with a CAA method. AIAA J. 2010, 48, 929–937. [Google Scholar] [CrossRef]
- Andrews, S.A.; Perez, R.E. Comparison of box-wing and conventional aircraft mission performance using multidisciplinary analysis and optimization. Aerosp. Sci. Technol. 2018, 79, 336–351. [Google Scholar] [CrossRef]












| Area (S) | Sref = 383.69 m2 |
| Mean Aerodynamic Chord (MAC) | cref = 7 m |
| Span (b) | b = 58.76 m |
| Aspect Ratio (AR) | 9 |
| Taper Ratio (λ) | 0.275 |
| Sweep (Λ) | 35° |
| Dihedral (Γ) | 0° (ground) 5° (cruise) |
| Altitude (ft) | Airspeed (Mach) | Re (cref = MAC = 7 m) | AoA (α) |
|---|---|---|---|
| 27,300 | 0.86 | 61 × 106 | 1°; 2°; 3° |
| 37,000 | 0.85 | 43 × 106 | 2.05°; 2.25° |
| 38,500 | 0.85 | 40 × 106 | 0°; 1°; 2.05°; 3° |
| 44,000 | 0.85 | 30 × 106 | 0°; 1°; 2.05°; 2.25°, 3°, 5.5° |
| 0.8; 0.75; 0.7 | 29 × 106; 27.2 × 106; 25.4 × 106 | 0°; 2.05° |
| Main Wing | Horizontal Tail | Fuselage | Total | |
|---|---|---|---|---|
| Lift | 126.63 | −6.03 | 17.48 | 138.08 |
| Drag | 4.82 | 0.54 | 1.62 | 6.99 |
| L/D | 26.25 | −11.11 | 10.74 | 19.74 |
| 1st Wing | 2nd Wing | 3rd Wing | Total/Reference | |
|---|---|---|---|---|
| Area (S) | 243.8 m2 | 247 m2 | 270.6 m2 | Sref = 761.4 m2 |
| MAC | 4.21 m | 4.05 m | 3.12 m | cref = 3.79 m |
| Span (b) | 60 m | 60 m | 80 m | bref = 60 |
| Aspect ratio (AR) | 14.7 | 14.5 | 23.6 | N/A |
| Taper ratio (λ) | 0.802 | 0.764 | 0.761 | N/A |
| Sweep (Λ) | 34° | 31° | −30° | N/A |
| Dihedral (Γ) | 2.56° | 2.62° | −1.22° | N/A |
| Altitude (ft) | Airspeed (Mach) | Re (cref = MAC = 3.79 m) | AoA (α) |
|---|---|---|---|
| 0 | 0.7 | 61.8 × 106 | 0° |
| 25,000 | 0.65 | 27.2 × 106 | −1° |
| 35,000 | 0.65 | 19.3 × 106 | −1° |
| 40,000 | 0.6 | 14.2 × 106 | 0° |
| 42,000 | 0.65 | 14.0 × 106 | −1°; 0° |
| 42,500 | 0.65 | 13.7 × 106 | −1° |
| 43,000 | 0.6; 0.65; 0.75 | 12.3 × 106; 13.4 × 106; 15.4 × 106 | 0°; −1° |
| 0.7 | 14.4 × 106 | −3°; −2°; −1.8°; −1.5°; −1.2°; −1°; −0.8°; 0°; 1°; 2°; 3° | |
| 43,500 | 0.65 | 13.0 × 106 | −1° |
| 44,000 | 0.65 | 12.7 × 106 | −1° |
| 0.7; 0.75; 0.8 | 13.7 × 106; 14.7 × 106; 15.7 × 106 | 0°; 2.05° | |
| 0.85 | 16.7 × 106 | 0°; 1°; 2°; 2.05°;3° | |
| 46,000 | 0.8 | 14.2 × 106 | 0° |
| 47,000 | 0.65 | 11.0 × 106 | −1° |
| 48,000 | 0.875 | 14.2 × 106 | 0° |
| 49,000 | 0.92 | 14.2 × 106 | 0° |
| 52,000 | 1.06 | 14.2 × 106 | 0° |
| 55,000 | 0.65 | 7.5 × 106 | −1° |
| 60,000 | 0.65 | 5.9 × 106 | −1° |
| 0.85 | 7.7 × 106 | 0° |
| 1st Wing | 2nd Wing | 3rd Wing | V-Tail | Fuselage | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | Alter. | Present | Alter. | Present | Alter. | Present | Alter. | Present | Alter. | Present | Alter. | |
| Lift | 48.94 | 45.24 | 52.35 | 48.43 | 59.58 | 53.96 | 2.34 | 1.99 | 2.77 | 2.61 | 165.98 | 152.23 |
| Drag | 1.83 | 1.63 | 2.64 | 2.28 | 4.60 | 3.85 | 0.51 | 0.43 | 1.00 | 1.01 | 10.58 | 9.20 |
| L/D | 26.74 | 27.75 | 19.83 | 21.24 | 12.95 | 14.02 | 4.59 | 4.63 | 2.77 | 2.58 | 15.69 | 16.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.; Redonnet, S.; Hernadi, A. Computational Investigation of a Novel Box-Wing Aircraft Concept. Appl. Sci. 2022, 12, 752. https://doi.org/10.3390/app12020752
Hasan M, Redonnet S, Hernadi A. Computational Investigation of a Novel Box-Wing Aircraft Concept. Applied Sciences. 2022; 12(2):752. https://doi.org/10.3390/app12020752
Chicago/Turabian StyleHasan, Mehedi, Stephane Redonnet, and Andras Hernadi. 2022. "Computational Investigation of a Novel Box-Wing Aircraft Concept" Applied Sciences 12, no. 2: 752. https://doi.org/10.3390/app12020752
APA StyleHasan, M., Redonnet, S., & Hernadi, A. (2022). Computational Investigation of a Novel Box-Wing Aircraft Concept. Applied Sciences, 12(2), 752. https://doi.org/10.3390/app12020752








