Design and Analysis for Hypoid Gears with Ease-Off Flank Modification
Abstract
:1. Introduction
2. Ease-Off Flank Modification Methodology for the Pinion
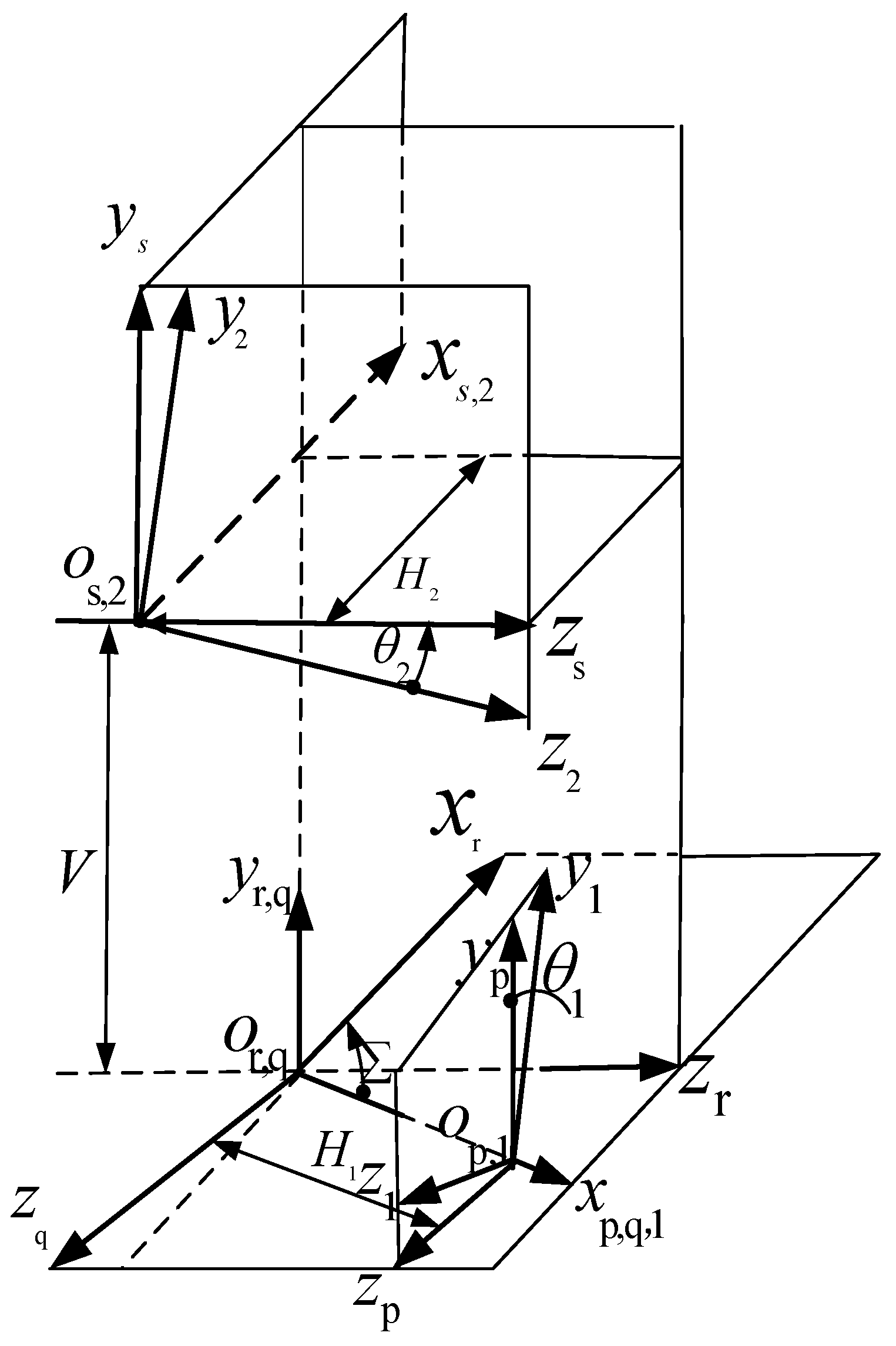
2.1. Tooth Representation of Pinion Globally Conjugated with the Gear
2.2. Tooth Representation of Pinion with Ease-Off Flank Modification Only Depending on Transmission Error
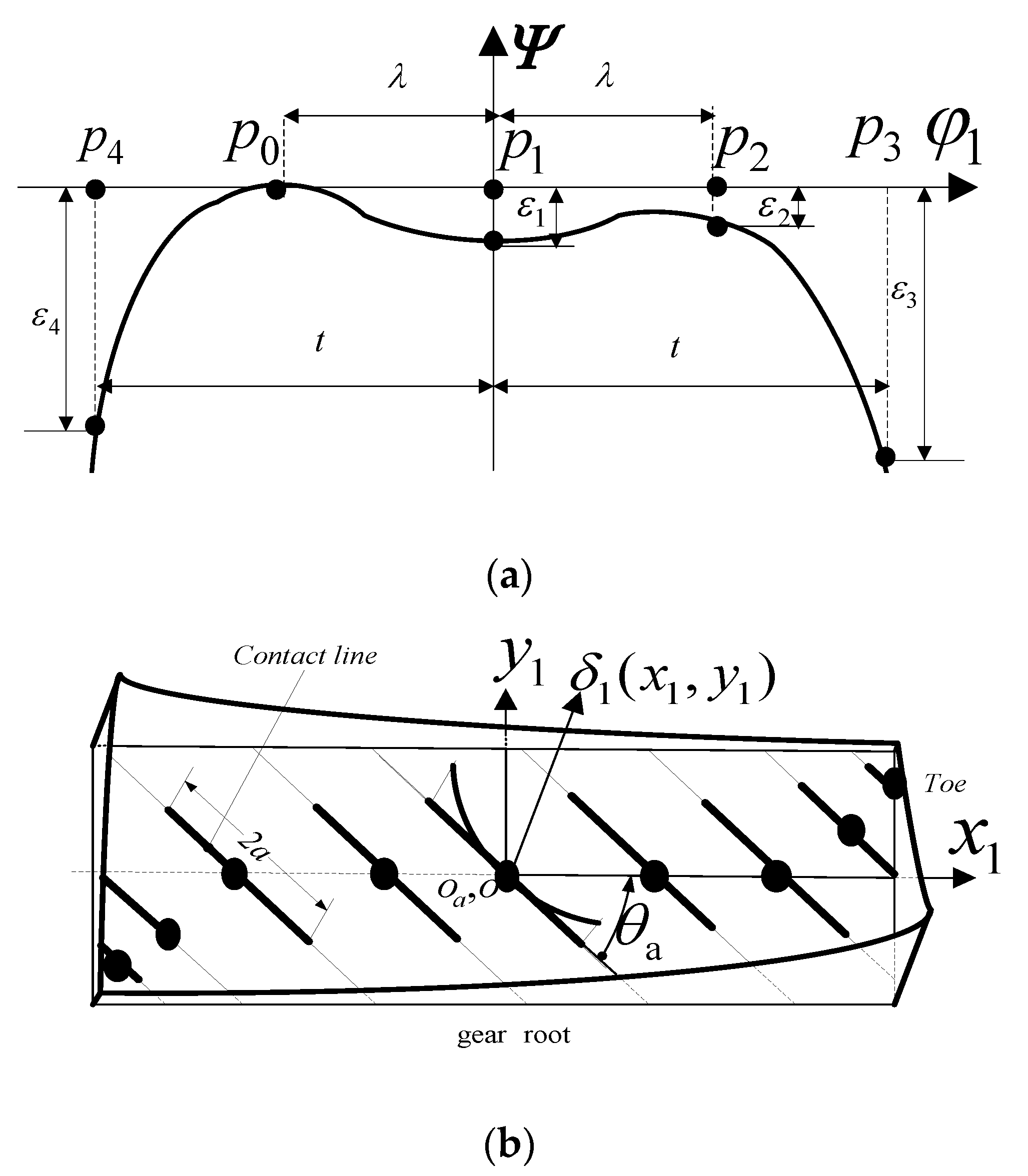
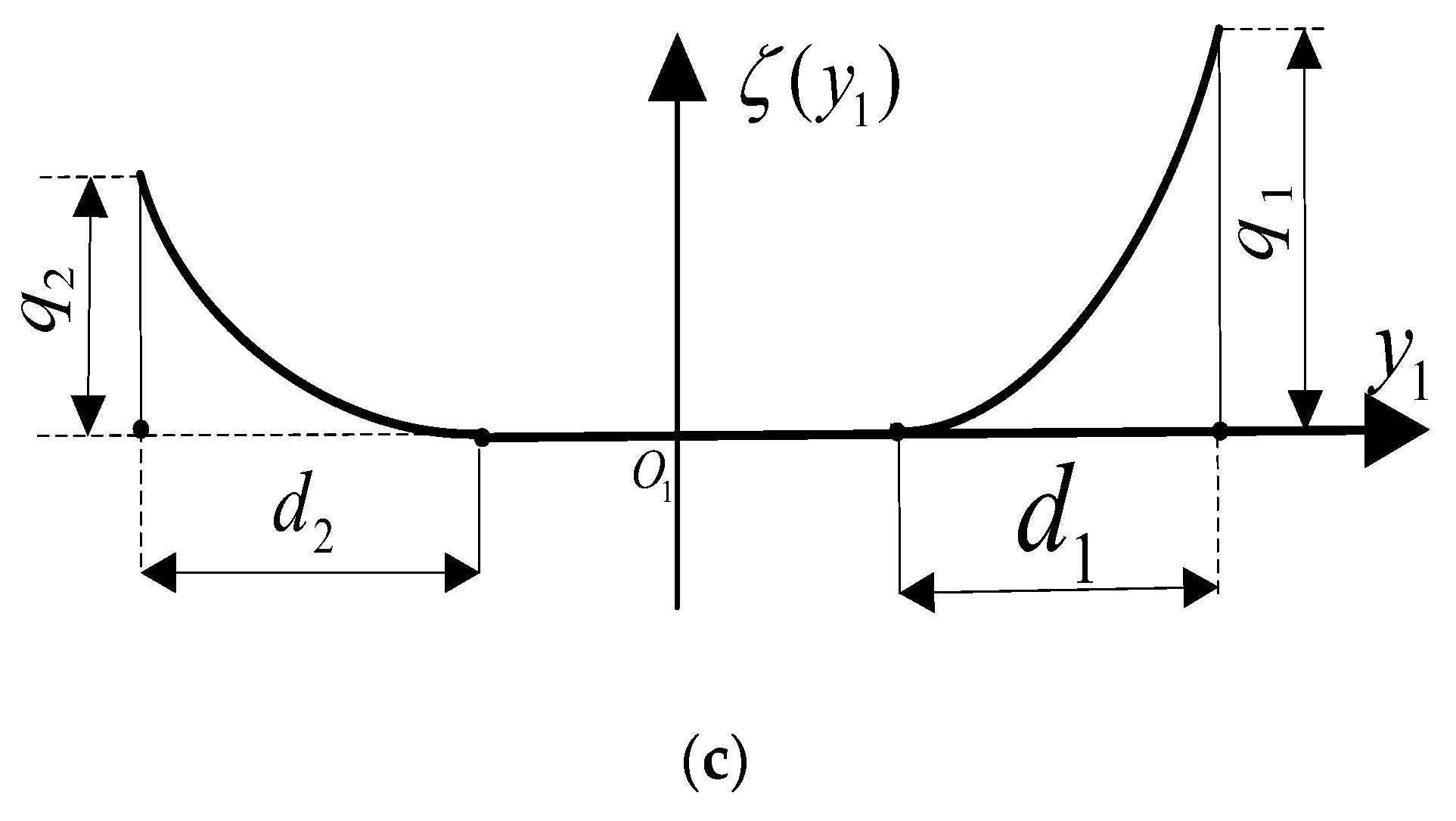
2.3. Tooth Expression of Pinion with Ease-Off Flank Modification Both Depending on Transmission Error and Length of Contact Line
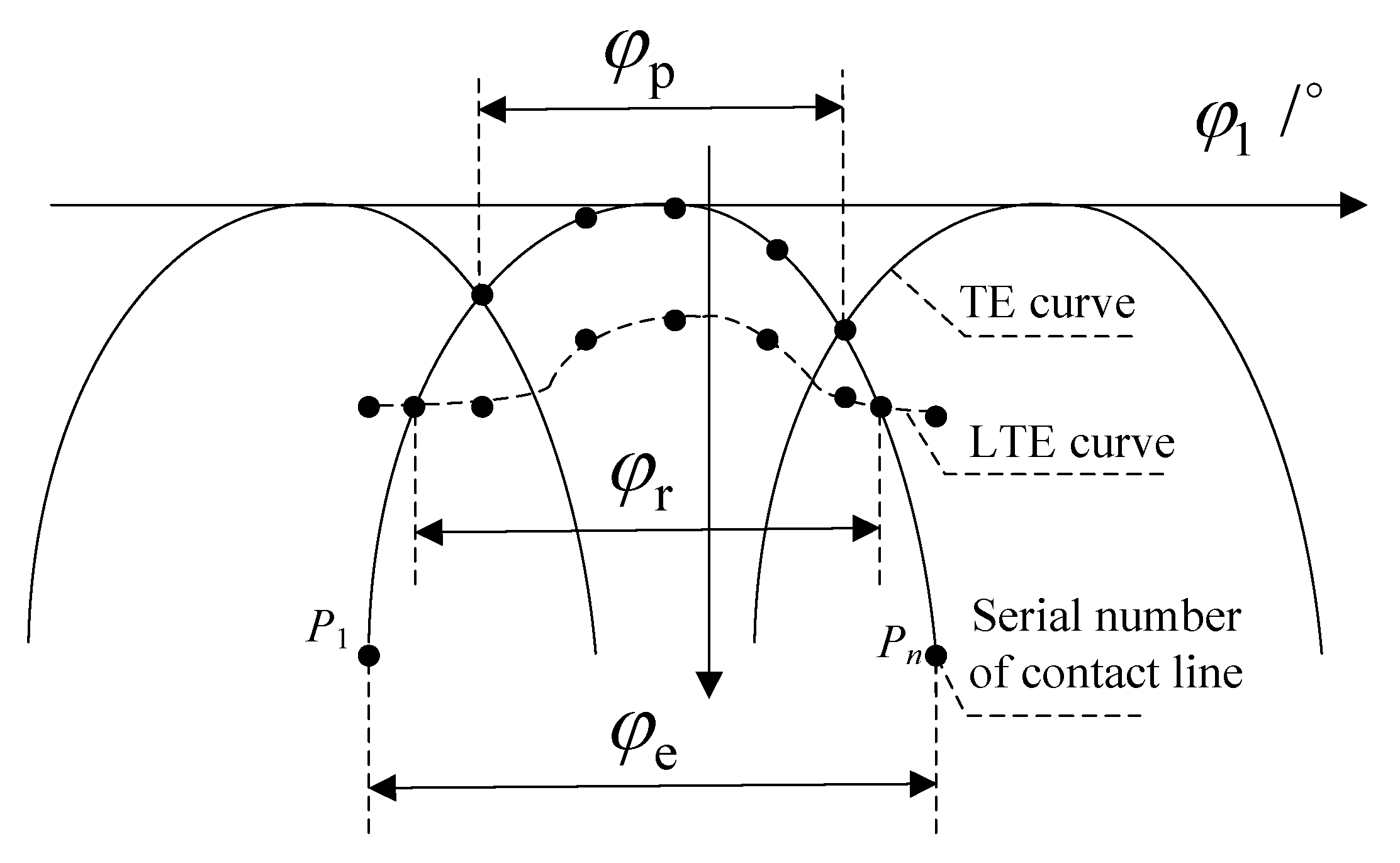
3. Determination of Ease-Off Flank Modification Parameters
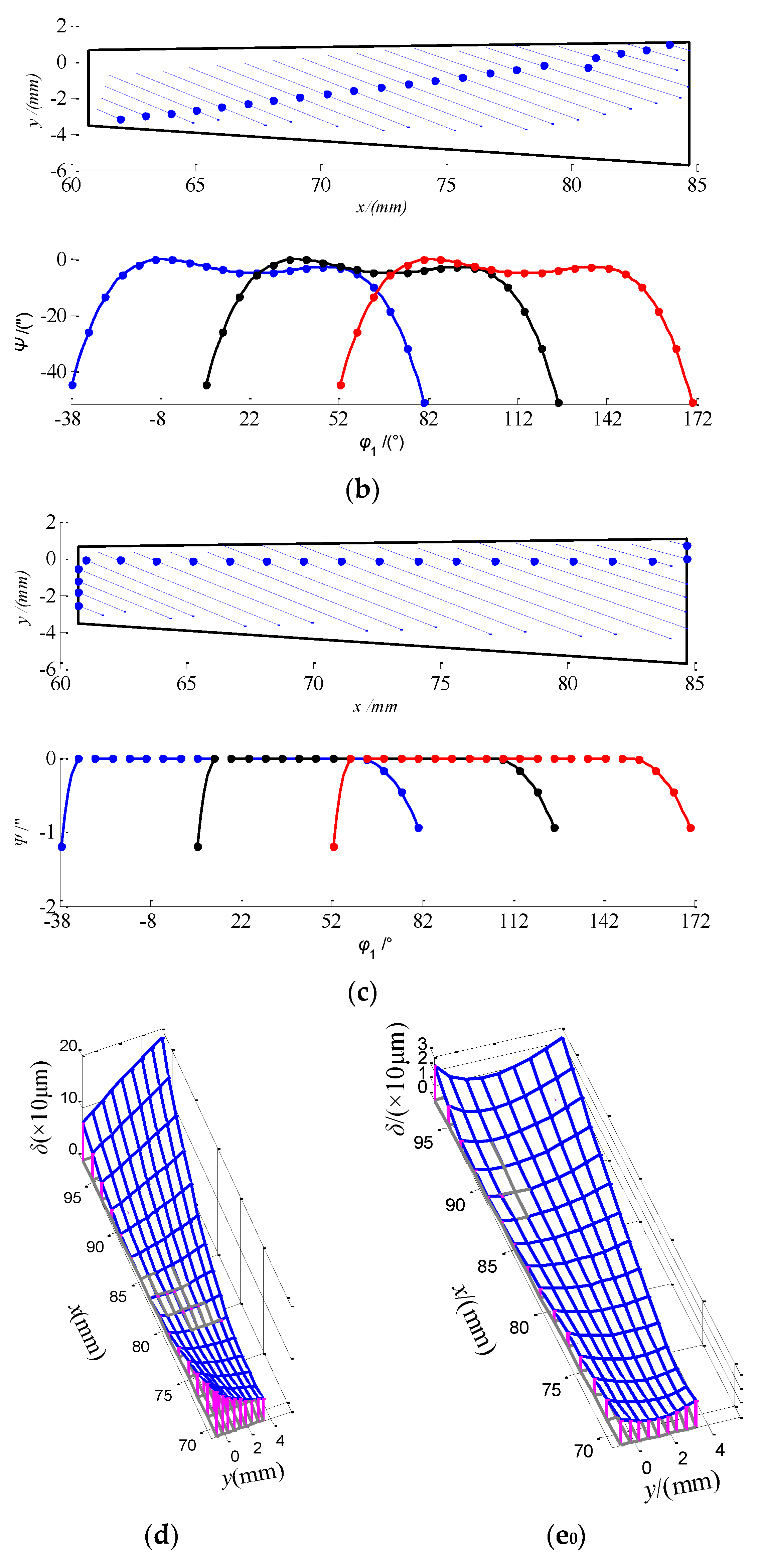
3.1. TCA Model for Hypoid Gears with Ease-Off Flank Modification
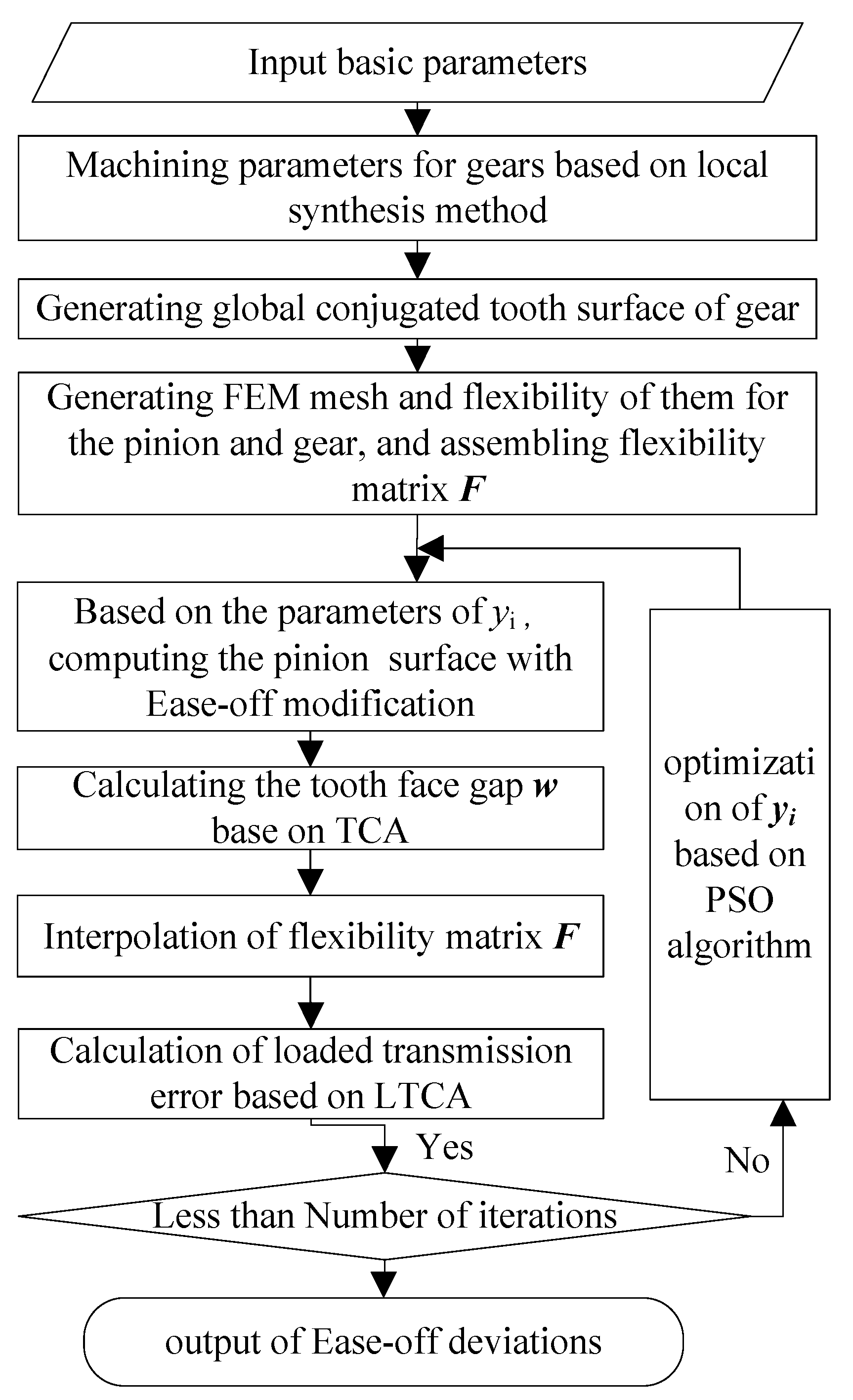
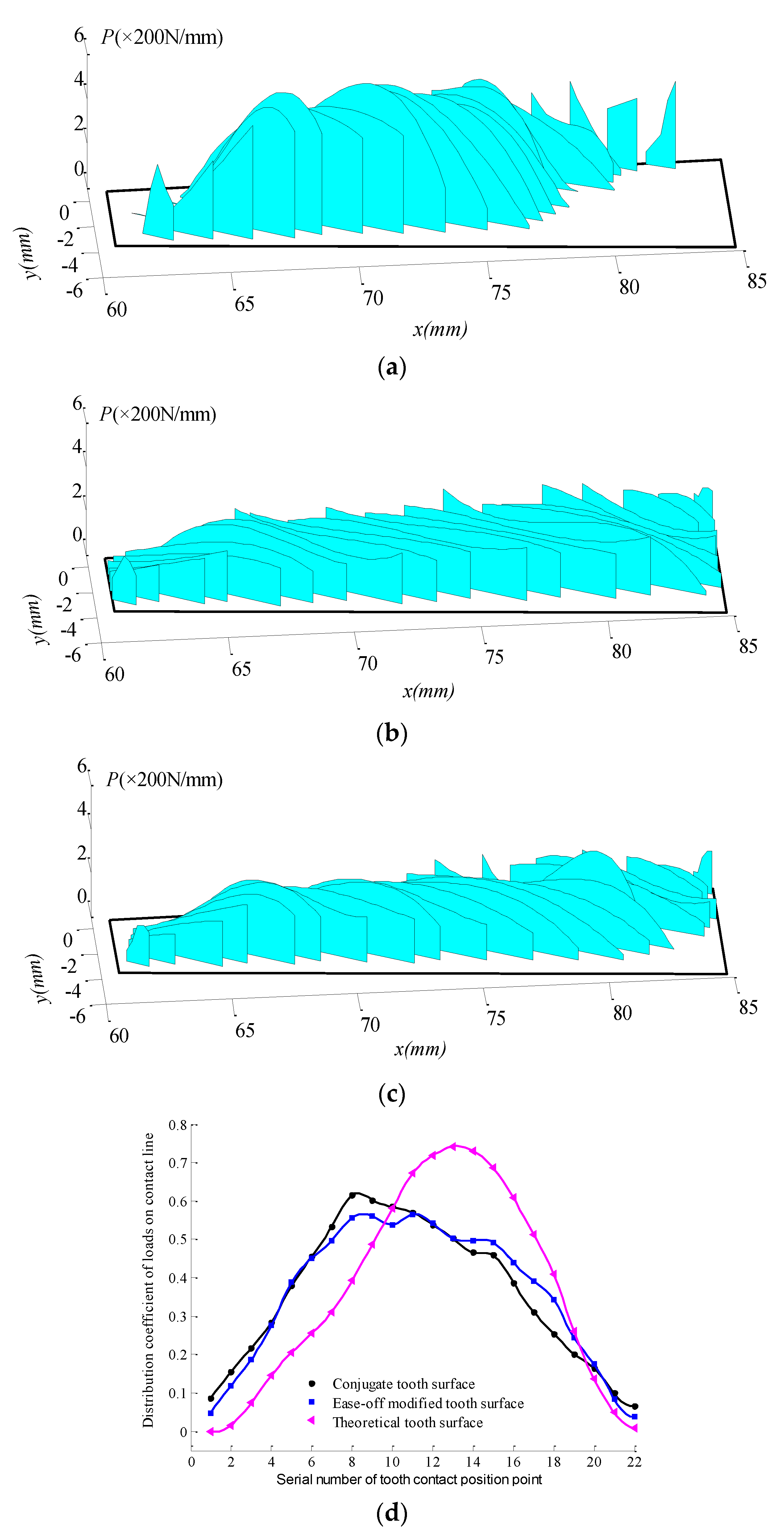
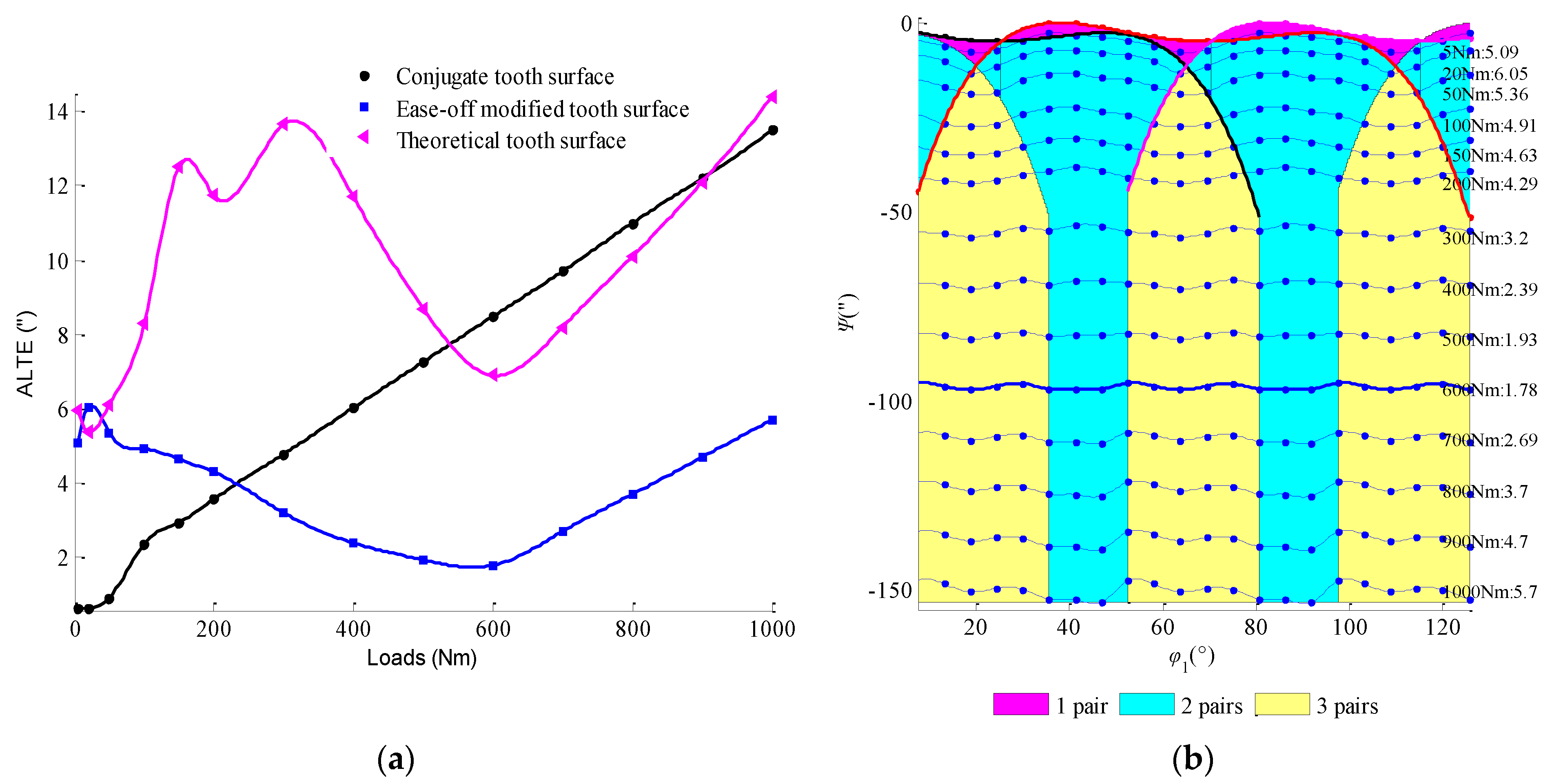
3.2. Determination of Ease-Off Flank Modification Parameters Based on LTCA
3.3. Actual Coincidence Degree of Modification Tooth Surface
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory, 2nd ed.; Cambridge University Press: New York, NY, USA, 2004; pp. 240–260. [Google Scholar]
- Zhang, Y.; Fang, Z. Analysis of transmission errors under load of helical gears with modified tooth surfaces. J. Mech. Des. 1997, 119, 1206. [Google Scholar] [CrossRef]
- Litvin, F.L.; Zhang, Y. Local Synthesis and Tooth Contact Analysis of Face-Milled Spiral Bevel Gears; Illinois Univ at Chicago Circle: Chicago, IL, USA, 1991. [Google Scholar]
- Stadtfeld, H.J.; Gaiser, U. The ultimate motion graph. J. Mech. Des. 2000, 122, 317–322. [Google Scholar] [CrossRef]
- Wang, P.Y.; Fong, Z.H. Fourth-Order Kinematic Synthesis for Face-Milling Spiral Bevel Gears. With Modified Radial Motion (MRM) Correction. J. Mech. Des. 2006, 128, 457–467. [Google Scholar] [CrossRef]
- Fang, Z.D.; Liu, T.; Deng, X.Z. Meshing analysis of spiral bevel gear based on transmission error design. J. Aeronaut. 2002, 23, 226–230. [Google Scholar]
- Zhou, K.H.; Tang, J.Y.; Yan, H.Z. Design method of point meshing tooth surface based on predetermined meshing characteristics. J. Aerosp. Power 2009, 24, 2612–2617. [Google Scholar]
- Cao, X.M.; Deng, X.Z.; Nie, S.W. Topological structure design of high order transmission error tooth surface of aviation spiral bevel gear based on conjugate tooth surface modification. J. Aerosp. Power 2015, 30, 195–200. [Google Scholar]
- Wang, P.; Zhang, Y.; Wan, M. Global synthesis for face milled spiral bevel gears with zero transmission errors. J. Mech. Des. 2016, 138, 033302. [Google Scholar] [CrossRef]
- Wang, X.; Fang, Z.D.; Mu, Y.M. The optimal design of HGT hypoid gear bearing transmission error. Vib. Shock. 2017, 36, 34–40. [Google Scholar]
- Gonzalez-Perez, I.; Fuentes-Aznar, A. Conjugated action and methods for crowning in face-hobbed spiral bevel and hypoid gear drives through the spirac system. Mech. Mach. Theory 2019, 139, 109–130. [Google Scholar] [CrossRef]
- Lee, Y.H.; Fong, Z.H. A mathematical model for grinding a stick blade profile to cut hypoid gears. J. Mech. Des. 2020, 142, 053401. [Google Scholar] [CrossRef]
- Fan, Q. Tooth surface error correction for face-hobbed hypoid gears. J. Mech. Des. 2010, 132, 011004. [Google Scholar] [CrossRef]
- Shih, Y.P.; Fong, Z.H. Flank correction for spiral bevel and hypoid gears on a six-axis CNC hypoid gear generator. J. Mech. Des. 2008, 130, 062604. [Google Scholar] [CrossRef]
- Simon, V.V. Generation of hypoid gears on CNC hypoid generator. J. Mech. Des. 2011, 133, 121003. [Google Scholar] [CrossRef]
- Hsu, R.H.; Shih, Y.P.; Fong, Z.H.; Huang, C.L.; Chen, S.H.; Chen, S.S.; Lee, Y.H.; Chen, K.H.; Hsu, T.P.; Chen, W.J. Mathematical Model of a Vertical Six-Axis Cartesian Computer Numerical Control Machine for Producing Face-Milled and Face-Hobbed Bevel Gears. J. Mech. Des. 2020, 142, 043301. [Google Scholar] [CrossRef]
- Ding, H.; Tang, J. Machine-tool settings driven high-order topology optimization to grinding tooth flank by considering loaded tooth contact pattern for spiral bevel gears. Int. J. Mech. Sci. 2020, 172, 105397. [Google Scholar] [CrossRef]
- Artoni, A.; Gabiccini, M.; Kolivand, M. Ease-off based compensation of tooth surface deviations for spiral bevel and hypoid gears: Only the pinion needs corrections. Mech. Mach. Theory 2013, 61, 84–101. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations. J. Mech. Des. 2010, 132, 071004. [Google Scholar] [CrossRef]
- Shih, Y.P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears. Mech. Mach. Theory 2010, 45, 1108–1124. [Google Scholar] [CrossRef]
- Artoni, A.; Kolivand, M.; Kahraman, A. An ease-off based optimization of the loaded transmission error of hypoid gears. J. Mech. Des. 2010, 132, 011010. [Google Scholar] [CrossRef]
- Su, J.Z.; He, Z.X. High precision profile modification of spiral bevel gears. J. South China Univ. Technol. 2014, 42, 91–96. [Google Scholar]
- Ding, H.; Tang, J.; Zhou, Y.; Jue, Z.; Zhong, J.; Wan, G. A multi-objective correction of machine settings considering loaded tooth contact performance in spiral bevel gears by nonlinear interval number optimization. Mech. Mach. Theory 2017, 113, 85–108. [Google Scholar] [CrossRef]
- Simon, V.V. Multi-objective optimization of hypoid gears to improve operating characteristics. Mech. Mach. Theory 2020, 146, 103727. [Google Scholar] [CrossRef]
- Artoni, A.; Gabiccini, M.; Guiggiani, M.; Kahraman, A. Multi-Objective Ease-Off Optimization of Hypoid Gears for Their Efficiency, Noise, and Durability Performances. ASME J. Mech. Des. Dec. 2011, 133, 121007. [Google Scholar] [CrossRef]
- Yan, H.Z.; Xiao, M.; Hu, Z.A. Based on Ease-off for sectional modification method of spiral bevel gear tooth surface. J. Cent. South Univ. 2018, 49, 824–830. [Google Scholar]
- Li, G.; Zhu, W.D. An active ease-off topography modification approach for hypoid pinions based on a modified error sensitivity analysis method. J. Mech. Des. 2019, 141, 093302. [Google Scholar] [CrossRef]
- Vivet, M.; Tamarozzi, T.; Desmet, W.; Mundo, D. On the modelling of gear alignment errors in the tooth contact analysis of spiral bevel gears. Mech. Mach. Theory 2021, 155, 104065. [Google Scholar] [CrossRef]
- Dooner, D.B. On the third law of gearing: A study on hypoid gear tooth contact. Mech. Mach. Theory 2019, 134, 224–248. [Google Scholar] [CrossRef]
- Ma, Z.Y. Contact Analysis of Spiral Bevel Gears Based on Ease-off Topological Surface; Henan University of Science and Technology: Luoyang, China, 2015. [Google Scholar]
- Fan, Q. Ease-Off and Application in Tooth Contact Analysis for Face-Milled and Face-Hobbed Spiral Bevel and Hypoid Gears. In Theory and Practice of Gearing and Transmissions; Springer: Cham, Germany, 2016; pp. 321–339. [Google Scholar]


| Parameters | Pinion | Gear |
|---|---|---|
| Tooth number | 8 | 41 |
| Mean helix angle/(deg) | 48.93 | 30.63 |
| Addendum height/(mm) | 5.77 | 1.05 |
| Dedendum height/(mm) | 1.16 | 5.73 |
| Pitch cone angle/(deg) | 12.53 | 76.82 |
| Face cone angle/(deg) | 17.45 | 77.73 |
| Root cone angle(deg) | 11.67 | 71.68 |
| Outer cone distance/(mm) | 97.19 | 84.72 |
| Face width/(mm) | 28 | 24 |
| Axial setting | 13.84 | −1.43 |
| Generation type | Generated | Formate |
| Offset distance/(mm) | 23 | |
| Shaft angle/(deg) | 90 | |
| Parameters | Pinion (Concave Surface) | Gear (Convex Surface) |
|---|---|---|
| Tilt angle/(deg) | 16.7 | 0 |
| Swivel angle/(deg) | 346.7 | 0 |
| Cutter radius/(deg) | 80.5 | 75.4 |
| Cutter angle/(deg) | 20 | 22.5 |
| Radial setting/(mm) | 73.95 | 74.04 |
| Basic cradle angle/(deg) | 83.6 | −66.3 |
| Vertical/(mm) | 19.6 | 0 |
| Axial/(mm) | 2.4 | 0.6 |
| Machine center to back/(mm) | 2.7 | 0 |
| Machine root angle/(deg) | −2 | 70.9 |
| Roll ratio | 5.064418 | —— |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jiang, J.; Chen, H.; Tian, J.; Su, Y.; Guo, J. Design and Analysis for Hypoid Gears with Ease-Off Flank Modification. Appl. Sci. 2022, 12, 822. https://doi.org/10.3390/app12020822
Wang Q, Jiang J, Chen H, Tian J, Su Y, Guo J. Design and Analysis for Hypoid Gears with Ease-Off Flank Modification. Applied Sciences. 2022; 12(2):822. https://doi.org/10.3390/app12020822
Chicago/Turabian StyleWang, Qin, Jinke Jiang, Hua Chen, Junwei Tian, Yu Su, and Junde Guo. 2022. "Design and Analysis for Hypoid Gears with Ease-Off Flank Modification" Applied Sciences 12, no. 2: 822. https://doi.org/10.3390/app12020822






