Multi-Objective Optimization of Hybrid Renewable Tri-Generation System Performance for Buildings
Abstract
:1. Introduction
1.1. Hybrid Trigeneration System
1.2. Simulation, Modeling, Optimization and Analysis Methodology
1.2.1. TRNSYS Simulation
1.2.2. Optimization Model
1.2.3. Objective Function
2. Constraints
3. Simulation Methodology
4. Input Parameters
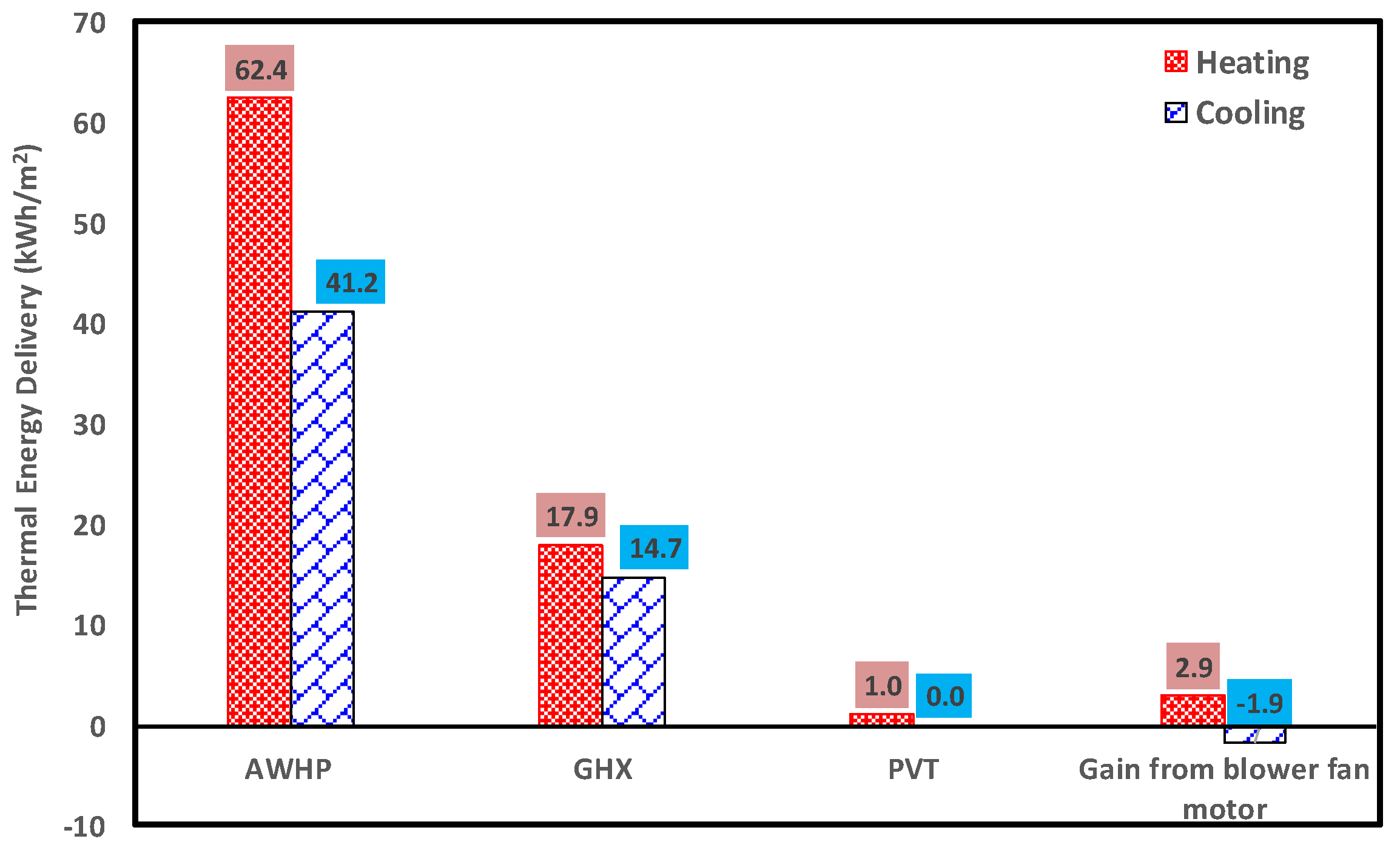
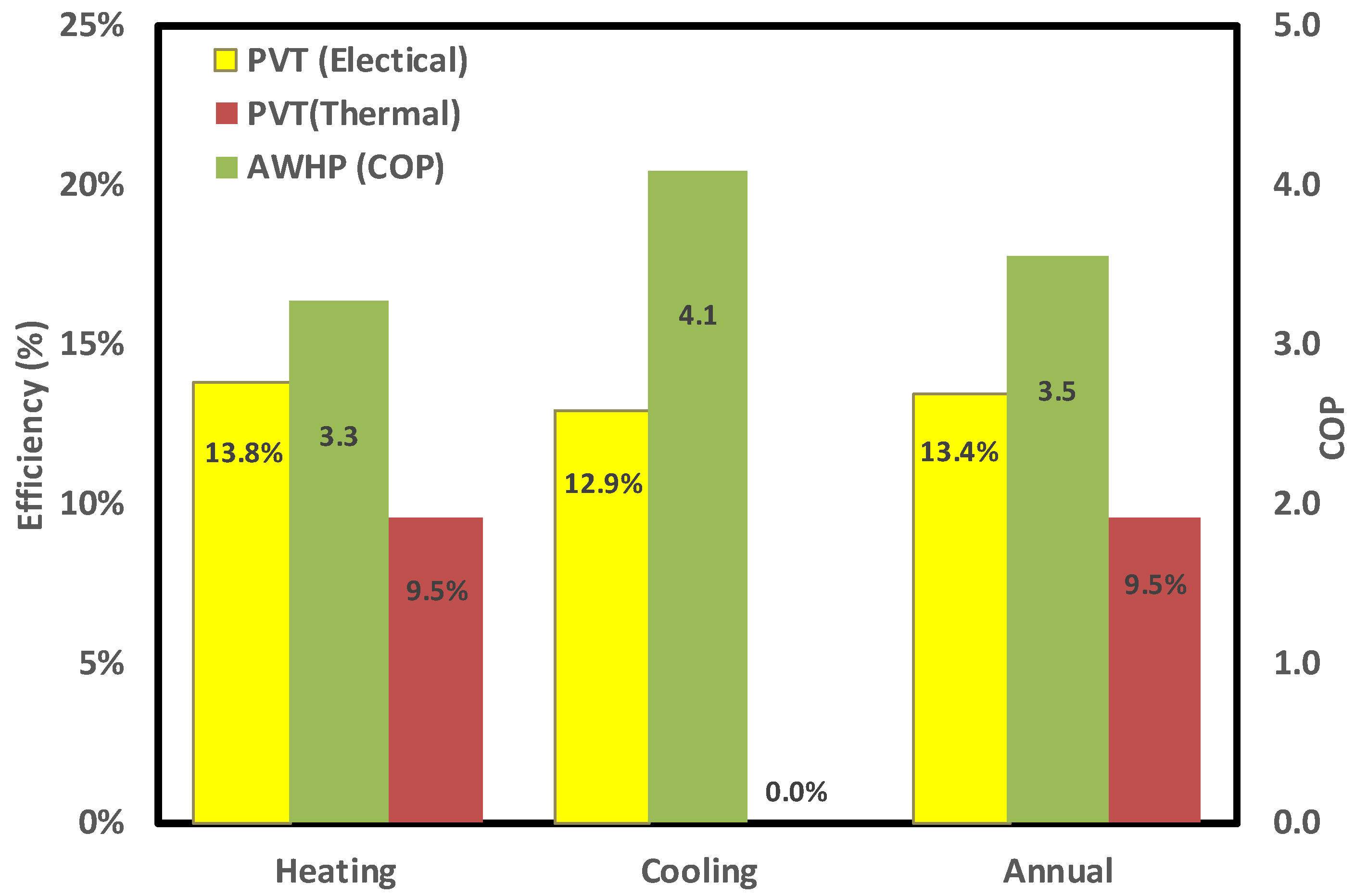
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Directive 2004/8/EC of the European Parliament and of the Council of the 11 February 2004 on the promotion of cogeneration based on the useful heat demand in the internal energy market and amending Directive 92/42/EEC. Off. J. Eur. Union 2004, 8, 50–60. Available online: https://eur-lex.europa.eu/eli/dir/2004/8/oj (accessed on 21 February 2004).
- Maghanki, M.M.; Ghobadian, B.; Najafi, G.; Galogah, R.J. Micro combined heat and power (MCHP) technologies and applications. Renew. Sustain. Energy Rev. 2013, 28, 510–524. [Google Scholar] [CrossRef]
- Evangelisti, S.; Lettieri, P.; Clift, R.; Borello, D. Distributed generation by energy from waste technology: A life cycle perspective. Process Saf. Environ. Prot. 2015, 93, 161–172. [Google Scholar] [CrossRef]
- Angrisani, G.; Roselli, C.; Sasso, M. Distributed micro-trigeneration systems. Prog. Energy Combust. Sci. 2012, 38, 502–521. [Google Scholar] [CrossRef]
- Sonar, D.; Soni, S.L.; Sharma, D. Micro-trigeneration for energy sustainability: Technologies, tools and trends. Appl. Therm. Eng. 2014, 71, 790–796. [Google Scholar] [CrossRef]
- Barbieri, E.; Spina, P.; Venturini, M. Analysis of innovative micro-CHP systems to meet household energy demands. Appl. Energy 2012, 97, 723–733. [Google Scholar] [CrossRef]
- Moghaddam, A.; Seifi, A.; Niknam, T.; Pahlavani, M. Multi-objective operation management of a renewable MG (micro-grid) with backup micro-turbine/fuel cell/battery hybrid power source. Energy 2011, 36, 6490–6507. [Google Scholar] [CrossRef]
- Shaneb, O.; Coates, G.; Taylor, P. Sizing of residential μCHP systems. Energy Build. 2011, 43, 1991–2001. [Google Scholar] [CrossRef]
- Kim, J.; Cho, W.; Lee, K. Optimum generation capacities of micro combined heat and power systems in apartment complexes with varying numbers of apartment units. Energy 2012, 35, 5121–5131. [Google Scholar] [CrossRef]
- Dorer, V.; Weber, A. Energy and CO2 emissions performance assessment of residential micro-generation systems with dynamic whole-building simulation programs. Energy Convers. Manag. 2009, 50, 648–657. [Google Scholar] [CrossRef]
- Gusdorf, J.; Douglas, M.; Swinton, M.; Szadkowski, F.; Manning, M. Testing a residential system including combined heat and power and ground heat source heat pumps at the Canadian Centre for Housing Technology. In Proceedings of the 1st International Conference on Microgeneration and Related Technologies, Ottawa, ON, Canada, 10–14 March 2008. [Google Scholar]
- Yang, L.; Douglas, M.A.; Gusdorf, J.; Szadkowski, F.; Limouse, E.; Manning, M.; Swinton, M. Residential total energy system testing at the Canadian Center for Housing Technology. In Proceedings of the ASME Power, San Antonio, CA, USA, 17–19 July 2007. [Google Scholar]
- Smith, M.; Few, P. Domestic-scale combined heat-and-power system incorporating a heat pump: Analysis of a prototype plant. Appl. Energy 2011, 70, 215–232. [Google Scholar] [CrossRef]
- Tempesti, D.; Manfrida, G.; Fiaschi, D. Thermodynamic analysis of two micro-CHP systems operating with geothermal and solar energy. Appl. Energy 2012, 97, 609–617. [Google Scholar] [CrossRef]
- Guo, T.; Wang, H.; Zhang, S. Selection of working fluids for a novel low-temperature geothermally-powered ORC based cogeneration system. Energy Convers. Manag. 2011, 52, 2384–2391. [Google Scholar] [CrossRef]
- Ribberink, H.; Lombardi, K.; Yang, L.; Entchev, E. Investigation of a hybrid renewable-microgeneration energy system for power and thermal generation with reduced emissions. Proc. Inst. Mech. Eng. Part A. J. Power Energy 2013, 227, 62–72. [Google Scholar] [CrossRef]
- Hawkes, A.; Leach, M. Cost-effective operating strategy for residential micro-combined heat and power. Energy 2007, 32, 711–723. [Google Scholar] [CrossRef]
- Entchev, E.; Gusdorf, J.; Swinton, M.; Bell, M.; Szadkowski, F.; Kalbfleisch, W.; Marchand, R. Micro-generation technology assessment for housing technology. Energy Build. 2004, 36, 925–931. [Google Scholar] [CrossRef]
- Hamada, Y.; Takeda, K.; Goto, R.; Kubota, H. Hybrid utilization of renewable energy and fuel cells for residential energy systems. Energy Build. 2011, 43, 3680–3684. [Google Scholar] [CrossRef]
- International Energy Agency, Energy Conversion in Buildings and Community System Program (ECBCS) Annex 42, The Simulation of Building-Integrated Fuel Cell and Other Cogeneration Systems (COGEN-SIM). Available online: www.ecbcs.org/annexes/annex42.htm (accessed on 15 May 2018).
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. Dynamic analysis of PEMFC-based CHP systems for domestic application. Appl. Energy 2012, 91, 13–28. [Google Scholar] [CrossRef]
- Calise, F.; Ferruzzi, G.; Vanoli, L. Transient simulation of polygeneration systems based on PEM fuel cells and solar heating and cooling technologies. Energy 2012, 41, 18–30. [Google Scholar] [CrossRef]
- Bang-Møller, C.; Rokni, M.; Elmegaard, B. Exergy analysis and optimization of a biomass gasification, solid oxide fuel cell and micro gas turbine hybrid system. Energy 2011, 36, 4740–4752. [Google Scholar] [CrossRef]
- Liso, V.; Olesen, A.; Nielsen, M.; Kær, S. Performance comparison between partial oxidation and methane steam reforming processes for solid oxide fuel cell (SOFC) micro combined heat and power (CHP) system. Energy 2011, 36, 4216–4226. [Google Scholar] [CrossRef]
- Thorsteinson, E. Performance testing of a 1 kWe PEM fuel cell cogeneration system. In Proceedings of the 2nd International Conference on Microgeneration and Related Technologies, Glasgow, UK, 1–3 April 2011. [Google Scholar]
- Obara, S.; Watanabe, S.; Rengarajan, B. Operation method study based on the energy balance of an independent microgrid using solar-powered water electrolyzer and an electric heat pump. Energy 2011, 36, 5200–5213. [Google Scholar] [CrossRef]
- Kumar, A.; Baredar, P.; Qureshi, U. Historical and recent development of photovoltaic thermal (PVT) technologies. Renew. Sustain. Energy Rev. 2015, 42, 1428–1436. [Google Scholar] [CrossRef]
- Chow, T.T. A review on photovoltaic/thermal hybrid solar technology. Appl. Energy 2010, 87, 365–379. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.; Nam, Y.; Lee, E.J.; Entchev, E. Heat Exchange Rate Analysis of a Low-depth Modular Ground Heat Exchanger through Real-scale Experiment. Energies 2021, 14, 1893. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, K.S.; Yang, L.; Entchev, E.; Lee, E.J.; Kang, E.C. Validation and Numerical Sensitivity Study of Air Baffle Photovoltaic-Thermal Module, International Journal Air conditioning and Refrigeration. Energies 2020, 13, 1990. [Google Scholar] [CrossRef] [Green Version]
- Bayer, P.; Saner, D.; Bolay, S.; Rybach, L.; Blum, P. Greenhouse gas emission savings of ground source heat pump systems in Europe: A review. Renew. Sustain. Energy Rev. 2012, 16, 1256–1267. [Google Scholar] [CrossRef]
- Self, S.J.; Reddy, B.V.; Rosen, M.A. Geothermal heat pump systems: Status review and comparison with other heating options. Appl. Energy 2013, 101, 341–348. [Google Scholar] [CrossRef]
- Omer, A.M. Ground-source heat pumps systems and applications. Renew Sustain Energy Rev. 2008, 12, 344–371. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- International Energy Agency, Energy Conversion in Buildings and Community System Program (ECBCS) Annex 54, Analysis of Micro-Generation & Related Energy Technologies in Buildings. Available online: www.ecbcs.org/annexes/annex54.htm (accessed on 3 June 2012).
- Chen, Y.; Zhang, T.; Yang, H.; Peng, J. Study on energy and economic benefits of converting a combined heating and power system to a tri-generation system for sewage treatment plants in subtropical area. Appl. Therm. Eng. 2016, 94, 24–39. [Google Scholar] [CrossRef]
- Feist, W.; Schnieders, J.; Dorer, V.; Haas, A. Re-inventing air heating: Convenient and comfortable within the frame of the passive house concept. Energy Build. 2005, 37, 1186–1203. [Google Scholar] [CrossRef]
- Chel, A.; Janssens, A.; Michel, D.P. Thermal performance of a nearly zero energy passive house integrated with the air-air heat exchanger and the earth–water heat exchanger. Energy Build. 2015, 96, 53–63. [Google Scholar] [CrossRef]
- Murphy, M. Leco. Simulating Earth to Air Heat Exchangers. Ventilation Preheating and Pre-Cooling; SINTEF: 2011; 70, Research Report. Available online: http://hdl.handle.net/11250/2420221 (accessed on 31 December 2011).
- Urchueguía, J.F.; Zacarés, M.; Corberán, J.M.; Montero, Á.; Martos, J.; Witte, H. Comparison between the energy performance of a ground-coupled water to water heat pump system and an air to water heat pump system for heating and cooling in typical conditions of the European Mediterranean coast. Energy Convers. Manag. 2008, 49, 2917–2923. [Google Scholar] [CrossRef]
- Calise, F.; Cappiello, F.L.; D’Accadia, D.M.; Vicidomini, M. Thermo-economic optimization of a novel hybrid renewable trigeneration plant. Renew. Energy 2021, 175, 532–549. [Google Scholar] [CrossRef]
- Jalalizadeh, M.; Fayaz, R.; Delfani, S.; Mosleh, H.J.; Karami, M. Dynamic simulation of a trigeneration system using an absorption cooling system and building integrated photovoltaic thermal solar collectors. J. Build. Eng. 2021, 43, 102482. [Google Scholar] [CrossRef]
- Cioccolanti, L.; Tascioni, R.; Bocci, E.; Villarini, M. Parametric analysis of a solar Organic Rankine Cycle trigeneration system for residential applications. Energy Convers. Manag. 2018, 163, 407–419. [Google Scholar] [CrossRef]
- Braun, R.; Haag, M.; Stave, J.; Abdelnour, N.; Eicker, U. System design and feasibility of trigeneration systems with hybrid photovoltaic-thermal (PVT) collectors for zero energy office buildings in different climates. Sol. Energy 2020, 196, 39–48. [Google Scholar] [CrossRef]
- Rad, M.; Leon-Garcia, A. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar]
- Rong, A.; Lahdelma, R. An efficient linear programming model and optimization algorithm for trigeneration. Appl. Energy 2005, 82, 40–63. [Google Scholar] [CrossRef]
- Ashouri, A.; Fux, S.; Benz, M.; Guzzella, L. Optimal design and operation of building services using mixed-integer linear programming techniques. Energy 2013, 59, 365–376. [Google Scholar] [CrossRef]
- Marachal, F.; Kalitventzeff, B. Process integration: Selection of the optimal utility system. Comput. Chem. Eng. 1998, 22, 149–156. [Google Scholar] [CrossRef]
- Bozchalui MHashmi SHassen HCanizares, C.; Bhattacharya, K. Optimal operation of residential energy hubs in smart grids. IEEE Trans. Smart Grid 2012, 3, 1755–1766. [Google Scholar]
- Chen ZWu, L.; Fu, Y. Real-time price-based demand response management for residential appliances via stochastic optimization and robust optimization. IEEE Trans. Smart Grid 2012, 3, 1822–1831. [Google Scholar] [CrossRef]
- Giorgio, A.; Pimpinella, L. An event-driven smart home controller enabling consumer economic saving and automated demand side management. Appl. Energy 2012, 96, 92–103. [Google Scholar] [CrossRef]
- Ha LJoumaa HPloix, S.; Jacomino, M. An optimal approach for electrical management problem in dwellings. Energy Build. 2012, 45, 1–14. [Google Scholar]
- Fazlollahi, S.; Maréchal, F. Multi-objective, multi-period optimization of biomass conversion technologies using evolutionary algorithms and mixed integer linear programming (MILP). Appl. Therm. Eng. 2013, 50, 1504–1513. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Wang, S.; Sun, Y.; Yan, C. Optimal scheduling of buildings with energy generation and thermal energy storage under dynamic electricity pricing using mixed-integer nonlinear programming. Appl. Energy 2015, 147, 49–58. [Google Scholar] [CrossRef]
- Babu, C.; Ashok, S. Peak load management in electrolytic process industries. IEEE Trans. Power Syst. 2008, 23, 399–405. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Shirazi, E.; Jadid, S. Optimal residential appliance scheduling under dynamic pricing scheme via hemdas. Energy Build. 2015, 93, 40–49. [Google Scholar] [CrossRef]
- TEES company (TRNSYS Website). Available online: http://www.trnsys.com/ (accessed on 20 November 2017).
- University of Wisconsin-Madison, TRNSYS 17—Mathematical Reference, Vol. 4. Available online: http://web.mit.edu/parmstr/Public/TRNSYS/04-MathematicalReference.pdf (accessed on 5 February 2012).
- Nam, Y.J.; Ooka, R.; Hwang, S.H. Development of a numerical model to predict heat exchange rates for a ground-source heat pump system. Energy Build. 2008, 40, 2133–2140. [Google Scholar] [CrossRef]
- General Algebraic Modeling System (GAMS website). Available online: https://www.gams.com/ (accessed on 7 June 2019).


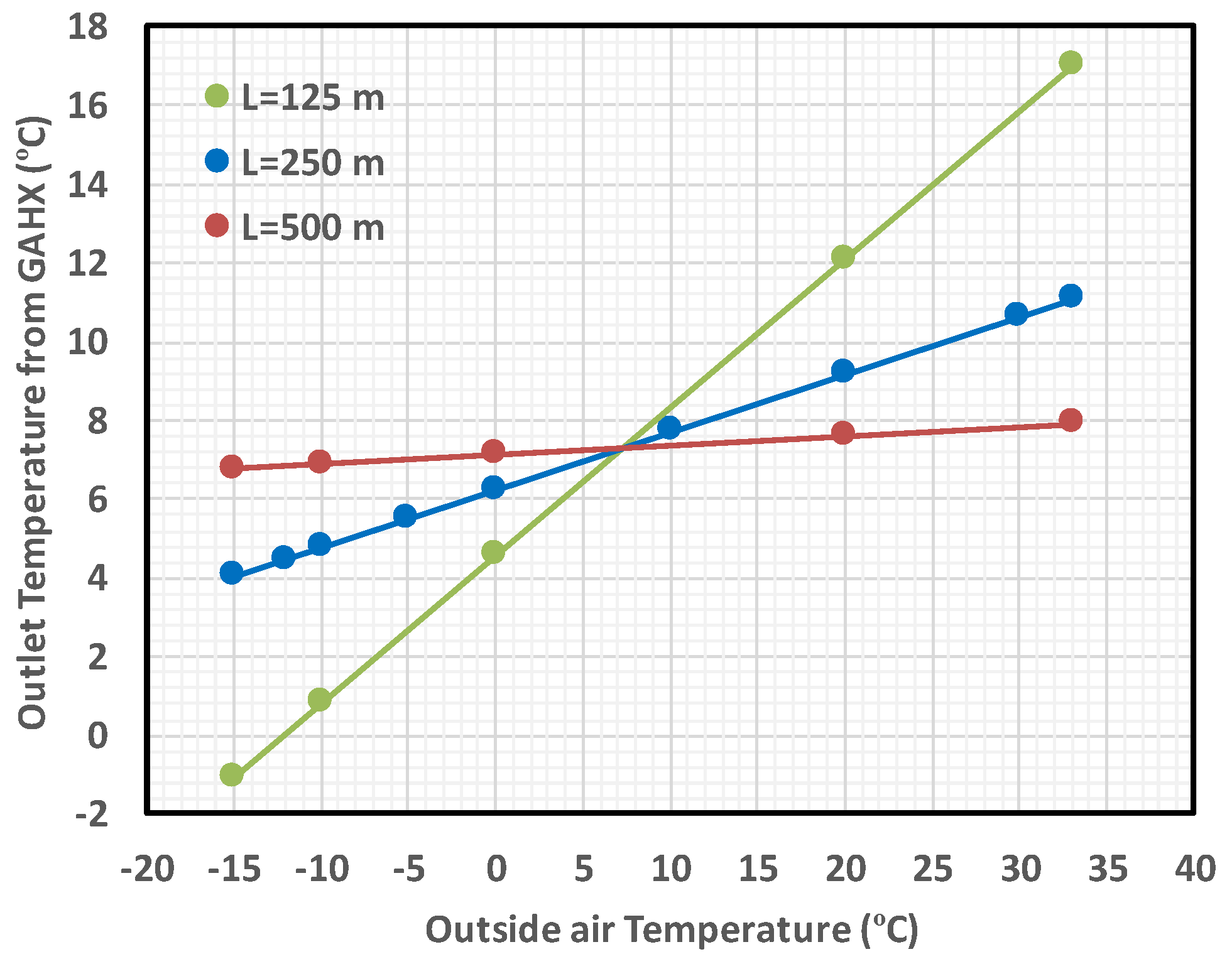
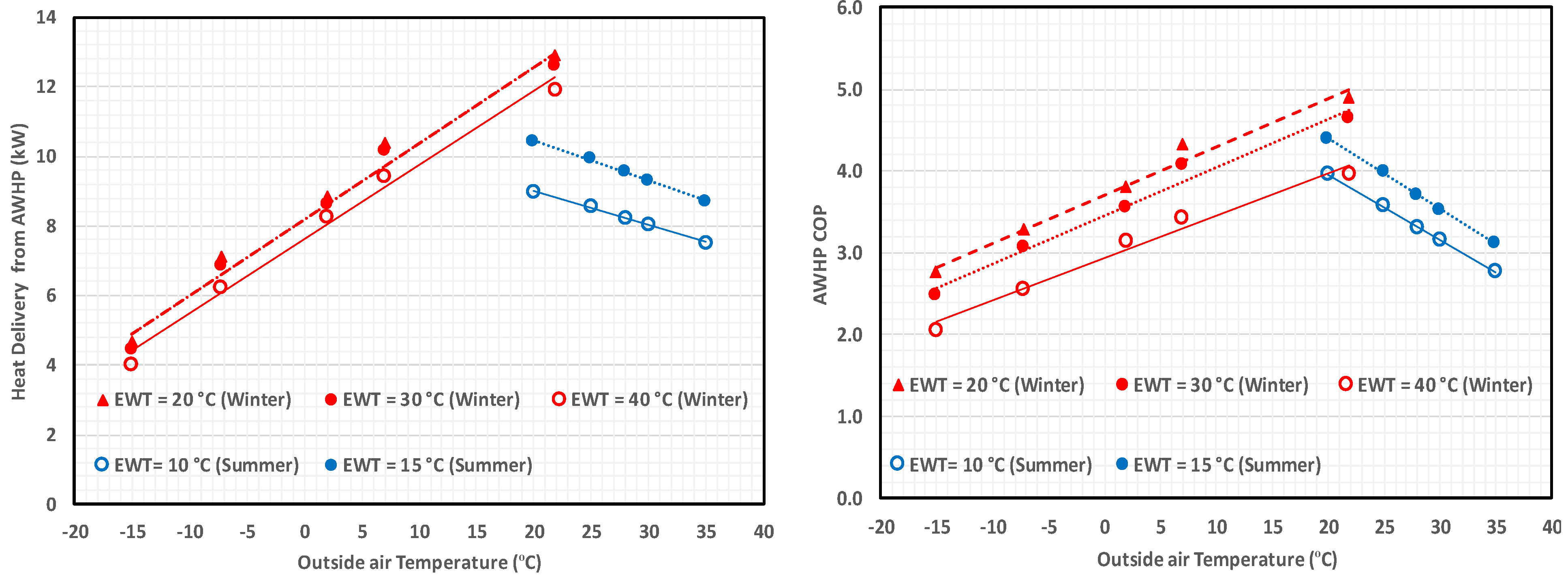
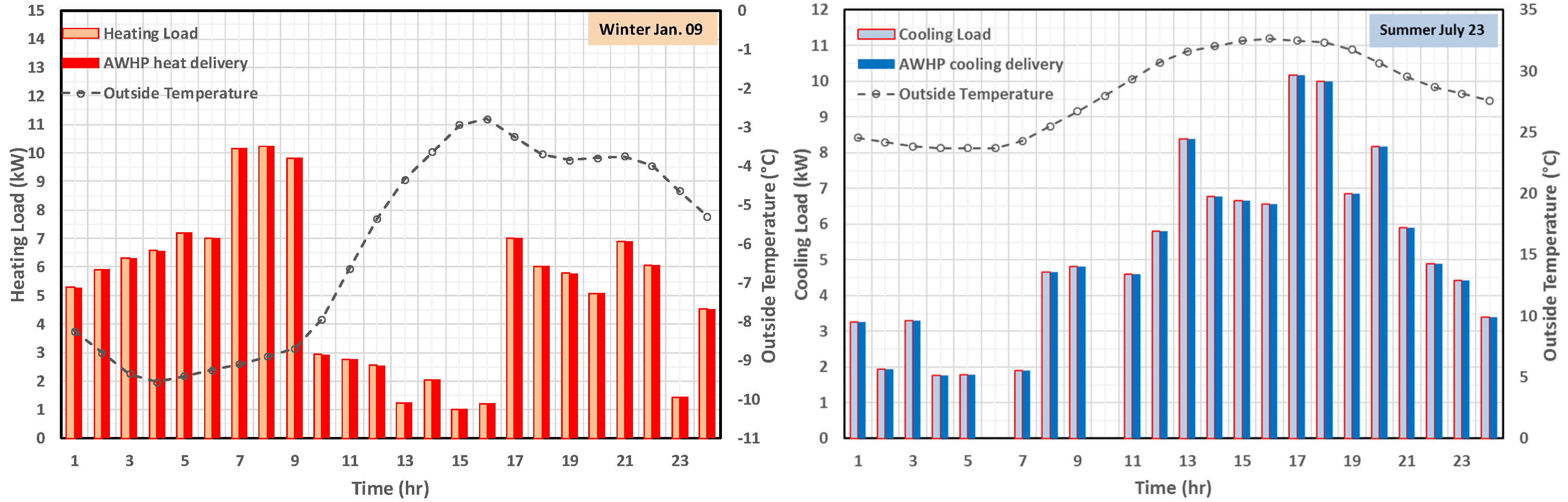
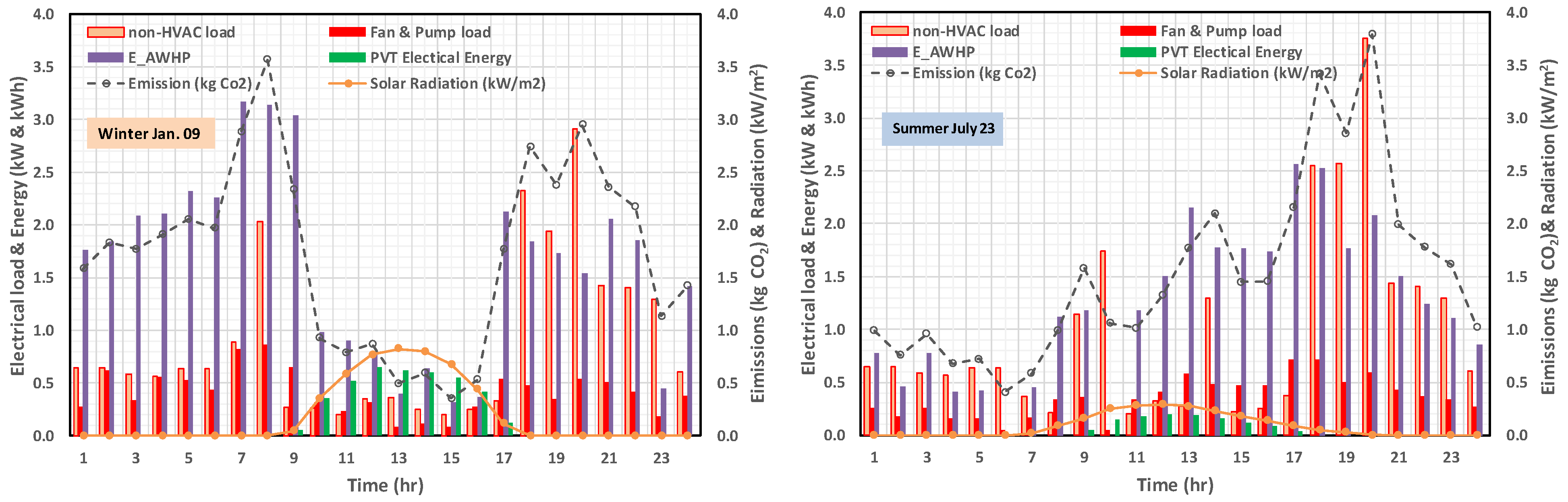

| Value | Unit | Comment | |
|---|---|---|---|
| Infiltration | 0.15 | ACH | |
| Window to area ratio | 35 | % | Vertical glazing of wall |
| Ventilation | 10 | L/s. person | |
| Internal equipment load | 8.07 | W/m2 | |
| Internal lighting load | 10.76 | W/m2 | |
| Roof U value | 0.27 | W/m2 k | |
| Exterior walls U value | 0.43 | W/m2 k | |
| Opaque doors U value | 3.97 | W/m2 k | |
| Slab on grade Floors | 0.934 | W/m k | |
| Windows U value | 3.12 | W/m2 k | Metal framing (SHGC 0.4) |
| Floor to ceiling height | 2.7 | M | |
| Attic height | 1.5 | M |
| System | Signal | Heating Mode | Cooling Mode |
|---|---|---|---|
| AWHP | ON | TTankB ≤ 40 °C | Troom ≤ Tset − 0.5 °C |
| OFF | TTankB ≥ 45 °C | Troom ≥ Tset + 0.5 °C | |
| PVT (preheating) | ON | TPVT – TGAHX ≥ 5 °C | N/A |
| OFF | TPVT – TGAHX ≤ 2 °C | N/A |
| Parameter | Cost/Value | Lifetime (yr.)/Unit |
|---|---|---|
| Ground Air Heat Exchanger | CAD 35/m | 25 |
| AWHP | CAD 1050 /kW | 20 |
| PVT | CAD 11/We | 25 |
| Storage tank | CAD 1300 | 15 |
| Pump | CAD 525 | 10 |
| Blower | CAD 600 | 10 |
| Fan Coil | CAD 608 | 10 |
| GAHX Subsidy | CAD 0 | - |
| AWHP Subsidy | CAD 0 | - |
| PVT Subsidy | CAD 0 | - |
| Emission cost | CAD 25/ton CO2 | - |
| Electrical price (Buy) | CAD 0.14/kWh | - |
| Electrical price (Sell) | CAD 0.14/kWh | - |
| Interest rate | 3.5% | - |
| Operation and maintenance | 0.5–1% from capital cost | |
| Emission Factor | 590 | CO2 g/kWhel |
| Variable | Boundary Range | Unit |
|---|---|---|
| Ground Heat Exchanger length | [125–500] | m |
| AWHP heating size | [6.6–17.2] | kW |
| AWHP cooling size | [5.6–10.5] | kW |
| PVT area | [10–200] | m2 |
| System | Cost (CAD/Yr.) |
|---|---|
| GAHX Capital | 265.5 |
| AWHP Capital | 809.1 |
| PVT Capital | 514 |
| Fan, Pump, Fan coil, etc. | 321.3 |
| Operation &Maintenance | 14.6 |
| Purchase Electricity | 2105.5 |
| Selling Electricity | 94.5 |
| Emission | 222.2 |
| Subsidy | 0 |
| Objective | 4157.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorab, M.; Yang, L.; Entchev, E.; Lee, E.-J.; Kang, E.-C.; Kim, Y.-J.; Bae, S.; Nam, Y.; Kim, K. Multi-Objective Optimization of Hybrid Renewable Tri-Generation System Performance for Buildings. Appl. Sci. 2022, 12, 888. https://doi.org/10.3390/app12020888
Ghorab M, Yang L, Entchev E, Lee E-J, Kang E-C, Kim Y-J, Bae S, Nam Y, Kim K. Multi-Objective Optimization of Hybrid Renewable Tri-Generation System Performance for Buildings. Applied Sciences. 2022; 12(2):888. https://doi.org/10.3390/app12020888
Chicago/Turabian StyleGhorab, Mohamed, Libing Yang, Evgueniy Entchev, Euy-Joon Lee, Eun-Chul Kang, Yu-Jin Kim, Sangmu Bae, Yujin Nam, and Kwonye Kim. 2022. "Multi-Objective Optimization of Hybrid Renewable Tri-Generation System Performance for Buildings" Applied Sciences 12, no. 2: 888. https://doi.org/10.3390/app12020888
APA StyleGhorab, M., Yang, L., Entchev, E., Lee, E.-J., Kang, E.-C., Kim, Y.-J., Bae, S., Nam, Y., & Kim, K. (2022). Multi-Objective Optimization of Hybrid Renewable Tri-Generation System Performance for Buildings. Applied Sciences, 12(2), 888. https://doi.org/10.3390/app12020888







